Introduction

Climate variability and its impact on farmer attitudes to risk are key drivers of both profitability and yield gaps in Australia’s broadacre dryland cereal cropping systems (Hochman & Horan, 2018; Monjardino et al., 2013, 2015; Zhang et al., 2019). This is due primarily to the importance of soil moisture to agronomic performance (Kirkegaard et al., 2014) and its impact on farmer investment in nitrogen (N; note that, in contrast to places like the European Union, farm businesses in Australia do not receive any government subsidies). In effect, the N management problem faced by Australian farmers boils down to one of: ‘given prevailing and expected seasonal conditions, will I have enough soil water available to produce a crop of desired commercial yield, and to therefore justify investment in sufficient N to produce it ?’ Because soils and their ability to supply a crop with water may be highly spatially variable (Rab et al., 2009), fertilizer management based on soil-specific management zones and underpinned by Precision Agriculture (PA) technologies, is one response to the uncertainty associated with these questions (Monjardino et al., 2013). However, the rate of adoption of sensing technologies aimed at supporting targeted, variable-rate, N management is low (Bramley & Ouzman, 2019). A possible reason for this is that the development of such sensors as aids to N management (e.g. Raun et al., 2005) has generally failed to recognise the complex multivariate nature of the drivers of crop response to N and its profitability (Colaço & Bramley, 2018). For example, Colaço and Bramley (2019) have highlighted the need to incorporate consideration of site and seasonal variation, and their consequences for soil moisture status, into the calibration and use of sensors to assist with N management. Indeed, where the optimisation of N management is a key goal, the need to factor soil moisture status into the decision-making process is critical (Lawes et al., 2019).

The importance of soil moisture as a primary determinant of yield potential is a major reason why cereal growers in Australia’s dryland wheatbelt have been encouraged to purchase soil moisture sensors, such as are commonly used to underpin irrigation management in winegrape (Nordestgaard, 2019) and other horticultural systems (Montagu & Stirzaker, 2008). However, no matter how well these are calibrated, the utility of such sensors is arguably constrained by the fact that they sense moisture status in a small volume of soil. As a result, their interpretation in the context of soil spatial variability at the field and farm scale is potentially problematic and somewhat reliant on the development of ‘rules of thumb’, especially given the low intensity of field-based characterisation of plant available water capacity (PAWC; Dalgleish et al., 2012; see also https://www.apsim.info/apsim-model/apsoil/). Accordingly, fewer than a quarter of Australian broadacre dryland cereal growers have adopted such sensors, with their use strongly skewed towards the eastern states of Australia and otherwise more focussed in higher rainfall areas (Bramley & Ouzman, 2019). Furthermore, of the approximately 500 dryland farmer clients of one provider of soil sensing services, around 70% have just a single sensor on their farm (L. Wilksch, Agbyte—pers. comm.) which is likely to be around 2,500 ha in area (Bramley & Ouzman, 2019). Methods of extrapolating soil moisture probe data away from the location of the probe are therefore of considerable interest, as is the question of how useful being able to do this is in the context of supporting PA, including targeted on-farm decision-making such as variable rate N application. Our objective in the present work was to develop a method for extrapolating soil moisture probe data to other parts of a field and so enable it to be interpreted throughout the field. The method relies on a combination of freely available satellite and weather data, along with a simple understanding of crop phenology and which, as such, should be readily implementable. We also consider the utility of the information generated by this method in light of the results obtained when it is implemented at two contrasting sites in the Australian grainbelt.

Methods and materials

Sites

Development and initial testing of the methodology (see below) was done using data collected in 2019 and 2020 from a 64 ha field located near Tarlee in the mid-north of South Australia, where annual rainfall is in the 425–525 mm range. As reported by Colaço et al. (2023), the growing season rainfall at this site was 218 mm in 2019 and 352 mm in 2020, whilst the mean yields achieved were 3.5 t/ha wheat in 2019 and 7.5 t/ha barley in 2020.

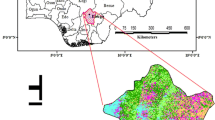
Several years of yield maps and an electromagnetic soil survey (Fig. 1a) promoted the delineation of three zones (Taylor et al., 2007) within the field (Fig. 1b). The soils in zone 1 are deep (> 1 m) black cracking vertosols (ASRIS, 2011). Those in zone 2 are a mix of a shallower variant of these black soils and the red vertosols that are common in the district, often with calcrete layers in the subsoil, the occurrence of which ranges in depth from around 40–80 cm. The soils in zone 3 are much shallower (generally < 80 cm) red calcarosols with more loamy textures, again with calcrete in the subsoil, often occurring as shallow as 35 cm. Notwithstanding the different soils in each zone, the average soil clay content in the top 30 cm derived from 21 soil sample locations (Fig. 1a; Colaço et al., 2023) was 38.8%. A soil moisture capacitance probe (EnviroPro EP100G-L-12, Entelechy Pty Ltd, Golden Grove, SA 5125, Australia) was installed in each zone. The locations of these were conditioned by the need for them to be located within ~ 15 m of the fence line to enable access to power and avoid interference with farm machinery, but they were otherwise located to reflect the different zones (Fig. 1b). Note that these probes measure soil moisture within a field of influence of 55 mm from the wall of the probe. As such, they are specified to assess soil moisture status in a total soil volume of 19.2 L. A soil moisture characterisation (Burk & Dalgliesh, 2013) was undertaken at a location close to (within ~ 15 m) each probe for estimation of plant available water capacity (PAWC), and samples were also collected close to the position of the probe in ad hoc time series for probe calibration. As part of other work on N decision making (Colaço et al., 2023), samples were also collected from the 21 locations distributed across the field (Fig. 1a) close to growth stage GS31 (Zadoks, 1974). In all cases, gravimetric soil moisture content was determined using oven drying at 105 °C for not less than 48 h. Other aspects of soil characterisation (estimation of bulk density and PAWC, etc.) were as described by Burk and Dalgleish (2013).

Fig. 1
figure 1

The 64 ha field near Tarlee in the mid-North region of South Australia used for the study. a Electromagnetic (EM38) soil survey (0–75 cm depth) of apparent electrical soil conductivity (ECa), and the locations of soil samples collected for mid-season soil moisture determination in 2019 (circle) and 2020 (square). b Management zones identified from analysis of ECa along with several years of prior yield maps, and the locations of soil moisture probes installed in these zones. c–f Cumulative NDVI (ΣNDVI) at either approximately GS31 or in late September in each of 2019 and 2020

Full size image

Further testing of the methodology described below made use of a contrasting 358 ha field located near Kalannie in Western Australia. Here, the soils are predominantly Kandosols (ASRIS, 2011), non-calcareous, and with no marked texture contrast down the profile, with a mean clay content in the top 30 cm of 11.7%, with some Chromosols (ASRIS, 2011) also present. The latter have a marked texture contrast with 10.0% clay in the top 10 cm and 37.3% at 30 cm; overall, the mean clay content in the top 30 cm in this field was 17.2% (Colaço et al., 2023). Growing season rainfall at this site was 194 mm in 2019 and 162 mm in 2020, with mean yields of wheat achieved of 2.2 and 2.5 t/ha in 2019 and 2020 respectively (Colaço et al., 2023).

Data and rationale

The method developed here relies on the ability to predict biomass from a time series of NDVI (Perry et al., 2022a, 2022b) coupled with the basic dependence of cereal crop phenology on temperature and water availability (Flohr et al., 2017). In particular, it is enabled by the observation that, during a cropping season, cumulative NDVI (ΣNDVI) obtained from the time series closely matches crop biomass accumulation (Perry et al., 2022a, 2022b). Since soil moisture status is a strong driver of crop biomass, the objective here was to see whether ΣNDVI could be used as a spatio-temporal covariate to enable extrapolation of soil moisture probe data away from the probe to other locations within a field during the growing season.

In brief, for both sites, publicly available Level-2A orthorectified and atmospherically corrected surface reflectance imagery obtained from the Sentinel-2A and B multispectral instrument was downloaded using the Google Earth Engine (Gorelick et al., 2017) for dates covering the growing season in 2019 and 2020. Note that such imagery can be obtained at no cost, making it an attractive basis for the approach used here. Following removal of images that were affected by cloud cover and/or cloud shadows, the retained images were fitted, on a per pixel basis (each pixel is 10 m × 10 m), with a smooth function to describe the NDVI time series during the growing season (Perry et al., 2022a, 2022b). Since NDVI is reflective of the amount of photosynthetically active biomass, it has values of approximately zero at sowing, rises slowly following crop emergence and then more steeply during the main period of vegetative growth, before reaching a plateau mid-season and then declining as the crop matures (Fig. 2a). As described by Perry et al., (2022a, 2022b), from the function fitted to the useable NDVI time series, daily values of NDVI were estimated for each pixel and from these, ΣNDVI calculated, again on a daily time step. As seen in Fig. 2b, and consistent with the foregoing, ΣNDVI increases slowly before rising more steeply and reaching a maximum immediately prior to senescence. The output from this process is the ability to generate maps of ΣNDVI for any day in the growing season, as shown in Fig. 1c–f; here, we have focussed on a date corresponding to GS31 (Zadoks, 1974) when a grower might be considering a mid-season N application, and a date in late September when a grower might be considering whether there is sufficient soil moisture to finish a crop, or whether it might be better to cut the crop for hay.

Fig. 2
figure 2

Change in a NDVI and b cumulative NDVI (ΣNDVI) with days after sowing for the location corresponding to the soil moisture probe located in zone 1 (Fig. 1) in 2020

Full size image

Daily temperature, rainfall and evaporation data were downloaded from the Bureau of Meteorology (BOM; http://www.bom.gov.au/climate/data/). For the South Australian site, which is approximately halfway between Clare (BOM station 23021) and Roseworthy (21131), data for the weather stations at these locations were accessed and mean values calculated. These Clare-Roseworthy means were assumed to provide a representative reflection of seasonal conditions at this SA site. For the site in Western Australian, BOM station 10070 (Kalannie) was used. Again, these data are available at no cost.

Crop phenology is highly temperature-driven and accordingly, the aforementioned daily temperature data were used to calculate the season growing degree days (GDD; base of 0 °C) with time-zero defined by the date of sowing. Since GDD provides a cumulative measure of temperature, and given the use of ΣNDVI in this work as a biomass predictor, rather than relying solely on daily rainfall to reflect the water impact on crop growth, we instead focussed on net precipitation (NP; i.e. daily rainfall—daily evaporation) and, to be consistent with the cumulative nature of GDD, calculated cumulative net precipitation (ΣNP).

Soil moisture data were downloaded from the probes on a daily time step with all dates converted to a ‘days after sowing’ (DAS) basis. Three probes were used at the South Australian site (Fig. 1) with the Western Australian site equipped with a single probe.

Statistical analysis and mapping

From the above, and on a daily time step, we had a dataset comprising the following: For each study field as a whole, daily temperature, rainfall, GDD, NP, ΣNP, and on a per pixel basis within these fields, ΣNDVI; at each soil probe location, in addition to the aforementioned data, we also had the soil moisture probe data to a depth of 1 m in increments of 10 cm. Note that for the purposes of our analysis, the daily weather indices were assumed to be spatially invariant throughout the field. We also acknowledge the difference in area between a single pixel in the NDVI Imagery and the much smaller area around which the probe was sensing soil moisture status (within 55m of the probe wall). Whilst this is certainly a source of error in our approach, we do not believe it has a material impact on the utility or otherwise of these data of differing areal support, as may be inferred from the results presented below.

Relationships between the soil moisture and other data were explored using normal and stepwise multiple linear regression in JMP (v. 16.0, SAS Institute Inc, Cary, NC, USA), which was also used for other statistical analysis. For the prediction of soil moisture probe data, our working model was:

$$\Theta_{{{\text{v}},p,d,t}} = a_{d} + b_{d} .\Sigma {\text{NDVI}}_{p,t} + c_{d} .\Sigma {\text{NP}}_{t} + e_{d} .{\text{GDD}}_{t}$$
(1)

where Θv,p,d,t is the volumetric soil moisture content (%) recorded by probe p (p = 1…3), at depth d (d = 0…100 cm in increments of 10 cm), on t days after sowing; ΣNDVIp,t is the value of ΣNDVI in the pixel that is co-incident with the location of probe p, on day t after sowing; ΣNPt and GDDt are the values of ΣNP and GDD on day t; and a, b, c and e are parameters which are specific for each depth increment (d).

Subsequently, following crop emergence (i.e. once there is a measurable NDVI), for each soil depth increment of interest (d), on any day (t), and at any location (xy) in the field, we sought to predict Θv as:

$$\Theta_{{{\text{v}},{\text{xy}},d,t}} = a_{d} + b_{d} .\Sigma {\text{NDVI}}_{xy,t} + c_{d} .\Sigma {\text{NP}}_{t} + e_{d} .{\text{GDD}}_{t}$$
(2)

where, for any depth (d), the parameters a, b, c and e take the values obtained from Eq. (1). At the WA site, where we only had access to one soil moisture probe, Eq. (2) was applied across the entire field. However, at the SA site, where three probes were available (Fig. 1), Eq. 1 was generated separately for each probe and consequently, it was also possible to apply three discrete versions of Eq. (2), one specific to each probe. This also meant that at the SA site, we could also constrain the locations (xy) for which Eq. 2 was applied to a zone-specific basis and explore the merits of averaging the predictions of Θv,xy,d,t generated by the 3 probes for the entire field.

The results of exploration of Eqs. (1) and (2) were used, along with raw soil moisture data (see below), as inputs to map display and analysis which was done using the ArcGIS software suite (v. 10.8.2; ESRI, Redlands, CA, USA).

For the SA site, evaluation of the utility of soil moisture predictions derived from Eq. (2) was done using samples collected from the 21 locations shown in Fig. 1a on 7 August 2019 and 28 July 2020 as part of other work reported by Colaço et al. (2023); these were the only dates during the growing season for which we had actual soil moisture measurements. Values of ΣNDVIxy,t, ΣNPt and GDDt pertinent to these dates were used to generate estimates of soil moisture content (Eq. 2) and these were regressed against measured soil moisture using simple linear regression. A similar approach was used for the WA site where soil moisture was measured in samples collected on 20 August 2019 and 14 August 2020.

Results

For the SA site (Fig. 1), ΣNDVI, ΣNP and GDD were all significant predictors (P < 0.0001) of soil moisture probe data logged by the probe in zone 1 at a depth of 20 cm across the two seasons (2019–2020) when either normal or stepwise multiple linear regression was used (R2adj = 0.87; Fig. 3); that is, Eq. (1) was found to be useful. When Eq. (1) was run on a per season basis, the result improved markedly in 2019 (R2adj = 0.99), compared to 2020 (R2adj = 0.82), most likely due to the effect of aberrant mid-season rainfall events in 2020 (Fig. 3). When the analysis was repeated for all depth increments, R2 for the predictions ranged from 0.78–0.99 in 2019, 0.62–0.83 in 2020 and 0.59–0.85 for both years combined (P < 0.0001 in all cases). In other words, the time series of ΣNDVI along with ΣNP and GDD could faithfully reproduce the time series of soil moisture status logged by the probe. Similar results were obtained for the probes located in zones 2 and 3 (Fig. 1b) and for the WA site (Fig. 4). Accordingly, the parameters ad, bd, cd and ed derived for each probe location could be used, along with the ΣNDVI imagery, to implement Eq. (2) and so extrapolate predicted soil moisture status across the entire field in depth increments of 10 cm—that is, for every pixel (xy) in the ΣNDVI imagery, on any date (t), using data from any of the probes (p) as input (Figs. 5, 6).

Fig. 3
figure 3

Prediction of soil moisture probe data at 20 cm depth in Zone 1 of the SA site (Fig. 1) in 2019 (red) and 2020 (blue) using a normal and b stepwise multiple linear regression over both seasons and c, d on a per season basis using just cumulative NDVI (ΣNDVI), cumulative net precipitation (ΣNP) and season growing degree days (GDD)

Full size image
Fig. 4
figure 4

Variation in soil moisture at either 30 or 100 cm depth at the WA site, either logged by the soil moisture probe (black lines) or predicted (red lines) using cumulative NDVI (ΣNDVI), cumulative net precipitation (ΣNP) and season growing degree days (GDD). Note that a logger error meant that some data were missing in the period from approximately 45–70 days after sowing

Full size image
Fig. 5
figure 5

Prediction of within-field soil moisture variation at GS31 in 2019 (22 July; 68 days after sowing) in a 64 ha field in the mid-North of South Australia using cumulative NDVI (ΣNDVI), cumulative net precipitation (ΣNP) and season growing degree days (GDD) and data logged by soil moisture probes (green triangles) located in each of three zones (Fig. 1). Predictions are shown in 10 cm increments down the profile (0–100 cm)

Full size image
Fig. 6
figure 6

Prediction of within-field soil moisture variation on 14 September 2019 (130 days after sowing) in a 358 ha field near Kalannie in Western Australia using cumulative NDVI (ΣNDVI), cumulative net precipitation (ΣNP) and season growing degree days (GDD) and data logged by a soil moisture probe located close to the edge of the field. Predictions are shown in 10 cm increments down the profile (0–100 cm)

Full size image

Figures 5, 6 suggest that when within-field variation in soil moisture is predicted using a single probe, variation in the estimated soil moisture content down the profile is greater than the within-field spatial variation in soil moisture content at any individual depth. At the SA site, this is despite the fact that soil characterisation highlighted the differences between the soils at the three probe locations. Thus, PAWC to a depth of 50 cm (below which no roots were observed during the study) was estimated at 60.2 and 77.4 mm in zones 1 and 2. In zone 3, it was only possible to determine PAWC (30.5 mm) to a depth of 40 cm due to interference from calcrete and calcareous stones; PAWC to the same 40 cm depth in zones 1 and 2 was measured at 58.5 and 72.2 mm. Given the existence of the three zones at the SA site (Fig. 1) and these measured differences in PAWC, it is of no surprise that the predictions of soil moisture status over the entire field based on individual zone-based probes also differed (Fig. 5) a result which, even assuming that all probes were equally well installed and calibrated to the soil conditions at each probe location, may present a dilemma for farmers purchasing such sensors. Note also that, as part of the soil characterisations, we found that the calibration of probe data against measured soil moisture was strongest at shallower depths (not shown).

Given the difficulties presented by the shallow and stony nature of soil in zone 3, along with the observation that probe calibration against measured soil water over the season (not shown) was better at shallower depths, calibration of predicted (extrapolated) soil moisture determined using Eq. (2) against measurements made at 21 locations (Fig. 1a) was confined to samples taken from the top 30 cm only. Figure 7 shows the derivation of ‘average’ and ‘zone-based’ maps for the SA site at GS31 in 2019. To calculate these, each probe-specific implementation of Eq. (2) for the whole field (Fig. 5) was adjusted using calibrations generated for each probe based on the volumetric water content of samples collected at each probe site during the season in 10 cm depth increments, and an average map was calculated across the three probes. The zone-based maps were derived from the same calibration-adjusted maps but using the selection of just those portions of each probe-specific map delimited by the zones (i.e. values of xy; Eq. 2) identified in Fig. 1b. One consequence of the zone-based approach is an apparent over-emphasis of between-zone soil differences by ‘hard boundaries’ between zones (Fig. 7). These are much less evident in the maps of ΣNDVI (Fig. 1c-f) which, nevertheless, do reflect any effects of between-zone differences on the crop. Nonetheless, the ‘average’ and ‘zone-based’ maps (Fig. 7) were used as the basis for evaluation of Eq. (2) by comparison with actual measurements of soil moisture made at 21 locations throughout the field (Fig. 1a) on 7 August 2019 and 28 July 2020. Note that, whereas hitherto, all soil moisture data used here (probe data and for probe calibration) were expressed on a volumetric basis, at the 21 sampling points (Fig. 1a), at which bulk density was not determined, soil moisture was determined on a gravimetric basis only. However, at each soil moisture probe location, a strong linear relationship was evident between volumetric and gravimetric soil moisture.

Fig. 7
figure 7

Average and zone-based soil moisture maps at GS 31 (22 July; 68 days after sowing) in 2019 at the SA site derived from probe-specific maps (Fig. 5) following adjustment based on the calibration for individual probes against actual soil moisture for each depth at each probe location (green triangles)

Full size image

In spite of between-zone soil differences being reflected in both NDVI and ΣNDVI (Fig. 1c-f), at our SA site, values of R2adj for regressions of observed against predicted soil moisture suggest that zone-based prediction (c.f. Figure 7) of mid-season soil moisture was markedly better than predictions based on single probes (Fig. 8). They were also better than the average prediction from three zone-based probes (not shown). Furthermore, if a single probe-based implementation of Eq. (2) was used for the prediction over the whole field (i.e. all xy), it made no difference which one of the three available probes was used. This last result makes sense given that on any date, the same ΣNDVI image and values of ΣNP and GDD are used as input, such that a simple linear transformation reflects the effect of between-probe differences in the actual prediction. Similarly, given the close linear relationship between gravimetric and volumetric soil moisture at any depth, there was no difference in the accuracy of prediction between gravimetric or volumetric soil moisture.

Fig. 8
figure 8

Calibration of measures of gravimetric soil moisture against predictions of volumetric soil moisture at a–c the SA and d WA sites derived from soil moisture sensor data at either a–c 20 cm or d 30 cm depth, cumulative NDVI (ΣNDVI), cumulative net precipitation (ΣNP) and season growing degree days (GDD). a August 7, 2019, top 10 cm predicted from the sensor in zone 1; b July 28, 2020, top 30 cm predicted from the sensor in zone 2; c both dates (2019, red; 2020 blue), top 10 cm using zone-based predictions derived from the sensors in each of zones 1–3 (Figs. 1b and 7); d 20 August, 2019, top 30 cm. In a, b and d, the predictions derived from sensor calibrations developed for the year of measurement only (c.f. Figure 3c–d). In c the prediction derived from calibrations developed over both years of the study combined

Full size image

There was no substantive difference in the accuracy of prediction of actual gravimetric soil moisture using relationships derived from either one (Fig. 3c) or two years of probe data (Fig. 3a, b). At the SA site, R2adj for zone-based prediction of soil moisture at the 21 locations in 2019 (Fig. 1a) was marginally better when the two-year prediction was used rather than that specific to 2019 (0.75 compared to 0.73 for the 0–10 cm depth; P < 0.0001 in both cases); in 2020, the season specific prediction was marginally better (R2adj of 0.54 and 0.56; P < 0.0001). Over the two years together (7 August 2019 and 28 July 2020; Fig. 8c) the two-year prediction was slightly better (R2adj of 0.69, P < 0.0001) than when season-specific predictions were used (R2adj of 0.67, P < 0.0001). However, as indicated by Fig. 8a,b, when only a single probe was available, the accuracy of soil moisture prediction was generally not sufficient (R2adj of approx. 0.4) to regard the extrapolation method (i.e. Eq. 2) as a satisfactory alternative to direct measurement if accurate estimates of soil moisture status are required. In other words, in variable fields, multiple, zone-based probes are required. Notwithstanding the lower range of soil moisture variation in the typically drier, sandy, topsoils at the WA site (Fig. 6), and that only one probe was available, the results obtained there were similar. However, presumably due to the lower water holding capacity at the WA site and the effect of evaporative demand on sandy topsoil moisture contents, a better prediction was obtained using probe data from 30 cm depth at this site (Fig. 8d) than at shallower depths (not shown), as used for the SA site (Fig. 8a–c).

Discussion

Our objective here was to see whether we could extrapolate soil moisture probe data away from the location of a probe, and so make it useful for dryland cereal growers as input to targeted (i.e. site-specific) management at the within-field scale. It is clear from Figs. 5 and 6 that, in general (i.e. for any probe or any date), variation in the estimated soil moisture content down the profile is considerably greater than the within-field spatial variation in soil moisture content at any individual depth—when within-field variation in soil moisture is predicted using a single probe. At a site such as our Western Australian site (Fig. 6), which does not exhibit marked soil variation either spatially or down the profile, it might therefore be concluded that being able to extrapolate soil moisture away from the location of a probe to other parts of a paddock may not inspire a targeted decision—at either GS31 or late in September—because for any depth, the magnitude of spatial variation in soil moisture is only a few %. The same conclusion might be drawn at the South Australian site (Fig. 5) if only a single probe were available—as is the case in most instances of soil moisture sensors being used by Australian dryland cereal growers. However, as both Figs. 7 and 8 illustrate, in our SA field in which marked soil variation is apparent and expressed in the existence of management zones, the use of a single soil moisture probe may be misleading in similarly suggesting that soil moisture variation down the profile is greater than its spatial variation at field scale, with the latter more appropriately highlighted by the use of zone-based probes. We suspect that for reasons of cost, along with the effort required for sensor calibration against site conditions, data management and analysis, dryland broadacre cereal growers are unlikely to want to pursue zone-based use of soil moisture sensors, especially given the accuracy of prediction illustrated here (Fig. 8). In other words, they are unlikely to perceive the value of the information provided by multiple probes as sufficient to warrant investment in them (Bramley & Ouzman, 2019). This may especially be the case at drier sandier sites, such as our WA field (Fig. 6, 8d). In general, therefore, and notwithstanding that our method provides a means of extrapolating away from the location of a probe, we conclude that the primary value in using soil moisture sensing in most dryland cereal cropping situations is likely to be in comparing seasons, and in understanding differences between them, rather than informing a targeted decision in-season. Thus, such sensors assist growers in assessing how similar this year is to last year or the year before in terms of water availability to a crop and so enable such similarities or contrasts to be factored into agronomic decision-making, such as in relation to mid-season N management, or the ability to finish a crop. Likewise, as demonstrated by Colaço and Bramley (2019), they may provide critical information to enable value to be accrued from other sensing technologies which are otherwise hamstrung by their present univariate approach to agronomic decision support. Indeed, and in respect of N management, the over-simplification of the myriad of agronomic and business factors which impact on an N decision in mechanistic crop models is arguably a major reason why data-driven approaches to decision making using machine learning have recently been shown to outperform such mechanistic approaches (Colaço et al., 2021, 2023) and thereby deliver benefits to growers from both profit enhancement and error reduction perspectives (Colaço et al., 2023).

Recent research (He et al., ) has pursued an inverse modelling approach, first attempted by Florin et al. (2011), for the estimation of PAWC using crop yield data, derived either from yield monitors or simulated using APSIM (Holzworth et al., 2015). This work has demonstrated that PAWC can be reliably predicted using such an approach and might therefore inform targeted management in broadacre cropping systems. Of course, it contrasts from the present study by focussing on spatial variation in the ‘size of the bucket’ (i.e. PAWC) rather than ‘how full the bucket is’. In our calibration of extrapolated against measured soil water status at the SA site, inclusion of a surrogate measure of PAWC provided by electromagnetic soil survey as a covariate did not improve prediction of soil water status, in spite of the results of a preliminary analysis (not shown) which suggested that the ECa data used as a part of the initial zone delineation (Fig. 1a), were correlated to PAWC. However, the integration of the present approach with that of Florin et al. (2011) and He et al. (2021, 2022) would enable understanding of spatial variation in not only the size of the bucket, but also how full the bucket is. Such information could indeed inform targeted agronomic decision making and is therefore worthy of further research.

In the absence of soil modification, PAWC is a static variable; soil moisture status is dynamic. Two obvious significant limitations of the present method therefore are that it only works during the season (i.e. when there is measurable NDVI), and that in the absence of improved weather forecasting, or even an ability to predict NDVI, its utility remains limited by lack of knowledge as to how the season might evolve. This first of these limitations means that the method cannot be used to inform a sowing decision, which is a key area of interest for growers. Whilst the second limitation can be partially overcome by continual updating of ΣNDVI and weather data, the ability to predict a dry finish, which may render a targeted mid-season decision worthless, remains elusive. It is for these kinds of reasons that alternative approaches to so-called ‘now-casting’ (Wimalathunge & Bishop, 2023) are the subject of much current effort. That of Wimalathunge and Bishop (2019) draws on the integration of water balance modelling with soil and weather information. It is currently limited by the resolution of available soil information (Han et al., 2022), and to support targeted decision-making, is likely reliant on farmers paying for bespoke digital soil maps of their farms at high spatial resolution (Wimalathunge & Bishop, 2023). The cost of these therefore makes the approach of He et al. (2021, 2022), perhaps combined with the present approach, an attractive one. Whilst the utility of ‘now-casting’ is likely to remain somewhat constrained by inability to predict the future, understanding how much soil water is available in real time, is clearly valuable for risk management (Monjardino et al., 2015). Overall, the integration of the present approach with those of He et al. (2021, 2022) and Wimalathunge and Bishop (2019, 2023), as multivariate input to a machine learning-based, data-driven tool (Colaço et al., 2021, 2023; Lawes et al., 2019; Richetti et al., 2023) may offer the best way forward.

Finally, we note that both the development and evaluation of our method was confined to fields in which wheat or barley was grown. Whilst the performance of other crops such as canola, lentils or lupins is also known to be reflected by NDVI, additional work will be required to evaluate the method for these crops if there is interest in using it when such crops are being grown. Similarly, exploration of the method for use in irrigated systems across a range of cereal and horticultural crops may well be of value.

Conclusions

Using cumulative NDVI, season growing degree days and cumulative net precipitation as covariates, extrapolation of soil moisture probe data to any location within a field on any day within a growing season is possible. However, the utility of being able to do this is of questionable value to farmers interested in targeted variable rate management, both in fields with limited soil variation, and also in those with well defined soil zones, but which do not have a probe in each zone. Accordingly, the main benefit of soil moisture sensors to dryland cereal growers is likely confined to better understanding seasonal variation in soil moisture and its implications for differential management between different cropping seasons. However, greater value from such technology may accrue through integration with other approaches to better understanding field scale variation in soil moisture.