Introduction

Global climate changes and population growth are demanding new strategies for enhancing yield potential of crops due to their great genetic diversity (Foley et al., 2011; Sharma et al., 2015). However, the full potential of such strategies has not been reached due to the technical difficulties encountered by plant breeders in evaluating new cultivars in different scenarios. This process has been improved with the emergence of aerial and terrestrial high-throughput plant phenotyping platforms (HTPPs), which can meet the needs of breeders (Phillips, 2010; Andrade-Sanchez et al., 2014; Araus & Cairns, 2014). Recent adavances in high-resolution remote sensing technologies and the development of HTPPs, have allowed breeders to obtain valuable crop information remotely (i.e., non-destructively), more quickly and cheaper than with traditional sampling methods (Fahlgren et al., 2015; Pérez-Ruiz et al., 2020; Li et al., 2021).

The leaf area index (LAI) is a key biophysical parameter that has been extensively studied for years to characterize vegetation dynamics and crop productivity. According to Watson (1947) LAI is defined as the photosynthetically active leaf area per unit of horizontal ground surface area, and has been related to crop development, crop water use, crop carbon uptake and yield (Asner et al., 2003; Kalisperakis et al., 2015; Yan et al., 2019). The LAI is therefore a relevant crop trait to be monitored with HTPPs in maize breeding programs to support breeders in the process of obtaining more productive cultivars.

From a literature review, there exist two widely used methods (direct and indirect) for retrieving LAI (Behera et al., 2010; Olivas et al., 2013). Direct methods are more accurate than indirect methods but their often destructive nature and the time required to process leaf samples at laboratory facilities (Stroppiana et al., 2006; Sonnentag et al., 2007) make them unsuitable for inclusion in the routine measurements undertaken by maize breeders. Indirect methods based on optical measurements provide fast LAI estimates but require costly equipment whereas the methods based on hemispheric/nadir-view RGB imagery and gap fraction theory provide more economical LAI estimates (Mougin et al., 2014; Sharifi, 2018; Yan et al., 2019). Although hemispherical bottom-up RGB images have been traditionally used for indirectly estimating LAI (Jonckheere et al., 2004), nadir-view and bottom-up hemispherical RGB images showed similar accuracies for LAI estimation (Mougin et al., 2014). Despite their usefulness for LAI determination, these methodologies based on the use of affordable RGB images require the use of post-processing software, slowing down the process of obtaining LAI data (Jonckdheere et al., 2004).

Allometric relationships are empirical functions that relate the leaf area to any other plant dimension, and they have also been widely studied to estimate LAI under different conditions and crops (McKee, 1964; Wiersma & Bailey, 1975; Aase, 1978). During the last 2 decades, many studies have found that leaf dimensions (length and width) can provide accurate LAI estimates using straightforward allometric relationships (Soltani et al., 2006; Colaizzi et al., 2017). Although allometric methods can be understood as indirect methods for LAI estimation, since they infer an LAI value from its relationship with other vegetation traits, they can also be considered direct methods because the allometric relations are obtained from leaves that were sampled and measured manually (Yan et al., 2019). In research or breeding trials where destructive sampling is not possible, allometric relationships provide an excellent method to be used as ground-truths for the validation of other indirect methods for LAI estimation.

Artificial intelligence (AI) algorithms represent a new approach for indirect LAI estimation from remotely-sensed data, including RGB imagery (Verrelst et al., 2012; Houborg & McCabe, 2018; Fang et al., 2019). In recent years, despite the widely recognized importance of LAI in various biophysical processes, only a few authors have published studies where remote sensing technologies along with convolutional neural networks (CNNs) based models have been used to estimate its value. A multi-feature learning method to quantify green fractional vegetation cover in wheat was suggested by Sadeghi-Tehran et al. (2017). The results were compared with actual LAI values, showing coefficients of determination greater than 0.8. Over the same period, Jin et al. (2020a) proposed a deep learning-based algorithm for non-destructive estimation of 3D plant architecture for predicting at plot level maize biomass using terrestrial LiDAR. However, although the capability of LiDAR sensor to estimate phenotypic traits (i.e., leaf area) at individual plant level showed great potential, its cost is still a challenge for small plant breeding companies (Jin et al., 2021). Harnessing the success of drones in agriculture, Yamaguchi et al. (2021) evaluated the feasibility of combining CNN with RGB images taken from unmanned aerial vehicles (UAVs). The results demonstrated that the DL model developed could be an alternative for rice LAI estimation, as long as images are taken without blur effect caused by the UAV’s high-speed flight. A recent study conducted in wheat by Apolo–Apolo et al. (2021) showed the feasibility of combining DL and RGB images obtained from a field HTPP platform (Pérez-Ruiz et al., 2020) to derive LAI values in wheat breeding plots. In the last decade, efforts have been made to develop methodologies for the determination of LAI in maize from optical sensors, including hyperspectral, multispectral, LiDAR and RGB sensors (Table 1). Among the methodologies employed by these authors to estimate maize LAI from images and optical data are empirical relationships with vegetation indices (Fei et al., 2012), the use of machine learning models such as deep neural networks (DNN), support vector regression (SVR) or partial least squares regression (PLSR) (Fei et al., 2012; Castro-Valdecantos et al., 2021; Liu et al., 2021), the use of look-up tables (LUT) (Fei et al., 2012; Duan et al., 2014; Richter et al., 2010; Zhao et al., 2018), or through the inversion of the PROSAIL canopy reflectance model. The coefficient of determination (R2) obtained with the different methodologies for estimating LAI in maize ranged from 0.66 to 0.87 (Table 1). In previous works conducted on other crop species, it has been shown that the development of DL models that fuse different data sources (e.g. RGB images and other crop features introduced in the form of numerical data) can significantly improve the DL model performance (Apolo-Apolo et al. 2021). The DL models developed to date for the determination of LAI in maize use a single source of data (Table 1), so it is necessary to evaluate the potential of DL models that combine different data sources to estimate LAI in maize.

Table 1 Performance and methodology used in previous studies for the estimation of LAI in maize
Full size table

Based on the above, the objectives of this study were (1) to develop and evaluate three different DL-based models using RGB imagery taken from a field-based HTPP for maize LAI estimation, and (2) to examine their accuracy as compared to a traditional indirect LAI estimation method based on RGB imagery and gap fraction analysis.

Materials and methods

Experimental design

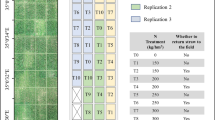
The experiment was performed at the facilities of a maize breeding company (Corteva Agrisciencies S.L.) located in La Rinconada, Sevilla, Spain (latitude: 37.4572° N; longitude: 5.9811° W; datum WGS84). The study was carried out over two crop seasons (2018 and 2019) in a maize breeding trial sown on 10th and 16th of April respectively, consisting of 20 hybrids, three replicates per cultivar and two irrigation treatments (well-watered and deficit irrigated) in a randomized block design (supplementary Fig. S1). Each plot consisted of two 6 m long maize rows with a plant spacing of 0.75 m × 0.15 m. A total of 32 maize plots, corresponding to two complete rows of plots from the well-watered block, were used in the experiment. During the two experimental seasons, the crops were managed following the usual agronomic practices in the region.

RGB images were taken throughout the two growing seasons in the selected plots and used to develop three DL-based models for indirect LAI estimation. Additionally, the RGB images were also used to obtain LAI estimates with the CAN-EYE software (V6.4.91), which provides indirect LAI estimations by gap fraction analysis. The latter is a method traditionally used for indirect LAI estimation from RGB images, which has been used in this study to compare its performance with that of the three DL-based models developed in this work. The accuracy of all indirect LAI estimation methods was assessed through comparison with ground-truth LAI data obtained during the sampling days. The following sections describe the above methods in more detail.

LAI ground-truth data

Direct LAI measurements were performed to be considered as ground-truth data for the validation of all indirect LAI estimation methods. Since leaf area measurements are often destructive and cannot be feasibly performed in breeding programs due to the error they would introduce in the final harvest, an allometric relationship similar to that proposed by other authors (Montgomery, 1911; McKee, 1964; Keating & Wafula, 1992; Birch et al., 1998) was developed to estimate the leaf area of individual maize leaves from their main dimensions (i.e., length and maximum width). By measuring the main dimensions of all the leaves of a plant, its total leaf area can thus be measured without destructive sampling. To obtain the allometric relationship, over 70 maize leaves with different sizes were destructively sampled in 2018. The main dimensions of all sampled leaves (length, L, and maximum width, W) were measured manually in the laboratory with a millimetre-precision tape measure (Tylon Tape 8 m, Stanley, Japan). In addition, the unitary leaf area (LA) of each leaf was measured with a leaf area meter (model Li-Cor 3100, Li-Cor, Lincoln, NE, USA). Using these variables, an allometric relationship was derived to estimate LA from the corresponding L and W measurements.

During the 2 years of experiments, two representative plants per plot were selected on each sampling date (three dates per growth cycle) and used for the direct estimation of the LAI to be used as ground-truth values. For each maize plot and sampling date, LAI was calculated as follows:

$$LAI=\frac{PLA \left({m}^{2}\right)}{PS \left({m}^{2}\right)}$$
(1)

where PLA denotes the total plant leaf area calculated by summing the individual LAs of all plant leaves obtained with the allometric relationship and PS denotes the plant spacing (estimated as the inverse of the plant density).

The measured LAI values were used as ground-truth data for the DL-based models training/validation as well as to assess the reliability of the indirect LAI estimates made by the CAN-EYE software.

Image acquisition

In this study, a smartphone iPhone X (Apple Inc, Cupertino, CA, USA), whose technical characteristics are shown in supplementary Table S1, was suspended at the front of an HTPP platform to take nadir-view images of maize canopy. Considering that the camera was centered in the interrow spacing of the plots, placed 1 m above the maize canopies and that its field of view is 60.983 (Table S1), it is very unlikely that leaves from adjacent treatment plants are interfering the LAI measurements. The device was used for recording RGB videos in QuickTime Movie (MOV) format across all the selected plots. The platform speed was set at 0.6 m s−1, which allowed a video to be recorded in an average of 10 s per plot.

The videos were disassembled into JPEG image frames with an automated script based on Python (Python programming language, v. 3.7) and OpenCV computer vision library (Open Source Computer Vision Library, v. 3.2.0). As a result, an average of 300 frames per plot were produced. Approximately 250 out of 300 images per plot were taken for the final analysis to avoid the border effect. The images were taken over six sampling dates, three belonging to the 2018 growing season, days of year (DOY) 143 (phenological period V8), 157 (V11) and 169 (V13), and the other three belonging to the 2019 growing season, DOY 151 (V9), 163 (V12) and 177 (VT). The platform was operated from 11:00 a.m. to 1:00 p.m. under diverse but dry weather conditions during the two growing seasons.

Deep learning (DL) models description

Three DL models were developed to estimate LAI from RGB images, termed (i) classification model, (ii) regression model and (iii) multi-input model. Although the three models are based on CNNs, the classification model predicts discrete LAI values (classes) whereas the regression and multi-input models predict any LAI value in a given range. The classification model was trained with a set of RGB images labelled with ground-truth LAI values (classes), whereas the regression and multi-input models use RGB images and numerical data, including ground-truth LAI values, for model training. The RGB images taken over the six sampling dates in 16 out of 32 plots were used as the training dataset, which was further split into a training set and a validation set with 80% and 20% of images, respectively. The images from the remaining 16 plots comprised the testing dataset, i.e. a completely independent set of images that were not used during the model fine-tuning process and that provides an unbiased evaluation of the models, avoiding the possibility of model overfitting or pre-learning, masking the actual performance of the model (Kuhn & Johnson, 2013).

The Keras application programming interface (API) (https://keras.io) and the open-source library TensorFlow as the backend (Abadi et al., 2015), were used to define the model architecture since this API is able to define a model that can take different data inputs, such as numerical, categorical and image data, as well as their combination. Thus, the Keras sequential approach was used for the classification CNN model and a functional approach was used for the regression and multi-input CNN models.

The classification CNN model proposed (Fig. 1), was a small version of the well-known VGGNet network introduced by Simonyan & Zisserman (2014). These kind of models are used to predict a class (categorical or discrete variable) for a given input (e.g., image). The model was developed using a dataset consisting of 24,473 original RGB images (1920 × 1080 pixels each) divided into 96 LAI classes, which corresponded to the measured LAI ground-truth values of each plot and day of measurement (16 plots and 6 sampling dates). The classes were completely mutually exclusive, and there was no overlap between them. It is well-known that overfitting can occur with small training datasets (Cogswell et al., 2015). Thus, data augmentation and the dropout technique were implemented to supply sufficient robustness to the model, since this approach generates and regularizes additional training data from an existing dataset (Srivastava et al., 2014). Since the shapes of the input images needed to be arranged for the first convolutional layer, the original RGB images were resized into 180 × 180 pixel RGB images (depth = 3) to reduce the computational cost of the model and to standardize the input images to an acceptable set of dimensions for training (Rosebrock, 2018). The CNN model consisted of three convolution blocks placed in a sequential manner (Fig. 1). Firstly, a 2D convolutional neural network contained the main portion of the network´s computational load. Next, a rectified linear unit (ReLU) activation function is used, where the threshold was set to zero each time. Finally, a max-pooling layer was used to reduce the spatial size of the representation, decreasing the number of computational cycles and weights. After that, a dropout was applied to the next layer to randomly reduce (20%) the number of output units by disconnecting nodes from the current layer and inputting them into the next layer. Finally, the next layer was flattened, and a fully connected layer was specified by the dense function (128) with ReLU function to round out the output of each class (96) label probability.

Fig. 1
figure 1

Schematic diagram showing the structure of the deep learning classification model for estimating LAI values. The model input was RGB images resized to 180 × 180 pixels. Three blocks of convolution and rectified linear unit (CONV + ReLU) placed sequentially were used, followed by a maximum pooling layer (Max pool) to reduce the spatial size of the representation for feature extraction. Finally, the next layer was flattened and fully connected to determine the probability that an image belongs to a certain class with the softmax activation function

Full size image

The regression and multi-input models were developed using a dataset consisting of RGB images and numerical data. The image dataset used as model input consists of 384 original RGB images with an image resolution of 1920 × 1080 pixels, which are tiled in a unique montage of 4 RGB images randomly selected per plot covering approximately two-thirds of the plot surface, 6 sampling dates and 16 plots. The new tiled image was compressed to 180 × 180 pixels as described in the previous classification model. The numerical data input was processed by a simple multilayer perceptron (MLP), and was defined by the measured LAI values (allometric relationship), plant height, number of days after sowing and cover fraction, since those four parameters were shown to be suitable as data inputs for this DL method (Apolo-Apolo et al., 2021). Cover fraction values were calculated for each image using a Python-based image segmentation method previously described in Apolo-Apolo et al. (2021).

The regression model architecture (Fig. 2) was based on RGB images and numerical data. It was composed of three convolutional layers with a kernel of (3, 3). Each convolution layer was followed by an activation function (ReLU), a batch-normalization layer and a MaxPooling2D with a pool size of (2, 2). Then, the next layer was flattened and two fully-connected layers with batch-normalization and dropout were added. Finally, another fully connected layer was applied to match with the numerical data. Finally, the final output variable is the LAI value of the plot, which is defined as a numerical (or continuous) variable. Unlike the multi-input model, the regression model requires only RGB images for predicting LAI.

Fig. 2
figure 2

Schematic diagram showing the structure of the deep learning regression model for estimating LAI values. The inputs are described as an unique montage of 4 RGB tiled images randomly selected per plot, with 180 × 180 pixels (px) dimension for one branch and a multi layer perceptron (MLP) for the numerical data. Convolutional layers (CONV), followed by rectified Linear Unit activation (ReLU), a batch-normalization layer and a MaxPooling2D were implemented

Full size image

The multi-input model architecture (Fig. 3), was based on two branches to handle each type of data, with the first branch set for image processing and the second branch set for numerical data processing. These branches operate independently of each other until they are concatenated. The first branch of the model was based on three convolutional layers placed in a sequential manner with a 2D convolutional neural network followed by batch normalization, ReLU activation and max-pooling, and a dropout rate of 50% was added at the end. Then, another set of one 2D convolutional neural network followed by a flattened, dense and dropout layers was added. The second branch with numerical data as input was processed by MLP composed of two fully-connected (dense and hidden) input layers both with ReLU activation. Finally, both outputs (from the two branches) were concatenated and used for the final step of the network, which comprissed a fully connected layer with two dense layers, where an activation regression function (linear) was added. The final output of the model is the predicted LAI value of the plot, which is defined as numerical (or continuous) variable. In addition to RGB images, the multi-input model requires plant height, number of days after sowing and cover fraction for predicting LAI.

Fig. 3
figure 3

Schematic diagram showing the structure of the deep learning multi-input (CNN + MLP) model. The inputs are described as an unique montage of 4 RGB tiled images randomly selected per plot, with 180 × 180 pixels (px) dimension for one branch and a multi layer perceptron (MLP) for the numerical data (LAI, fraction of vegetation cover -FC-, plant height and days after sowing). Convolutional layers (CONV), followed by rectified Linear Unit activation (ReLU), a batch-normalization layer and a MaxPooling2D were implemented. Unlike the regression model (Fig. 2), the multi-input model uses RGB images and numerical data also for LAI predictions

Full size image

The classification model was compiled using “sparse categorical cross-entropy” loss function, whereas the regression and multi-input models used the “mean absolute percentage error” for their loss functions. All the models used the Adam optimization algorithm (Kingma & Ba, 2014) as the optimizer, a learning rate of 0.001 and a batch size of 16, 100 and 300. In addition, 100 epochs were used with the classification model and 500 epochs were used with the regression and multi-input model due to their dual structure of images and numerical data. A weight decay factor of 0.001/2500 and 0.001/500 were utilized for the regression and multi-input models, respectively.

Indirect LAI estimation using the CAN-EYE software

Maize LAI was also estimated with a classical indirect method based on RGB imagery and gap fraction theory using the CAN-EYE software (developed by the French National Institute of Agronomic Research–INRA). Three equal batches of 10 random images were selected from each plot and sampling date to be analysed with the software. The software uses a series of images processed simultaneously to estimate the LAI (Demarez et al., 2008), so the 10-image batches were processed at one time, and the LAI averages per plot were calculated by averaging the LAI values derived from each batch of 10 images. Before analysing the images, they were preprocessed following the software instructions. Image processing followed a segmentation step, in which all pixels were classified into two categories established by the software, defined as the background (soil) and foreground (vegetation). The software also provided estimates of the leaf clumping index (Chen & Black, 1992), which is computed based on the assumption that vegetation elements are locally assumed randomly distributed, so true LAI values could be determined and used in this work. To compare the different indirect methods, only the images used as test dataset in the DL-based models (n = 96) were used to estimate LAI with the CAN-EYE software.

Statistical analysis

Linear regressions were used to compare the estimated LAI values by CAN-EYE software and the three DL models against the ground-truth LAI values. The mean absolute error (MAE) and the root mean square error (RMSE) values were calculated with RStudio team (2020; Version 1.3.959) to analyse the predictive performance of the CAN-EYE software and the DL models.

Results

Figure 4 shows the allometric relationship obtained to estimate the area of individual maize leaves from their corresponding main dimensions (length and maximum width). The relationship explained 96% of the observed LA variability, with a slope of 0.78 cm2 cm−2 and an intercept of + 4.21 cm2. The relationship was used to determine the ground-truth LAI values for each plot and sampling date.

Fig. 4
figure 4

Allometric relationship between each unitary leaf area and the corresponding main leaf dimensions (L: length, W: maximum width). Each symbol represents an individual leaf. The solid line depicts the regression line, whereas the dashed line depicts the 1:1 line

Full size image

The accuracy and loss values of the three DL-based models that were obtained during model training and validation are shown in Table 2. After 100 epochs, the accuracy and loss values of the classification model were approximately 0.95 and 0.12%, respectively, in both the training and validation sets, indicating the high level of performance achieved by the model. After 500 epochs, the mean absolute percentage errors (loss function) of the regression model were approximately 12.8% and 20.3% for the training and validation datasets, respectively. The multi-input model showed, after 500 epochs, loss values of approximately 1.36% and 1.89% for the training and validation sets, respectively.

Table 2 Training and validation accuracy and loss values obtained for each DL model
Full size table

The relationships between ground-truth LAI and LAI estimated with the CAN-EYE software and the three DL-based models are shown in Fig. 5. An independent set of 96 images corresponding to 16 plots out of 32 and 6 sampling dates was used to test all the indirect LAI estimation methods. The CAN-EYE LAI estimations explained 67% of the observed LAI variability, with a slope of 0.82 and an intercept of + 1.56 (Fig. 5a). The CAN-EYE method tended to overestimate the LAI and presented MAE and RMSE values of 1.23 and 1.41, respectively (Table 3).

Fig. 5
figure 5

Relationship between measured ground-truth LAI values and LAI values estimated with the CAN-EYE software (a), the DL-based classification model (b), the DL-based regression model (c) and the DL-based multi-input model (d). Each symbol represents an individual RGB image selected from each plot and sampling date. The solid line depicts the regression line, whereas the dashed line depicts the 1:1 line

Full size image
Table 3 Summary of the statistical indicators obtained with the four LAI estimation methods evaluated: the CAN-EYE software, classification model, regression model and multi-input model
Full size table

The DL-based classification model explained 78% of the observed LAI variability (Fig. 5b). The regression line between measured and estimated LAI values had a slope of 0.76 and an intercept of + 0.44, denoting a certain degree of model overestimation and underestimation for LAI values lower and greater than 2, respectively. Compared to the CAN-EYE method, the classification model exhibited higher accuracy for predicting maize LAI, with MAE and RMSE values notably lower (MAE = 0.39, RMSE = 0.52) than those observed with the CAN-EYE software (MAE = 1.23, RMSE = 1.41) (Table 3). The relationship between the LAI values estimated by the DL-based regression model and the measured LAI showed a slope of 0.81 and an intercept of + 0.45 (Fig. 5c). The relationship showed much lower scattering (R2 = 0.89) than those obtained with the CAN-EYE software and the DL-based classification model. The MAE (0.3) and RMSE (0.35) obtained with the regression model were somewhat lower than those obtained with the classification model (Table 3). As with the classification model, the regression model tended to over-estimate and under-estimate LAI values lower than 2 and higher than 3, respectively. The relationship between measured LAI and LAI values estimated with the DL-based multi-input model showed a slope of 0.96 and an intercept of + 0.08 (Fig. 5d). The relationship showed much lower scattering (R2 = 0.97) than those obtained with the CAN-EYE software and the other DL-based (classification and regression) models. The multi-input model error was also lower than that obtained with the classification and regression models, with MAE and RMSE values of 0.13 and 0.19, respectively (Table 3).

Discussion

The reliability and accuracy of three deep learning based models that utilize nadir-view RGB images to estimate the LAI of maize breeding microplots has been evaluated and compared with that of a traditional image-based indirect method for LAI estimation. One of the main advantages of using DL-based models over traditional image-based indirect methods for LAI estimation is the absence of the image post-processing steps required by other methodologies, such as the CAN-EYE software. As for indirect methods that estimate LAI from diffuse radiation intercepted by vegetation at different zenith and azimuth angles (e.g. LI-2200 C PCA, Li-COR, Nebraska, USA), the use of DL models sourced with RGB images allows estimating LAI in a more affordable way and without the limitation of having to perform the measurements under diffuse solar radiation conditions, as is the case of the aforementioned instrument.

In terms of model accuracy, the three DL-based models evaluated showed substantially lower LAI estimation errors than that obtained with the CAN-EYE software, as well as less data scattering (Table 3). In fact, the CAN-EYE method provided LAI estimations with similar accuracy to that of previous works that used either spectral indices (Fei et al., 2012) or machine learning algorithms, such as SVR, DNN or RFR (Fei et al., 2012; Liu et al., 2021), for maize LAI estimation (Table 1). Of the three DL models assessed, the regression and multi-input models reduced data scattering significantly with respect to the classification model, being the multi-input model the one that showed the lowest LAI estimation errors (MAE = 0.13, RMSE = 0.19) (Table 3). The errors observed with the regression and multi-input models are notably lower than those found in previous works where maize LAI was estimated from remotely sensed dada and various types of models (Table 1). Only Richter et al. (2010) obtained error values within the same order of magnitude (RMSE = 0.42) by estimating maize LAI through PROSAIL model inversion and look-up tables (Table 1). The reason why these two models (regression and multi-input models) outperformed the classification model may be due to the fact that they can predict continuous LAI values within the range of LAI values used for model training, whereas the LAI predictions made by the classification model must match one of the LAI classes used in the training dataset. Although both models (regression and multi-input) use two sources of information (images and numerical data) for model training, the fact that the multi-input model also requires both types of data sources to make LAI predictions may explain its better performance (Apolo-Apolo et al., 2021; Yamaguchi et al., 2021). On the other hand, although the performance of the regression model is slightly poorer than that of the multi-input model, the fact that it uses numerical data only during model training and that reasonably accurate LAI predictions are obtained from RGB images alone, makes it a very promising method in terms of simplicity. Although the multi-input model can achieve much higher accuracies than those previously observed with other methods (Table 1), the fact that it requires fusing different data sources (i.e. crop height from LiDAR point cloud processing, RGB imagery, etc.) makes it a more complex method for breeders to adopt.

Deep learning has already been considered as a promising tool for solving different kinds of problems in agriculture (Kamilaris and Prenafeta-Boldu, 2018; Zhu et al., 2018; Zheng et al., 2019). However, despite the excellent performance of the DL models tested in this study and the growing number of available DL-based applications in agriculture, there is still room for models improvement by, for example, enhancing the training dataset of images by using tools such as flipping or changing the brightness of each image (Yamaguchi et al., 2021). The suitability of estimating LAI from spectral indices derived from optical devices has been successfully evaluated in the past and recent years (Fei et al., 2012; Liu et al., 2021), but these approaches normally use costly equipment (e.g. hyperspectral and multi-spectral cameras on-board UAVs or HTPPs) or provide spatial resolutions (e.g., satellite-based applications) that are not suitable for use in some agricultural applications (Richter et al., 2010; Zhao et al., 2018), such as LAI monitoring in breeding trials with very small plot sizes (Gitelson et al., 2003; Jin et al., 2020b). For the latter practical application, the multi-input model developed in this work offers higher accuracies than those observed by Liu et al. (2021) with various machine learning models based on the use of RGB images captured from drones (Table 1). The use of data sources of different nature in DL-based models seems, therefore, to be a way to increase their predictive potential as compared to models that rely exclusively on RGB images.

The DL-based models developed in this work offer, therefore, an accurate, affordable and fast alternative for LAI estimation in maize. The deep learning models also have the advantage of being able to continue to be trained with new images that are incorporated into the dataset, allowing a progressive increase in their predictive potential.

Conclusions

In this research, it was studied whether DL-based models using down-facing RGB images as input could be an alternative to existing semi-automated approaches for the indirect estimation of LAI in maize. It was observed that the developed DL models outperformed a classical indirect method for LAI estimation based on gap fraction analysis and RGB imagery. In addition, among the three DL models developed, the multi-input model presented less data scattering and less prediction error than the classification and regression models. Future work includes improving the model through re-training with new images to be incorporated into the training dataset, and incorporating the model into the workflow of an HTPP for real-time determination of LAI in maize breeding plots.