Introduction

Emerging in the mid-1980s, precision agriculture (PA) is a farming management concept based on observing, measuring and responding to the spatio-temporal variability in weather, soil and agricultural production. It involves the employment of appropriate technologies for the location, in a timely manner and in the right way to improve production while minimizing environmental impacts (Gebbers and Adamchuk 2010). Positioning accuracy is of prime importance for precise management of agricultural operations. Different PA applications require different positioning accuracies (Perez-Ruiz and Upadhyaya 2012): (i) low accuracy (meter level) can be used for asset management, tracking and tracing; (ii) medium accuracy (sub-meter level) can be used for tractor guidance, via manual control, for lower accuracy operations such as spraying (Xue et al. 2016), spreading, harvesting bulk crops and for area measurement and field mapping (Auernhammer et al. 1994); (iii) high accuracy (cm level) can be used for auto-steering systems on tractors and self-propelled machines (harvesters and sprayers) (Gan-Mor et al. 2007; Dijksterhuis et al. 1998; Bell 2000) and for precision operations such as planting (Sun et al. 2010; Ehsani et al. 2004). In PA, it is well recognized that Global Navigation Satellite Systems (GNSS) are the major enabler of ‘precision’ (Larsen et al. 1994; Krüger et al. 1994).

GNSS represents a constellation of satellites providing signals from space, transmitting positioning and timing data with global coverage. A GNSS receiver employs trilateration to determine its position on or near the Earth’s surface by timing signals from four or more GNSS satellites. There are two fully operational GNSS systems at present—the United States’ Global Positioning System (GPS), and the Russian Federation’s Global Navigation Satellite System (GLONASS): and two systems under development—the Chinese Beidou Navigation Satellite System (BeiDou), and the European Union’s Galileo system, which are both expected to achieve full global coverage capability by 2020. In addition, the Japanese Quasi-Zenith Satellite System (QZSS) and Indian Navigation with Indian Constellation (NAVIC) are two regional systems. Over the past three decades, the US GPS system has been the most accurate and reliable means for positioning, navigation and timing (PNT) services, and has made great contributions to earth sciences and engineering applications. Up to now, 32 GPS satellites consisting of BLOCK IIR, BLOCK IIR-M, and BLOCK IIF are operational and equally distributed in three independent orbit planes. Unlike previous BLOCK II/IIA satellites, BLOCK IIF satellites can broadcast a third signal, allowing acceleration and improvement of the positioning accuracy further. The Soviet Union started to develop the GLONASS system in 1976. Due to subsequent political and economic issues, retired satellites were not replaced, resulting in insufficient satellites in orbit to provide services during the late 1990s and the first decade of 2000s. With a modernized plan, the constellation has been recovered since 2011. Currently, 24 satellites are operational to provide PNT services. The new and emerging BeiDou and Galileo systems provide potential for more precise and reliable GNSS applications and services around the world, or in certain regions. BeiDou, declared to be operational to provide regional PNT services in December 2012, consisted then of 5 Geostationary Orbit (GEO), 5 Inclined Geosynchronous Orbit (IGSO), and 4 Medium Earth Orbit (MEO) satellites. With the launch of new generation BeiDou IGSO and MEO satellites in 2015 and 2016, the system is starting to become a global navigation satellite system, and this phase will be completed in 2020. By then, the space segment of BeiDou will consist of 5 GEO, 3 IGSO, and 27 MEO satellites (CSNO 2013). Galileo is aiming to provide a highly accurate, guaranteed global positioning service under civilian control. Its In-Orbit Validation (IOV) phase has been completed, and the system is moving to the Full Operational Capability (FOC) phase. As part of the IOV phase, 4 Galileo-IOV experimental satellites were sent into orbit on 21 October 2011 and 12 October 2012; fourteen FOC satellites have been successfully launched since then. The initial services started on 15 December 2016, and the full operation of the Galileo constellation will be accomplished with 30 satellites in three orbital planes in 2020 (EU 2016). More than 80 GNSS satellites in total are now in orbit around the Earth, and about 120 satellites will be available once all the four global GNSS systems are fully deployed in the near future. Increasing the number of operational systems is expected to improve the observation geometry, which in turn will benefit the positioning accuracy, availability, integrity and continuity.

It is well known that a common approach to achieve real-time high accuracy positioning results for a moving device in PA is Real Time Kinematic GPS (RTK GPS), in which two or more GPS receivers (at least one rover and one reference) track similar satellites, and both pseudo-range and phase measurements are used to provide up to centimeter-level positioning accuracy. As the co-ordinates of the reference stations are known, a range of common errors (e.g. orbital, ionospheric and tropospheric effects) between the reference and the rover receivers can be estimated and then used to improve the positioning accuracy of the rovers. Note that the correlation of errors decreases with increased distance between the reference and rover receivers. The deployment of two GPS receivers along with a radio data link for agricultural applications could be expensive in many instances. An alternative, to reduce the cost without degrading the positional accuracy, is to use Network RTK (Sun et al. 2010; Gan-Mor et al. 2007; Dijksterhuis et al. 1998; Bell 2000). However, the subscription fee of the Network RTK service is high, particularly for those seeking centimeter level accuracy. In contrast to RTK, precise point positioning (PPP) uses dual-frequency pseudo-range and carrier phase observables from a single receiver, as well as precise satellite positions and clocks, to determine its absolute co-ordinate at the same level of accuracy as RTK, but with higher flexibility, potentially lower capital and running costs and global capability (Zumberger et al. 1997). In this case, no correction from reference stations is required for PPP, except for precise satellite position and clock products that are freely provided by the International GNSS Service (IGS) (Dow et al. 2009).

GPS PPP has not been used in PA, let alone Multi-GNSS PPP, although previous research has demonstrated that Multi-GNSS can provide higher accuracy and more stable positioning for PA (Kabir et al. 2016). This paper attempts to examine the feasibility of multi-GNSS PPP in PA through a series of experiments with different working modes (i.e. stationary and moving) under different observation conditions (e.g. open sky, with buildings or with canopy). All operational systems—GPS, GLONASS, Galileo and BeiDou—were used in this study.

Materials and methods

Field sites

In order to assess the feasibility of Multi-GNSS PPP for PA applications and evaluate the performance of Multi-GNSS PPP, three experiments were carried out in different working modes at different sites (Fig. 1): (i) the stationary (static) experiment, labeled as EPs1, was carried out on the roof of the Drummond Building of Newcastle University (UK) with two Leica receivers under the open sky on 2 March 2016; (ii) the first moving (kinematic) experiment was conducted in Cockle Park Farm of Newcastle University (UK) with three Leica receivers on a truck on 2 September 2015 (indicated as EPm1 hereafter); and (iii) the second moving experiment was carried out at Xiaotangshan Farm of the National Engineering Research Center for Information Technology in Agriculture (NERCITA), Beijing, China with two Trimble NetR9 receivers on a tractor on 14 September 2015 (labeled as EPm2 hereafter).

Fig. 1
figure 1

The experiment sites and trajectories of EPs1 (a), EPm1 (b), and EPm2 (c), respectively. The red dot in (a) represents the location for the stationary experiment. The red square in (b) indicates the field shown in the insert. The blue and yellow circles represent the locations where the two drivers stopped for a break in (b) and (c), respectively (Color figure online)

Full size image

For EPm1, the truck was systematically driven around a field at Cockle Park Farm (indicated by a red rectangle, Fig. 1b) from 10:38 (UTC time). About 2 h later, the truck left the field for a return to the main University campus by a fast southbound route (distance 30 km). On the way, the driver stopped for a break (at the village of Stannington, indicated by a blue circle in Fig. 1b) during the period from 13:00 to 13:45. For EPm2, the tractor kept moving and repeated the same bounding route around the Xiaotangshan farm (Fig. 1c), except for the period from 03:40 to 05:00 (UTC time), when the driver stopped for a break. There were trees and some huts at the side (or sometimes both sides) of the route as shown in the inserts of Fig. 1c.

Multi-GNSS receivers and configuration

Three different types of Multi-GNSS receiver were used in this study, the Leica Viva GS10 and GS15 for EPs1 and EPm1, and the Trimble NetR9 for EPm2. The Leica Viva GS10 receiver is a 555-channel Multi-GNSS receiver and can collect a range of GNSS signals (GPS L1, L2, L2C, L5; GLONASS L1, L2; BeiDou B1, B2, B3; Galileo E1, E5a, E5b, Alt-BOC, E6; and QZSS L1, L2, L5, LEX). The Leica Viva GS15 can track similar multi-frequency signals, except for Galileo E6 and BeiDou B3, and has 150 channels. Both Leica Viva GS10 and GS15 can access the Leica SmartNet service to provide a Network RTK solution with an accuracy of better than 8 mm + 0.5 ppb for horizontal components. The Trimble NetR9 has 440 channels to track multi-frequency signals from GPS, GLONASS, BeiDou, Galileo, and QZSS with RTK capabilities similar to the Leica receivers.

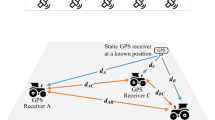
For EPs1, two Leica AS10 antennas connecting separately to Leica Viva GS10 receivers were set up on a steel bar with a fixed inter-antenna distance of 500.0 mm, and a Leica Viva GS15 antenna was set up in the middle of the bar to provide the Leica SmartNet solution (Takac and Lienhart 2008), as shown in Fig. 2a. An identical configuration was also used for EPm1 with a fixed inter-antenna distance of 763.0 mm, but the steel bar was mounted on a truck, as shown in Fig. 2b. For EPm2, two Trimble R8-4 antennas connecting to Trimble NetR9 receivers were mounted on a tractor, and the length between the two anchorage points (called baseline hereafter) was 432.0 mm (Fig. 2c). The specifications and configurations of the receivers used in this study are listed in Table 1.

Fig. 2
figure 2

Equipment configurations. (a) Leica Viva GS10 and GS15 used in Drummond Building (Newcastle upon Tyne, UK) (b) Leica Viva GS10 and GS15 used in Cockle Park Farm (Morpeth, UK), and (c) Trimble NetR9 used in Xiaotangshan Farm (Beijing, China)

Full size image
Table 1 Equipment, observation periods and the baseline lengths for the three experiments
Full size table

Multi-GNSS precise point positioning (PPP)

Precise point positioning (PPP) is a satellite positioning technique in which dual-frequency pseudo-range and carrier phase observables from a single receiver, together with precise satellite orbit and clock products, are used to determine the receiver’s precise position (Zumberger et al. 1997). For PPP, errors from a range of sources including ionospheric delay, tropospheric delay, receiver clock, multipath and measurement noises need to be carefully handled. In general, the ‘ionosphere-free’ combination of double frequency measurements is usually formed to remove the ionospheric delay, and the tropospheric delay and receiver clock offset are estimated with the site co-ordinates simultaneously. No model is available for removing the multipath errors, hence it has been left to be absorbed by the post-fit residuals. Other error sources, such as satellite and receiver antenna phase center variations (PCVs) as well as offsets (PCOs), relativistic effects, phase wind-up, earth tides, ocean loading and atmosphere loading can be corrected with appropriate models (Kouba and Héroux 2001). As the site co-ordinates and receiver clock need to be estimated, a minimum of four measurements are required. PPP can be conducted globally and is currently able to provide millimeter-level accuracy in a stationary mode and centimeter-level accuracy in a moving mode (Li and Zhang 2012). PPP has a few advantages over relative positioning techniques such as RTK: no restriction with inter-station distances, direct determination of position solution, simple data processing and global capability. As a result, PPP is widely applied to near real-time meteorology (Rocken et al. 2005; Lu et al. 2016), crustal deformation monitoring (Calais et al. 2006), orbit determination of low earth orbit satellites (Zehentner and Mayer-Gürr 2015), earthquake and tsunami monitoring and early warning (Li et al. 2013; Chen et al. 2015), and other geoscience applications.

As a satellite-based navigation and positioning system, the accuracy and reliability of GNSS PPP solutions are highly dependent on the number of visible satellites. When using GPS only, the number of visible satellites is insufficient to provide a position solution under some situations such as in urban canyons, open-pit mines, mountainous areas and tree cover areas in agriculture. With the recent revitalization of the GLONASS constellation and two newly emerging constellations of BeiDou and Galileo, it is now feasible to conduct Multi-GNSS PPP with about 80 operational satellites, increasing the number of visible satellites significantly.

The data collected in the above three experiments were analyzed using the PPP approach with the positioning and navigation data analyst (PANDA) software package (Liu and Ge 2003). The analyses were based on the sequential least squares approach (Koch 1999) and performed independently with GPS-only or Multi-GNSS measurements (GPS, GLONASS, Galileo and BeiDou). Among the four systems, GPS can provide the best individual solution due to the larger number of satellites in orbit, as well as the best quality of orbit and clock products. Hence, in this study, GPS was used to assess the PPP performance of a single system, whilst a combination of GPS, GLONASS, BeiDou and Galileo was employed to assess the PPP performance with multiple systems. GNSS data were processed in a post-mission mode, and the GFZ final orbit and 30 s clock products of IGS Multi-GNSS Experiment (MGEX) were used. For Multi-GNSS PPP, additional inter-system bias (ISB) and inter-frequency bias (IFB) parameters also needed to be estimated, as those parameters are used to account for the signal biases of different GNSS systems or frequencies. Table 2 presents the data processing strategy in detail.

Table 2 Data processing strategies and models for Multi-GNSS PPP
Full size table

‘Precision’ and ‘accuracy’ are often used to describe how good the position acquired by the GNSS actually is. These terms are technically different as ‘precision’ refers to the closeness to the mean observation and ‘accuracy’ refers to truth. Usually, the precision has been obtained and is used as no absolute truth is available. In order to assess the accuracy achieved by PPP, two receivers were set up on the steel bar as described above (Fig. 1) with a fixed, precisely known, inter-antenna distance in each experiment. After performing PPP for each receiver, the co-ordinates of each could be obtained to compute the length of the inter-antenna distance (referred as baseline length hereafter), which can be compared with the truth. Hence, the Root Mean Square Error (RMSE) and standard derivation (Stdev) of this dataset are used to describe the accuracy and precision of PPP, respectively in this study.

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {b_{i} - \tilde{b}} \right)^{2} } }$$
(1)
$$Stdev = \sqrt {\frac{1}{n - 1}\sum\limits_{i = 1}^{n} {\left( {b_{i} - b_{avg} } \right)^{2} } }$$
(2)
$$b_{avg} = \frac{1}{n}\sum\limits_{i = 1}^{n} {b_{i} }$$
(3)

where \(b_{i}\) is the derived length of baseline for the epoch i, \(\tilde{b}\) is the precisely known inter-antenna distance, \(b_{avg}\) is the mean of the baseline length, \(n\) is the number of epochs. As the baseline length was obtained by differencing two receivers’ co-ordinates, the RMSE will be \(\sqrt 6\) times the 1D accuracy of PPP co-ordinates, given the same errors for 1D PPP co-ordinates of the two receivers at either end of the baseline. In addition, as the RTK solution could be obtained by the Leica Viva GS15 receiver in EPs1, the PPP derived co-ordinates of the antennae at either end of the bar can also be used to derive the positions of the Leica Viva GS15 antenna and compare with Leica SmartNet RTK solutions, thus assessing the precision of PPP.

Results and discussion

Stationary experiment

Figure 3a shows the number of visible satellites for each GNSS system (i.e. GPS (G), GLONASS (R), Galileo (E), and BeiDou (C)) as well as the total number of all GNSS systems (G + R+E + C) for EPs1. Up to three Galileo satellites were tracked, but one was only observed for a quite short period (about 1 min). Similarly, only two BeiDou satellites were tracked, as BeiDou provided best coverage in the Asia–Pacific region at the time of this experiment. Although more than 8 GPS satellites were observed in most periods of the experiment, there was only one satellite available during the beginning 10 min (14:54:10–15:04:07). More than 4 GLONASS satellites were tracked, and the number gradually increased to 7. In sum, no more than 9 satellites were tracked during the first 10 min, and half of them were GLONASS satellites. After that, at least 16 satellites were observed. Figure 3b shows the PDOP (Positioning Dilution of Precision) values for positioning with GPS, GLONASS and Multi-GNSS systems. No PDOP of BeiDou or Galileo is included in Fig. 3b due to the insufficient number of satellites (< 4 for both systems). Similarly, there were no PDOP values for GPS only PPP in the first 10 min, as only one GPS satellite was tracked. In general, the GPS PDOP values mainly varied between 1.5 and 4 m, while the GLONASS PDOP values were about 2–6 m. However, once all satellites were used, the PDOP values significantly reduced, to 1.5 m or lower. In particular, thanks to the contribution from GLONASS, a positioning solution was possible for the first 10 min. These enhancements suggest a definite advantage of Multi-GNSS over a single system. A high correlation between PDOP and the number of satellites could be easily observed: the more satellites, the lower PDOP can be.

Fig. 3
figure 3

The number of tracked satellites (a) and PDOP (b) for EPs1. The number of GPS (G), GLONASS (R), Galileo (E), BeiDou (C), and all satellites (G + R+E + C) are shown in dark blue, blue, cyan, green, and orange lines, respectively, and the same for PDOP (Color figure online)

Full size image

Three PPP solutions were obtained, by using GPS (GPS-only), GPS and GLONASS (GPS + GLONASS), and quad-constellation (ALL) measurements for EPs1, respectively. Figure 4 shows the derived epoch-wise baseline lengths from the three different PPP solutions, and the corresponding statistical results are listed in Table 3. It should be noted that there was no solution for GPS PPP during the period from 14:54:10 to 15:04:07, as there was only one GPS satellite tracked by the receiver. Compared with the GPS/GLONASS and four-system combined solutions, the GPS solution showed the lowest repeatability and precision, as indicated by the calculated standard deviation (Stdev). There was an increasing trend for the epoch-wise baseline lengths, and it was caused by the change of observation geometry. Once the GLONASS satellites were added, the positioning could be obtained for the first 10 min, as the number of tracked satellites increased to 6 (Fig. 3a). The position repeatability was also improved, as the Stdev decreased from 19.0 mm to 12.0 mm. A sudden change occurred around 15:04:07 when many more GPS satellites became visible. For the four-system combined solution (ALL), the peak-to-peak variation was below 40.0 mm with a Stdev of 6.0 mm; and the change occurred at 15:04:07 but it was smaller due to better constraints from the BeiDou and Galileo satellites. The mean baseline length of GPS solution (491.0 mm) was closest to the truth (500.0 mm); almost the same value was obtained by the four-system combined solution (490.0 mm), and it was 487.0 mm for GPS/GLONASS combined solution. However, the GPS solution has the lowest accuracy (62.0 mm), and this was improved to 41.0 and 34.0 mm, respectively by using GPS/GLONASS, or all GNSS systems for PPP. Hence, the 1D accuracy reached to 13.9 mm (\(\approx 34.0/\sqrt 6\) mm) under the above mentioned assumption, and the corresponding horizontal accuracy was about 19.6 mm (\(\approx 34.0/\sqrt 3\) mm). Thus, the PPP probably meets the positioning requirement of PA.

Fig. 4
figure 4

The epoch-wise length of baseline derived from GPS (GPS-only, blue), GPS and GLONASS (GPS + GLONASS, green), and quad-constellation combined (ALL, red) PPP solutions for EPs1 (Color figure online)

Full size image
Table 3 Statistical results for the three experiments (unit: m)
Full size table

As the raw data were not recorded for the Leica Viva GS15 receiver during experiments EPs1 and EPm1, positioning directly derived from PPP was impossible. However, as it was located in the middle of the two Leica Viva GS10 receivers, its epoch-wise co-ordinates could be obtained by simply averaging the PPP solutions from the two GS10 Viva receivers. In that case, the derived positions could be compared with the Leica SmartNet RTK solution. Figure 5 illustrates the corresponding co-ordinate differences between RTK and quad-constellation PPP solutions in the east (E), north (N) and up (U) components, and the statistical results are listed in Table 4. In general, the differences were quite stable, except for the discontinuity that occurred around 15:53:00 in the up component. This was caused by the jump in the estimated troposphere delays of PPP, estimated as a piece-wise constant every 1 h. Once only one troposphere parameter was estimated, the bias disappeared (Fig. 5b). Systematic biases between the Leica SmartNet RTK and Multi-GNSS PPP solutions can be observed in both horizontal and vertical components for two reasons. Firstly, these two solutions were in two different reference frames. The RTK solution was in the WGS84 frame, whereas the PPP solution was in the IGb08 frame. Secondly, the unmeasured offset between the reference point of Leica GS15 antenna and mounted point on the bar biased the solutions. However, once the biases are removed, the two solutions are in good agreement with Stdev of about 6.0, 7.0, and 32.0 mm in the east, north and up components, respectively. This further confirms that Multi-GNSS PPP can have a similar positioning accuracy to RTK, at least in a stationary mode.

Fig. 5
figure 5

The co-ordinate differences between RTK and quad-constellation combined PPP solution in East (E, blue), North (N, green), and Up (U, red) component by estimating piece-wise constant troposphere in each 1 h (a) or only one constant troposphere (b) (Color figure online)

Full size image
Table 4 Statistical results for the co-ordinate differences between RTK and PPP solutions for the stationary experiment (unit: m)
Full size table

This stationary experiment suggests that centimeter level accuracy can be achieved by the PPP approach. In addition, Multi-GNSS can not only improve the repeatability of PPP, but also make positioning possible when a limited number of satellites from a single GNSS system have been tracked.

Multi-GNSS moving experiments

Like the stationary experiment, Multi-GNSS has positive impacts on improving the accuracy and reliability of PPP. For EPm1, there were no more than 3 Galileo satellites observed (Fig. 6). However, up to four BeiDou satellites were tracked throughout most of the experiment. For the period when the truck was in the field or stopped at Stannington, at least 6 GLONASS and 7 GPS satellites were observed. However, the number of tracked satellites varied significantly on the road southwards due to the obstruction of trees and constructions. In sum, more than 18 satellites could be used for positioning when the truck was in the field or stopped at Stannington, but most of the GNSS satellites were obstructed when the truck was on the road. High correlation between PDOP and the number of tracked satellites was also identified. Similar to EPs1, the smallest PDOP were obtained once all tracked satellites were used for PPP, whereas it was measured as 1.5–4 m and 2–6 m for GPS and GLONASS-only solutions respectively. Although more than four satellites were available for the obstruction period, the PDOP values fluctuated significantly and it was difficult (if not impossible) to determine the co-ordinates even using Multi-GNSS satellites. Hence, in this study, only the data when the truck was in the field was selected for further analysis.

Fig. 6
figure 6

The number of tracked satellites (a) and PDOP (b) for EPm1. The number of GPS (G), GLONASS (R), Galileo (E), BeiDou (C), and all satellites (G + R+E + C) are shown in dark blue, blue, cyan, green, and orange lines, respectively, and the same for PDOP (Color figure online)

Full size image

Figure 7 shows two PPP solutions for EPm1, one using GPS (GPS-only) and the other with quad-constellation (ALL) measurements. The corresponding statistical results presented in Table 3, suggest similar performances for both PPP solutions in general. The Stdev was only 11.0 mm for both solutions, while the differences of mean values compared to the true length of baseline were 5.0 mm and 4.0 mm for GPS-only and Multi-GNSS solution, respectively. The four-system combined solution (12.0 mm) had slightly higher accuracy than that of the GPS-only solution (13.0 mm). In addition, for the period when the tractor stopped from about 10:51–11:22, the Multi-GNSS solution showed less variation and higher accuracy compared with the GPS-only solution.

Fig. 7
figure 7

The epoch-wise length of baseline derived from GPS-only (blue), and Multi-GNSS (ALL, red) PPP solutions for EPm1 (Color figure online)

Full size image

Whilst experiments EPs1 and EPm1 were carried out in the UK, EPm2 was conducted in China. Up to 10 BeiDou satellites were tracked, including GEO and IGSO satellites (Fig. 8). Similar to the other two experiments, both GPS and GLONASS satellites had good visibility, each with 7 or more satellites, particularly when the tractor stopped for its break. The total number of all the tracked satellites was up to 26 with periodic variations, because the tractor repeated the same route and GNSS signals were regularly obstructed by trees and buildings along the roads in the west and south (Fig. 3c). However, different from EPm1, at least eight satellites were available to ensure the reliability and robustness of GNSS PPP solutions even in the obstructed period, and the PDOP was less than 4 m for the Multi-GNSS combined solution.

Fig. 8
figure 8

The number of tracked satellites (a) and PDOP (b) for EPm2. The number of GPS (G), GLONASS (R), BeiDou (C), and all satellites (G + R+C) are shown in dark blue, blue, green, and orange lines, respectively, and the same for PDOP (Color figure online)

Full size image

Two PPP solutions were obtained by using GPS (GPS-only) and Multi-GNSS (ALL) measurements for EPm2, respectively. The epoch-wise lengths of baseline obtained are plotted in Fig. 9, and the corresponding statistical results are in Table 3. It can be seen that the GPS-only solution showed more obvious variation than the Multi-GNSS solution. Furthermore, many discontinuities can be observed in the GPS-only solutions when the tractor moved, as the GPS signals were obstructed by the trees and buildings along the road. Once the Multi-GNSS observations were used, much more stable results were obtained, and the jumps were reduced significantly with the Stdev decreasing from 110.0 to 48.0 mm. The difference of mean to the truth of the baseline length was reduced to 3.0 mm from 62.0 mm by using Multi-GNSS observations. The accuracy of baseline measurement reached 35.0 mm (equivalent to 20.2 mm (\(\approx 35.0/\sqrt 3\) mm) accuracy in the horizontal direction and 14.3 mm (\(\approx 35.0/\sqrt 6\) mm) in 1D) with about 4 times improvement compared to the GPS only solution (126.0 mm). This demonstrates the superiority of Multi-GNSS PPP over a single system, the accuracy and stability of positioning could be improved by using such Multi-GNSS signals, particularly with some obstructions.

Fig. 9
figure 9

The epoch-wise length of baseline derived from GPS-only (blue), and Multi-GNSS (ALL, red) PPP solutions (Color figure online)

Full size image

From the moving test results, Multi-GNSS improved the satellite availability and then enhanced the accuracy and stability of positioning better than the single-GNSS PPP, notably where there were obstructions to GNSS satellites such as in mountainous or highly urbanized areas. In addition, the precision of baseline was also at centimetre level, which can be compared with that of RTK. Therefore, Multi-GNSS can be an option for agricultural users for high accuracy requirement applications in precision agriculture.

Conclusions

In this study, the performance and feasibility of PPP with Multi-GNSS systems in PA were assessed with one stationary and two moving experiments. The following concluding remarks can be drawn from this study:

  • The number of Multi-GNSS satellites tracked was higher than the single-GNSS under both stationary and moving conditions.

  • Multi-GNSS PPP showed better precision compared to that of PPP with a single GNSS system where there are obstructions to GNSS satellites.

  • Multi-GNSS PPP showed better repeatability in all experiments compared to that of PPP with a single GNSS system. Hence, it has potential to work in conditions with poor visibility.

  • The tests have also demonstrated that an accuracy of better than 20 mm in 1D can be achieved by GNSS PPP for both stationary and moving conditions. The accuracy can be compared with that of RTK. However, the accuracy of a RTK solution is dependent on the distance between the rover and reference station, and the shorter the inter-station distance, the better position results can be obtained. For RTK GNSS, a dense reference station network is required to ensure its accuracy and reliability, which will inevitably increase the infrastructure cost and service fees. In contrast, GNSS PPP only needs precise orbit and clock products, which can be obtained from IGS or other institutions freely, and does not require access to observations from reference stations. Hence, PPP has higher flexibility and lower capital and running cost, and similar accuracy can be obtained globally.

Precise position is demanded in diverse precision agricultural applications. The above results have demonstrated that centimeter level can be achieved with GNSS PPP. It is believed that, due to its effectiveness and low cost, PPP will be a great opportunity for agriculture, meeting the high accuracy requirement in PA in the near future.