Integrating super resolution mapping and SEBS modeling for evapotranspiration mapping at the field scale

Abstract

This study addresses the use of super resolution mapping (SRM) for precision agriculture. SRM was applied to a high resolution GeoEye image of a vineyard in Iran with the aim to determine the actual evapotranspiration (AET) and potential evapotranspiration (PET). The Surface Energy Balance System applied for that purpose requires the use of a thermal band, provided by a Landsat TM image of a 30 m resolution. Image fusion downscaled that information towards the 0.5 by 0.5 m² scale level. The geometry was validated with an UltraCam aerial photo. Grape trees in the vineyard were planted in rows and three levels were distinguished: the field, rows and individual trees. AET values thus obtained ranged within rows from 5.32 (SD = 0.26) to 5.39 (SD = 0.24), whereas values for individual plants ranged from 5.29 (SD = 0.22) through 5.33 (SD = 0.39) to 5.36 (SD = 0.23). The study showed that AET values were obtained close to 5.71 mm day⁻¹ derived by standard calculations at the field scale, but spatial variability was clearly present. The study concluded that modern satellite derived information in combination with recently developed image analysis methods is able to provide reliable AET values at the row level, but not yet for every individual grape tree.

Introduction

Precision agriculture (PA) is a relatively new and advanced form of agriculture that emerged as a concept in the nineteen nineties (Bouma 1997). It allows farmers to manage their crops by maximizing the cost-benefit ratio in terms of field variation (Brisco et al. 1998). Good management depends upon collecting timely and precise information about the status of crops and resources. Remote sensing (RS) tools can be useful in this respect. In particular, PA benefits from integrating advanced geomatical technologies such as a Global Positioning System (GPS), a geospatial information system (GIS) and RS products in supporting agricultural activities. PA aims at providing the optimal management strategy with multiple sources to support farm managers and decision makers such as crop water requirement related to the adoption of a proper policy on available agricultural area. Crop water requirements are to be assessed, evaluated and managed on the basis of modeling, and in this way it is affected by uncertainty (Zhang et al. 2002).

Nowadays, the management system scale is much more precise than before. The smallest unit is the plant scale or even the scale of individual leaves in contrast to traditional agriculture management system scales where the field was the smallest unit.

Determining the amount of water to be supplied to various crop types is an important management decision (Wu et al. 2012). Water deficit, defined as the difference between supply and requirement is increasingly the result of improper water resource management. An important variable in this respect is crop EvapoTranspiration (ET). Water will be lost from the crop and soil due to ET, depending upon crop type, vegetation cover and weather factors. In agricultural irrigation systems, enough water is used to compensate for crop ET; the so-called actual crop water requirement. Two types of ET can be distinguished, potential evapotranspiration (PET) and actual evapotranspiration (AET). AET is defined as the actual elimination of water from the soil surface and the plant, whereas PET is atmospheric capability to remove the water from the surface as a consequence of evaporation and transpiration (Pidwirny 2006) if crop is not faced with any water shortage.

Remotely sensed data are useful to supply crop information from satellite data. With spatial resolutions down to 0.5 m, more and more information becomes available at a very high resolution. This scale level, however, is still too coarse to be of much value at the plant scale of many crops. In this study super resolution mapping (SRM) is used to partition pixels into smaller sub-pixels in order to achieve a high spatial resolution image from a coarser resolution image (Atkinson 2009); (Ardila et al. 2011). SRM creates hard classification maps at a finer resolution by increasing the spatial resolution of input imagery using a spatial optimization method (Atkinson 2009). SRM takes the spatial dependency into account between neighboring pixels based on spatial distance. SRM has been proposed using diverse algorithms. Tatem et al. (2001) developed SRM with a Hopfield neural network. Verhoeye and De Wulf (2002) proposed the application of linear optimization techniques for sub-pixel mapping. Mertens et al. (2003) applied genetic algorithms in SRM. Boucher and Kyriakidis (2006) implemented indicator kriging in SRM to evaluate the spatial variability of classes. Kasetkasem et al. (2005) introduced SRM based on Markov random field (MRF). Tolpekin and Stein (2009) adapted SRM based MRF to variation in class separability. Lopez (Ardila et al. 2011) proposed MRF based SRM for identification of urban trees in very high resolution images on the basis of an energy function, spatial smoothness, and prior and conditional probability.

This study considers the Surface Energy Balance System (SEBS) to use RS information in PA. SEBS estimates atmospheric turbulent fluxes, evaporative fraction and actual ET using satellite image data and meteorological information (Su 2002). It includes a toolbox for determining physical parameters of land surface such as albedo, land surface emissivity and land surface temperature (LST) from spectral radiance and reflectance measurements of satellite earth observation data.

PA in Iran is in its infancy, and possibly much can be gained from further development and applications. An interesting crop is the grape tree. It is grown in the Northern part of Iran, close to the Caspian Sea. In that area water is scarce and optimal water application is required to maintain and possibly increase productivity. Water application is commonly done at the field scale. Grape trees, however, are planted in rows and the question was raised whether PA can benefit from RS imagery at the row level, or even at the individual plant level. In this way, the scarce water could be applied at those locations where it was maximally beneficial.

Remotely sensed observations and management scale practices do not fully coincide yet. High spatial resolution satellite images can be used to identify the contours of relatively large individual plants and study their spatial characteristics, but the spatial resolution is still too coarse to extract information that is relevant for PA. In this study we explore location and spectral information of individual plants at it was extracted by SRM based on MRF of a very high resolution image. We focused on obtaining crop water requirement, and applied SEBS at coarse resolution images to retrieve the actual information.

The objective of this research was to investigate to which degree current RS images can be of help in PA. The aim is to obtain high resolution information on the basis of rows and individual plants of vineyard from images of coarse spatial and spectral resolution.

Study area and data

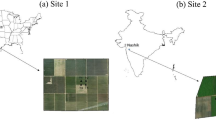
The study area is a vineyard with geographical coordinates 36°11′21″N, 50°13′19″E, located close to the city of Sharifabad, in the center of the Qazvin province North-western Iran. In this region, water is scarce and ground water level is lowering every year by approximately 80 cm. The area is an open homogeneous land planted with grape trees and is also referred to as an industrial type agricultural field (Fig. 1). Gardens and agricultural fields like vineyards are abundant in this region. The main reason of focusing on grape trees is the economic importance of grape fruit and potential capacity of RS based information in assessing the crop water requirement at row and possibly at plant levels. The selected field consists of grape trees planted in 22 rows. The length of each row is 40 m and there are 16 plants per row, the distance between trees in a row is 2 m, whereas the plant diameter is approximately 60 cm. The growing season of grape trees takes place between spring and leaf fall in autumn. That means the growing season starts from April until October for both traditional and industrial grape trees. The study period is selected such that grape trees are in the mid-season of growing and that interlocks between canopy covers in rows can be observed.

Fig. 1

The study area located in the Northern part of Iran. a The GeoEye satellite image at 2 m multispectral and a 0.5 m panchromatic resolution. b The Landsat 5 TM image at 30 m resolution. c The UltraCam digital aerial photo at 14 cm resolution

Remote sensing imagery

Three types of images were obtained from this field: a GeoEye satellite image, an UltraCam digital aerial photo and a Landsat 5 TM satellite image (Fig. 1). GeoEye-1 is a high resolution satellite image of a 0.41 m spatial resolution in panchromatic mode and 1.65 m in multispectral mode. The GeoEye image provides both image products as panchromatic images and multispectral images separately as well as simultaneously as a panchromatic and multispectral (pan-sharpened) product. A four band pan-sharpened, multispectral image and a panchromatic GeoEye image were collected for the study area on June 19, 2011. Images were projected in Universal Transfer Mercator (UTM) with the standard spheroidal reference surface WGS 84. A panchromatic image and multispectral images of GeoEye are very well co-registered. A Landsat 5 TM image was taken on August 1, 2011 (Fig. 1) which has seven multispectral bands such as the visible (from 0.45 to 0.69 µm), near infrared (from 0.76 to 0.90 µm), middle infrared (from 1.55 to 1.75 and 2.08 to 2.35 µm) and a resampled thermal band (from 10.40 to 12.5 µm), all at a 30 m spatial resolution. For atmospheric correction of the Landsat image, the simplified method in the atmospheric correction (SMAC) is used (Rahman and Dedieu 1994). An UltraCam digital aerial photo was taken on July 17, 2012 at 0.14 m ground resolution in the visible and near infrared multispectral range. The digital photo was taken by a high resolution multichannel RGBI sensor on an airborne platform at a 6 µm physical pixel size. The digital aerial photo was orthorectified to eliminate camera tilt, lens distortion and topographic correction. To overlay the aerial photo with the GeoEye satellite image, it was georeferenced using ground control points (GCPs) extracted from the GeoEye satellite image, using the GeoEye image as the master image for geo-registration (Fig. 1).

Meteorological data

A main issue in PA is to indicate the water stress with respect to the ET. For this purpose the SEBS model presented below has been used at rows and individual pixels in the field. Variability of ET depends upon crop-, soil-, water-, management and weather-related variables. Weather data were collected by the Qazvin weather station during a day of August 1, 2011. The weather station with coordinates 36°15′00″ N, 50°30′00″ E is located at approximately 17 km north of the city of Qazvin (Table 1). Recorded weather data include the maximum and minimum temperature, wind speed, sunshine hours, air pressure and humidity.

Table 1 The ground meteorological data (at the Qazvin weather station). Time of recording information is at 6 am GMT

Field data

For the field data, we considered a field, denoted by F, of 3040 m². In this field, grape trees were planted in 22 rows, labeled as $R_{1} , \ldots ,R_{22}$, each row containing 16 plants. This field was selected as it had regularly spaced grape trees, and had a shared coverage in both GeoEye satellite image and UltraCam photo. Visual interpretation was based on the UltraCam image, whereas the Geoeye panchromatic image was applied to delineate individual plants and create reference data for validation (Fig. 2). Delineating plants was not possible for some rows and plants because several plants were not pruned, resulting in an interlock between them. To study the effects of SRM in more detail a subset R = {R ₁₅ , R ₁₆ , R ₁₇ } of three rows was identified with relatively little interlock. Within $R_{16}$ we defined the subset P = $\{ P_{1} , P_{2} , P_{3} \}$ consisting of three individual plants that had relatively low coverage, so that only a few interlocks occurred between canopies of the plants.

Fig. 2

Identification of three individual plants as the subset P: a from the GeoEye panchromatic image and b as reference polygons from the aerial photo (Color figure online)

Methodology

The methodology of this research is divided into three stages. The first step uses MRF based SRM to detect rows and plants within rows. The second step uses SEBS to determine the ET at a rather coarse level (30 m resolution). The third step applies image fusion to integrate the results from SEBS and SRM to assess the ET at row and plant levels to support PA.

Super resolution mapping based on Markov random field

We consider a coarse resolution multispectral image $y$ of $M \times N$ pixels and a fine resolution multispectral image $x$. $S$ is the scale factor between $y$ and $x$ as ratio of pixel size where pixel is modeled with square footprint whereas the pixel size is the side of the square. If S is integer, then each pixel $y$ contains $S^{2}$ pixels from $x$, whereas if $S$ is non-integer that number may vary. It is assumed that $x$ only contains pure pixels whereas $y$ also contains mixed pixels. A pixel in y is represented as b _i (i.e., $i \in \left\{ {1, \ldots ,M \times N} \right\}$) and a pixel in $x$ as $a_{i|j}$, where the notation i|j indicates that the center of the pixel is inside the footprint of pixel $b_{i}$. If the footprint of b _i contains $W(b_{i} )$ centroids of a _i|j then a general equation expressing the relation between $x$ and $y$ is represented as a weighted average with weights θ _j equals:

$$ y(b_{i} ) = \frac{1}{{W\left( {b_{i} } \right)}}\mathop \sum \limits_{j = 1}^{{W\left( {b_{i} } \right)}} \theta_{j} x\left( {a_{i|j} } \right). $$

(1)

For integer valued S and aligned grids of $a$ and $b$, $W\left( {b_{i} } \right)$ = S ² pixels a _i|j compose b _i , whereas for non-integer valued S, fractions of a _i|j compose b _i and $W\left( {b_{i} } \right)$ can have various values between [S]² and ([S] + 1)², with [S] denoting the integer part of S. It is convenient to choose a grid of $a$ to match the direction of rows in R, whereas in practice grid b is not aligned with the rows in R. To deal with misaligned grids we use geographic coordinates to relate b _i and a _i|j . For each pixel b _i , thus all pixels $a_{i|j}$ with centroid in b _i are identified.

In (1) we do not further explore weighing of the sub-pixels, and take $\theta_{j} = 1$ throughout. MRF as a contextual classification method uses the spatial dependence between finer scale pixels ($a$) to assign class label $c\left( {a_{i|j} } \right)$ to each $a_{i|j}$ at the finer scale image. The label set is denoted by L whereas $c$ is a super-resolution map. In MRF, a context is prior information that is used when constructing the global energy in a Bayesian way. MRF can be specified by means of a Gibbs random field (GRF) (Li 2009). For super-resolution map $c$, the prior probability density function in a GRF is written as:

$$ P\left( c \right) = \frac{1}{Z}{ \exp }\left[ { - \frac{U\left( c \right)}{T}} \right], $$

(2)

where $U\left( c \right)$ is the prior energy function of $c$, $T$ is a constant termed of the temperature and $Z$ is a partition function, ensuring normalization of $P\left( c \right)$.

Let $U\left( {c\left( {a_{i|j} } \right)\left| {c\left( {D\left( {a_{i|j} } \right)} \right)} \right.} \right)$ be the local prior energy of pixel in a _i|j and let $D\left( {a_{i|j} } \right)$ be the neighborhood of pixel $a_{i|j}$. This can be expressed as $U\left( {c\left( {a_{i|j} } \right)\left| {c\left( {D\left( {a_{i|j} } \right)} \right)} \right.} \right)$ following Tolpekin and Stein (2009). This energy function takes the value zero if all neighbor pixels are assigned to the same class, whereas it takes larger value for heterogeneous class labels in $\left( {a_{i|j} } \right)$. Further, let $U\left( {x_{i} |c_{i} } \right)$ be the local conditional energy of pixel $a$ and $U\left( {c_{i} \left| {x_{i} } \right.} \right)$ the local posterior energy of the pixel $a$. The following equation expresses the posterior energy applying Bayes formula to a single pixel $a_{i|j}$:

$$ U\left( {c\left( {a_{i|j} } \right)\left| {x\left( {a_{i|j} } \right)} \right.,c\left( {D\left( {a_{i|j} } \right)} \right)} \right) = U\left( {x\left( {a_{i|j} } \right)\left| {c\left( {a_{i|j} } \right)} \right.} \right) + U\left( {c\left( {a_{i|j} } \right)\left| {c\left( {D\left( {a_{i|j} } \right)} \right)} \right.} \right). $$

(3)

Further, let $\lambda$ ($0 \le \lambda < 1$) be an MRF parameter that balances the prior and conditional energy functions and let $\lambda_{pan}$ ($0 \le \lambda_{pan} < 1$) be the likelihood energy parameter that balances the conditional energies of the multispectral and panchromatic GeoEye images. The energy function with respect to coarse resolution image $y$ and panchromatic image $q$ is then written following Ardila et al. (2011):

$$ U\left( {c\left( {a_{i|j} } \right) |c\left( {D\left( {a_{i|j} } \right)} \right),y(b_{i} ),q\left( {a_{i|j} } \right)} \right) = \lambda U\left( {c\left( {a_{i|j} } \right)\left| {c\left( {D\left( {a_{i|j} } \right)} \right)} \right.} \right) + \left( {1 - \lambda } \right)\left( {\lambda_{pan} U\left( {q\left( {a_{i|j} } \right) |c\left( {a_{i|j} } \right)} \right) + \left( {1 - \lambda_{pan} } \right)U\left( {y\left( {b_{i} } \right) |c\left( {a_{i|j} } \right)} \right)} \right). $$

(4)

The global posterior energy function is then obtained as:

$$ U\left( {c\left| {y,q} \right.} \right) = \mathop \sum \limits_{i,j} U\left( {c\left( {a_{i|j} } \right) |c\left( {D\left( {a_{i|j} } \right)} \right),y(b_{i} ),q\left( {a_{i|j} } \right)} \right). $$

(5)

The equations can be interpreted as follows. First, $x$ is not observed and we only have $y$ and $q$. The solution of MRF based SRM is then found by finding the super-resolution map $c$ that leads to the minimum of the global posterior energy function (5). To apply SRM based MRF, the posterior energy (5) is optimized in terms of smoothness parameters (λ, $\lambda_{pan}$). Our finding with the values of smoothness parameter agrees with the values of other studies Tolpekin and Stein (2009) and Ardila et al. (2011) for the same scale factor and class separability. A maximum a posteriori (MAP) estimated is then obtained by applying Simulated Annealing (SA). In order to minimize the posterior energy for estimating MAP, a convenient class label is defined for each pixel. SA reaches the highest classification accuracy and the lowest energy as compared to other algorithms (Tso and Mather 2009). It is a stochastic algorithm that includes as the annealing parameters the initial temperature $T_{0}$ and the cooling rate η$< 1$ controls the temperature reduction rate. The temperature is decreased as $T_{k + 1} = T_{k} \times \eta$. A high temperature corresponds to large randomness and thus increases the probability of labeling pixels by replacing classes with a new class of a higher energy. We set T ₀ = 3 after testing values between 0 and 3, and $\eta =$ 0.9, as taking a larger η value resulted in a high increase of the number of iterations to reach convergence for assigning class labels. Those experimentally determined values agreed with those from Tolpekin and Stein (2009). We defined two classes as canopy and soil and estimated the mean and covariance matrices of these classes. The scale factor value was set equal to four, resulting in each pixel at the SRM map having a 0.5 m spatial resolution, thus allowing a good integration of SEBS and the SRM based map.

After optimizing the smoothness parameters and the posterior energy, the appropriate class label is defined for each pixel. The application of MAP criterion ensures that the obtained SRM is optimal both with respect to the image data and with respect to the spatial configuration of land cover classes.

EvapoTranspiration

EvapoTranspiration (ET) refers to two simultaneous processes related to plant—atmosphere interaction: evaporation, being the loss of water from the soil surface, and transpiration the removal of water from wet vegetation through the atmosphere (Allen et al. 1998). Commonly, AET is distinguished from PET, where AET is the actual elimination of water from the surface, and PET is the capability of the atmosphere to remove the water from the surface as a consequence of evaporation and transpiration (Pidwirny 2006) when a crop is not faced with any water shortage. In agricultural irrigation management systems, the amount of water that is needed to maximize crop productivity, is equal to PET, and the so-called crop water stress (CWS), equals the difference between AET and PET (Pidwirny 2006):

$$ CWS = PET - AET. $$

(6)

CWS is thus the deficit, which in principle has to be supplied to crop if CWS $> 0$.

The SEBS was developed for the assessing of atmospheric turbulent fluxes and daily ET per pixel using RS data (Su 2002). The surface energy balance is written as:

$$ R_{n} = H + \lambda^{*} E + G_{0} . $$

(7)

The net radiation flux R _n is thus the sum of the sensible heat flux H which is the heat transferred between the air and surface by turbulence, the latent heat flux $\lambda^{*} E$ where $\lambda^{*}$ is the latent heat of vaporization and E is the AET. $G_{0}$ is the soil surface heat flux that is the energy for warming the subsurface of the earth, each expressed in Wm⁻². SEBS requires three sets of input data:

• 1. Land surface emissivity, albedo, temperature and the Normalized Difference Vegetation Index (NDVI) data derived from remotely sensed images. Land surface emissivity (LSE) is estimated from the visible and near infrared bands of Landsat 5 TM following Sobrino (2004). Su (2002) assumed a linear relationship between soil heat flux and net radiation. Sensible heat flux (H) is modeled by Monin–Obukhov similarity (Brutsaert 1982). Finally the daily actual ET ($ET_{daily}$, ${\text{mm day}}^{ - 1}$) is estimated as (Su 2002):

  $$ ET_{daily} = 8.64 \times 10^{7} \times \varLambda_{daily} \times \frac{{\overline{{R_{n} }} - \overline{{G_{0} }} }}{{\lambda^{*} \rho_{w} }}. $$

  (8)

  Here $\overline{{R_{n} }}$ is the daily net radiation (J m⁻² day⁻¹), $\lambda^{*}$ is the latent heat of vaporization $\left( {\lambda^{*} = \left( {2.501 - 0.00237 \times T_{air} } \right) \times 10^{6} } \right)$ (J kg⁻¹), ∧_daily is the daily average evaporative fraction that can be found in Su (2002) and $\rho_{w}$ is the density of water $(1000 {\text{kg m}}^{ - 3} )$. In addition, the soil heat flux $\overline{{G_{0} }}$ during 24 h is assumed to be small, and therefore was neglected. Further, LST is taken from the thermal band using the method by Sobrino et al. (2004), whereas the surface albedo for shortwave radiation ($\alpha$) is derived from narrowband to broadband conversion by Liang (2001). SEBS can use Landsat images with a combination of ground meteorological data as input for calculating the surface energy balance, but is not applicable to GeoEye or Ultracam images, as they do not have a thermal band.

• 2. Air pressure, humidity, temperature and wind speed data at reference height, obtained from weather stations.

• 3. Downward shortwave radiation and downward longwave radiation data that can be measured directly or can be obtained from a radiation model. The net radiation flux (R_n) is estimated by incorporating the retrieved surface emissivity, the LST and α from the Landsat 5 TM data and by the use of the downward longwave and solar radiation.

The output of SEBS is provided at spatial resolution of the thermal band of the input image (Su 2002).

In this research, SEBS is applied to estimate AET and PET on a daily basis, whereas SRM is used to detect the rows or the individual plants. To do so, the raw data of each image band is converted first to radiance and reflectance.

Image fusion for integration of actual ET and NDVI

In this research, the result of AET from SEBS from the 30 ${\text{m }}$ lower coarse resolution image was fused with the NDVI image extracted from the GeoEye satellite image. To do so, it was assumed that the NDVI at the fine resolution image includes both vegetation with a high AET and soil with a low daily AET. The Gram–Schmidt (GS) spectral sharpening (Laben and Brower 2000) was applied for image fusion of the fine scaled GeoEye image with the coarse scale Landsat image. GS consists of four steps. Step 1 simulates a coarse spatial resolution image of AET maps at 30 m spatial resolution. Step 2 performs a GS transformation on the simulated coarser resolution image. Step 3 adjusts the statistical information at the finer spatial resolution image of NDVI at 0.5 m spatial resolution and compares it with statistical information of the first transform GS providing an adapted finer resolution image. Step 4 applies the inverse GS transformation and provides the enhanced spatial resolution image. All processes were carried out following (Ha et al. 2012) in ENVI (Environment for Visualizing Image) software, developed by ITT^®.

Comparison with existing methods

We validated the SRM results from each row and individual plants using the UltraCam photo and the panchromatic image of the GeoEye satellite image respectively.

SRM is performed both at subset R, and for the three individual plants in P. A reference map displaying the rows and individual plants was created from the UltraCam digital aerial photo and the panchromatic image of GeoEye satellite image. In this process, selected rows and individual plants were presented as a red polygon (Fig. 2). The number of pixels classified inside a polygon served as a reference for the total number of classified pixels. Accuracy of SRM results was assessed using Cohen’s kappa statistics (Richards 2012).

The quality and accuracy of estimated AET determined through SEBS should be assessed in comparison with field measurements (Su 2002). However, due to the absence of in situ data, we followed a standard FAO-56 method, i.e. the FAO Penman–Monteith methodology (Allen et al. 1998) of determining daily PET and to validate the result of ET obtained from SEBS. In this process ET is estimated as follows:

$$ ET_{c} = ET_{0} \times K_{c} , $$

(9)

where $ET_{c}$ is the potential crop evapotranspiration under standard conditions, $ET_{0}$ is the ET of grass as the reference crop and $K_{c}$ is the coefficient factor for the well watered crop under optimal agronomic conditions. The $K_{c}$ is a single crop coefficient for the grape tree was chosen at the mid-season stage of crop development. PET was determined as well from meteorological data using (9) that was then compared to the assumed maximum value of AET from SEBS.

Results

SRM from the GeoEye satellite image

We begin by considering optimization of the smoothness parameters for applying SRM based MRF, λ and $\lambda_{pan}$. For subset R, values equal to λ = 0.9 and $\lambda_{pan} = 0.4$ resulted in the highest accuracy for row detection. The optimized SRM showed a much more coherent pattern of the three rows. Convergence was reached after 70 iterations, when the total energy after a reduction with more than 50 % did not decrease any further (Fig. 3). Using a $\eta = 0.95$ value, we observed the highest quality of agreement ($\kappa$ = 0.72), whereas the total energy included a local and global minimum values. This value needed 174 iterations to converge. Choosing $\eta$ = 0.9 updated the pixels and changed their classes during 63 iterations. The curve shows that the energy minimization values converged from a local minimum value equal to 7.2 to a global minimum value of 6.5. Optimization was repeated for each of the three rows individually (Fig. 4), observing slightly different structures for the rows of plants.

Fig. 3

The result of SRM based MRF for subset R with using the starting parameters S = 4 $T_{0}$ = 3 and $\eta$ = 0.9 and the optimized parameters λ = 0.9 and $\lambda_{pan}$ = 0.4; red polygons are reference data (Color figure online)

Fig. 4

Result of SRM based MRF for the three rows in subset R individually: a $R_{15}$, b $R_{16}$ and c $R_{17} ;$ red polygons are reference data (Color figure online)

Figure 5 displays the result of initial and optimized SRM for the subset P. Values of $\kappa$ were equal to 0.64, 0.60 and 0.71 respectively. Plant $P_{1}$, was covered by 18 pixels as canopy class after the initial SRM, whereas by the optimal SRM it was covered by 9 pixels. For plants $P_{2}$ and $P_{3}$ the original coverage of 22 and 17 reduced to 17–12, respectively.

Fig. 5

The initial (left) and the optimized (right) SRM results for individual plants of subset P located in $R_{16}$: a $P_{1}$, b $P_{2}$, c $P_{3}$. In the optimized results a more coherent pattern is observed that better corresponds with the red polygons as reference data (Color figure online)

Daily ET from the Landsat 5 TM satellite image

AET values around the field F with its 22 rows obtained using the RS data and the weather data in SEBS is presented in Fig. 6. Daily AET values in this field ranged from 4.50 up to 5.76 mm day⁻¹. The AET value of 5.76 mm day⁻¹ was taken as the PET value. This value is comparable to the PET derived with the FAO Penman–Monteith methodology, equal to 5.71 mm day⁻¹. Comparison of these two values shows a small difference, confirming the acceptability of SEBS. We observed that there was a lower AET variation along the top of the vineyard as compared to the bottom side.

Fig. 6

Retrieval daily AET values at a 30 m resolution based on the SEBS model overlaid with the whole field F (Color figure online)

Image fusion of AET and NDVI maps

After image fusion of the coarse resolution image (Fig. 7a) and the fine resolution image (Fig. 7b), Fig. 7c illustrates the resampled coarse resolution image as the AET values (Fig. 7b). High AET values shown as light colors appear within the rows, whereas low values, shown as dark colors, appear between the rows. Therefore, the high AET values correspond with the canopy, whereas low AET values refer to the soil between the rows. Because of the coarse resolution of the Landsat image and the high resolution of the GeoEye image, the observed pattern looks similar to the GeoEye image, whereas the values correspond with the AET values obtained from the Landsat image.

Fig. 7

The high resolution NDVI image (a), the AET image obtained from SEBS (b) and the result after image fusion (c) using the GS method

In this part, the results of applying SRM for the fused image at the 0.5 m resolution are presented first for rows 15–17 and then for three individual plants (Fig. 8). Rows are clearly identified, whereas individual plants are more difficult to separate. Table 2 indicates the results AET for R and P, respectively, where for assigning AET to each row or individual plant the mean pixel value was taken per row and individual plant. For rows we observe AET values ranging between 5.32 (SD = 0.26) and 5.39 (SD = 0.24), whereas values for individual plants the AET values ranged from 5.29 (SD = 0.22) for P₁, through 5.33 (SD = 0.39) for P₂ to 5.36 (SD = 0.23) for P₃. The standard deviation indicates the amount variation from the mean, i.e. a low sd indicates that AET values are close to the mean AET value. So, we observed that plant $P_{2}$ has the highest sd and $P_{1}$ with has the lowest sd. Furthermore, the AET value of $P_{1}$ is close to the mean AET as compared to the other individual plants and rows. Hence the main difference is, as expected, at the within-plant level. Because, $P_{2}$ is located between $P_{1}$ and $P_{3}$, the effect of extracting individual plants that was based on visual interpretation, resulted in the high sd value for $P_{2}$ as compared to $P_{1}$ and $P_{3}$. For the individual plants $P_{1} , P_{2} , P_{3}$ the AET values slightly below the FAO-56 PET value.

Fig. 8

Combination of SRM result with the actual ET a for subset R and b zooming in at subset P

Table 2 Mean AET values and their standard deviation for subareas R and P

Application of SRM and SEBS for precision agriculture

We found that rows are clearly identified, whereas individual plants are more difficult to separate. Hence, PA that is based on the satellite with the finest resolution and the use of SEBS should focus on rows rather than on plants. Spatially varying water application should therefore best be done at the row level. Application of SRM may then proceed as follows. First, the relation between the SRM produced map and the actual ET per row and individual plant is constructed. This is followed by the specification of the NDVI map as vegetation index indicates for rows and individual plants.

Discussion

In this part, the results are discussed of applying SRM based MRF for obtaining AET from SEBS as reported in the “Result” section. Further, the applicability of using SRM and the SEBS in a more general setting is discussed in detail to support the crop water requirement in PA.

An important problem for linking SEBS and SRM results concerns the resolution of the thermal band available from RS images. The Geoeye image has a high spatial resolution, whereas the Landsat 5 TM produces medium spatial resolution images. To overcome this problem, image fusion using the Gram–Schmidt (GS) method applied to increase the spatial resolution of the actual ET image from 30 m resolution to 0.5 m spatial resolution equivalent to the resolution of the SRM result. To apply downscaling, the NDVI image from the pan-sharpened GeoEye image was used. It was further assumed that vegetation in the NDVI map represents a higher AET value than the soil.

For implementing SRM based MRF, the set of training pixels for canopy and soil was chosen from the multispectral and panchromatic bands. There was a limitation for selecting land cover classes in the multispectral GeoEye image, because of the absence of variation between soil and canopy pixels. Therefore, when choosing training pixels from the soil class, we selected an area close to the area of interest. For η, Kassaye (2006) recommended values between 0.8 and 0.9 as being optimal for simple and complex scenes respectively.

The highest κ values, equal to 0.64, 0.60 and 0.71, were observed for one subset of three individual plants respectively. An important reason that relatively low accuracies are achieved is due to the use of the UltraCam digital aerial photo as reference data. The time of acquisition of the GeoEye image and the aerial photo differs by more than a year. Therefore, changes during the growing season could affect the selection of an appropriate boundary for each row and individual plants. The observed values, though, are well compatible with values of 0.73, 0.67, 0.68 and 0.54, respectively, observed e.g. by Ardila Lopez (2012) for four subsets of urban trees.

The current study is potentially useful for farmers who want to obtain information regarding the health of individual plants. The reason is that NDVI as a vegetation index is informative on general vegetation status that is in turn affected by crop stress. Hence, using SRM at the individual row and plant scale and combining that result at the 0.5 ${\text{m}}$ pixel resolution results into a 50 ${\text{cm}}$ resolution NDVI map. Farmers will thus be able to control crop health at that scale level. PA aims at providing management strategies from multiple sources to support the decision makers and farm managers with crop production (Oliver 2010). Using advanced technologies in Geomatic science such as integration RS, GIS and GPS data thus leads to an important and reproducible strategy. In particular in this study, crop water requirement was the main issue for farmers and decision makers. Farmers who want to develop a strategy for managing water supply though irrigation networks of agricultural fields can use crop water requirement derived from RS data using the SEBS model and SRM as shown in this study. Such a product helps farmers and decision makers to decide on the amount of water requirements to maximize the cost benefit ratio of crop productivity. In this study, the target area was a vineyard, and crop water requirement was studied at the plant scale. The AET map can be utilized to assess the water stress at row and plant levels, and develop strategy for irrigation and select those irrigation methods that are appropriate to use. In turn, the NDVI map can be instrumental to make a fertilization plan.

Taking the maximum AET value as the PET value we were able to estimate crop water requirement for each row and individual plants: if PET exceeds AET then water stress occurs and the crop should be irrigated. Water requirement is spatially varying for stochastic reasons. Besides there is a temporal effect on the variation of AET values during the growing season and even within a single day. Finally, different crop varieties could in principle occur. In agricultural production situations, such as those for grape trees in a vineyard area in Iran, only a single variety is cultivated. At From the AET and PET obtained in the study area, there is limited water stress on these crops and plants have to be irrigated when stress is becoming considerable.

Conclusions

The aim of this research was to achieve high resolution information on the basis of rows and individual plants of vineyard from images of coarse spatial and spectral resolution. We derived the following conclusions:

• SRM is able to provide reliable positional information of the position and the extent of plants in rows, but that the information for individual plants has a higher uncertainty.

• Evapotranspiration values provided by the standard SEBS are in good agreement with values derived by standard FAO methods.

• Further improvements are to be expected when satellite information also in the thermal band becomes available at a finer resolution.