Abstract
Previous studies have shown the importance of soil moisture (SM) in estimating crop yield potential (YP). The sensor based nitrogen (N) rate calculator (SBNRC) developed by Oklahoma State University utilizes the Normalized Difference Vegetation Index (NDVI) and the in-season estimated yield (INSEY) as the estimate of biomass to assess YP and to generate N recommendations based on estimated crop need. The objective was to investigate whether including the SM parameter into SBNRC could help to increase the accuracy of YP prediction and improve N rate recommendations. Two experimental sites (Lahoma and Perkins) in Oklahoma were established in 2006/07 and 2007/08. Wheat spectral reflectance was measured using a GreenSeeker™ 505 hand-held optical sensor (N-Tech Industries, Ukiah, CA). Soil–water content measured with matric potential 229-L sensors (Campbell Scientific, Logan, UT) was used to determine volumetric water content and fractional water index. The relationships between NDVI, INSEY and SM indices at planting and sensing at 5, 25, 60 and 75-cm depths versus grain yield (GY) were evaluated. Wheat GY, NDVI at Feekes 5 and soil WC at planting and as sensed at three depths were also analyzed for eight consecutive growing seasons (1999–2006) for Lahoma. Incorporation of SM into NDVI and INSEY calculations resulted in equally good prediction of wheat GY for all site-years. This indicates that NDVI alone was able to account for the lack of SM information and thus lower crop YP. Soil moisture data, especially at the time of sensing at the 5-cm depth could assist in refining winter wheat YP prediction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
For the major crop production systems, nitrogen use efficiency (NUE) values for most cereal crops including wheat (Triticum aestivum L.), corn (Zea mays L.) and rice (Oryza sativa L.) are estimated to be approximately 33 % worldwide (Raun and Johnson 1999). Failure to accurately assess a crop’s fertilizer requirement, ignoring the impact of spatial and temporal variability, and difficulty identifying the most appropriate timing for fertilizer application results in inefficient fertilizer management. Low NUE values in crop production are generally due to loss of applied N from the soil–plant system via various pathways including gaseous plant emission, denitrification, leaching, surface runoff and volatilization. An increase of NUE in production of three major cereal crops—wheat, maize and rice—by just 10 % would result in savings of about US $5 billion per year and substantial improvement in environmental quality (Gupta and Khosla 2012).
Grain yield (GY) is a function of combined growth factors present within a particular growing environment (Raun and Johnson 1999) and yield potential (YP) is “the yield of a cultivar when grown in environments to which it is adapted, with nutrients and water non-limiting and with pests, diseases, weeds, lodging and other stresses effectively controlled” Evans and Fischer (1999). Raun et al. (2001) emphasized that potential yield is associated with soil- and weather-specific conditions. They refer to the “highest yield obtainable in ideal conditions” as the maximum yield. Therefore, in addition to nutrient management practices, environmental factors are significantly affecting the efficiency of applied fertilizers. Soil moisture is one of the most important environmental factors that influence plant growth and development, including grain production. Soil–water content significantly affects both nutrient release from applied fertilizers and mineralization reactions (Koerselman et al. 1993). Furthermore, the changes in soil moisture regime cause variation in soil solution chemistry (Litaor 1988) and, therefore, affects uptake by plants (Aparna and Germund 2000).
It is apparent that fertilizer use efficiency is a function of available water (Fiez et al. 1994; Gutierrez-Boem and Thomas 1998). Thus, temporal variability in soil moisture (SM) clearly translates into temporal variability of crop response to N. It has been shown that crops response to N varies significantly from year to year, and that the magnitude of response is difficult to predict from 1 year to the next. This emphasizes the fact that fertilizer management decisions should be made in-season (Johnson and Raun 2003). The response index (RI) as proposed by Johnson and Raun (2003) projects the actual crop response to applied fertilizer N. Response index values help to identify responsive and non-responsive site-years and assist in determining of N fertilizer needs, and clearly demonstrate temporal dependency on GY.
Precision agriculture tools such as remote sensors enable us to evaluate crops vigor, biomass production, canopy greenness and overall plant health. Knowledge of crop nutrient status and its YP mid-season allows producers to adjust top-dress N rates accordingly. Normalized difference vegetation index (NDVI) and other indices derived from measurements of canopy reflectance have been widely used for in-season estimation of GY in various crops. Raun et al. (2001) established a non-destructive method for accurate estimation of YP using spectral measurements. Raun et al. (2002) combined mid-season YP prediction and N response using in-season estimated yield (INSEY) and RI to develop an algorithm for mid-season topdress N fertilization. Because INSEY utilizes the number of days from planting to sensing, where growing degree days were above zero (GDD > 0), it helps to account for period(s) during the cropping season with no plant growth due to low temperatures, regardless of SM status.
Previous studies have shown the importance of SM in estimating crop GY. Humphreys et al. (2004) concluded that incorporation of soil characteristics such as soil texture and SM capacity can help explain more about the growing conditions and thereby improve the accuracy of YP prediction using the INSEY approach. Kumar et al. (2006) investigated the relationship between seasonal crop water stress index (based on evapotranspiration deficits and NDVI) and sorghum GYs. They concluded that improved GY estimates could be obtained mid-season when spectral indices (i.e. NDVI) along with soil water parameters were incorporated in the model.
Several authors investigated the importance of adequate SM at different times during the growing season for maximizing crops yield. Musick et al. (1994) reported that increasing available SM at planting in wheat production systems in the U.S. southern plains appears to be just as important as irrigation during the growing season to eliminate or minimize water stress. Results by French and Schultz (1984) indicated that amount of water present within the soil profile at planting is vital in promoting GY. It also has been shown that yields can be maximized if the amount of plant available soil water is consistently adequate throughout the growing season (Irmak et al. 2002).
Another important point to consider is the potential affect of SM on soil color which in turn could affect the NDVI values. Results by Eklundh (1998) indicated that 10 and 36 % of variation in NDVI values could be explained by variation in rainfall on 10-day and monthly scales, respectively. The author noted, however, that the use of rainfall data to predict vegetative growth may be constrained by variability in soil characteristics such as soil type, soil water holding capacity, as well as rainfall duration and intensity. Eklundh (1998) pointed out the importance of more detailed research on understanding the SM-NDVI-yield relationship. Daughtry et al. (2000) suggested that changes in surface SM significantly contribute to differences in crop canopy reflectance (even for homogeneous canopies), making plant stress identification and quantification more challenging.
Improving NUE in cereal crops is a challenging task that encompasses the ability to accurately estimate a crops need for N and developing nutrient management practices that would provide the best return from fertilizer application. Precision agriculture techniques such as remote sensing for variable-rate fertilizer application and site-specific nutrient management help to maximize crop yield and improve grain quality while minimizing the negative impact of agricultural practices on the environment. Since 2002, the sensor based nitrogen rate calculator (SBNRC), an interactive on-line tool, has been offered by Oklahoma State University. The calculator was developed to help make more informed decisions regarding soil nutrient management and provides crop producers with more accurate mid-season fertilizer N recommendations tailored for many different crops (winter wheat, spring wheat, rainfed and irrigated corn, canola (Brassica napus L.), Bermuda grass (Cynodon dactylon L.), grain sorghum and rice (Oryza sativa L.)) and regions (USA, Mexico, Australia, Argentina, Canada and China). The SBNRC utilizes mid-season crop canopy reflectance measurements and other site-specific information like GDD and average maximum yield for the region to generate the appropriate fertilizer N rates. The calculator also accounts for the current fertilizer price and the projected grain price to estimate the gross return on fertilizer investment associated with the prescribed fertilizer rate. Results from long-term research and on-farm trials suggest that farmer profits can be increased by more than $4/ha in wheat production and $8/ha in corn production systems by implementation of SBNRC-derived N fertilizer top-dress rates (www.nue.okstate.edu 2012).
It is clear that SM can have a significant effect on N availability and uptake and NUE. Furthermore, SM has the potential to improve our ability to estimate crops response to N and predict YP mid-season, which would help improve N fertilizer rate recommendations. With ongoing development of advanced sensor-based tools for improving NUE, numerous methodologies are being proposed in an attempt to use both direct and indirect measurements of crop parameters to estimate crop N requirements. These methodologies often fail to account for the effect of temporal variability in environmental factors like SM, which are closely tied with temporal variability in crop yield (Raun et al. 2011). Developing a deeper understanding of the SM-GY relationship must be attained for SM parameters to be successfully used in YP prediction. When sound methodologies for practical use of the SM measurements are developed, crop producers will benefit fully from an impressive volume of historical and current SM data which is readily available from numerous sources. Considering all of the above, it appears that incorporating the SM parameter into SBNRC could help to significantly improve fertilizer N recommendations and increase NUE. The objective of this study was to determine the effect of soil profile moisture on the accuracy of YP prediction in winter wheat based on mid-season canopy reflectance.
Materials and methods
This study aimed to simulate a scenario where wheat producers would use SM data—obtained from either the closest weather station such as the Oklahoma Mesonet (OM) web site-or from a set of sensors installed in their field—in addition to crop reflectance measurements to obtain an estimate of YP and to generate topdress fertilizer N rates. This was a two-part project consisting of a field study and analysis of long-term data. Two long-term experiments were used to collect the data for the field study in 2007 and 2008: experiment 502 at the North Central Research Station (36.39°N, 98.09°W) in Lahoma, Oklahoma (established in 1971) and experiment 801—at the Cimarron Valley Agronomy Research Station in Perkins (35.98°N, 97.02°W), Oklahoma (initiated in 1996). The soil at Lahoma is a well-drained, deep and moderately permeable Grant silt loam (fine-silty, mixed, thermic Udic Argiustoll) and at Perkins—a Teller sandy loam; fine-loamy, mixed, thermic Udic Argiustoll. The treatment structures for experiments 502 and 801 are reported in Tables 1 and 2, respectively. Yield potential sub-plots—4 m2 squares that were originally setup within the plots of experiments 502 and 801 (treatments 1 through 7 at Lahoma, and treatments 3, 6, 9 and 12 at Perkins) (Tables 1, 2) to compile the records of YP equations—were used to collect soil moisture measurements, canopy reflectance readings and final winter wheat GY data.
Soil volumetric water content (WC) and fractional water index (FWI) at the time of planting (average from 15 days before to 15 days after planting) and at the time of sensing (average from 15 days before to 15 days after sensing), at 5, 25, 60 and 75-cm depths were evaluated. The SM measurements used for both the field study and long-term data analysis were derived from 229-L water matrix potential (MP) sensors manufactured by Campbell Scientific, Logan, Utah, USA. For the field study, a set of four 229-L sensors were installed prior to planting at each experimental site at depths of 5, 25, 60 and 75 cm to record SM observations. Each 229-L sensor was individually calibrated by collecting ΔT values to obtain the threshold temperature values, two temperatures were measured: ΔTmin (the wettest value obtained by saturating the ceramic matrix of a sensor in water) and ΔTmax (the driest value determined by drying the sensor ceramic matrix with a desiccant). A linear regression: TR = m * ΔT + b, where TR is referred to as the ΔTref temperature, was used to “normalize” the response of each sensor (ΔTsensor) to the response of a reference sensor. This idealized reference sensor has the following characteristics: ΔTmax = 3.96 °C, ΔTmin = 1.38 °C. The regression coefficients m and b were determined using the following equation:
and
Thus, each sensor has its own unique coefficients for normalizing its response.
Estimates of SM including: MP or WC and FWI were then derived from TR values.
The following equation was applied to determine MP
where MP is the MP (bars), TR is the ΔT reference (°C), a = 1.788, c = 0.717.
The MP values were then converted into soil water content as follows:
where WC is the soil water content on a volume basis (m3 water/m3 soil), WCr is residual water content (m3 water/m3 soil), WCs is the saturated water content (m3 water/m3 soil), a and n is empirical constants, MP is the matric (soil–water) potential (bars).
The coefficients (WCr, WCs, a and n) for each depth for each site are available from the OM database. These coefficients are influenced by the following soil properties: soil texture, bulk density, porosity, etc.
Fractional water index values were determined using the following equation:
where FWI is the FWI (unitless), TR is ΔT reference (°C), ΔTdry is 3.96 °C, ΔTwet is the 1.38 °C. All equations were obtained from Oklahoma Mesonet.
For long-term data analysis, publicly available 229-L data from Oklahoma Mesonet station #55 was closest to the experimental site (1.6 km west-southwest of Lahoma, Major County, Oklahoma). The Oklahoma Mesonet, an automated statewide system of 115 remote meteorological stations, installed a set of four MP sensors to measure SM at 5, 25 and 60 cm (Brock et al. 1995). Soil moisture observations are available within the Oklahoma Mesonet network through an interactive web site. Soil moisture data compiled by Oklahoma Mesonet contributes to research (drought studies, investigation of moisture impact on soil conditions) and public knowledge (precipitation patterns, duration and intensity, agricultural modeling) (Brock et al. 1995).
Long-term data analysis of winter wheat GY data, NDVI at the Feekes 5 growth stage, and WC was conducted for eight consecutive cropping seasons (1999 through 2006) for experiment 502 at Lahoma, Oklahoma. Soil WC was evaluated at 5, 25 and 60-cm depths for 15-day periods before and after planting and sensing.
Within each of the YP sub-plots, wheat spectral reflectance was measured using a GreenSeeker™ hand-held optical sensor at the Feekes 5 growth stage. The GreenSeeker sensor employs a patented technology to measure crop reflectance and calculate NDVI
where ρNIR is the fraction of emitted near infrared (NIR) radiation returned from the sensed area(reflectance), and ρRed is the fraction of emitted red radiation returned from the sensed area (reflectance). The INSEY values were calculated as NDVI at Feekes 5 divided by GDD > 0.
Yield potential sub-plots were harvested with a Massey Ferguson 8XP self propelled combine to record wheat GY. Grain yields were extremely low at Perkins in 2009 ranging from 8 kg ha−1 for the unfertilized check plot to 685 kg ha−1 for treatments that received 168 kg N ha−1. These low yields were due to several hail storms, including observation of baseball-sized hailstones at Perkins in the spring of 2009. Data for Perkins for the 2008–2009 growing season were not included in the analysis. The relationship of NDVI (at Feekes 5) and INSEY with winter wheat GY were analyzed. For the field study, a total of 64 combinations of NDVI and INSEY at Feekes 5 growth stage, along with SM (WC and FWI) at four depths (5, 25, 60 and 75 cm) and different times (planting and sensing periods) were evaluated to determine if SM can help to estimate winter wheat GY. For example, the following combination was evaluated: NDVI at Feekes 5 multiplied by FWI at the 5-cm depth at sensing. For long-term data analysis, the relationship of NDVI (at Feekes 5) and INSEY with winter wheat GY was assessed. Also, 24 combinations of WC at three depths (5, 25 and 60 cm) for the planting and sensing periods were obtained from the Oklahoma Mesonet database and evaluated for the relationship with winter wheat GY. For example: INSEY at Feekes 5 was multiplied by the 30-day average WC at planting for the 60-cm depth.
Results and discussion
Field study
Climate conditions
During the 2007–2008 growing season, much more abundant precipitation was observed at Lahoma compared to Perkins. Lahoma received 727 mm of precipitation—over 180 mm more than Perkins. Average air temperatures at Lahoma were more than 10 °C higher than at Perkins: 20 °C at Lahoma compared to 9 °C at Perkins (Table 3). The average air temperature at Perkins was substantially lower than the 8-year average (1999–2007) of 14 °C for this site.
A drastic difference in weather conditions was experienced at Lahoma between the 2007–2008 and 2008–2009 growing seasons. Cooler and drier conditions were experienced during the second year of the study. Precipitation received at Lahoma in 2008–2009 was 381 mm less than in 2007–2008. During the first growing season of this study (2007–2008), the average air temperature of 20 °C was substantially higher than the previous 8-year average (1999–2007) of 12 °C. The average air temperature of 10 °C at Lahoma in 2008–2009 was comparable to the 8-year average (Table 3). While average temperatures at Lahoma in 2008–2009 were comparable to those at Perkins in 2007–2008, Perkins received 200 mm more precipitation than Lahoma (Table 3).
In summary, all three site-years were very different weather wise. Lahoma in 2007–2008 was the warmest and the wettest of all site-years with its significantly warmer air temperatures compared to the 8-year average observations. While Perkins, in 2007–2008, was the coolest site-year, Lahoma in 2008–2009 was the driest compared to others.
Grain yield and NDVI
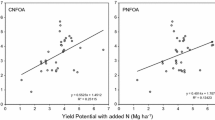
Winter wheat responded to N fertilization in that grain yields for all site-years increased with increased N rates applied (Fig. 1a–c). Specifically, 81, 99 and 91 % of GY was explained by the amount of total N applied at Lahoma in 2008, at Perkins in 2008 and at Lahoma in 2009, respectively. Grain yield, reflectance measurement and SM data were analyzed by site-year because the experimental design does not allow for proper across site-year comparison. However, the analysis yielded similar results for each site-year evaluated, which suggests a consistent trend and a high potential for robustness across site-years. In 2008, NDVI at the Feekes 5 growth stage was able to explain 82 % of variation in winter wheat GY at Lahoma (R2 = 0.82) (Fig. 2a) and 69 % at Perkins (R2 = 0.69) (Fig. 2b). Also, at Lahoma in 2009, NDVI at the Feekes 5 growth stage explained 88 % of variation in winter wheat GY (Fig. 2c). Interestingly, accounting for number of days with GDD > 0 did not help improve the accuracy of YP prediction. In particular, INSEY explained the same amount of variation in GY as NDVI. Specifically, both NDVI and INSEY explained 82, 69 and 88 % of variation in GY at Lahoma in 2008, at Perkins in 2008 and at Lahoma in 2009, respectively (data not shown). Also, for each site year, the accuracy of YP prediction was the same for all 4 evaluated depths (5, 25, 60 and 75 cm) as well as for both SM index types (FWI and WC) (data not shown).
The GreenSeeker sensor is marketed primarily as a biomass sensor, not an N-sensor. GreenSeeker reflectance measurements can be utilized to index basic nutrient response, crop condition, yield potential, water stress, and pest and disease impact in a quantitative and objective manner (www.trimble.com 2012). Sensing the crop with a GreenSeeker has been compared to a complete plant physical examination, which allows assessing the crops’ overall health and YP. Greener biomass is expected to reflect greater amounts of NIR light than in the visible range. In water-limited conditions, as plants experience water-stress significantly less light in the NIR range is reflected. This was the case at Lahoma, where GreenSeeker NDVI was a better predictor of final winter wheat GY in the dry site-year (2008–2009); it indicated that NDVI values accurately reflected the lack of SM and, in turn, lower winter wheat YP due to water stress.
Long-term data analysis
Figure 3a shows that NDVI alone at the Feekes 5 growth stage was correlated with winter wheat GY (R2 = 0.44). When WC at the 5-cm depth at planting was used (NDVI multiplied by WC at 5 cm at planting), the relationship with winter wheat GY was improved significantly (R2 = 0.93) over using NDVI alone (Fig. 3b). In fact, WC at 5 cm at planting delivered the best improvement in accuracy of YP prediction compared to all other indices (data not shown). Incorporating WC at the 5-cm depth at sensing substantially increased the relationship with GY compared to using NDVI alone. Fifty-two percent of the variation in winter wheat GY was explained by NDVI multiplied by WC at 5-cm depth at sensing (Fig. 3c). As illustrated in Fig. 4a, INSEY explained approximately 30 % of the variation in winter wheat GY. Incorporating WC at the 5-cm depth, at sensing, greatly improved the relationship with GY. Over 60 % of the variation in GY was explained by the INSEY multiplied by WC at 5-cm depth at sensing (Fig. 4b).
Relationship between NDVI at Feekes 5 growth stage and winter wheat grain yield (a), between NDVI at Feekes 5 growth stage multiplied by volumetric soil water content at the 5-cm depth at the time of planting and winter wheat grain yield (b), and between NDVI at Feekes 5 growth stage multiplied by volumetric soil water content at the 5-cm depth at the time of sensing and winter wheat grain yield (c), Lahoma, OK, 1999–2006
Analysis of long-term GY, NDVI and INSEY data confirmed that NDVI and INSEY can be used to estimate YP in winter wheat (Figs. 3 and 4). Also, analysis of this particular data set suggests that SM, especially at the 5-cm depth at planting and sensing, along with using the number of days where GDD > 0, could further improve the accuracy of YP prediction. Using the number of days from planting to sensing where GDD > 0 is intended to account for those days where growth was not possible due to low temperatures. It is important to note that for days when the temperature is not a limiting factor, plant growth could be still restricted by other environmental conditions, such as lack of plant available SM. The results suggest that three indices: NDVI multiplied by WC at 5-cm depth at planting, NDVI multiplied by WC at 5-cm depth at sensing and INSEY multiplied by WC at 5-cm depth at sensing have the greatest potential to increase the accuracy of YP estimation in winter wheat.
Notably, all indices that helped to improve the relationship with GY incorporated WC at the 5-cm depth. This indicates the particular importance of adequate SM within the top 5 cm of soil for winter wheat. Winter wheat has a primary root system and a fibrous root system that develops throughout the growing season. Fibrous roots develop from nodes at or near the soil surface. As these fine roots grow, crop water and nutrient uptake surface increases accordingly. While root depth and density are affected by soil water availability and the presence of nutrients and oxygen in the soil, the active rooting depth in winter wheat can reach up to 1.2 m. Water uptake is related to wheat root density. However, the volume of water uptake decreases significantly with soil depth. In fact, the majority of total water uptake (up to 60 %) occurs in the first 30 cm of soil (FAO 2010). Also, moisture within the top layers of soil is probably the most variable because it is most affected by environmental changes. The top layers of soil are the first to become saturated during a rainfall event, and also the first to dry out during dry periods. Thus, the results of the long-term data analysis are consistent with the concept that fine fibrous roots located near the soil surface play the key role in water uptake in winter wheat. In conclusion, knowledge of soil water status at the time of sensing and planting, especially at the 5-cm depth, could assist in winter wheat YP prediction, which, in turn, could result in improved fertilizer N rate recommendations and increased NUE in wheat production systems.
Conclusions
Considering both long-term data analysis and field study results, we can conclude the following. First, NDVI and INSEY can be utilized as predictors of GY in winter wheat. Second, SM can help to significantly improve the accuracy of YP prediction in winter wheat. In this study, the incorporation of number of days where GDD > 0, did not improve the accuracy of YP prediction. This emphasizes the point that on the days that the temperature is not a limiting factor, plant growth could still be restricted by other environmental conditions such as lack of plant available SM.
Results from this field study showed that all four evaluated depths delivered the same improvement in YP prediction accuracy, suggesting that SM data at all depths was equally important. On the other hand, the analysis of long-term data clearly showed that SM data at the 5-cm depth was more useful in estimating YP mid-season compared to other depths. Considering the fact that the long-term study presents a more comprehensive outlook on data, it is reasonable to suggest that a particular strategy, such as a single depth being more useful than other depths, could be discovered.
Overall, the results suggested that three indices—NDVI multiplied by WC at 5-cm depth at planting, NDVI multiplied by WC at 5-cm depth at sensing, and INSEY multiplied by WC at 5-cm depth at sensing—have the highest potential to increase the accuracy of YP estimation in winter wheat mid-season, which, in turn, could translate into improved NUE in wheat production systems. It follows that SM data can help improve the efficiency of N management because it substantially enhances our ability to properly address temporal and spatially variable N requirements. Including SM into the vegetation indices at the time of sensing is feasible if NDVI and SM data can be collected simultaneously. Incorporating SM parameters, especially at the time of sensing, in algorithm-based calculators such as SBNRC could help to significantly improve fertilizer N recommendations and increase NUE.
Abbreviations
- FWI:
-
Fractional water index
- INSEY:
-
In-season estimated yield
- NDVI:
-
Normalized difference vegetation index
- NUE:
-
Nitrogen use efficiency
- SBNRC:
-
Sensor based nitrogen rate calculator
- SED:
-
Standard error of the difference between two equally replicated means
- YP:
-
Yield potential
- WC:
-
Volumetric water content
References
Aparna, M., & Germund, T. (2000). Effect of wet and dry cycles in calcareous soil on mineral nutrient uptake of two grasses, Agrostis stolonifera L. and Festuca ovina L. Plant Ecology and Systematics, 224(2), 297–303.
Brock, F. V., Crawford, K. C., Elliott, R. L., Cuperus, G. W., Stadler, S. J., Johnson, H. L., et al. (1995). The Oklahoma Mesonet: A technical overview. Journal of Atmospheric and Oceanic Technology, 12(1), 5–19.
Daughtry, C. S. T., Walthall, C. L., Kim, M. S., Brown de Colstoun, E., & McMurtrey, III. J. E. (2000). Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sensing of Environment, 74(2), 229–239.
Eklundh, L. (1998). Estimating relations between AVHRR NDVI and rainfall in East Africa at 10-day and monthly time scales. Remote Sensing, 19(3), 63–570.
Evans, L. T., & Fischer, R. A. (1999). Yield potential: Its definition, measurement, and significance. Crop Science, 39(6), 1544–1551.
Fiez, T. E., Miller, B. C., & Pan, W. L. (1994). Winter wheat yield and grain protein across varied landscape positions. Agronomy Journal, 86(6), 1026–1032.
French, R. J., & Schultz, J. E. (1984). Water use efficiency of wheat in a Mediterranean-type environment. I. The relation between yield, water use and climate. Australian Journal of Agricultural Research, 35(6), 743–764.
Gupta, M.L., & Khosla, R. (2012). Precision nitrogen management and global nitrogen use efficiency. In K. Harald & G. Martha Patricia Butron (Eds.), Proceedings of the 11th International Conference on Precision Agriculture, Indianapolis, USA.
Gutierrez-Boem, F. H., & Thomas, G. W. (1998). Phosphorus nutrition affects wheat response to water deficits. Agronomy Journal, 90(2), 166–171.
Humphreys, M. T., Raun, W. R., Martin, K. L., Freeman, K. W., Johnson, G. V., & Stone, M. L. (2004). Indirect estimates of soil electrical conductivity for improved prediction of wheat grain yield. Communications in Soil Science and Plant Analysis, 35(17–18), 2639–2653.
Irmak, A., Batchelor, W. D., Jones, J. W., Irmak, S., Paz, J. O., Beck, H. W., et al. (2002). Relationship between plant available soil water and yield for explaining soybean yield variability. Applied Engineering in Agriculture, 18(4), 471–482.
Johnson, G. V., & Raun, W. R. (2003). Nitrogen response index as a guide to fertilizer management. Journal of Plant Nutrition, 26(2), 249–262.
Koerselman, W., Van Kerkhoven, M. B., & Verhoeven, J. T. A. (1993). Release of inorganic N, P and K in peat soils; effect of temperature, water level. Biogeochemistry, 20, 63–81.
Kumar, M.U., Victor, U.S., Srivastava, N.N., Sharma, K.L., Ramesh, V., Vanaja, M., et al. (2006). Use of a root zone soil moisture model and crop spectral characteristics to estimate sorghum yields in a dryland Alfisol toposequence. Proceedings of the SPIE, the International Society for Optical Engineering, Goa, India, (vol. 6411).
Litaor, M. I. (1988). Soil solution chemistry in an alpine watershed, Front Range, Colarado, USA. Arctic and Alpine Research, 20, 485–491.
Musick, J. T., Jones, O. R., Stewart, B. A., & Dusek, D. A. (1994). Water-yield relationships for irrigated and dryland wheat in the U.S. southern plains. Agronomy Journal, 86(6), 980–986.
Raun, W. R., & Johnson, G. V. (1999). Improving nitrogen use efficiency for cereal production. Agronomy Journal, 91(3), 357–363.
Raun, W. R., Solie, J. B., Johnson, G. V., Stone, M. L., Lukina, E. V., Thomason, W. E., et al. (2001). In-season prediction of potential grain yield in winter wheat using canopy reflectance. Agronomy Journal, 93(1), 131–138.
Raun, W. R., Solie, J. B., Johnson, G. V., Stone, M. L., Mullen, R. W., Freeman, K. W., et al. (2002). Improving nitrogen use efficiency in cereal grain production with optical sensing and variable rate application. Agronomy Journal, 94(4), 815–820.
Raun, W. R., Solie, J. B., & Stone, M. L. (2011). Independence of yield potential and crop nitrogen response. Precision Agriculture, 12(4), 508–518.
Nitrogen Use Efficiency web site. (2012). Introduction, sensor based N rate calculator (SBNRC). Retrieved September 7, 2012, from www.nue.okstate.edu; http://www.nue.okstate.edu/Hand_Held/SBNRC_Introduction.htm.
GreenSeeker Handheld. (2012). GreenSeeker data collection and mapping system. Retrieved September 7, 2012, from www.trimble.com; http://www.ntechindustries.com/handheld.html.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Walsh, O.S., Klatt, A.R., Solie, J.B. et al. Use of soil moisture data for refined GreenSeeker sensor based nitrogen recommendations in winter wheat (Triticum aestivum L.). Precision Agric 14, 343–356 (2013). https://doi.org/10.1007/s11119-012-9299-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11119-012-9299-9