Abstract
A mixed lattice group is a generalization of a lattice ordered group. The theory of mixed lattice semigroups dates back to the 1970s, but the corresponding theory for groups and vector spaces has been relatively unexplored. In this paper we investigate the basic structure of mixed lattice groups, and study how some of the fundamental concepts in Riesz spaces and lattice ordered groups, such as the absolute value and other related ideas, can be extended to mixed lattice groups and mixed lattice vector spaces. We also investigate ideals and study the properties of mixed lattice group homomorphisms and quotient groups. Most of the results in this paper have their analogues in the theory of Riesz spaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of mixed lattice semigroups was developed by Arsove and Leutwiler in [4,5,6,7]. Their aim was to develop an axiomatic approach to classical potential theory from a purely algebraic point of view. Their theory unified and generalized some of the earlier axiomatizations of potential theory, such as the theory of cones of potentials, developed by Mokobodzki and Sibony (see [7] and references therein), and the theory of H-cones developed by the Romanian group of mathematicians, Boboc, Bucur and Cornea [9]. These theories can be regarded as special cases of the Arsove–Leutwiler theory. Since the properties of mixed lattice semigroups had been extensively studied, it seemed natural to investigate the mixed lattice structure in the group setting. This was done by Eriksson–Bique in [10, 11]. Group extensions of mixed lattice semigroups were considered in [10], where it was shown that the mixed lattice structure is indeed preserved in such extensions. A more general definition of a mixed lattice group was given in [11], and some of the basic properties of mixed lattice groups were derived there. However, after the publication of the aforementioned papers the research on the subject has been virtually nonexistent. The purpose of the present paper is to initiate a systematic study of mixed lattice groups.
A mixed lattice group is a partially ordered Abelian group with two partial orderings. The usual supremum and infimum of two elements is replaced by unsymmetrical mixed envelopes which are formed with respect to the two partial orderings. It is then required that these mixed upper and lower envelopes exist for every pair of elements. If the two partial orderings are identical, then the mixed upper and lower envelopes become the usual supremum and infimum, and the mixed lattice group reduces to an ordinary lattice ordered group. In this sense, a mixed lattice group is a generalization of a lattice ordered group. However, due to the unsymmetrical nature of the mixed envelopes, some familiar properties of lattice ordered groups (such as the distributive laws) no longer hold in a mixed lattice group.
Since we are considering a generalization of lattice ordered groups and Riesz spaces, it is natural to begin our study by considering some of the most fundamental concepts in these structures, such as the absolute value and ideals, and examine how these concepts could be carried over to the theory of mixed lattice structures. In Sect. 2 of the present paper we give the essential definitions and results that will be needed in the subsequent sections. These include the concept of a mixed lattice vector space which has not been studied before. We also introduce a classification of mixed lattice groups based on their algebraic structure, and present some examples to illustrate the relationships between different classes of mixed lattice groups. Roughly speaking, these so-called regularity classes describe how closely the set of positive elements resembles a mixed lattice semigroup. The importance of this classification becomes apparent as we develop our theory further.
In Sect. 3 we define the generalized absolute values and derive their basic properties. The generalized absolute values are defined in terms of upper and lower parts, which are analogous to the positive and negative parts in the theory of Riesz spaces, but now we have two partial orderings which leads to two distinct upper and lower parts for each element. The fundamental identities as well as the triangle inequalities for the generalized absolute values are given in Theorems 3.2, 3.4 and 3.5. In addition to these we give some other interesting results, such as Theorem 3.6, which is the mixed lattice version of the representation of an element as a difference of two disjoint elements, a well known result in Riesz space theory. To finish Sect. 3, we study the behavior of mixed envelopes under scalar multiplication in vector spaces and the relationship between the ordinary absolute value and the generalized absolute values.
The related concept of mixed lattice ideal is introduced in Sect. 4, and some basic facts concerning ideals will be presented there. The definitions of ideals are based on the notion of order convex sets. We give characterizations of mixed lattice ideals and examine their relationship with lattice ideals.
In Sect. 5 we study homomorphisms between mixed lattice groups. First we give the fundamental characterization of mixed lattice homomorphisms (Theorem 5.2) and show that a mixed lattice homomorphism preserves the regularity properties of its domain (Theorem 5.8). We study the kernel of a mixed lattice homomorphism and show that the kernel has similar ideal properties as the kernels of Riesz homomorphisms between two Riesz spaces (Theorem 5.9). Theorem 5.10 characterizes mixed lattice isomorphisms, and in Theorem 5.13 we show that a mixed lattice semigroup homomorphism can be extended to a mixed lattice group homomorphism. The closely related idea of a quotient group is discussed in Sect. 6, where we give necessary conditions for the quotient group to be a mixed lattice group (Theorem 6.2).
Most of the concepts and results in the present paper have their counterparts in the theory of Riesz spaces and lattice ordered groups. For a comprehensive treatment of these topics, we refer to [8, 12, 15, 16]. We should point out that although the proofs of some results in this paper may appear to be similar to their counterparts in Riesz spaces, the algebraic structure of mixed lattice groups is different than the structure of Riesz spaces. In fact, many well known fundamental properties of Riesz spaces such as the commutativity of the lattice operations no longer hold in mixed lattice groups. To emphasize these differences, we will give references on Riesz spaces and lattice ordered groups at many places. Moreover, since this is a rather unexplored topic, we try to give fairly complete proofs for most results. It is our hope that this paper will serve as a good starting point for future research on mixed lattice groups and mixed lattice vector spaces.
2 Mixed lattice semigroups and groups
We begin by stating the definitions of the basic structures. Let \(({{\mathcal {S}}},+,\le )\) be a positive partially ordered Abelian semigroup with zero element. That is, we require that \(u\ge 0\) for all \(u\in {{\mathcal {S}}}\), and \(u\le v\) implies \(u+w\le v+w\). In what follows, we will also assume that the cancellation law
holds in \({{\mathcal {S}}}\). This partial order \(\le \) is called the initial order. It follows from the assumptions that the initial order has the following property.
Indeed, if the above assumptions hold then \(u+v=a+b\le a+v\), and so by (2.1) we have \(u\le a\). But by assumption \(a\le u\), so \(u=a\). A similar argument shows that \(v=b\) and (2.2) follows.
The semigroup \({{\mathcal {S}}}\) itself gives rise to another partial ordering. This intrinsic order on \({{\mathcal {S}}}\) is called the specific order, and it is defined by
Clearly, (2.3) means that \(u\succcurlyeq 0\) for all \(u\in {{\mathcal {S}}}\) (since \(u=u+0\)). Hence, if we formally use the difference notation \(v-u\) to denote the unique element that satisfies \(u+(v-u)=v\) (whenever such an element exists), then the above definition is equivalent to
but traditionally definition (2.3) is used for the specific order since there are no negative elements in \({{\mathcal {S}}}\). Note that (2.3) does not hold for the initial order, in general.
We should still verify that \(\preccurlyeq \) is a partial ordering which is compatible with the semigroup structure and satisfies (2.1). It is easy to see that \(\preccurlyeq \) is reflexive and transitive. To prove antisymmetry, assume \(u\preccurlyeq v\) and \(v\preccurlyeq u\). Then \(u=v+v'\) and \(v=u+u'\) for some \(u',v'\in {{\mathcal {S}}}\). Adding \(v'\) to the last equality gives \(u=v+v'=u+u'+v'\). As \(u'+v'\ge 0\), it follows by (2.2) that \(u'+v'=0\). But this implies that \(u'=v'=0\), again by (2.2). Hence, \(u=v\). This proves that \(\preccurlyeq \) is a partial order. Next, if \(u\preccurlyeq v\) then \(v=u+u'\) for some \(u'\in {{\mathcal {S}}}\). It follows that \(v+w=u+w+u'\) for any element \(w\in {{\mathcal {S}}}\), and so \(u+w\preccurlyeq v+w\). Conversely, if \(u+w\preccurlyeq v+w\), then \(v+w=u+w+u'\) for some \(u'\in {{\mathcal {S}}}\). Since equality is just a special case of the relation \(\le \), it follows by (2.1) that \(v=u+u'\), or equivalently \(u\preccurlyeq v\). Hence, the specific order \(\preccurlyeq \) is compatible with the semigroup structure and has the cancellation property (2.1).
If we equip the semigroup \({{\mathcal {S}}}\) with the partial order \(\preccurlyeq \), then \(({{\mathcal {S}}},+,\le ,\preccurlyeq )\) is a positive partially ordered semigroup with respect to two partial orderings \(\le \) and \(\preccurlyeq \), both satisfying (2.1). Notice that \(u\preccurlyeq v\) implies \(u\le v\) in \({{\mathcal {S}}}\), but not conversely. Moreover, it follows from positivity and (2.2) that no nonzero element of \({{\mathcal {S}}}\) has an inverse in \({{\mathcal {S}}}\). In particular, \({{\mathcal {S}}}\) cannot be a group, unless \({{\mathcal {S}}}=\{0\}\).
With these two partial orders \(\le \) and \(\preccurlyeq \) we define the mixed lower and upper envelopes

and

respectively, where the minimum and maximum are taken with respect to the initial order \(\le \), whenever they exist. The following definition was given by Arsove and Leutwiler in [7].
Definition 2.1
Let \(({{\mathcal {S}}},+,\le ,\preccurlyeq )\) be a partially ordered Abelian semigroup with zero element and two partial orders \(\le \) and \(\preccurlyeq \) such that \(u\ge 0\) for all \(u\in {{\mathcal {S}}}\) and (2.1) holds in \({{\mathcal {S}}}\), and \(\preccurlyeq \) is given by (2.3). If the mixed upper and lower envelopes  and
and  exist in \({{\mathcal {S}}}\) for all \(u,v\in {{\mathcal {S}}}\), and they satisfy the identity
exist in \({{\mathcal {S}}}\) for all \(u,v\in {{\mathcal {S}}}\), and they satisfy the identity

then \(({{\mathcal {S}}},+,\le ,\preccurlyeq )\) is called a mixed lattice semigroup.
Remark 2.2
There are other equivalent formulations for the definition of a mixed lattice semigroup given in [7]. We have chosen to use the above definition in this paper, as it is the most convenient for our purposes. We do not discuss the other possible formulations here, but we would like to remark that the additional identity in Definition 2.1 does not follow from the other assumptions and it is needed in order to make these different formulations equivalent. The existence of the mixed envelopes is not sufficient for that, and it is possible to construct a semigroup where all the other assumptions hold except the last identity in Definition 2.1. The next example clarifies this.
Example 2.3
Consider the semigroup \({{\mathcal {S}}}=\{0\}\cup [2,\infty )\) with the usual addition of real numbers. Let \(\le \) be the usual order inherited from \({{\mathbb {R}}}\) and define \(\preccurlyeq \) as the partial order induced by \({{\mathcal {S}}}\) itself, that is, \(y\succcurlyeq x\) if and only if \(y=x\) or \(y\ge x+2\). Note that this is equivalent to \(y=x+w\) for some \(w\in {{\mathcal {S}}}\). Clearly, \(\le \) and \(\preccurlyeq \) are partial orderings that are compatible with the semigroup structure of \({{\mathcal {S}}}\) and satisfy condition (2.1). Moreover, the elements  and
and  exist in \({{\mathcal {S}}}\) for all \(x,y\in {{\mathcal {S}}}\). For example, the element
exist in \({{\mathcal {S}}}\) for all \(x,y\in {{\mathcal {S}}}\). For example, the element  is given by
is given by

Thus \(({{\mathcal {S}}},+,\le ,\preccurlyeq )\) satisfies all the assumptions of Definition 2.1, except that the identity  does not hold in \({{\mathcal {S}}}\). For instance,
does not hold in \({{\mathcal {S}}}\). For instance,  . Hence \({{\mathcal {S}}}\) is not a mixed lattice semigroup.
. Hence \({{\mathcal {S}}}\) is not a mixed lattice semigroup.
Remark 2.4
The ideas introduced so far can be given a more informal description. Loosely speaking, the construction of a mixed lattice semigroup is as follows. We start with some ”initial” partially ordered Abelian semigroup \(({{\mathcal {S}}}_0,+,\le )\) with zero element (hence the term initial order), assuming that \(({{\mathcal {S}}}_0,+,\le )\) is positive with respect to \(\le \), and the cancellation property (2.1) holds. Then we take some specific subsemigroup \({{\mathcal {S}}}\) of \({{\mathcal {S}}}_0\) and define the specific order as the partial order determined by \({{\mathcal {S}}}\). Thus we end up with a semigroup \(({{\mathcal {S}}},+,\le ,\preccurlyeq )\) with two partial orders, which is then a mixed lattice semigroup, provided that all the assumptions regarding the mixed envelopes are satisfied. In this process, some elements of the initial semigroup \({{\mathcal {S}}}_0\) are ”left out” and the semigroup \({{\mathcal {S}}}\) does not contain all the original elements that are positive with respect to the initial order \(\le \), but it consists precisely of those elements that are positive with respect to the specific order \(\preccurlyeq \). Many of the examples given in this paper are also constructed in this manner.
Now we come to the topic of mixed lattice groups rather than semigroups. The following definition of a mixed lattice group was given by Eriksson–Bique in [11].
Definition 2.5
Let \(({{\mathcal {G}}},+,\le ,\preccurlyeq )\) be a partially ordered Abelian group with respect to two partial orders \(\le \) and \(\preccurlyeq \). If the mixed lower envelope  exists for all \(x,y\in {{\mathcal {G}}}\), then \(({{\mathcal {G}}},+,\le ,\preccurlyeq )\) is called a mixed lattice group.
exists for all \(x,y\in {{\mathcal {G}}}\), then \(({{\mathcal {G}}},+,\le ,\preccurlyeq )\) is called a mixed lattice group.
We note that the above definition is not as restrictive as the definition of a mixed lattice semigroup. Most importantly, the two partial orders are not required to be related in any way. Definition 2.5 also clearly shows that a lattice ordered group is a special case of a mixed lattice group. Indeed, if the two partial orderings \(\le \) and \(\preccurlyeq \) are chosen to be identical, then the mixed lattice group reduces to an ordinary lattice ordered group.
Eriksson–Bique [10] has also shown that every mixed lattice semigroup \({{\mathcal {S}}}\) can be extended to a group of formal differences of elements of \({{\mathcal {S}}}\) and the mixed lattice structure is preserved in this extension. Many important examples of mixed lattice groups arise in this way. We will now discuss this construction in more detail.
Let \({{\mathcal {S}}}\) be a mixed lattice semigroup and define an equivalence relation on \({{\mathcal {S}}}\times {{\mathcal {S}}}\) by putting
The equivalence class generated by (u, v) is denoted by [(u, v)] and the set of all equivalence classes by \([({{\mathcal {S}}},{{\mathcal {S}}})]\). We define addition in \([({{\mathcal {S}}},{{\mathcal {S}}})]\) by
Now the zero element of \([({{\mathcal {S}}},{{\mathcal {S}}})]\) is [(0, 0)] and \([(u,0)]+[(0,u)]=[(0,0)]\), and so \([(u,0)]=-[(0,u)]\) for all \(u\in {{\mathcal {S}}}\). Thus, \([({{\mathcal {S}}},{{\mathcal {S}}})]\) is a group. Next we define partial ordering by
It is not difficult to show that the addition and partial ordering are well-defined. The above definitions imply that the property
holds in \([({{\mathcal {S}}},{{\mathcal {S}}})]\), and hence \([({{\mathcal {S}}},{{\mathcal {S}}})]\) is a partially ordered group. Moreover, We observe that the sets \({{\mathcal {S}}}\) and \(\{[(u,0)]: u\in {{\mathcal {S}}}\}\) are isomorphic, so we identify [(u, 0)] with u, and similarly we identify [(0, u)] with \(-u\). We now denote this group by \([({{\mathcal {S}}},{{\mathcal {S}}})]={{\mathcal {S}}}-{{\mathcal {S}}}\) and we call \({{\mathcal {S}}}-{{\mathcal {S}}}\) the group of formal differences of elements of \({{\mathcal {S}}}\).
The specific order in \({{\mathcal {S}}}-{{\mathcal {S}}}\) is defined as
The following results are due to Eriksson–Bique.
Lemma 2.6
([10, Lemma 3.1]) The specific order in \({{\mathcal {S}}}-{{\mathcal {S}}}\) defined above is a partial order that is well-defined and compatible with the group structure of \({{\mathcal {S}}}-{{\mathcal {S}}}\). Moreover, it has the property
for \(u,v,x,y\in {{\mathcal {S}}}\).
Theorem 2.7
([10, Theorem 3.2]) Let \({{\mathcal {S}}}\) be a mixed lattice semigroup and \(u_1,u_2,v_1,v_2\in {{\mathcal {S}}}\). Then the mixed envelopes of elements \(u_1-u_2\) and \(v_1-v_2\) in \({{\mathcal {S}}}-{{\mathcal {S}}}\) exist and they are given by

and

In particular, \({{\mathcal {S}}}-{{\mathcal {S}}}\) is a mixed lattice group.
Let \({{\mathcal {G}}}\) be a mixed lattice group. The definition of the mixed envelopes implies that the inequalities

hold for all \(x,y\in {{\mathcal {G}}}\). In the sequel, we will use these inequalities without further reference. There are several other identities and calculation rules that we will apply frequently. For easy reference, we list all these fundamental properties of mixed lattice groups below. The following properties hold for all elements x, y and z in an arbitrary mixed lattice group.

Identities (P1), (P2a), (P2b) and (P3) were proved in [11, Lemma 3.1]. Note, in particular, that in a mixed lattice group (P1) is a consequence of the definitions of the mixed envelopes and the existence of negative elements, while in the definition of mixed lattice semigroup (P1) must be included as an axiom. Properties (P4), (P5a) and (P5b) are easy consequences of the definition of the mixed envelopes.
A subset \({{\mathcal {S}}}\) of \({{\mathcal {G}}}\) is said to be a mixed lattice subsemigroup in \({{\mathcal {G}}}\) if \({{\mathcal {S}}}\) is a mixed lattice semigroup and the mixed envelopes  and
and  in \({{\mathcal {S}}}\) are the same as in \({{\mathcal {G}}}\) for all \(x,y\in {{\mathcal {S}}}\). It follows from the definition of the mixed lattice semigroup that if the semigroup \({{\mathcal {U}}}=\{w\in {{\mathcal {G}}}: w\succcurlyeq 0\}\) is a mixed lattice subsemigroup in \({{\mathcal {G}}}\) then it is the largest (with respect to set inclusion) mixed lattice subsemigroup in \({{\mathcal {G}}}\).
in \({{\mathcal {S}}}\) are the same as in \({{\mathcal {G}}}\) for all \(x,y\in {{\mathcal {S}}}\). It follows from the definition of the mixed lattice semigroup that if the semigroup \({{\mathcal {U}}}=\{w\in {{\mathcal {G}}}: w\succcurlyeq 0\}\) is a mixed lattice subsemigroup in \({{\mathcal {G}}}\) then it is the largest (with respect to set inclusion) mixed lattice subsemigroup in \({{\mathcal {G}}}\).
In addition to properties (P1)–(P5), there are the following ”regularity properties” which require certain additional assumptions that will be discussed below.

We begin with properties (R2a) and (R2b), which have the following characterization.
Theorem 2.8
([11, Theorem 3.5]) Let \({{\mathcal {G}}}\) be a mixed lattice group and let \({{\mathcal {U}}}=\{w\in {{\mathcal {G}}}: w\succcurlyeq 0\}\). Then the following conditions are equivalent.
-
(a)
\({{\mathcal {U}}}\) is a mixed lattice subsemigroup of \({{\mathcal {G}}}\).
-
(b)
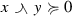 for all \(x,y\in {{\mathcal {U}}}\), where
for all \(x,y\in {{\mathcal {U}}}\), where  is the mixed lower envelope in \({{\mathcal {G}}}\).
is the mixed lower envelope in \({{\mathcal {G}}}\). -
(c)
\({{\mathcal {G}}}\) has the properties (R2a) and (R2b).
Property (R1) holds in every mixed lattice semigroup, where it is a simple consequence of the definition of specific order. As we develop our theory further in the following sections, it turns out that this property is quite important in many situations. We will show below that (R0) is implied by (R1). Moreover, (R2a) and (R2b) are also essential for certain results and, in many cases, a mixed lattice group can be viewed as a group extension of some mixed lattice semigroup. Due to the importance of these properties, we introduce the following classification of mixed lattice groups.
Definition 2.9
Let \({{\mathcal {G}}}\) be a mixed lattice group.
-
(i)
\({{\mathcal {G}}}\) is called pre-regular if \(x\preccurlyeq y\) implies that \(x\le y\) in \({{\mathcal {G}}}\).
-
(ii)
\({{\mathcal {G}}}\) is called quasi-regular if the set \({{\mathcal {S}}}=\{w\in {{\mathcal {G}}}: w\succcurlyeq 0\}\) is a mixed lattice subsemigroup in \({{\mathcal {G}}}\).
-
(iii)
\({{\mathcal {G}}}\) is called regular if it is quasi-regular and the set \({{\mathcal {S}}}\) defined above is generating, that is, \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\).
-
(iv)
A mixed lattice group that is not pre-regular is called irregular.
By Theorem 2.8, \({{\mathcal {G}}}\) is quasi-regular if and only if the properties (R2a) and (R2b) hold in \({{\mathcal {G}}}\). It is now a simple matter to show that every regular mixed lattice group is quasi-regular, and every quasi-regular mixed lattice group is pre-regular. Moreover, pre-regularity implies property (R0). The converse implications do not hold in general (see Examples 2.17 through 2.23 below).
Theorem 2.10
The following hold.
-
(a)
Every regular mixed lattice group is quasi-regular.
-
(b)
Every quasi-regular mixed lattice group is pre-regular.
-
(c)
Every pre-regular mixed lattice group has the property (R0).
Proof
(a) Obvious.
(b) Assume that \({{\mathcal {G}}}\) is quasi-regular and \(x\succcurlyeq y\). Then \(x-y\succcurlyeq 0\), and the set \(\{w\in {{\mathcal {G}}}:w\succcurlyeq 0\}\) is a mixed lattice semigroup, where (R1) holds. So we have \(x-y\ge 0\), or \(x\ge y\). Hence, \({{\mathcal {G}}}\) is pre-regular.
(c) Assume first that \(x\le y\). Since \(y\preccurlyeq y\), by (P5) we have  , and so by (P1) we get
, and so by (P1) we get  . This implies that
. This implies that  . On the other hand, we have
. On the other hand, we have  , and so by (R1) we have
, and so by (R1) we have  . Hence
. Hence  . Conversely, if
. Conversely, if  then \(x\le y\). For the other equivalence, note that if
then \(x\le y\). For the other equivalence, note that if  then the identity
then the identity  implies that
implies that  . The reverse implication is proved similarly. \(\square \)
. The reverse implication is proved similarly. \(\square \)
The foregoing theory can also be formulated in vector spaces. For this, recall that \(({{\mathcal {V}}},\le )\) is a partially ordered vector space if
hold for all \(u,v,w\in {{\mathcal {V}}}\) and \(\alpha \ge 0\). We now define a mixed lattice vector space by introducing another partial ordering and requiring that the mixed envelopes exist for every pair of elements. In this paper, we only consider real vector spaces.
Definition 2.11
Let \(({{\mathcal {V}}},\le ,\preccurlyeq )\) be a partially ordered real vector space with respect to two partial orders \(\le \) and \(\preccurlyeq \). If the mixed upper and lower envelopes  and
and  exist for all \(x,y\in {{\mathcal {V}}}\), then \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is called a mixed lattice vector space. The partial orderings \(\le \) and \(\preccurlyeq \) are called initial order and specific order, respectively.
exist for all \(x,y\in {{\mathcal {V}}}\), then \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is called a mixed lattice vector space. The partial orderings \(\le \) and \(\preccurlyeq \) are called initial order and specific order, respectively.
Definition 2.11 clearly implies that a Riesz space is a special case of a mixed lattice vector space. Indeed, if the two partial orderings \(\le \) and \(\preccurlyeq \) coincide, then the mixed upper and lower envelopes become the usual supremum and infimum, and the mixed lattice vector space reduces to an ordinary Riesz space. Thus every Riesz space is a mixed lattice vector space, and every mixed lattice vector space is an ordered vector space, but the converse inclusions do not hold. In this sense, the concept of a mixed lattice vector space is intermediate between a Riesz space and a general ordered vector space.
Most results in this paper are given in the more general group setting and the proofs can be translated to vector spaces with no difficulty. In fact, many of our results do not depend on the scalar multiplication at all. Therefore, we shall formulate our results in mixed lattice vector spaces only if they are not applicable to the group setting.
Before discussing the examples, we give a useful result that helps to determine whether a given structure is actually a mixed lattice group. The next theorem is an extension of [11, Theorem 3.3], in which the equivalence (a)\(\iff \)(e) was proved.
Theorem 2.12
Let \({{\mathcal {G}}}\) be a partially ordered group with two partial orderings \(\le \) and \(\preccurlyeq \). Then the following conditions are equivalent:
-
(a)
\({{\mathcal {G}}}\) is a mixed lattice group.
-
(b)
The mixed lower envelope
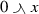 exists for all \(x\in {{\mathcal {G}}}\).
exists for all \(x\in {{\mathcal {G}}}\). -
(c)
The mixed upper envelope
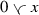 exists for all \(x\in {{\mathcal {G}}}\).
exists for all \(x\in {{\mathcal {G}}}\). -
(d)
The mixed lower envelope
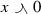 exists for all \(x\in {{\mathcal {G}}}\).
exists for all \(x\in {{\mathcal {G}}}\). -
(e)
The mixed upper envelope
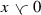 exists for all \(x\in {{\mathcal {G}}}\).
exists for all \(x\in {{\mathcal {G}}}\).
Proof
The equivalence (a)\(\iff \)(e) was proved in [11, Theorem 3.3]. The other equivalences (a)\(\iff \)(b), (a)\(\iff \)(c), and (a)\(\iff \)(d) are proved similarly. \(\square \)
We now discuss several examples of mixed lattice structures. The first one is due to Arsove and Leutwiler [7].
Example 2.13
The historical background of mixed lattice semigroups is in potential theory, and an archetypical example of a mixed lattice semigroup is the set \({{\mathcal {U}}}\) of positive superharmonic functions on some region D in \({{\mathbb {R}}}^n\). Here the initial order is defined pointwise, that is, \(f\le g\) if \(f(x)\le g(x)\) for almost every \(x\in D\) and the specific order is defined by \(f\preccurlyeq g\) if \(f\le g\) and \(g-f\) is superharmonic on D. Then \(({{\mathcal {U}}},\le ,\preccurlyeq )\) is a mixed lattice semigroup [7, Theorem 21.2].
A special case of positive superharmonic functions is the semigroup of positive concave real functions on some interval [a, b]. Hence, the set of those functions that can be written as a difference of two positive concave functions is a mixed lattice vector space. Differences of concave functions typically arise in certain optimization problems.
The next example is from probability theory, and it was also given by Arsove and Leutwiler [7, pp. 126–127].
Example 2.14
A sub-stochastic matrix is a (possibly infinite) non-negative matrix \(P=(p_{ij})\) such that the elements of P satisfy the condition \(\displaystyle \sum \nolimits _{j} p_{ij}\le 1\) for all i. Vectors are ordered in the usual way, that is, \(x\le y\) if \(x_i\le y_i\) for all i. A vector \(x\ge 0\) is called excessive with respect to the sub-stochastic matrix P if \(Px\le x\). Define the specific order by \(x\preccurlyeq y\) if \(x\le y\) and \(P(y-x)\le y-x\), or \((I-P)(y-x)\ge 0\). For a given sub-stochastic matrix P, let \({{\mathcal {U}}}\) be the set of all bounded vectors that are excessive with respect to P. Then \(({{\mathcal {U}}},\le ,\preccurlyeq )\) is a mixed lattice semigroup.
The dual concept of excessive measure is defined as a non-negative row vector \(x^T\) such that \(x^T P\le x^T\). The set of finite measures that are excessive with respect to P is similarly a mixed lattice semigroup.
More generally, it has been shown that the cones of excessive functions and excessive measures associated with Markov processes with continuous state-space have a mixed lattice structure. For proofs and more details, see [13, Theorems 5.9 and 5.11]
The following example of a regular mixed lattice group (indeed, a mixed lattice vector space) was given in [11, Example 1].
Example 2.15
Let \({{\mathcal {G}}}=BV([a,b])\) be the set of all functions of bounded variation on an interval [a, b]. Functions of bounded variation have the following well known characterization (see for example [3, Theorem 6.13]): \(f\in BV([a,b])\) if and only if \(f=f_1-f_2\), where \(f_1\) and \(f_2\) are positive increasing functions. It was shown in [7, Theorem 21.2], that the set \({{\mathcal {S}}}\) of all positive increasing functions is a mixed lattice semigroup. Hence, we can write \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\) and so \({{\mathcal {G}}}\) is a mixed lattice group where the initial and specific orders are defined by
and
respectively. It is well known that the space BV([a, b]) is a Riesz space with respect to both partial orders defined above (see [1, Section 9.8]). So, in a sense, this mixed lattice vector space is a ”mixture” of the two Riesz spaces \((BV([a,b]),\le )\) and \((BV([a,b]),\preccurlyeq )\).
Next we consider different positive cones in \({{\mathbb {R}}}^n\) to obtain more examples of mixed lattice vector spaces.
Example 2.16
Let \({{\mathcal {V}}}=({{\mathbb {R}}}^n,\le ,\preccurlyeq )\) where \(\le \) is given by the standard positive cone, that is, \(x\ge 0\) if \(x_k\ge 0\) for all \(k=1,2,\ldots ,n\) and define \(\preccurlyeq \) by the positive cone \(C=\{x: x_{k+1}\ge x_k\ge 0, k=1,2,\ldots ,n-1 \}\). Then the cone C is generating and the element  exists for every \(x\in {{\mathcal {V}}}\) and hence \({{\mathcal {V}}}\) is a regular mixed lattice vector space. In fact, u is a vector such that
exists for every \(x\in {{\mathcal {V}}}\) and hence \({{\mathcal {V}}}\) is a regular mixed lattice vector space. In fact, u is a vector such that
for \(k=1,2,\ldots ,n-1\). This example applies also for the infinite dimensional sequence space consisting of those sequences \((x_k)\), where \(x_k\) is defined as above for \(k=1,2,3,\ldots \). In this case, the definition of the specific order can be written as \(x\succcurlyeq 0\) if \(x\ge 0\) and x is increasing.
In the sequel, we denote the supremum and infimum formed with respect to initial order by \(\sup \) and \(\inf \), respectively (whenever they exist), and the supremum and infimum formed with respect to specific order by \(\text {sp sup}\) and \(\text {sp inf}\), respectively (whenever they exist). Our next examples are mixed lattice vector spaces that are quasi-regular but not regular.
Example 2.17
Let \({{\mathcal {V}}}={{\mathbb {R}}}^3\) and define \(\le \) as the partial order induced by the positive cone \(C_1=\{(x,y,z): z\ge \sqrt{x^2+y^2}\}\). Define specific order \(\preccurlyeq \) as the partial order with the positive cone \(C_2=\{(x,y,z): x=y=0, z\ge 0\}\). Geometrically it is obvious that the element  exists for all \(x\in {{\mathbb {R}}}^3\), since the cone \(C_1\) and any line parallel to z-axis always intersect. Moreover, the two partial orders \(\le \) and \(\preccurlyeq \) coincide on the z-axis and hence the set \(\{x\in {{\mathcal {G}}}: x\succcurlyeq 0\}\) can be identified with the set of positive real numbers with the usual ordering. This set is obviously a very special case of a mixed lattice semigroup. Thus \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice group (in fact, a mixed lattice vector space) which is quasi-regular, but not regular since the specific cone \(C_2\) is not generating. This example also shows that a mixed lattice group need not be a lattice with respect to either partial ordering. Again, this is easy to see geometrically for partial order \(\le \), since the intersection of two circular cones of type \(C_1\) is not necessarily a circular cone and thus the element \(\sup (x,y)\) does not exists if the elements x and y are not comparable. \({{\mathcal {G}}}\) is also not a lattice with respect to \(\preccurlyeq \), since the element \(\text {sp sup} \{x,y\}\) does not exist, unless the points x and y both lie on the same line parallel to the z-axis.
exists for all \(x\in {{\mathbb {R}}}^3\), since the cone \(C_1\) and any line parallel to z-axis always intersect. Moreover, the two partial orders \(\le \) and \(\preccurlyeq \) coincide on the z-axis and hence the set \(\{x\in {{\mathcal {G}}}: x\succcurlyeq 0\}\) can be identified with the set of positive real numbers with the usual ordering. This set is obviously a very special case of a mixed lattice semigroup. Thus \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice group (in fact, a mixed lattice vector space) which is quasi-regular, but not regular since the specific cone \(C_2\) is not generating. This example also shows that a mixed lattice group need not be a lattice with respect to either partial ordering. Again, this is easy to see geometrically for partial order \(\le \), since the intersection of two circular cones of type \(C_1\) is not necessarily a circular cone and thus the element \(\sup (x,y)\) does not exists if the elements x and y are not comparable. \({{\mathcal {G}}}\) is also not a lattice with respect to \(\preccurlyeq \), since the element \(\text {sp sup} \{x,y\}\) does not exist, unless the points x and y both lie on the same line parallel to the z-axis.
Example 2.18
Let \({{\mathcal {V}}}\) be the vector space of all bounded differentiable real functions on an interval (a, b) and define the initial order \(\le \) as the usual pointwise ordering, and specific order by \(f\preccurlyeq g\) if \(g-f\ge 0\) and \(g-f\) is a constant function. Let \(f\in {{\mathcal {V}}}\) and put \(m=\inf \{f(x):x\in (a,b)\}\) and \(m_f=\min \{0,m\}\). Then  exists and \(g(x)= f(x)-m_f\) for all \(x\in (a,b)\). Clearly, \(g\in {{\mathcal {V}}}\) and so \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice vector space that is quasi-regular but not regular since the specific positive cone \(C_s=\{f\in {{\mathcal {V}}}:f\ge 0 \text { and } f \text { is constant}\}\) is not generating.
exists and \(g(x)= f(x)-m_f\) for all \(x\in (a,b)\). Clearly, \(g\in {{\mathcal {V}}}\) and so \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice vector space that is quasi-regular but not regular since the specific positive cone \(C_s=\{f\in {{\mathcal {V}}}:f\ge 0 \text { and } f \text { is constant}\}\) is not generating.
Example 2.19
Let \({{\mathcal {G}}}\) be the set of real \(n\times n\) matrices and let \({\mathcal {B}}\) be the class of all symmetric \(n\times n\) matrices. We define order relations \(A\le B\) if \(a_{ij}\le b_{ij}\) for all \(i,j=1,\ldots ,n\) and \(A\preccurlyeq B\) if \(A\le B\) and \(B-A\in {\mathcal {B}}\). Then  exists for every \(A\in {{\mathcal {G}}}\) and the elements of C are given by \(c_{ij}=\max \{0,a_{ij},a_{ji}\}\). Hence, \({{\mathcal {G}}}\) is a mixed lattice group. \({{\mathcal {G}}}\) is easily seen to be quasi-regular (by the condition (b) of Theorem 2.8) but not regular since \({\mathcal {B}}\) does not generate \({{\mathcal {G}}}\).
exists for every \(A\in {{\mathcal {G}}}\) and the elements of C are given by \(c_{ij}=\max \{0,a_{ij},a_{ji}\}\). Hence, \({{\mathcal {G}}}\) is a mixed lattice group. \({{\mathcal {G}}}\) is easily seen to be quasi-regular (by the condition (b) of Theorem 2.8) but not regular since \({\mathcal {B}}\) does not generate \({{\mathcal {G}}}\).
Note that \({\mathcal {B}}\) could be replaced by some other suitable class of matrices, such as integer matrices. This choice for \({\mathcal {B}}\) yields a different mixed lattice group.
Example 2.20
Let \({{\mathcal {V}}}\) be the space of continuous real functions on the interval \([-1,1]\). Let \(f\le g\) be the usual pointwise ordering and \(f\preccurlyeq g\) if \(f\le g\) and \(g-f\) is an even function. Then  exists in \({{\mathcal {V}}}\) for every \(f\in {{\mathcal {V}}}\), and \(h(x)=\max \{0,f(x),f(-x)\}\). Hence, \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice vector space.
exists in \({{\mathcal {V}}}\) for every \(f\in {{\mathcal {V}}}\), and \(h(x)=\max \{0,f(x),f(-x)\}\). Hence, \(({{\mathcal {V}}},\le ,\preccurlyeq )\) is a mixed lattice vector space.
The following two examples are due to Eriksson–Bique [11].
Example 2.21
Consider the partially ordered group \(({{\mathbb {Z}}},\le ,\preccurlyeq )\), where \(\le \) is the usual order. Let p be a strictly positive integer and define specific order \(\preccurlyeq \) by setting
Then \(({{\mathbb {Z}}},\le ,\preccurlyeq )\) is a quasi-regular mixed lattice group [11, Example 2].
Example 2.22
The set \({{\mathbb {R}}}\) of real numbers is a mixed lattice group with \(\le \) as the usual order and specific order defined by \(x\preccurlyeq y\) if \(y-x\ge 0\) and \(y-x\in {{\mathbb {Z}}}\). Now, for example, if \(n\in {{\mathbb {Z}}}\) then

where \(\lfloor x \rfloor \) is the greatest integer less than or equal to x. [11, Example 3]
Note that the above construction could also be applied to \({{\mathbb {Q}}}\) or any subfield of \({{\mathbb {R}}}\) to yield a mixed lattice group.
Next we give an example of a pre-regular mixed lattice group that is not quasi-regular.
Example 2.23
Let \({{\mathcal {G}}}=({{\mathbb {Z}}}\times {{\mathbb {Z}}},\le ,\preccurlyeq )\) and define partial orders \(\le \) and \(\preccurlyeq \) as follows. If \(x=(x_1,x_2)\) and \(y=(y_1,y_2)\) then \(x\le y\) iff \(x_1\le y_1\) and \(x_2\le y_2\). In addition, \(x\preccurlyeq y\) iff \(x=y\) or \(y_1\ge x_1+1\) and \(y_2\ge x_2+1\). Using Theorem 2.12 it is easy to check that \({{\mathcal {G}}}\) is a mixed lattice group which is clearly pre-regular. Now let \(x=(1,1)\) and \(y=(1,2)\), and let \(W=\{w\in {{\mathcal {G}}}:w\succcurlyeq 0\}\). Then \(x\in W\) and \(y\in W\) but  . By Theorem 2.8 the set W is not a mixed lattice subsemigroup of \({{\mathcal {G}}}\) and so \({{\mathcal {G}}}\) is not quasi-regular.
. By Theorem 2.8 the set W is not a mixed lattice subsemigroup of \({{\mathcal {G}}}\) and so \({{\mathcal {G}}}\) is not quasi-regular.
Remark 2.24
There is an interesting problem related to the previous example and the regularity properties of mixed lattice vector spaces. The above counterexample was based on the fact that the set of positive elements in a mixed lattice group is not necessarily convex. However, in an ordered vector space the positive cone is always convex, so this raises the following question: Does there exist a pre-regular mixed lattice vector space that is not quasi-regular? A negative answer to this question would result in a somewhat simplified theory for mixed lattice vector spaces.
The next example presents a mixed lattice group which is irregular, and does not have properties (R0), (R1) and (R2).
Example 2.25
Let \({{\mathcal {G}}}=({{\mathbb {Z}}}\times {{\mathbb {Z}}},\le ,\preccurlyeq )\), where \(\le \) and \(\preccurlyeq \) are lexicographic orders defined as
and
Then \({{\mathcal {G}}}\) is a partially ordered group with the usual coordinatewise addition, and since both partial orders are total orders they obviously have the properties
Clearly, the element  exists for every \(x\in {{\mathcal {G}}}\), and so \({{\mathcal {G}}}\) is a mixed lattice group. However, none of the regularity properties (R1)–(R2) hold in \({{\mathcal {G}}}\). To see this, let \(x=(0,1)\) and \(y=(1,0)\). Then \(x\le y\) but
exists for every \(x\in {{\mathcal {G}}}\), and so \({{\mathcal {G}}}\) is a mixed lattice group. However, none of the regularity properties (R1)–(R2) hold in \({{\mathcal {G}}}\). To see this, let \(x=(0,1)\) and \(y=(1,0)\). Then \(x\le y\) but  . Hence, (R0) does not hold and this implies that (R1) and (R2) do not hold either.
. Hence, (R0) does not hold and this implies that (R1) and (R2) do not hold either.
Irregular mixed lattice structures are perhaps a bit too general to be very useful. It turns out that more interesting results can be obtained under the pre-regularity assumption, and in later sections we will mostly focus on the pre-regular case.
3 Generalized absolute values
One of the fundamental concepts in the theory of Riesz spaces and lattice ordered groups is the absolute value of an element. However, in mixed lattice groups this idea is completely unexplored. In this section we introduce the generalization of the absolute value for elements of mixed lattice groups and mixed lattice vector spaces.
We start by introducing the upper and lower parts of an element which play the roles of the positive and negative parts of an element in a lattice ordered group.
Definition 3.1
Let \({{\mathcal {G}}}\) be a mixed lattice group and \(x\in {{\mathcal {G}}}\). The elements  and
and  are called the upper part and lower part of x, respectively. Similarly, the elements
are called the upper part and lower part of x, respectively. Similarly, the elements  and
and  are called the specific upper part and specific lower part of x, respectively.
are called the specific upper part and specific lower part of x, respectively.
From the above definitions we observe that for the specific upper and lower parts we have \(x^{u}\succcurlyeq 0\) and \(x^{l}\succcurlyeq 0\), and for the upper and lower parts \(^{u}x\ge 0\) and \(^{l}x\ge 0\). By Theorem 2.12, a partially ordered group \({{\mathcal {G}}}\) is a mixed lattice group if and only if one of the upper or lower parts exists for all \(x\in {{\mathcal {G}}}\).
The upper and lower parts have the following basic properties.
Theorem 3.2
Let \({{\mathcal {G}}}\) be a mixed lattice group and \(x\in {{\mathcal {G}}}\). Then we have
-
(a)
\(^{ u }x=^{ l }(-x)\) and \(x^{ u }=(-x)^{ l }\).
-
(b)
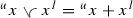 and
and 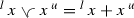
-
(c)
\(x = x^{ u } - ^{ l }x = ^{ u }x - x^{ l }\)
-
(d)
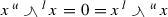
-
(e)
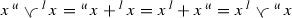
-
(f)
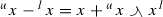 and
and 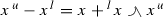 .
.
Proof
(a) These follow immediately from the definitions.
(b) Using (P2a) repeatedly we get

The proof for the second equality is similar.
(c) Using (P1) and (P3) we get

Similarly, \(x^{ u } - ^{ l }x = x\).
(d) Combining (P1) and (b) gives

From this it follows that  . The other equality is similar.
. The other equality is similar.
(e) For the first equality, we use (P2a) twice to get

The last equality is proved similarly. The middle equality follows from (c).
(f) First we note that by (P2a) and (P3)

and

So by adding \(-x^{ u }-^{ l }x\) and \(-^{ u }x - x^{ l }\), respectively, to the two equations in (e) we get

Now we use (c) and substitute \(x^{ u }=x+^{ l }x\) into the first equality and \(x^{ l }=^{ u }x-x\) into the second equality to get  and
and  . \(\square \)
. \(\square \)
From the preceding theorem we observe that both ”unsymmetrical” expressions  and
and  have properties that are similar to the absolute value of an element in lattice ordered groups, and they can be expressed as the sum of upper and lower parts, just as the absolute value can be expressed as the sum of positive and negative parts. These observations motivate the following definition.
have properties that are similar to the absolute value of an element in lattice ordered groups, and they can be expressed as the sum of upper and lower parts, just as the absolute value can be expressed as the sum of positive and negative parts. These observations motivate the following definition.
Definition 3.3
Let \({{\mathcal {G}}}\) be a mixed lattice group and \(x\in {{\mathcal {G}}}\). The elements \(^{ u }x^{ l }= ^{ u }\!x + x^{ l }\) and \(^{ l }x^{ u }=^{ l }\!x + x^{ u }\) are called the unsymmetrical generalized absolute values of x.
We will now examine the basic properties of the generalized absolute values. As we might expect, they turn out to have many similarities with the ordinary absolute value, as the next few theorems show.
Theorem 3.4
Let \({{\mathcal {G}}}\) be a mixed lattice group and \(x\in {{\mathcal {G}}}\). Then we have
-
(a)
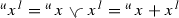 and
and 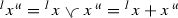 .
. -
(b)
\(^{ u }x^{ l } =^{ l }(-x)^{ u }\).
-
(c)
\(x\succcurlyeq 0\) if and only if \(x=^{ l }x^{ u }=x^{ u }\) and \(^{ l }x=0\).
-
(d)
\((x^{ u })^{ u }=^{ l }(x^{ u })^{ u }=x^{ u }\) and \((x^{ l })^{ u }=^{ l }(x^{ l })^{ u }=x^{ l }\).
-
(e)
\(^{ u }x^{ l }+^{ l }x^{ u }\succcurlyeq 0\) and \(^{ u }x^{ l }+^{ l }x^{ u }\ge 0\).
Proof
(a) is just a restatement of Theorem 3.2.
(b) By Theorem 3.2 (a) we have  .
.
(c) If \(x=x^{ u }\) then \(x\succcurlyeq 0\). Conversely, let \(x\succcurlyeq 0\). Then  and since \(-x\preccurlyeq 0\) and \(0\le 0\), it follows by (P5) that
and since \(-x\preccurlyeq 0\) and \(0\le 0\), it follows by (P5) that  . Hence, \(^{ l }x=0\). This implies that \(x=x^{ u }-^{ l }x=x^{ u }\) and \(^{ l }x^{ u }=^{ l }x +x^{ u }=x^{ u }=x\).
. Hence, \(^{ l }x=0\). This implies that \(x=x^{ u }-^{ l }x=x^{ u }\) and \(^{ l }x^{ u }=^{ l }x +x^{ u }=x^{ u }=x\).
(d) These identities follow immediately from (f), since \(x^{ u }\succcurlyeq 0\) and \(x^{ l }\succcurlyeq 0\).
(e) These follow from (c) and Theorem 3.2 (e), since
\(^{ u }x^{ l }+^{ l }x^{ u }= ^{ u }x + ^{ l }x+ x^{ l } + x^{ u } =2(^{ u }x + ^{ l }x)=2(x^{ l } + x^{ u }).\) \(\square \)
The next theorem gives some useful additional properties of the generalized absolute values. The first two are the triangle inequalities.
Theorem 3.5
Let \({{\mathcal {G}}}\) be a mixed lattice group. For all \(x,y\in {{\mathcal {G}}}\) the following hold.
-
(a)
\(^{ u }x+^{ u }y \ge ^{ u }(x+y)\), \(x^{ l }+y^{ l } \ge (x+y)^{ l }\) and \(^{ u }x^{ l }+^{ u }y^{ l } \ge ^{ u }(x+y)^{ l }\)
-
(b)
\(x^{ u }+y^{ u } \ge (x+y)^{ u }\), \(^{ l }x+^{ l }y \ge ^{ l }(x+y)\) and \(^{ l }x^{ u }+^{ l }y^{ u } \ge ^{ l }(x+y)^{ u }\)
-
(c)
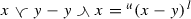 and
and 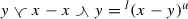
-
(d)
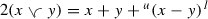 and
and 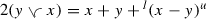 .
.
Proof
(a) Since  and
and  and similarly
and similarly  and
and  , it follows by (P5) that
, it follows by (P5) that  . The proof for the second inequality is similar. It then follows that
. The proof for the second inequality is similar. It then follows that
(b) Just repeat the arguments in (a).
(c) Applying Theorem 3.2 we get

The second equality follows from the first one by exchanging x and y and applying Theorem 3.2 (a).
(d) From (P1) we get  . The desired result follows by substituting this into (c). The second identity is similar. \(\square \)
. The desired result follows by substituting this into (c). The second identity is similar. \(\square \)
In Theorem 3.2 we showed that any \(x\in {{\mathcal {G}}}\) can be written as a difference of upper and lower parts. Just as in Riesz space theory, these decompositions \(x = x^{ u } - ^{ l }x\) and \(x= ^{ u }x - x^{ l }\) with  are minimal in the sense of the following theorem.
are minimal in the sense of the following theorem.
Theorem 3.6
Let \({{\mathcal {G}}}\) be a mixed lattice group. If \(x\in {{\mathcal {G}}}\) and \(x=u-v\) then the following hold.
-
(a)
If \(u\succcurlyeq 0\) and \(v\ge 0\) then \(u\ge x^{ u }\) and \(v\ge ^{ l }x\),
-
(b)
if \(u\ge 0\) and \(v\succcurlyeq 0\) then \(u\ge ^{ u }x\) and \(v\ge x^{ l }\),
and conversely,
-
(c)
if \(x=u-v\) with
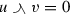 then \(u= x^{ u }\) and \(v= ^{ l }x\),
then \(u= x^{ u }\) and \(v= ^{ l }x\), -
(d)
if \(x=u-v\) with
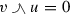 then \(u= ^{ u }x\) and \(v= x^{ l }\).
then \(u= ^{ u }x\) and \(v= x^{ l }\).
Proof
(a) Let \(x=u-v\) with \(u\succcurlyeq 0\) and \(v\ge 0\). Then \(u=x+v\ge x\) and it follows by (P5a) and (P4) that  . Then, using (P5) again we get
. Then, using (P5) again we get

(b) Similar.
(c) Assume that \(x=u-v\) with  . Then we have
. Then we have

and so \(u=x^{ u }\). It now follows that \(v=u-x=x^{ u }-x=^{ l }x\).
(d) Similar. \(\square \)
The preceding theorem corresponds to the representation of elements in a Riesz space as a difference of two disjoint elements. The theory of disjointness in mixed lattice semigroups has been studied by Arsove and Leutwiler [7].
In an arbitrary mixed lattice group, the generalized absolute values can behave somewhat unexpectedly. However, in pre-regular mixed lattice groups we can say more about the upper and lower parts as well as the generalized absolute values.
Theorem 3.7
Let \({{\mathcal {G}}}\) be a pre-regular mixed lattice group and \(x\in {{\mathcal {G}}}\). Then the following hold.
-
(a)
\(x\succcurlyeq 0\) if and only if \(x=^{ l }x^{ u }=^{ u }x^{ l }=^{ u }x=x^{ u }\) and \(^{ l }x=x^{ l }=0\).
-
(b)
\(x\ge 0\) if and only if \(x=^{ u }x^{ l }=^{ u }x\) and \(x^{ l }=0\).
-
(c)
\(^{ u }x^{ l }\ge 0\) and \(^{ l }x^{ u }\ge 0\). Moreover, \(^{ u }x^{ l }=^{ l }x^{ u }= 0\) if and only if \(x=0\).
-
(d)
\(^{ u }(^{ u }x)=^{ u }(^{ u }x)^{ l }=^{ u }x\) and \(^{ u }(^{ l }x)=^{ u }(^{ l }x)^{ l }=^{ l }x\).
-
(e)
\(^{ u }(^{ u }x^{ l })^{ l }=^{ u }x^{ l }\) and \(^{ u }(^{ l }x^{ u })^{ l }=^{ l }x^{ u }\).
Proof
(a) Let \(x\succcurlyeq 0\). By (P4) it follows that  . Then we have \(x=x^{ u }=x^{ u }-^{ l }x\) and it follows that \(^{ l }x=0\) and \(^{ l }x^{ u }=^{ l }x +x^{ u }=x^{ u }=x\). Furthermore, we have
. Then we have \(x=x^{ u }=x^{ u }-^{ l }x\) and it follows that \(^{ l }x=0\) and \(^{ l }x^{ u }=^{ l }x +x^{ u }=x^{ u }=x\). Furthermore, we have  , which implies that \(x^{ l }\ge 0\) by (R1). But if \(x\succcurlyeq 0\) then \(-x\preccurlyeq 0\), which implies that \(-x\le 0\). Hence, since \(0\preccurlyeq 0\), by (P5) we have
, which implies that \(x^{ l }\ge 0\) by (R1). But if \(x\succcurlyeq 0\) then \(-x\preccurlyeq 0\), which implies that \(-x\le 0\). Hence, since \(0\preccurlyeq 0\), by (P5) we have  . Thus \(x^{ l }=0\) and so \(x=^{ u }x-x^{ l }=^{ u }x\) and \(^{ u }x^{ l }=^{ u }x+x^{ l }=^{ u }x=x\). Conversely, if
. Thus \(x^{ l }=0\) and so \(x=^{ u }x-x^{ l }=^{ u }x\) and \(^{ u }x^{ l }=^{ u }x+x^{ l }=^{ u }x=x\). Conversely, if  then
then  and so
and so  and it follows from (P4) that \(x\succcurlyeq 0\).
and it follows from (P4) that \(x\succcurlyeq 0\).
(b) Similar.
(c) Clearly, \(^{ u }x^{ l }\ge 0\) and \(^{ l }x^{ u }\ge 0\). If \(x=0\) then evidently \(^{ u }x^{ l }=^{ l }x^{ u }= 0\). Conversely, assume that \(^{ l }x^{ u }= ^{ l }x+x^{ u }=0\). Then \(x^{ u }=-^{ l }x\), which implies that \(2x^{ u }=x^{ u }-^{ l }x=x\). Now \(x=2x^{ u }\succcurlyeq 0\), and so by (a) we have \(x=^{ l }x^{ u }=0\). If \(^{ u }x^{ l }= 0\) then similar arguments show that \(x=0\).
(d) These follow immediately from (b), since \(^{ u }x\ge 0\) and \(^{ l }x\ge 0\).
(e) This follows immediately from (a) and (b). \(\square \)
Remark 3.8
The last theorem is not valid without the pre-regularity condition, and the generalized absolute value may even be negative. The next example clarifies these points.
Example 3.9
Consider the lexicographically ordered mixed lattice group of Example 2.25. If \(x=(1,-1)\) then \(x\ge 0\) but \(^{ u }x=(0,0)\le x\). Moreover, \(x^{ l }=-x\le 0\) and so \(^{ u }x^{ l }=^{ u }x+x^{ l }=-x\le 0\). This shows that in general, one of the generalized absolute values as well as the upper or lower part can actually be negative with respect to one of the partial orders. However, Theorem 3.4 (e) implies that both unsymmetrical absolute values cannot be negative at the same time.
Next we will study the behavior of the mixed envelopes and generalized absolute values under scalar multiplication. In a mixed lattice vector space the generalized absolute values have alternative expressions, which bear close resemblance to the definition of the absolute value in Riesz spaces, that is \(|x|=x\vee (-x)\).
Proposition 3.10
Let \({{\mathcal {V}}}\) be a mixed lattice vector space. Then for all \(x,y\in {{\mathcal {V}}}\) the following hold.
-
(a)
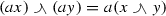 and
and 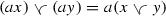 for all \(a\ge 0\),
for all \(a\ge 0\), -
(b)
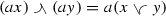 and
and 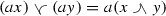 for all \(a< 0\),
for all \(a< 0\), -
(c)
\(^{ u }(ax)^{ l }=a ^{ u }x^{ l }\) and \(^{ l }(ax)^{ u }=a ^{ l }x^{ u }\) for all \(a\ge 0\),
-
(d)
\(^{ u }(ax)^{ l }=|a| ^{ l }x^{ u }\) and \(^{ l }(ax)^{ u }=|a| ^{ u }x^{ l }\) for all \(a<0\).
-
(e)
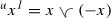 and
and 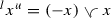 .
.
Proof
(a) Assume that \(a>0\) (the case \(a=0\) is trivial). Then by the definition of the lower envelope we have

The proof for the upper envelope is similar.
(b) These identities follow from (a) and property (P3).
(c) These follow from (a) and (b) and Theorem 3.2.
(d) Note that if \(a<0\) then \(a=-|a|\), and apply part (c) and Theorem 3.2(b).
(e) By Theorem 3.2 and part (b) we have

This proves the first identity in (e). The second identity is proved in a similar manner. \(\square \)
To conclude this section, we show that under certain conditions the results of the preceding proposition hold also in mixed lattice groups. For the discussion that follows, we will need the next definition.
Definition 3.11
A mixed lattice group \({{\mathcal {G}}}\) is called Archimedean if the condition \(nx\le y\) for all \(n\in {{\mathbb {N}}}\) implies \(x\le 0\).
Erkisson–Bique has proved the following result concerning Archimedean mixed lattice semigroups.
Theorem 3.12
([10, Theorem 4.1]) If \({{\mathcal {S}}}\) is an Archimedean mixed lattice semigroup, then

Combining the result of Theorem 3.12 with property (P3) and the identities in Theorem 2.7 yields the following corollary.
Corollary 3.13
If \({{\mathcal {G}}}\) is a regular Archimedean mixed lattice group, then the following hold for all \(x,y\in {{\mathcal {G}}}\).
-
(a)
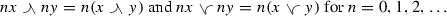
-
(b)
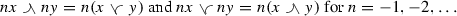 .
. -
(c)
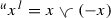 and
and 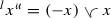 .
.
Remark 3.14
It should be noted that the Archimedean property in the preceding theorem is not a necessary condition, as the above result holds in every non-Archimedean Riesz space. In general, the identities in Corollary 3.13 do not hold as the following example shows.
Example 3.15
Consider the partially ordered group \(({{\mathbb {Z}}},\le ,\preccurlyeq )\) of Example 2.21, where \(\le \) is the usual order and
Choose \(p=3\). Then we find that  but
but  and so the identity (a) of Corollary 3.13 fails to hold. Next, let \(x=-1\) and compute
and so the identity (a) of Corollary 3.13 fails to hold. Next, let \(x=-1\) and compute  and
and  . Then by Theorem 3.2 we have \(^{ u }x^{ l }=2+3=5\). However, if we try to use the formula of Corollary 3.13 (c) we get
. Then by Theorem 3.2 we have \(^{ u }x^{ l }=2+3=5\). However, if we try to use the formula of Corollary 3.13 (c) we get  .
.
If \({{\mathcal {G}}}\) is a lattice with respect to specific order \(\preccurlyeq \) then the absolute value with respect to \(\preccurlyeq \) exists for all \(x\in {{\mathcal {G}}}\) and we denote it by \({{\,\mathrm{sp}\,}}|x|={{\,\mathrm{sp \;sup}\,}}\{x,-x\}\). Similarly, we denote the positive and negative parts with respect to \(\preccurlyeq \) by \({{\,\mathrm{sp}\,}}(x^+)\) and \({{\,\mathrm{sp}\,}}(x^-)\), respectively.
Proposition 3.16
Let \({{\mathcal {G}}}\) be a quasi-regular mixed lattice group that is a lattice with respect to its specific order. Then
-
(a)
\({{\,\mathrm{sp}\,}}|x| ={{\,\mathrm{sp \;sup}\,}}\{^{ u }x^{ l },^{ l }x^{ u }\}\) for all \(x\in {{\mathcal {G}}}\).
-
(b)
\({{\,\mathrm{sp}\,}}(x^+)={{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\) for all \(x\in {{\mathcal {G}}}\).
-
(c)
\({{\,\mathrm{sp}\,}}(x^-)={{\,\mathrm{sp \;sup}\,}}\{^{ l }x,x^{ l }\}\) for all \(x\in {{\mathcal {G}}}\).
Proof
(a) We have  and
and  . From this it follows that \({{\,\mathrm{sp \;sup}\,}}\{^{ u }x^{ l },^{ l }x^{ u }\} \succcurlyeq {{\,\mathrm{sp \;sup}\,}}\{x,-x\}={{\,\mathrm{sp}\,}}|x|\). On the other hand, we have \({{\,\mathrm{sp}\,}}|x|\succcurlyeq x\), \({{\,\mathrm{sp}\,}}|x|\succcurlyeq -x\) and \({{\,\mathrm{sp}\,}}|x|\succcurlyeq 0\). Then by (R2)
. From this it follows that \({{\,\mathrm{sp \;sup}\,}}\{^{ u }x^{ l },^{ l }x^{ u }\} \succcurlyeq {{\,\mathrm{sp \;sup}\,}}\{x,-x\}={{\,\mathrm{sp}\,}}|x|\). On the other hand, we have \({{\,\mathrm{sp}\,}}|x|\succcurlyeq x\), \({{\,\mathrm{sp}\,}}|x|\succcurlyeq -x\) and \({{\,\mathrm{sp}\,}}|x|\succcurlyeq 0\). Then by (R2)  and
and  . So
. So  . Similarly we show that \({{\,\mathrm{sp}\,}}|x|\succcurlyeq ^{ u }x^{ l }\). Hence, \({{\,\mathrm{sp \;sup}\,}}\{^{ u }x^{ l },^{ l }x^{ u }\}\preccurlyeq {{\,\mathrm{sp}\,}}|x|\) and the proof is complete.
. Similarly we show that \({{\,\mathrm{sp}\,}}|x|\succcurlyeq ^{ u }x^{ l }\). Hence, \({{\,\mathrm{sp \;sup}\,}}\{^{ u }x^{ l },^{ l }x^{ u }\}\preccurlyeq {{\,\mathrm{sp}\,}}|x|\) and the proof is complete.
(b) Since \(^{ u }x\succcurlyeq x\) and \(x^{ u }\succcurlyeq 0\) we get \({{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\succcurlyeq {{\,\mathrm{sp \;sup}\,}}\{x,0\}={{\,\mathrm{sp}\,}}(x^+)\). On the other hand, \({{\,\mathrm{sp}\,}}(x^+)\succcurlyeq 0\) and \({{\,\mathrm{sp}\,}}(x^+)\succcurlyeq x\), and so  and
and  . It follows that \({{\,\mathrm{sp}\,}}(x^+)\succcurlyeq {{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\). Hence, \({{\,\mathrm{sp}\,}}(x^+)={{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\). The proof for (c) is similar. \(\square \)
. It follows that \({{\,\mathrm{sp}\,}}(x^+)\succcurlyeq {{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\). Hence, \({{\,\mathrm{sp}\,}}(x^+)={{\,\mathrm{sp \;sup}\,}}\{^{ u }x,x^{ u }\}\). The proof for (c) is similar. \(\square \)
4 Mixed lattice ideals
Ideals play a fundamental role in the theory of Riesz spaces. In this section we extend the study of ideals to mixed lattice groups. A lattice ideal in a Riesz space E is defined as a subspace A of E such that if \(x\in A\) and \(|y|\le |x|\) then \(y\in A\). We could define ideals in a mixed lattice group similarly with respect to initial and specific orders. However, for the specific order such a definition is problematic, since the absolute values \(^{ u }x^{ l }\) and \(^{ l }x^{ u }\) are not necessarily positive with respect to specific order. The notion of an order convex subspace can be used as a generalization of the lattice ideal in an ordered vector space, and lattice ideals in Riesz spaces are precisely those sublattices that are order convex. We use this approach to define ideals in mixed lattice structures.
Definition 4.1
-
(i)
A subgroup \({{\mathcal {S}}}\) of a mixed lattice group \({{\mathcal {G}}}\) is called a mixed lattice subgroup of \({{\mathcal {G}}}\) if
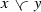 and
and 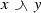 belong to \({{\mathcal {S}}}\) whenever x and y are in \({{\mathcal {S}}}\). Here
belong to \({{\mathcal {S}}}\) whenever x and y are in \({{\mathcal {S}}}\). Here 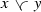 and
and 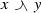 are the upper and lower mixed envelopes in \({{\mathcal {G}}}\).
are the upper and lower mixed envelopes in \({{\mathcal {G}}}\). -
(ii)
A subset \(U\in {{\mathcal {G}}}\) is called order convex, if \(x\le z\le y\) and \(x,y\in U\) imply that \(z\in U\). Similarly, a subset \(U\in {{\mathcal {G}}}\) is called specifically order convex, if \(x\preccurlyeq z\preccurlyeq y\) and \(x,y\in U\) imply that \(z\in U\).
-
(iii)
If \({{\mathcal {A}}}\) is an order convex mixed lattice subgroup of \({{\mathcal {G}}}\) then \({{\mathcal {A}}}\) is called a mixed lattice ideal of \({{\mathcal {G}}}\). Similarly, a specifically order convex mixed lattice subgroup of \({{\mathcal {G}}}\) is called a specific mixed lattice ideal of \({{\mathcal {G}}}\).
Next we state a useful characterization for mixed lattice ideals in a pre-regular mixed lattice group. The conditions (c)–(f) correspond to the usual definition of a lattice ideal.
Theorem 4.2
Let \({{\mathcal {G}}}\) be a pre-regular mixed lattice group and \({{\mathcal {A}}}\) a subgroup of \({{\mathcal {G}}}\). The following conditions are equivalent.
-
(a)
\({{\mathcal {A}}}\) is a mixed lattice ideal in \({{\mathcal {G}}}\)
-
(b)
The following two conditions hold.
(i) \(x\in {{\mathcal {A}}}\) implies \(^{ u }x^{ l }\in {{\mathcal {A}}}\). (ii) \(0\le x \le y\) with \(y\in {{\mathcal {A}}}\) implies \(x\in {{\mathcal {A}}}\).
-
(c)
If \(^{ u }y^{ l }\le ^{ u }x^{ l }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(d)
If \(^{ l }y^{ u }\le ^{ u }x^{ l }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(e)
If \(^{ l }y^{ u }\le ^{ l }x^{ u }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(f)
If \(^{ u }y^{ l }\le ^{ l }x^{ u }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
Proof
The implication \((a)\implies (b)\) is evident.
To show that \((b)\implies (c)\), assume that conditions (i) and (ii) in (b) hold. If \(0\le ^{ u }y^{ l } \le ^{ u }x^{ l }\) and \(x\in {{\mathcal {A}}}\), then \(^{ u }x^{ l }\in {{\mathcal {A}}}\) by (i). Then (ii) implies that \(^{ u }y^{ l }\in {{\mathcal {A}}}\) and the inequality \(0\le ^{ u }y\le ^{ u }y^{ l }\) together with (ii) imply that \(^{ u }y\in {{\mathcal {A}}}\). So \(^{ u }y^{ l }-^{ u }y=y^{ l } \in {{\mathcal {A}}}\), and hence \(^{ u }y-y^{ l }=y\in {{\mathcal {A}}}\).
Next we show that \((c)\implies (a)\). Assuming that (c) holds, let \(x\in {{\mathcal {A}}}\). Then \(0\le ^{ u }x = ^{ u }(^{ u }x)^{ l }\le ^{ u }x^{ l }\) and so \(^{ u }x\in {{\mathcal {A}}}\). This proves that \({{\mathcal {A}}}\) is a mixed lattice subgroup (by Theorem 2.12). Next, assume that \(u\le z\le v\) with \(u,v\in {{\mathcal {A}}}\). We want to show that \(z\in {{\mathcal {A}}}\). Now \(0\le z-u\le v-u\), and it follows that \(0\le ^{ u }(z-u)^{ l }\le ^{ u }(v-u)^{ l }\). Since \({{\mathcal {A}}}\) is a subgroup, we have \(v-u\in {{\mathcal {A}}}\) and so by assumption \(z-u\in {{\mathcal {A}}}\). Thus, \(z=u-(z-u)\in {{\mathcal {A}}}\) and \({{\mathcal {A}}}\) is order convex, and hence a mixed lattice ideal.
For \((c)\implies (d)\), let \(x\in {{\mathcal {A}}}\) and observe that the inequality \(^{ l }y^{ u }\le ^{ u }x^{ l }\) is equivalent to \(^{ u }(-y)^{ l }\le ^{ u }x^{ l }\). If the condition (c) holds, then \(-y\in {{\mathcal {A}}}\) and since \({{\mathcal {A}}}\) is a subgroup, we have \(y\in {{\mathcal {A}}}\). This establishes (d). The implications \((d)\implies (e)\), \((e)\implies (f)\) and \((f)\implies (c)\) are proved similarly. \(\square \)
As it turns out, the equivalent conditions for specific mixed lattice ideals are slightly different. More details are given in the following results.
Proposition 4.3
Let \({{\mathcal {G}}}\) be a pre-regular mixed lattice group and \({{\mathcal {A}}}\) a subgroup of \({{\mathcal {G}}}\). The following conditions are equivalent.
-
(a)
\({{\mathcal {A}}}\) is a specific mixed lattice ideal in \({{\mathcal {G}}}\)
-
(b)
The following two conditions hold.
(i) \(x\in {{\mathcal {A}}}\) implies \(^{ u }x^{ l }\in {{\mathcal {A}}}\). (ii) \(0\preccurlyeq x \preccurlyeq y\) with \(y\in {{\mathcal {A}}}\) implies \(x\in {{\mathcal {A}}}\).
Proof
The implication \((a)\implies (b)\) is clear.
To prove that \((b)\implies (a)\), suppose that conditions (i) and (ii) in (b) hold. If \(x\in {{\mathcal {A}}}\) then \(^{ u }x^{ l }\in {{\mathcal {A}}}\) and this implies that \({{\mathcal {A}}}\) is a mixed lattice subgroup. Moreover, if \(x,y\in {{\mathcal {A}}}\) and \(x\preccurlyeq z\preccurlyeq y\) holds, then \(0\preccurlyeq z-x\preccurlyeq y-x \in {{\mathcal {A}}}\) and by condition (ii) we have \(z-x\in {{\mathcal {A}}}\), and consequently, \(x+(z-x)=z\in {{\mathcal {A}}}\). Hence \({{\mathcal {A}}}\) is a specific mixed lattice ideal. \(\square \)
The related conditions (c)–(f) of Theorem 4.2 are not equivalent for specific mixed lattice ideals, but they imply the conditions given in Proposition 4.3.
Proposition 4.4
Let \({{\mathcal {G}}}\) be a pre-regular mixed lattice group and \({{\mathcal {A}}}\) a subgroup of \({{\mathcal {G}}}\). If one of the following equivalent conditions holds then \({{\mathcal {A}}}\) is a specific mixed lattice ideal.
-
(a)
If \(^{ u }y^{ l }\preccurlyeq ^{ u }x^{ l }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(b)
If \(^{ l }y^{ u }\preccurlyeq ^{ u }x^{ l }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(c)
If \(^{ l }y^{ u }\preccurlyeq ^{ l }x^{ u }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
-
(d)
If \(^{ u }y^{ l }\preccurlyeq ^{ l }x^{ u }\) and \(x\in {{\mathcal {A}}}\) then \(y\in {{\mathcal {A}}}\).
Proof
The equivalence of the conditions is proved in the same way as in Theorem 4.2. Assume that (a) holds. If \(x\in {{\mathcal {A}}}\) then it follows from the identity \(^{ u }(^{ u }x^{ l })^{ l }=^{ u }x^{ l }\) that \(^{ u }x^{ l }\in {{\mathcal {A}}}\). Moreover, if \(0\preccurlyeq y\preccurlyeq x\) then \(0\preccurlyeq ^{ u }y^{ l }\preccurlyeq ^{ u }x^{ l }\) and so \(y\in {{\mathcal {A}}}\). Hence by Proposition 4.3\({{\mathcal {A}}}\) is a specific mixed lattice ideal. \(\square \)
The next counterexample shows that the conditions of Propositions 4.3 and 4.4 are not equivalent.
Example 4.5
Consider \({{\mathbb {Z}}}\times {{\mathbb {Z}}}\) with the lexicographic order \(\le \) given in Example 2.25 and define \(\preccurlyeq \) by \((x,y)\preccurlyeq (u,v)\) if \(x\le u\) and \(y\le v\). Then \({{\mathcal {G}}}=({{\mathbb {Z}}}\times {{\mathbb {Z}}},\le ,\preccurlyeq )\) is a regular mixed lattice group. Consider the subgroup \({{\mathcal {A}}}=\{(x,y): y=0\}\). It is easy to see that the condition (b) of Theorem 4.3 holds in \({{\mathcal {A}}}\) and so \({{\mathcal {A}}}\) is a specific mixed lattice ideal in \({{\mathcal {G}}}\). However, the conditions of Proposition 4.4 do not hold in \({{\mathcal {A}}}\). Choose for example \(x=(2,0)\) and \(y=(1,-1)\). Then \(x\in {{\mathcal {A}}}\) and \(y=^{ u }y^{ l }\preccurlyeq ^{ u }x^{ l }=x\), but \(y\notin {{\mathcal {A}}}\).
As an easy consequence of the preceding results we have the following relationship between lattice ideals and mixed lattice ideals.
Proposition 4.6
-
(a)
If \({{\mathcal {G}}}\) is a mixed lattice group that is a lattice with respect to initial order \(\le \) then every mixed lattice ideal is a lattice ideal (with respect to \(\le \)).
-
(b)
If \({{\mathcal {G}}}\) is a mixed lattice group that is a lattice with respect to specific order \(\preccurlyeq \) then every lattice ideal (with respect to \(\preccurlyeq \)) is a specific mixed lattice ideal.
Proof
(a) Let \({{\mathcal {A}}}\) be a mixed lattice ideal in \({{\mathcal {G}}}\) and \(x\in {{\mathcal {A}}}\). Assume that \(|y|\le |x|\). By Theorem 4.2 we have \(^{ u }x^{ l },^{ l }x^{ u }\in {{\mathcal {A}}}\) and inequalities \(x\le ^{ l }x^{ u }\) and \(-x\le ^{ u }x^{ l }\) imply that \(0\le |x|\le ^{ u }x^{ l }+^{ l }x^{ u }\). Then Theorem 4.2 implies that \(|x|\in {{\mathcal {A}}}\). Since \(0\le y^+\le |y|\le |x|\), it follows that \(y^+\in {{\mathcal {A}}}\). Similarly, \(y^-\in {{\mathcal {A}}}\) and so \(y=y^+-y^-\in {{\mathcal {A}}}\). This proves that \({{\mathcal {A}}}\) is a lattice ideal in \({{\mathcal {G}}}\).
(b) Let \({{\mathcal {A}}}\) be a lattice ideal with respect to \(\preccurlyeq \) and \(x\in {{\mathcal {A}}}\). Then \(0\preccurlyeq x^{ u } = {{\,\mathrm{sp}\,}}|x^{ u }| \preccurlyeq {{\,\mathrm{sp}\,}}|x|\). This implies that \(x^{ u }\in {{\mathcal {A}}}\) and so \(^{ l }x=x^{ u }-x\in {{\mathcal {A}}}\). Hence \(^{ u }x^{ l }=x^{ u }+^{ l }x\in {{\mathcal {A}}}\). Moreover, if \(0\preccurlyeq y\preccurlyeq x\) with \(x\in {{\mathcal {A}}}\) then \(0\preccurlyeq {{\,\mathrm{sp}\,}}|y|\preccurlyeq {{\,\mathrm{sp}\,}}|x|\) and since \({{\mathcal {A}}}\) is a lattice ideal, this implies that \(y\in {{\mathcal {A}}}\). Hence the conditions of Proposition 4.3 hold and \({{\mathcal {A}}}\) is a specific mixed lattice ideal. \(\square \)
The converse of Proposition 4.6 does not hold (see Example 4.10 below).
The following facts are now evident.
Proposition 4.7
In a mixed lattice group \({{\mathcal {G}}}\) the following hold.
-
(a)
If \({{\mathcal {G}}}\) is pre-regular and \({{\mathcal {A}}}\) is a mixed lattice ideal in \({{\mathcal {G}}}\), then \({{\mathcal {A}}}\) is a specific mixed lattice ideal in \({{\mathcal {G}}}\).
-
(b)
Intersections of (specific) mixed lattice ideals are (specific) mixed lattice ideals.
Before discussing examples we give the following simple but useful result.
Lemma 4.8
If \({{\mathcal {G}}}\) is a quasi-regular mixed lattice group and \({{\mathcal {U}}}=\{w:w\succcurlyeq 0\}\) then the subgroup \({{\mathcal {S}}}\) generated by \({{\mathcal {U}}}\) (i.e. \({{\mathcal {S}}}={{\mathcal {U}}}-{{\mathcal {U}}}\)) is a specific mixed lattice ideal in \({{\mathcal {G}}}\).
Proof
If \(x\in {{\mathcal {S}}}\) then \(x=u-v\) for some \(u,v\succcurlyeq 0\) and  and so
and so  . This proves that \({{\mathcal {S}}}\) is a mixed lattice subgroup of \({{\mathcal {G}}}\). Moreover, \(0\preccurlyeq y\preccurlyeq x\) clearly implies that \(y\in {{\mathcal {S}}}\) and hence \({{\mathcal {S}}}\) is a specific mixed lattice ideal. \(\square \)
. This proves that \({{\mathcal {S}}}\) is a mixed lattice subgroup of \({{\mathcal {G}}}\). Moreover, \(0\preccurlyeq y\preccurlyeq x\) clearly implies that \(y\in {{\mathcal {S}}}\) and hence \({{\mathcal {S}}}\) is a specific mixed lattice ideal. \(\square \)
In the remainder of this paper, we shall use simply the terms ideal and specific ideal for mixed lattice ideals and specific mixed lattice ideals, respectively, if there is no danger of confusion.
Example 4.9
Consider the mixed lattice group \(({{\mathcal {G}}},\le ,\preccurlyeq )\) of Example 2.21. The only ideals in this mixed lattice group are \(\{0\}\) and \({{\mathcal {G}}}\). Indeed, if \({{\mathcal {S}}}\) is an ideal in \({{\mathcal {G}}}\) and \(x\in {{\mathcal {S}}}\) with \(x\ge 1\ge 0\), then since \({{\mathcal {G}}}\) is pre-regular, we have \(^{ u }x^{ l }=x\ge 1\), and so \(^{ u }1^{ l }=1\le ^{ u }x^{ l }\). Hence \(1\in {{\mathcal {S}}}\), and consequently, \(n\cdot 1=n\in {{\mathcal {S}}}\) for every \(n\in {{\mathbb {Z}}}\). Thus \({{\mathcal {S}}}={{\mathcal {G}}}\).
The subgroup \({{\mathcal {A}}}=\{pn:n\in {{\mathbb {Z}}}\}\) is a specific ideal in \({{\mathcal {G}}}\), by Lemma 4.8.
Example 4.10
Let \({{\mathcal {G}}}={{\mathbb {R}}}^2\) and define \(\le \) as the partial order induced by the positive cone \(C_1=\{(x,y):x\ge 0 \text {and} y\ge 0\}\). Define specific order \(\preccurlyeq \) as the partial order with the positive cone \(C_2=\{(x,x):x\ge 0 \}\). Both of these are compatible partial orders in \({{\mathbb {R}}}^2\). An easy verification shows that the element  exists for all \(x\in {{\mathcal {G}}}\). Thus, by Theorem 2.12, \(({{\mathcal {G}}},\le ,\preccurlyeq )\) is a mixed lattice vector space which is clearly pre-regular but not regular, since the cone \(C_2\) does not generate the whole space \({{\mathbb {R}}}^2\). It should be clear, however, that the set \({{\mathcal {S}}}=\{x\in {{\mathcal {G}}}:x\succcurlyeq 0\}\) is a mixed lattice semigroup and thus \({{\mathcal {G}}}\) is quasi-regular.
exists for all \(x\in {{\mathcal {G}}}\). Thus, by Theorem 2.12, \(({{\mathcal {G}}},\le ,\preccurlyeq )\) is a mixed lattice vector space which is clearly pre-regular but not regular, since the cone \(C_2\) does not generate the whole space \({{\mathbb {R}}}^2\). It should be clear, however, that the set \({{\mathcal {S}}}=\{x\in {{\mathcal {G}}}:x\succcurlyeq 0\}\) is a mixed lattice semigroup and thus \({{\mathcal {G}}}\) is quasi-regular.
In \(({{\mathcal {G}}},\le ,\preccurlyeq )\), the set \({{\mathcal {A}}}=\{(x,y):x=y\}\) is a specific mixed lattice ideal by Lemma 4.8, but not a mixed lattice ideal. To show that \({{\mathcal {A}}}\) is not a mixed lattice ideal, choose \(x=(1,1)\) and \(y=(1,0)\). Then \(x\in {{\mathcal {A}}}\) and \(y=^{ u }y^{ l }\le ^{ u }x^{ l }=x\), but \(y\notin {{\mathcal {A}}}\). Finally, note that \({{\mathcal {G}}}\) is a lattice with respect to \(\le \) and the x-axis is a lattice ideal in \({{\mathcal {G}}}\) but not a mixed lattice ideal. Hence, the converse of Proposition 4.6 does not hold.
Example 4.11
As another example, consider \({{\mathcal {G}}}=BV([0,1])\), the functions of bounded variation on [0, 1] (see Example 2.15). Let \({{\mathcal {S}}}\) be the set of all constant functions. Then \({{\mathcal {S}}}\) is clearly a subgroup of \({{\mathcal {G}}}\), and it is also a mixed lattice subgroup, where the upper and lower envelopes are given by  and
and  . However, \({{\mathcal {S}}}\) is not a (specific) ideal in \({{\mathcal {G}}}\). This can be seen by choosing \(f(x)=1\) and \(g(x)=1-x\). Then \(g\ge 0\) and \(f\succcurlyeq 0\), and since \({{\mathcal {G}}}\) is regular, we have \(g=^{ u }g^{ l }\) and \(f=^{ u }f^{ l }\). Now \(^{ u }g^{ l }\le ^{ u }f^{ l }\) and \(^{ u }g^{ l }\preccurlyeq ^{ u }f^{ l }\), and \(f\in {{\mathcal {S}}}\) but \(g\notin {{\mathcal {S}}}\). Hence \({{\mathcal {S}}}\) is not an ideal or a specific ideal in \({{\mathcal {G}}}\).
. However, \({{\mathcal {S}}}\) is not a (specific) ideal in \({{\mathcal {G}}}\). This can be seen by choosing \(f(x)=1\) and \(g(x)=1-x\). Then \(g\ge 0\) and \(f\succcurlyeq 0\), and since \({{\mathcal {G}}}\) is regular, we have \(g=^{ u }g^{ l }\) and \(f=^{ u }f^{ l }\). Now \(^{ u }g^{ l }\le ^{ u }f^{ l }\) and \(^{ u }g^{ l }\preccurlyeq ^{ u }f^{ l }\), and \(f\in {{\mathcal {S}}}\) but \(g\notin {{\mathcal {S}}}\). Hence \({{\mathcal {S}}}\) is not an ideal or a specific ideal in \({{\mathcal {G}}}\).
Next, consider the subset \({{\mathcal {A}}}=\{f\in {{\mathcal {G}}}:f(0)=0\}\). This is both an ideal and a specific ideal in \({{\mathcal {G}}}\). To see this, let \(f\in {{\mathcal {A}}}\) and \(^{ u }g^{ l }\le ^{ u }f^{ l }\). By the definitions of initial and specific orders (see Example 2.15), it is clear that \(^{ u }f(0)=f^{ l }(0)=0\), and so \(^{ u }f^{ l }\in {{\mathcal {A}}}\). Moreover, since \({{\mathcal {G}}}\) is regular, we have \(0\le ^{ u }g^{ l }\) and hence \(0\le ^{ u }g^{ l }(0)\le ^{ u }f^{ l }(0)=0\). This implies that \(^{ u }g^{ l }(0)=0\) and so \(g\in {{\mathcal {A}}}\). Hence, \({{\mathcal {A}}}\) is an ideal in \({{\mathcal {G}}}\), and it then follows from Proposition 4.7 that \({{\mathcal {A}}}\) is also a specific ideal in \({{\mathcal {G}}}\).
Example 4.12
Let \({{\mathcal {V}}}\) be the mixed lattice vector space of Example 2.18 with the specific positive cone \(C_s=\{f\in {{\mathcal {V}}}:f\ge 0 \text { and } f \text { is constant}\}\). The subspace \(S=C_s-C_s\) consisting of all constant functions is a specific ideal in \({{\mathcal {V}}}\) but not an ideal.
Example 4.13
Let \({{\mathcal {G}}}\) be the mixed lattice group of Example 2.19. It is easy to verify that the set of diagonal matrices is a mixed lattice ideal in \({{\mathcal {G}}}\) and the set of symmetric matrices is a specific mixed lattice ideal in \({{\mathcal {G}}}\) (by Lemma 4.8) but not an ideal. Finally, the set of integer matrices is a mixed lattice subgroup in \({{\mathcal {G}}}\) but not a specific mixed lattice ideal.
5 Mixed lattice homomorphisms
Next we use the results of the preceding sections to study mixed lattice group homomorphisms.
Definition 5.1
Let \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) be mixed lattice (semi)groups. An additive mapping \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) is a mixed lattice (semi)group homomorphism if  and
and  for all \(x,y\in {{\mathcal {G}}}\).
for all \(x,y\in {{\mathcal {G}}}\).
If T is a mixed lattice group homomorphism, then by additivity \(T(0)=0\) and \(T(-x)=-Tx\) for all \(x\in {{\mathcal {G}}}\).
Our next result gives a characterization of mixed lattice group homomorphisms. Similar characterizations are well known in Riesz spaces ([2, Theorem 2.14]) and lattice ordered groups ([14, Theorem 4.5]).
Theorem 5.2
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be an additive mapping between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\). Then the following statements are equivalent.
-
(a)
T is a mixed lattice group homomorphism.
-
(b)
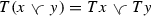 for all \(x,y\in {{\mathcal {G}}}\).
for all \(x,y\in {{\mathcal {G}}}\). -
(c)
\(T(x^{ l })=(Tx)^{ l }\) for all \(x\in {{\mathcal {G}}}\).
-
(d)
\(T(x^{ u })=(Tx)^{ u }\) for all \(x\in {{\mathcal {G}}}\).
-
(e)
\(T(^{ l }x)=^{ l }(Tx)\) for all \(x\in {{\mathcal {G}}}\).
-
(f)
\(T(^{ u }x)=^{ u }(Tx)\) for all \(x\in {{\mathcal {G}}}\).
-
(g)
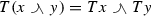 for all \(x,y\in {{\mathcal {G}}}\).
for all \(x,y\in {{\mathcal {G}}}\). -
(h)
If
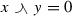 in \({{\mathcal {G}}}\), then
in \({{\mathcal {G}}}\), then 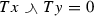 holds in \({{\mathcal {H}}}\).
holds in \({{\mathcal {H}}}\).
Proof
(a)\(\implies \)(b) Obvious.
(b)\(\implies \)(c) Assuming that (b) holds, we have

(c)\(\implies \)(d) If (c) holds, then by Theorem 3.2 (a) we have
(d)\(\implies \)(e) Assume (d) holds. From the identity \(^{ l }x=x^{ u }-x\) it follows that
(e)\(\implies \)(f) If (e) holds, then
(f)\(\implies \)(g) First we note that for any elements u and v in a mixed lattice group we have

so by additivity of T and part (f) we have

(g)\(\implies \)(h) If  then (g) implies
then (g) implies  .
.
(h)\(\implies \)(g) First we note that  , so by (h) we have
, so by (h) we have

Hence,  .
.
(g)\(\implies \)(a) If (g) holds, then

\(\square \)
Under the additional assumption that \({{\mathcal {H}}}\) contains no elements of order 2 we can add the following conditions to the list of the preceding theorem.
Proposition 5.3
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be an additive mapping between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\). If \({{\mathcal {H}}}\) contains no elements of order 2 then the following statements are equivalent.
-
(a)
T is a mixed lattice homomorphism.
-
(b)
\(T(^{ l }x^{ u })=^{ l }(Tx)^{ u }\) for all \(x\in {{\mathcal {G}}}\).
-
(c)
\(T(^{ u }x^{ l })=^{ u }(Tx)^{ l }\) for all \(x\in {{\mathcal {G}}}\).
Proof
(a)\(\implies \)(b) Applying Theorem 5.2 we get
(b)\(\implies \)(c) Follows by the identity \(^{ u }x^{ l }=^{ l }(-x)^{ u }\) in Theorem 3.4.
(c)\(\implies \)(a) By Theorem 3.5 (d) we have  , so by additivity of T we get
, so by additivity of T we get

It follows that  , and since \({{\mathcal {H}}}\) contains no elements of order 2, this implies that
, and since \({{\mathcal {H}}}\) contains no elements of order 2, this implies that  . Hence T is a mixed lattice homomorphism.
. Hence T is a mixed lattice homomorphism.
\(\square \)
In particular, the additional assumption in the preceding proposition holds in mixed lattice vector spaces. Moreover, it holds if the range of T is a mixed lattice group that is a lattice with respect to one of the partial orderings. In fact, we have the following well-known result.
Lemma 5.4
([8, Corollary 1, pp. 294]) If G is a lattice ordered group with \(x\in G\) and \(n\in {{\mathbb {N}}}\), then \(nx=0\) implies that \(x=0\).
The conclusion of the above lemma holds also in a regular Archimedean mixed lattice group. For this, we need the following lemma (which is due to the referee, to whom we are grateful).
Lemma 5.5
If \({{\mathcal {G}}}\) is a regular Archimedean mixed lattice group with \(x\in G\) and \(n\in {{\mathbb {N}}}\), then \(nx=0\) implies that \(x=0\).
Proof
First assume that \(x \ge 0\). Then \(0 \le x \le 2x \le \cdots \le nx = 0\), so \(x = 0\). Now let x be arbitrary. It follows from Corollary 3.13 that
Moreover, Theorem 3.7(c) shows that \(^{ u }x^{ l } \ge 0\) and \(^{ l }x^{ u } \ge 0\), so the first line of our proof implies that \(^{ u }x^{ l } = 0\) and \(^{ l }x^{ u } = 0\). Consequently, \(x = 0\), again by Theorem 3.7(c). \(\square \)
Combining the results of Proposition 5.3, Lemma 5.4 and Lemma 5.5 we get the following special cases of Proposition 5.3.
Corollary 5.6
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be an additive mapping between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\). Consider the following statements.
-
(a)
T is a mixed lattice group homomorphism.
-
(b)
\(T(^{ l }x^{ u })=^{ l }(Tx)^{ u }\) for all \(x\in G\).
-
(c)
\(T(^{ u }x^{ l })=^{ u }(Tx)^{ l }\) for all \(x\in G\).
The statements (a), (b) and (c) are equivalent if at least one of the following conditions hold.
-
(i)
\({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) are mixed lattice vector spaces.
-
(ii)
\({{\mathcal {H}}}\) is a lattice with respect to one of the partial orderings.
-
(iii)
\({{\mathcal {H}}}\) is a regular Archimedean mixed lattice group.
Remark 5.7
Note that in Example 2.17 we showed that there does exist mixed lattice groups that are not lattices with respect to either partial ordering. We should also point out that the conditions (b) and (c) in the above corollary always hold for any mixed lattice homomorphism but they are not necessarily equivalent to T being a homomorphism. Furthermore, the assumption in Lemma 5.4 that \({{\mathcal {G}}}\) is a lattice is not a necessary condition.
We shall say that a mapping \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) is increasing if \(x\le y\) in \({{\mathcal {G}}}\) implies that \(Tx\le Ty\) in \({{\mathcal {H}}}\). Similarly, T is specifically increasing, if \(x\preccurlyeq y\) in \({{\mathcal {G}}}\) implies that \(Tx\preccurlyeq Ty\) in \({{\mathcal {H}}}\). We now prove the following result which gives some additional basic facts about mixed lattice homomorphisms.
Theorem 5.8
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be a mixed lattice group homomorphism between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\). Then the following hold.
-
(a)
T is specifically increasing. In addition, if \({{\mathcal {G}}}\) is pre-regular then T is increasing.
-
(b)
If \({{\mathcal {S}}}\subset {{\mathcal {G}}}\) is a mixed lattice subgroup (or subsemigroup) of \({{\mathcal {G}}}\), then \(T({{\mathcal {S}}})\) is a mixed lattice subgroup (or subsemigroup) of \({{\mathcal {H}}}\).
-
(c)
If \({{\mathcal {G}}}\) is pre-regular then \(T({{\mathcal {G}}})\) is pre-regular.
-
(d)
If \({{\mathcal {G}}}\) is (quasi-)regular then \(T({{\mathcal {G}}})\) is (quasi-)regular.
-
(e)
If \({{\mathcal {G}}}\) is pre-regular and \({{\mathcal {A}}}\) is a (specific) ideal in \({{\mathcal {G}}}\), then \(T({{\mathcal {A}}})\) is a (specific) ideal in \(T({{\mathcal {G}}})\).
-
(f)
If T is bijective then \(T^{-1}\) is also a mixed lattice homomorphism.
Proof
(a) If \(x\succcurlyeq y\) then \(x-y\succcurlyeq 0\), and by Theorem 3.4 we have \((x-y)^{ u }=x-y\). Since T is a homomorphism, it follows that
and so \(Tx\succcurlyeq Ty\).
If \({{\mathcal {G}}}\) is pre-regular, then \(x\ge 0\) if and only if \(x=^{ u }x\), by 3.7. Similar arguments as above now establish that \(x\ge y\) implies that \(Tx\ge Ty\).
(b) These statements are evident by the definition of a mixed lattice homomorphism.
(c) It is sufficient to show that if \(y\in T({{\mathcal {G}}})\), then \(y\succcurlyeq 0\) implies that \(y\ge 0\). If \(y\succcurlyeq 0\) then by Theorem 3.4 (f) \(y=y^{ u }\). There exists \(x\in {{\mathcal {G}}}\) such that \(y=Tx\), and we have \(y=y^{ u }=(Tx)^{ u }=T(x^{ u })\). Now \(x^{ u }\succcurlyeq 0\) and \({{\mathcal {G}}}\) is pre-regular, so it follows that \(x^{ u }\ge 0\). By (a) T is increasing, and so \(y=T(x^{ u })\ge 0\). Hence \(T({{\mathcal {G}}})\) is pre-regular.
(d) Assume that \({{\mathcal {G}}}\) is quasi-regular. Let \({{\mathcal {U}}}=\{w\in T({{\mathcal {G}}}):w\succcurlyeq 0\}\). We need to show that \({{\mathcal {U}}}\) is a mixed lattice semigroup. If \(u,v\in {{\mathcal {U}}}\), then \(u=u^{ u }\) and \(v=v^{ u }\) by Theorem 3.4, and there exist elements \(x,y\in {{\mathcal {G}}}\) such that \(u=Tx\) and \(v=Ty\). Since \(x^{ u }\succcurlyeq 0\), \(y^{ u }\succcurlyeq 0\) and \({{\mathcal {G}}}\) is quasi-regular, it follows by Theorem 2.8 that  . By (a) T is specifically increasing, so we have
. By (a) T is specifically increasing, so we have

Hence, by Theorem 2.8 the set \({{\mathcal {U}}}\) is a mixed lattice semigroup and so \(T({{\mathcal {G}}})\) is quasi-regular. Moreover, if \({{\mathcal {G}}}\) is regular, then \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\) and \(T({{\mathcal {G}}})=T({{\mathcal {S}}})-T({{\mathcal {S}}})\), where \(T({{\mathcal {S}}})\) is a mixed lattice semigroup, as we have just proved. Hence \(T({{\mathcal {G}}})\) is regular.
(e) By Theorem 4.2 we need to show that if \(0\le Tx\le Ty\) with \(Ty\in T({{\mathcal {A}}})\), then \(Tx\in T({{\mathcal {A}}})\). Since \(Tx\ge 0\) it follows that \(Tx=^{ u }(Tx)\). Hence, \((Tx)^{ l }=T(x^{ l })=0\), which implies that \(x^{ l }=0\), and so \(x\ge 0\). Moreover, \(0\le Tx\le Ty\) implies that \(T(y-x)\ge 0\), and again similar reasoning shows that \(y-x\ge 0\). Hence we have \(0\le x\le y\) with \(y\in {{\mathcal {A}}}\), and since \({{\mathcal {A}}}\) is an ideal, it follows that \(x\in {{\mathcal {A}}}\) and so \(Tx\in T({{\mathcal {A}}})\). Moreover, since \(^{ u }(Tx)^{ l }=T(^{ u }x^{ l })\) and \({{\mathcal {A}}}\) is an ideal it follows that \(^{ u }(Tx)^{ l }\in T({{\mathcal {A}}})\) if and only if \(Tx\in T({{\mathcal {A}}})\). Hence, \(T({{\mathcal {A}}})\) is an ideal, by Theorem 4.2. The proof is essentially the same for specific ideals.
(f) Let \(y\in {{\mathcal {H}}}\) and set \(x=T^{-1}y\). Then \(T(x^{ u })=y^{ u }\), and we have \(T^{-1}(y^{ u })=x^{ u }=(T^{-1}y)^{ u }\). Thus \(T^{-1}\) is a mixed lattice homomorphism, by Theorem 5.2. \(\square \)
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be a group homomorphism, and recall that the kernel of T is the set \(N(T)=\{x\in {{\mathcal {G}}}: Tx=0\}\). We give the following result concerning the kernel of a mixed lattice homomorphism.
Theorem 5.9
Let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be a mixed lattice group homomorphism between two mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\). If \({{\mathcal {G}}}\) is pre-regular then the kernel N(T) is an ideal, and hence a specific ideal.
Proof
The kernel N(T) is certainly a subgroup of \({{\mathcal {G}}}\), and it is also a mixed lattice subgroup of \({{\mathcal {G}}}\), for if \(x,y\in N(T)\) then  , hence
, hence  . Assume then that \({{\mathcal {G}}}\) is pre-regular. Then by 3.7 we have \(^{ u }x^{ l }\ge 0\) for all \(x\in {{\mathcal {G}}}\). Suppose now that \(0\le ^{ u }y^{ l }\le ^{ u }x^{ l }\) with \(x\in N(T)\). By Theorem 5.8T is increasing, and so we have
. Assume then that \({{\mathcal {G}}}\) is pre-regular. Then by 3.7 we have \(^{ u }x^{ l }\ge 0\) for all \(x\in {{\mathcal {G}}}\). Suppose now that \(0\le ^{ u }y^{ l }\le ^{ u }x^{ l }\) with \(x\in N(T)\). By Theorem 5.8T is increasing, and so we have
Hence, \(T(^{ u }y^{ l })=^{ u }(Ty)^{ l }=0\), and it follows by Theorem 3.7 (c) that \(Ty=0\), or \(y\in N(T)\). This shows that N(T) is an ideal in \({{\mathcal {G}}}\), and hence a specific ideal by Proposition 4.7. \(\square \)
The converse of the preceding theorem holds too, in the sense that if \({{\mathcal {A}}}\) is an ideal in a pre-regular mixed lattice group \({{\mathcal {G}}}\), then there exists a mixed lattice homomorphism whose kernel is \({{\mathcal {A}}}\). We will prove this later in Theorem 6.3.
If \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) is a bijective mixed lattice homomorphism, then so is \(T^{-1}\) (by Theorem 5.8), and T is called a mixed lattice isomorphism, and the mixed lattice groups \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) are said to be isomorphic. In pre-regular mixed lattice groups, isomorphisms have the following characterization, which is analogous to the characterization of Riesz isomorphisms between two Riesz spaces (see [16, Theorem 18.5]). Additionally, Eriksson–Bique has proved a similar result for isomorphisms between two mixed lattice semigroups ([10, Theorem 4.3]).
Theorem 5.10
Let \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) be pre-regular mixed lattice groups and \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) a bijective additive mapping. Then T is a mixed lattice isomorphism if and only if both T and \(T^{-1}\) are increasing and specifically increasing.
Proof
If T is an isomorphism, then \(T^{-1}\) is also an isomorphism and they are both increasing and specifically increasing by Theorem 5.8. Conversely, assume that T and \(T^{-1}\) are increasing and specifically increasing. If \(x,y\in {{\mathcal {G}}}\), then  and
and  , which implies that
, which implies that  and
and  . Hence,
. Hence,  . Similar reasoning shows that
. Similar reasoning shows that  for all \(u,v\in {{\mathcal {H}}}\). Since T is bijective, there exist unique u and v in \({{\mathcal {H}}}\) such that \(u=Tx\) and \(v=Ty\). So we have
for all \(u,v\in {{\mathcal {H}}}\). Since T is bijective, there exist unique u and v in \({{\mathcal {H}}}\) such that \(u=Tx\) and \(v=Ty\). So we have  . Now since T is increasing, we can apply T and obtain
. Now since T is increasing, we can apply T and obtain  . Hence,
. Hence,  , and so T is a mixed lattice homomorphism. Since T was assumed to be bijective, T is an isomorphism. \(\square \)
, and so T is a mixed lattice homomorphism. Since T was assumed to be bijective, T is an isomorphism. \(\square \)
Mixed lattice homomorphisms also have a domination property described in the next theorem. For a similar result in Riesz spaces, see ([15, 2.6.9]).
Proposition 5.11
Let \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) be mixed lattice groups and \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) a mixed lattice homomorphism. If \(S:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) is an additive mapping such that S and \(T-S\) are both increasing and specifically increasing, then S is a mixed lattice homomorphism.
Proof
Let x and y be elements of \({{\mathcal {G}}}\) satisfying  . This implies that \(x\succcurlyeq 0\) and \(y\ge 0\). To see this, we write
. This implies that \(x\succcurlyeq 0\) and \(y\ge 0\). To see this, we write  , or \(x=(x-y)^{ u }\succcurlyeq 0\). Similarly we get \(y=^{ u }(y-x)\ge 0\). By our hypothesis it follows that \(0\preccurlyeq Sx\preccurlyeq Tx\) and \(0\le Sy\le Ty\). Since T is a homomorphism, we have
, or \(x=(x-y)^{ u }\succcurlyeq 0\). Similarly we get \(y=^{ u }(y-x)\ge 0\). By our hypothesis it follows that \(0\preccurlyeq Sx\preccurlyeq Tx\) and \(0\le Sy\le Ty\). Since T is a homomorphism, we have  . Hence
. Hence  and so by Theorem 5.2S is a mixed lattice homomorphism. \(\square \)
and so by Theorem 5.2S is a mixed lattice homomorphism. \(\square \)
We will now examine the extensions of mixed lattice semigroup homomorphisms to mixed lattice group homomorphisms. The following lemma is a slight modification of Kantorovich’s classical extension lemma in Riesz spaces (see [2, Theorem 1.10]).
Lemma 5.12
Let \({{\mathcal {S}}}\) and \({{\mathcal {T}}}\) be Abelian semigroups and \(T:{{\mathcal {S}}}\rightarrow {{\mathcal {T}}}\) an additive mapping. If \({{\mathcal {G}}}\) and \({{\mathcal {H}}}\) are the groups generated by \({{\mathcal {S}}}\) and \({{\mathcal {T}}}\), respectively (i.e. \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\) and \({{\mathcal {H}}}={{\mathcal {T}}}-{{\mathcal {T}}}\)), then there exists a unique additive mapping \(S:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) such that S extends T, that is, \(Sx=Tx\) for all \(x\in {{\mathcal {S}}}\).
The next result shows that if a mixed lattice group is extended to a group of formal differences, then a mixed lattice semigroup homomorphism can be extended to a mixed lattice group homomorphism.
Theorem 5.13
Let \(T:{{\mathcal {S}}}\rightarrow {{\mathcal {T}}}\) be a mixed lattice semigroup homomorphism between two mixed lattice semigroups \({{\mathcal {S}}}\) and \({{\mathcal {T}}}\). If \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\) and \({{\mathcal {H}}}={{\mathcal {T}}}-{{\mathcal {T}}}\) are the mixed lattice group extensions of \({{\mathcal {S}}}\) and \({{\mathcal {T}}}\), then T can be extended to a mixed lattice group homomorphism \(S:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\).
Proof
Let \(T:{{\mathcal {S}}}\rightarrow {{\mathcal {T}}}\) be a mixed lattice semigroup homomorphism. Since T is an additive map, by Lemma 5.12 it has an additive extension \(S:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) where \({{\mathcal {G}}}={{\mathcal {S}}}-{{\mathcal {S}}}\) and \({{\mathcal {H}}}={{\mathcal {T}}}-{{\mathcal {T}}}\) are the mixed lattice group extensions of \({{\mathcal {S}}}\) and \({{\mathcal {T}}}\), respectively. We need to show that the extension S preserves the mixed lattice operations. Let \(w,z\in {{\mathcal {G}}}\) and write \(w=u-v\) and \(z=x-y\) where \(u,v,x,y\in {{\mathcal {S}}}\). Then by Theorem 2.7

Since \(S=T\) on \({{\mathcal {S}}}\), we get

for all \(w,z\in {{\mathcal {G}}}\). It now follows from Theorem 5.2 that S is a mixed lattice group homomorphism. \(\square \)
6 Quotient mixed lattice groups
In this section we examine how quotient group constructions work in mixed lattice groups, and we obtain results that have analogues in Riesz space theory. For these we refer to [16, Chapter 3, §18].
Let \({{\mathcal {G}}}\) be an additive group and \({{\mathcal {S}}}\) a subgroup of \({{\mathcal {G}}}\). An equivalence relation \(\sim \) in \({{\mathcal {G}}}\) is defined as \(x\sim y\) iff \(x-y\in {{\mathcal {S}}}\). The equivalence class (or coset) of \(x\in {{\mathcal {G}}}\) is denoted by [x], and we identify \({{\mathcal {S}}}=[0]\). The quotient group of \({{\mathcal {G}}}\) modulo \({{\mathcal {S}}}\) is denoted by \({{\mathcal {G}}}/{{\mathcal {S}}}\). The set \({{\mathcal {G}}}/{{\mathcal {S}}}\) with addition defined by
is a group, where \(-[x]=[-x]\).
Assume now that \({{\mathcal {G}}}\) is a pre-regular mixed lattice group. We will prove that if \({{\mathcal {A}}}\) is an ideal in \({{\mathcal {G}}}\) then we can define initial and specific orders in \({{\mathcal {G}}}/{{\mathcal {A}}}\) in such manner that \({{\mathcal {G}}}/{{\mathcal {A}}}\) becomes a mixed lattice group. First we define the partial orderings.
Definition 6.1
Let \({{\mathcal {A}}}\) be an ideal in a pre-regular mixed lattice group \({{\mathcal {G}}}\). If \([x],[y]\in {{\mathcal {G}}}/{{\mathcal {A}}}\) then we define \([x]\le [y]\) whenever there exists elements \(x\in [x]\) and \(y\in [y]\) such that \(x\le y\) in \({{\mathcal {G}}}\). Similarly, \([x]\preccurlyeq [y]\) whenever there exists elements \(x\in [x]\) and \(y\in [y]\) such that \(x\preccurlyeq y\) in \({{\mathcal {G}}}\).
Before we proceed we need to verify that the relations given in the above definition are indeed partial orderings in \({{\mathcal {G}}}/{{\mathcal {A}}}\). We will begin with the initial order. Reflexivity is obvious. For transitivity, assume that \([x]\le [y]\) and \([y]\le [z]\). Let \(x\in [x]\), \(y_1,y_2\in [y]\) and \(z\in [z]\) be such that \(x\le y_1\) and \(y_2\le z\). Then
but by definition \(y_1-y_2\in {{\mathcal {A}}}\), and so \(z + (y_1 - y_2)\in [z]\). This shows that \([x]\le [z]\).
Finally, to prove antisymmetry, let \([x]\le [y]\) and \([y]\le [x]\). Then there exist \(x_1,x_2\in [x]\) and \(y_1,y_2\in [y]\) such that \(x_1\le y_1\) and \(y_2\le x_2\). Since \({{\mathcal {A}}}\) is a subgroup, it follows that
Since \({{\mathcal {A}}}\) is an ideal, it follows that \(y_1-x_1 \in {{\mathcal {A}}}\), that is, \([x]=[y]\). Noting that \({{\mathcal {A}}}\) is also a specific ideal (by Proposition 4.7), we can show similarly that the specific order given in Definition 6.1 is likewise a partial ordering in \({{\mathcal {G}}}/{{\mathcal {A}}}\).
We will now show that with these orderings the set \({{\mathcal {G}}}/{{\mathcal {A}}}\) becomes a pre-regular mixed lattice group.
Theorem 6.2
If \({{\mathcal {A}}}\) is an ideal in a pre-regular mixed lattice group \({{\mathcal {G}}}\), then \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a pre-regular mixed lattice group with respect to initial and specific orders given in Definition 6.1.
Proof
First we must show that these partial orderings are compatible with the group structure, that is, \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a partially ordered group with respect to orderings \(\le \) and \(\preccurlyeq \). To this end, assume that \([x]\le [y]\) and choose \(x\in [x]\) and \(y\in [y]\) such that \(x\le y\), and let \(z\in [z]\). Then \(x+z\le y+z\), and so \([x+z]\le [y+z]\). By definition of addition in \({{\mathcal {G}}}/{{\mathcal {A}}}\), this is equivalent to \([x]+[z]\le [y]+[z]\). The specific order \(\preccurlyeq \) is treated similarly.
It remains to show that \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a mixed lattice group. We will do this by showing that \([x]^{ u }\) exists for all \(x\in {{\mathcal {G}}}\) and it is equal to \([x^{ u }]\). Let \(x\in {{\mathcal {G}}}\) and notice that \(x^{ u }\ge x\) and \(x^{ u }\succcurlyeq 0\), so we have \([x]\le [x^{ u }]\) and \([0]\preccurlyeq [x^{ u }]\). Assume then that \([x]\le [y]\) and \([0]\preccurlyeq [y]\). Then there exist \(x_1\in [x]\) and \(y_1,y_2\in [y]\) such that \(x_1\le y_1\) and \(0\preccurlyeq y_2\). It follows that  and
and  . This implies that
. This implies that

Now we also have
and therefore

Now, since \(y_1,y_2\in [y]\) and \(x,x_1\in [x]\), we have \(y_1-y_2 \in {{\mathcal {A}}}\) and \(x-x_1 \in {{\mathcal {A}}}\), and since \({{\mathcal {A}}}\) is a mixed lattice subgroup, it follows that \((y_1-y_2)^{ u }\in {{\mathcal {A}}}\) and \((x-x_1)^{ u }\in {{\mathcal {A}}}\). Hence we have
Thus, \([x^{ u }]\le [y]\) and so we have proved that

and so \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a mixed lattice group, by Theorem 2.12.
Finally, assume that \({{\mathcal {G}}}\) is pre-regular and let \([x]\preccurlyeq [y]\). Then there exist \(x\in [x]\) and \(y\in [y]\) satisfying \(x\preccurlyeq y\) in \({{\mathcal {G}}}\). Since \({{\mathcal {G}}}\) is pre-regular, this implies that \(x\le y\). Consequently, \([x]\le [y]\) and so \({{\mathcal {G}}}/{{\mathcal {A}}}\) is pre-regular. \(\square \)
The mixed lattice group \({{\mathcal {G}}}/{{\mathcal {A}}}\) is called the quotient mixed lattice group of \({{\mathcal {G}}}\) modulo \({{\mathcal {A}}}\).
Now we observe that there is a close connection between mixed lattice homomorphisms and quotient mixed lattice groups.
Theorem 6.3
If \({{\mathcal {A}}}\) is an ideal in a pre-regular mixed lattice group \({{\mathcal {G}}}\), then \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a mixed lattice homomorphic image of \({{\mathcal {G}}}\) under the canonical mapping \(x\mapsto [x]\). Conversely, if \({{\mathcal {G}}}\) is pre-regular and \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) is a surjective mixed lattice homomorphism with kernel N(T), then \({{\mathcal {G}}}/N(T)\) and \({{\mathcal {H}}}\) are isomorphic.
Proof
Let \({{\mathcal {G}}}\) be a pre-regular mixed lattice group and \({{\mathcal {A}}}\) an ideal in \({{\mathcal {G}}}\). Inspecting the proof of Theorem 6.2 reveals that \([x^{ u }]=[x]^{ u }\) in \({{\mathcal {G}}}/{{\mathcal {A}}}\), and so by Theorem 5.2 the mapping \(x\mapsto [x]\) is a mixed lattice homomorphism of \({{\mathcal {G}}}\) onto \({{\mathcal {G}}}/{{\mathcal {A}}}\), and \({{\mathcal {A}}}\) is the kernel of this homomorphism.
Conversely, let \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {H}}}\) be a surjective mixed lattice homomorphism with kernel N(T). Then by Theorem 5.9, N(T) is an ideal in \({{\mathcal {G}}}\), and \({{\mathcal {G}}}/N(T)\) is a mixed lattice group by Theorem 6.2. Now the mapping \(f:{{\mathcal {G}}}/N(T)\rightarrow {{\mathcal {H}}}\), where \(f([x])=Tx\), is a mixed lattice isomorphism of \({{\mathcal {G}}}/N(T)\) onto \({{\mathcal {H}}}\). To prove this, we need to show that f is a bijective mixed lattice homomorphism. First, if \(Tx=Ty\) then \(T(x-y)=0\), and so \(x-y\in N(T)\). But this means that x and y belong to the same equivalence class in \({{\mathcal {G}}}/N(T)\), that is, \([x]=[y]\). Thus f is injective. Next, let \(z\in {{\mathcal {H}}}\). Since T is surjective, there exists an element \(x\in {{\mathcal {G}}}\) such that \(z=Tx\). Now we have \(f([x])=Tx=z\), and so f is surjective. Finally, since \([x^{ u }]=[x]^{ u }\) in \({{\mathcal {G}}}/N(T)\), and T is a homomorphism, it follows that
Hence, f is a bijective homomorphism, and therefore an isomorphism. \(\square \)
Combining the two preceding theorems with Theorem 5.8(d) we get the following result.
Corollary 6.4
If \({{\mathcal {A}}}\) is an ideal in a quasi-regular (regular) mixed lattice group \({{\mathcal {G}}}\), then \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a quasi-regular (regular, respectively) mixed lattice group with respect to initial and specific orders given in Definition 6.1.
We conclude this section with an example.
Example 6.5
Let \({{\mathcal {G}}}=BV([0,1])\) be the set of all functions of bounded variation on the interval [0, 1] (see Example 2.15). In Example 4.11 we saw that the set \({{\mathcal {S}}}\) of all constant functions is a mixed lattice subgroup of \({{\mathcal {G}}}\), but not an ideal. In Example 4.11 we also considered the set \({{\mathcal {A}}}=\{f\in {{\mathcal {G}}}:f(0)=0\}\), which was seen to be an ideal in \({{\mathcal {G}}}\). As a group, the quotient group \({{\mathcal {G}}}/{{\mathcal {S}}}\) can be identified with the subgroup \({{\mathcal {A}}}\) of \({{\mathcal {G}}}\). If we define a mapping \(T:{{\mathcal {G}}}/{{\mathcal {S}}}\rightarrow {{\mathcal {A}}}\) by \(T([f])=f-f(0)\), then T is clearly an additive map (that is, a group homomorphism), which is bijective. Indeed, if \(T([f])=T([g])\) and choose any \(f\in [f]\) and \(g\in [g]\), then \(f-f(0)=g-g(0)\), or \(f-g=f(0)-g(0)\). Now \(f(0)-g(0)\) is a constant and so \(f-g\in {{\mathcal {S}}}\), or \([f]=[g]\). Thus T is injective. Let \(f\in {{\mathcal {A}}}\). Then \(f\in {{\mathcal {G}}}\) and so \(f\in [f]\in {{\mathcal {G}}}/{{\mathcal {S}}}\), and we have \(T([f])=f-f(0)=f\), since \(f(0)=0\) for all \(f\in {{\mathcal {A}}}\). Hence T is surjective. This shows that the groups \({{\mathcal {G}}}/{{\mathcal {S}}}\) and \({{\mathcal {A}}}\) are isomorphic.
Now, since \({{\mathcal {S}}}\) is not an ideal, Theorem 6.1 does not apply here. In particular, the canonical mapping \(x\mapsto [x]\) is not a mixed lattice homomorphism, because the kernel of this mapping is \({{\mathcal {S}}}\), and the kernel of a mixed lattice homomorphism is necessarily an ideal (by Theorem 5.9).
Since \({{\mathcal {A}}}\) is an ideal in \({{\mathcal {G}}}\) (see Example 4.11), the quotient group \({{\mathcal {G}}}/{{\mathcal {A}}}\) is a mixed lattice group and the canonical map \(f\mapsto [f]\) is a mixed lattice homomorphism. We observe that the elements of \({{\mathcal {G}}}/{{\mathcal {A}}}\) are the equivalence classes determined by constant functions, that is, \({{\mathcal {G}}}/{{\mathcal {A}}}=\{[f]: f \text { is constant} \}\). Indeed, if f and g are in [f], then \(f-g\in {{\mathcal {A}}}\), or \((f-g)(0)=0\). This implies that \(f(0)=g(0)\) and hence \([f]=[g]\) if and only if \(f(0)=g(0)\). Since f(0) is a constant, we have \([f]=[f(0)]\).
Now the mapping \(T:{{\mathcal {G}}}\rightarrow {{\mathcal {S}}}\) defined by \(Tf=f(0)\) is a surjective mixed lattice homomorphism, since

and the kernel of T is \({{\mathcal {A}}}\). Hence, by Theorem 6.3, \({{\mathcal {G}}}/{{\mathcal {A}}}\) and \({{\mathcal {S}}}\) are isomorphic mixed lattice groups.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Aliprantis, C.D., Border, K.C.: Infinite Dimensional Analysis, 3rd edn. Springer, Berlin (2006)
Aliprantis, C.D., Burkinshaw, O.: Positive Operators. Springer, Berlin (2006)
Apostol, T.: Mathematical Analysis, second edn. Pearson, London (1974)
Arsove, M., Leutwiler, H.: Quasibounded and singular functions. Trans. Am. Math. Soc. 189, 275–302 (1974)
Arsove, M., Leutwiler, H.: Infinitesimal generators and quasi-units in potential theory. Proc. Natl. Acad. Sci. U.S.A. 72, 2498–2500 (1975)
Arsove, M., Leutwiler, H.: Quasi-units in mixed lattice structures. Potential Theory, Copenhagen 1979. Lecture Notes in Mathematics, vol. 787, pp. 35–54. Springer, Berlin (1980)
Arsove, M., Leutwiler, H.: Algebraic Potential Theory. Memoirs of the American Mathematical Society, vol. 226. American Mathematical Society, Providence (1980)
Birkhoff, G.: Lattice Theory, 3rd edn. American Mathematical Society, Providence (1973)
Boboc, N., Bucur, G., Cornea, A.: Order and Convexity in Potential Theory: H-Cones. Lecture Notes in Mathematics, vol. 853. Springer, Berlin (1981)
Eriksson-Bique, S.-L.: Generalized Riesz spaces. Rev. Roumaine Math. Pures Appl. 36(1–2), 47–69 (1991)
Eriksson-Bique, S.-L.: Mixed lattice groups. Rev. Roumaine Math. Pures Appl. 44(2), 171–180 (1999)
Fuchs, L.: Partially Ordered Algebraic Systems. Pergamon Press, Oxford (1963)
Getoor, R.K.: Excessive Measures. Birkhauser, Boston (1990)
Hong, L.: Locally solid topological lattice-ordered groups. Arch. Math. (Brno) 51, 107–128 (2015)
Jameson, G.: Ordered Linear Spaces. Lecture Notes in Mathematics, vol. 141. Springer, Berlin (1970)
Luxemburg, W.A.J., Zaanen, A.C.: Riesz Spaces, vol. I. North-Holland Publishing Company, Amsterdam (1971)
Acknowledgements
The authors would like to thank Dr. David Seifert and the anonymous referee for several helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
L. Paunonen is funded by the Academy of Finland Grant Number 298182.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eriksson, SL., Jokela, J. & Paunonen, L. Generalized absolute values, ideals and homomorphisms in mixed lattice groups. Positivity 25, 939–972 (2021). https://doi.org/10.1007/s11117-020-00794-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11117-020-00794-2
Keywords
- Mixed lattice
- Mixed lattice group
- Mixed lattice semigroup
- Riesz space
- Lattice ordered group
- Absolute value
- Ideal



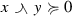 for all
for all  is the mixed lower envelope in
is the mixed lower envelope in 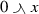 exists for all
exists for all 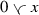 exists for all
exists for all 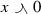 exists for all
exists for all 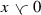 exists for all
exists for all 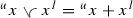 and
and 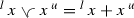
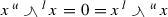
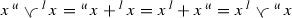
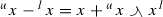 and
and 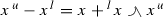 .
.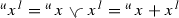 and
and 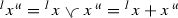 .
.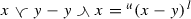 and
and 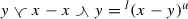
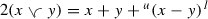 and
and 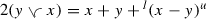 .
.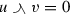 then
then 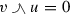 then
then 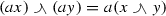 and
and 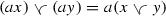 for all
for all 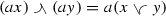 and
and 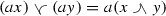 for all
for all 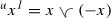 and
and 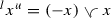 .
.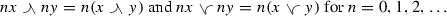
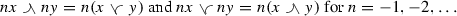 .
.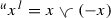 and
and 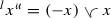 .
. and
and 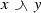 belong to
belong to 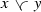 and
and 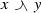 are the upper and lower mixed envelopes in
are the upper and lower mixed envelopes in 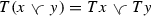 for all
for all 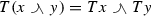 for all
for all 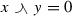 in
in 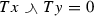 holds in
holds in