Introduction

Public investment to alleviate congestion on national road networks attracts much scrutiny due to the high costs involved and the essential nature of key infrastructure. Having accurate models of road traffic to allow policy makers to undertake long-term planning are therefore necessary. Static Traffic Assignment (TA) models are frequently used for strategic transportation planning within travel demand models (Department for Transport 2022). Much of current research focuses on dynamic TA which can model congestion more accurately, however static TA still has a specific use for the economic appraisal of long-term future changes to traffic patterns at the entire network level (Patil et al. 2021; Tsanakas et al. 2020).

Origin–Destination (O-D) demand estimation is a key challenge for static TA models and road transportation planning. O-D demand matrices represent the number of trips taken by drivers between distinct origins and destinations on the road network within a specific analysis time period (Abrahamsson 1998). In the literature there are a range of different approaches for their estimation (Bera and Rao 2011).

An established way of obtaining O-D matrices is through manual surveys of road users. However, these can be expensive and laborious, having low sample rates leading to high sampling bias risk and missed movements (Hazelton 2000). As an alternative in recent years there has been interest in new forms of historic trip data which provide information on driver trajectories from sources such as mobile phone GSM, GPS and Automatic Number Plate Recognition (ANPR) (Cvetek et al. 2021; Landmark et al. 2021; Liao et al. 2022). However, these types of data have issues relating to privacy and integration into the road network which limits their accessibility for data-driven modelling (Mahajan et al. 2021). Further approaches include utilising zone-based activity and socio-economic data to simulate approximate theoretical demands (Horni et al. 2016; Ren et al. 2014), and toll gate data in closed highway systems (Zeng et al. 2021).

In many countries, inductive loops under the main strategic roads are used to monitor traffic. Often this data is publicly available and does not entail privacy concerns (GraphHopper 2021). However, inductive loops do not provide any information on the routes drivers take. Techniques in the literature exist which can use flow count data from loop detectors to estimate O-D demand without the additional need for survey or historic trip data.

Attempting to estimate the O-D matrix solely from mean traffic flows entails problems relating to identifiability as the number of edge flow counts is less than the number of O-D demand pairs to be estimated, so it is difficult to know which vehicles on a road are travelling between which O-D nodes (Hazelton 2003).

Network tomography-based approaches such as Hazelton (2000); Vardi (1996); Lo et al. (1996); Dey et al. (2020) attempt to use the stochastic nature of traffic counts to estimate O-D demands using multiple samples of edge flows on the network for the estimation time period. Assuming the Poisson distribution of demands and a non-congested network, the Generalised Least Squares (GLS) as formulated in Hazelton (2003) is a practical version of this approach which has been applied to real world highway networks in static TA models (Zhang et al. 2018). Although its assumptions may be strong (Tebaldi and West 1998), due to its relatively lower computational requirements compared to the other network tomography-based approaches, the GLS is useful for gaining a prior matrix to be subsequently refined to include the effects of congestion through O-D adjustment algorithms (Spiess 1990; Lundgren and Peterson 2008). Other related flow count techniques are reported to have superior accuracy, however they require additional data sources such as privacy sensitive ANPR (Rostami Nasab and Shafahi 2020; Yang et al. 2017; Parry and Hazelton 2012).

GLS and network tomography-based techniques in general have difficulties working with large network sizes due to high space and time complexity in the involved processes (Brander and Sinclair 1996). Previous real-world applications of GLS have been limited to 34 node road networks with routes between O-D pairs limited to one (Zhang et al. 2018). Other network tomography-based approaches have been applied to smaller sized road networks (Dey et al. 2020; Hazelton 2001).

In this article, we propose a novel method to apply edge flow count O-D estimation to large-scale real-world road networks. This is done by partitioning the network into communities of smaller subnetworks to apply estimation to. We carry out an analysis of how partitioning a road network into a range of sizes affects accuracy and computational requirements.

Our partitioning approach uses community detection. Many networks representing complex systems contain a modular structure where the nodes cluster into communities of relative high density of connections with fewer connections between (Traag et al. 2019). A well-known performance measure to detect such community structure is network modularity (Fortunato 2010). One of the most used algorithms to evaluate modularity, which is an NP-complete problem (Brandes et al. 2006; Leeuwen et al. 2019), is the Louvain algorithm which allows the evaluation of a hierarchy of community partitions to be made (Blondel et al. 2008). A resolution parameter can determine the size of clusters that are identified. Applied to a road network, this can group areas of the network into clusters which are internally well-connected and externally less strongly. Basing community detection and the resulting partitioning on modularity utilises the network distance and not geographic distance between pairs which can be different. The grouping of nodes closer together on the network benefits the GLS estimation as the method does not account for geography constraints explicitly (Dey et al. 2020).

Previously, modularity and Louvain have been used to investigate high-level spatial and temporal patterns in travel demand when the demand is known, finding a strong relation between demand and geographic closeness of O-D pairs (Leeuwen et al. 2019). This provides evidence that the structure of travel demand could work with partitioned estimation.

Other works in transport literature have partitioned road networks with different approaches, utilising it for microscopic simulation (Ahmed and Hoque 2016), macroscopic fundamental diagrams (Dantsuji et al. 2019; Lin and Xu 2020), and traffic management through travel speed correlation (Yu et al. 2021). As far as we know, previous research has not used partitioning the road network via network modularity for flow-count demand estimation within static TA.

Our work develops several ways of applying partitioning to the estimation problem. The partitions can be the basis of reducing the road network down to a smaller, degenerated network with single nodes representing each community. Such a model could be integrated into infrastructure models such as NISMOD in the UK (Blainey and Preston 2019) which work at the scale of large urban areas but lack accurate treatment of traffic modelling. Previous works (e.g., Arnold et al. 2004) define cities or centroids of pre-determined zones as the nodes of networks, however, such approaches do not directly consider network properties in the creation of these zones. By utilising modularity as a basis for partitioning, the degenerate method can utlise network properties and avoid inaccuracies from grouping nodes that are close together geographically but not by network distance (or are even disconnected).

The partitions are also used within non-degenerate approaches, which preserve the road network in full but utilise the different scales of analysis, internal and external to the partitions, to estimate a full network demand matrix with increased agility.

Standard validation techniques are often inadequate to assess the effects of the partitioning on the estimates (Dey et al. 2020). Comparing the estimated matrix to another validation data source, such as historic trips, is problematic as that is still only a sample of the movements. It is impractical to account for all the movements on a large-scale road network for a ground-truth matrix. For this reason the validation of the results is done via the relative accuracy, predicting the flow and travel times through the user-equilibrium flow pattern of a derived static TA model.

To test this approach primarily we use flow count data from the England Strategic Road Network (SRN), a large real-world non-closed highway network suitable as a case study. This new technique is applied to a sample subnetwork connecting major metropolitan areas in England, using traffic flow count data obtained from the Motorway Incident Detection and Automatic Signalling (MIDAS) system used by National Highways (England) on the National Traffic Information Service (NTIS) model.

Summary of contribution

In this work, we propose a novel integrated and scalable method to obtain O-D estimations for large real-world highway networks and evaluate its performance producing accurate user-equilibrium flow patterns with static TA models. We do this by using network modularity as a basis for dividing up the road network into partitioned subnetworks to reduce the computational difficulty of the O-D estimation problem. This new technique is applied to a large portion of England’s SRN. It is demonstrated that the incorporation of partitioned O-D estimation within user-equilibrium flow pattern calculation has the effect of enabling reasonable estimates of the predicted flows and travel times compared to the unpartitioned case while greatly reducing the computational requirements. It is shown in the results that non-degenerate internal-only and internal-external combined approaches with large partitions leads to the best accuracy.

The primary contributions of our work are summarized as:

  • A new method of producing O-D matrices from flow counts is proposed which utilises network modularity to determine the optimal way to partition the network effectively and automatically.

  • The new method is applied in the calculation of user-equilibrium flow patterns solely from loop detector data on large scale real-world networks without the current size limitations of similar existing O-D estimation techniques.

  • Different approaches to utilising the partitioning are investigated: one degenerates the network based on the partitioning; others use the partitioning to focus on estimating the prior matrix from the internal and/or external movements of the partitioned nodes. It is found that using within-the-partition internal estimates for the O-D appraisal provides the best accuracy. Including the external between-the-partition estimates can help computation time.

The overall structure of this paper is summarized as follows. The "Traffic assignment model description" section describes the overall methodology for creating a full single-class, static TA model using network and loop detector data. In the "Network simplification and partitioned demand profile calculation" section, the method of network simplification is presented. The "Application on the England Strategic Road Network" section provides a summary description of the MIDAS and NTIS datasets used for the case study. In the "Results" section the main results are presented. Lastly, the paper is concluded with a discussion in the "Discussion" section, followed by a conclusion in the "Conclusion" section.

Traffic assignment model description

Preliminaries and notation

Notation

In this work all the vectors are column vectors. For example, the column vector x is written as \({\textbf {x}} =\{x_i,...,x_{dim({\textbf {x}})}\}\), where dim(x) is the dimension of x. We use a ’prime’ (e.g. x’) to denote the transpose of a matrix or vector. \({\mathbb {R}}_+\) denotes the set of all non-negative real numbers. Matrix Q \(\ge\) 0 or vector x \(\ge\) 0 indicates that all entries of a matrix Q or vector x are non-negative. Also, \(\vert {\mathcal {X}}\vert\) represents the cardinality of a set \({\mathcal {X}}\), and \([\![{\mathcal {X}}]\!]\) is used for the set \(\{1,...,\vert {\mathcal {X}}\vert \}\).

Network definition

We model the road network as a directed graph with a set of nodes \({\mathcal {V}}\) and a set of edges \({\mathcal {A}}\). The model assumes the graph is strongly connected and is defined by the node-edge incidence matrix with \({\textbf {N}} \in \{0,1,-1\}^{(\vert {\mathcal {V}}\vert \times \vert {\mathcal {A}}\vert )}\). On road networks in general, and the English SRN in particular, there is a path between all pairs of nodes so the assumption is valid.

The set of all O-D pairs on the network is denoted by \({\mathcal {W}} =\{{\textbf {w}}_i:{\textbf {w}}_i =(w_{si},w_{ti}),i=1,...,\vert {\mathcal {W}}\vert \}\), where \(w_{si}\) is the origin node and \(w_{ti}\) is the destination node of O-D pair i. The amount of travel demand between any single O-D pair \({\textbf {w}}=(w_s,w_t)\) is represented by \(\hat{d}^{\textbf {w}}\ge 0\). Using this, \(\textbf{d}^\textbf{w}\in {\mathbb {R}}^{\vert {\mathcal {V}}\vert }\) is defined as a vector with all zeros except for two entries of \(-\hat{d}^{{\textbf {w}}}\) for node \(w_s\) and a \(\hat{d}^{{\textbf {w}}}\) for node \(w_t\). Then, \({\textbf {d}}^{{\textbf {w}}_i}\) is a demand vector for O-D pair i, which can be combined for all O-D pairs to create the O-D demand matrix represented using \({\textbf {D}}\in {\mathbb {R}}^{\vert {\mathcal {V}}\vert \times \vert {\mathcal {W}}\vert }\).

For the demand estimation in the "Calculation of O-D demand matrices from flow counts" section, the O-D demand matrix \({\textbf {D}}\) is denoted in a simplified vector form as \({\textbf {g}}=(g_i; i\in [\![{\mathcal {W}}]\!])\) with each \(g_i\) equivalent to \(\hat{d}^{{\textbf {w}}_i}\). \({\mathcal {R}}_i\) is the index set of simple routes (without cycles) connecting O-D pair \(i\in [\![{\mathcal {W}}]\!]\), each \(r\in {\mathcal {R}}_i\) is a different sequence of edges which connect the O-D pair.

Let \({\textbf {x}}\in {\mathbb {R}}_+^{\vert {\mathcal {A}}\vert }\) be the vector of the total edge flow \(x_a\) on edge \(a\in {\mathcal {A}}\). Then the set of feasible flow vectors \({\mathcal {F}}\) is defined by:

$$\begin{aligned} {\mathcal {F}} {\mathop =\limits ^{{\rm def}}}\{{\textbf {x}}: \exists ~{\textbf {x}}^{{\textbf {w}}_i}\in {\mathbb {R}}_+^{\vert {\mathcal {A}}\vert } ~s.t. \; {\textbf {x}} = \sum _{i=1}^{\vert {\mathcal {W}}\vert } {\textbf {x}}^{{\textbf {w}}_i},\,\textbf{Nx}^{{\textbf {w}}_i}={\textbf {d}}^{{\textbf {w}}_i} \,\,\forall {}{} {\textbf {w}}_i\in {{\mathcal {W}}} \}, \end{aligned}$$
(1)

where \({\textbf {x}}^{{\textbf {w}}_i}\) indicates the flow vector attributed to O-D pair \(i\in [\![{\mathcal {W}}]\!]\). This implies that the total flow vector x is consistent with the demands \({\textbf {d}}^{{\textbf {w}}_i}\) between all O-D pairs.

The methods described in the following sections use different days of flow data on the network. They are seen as “snapshots” of the network at different points in time, with \(\vert {\mathcal {J}}\vert\) samples of the edge flow vector x. j \(\in [\![{\mathcal {J}}]\!]\) where j is the index of different snapshots of the network with corresponding average time bin hourly flows.

Time bins are selected periods of time that are commonly used to approximate travel demand in static TA models (e.g. 6 am - 10 am) (Zhang et al. 2018). The travel demand is assumed to be the same for each hour of the time bin, an average of the profile in the period.

The travel time on an edge \(a\in {\mathcal {A}}\) is denoted by \(t_a\). In the analysis of the results ("Results" section), there is a comparison between estimated model values and observed values of flow and time. In time bin p on edge a, estimated values are indicated with \(x^{user}_{p,a}\) and \(t^{user}_{p,a}\), and observed values are indicated with \(x^{obs}_{p,a}\) and \(t^{obs}_{p,a}\).

A collection of the network variables is provided in Table 1.

Table 1 Notation for Network Definition
Full size table

Congestion functions

Accurate congestion functions are key to TA models as they connect the travel time \(t_a\) to the vehicle flows \(x_a\) on edge \(a\in {\mathcal {A}}\). In the network model they take the form:

$$\begin{aligned} t_a(x_a)=t_a^0\,f\left( \frac{x_a}{m_a}\right) , \end{aligned}$$
(2)

where \(t_a^0\) is the free-flow travel time of an edge \(a \in {\mathcal {A}}\) and \(f(\cdot )\) is a strictly increasing and continuously differentiable function dependent on the flow \(x_a\) divided by the flow capacity \(m_a\) of that edge \(a \in {\mathcal {A}}\).

The Bureau of Public Roads (BPR) equation is consistent with Eq. 2 and is widely used in TA models (de Grange et al. 2017; Youn et al. 2008). In its more general form it is:

$$\begin{aligned} t_a(x_a)=t_a^0\left( 1+\alpha {(\frac{x_a}{{{m}_a}})}^\beta \right) , \end{aligned}$$
(3)

where the values of \(\upalpha\) and \(\upbeta\) are coefficients commonly taken as 0.15 and 4, respectively (Sheffi 1985). In this work we use this form of BPR and coefficients for all edges. The congestion functions are used in the O-D adjustment ("Calculation of O-D demand matrices from flow counts" section) and solution of the Traffic Assignment Problem (TAP) ("Flow pattern calculation" section)

On the English SRN, as in Dervisoglu et al. (2009), we use the maximum of the observed hourly mean flows on a edge as its capacity \(m_a\). The NTIS provided values of capacity are used for edges without sufficient congestion data for this estimation. The free-flow travel time \(t^{0}_a\) is obtained by taking the 95\(^\text {th}\) percentile of the observed hourly mean speeds (Casey et al. 2020; Silvano et al. 2020) as the free-flow speed then converting it to the travel time through the edge length.

Calculation of O-D demand matrices from flow counts

We use the GLS method together with the Bi-Level optimisation problem (BiLev) algorithm to estimate the O-D demand matrix from flow counts alone. Described here are the existing techniques that are applied within the novel network partitioning O-D matrix estimation presented in the "Network simplification and partitioned demand profile calculation" section.

Prior O-D demand matrix estimation

The GLS method assumes the edges are uncongested so that for each O-D pair the route choice probabilities are independent of the traffic flows. It obtains the estimated vectorised O-D demand matrix g (\(\ge\)0) through the following optimisation problem (see Hazelton 2000 for details):

$$\begin{aligned}&\min _{{\textbf {P}}\ge {\textbf {0}},{\textbf {g}}\ge {\textbf {0}}}\quad \sum _{j=1}^{\vert {\mathcal {J}}\vert }({\textbf {x}}^j -{\textbf {BP'g}})'S^{-1}({\textbf {x}}^j-{\textbf {BP'g}}),\nonumber \\&s.t.\quad p_{ir}=0\;\forall \;(i,r) \in \{(i,r):r\not \in {\mathcal {R}}_i\},\nonumber \\&\quad \quad {\textbf {P1}}={\textbf {1}}, \end{aligned}$$
(4)

where \(\varvec{P}=[p_{ir}]\) is the route choice probability matrix, \(\varvec{1}\) is a vector of ones and S is the sample covariance matrix for flows.

For all \(a \in {\mathcal {A}}\), \(r \in {\mathcal {R}}_i\), and \(i\in {1,...,\vert {\mathcal {W}}\vert }\), the edge-route incidence matrix entry \(B_{ra}^i\) is 1 if route \(r \in {\mathcal {R}}_i\) uses edge a, or 0 otherwise. We find the feasible routes for each O-D node pair using Yen’s multiple shortest paths algorithm (Brander and Sinclair 1996) and use them to create the edge-route incidence matrix B. We limit feasible routes to the two shortest routes by distance, if available, as it is commonly the case for the majority of the route flows to use the best couple of choices (Bonsall et al. 1997).

O-D demand matrix adjustment

To account for the effects of congestion and improve the accuracy of the vectorised initial prior demand estimate g\(^{{\textbf {0}}}\), the congestion functions can be used to find an improved solution through a gradient-based BiLev algorithm. With the observed flow vector denoted by x̃ = (\(\tilde{x}_a; a \in {\mathcal {A}}\)) and the estimated user-equilibrium flow vector x(g) for any feasible non-negative vector g (\(\ge\)0). The problem is expressed through the following objective function:

$$\begin{aligned} \min _{{\textbf {g}}\ge {\textbf {0}}} \quad F({\textbf {g}}) =\, \sum _{i=1}^{\vert {\mathcal {W}}\vert }(g_i-g_i^0)^2+ \sum _{a=1}^{\vert {\mathcal {A}}\vert }(x_a({\textbf {g}})-\tilde{x}_a)^2. \end{aligned}$$
(5)

The symbols are as defined in Table 1. Further details can be found in Spiess (1990) and Lundgren and Peterson (2008).

Flow pattern calculation

The predicted user-equilibrium flow pattern can be calculated using the congestion functions ("Congestion functions" section) and adjusted O-D demand matrix ("Calculation of O-D demand matrices from flow counts" section) through the Frank-Wolfe algorithm with the following optimisation of the Traffic Assignment Problem (TAP) (Patriksson 2015):

$$\begin{aligned} \min _{{\textbf {x}} \in {\mathcal {F}}} \sum _{a=1}^{\vert {\mathcal {A}}\vert } \int _{0}^{x_a} t_a(s) ds . \end{aligned}$$
(6)

The Frank-Wolfe algorithm uses a convergence criterion based on the size of relative gap between consecutive iterations (see Patriksson (2015) for details). In this work a non-dimensional relative gap of \(10^{-5}\) is used for the convergence of the edge flows (Patil et al. 2021). The user-equilibrium flow pattern results from drivers pursuing their selfish best route and throughout this work it is assumed to match the observed flows as commonly done in other works (Zhang et al. 2018; de Grange et al. 2017).

Network simplification and partitioned demand profile calculation

Network partitioning

Clustering is performed on the topographic representation based on a community partitioning using network modularity via the Louvain algorithm.

Network modularity measures the relative density of edges inside communities compared to the edges outside communities. It is measured with a scale value ranging from \(-\)0.5 to 1 (non-modular to fully modular clustering). By achieving the optimal value for modularity (closest to 1) the results should be the best possible grouping of the network nodes. The Louvain algorithm works by first finding small communities based on optimising modularity on all the nodes locally. Then those small communities are regrouped as single nodes in a condensed graph and the modularity between them is calculated. A change in modularity process is applied to this new network to see if there are increases in modularity from combining the new community partitions. If no increase in modularity occurs then that partition is optimal, otherwise the process of regrouping the nodes of the condensed graph repeats combining the communities further. See Blondel et al. (2008) and Traag et al. (2019) for more details.

The algorithm uses the following definition for modularity (Blondel et al. 2008):

$$\begin{aligned} Q= \frac{1}{2m} \sum _{i=1}^{\vert {\mathcal {V}}\vert }\sum _{j=1}^{\vert {\mathcal {V}}\vert } \left[ A_{ij} - \frac{k_{i}k_{j}}{2m} \right] \delta (c_i,c_j) . \end{aligned}$$
(7)

\(A_{ij}\) is the weight of the edge between nodes i and j, where \(i, j \in {\mathcal {V}}\). It is taken as the inverse of the edge length. The sum of the weights of the edges attached to node i is represented by \(k_i=\sum _{j=1}^{\vert {\mathcal {V}}\vert } A_{ij}\). The \(\updelta\)-function \(\updelta\) (\(c_{i}\), \(c_{j}\)) is 1 if \(c_i=c_j\) and 0 otherwise, such that \(c_i\) is the community to which node i is assigned. Also, \(m=\frac{1}{2} \sum _{i=1}^{\vert {\mathcal {V}}\vert }\sum _{j=1}^{\vert {\mathcal {V}}\vert } A_{ij}\) is based on the total weight of network edges.

We partition the topographic representation using the inverse of the edge distances as the network edge weights as opposed to the true road distance. This is so that nodes closer on the topographic network are treated as having a stronger connection. In the process, we replace pairs of parallel edges that have opposite flow directions with undirected edges due to the Louvain implementation used being limited to undirected graphs (Aynaud 2020). This does not affect the final result due to carriageways being in identical pairs.

With efficiency for large networks, the Louvain algorithm finds different high modularity partitions and provides a complete hierarchical community structure that gives access to different resolutions of community detection (Blondel et al. 2008). The resolution parameter in the algorithm implementation used (Aynaud 2020) controls the size of communities outputted from this hierarchical structure. Making the resolution size larger leads to a smaller number of partitions being produced with a greater number of nodes inside each one. We vary the size of the resolution over a range to produce partition sizes from unpartitioned (resolution equals zero) to the largest partitions when there are only two separate communities (a resolution value which depends on network size). Not every resolution produces a unique number of communities. We selected the lowest resolution that found each unique number of communities.

Each time the Louvain algorithm is run with the same inputs it can produce a variation on the exact partitioning produced due to randomized cluster initialization (Leeuwen et al. 2019). As we are primarily using partitioning to find communities of different sizes, control of the exact nodes in each partition is not a great concern.

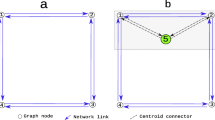
Once we have produced a result for the given resolution, the new community topographic representation is created from the groupings. The nodes of each partition are grouped into community supernodes. We use a modified Depth First Search (Mehlhorn and Sanders 2008) to find the neighbours of each partition and establish the community superedges of a new community topographic representation. An example of the process can be seen in Fig. 1.

The traffic measurements and parameters on the simplified community topographic representation are obtained from the original topographic representation using the following steps if multiple edges connect the partitions in parallel. The mean free-flow travel time of the edges weighted by mean measured flow in all time bins is used as the community superedge free-flow travel time. The sum of the capacities and measured flows on the constituent edges are used as the community superedge capacity and flow, respectively. The measured travel times for the community topographic edge are obtained from the mean of the observed travel times on the edges weighted by the measured flow in all time bins. We use this way of obtaining the traffic measurements and parameters because it approximates the effect of combining the multiple parallel edges of the original topographic into the community topographic. More roads have increased flow of vehicles and more capacity so these are summed; however, the time is the average per vehicle so the observed travel time and free-flow travel times are calculated through means weighted by the combined flows.

Fig. 1
figure 1

Example of community topographic representation after partitioning via Louvain algorithm

Full size image

Partitioned network O-D estimation

The community topographic representation can be used to obtain estimates of the uncongested prior O-D demand matrix using the GLS method. We investigate four different ways of utilising the representation for this purpose to understand the effects on TA result accuracy and computational requirements: (i) degenerate; (ii-A) non-degenerate internal-only; (ii-B) non-degenerate external-only; (ii-C) non-degenerate internal-external combined. Figure 2 shows an illustrative example of a nine node undirected simple graph network to demonstrate the partition grouping with internal and external O-D movements.

Fig. 2
figure 2

Example nine node topographic network (black) partitioned into three communities. Community topographic is in blue. The green dashed lines are the partitions’ external O-D movements, the red dashed are the partitions’ internal O-D movements

Full size image

(i) Degenerate

In the degenerate O-D estimation, the community topographic representation (Fig. 2 - blue graph) is used as a substitute network for original topographic representation (Fig. 2 - black graph). The O-D estimation and adjustment are applied to the flows and structure of the community topographic representation and not the original topographic representation.

In the nine node example, the partitioned community topographic representation is used to produce an O-D estimate, \(H_{com}\), for the partitions A, B and C.

$$\begin{aligned} \mathbf {H_{com}} = \begin{bmatrix} 0 &{} H_{com}^{AB} &{} H_{com}^{AC}\\ H_{com}^{BA} &{} 0 &{} H_{com}^{BC}\\ H_{com}^{CA} &{} H_{com}^{CB} &{} 0 \end{bmatrix}, \end{aligned}$$
(8)

where each non-zero entry (e.g. \(H_{com}^{XY}\)) is an estimate of the demand travelling between the pair of partitions (e.g. X and Y) based on the edge flows of the community superedges (Fig. 2 - green dashed lines).

This approach reduces the network size as shown in Fig. 1. It loses the detail of individual road junctions but seeks to preserve some of the main network structure. \(\mathbf {H_{com}}\) is used within the TA model to produce estimates of flows and travel times between the partitions on the community topographic representation.

(ii) Non-degenerate

The non-degenerate approaches aim to find an estimate of the demand for each O-D pair of the original topographic representation through breaking down the problem with the simpler community topographic representation.

In all the non-degenerate approaches, the prior matrix \(\textbf{H}\) is used in the O-D adjustment algorithm to produce a final O-D demand matrix which is used in a static TA model for the whole topographic network.

(ii-A) Non-degenerate internal-only

The internal approach applies O-D estimation to separately estimate demands for the internal O-D pairs of each partition by applying GLS to the flows and structure of that partition’s subnetwork (Fig. 2 - red dashed lines). For example, for Partition A in the nine node example, we can express a matrix of demands \(\mathbf {H_{int}^{A}}\):

$$\begin{aligned} \mathbf {H_{int}^{A}} = \begin{bmatrix} 0 &{} H^{12} &{} H^{13}\\ H^{21} &{} 0 &{} H^{23}\\ H^{31} &{} H^{32} &{} 0 \end{bmatrix}, \end{aligned}$$
(9)

where each non-zero entry is an estimate of the demand travelling between the pair of nodes based on the edge flows of the topographic representation (Fig. 2 - black graph). It follows the same form for other partitions.

For each partition, the O-D values between the internal nodes will be larger than what would be estimated if the whole unpartitioned network was being used as all the flows are assumed to be going only between the internal nodes. This is corrected with the help of the O-D adjustment algorithm.

In the non-degenerate internal-only approach, the matrices of demands for each of the partitions are combined into a prior matrix \(\textbf{H}\) by assuming zero demand for the inter-partition O-D pairs. Such that for the nine node example the prior matrix estimate is,

$$\begin{aligned} \textbf{H}&= \begin{bmatrix} \mathbf {H_{int}^{A}} &{} \textbf{0} &{} \textbf{0}\\ \textbf{0} &{} \mathbf {H_{int}^{B}} &{} \textbf{0}\\ \textbf{0} &{} \textbf{0} &{} \mathbf {H_{int}^{C}} \end{bmatrix}, \end{aligned}$$
(10)

where \(\varvec{0}\) is a matrix of zeros the size of the inter-partition O-D pairs. For the example in Fig. 2, there are three nodes in each partition and nine inter-partition O-D pairs between a permutation of two partitions. This corresponds to a 3 × 3 matrix for \(\varvec{0}\).

(ii-B) Non-degenerate external-only

The non-degenerate external-only approach uses the external partition O-D estimate, \(\mathbf {H_{com}}\), obtained from the community topographic representation. The external partition O-D demands are divided equally between the nodes which comprise the relevant partitions to spread the demand amongst the O-D pairs of the topographic representation (black graph).

To obtain estimates for the inter-partition demands, the community O-D matrix demands \(H_{com}\) are divided by the number of topographic O-D pairs that comprise each partition pair. For example, for partition pair AB, the number of nodes in A, \(u^A\), is three and the number of nodes in B, \(u^B\), is three so the number of O-D pairs is \(u^{AB} = u^A * u^B = 9\). The value for each pair is then \(H_{com}^{AB}/9\). Then, in matrix form, for partition pair AB with \({\textbf {l}}_A\) as a column vector of ones the length of \(u^A\), and \({\textbf {l}}_B\) as a column vector of ones the length of \(u^B\),

$$\begin{aligned} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{AB}}} = \frac{H^{AB}_{com}}{u^{AB}}{} {\textbf {l}}_{A}{} {\textbf {l}}_{B}'. \end{aligned}$$
(11)

External-only assumes zero values for the demands between the O-D pairs internal to the partitions, resulting in the following prior matrix,

$$\begin{aligned} \textbf{H}&= \begin{bmatrix} \textbf{0} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{AB}}} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{AC}}}\\ {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{BA}}} &{} \textbf{0} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{BC}}}\\ {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{CA}}} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{CB}}} &{} \textbf{0} \end{bmatrix}, \end{aligned}$$
(12)

where \(\varvec{0}\) is a matrix of zeros the size of the intra-partition O-D pairs. For the example in Fig. 2, there are three nodes in each partition and six O-D pairs between them. As in Eq. 9, the demand from a node to itself is included but set to zero. This then corresponds to a 3x3 matrix for \(\varvec{0}\).

(ii-C) Non-degenerate internal-external combined

In the non-degenerate internal-external combined approach, a prior matrix is formed using both internal and external estimations without any O-D demands assumed zero:

$$\begin{aligned} \textbf{H}&= \begin{bmatrix} \mathbf {H_{int}^{A}} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{AB}}} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{AC}}} &{} \\ {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{BA}}} &{} \mathbf {H_{int}^{B}} &{} {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{BC}}} &{} \\ {\hat{\textbf{H}}_{\textbf{ext}}^{\textbf{CA}}} &{} {\hat{\textbf{H}}_\textbf{ext}^\textbf{CB}} &{} \mathbf {H_{int}^{C}} \\ \end{bmatrix}, \end{aligned}$$
(13)

Summary of process of network O-D estimation

We summarise the process of applying the described network partitioning O-D estimation process in Algorithm 1.

figure d

Application on the England Strategic Road Network

Raw dataset description

The dataset used in this work takes the traffic data obtained through the MIDAS system installed on the main motorways and A-roads of the England SRN. MIDAS mostly records traffic through under-road inductive loops spaced approximately every 500 m. The dataset includes the data for the weekdays in September 2018 to June 2019. The MIDAS system measures speed, flow, occupancy and headway at approximately 7000 sites on the SRN. The data is given on a per-lane basis and aggregated over 1-minute intervals. It is assumed that the network does not have intersection control devices such as traffic lights. The SRN is without gated entry and exit so individual vehicles are not systematically identified as they join and leave the network (National Highways 2022).

The NTIS Network and Asset Model contains the information on the details and location of the different systems National Highways uses to monitor and control traffic on the SRN. It contains information on the location of MIDAS sensor sites and geospatial information of the road junctions and motorways that can be converted into a graph representation of the network. Attributes are also available to determine the direction of travel, capacity and length of the associated weighted graph’s edges (National Highways 2022).

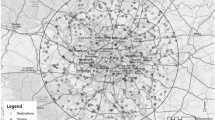
After conventional data selection and removal of faulty sensor observations, the central portion of the network was selected for analysis, comprising the main carriageways with relevant MIDAS sensor sites connecting a selection of major cities in England (Fig. 3).

Fig. 3
figure 3

Graph representation of the NTIS model of the SRN in the central subnetwork area. Map underlay from Google Maps (2021)

Full size image
Fig. 4
figure 4

Topographic representation for the subnetwork of the main roads connecting the central SRN

Full size image

Network graph topographic representation

The scale of the model is not concerned with navigation through the junctions between roads but instead with modelling the overall flows around the network. Therefore, an arterial road topographic representation is created for the English SRN. The NTIS model edges and nodes are grouped into superedges and supernodes that are used to create the simplified topographic representation (Fig. 4). Each supernode is a group of NTIS model nodes which comprise motorway junctions. Each superedge is a collection of the NTIS model edges that comprise each carriageway between the junctions. The combination of NTIS edges into superedges involves averaging the flows recorded by the sensors on the NTIS edges that compose them ("MIDAS data extraction" section). After the process of node and edge combination, the supernodes and superedges that constitute the simplified topographic representation are referred to as its nodes and edges. The resulting topographic representation of the English SRN we use in our analysis has 73 nodes, 156 edges and 5256 O-D pairs.

MIDAS data extraction

MIDAS data from the available sensors are extracted and matched to the associated topographic edge through the NTIS dataset. The flow data recorded are grouped into time bins of three distinct periods, AM: 6am - 10am, MD (midday): 10am - 4pm, PM: 4pm - 8pm. For each time period, the mean hourly flow is calculated over the respective period. The three time bins are selected to cover the morning and evening commuting traffic, and the less busy middle of the day, for which the demand patterns can vary considerably. They are similar to those used in previous data-driven static TA models (Zhang et al. 2018).

Loop detector data can be noisy and needs to be processed correctly (Knoop and Daamen 2017). When multiple sensors are available on the same edge, the median flow readings are used. This both minimises the effect of outliers and filters out erroneous readings, as those differing from the median by more than twice the median absolute deviation. This allows the central tendency of measured flows to be resistant to sensors with faults or which do not measure the main carriageway flow even after the slipway sensors are excluded through their database names.

The TA models are fitted to the MIDAS data taken from September 2018 to May 2019.

Results

Accuracy of different applications of the partitioning on the English SRN

To investigate the effect of partition resolution on each of the types of partitioning matrix estimation techniques, the Louvain resolution parameter was varied to evaluate the effect on the TA model accuracy and computation requirements of the resulting partitions. The analysis was carried out on the topographic representation of the SRN using MIDAS data taken from September 2018 to May 2019 for the three time bins (AM, MD, PM). Making an assessment based on flow and travel time estimation is a practical way to validate the accuracy of the calculated O-D matrices. The computation time results refer to the time taken to calculate the prior O-D demand matrix, O-D adjustment and solve the TAP.

Relative errors in the flow and travel times of the UE assignment prediction are used to evaluate the performance. The Absolute Percentage Errors (APE) are calculated as:

$$\begin{aligned} APE_{p,\hat{a}}^t = \frac{\vert t_{p,\hat{a}}^{user} - t_{p,\hat{a}}^{obs}\vert }{t_{p,\hat{a}}^{obs}}, \end{aligned}$$
(14)

for travel time, while

$$\begin{aligned} APE_{p,\hat{a}}^x = \frac{ \vert x_{p,\hat{a}}^{user} - x_{p,\hat{a}}^{obs}\vert }{x_{p,\hat{a}}^{obs}}, \end{aligned}$$
(15)

is used for flows. We use \(\hat{a}\) to indicate an edge on the topographic representation (i.e. Figure 2 - black graph) in the non-degenerate cases, or an edge on the community topographic representation (i.e. Figure 2 - blue graph) in the degenerate case. For each time bin p and edge \(\hat{a}\), \(x_{p,\hat{a}}^{obs}\) is the observed flow and \(t_{p,\hat{a}}^{obs}\) is the observed travel time derived from the edge length divided by observed average speed. The values are the mean flow or time on each edge within each time bin over the nine month fitting period. \(t_{p,\hat{a}}^{user}\) is the predicted travel time derived from the congestion function (Eq. 3) using \(x_{p,\hat{a}}^{user}\), which is the edge flow value predicted by the model through solving the UE TAP with the calculated O-D matrix. The APE values for all time bins on all edges are grouped together to provide the sample. For the case of the non-degenerate methods applied to the SRN, this means a \(3*156=468\) sample size that is used to create the boxplots. The number of observations in the sample is reduced for the degenerate approach, as the number of edges for the network varies with the size of the community topographic representation.

The results for the four estimation approaches can be seen to exhibit different patterns as the size of the partitions varies (Fig. 5 and 6). The error in flow and travel time prediction can be compared to the result for the unpartitioned case, which is a benchmark for the methods. The unpartitioned case gives the same value for all methods except internal-only, for which it was unattainable as each community only contains one node in that case.

Comparing the different approaches for using the partitioning, it can be seen that there is considerably different behaviour between degenerate and non-degenerate approaches (Fig. 5). The flow prediction accuracy for degenerate varies less for the partitions with a smaller percentage of the total nodes inside (a larger number of partitions); however, as the size of the partitions increases, the flow prediction has a larger variance between resolutions. The relative error for flow is low for the largest partition size. This can be attributed to the network being degenerated to a two node, two edge system so the demand prediction through GLS becomes trivial. It can be seen that the time prediction accuracy for the degenerate method stays broadly similar before decreasing slightly as the partitions become larger and less numerous.

Between the other non-degenerate methods (internal-only; external-only; internal-external combined), in Figs. 5 and 6 several trends can be seen. With internal-only, as the size of the partitions increases to include more nodes, the results for both flow and time improve up to the 11% point. Between 11-50% the median is approximately constant. In Fig. 7, the computation time for internal-only also begins to level off past the 11% point. This implies the results for using the internal-only approach are similar for the 11-50% partition size range in both accuracy and computation time. The results for internal-only were not available for the smallest five resolutions of partitioning. This is because the estimate of the prior matrix was too inaccurate for the O-D adjustment process to converge.

As the percentage of average nodes in a partition increases, the results for the external-only method show a broadly linear increase in error for flow and time prediction as well as computation time. This is due to the prior matrix increasingly basing the individual O-D movements on a smaller subset of topographic edges. Less information is available so the prior matrix moves further from its best estimate which is the unpartitioned case.

When internal and external estimates are combined to create the prior matrix, it can be seen that there is a degradation in accuracy for flow and time prediction from the unpartitioned case to the point of approximately 7% of total nodes. After this, the results for both flow and time improve with increases in the partition size before they start to level off. At the largest partition size it can be seen that the accuracy matches the internal-only result but with less computation time (Fig. 7).

For all the approaches, the travel time APEs are generally lower than the flow APEs. The differences in patterns between flow and travel time can be explained by the non-linearity of the congestion functions that are used to obtain the UE modelled travel times from the UE modelled flows.

To provide some context to the errors obtained, the results can be compared with other recent work such as Dey et al. (2020). The analysis in that work used a more capable but computationally demanding method of network tomography than GLS to obtain an O-D matrix for a smaller network in Melbourne, Australia city centre (23 nodes, 54 edges). They found a mean APE of 24.18% for flow using simulated data. Using travel time data from Uber and Syic, they found mean APEs in travel time predictions of 18-33%. Although these results are not directly comparable, as the networks and methods are different, it highlights the approximate size of error for current static TA models using network tomography O-D estimation.

Fig. 5
figure 5

Plot of Absolute Percentage Error in user-equilibrium flow prediction for each partition size investigated on the topographic representation of the Strategic Road Network for September 2018 to May 2019. Solid line is median error and dashed lines indicate the IQR. Lines are used as visual aid for the individual point results

Full size image
Fig. 6
figure 6

Plot of Absolute Percentage Error in user-equilibrium travel time prediction for each partition size investigated on the topographic representation of the Strategic Road Network for September 2018 to May 2019. Solid line is median error and dashed lines indicate the IQR. Lines are used as visual aid for the individual point results

Full size image

For the road network, the memory requirement of the four techniques for all partition sizes did not vary much, staying between 20.8\(-\)20.9 GB in all cases. The network is not particularly large (73 nodes, 156 edges) so memory is not the concern (see section "Computational Requirements"). The calculations for the results were all performed on a Dell PowerEdge C6320 with 2.4GHz Intel Xeon E5-2630 v3 CPU. The implication of the results is that the best option would be to use the largest partition possible with the internal-external combined or the internal-only methods.

Fig. 7
figure 7

Computation time of results for each partition size investigated on the topographic representation of the Strategic Road Network for September 2018 to May 2019. The time includes the calculation of the Origin–Destination (O-D) demand matrix and solution of the Traffic Assignment Problem (TAP). Lines are used as visual aid for the individual point results

Full size image

Comparison of the results with different sized networks

To investigate how the size of the network influences the results of the different methods, the same tests were carried out on additional artificially-generated networks of a range of sizes ("Appendix" section) and the Sioux Falls test network commonly used in TA model testing (TNFR 2022). The analysis was carried out on a single time bin of simulated flow data without travel time, generated according to the process outlined in the "Appendix" section.

Fig. 8
figure 8

Plot of Median Absolute Percentage Error in user-equilibrium flow prediction for each partition size investigated on different artificially-generated networks, the 73 node SRN network and the 24 node Sioux Falls network. Lines are used as visual aid for the individual point results

Full size image

Similar trends to the English SRN can be seen when the techniques are applied to the artificially-generated networks (Fig. 8). For internal-only, there is a peak in error for small partition sizes with no results produced for the smallest partitions. The internal-only results level out after around 11-13% of nodes (i.e. eight or nine partitions). This pattern can be explained by less of the O-D pairs having an estimated non-zero value in the prior matrix for smaller partition sizes. In the case of each partition only containing one node that means no O-D pair has an estimated value, which is why internal-only cannot obtain a TAP result. As the partitions get larger, internal-only includes more estimated O-D pairs in the prior matrix. This provides a more accurate starting matrix for O-D adjustment to work with, which leads to lower errors.

For external-only there is a steady increase in flow error as the partition size increases. As opposed to internal-only, this pattern can be explained by less of the O-D pairs having an estimated non-zero value in the prior matrix for larger partition sizes. For all partition sizes, at least some of the O-D pairs have an non-zero estimate so the TAP can be solved in all cases. As the partitions get larger, external-only includes more zero value non-estimated O-D pairs in the prior matrix. This provides a less accurate starting matrix for O-D adjustment to work with, which leads to higher errors.

The results for the internal-external combined method show the same characteristic triangle shape with an initial increase followed by a decrease in error. This pattern can be explained by it being a combination of the effects present for internal-only and external-only. At smaller partition sizes, the external estimates make up the majority of the O-D pair estimates, whereas, at the larger partition sizes the internal estimates constitute the majority. This means the errors are small for a large number of small partitions, which suits external estimation, and a small number of larger partitions, which suits internal estimation.

For the degenerate method the trend is similar for Sioux Falls but different for the artificially-generated networks. With the artificially-generated networks, there is a peak in error between 0-10% and then the error reduces to almost zero for the larger partition sizes. This can be attributed to the artificially-generated networks having no congestion and the simulated flows being created with a Poisson distribution, so that for the smaller network sizes (larger partitions) very accurate estimates of the demand are obtained.

Computational requirements

The computational requirements of the partitioning approaches were investigated using the artificially-generated networks for a single time bin as described in the "Appendix" section.

Computational requirements without partitioning

When the GLS method of O-D estimation is applied to a network without partitioning being used, it can be seen in Fig. 9 that the median error in flow prediction remains constant as the network size (number of nodes) grows, but the required computational time and memory increase steeply. For the results in Fig. 9, the O-D estimation and adjustment algorithms are being applied to the entire network. Due to the steeply increasing computational requirements, there is a limit on the number of nodes that O-D estimation can be applied to at one time. The main driving factor for memory requirements is the number of O-D pairs in the network and the assumed number of routes between them for GLS application. This is because these two factors determine the number of decision variables in the GLS mathematical optimisation formulation. As the number of nodes increases in the network, the number of O-D pairs and therefore the number of decision variables increases by order \({\mathcal {O}}(n(n-1))\). If the number of decision variables is too high, it can lead to infeasibly large memory requirements and breach the limit of the Gurobi solver used (Gurobi 2023). The number of days of data also contributes to increased memory requirements but is not the main driving factor. Further details on the networks investigated (i.e. the number of O-D pairs) for computational requirements without partitioning can be found in Table 2 in the "Appendix" section.

Fig. 9
figure 9

(a) Flow prediction error and (b) computational requirements for a range of network sizes when the Origin-Destination (O-D) estimation and adjustment are applied to a range of networks without the use of partitioning. In (a) the solid line is median error and dashed lines indicate the IQR. Lines are used as visual aid for the individual point results

Full size image

Computational requirements on larger networks with partitioning

The analysis of the artificially-generated networks was expanded to larger sizes for the internal-only and internal-external combined methods which are the best performers of the non-degenerate partitioning approaches. As the networks grow in size it can be seen in Fig. 10 (a) that the memory requirements for both methods increase at the extreme ranges of partitioning. Comparing between Figs. 9 and 10, the effectiveness of using partitioning to reduce the computational requirements for larger networks can be seen. For example, by using two partitions (internal-only and internal-external) the 243 node network has a similar RAM requirement and computation time to the unpartitioned 135 node network.

At very small partitions the memory requirements increase very steeply. The 216 and 243 node networks were unable to be calculated unpartitioned, this is due to the size of memory required and limitations with the Gurobi solver used. Of most interest is the increase in memory at the largest partition sizes. It can be seen that as the total network size grows, the memory for the larger partitions starts to become very high as each subnetwork within a partition is larger. Computation time shows a similar trend to memory for the two methods (Fig. 10 (b)), with internal-external having an advantage over internal-only for large partition sizes with larger networks.

Based on the results in Figs. 8 and 10, for the internal-only the error levels off between 11-50% and the computation requirements start to increase at 25%, so the optimal range for partition sizes is between 11-25% (or 9 to 4 partitions). For the internal-external approach, the error in Fig. 8 is lowest for the largest partitions (i.e. 50%), so it is best to go for as large a partition as is computationally affordable. In the case of the tested networks this would be 25%, however, for larger networks than those tested, this partition size would reduce. As internal-only has better errors than internal-external for smaller partitions, it is internal-only that is the better choice if result accuracy and memory are the primary concerns. If computation time is more important then internal-external is faster at the larger partition sizes.

To determine the optimal partition size before applying the method, consideration needs to be made of the computing resources available and what is most important out of result accuracy, computation time and memory requirements. The optimal size and number of partitions also depends on the size of the overall network and the number of routes between O-D pairs. As memory requirements are usually the main limiting factor for applying this type of O-D estimation, from the networks analysed, we can recommend starting with 9 partitions using internal-only and then reducing that number until the memory and computation time requirements become too onerous.

Fig. 10
figure 10

Computational requirements for each partition size investigated for a 153, 216 and 243 node artificially-generated network: a Memory; b Computation Time. Lines are used as visual aid for the individual point results

Full size image

Discussion

In proposing a method of partitioning a road system through network modularity, in this work we have demonstrated its potential for the calculation of the key O-D demand input for static TA models from loop detector data. This opens up the opportunity to estimate flow patterns for large road networks such as national highway systems without the need for additional routing data sources (i.e. travel surveys).

The results show that partitioning the network into small communities of nodes is tolerable for a degenerate approach to reduce the size of the network being analysed. This degenerate approach could be well suited for use in infrastructure assessment models such as NISMOD where the scale of analysis is more coarse, for instance at the inter-city level.

Applying partitioning in a non-degenerate way showed that a similar level of error in user-equilibrium flow and travel time predictions to the unpartitioned case can be obtained by dividing the network into a small number of larger partitions. The results show that the best accuracy results came from only using the internal O-D estimates of the partitions for the larger partition sizes. However, the results show that by also including the external partition estimates there can be a reduction in computation time in some cases. For the English SRN case study, it appears that the best option is to partition the network into two large communities. In very large networks where the size is such that a two community partition is still infeasibly large, the results show that for community partitions numbering three and greater it would be better to use the internal-only approach unless the communities contain such a small proportion of the nodes that the flow error starts to rise (approx. 12.5% of nodes or eight community partitions).

The use of partitioning unlocks the ability to utilise existing network tomography-based approaches on much larger networks with higher numbers of O-D pairs. It should be noted, however, for cases where the full-sized network is not too computationally onerous, it would be better to apply the O-D estimation without partitioning as that still provides the best accuracy.

For the England SRN case study, results were obtainable for the unpartitioned case as the network size and number of O-D pairs were small enough to be computationally feasible. This allowed the comparison of new partitioning methods to the baseline unpartitioned results on a real road network. If that case study were expanded to include a larger road system, partitioning would eventually become essential.

The non-degenerate approach is useful for application in more detailed traffic planning. The traffic assignment models which it can create are well suited to estimating alternative flow patterns of vehicles such as system-optimal, under which the global travel cost of all drivers is minimised through the routes they are assigned. This can be used for producing performance comparisons of different national road systems through metrics such as the Price of Anarchy and evaluating network improvement options (Youn et al. 2008).

The performance of the methods in this work is assessed by the prediction accuracy of the TA models using the estimated O-D matrices. The O-D matrices produced are not necessarily close representations of the true demand profile. The matrix obtained through the partitioning provides the prior matrix for the O-D adjustment algorithm to create a suitable demand input for the TA model to predict flows and travel times with the accuracy presented.

Future work could look to apply this type of multi-scale demand estimation with alternative techniques to GLS, which may be more suitable. Further research could look into incorporating separate terms in the O-D adjustment for the internal and external estimations of the prior matrix. Future work could also incorporate other data sources to inform the division between the O-D pairs of the externally estimated O-D movements. For example, in the AM period a greater share of demand could be distributed to the destinations where more employment is located. In this work we used the standard formulation and coefficients for the congestion functions, more accuracy is possible through the use of more advanced function estimates. Lastly, this work assumes that all the edges on the network have flow measurements, future work could look into adapting the method for situations where a number of measurements are missing. For example, flows on edges without measurements could possibly be reconstructed from the measurements on edges that feed into them.

Conclusion

In this work we developed a method of network partitioning through modularity to estimate O-D demand matrices for large road networks to be used in static TA models. We applied it to the central subnetwork of the English SRN and several artificially-generated networks to allow different levels of partition resolution to be tested for their effects on the results of TA models derived solely from loop detector traffic data.

We show that the approach developed allows for traffic to be analysed nationally at different scales. It can be used within infrastructure models to improve their analysis of congestion. It can also be used to create static TA models for strategic analysis and planning with a data source accessible to many transport planners. Future investigations could seek to implement the technique with more accurate techniques for O-D estimation from edge counts and improved adjustment algorithms.