Abstract
Freight forecasting models have been significantly improved in recent years, especially in the field of goods vehicle behavior modeling. On the other hand, the improvements to commodity flow modeling, which provide inputs for goods vehicle simulations, were limited. Contributing to this component in urban freight modeling systems, we propose an error component logit mixture model for matching a receiver to a supplier that considers two-layers in supplier selection: distribution channels and specific suppliers. The distribution channel is an important element in freight modeling, as the type of distribution channel is relevant to various aspects of shipments and vehicle trips. The model is estimated using the data from the Tokyo Metropolitan Freight Survey. We demonstrate how typical establishment survey data (i.e. establishment and outbound shipment records) can be used to develop the model. The model captures the correlation structure of potential suppliers defined by business function and provides insights on the differences in the supplier choice by distribution channel. The reproducibility tests confirm the validity of the proposed approach, which is currently integrated into a metropolitan-scale agent-based freight modeling system, for practical use.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Urban freight has become a globally important policy subject. Efficient operations of urban freight systems are critical in the metropolitan regions that become larger and denser. Furthermore, the evolution of logistics and supply chain practices has rapidly transformed the way freight operations take place. In this context, it is of utmost importance to develop a comprehensive and flexible urban freight simulator that can analyze the impacts of relevant policies such as land use changes, vehicle restrictions, the use of urban freight consolidation centers, the designation of loading/unloading spaces, crowdsourced deliveries, and other “smart” measures for freight operations.
Several urban freight modeling systems have been proposed in the literature (e.g. Boerkamps et al. 2000; Fischer et al. 2005; Wisetjindawat et al. 2005, 2006; Hunt and Stefan 2007; Nuzzolo and Comi 2014; Moeckel and Donnelly 2016; Alho et al. 2017) and, overall, freight modeling has been advanced significantly during the last few decades. However, the models for the commodity flows within a metropolitan area are underdeveloped (Comi et al. 2012). This is attributable to the heterogeneity of urban freight agents and the commodities handled as well as the difficulty of obtaining data, particularly disaggregate data. For urban freight, it is especially important to consider the nuances of sourcing behaviors by receiver type, such as offices, stores, restaurants, logistics facilities, factories, cultural and educational facilities, and residential facilities, which are relevant to commodity flows. Due to the data limitations, it is quite common to use aggregate economic statistics such as input–output tables to estimate commodity flows in freight traffic simulations (Ben-Akiva and de Jong 2013). On the other hand, a lot of efforts and resources were spent on collecting disaggregate data until this day. Several metropolitan-scale establishment surveys, which are also called commodity flow surveys, were conducted in recent years or are currently ongoing for informing urban freight models (Hunt et al. 2006; Alho and e Silva 2015; Toilier et al. 2016; Cheah et al. 2017; Oka et al. 2018). Exploring urban freight modeling approaches that make full use of those survey data is one of the important research topics.
One of the research gaps in urban commodity flow modeling is the consideration of distribution channels. Without the consideration of distribution channels, the model, for example, cannot differentiate direct and indirect shipments that go through logistics facilities, i.e. warehouses, distribution centers, truck terminals, and other intermediate facilities. While many freight models that deal with commodity flows were proposed in the past, the use of the facilities is considered mostly in the context of inter-city commodity flows (Huber et al. 2015); only a small number of the models explicitly consider the use of logistics facilities in the urban commodity flow estimation. Although an entire supply chain does not fit within a metropolitan region in many cases, the spatial distribution of urban logistics facilities is suspected to influence freight traffic flows (Dablanc and Rakotonarivo 2010; Sakai et al. 2015a). Furthermore, without considering the distribution channels, one cannot analyze the impact of the changes in urban structure. If some factories that have mainly been serving local markets move out, the local demands should be served by other suppliers, which could be other factories in the area or the logistics facilities that receive goods from outside. This paper aims to fill this research gap by proposing and testing a new approach that reproduces aggregated logistics chain structures within a metropolitan area through the estimation of the commodity flows. Here, we define a “logistics chain” as the connection between the locations of production and consumption, consisting of means of transportation, mainly goods vehicles in urban freight, and the intermediate locations that goods go through. Our approach is particularly appealing as it requires only typical establishment survey data, i.e. establishment and outbound shipment records.
For the model specification, we assume that commodity flows are demand-driven; a receiver, directly or indirectly through the cost minimization principle, determines a distribution channel (defined by the supplier function type, i.e. factory, logistics facility, office/store), and a supplier which has a specific location. While this is a strong assumption, it makes a simple and robust model specification possible. We present a framework for the supplier choice model and develop an error components logit mixture model that considers the complex correlation structure among alternative suppliers. We use the data from the Tokyo Metropolitan Freight Survey (TMFS) conducted in 2013 to estimate the model. The focus of this paper is the modeling approach, but the estimated parameters in the models using Tokyo’s data also provide interesting insights on the supplier choice mechanism. The proposed framework is integrated into a comprehensive metropolitan-scale agent-based modeling system, named “SimMobility” (Adnan et al. 2016). The SimMobility accommodates various decisions and behavioral aspects related to urban freight traffic, ranging from those based on long-term “strategic” visions, e.g. business characteristics and overnight parking locations for goods vehicles, to those relevant to daily logistics operations, e.g. vehicle touring, route choice, and delivery/pick-up parking (Alho et al. 2017). The proposed approach is also applicable to the commodity flow estimation in other existing urban freight modeling systems.
The rest of the paper consists of the following: in second section, the recent developments of freight models are reviewed, focusing on disaggregate commodity flow estimations and the consideration of distribution channels in the models; in third section, a proposed model structure and the calibration data are presented; in fourth section, the model specifications and the estimation process are detailed; in fifth section, the estimated models and the elasticity effects are discussed; in sixth section, tests for the model reproducibility are presented; and finally, in seventh section, the conclusions of this research are provided.
Literature review
In the last two decades, a number of freight forecasting models were proposed, considering the behaviors of individual agents and/or the decision-making processes in logistics operations (Chow et al. 2010; Comi et al. 2012; De Jong et al. 2013). These models are used for testing various logistics practices and policies, for which traditional aggregate-level freight models are not suited. Chow et al. (2010) provide a review of the two emerging groups of freight forecast models, “logistics models” and “vehicle touring models”, and De Jong et al. (2013) summarize the recent model development (2004 and after) mainly focusing on European models. There are various behavioral aspects that are considered in freight models, such as freight/trip production and consumption, commodity flow, mode choice, shipment frequency and size, vehicle scheduling and routing, and vehicle parking. The commodity flow estimation, the focus of this research, is one of the most essential components in a forecast model regardless of its scale, i.e. regional, national or urban.
A large number of approaches for the commodity flow estimation were proposed in the past, most of which are based on aggregate data. As disaggregate (i.e. establishment level) commodity flow data are often not available, the zone-to-zone level commodity flow estimation is still widely applied. Even recently proposed urban freight modelling systems, such as Nuzzolo and Comi (2014) and Moeckel and Donnelly (2016), treat commodity flows at an aggregate level. However, the aggregate models are passible of aggregation biases. Furthermore, the aggregate commodity flows have limitations for their use in a microsimulation of logistics behaviors (Ben-Akiva and de Jong 2013). Ben-Akiva and de Jong propose an Aggregate-Disaggregate-Aggregate (ADA) freight model system that specifies the procedure to disaggregate zone-to-zone flows to establishment-to-establishment flows. The ADA freight model system was implemented in the Swedish national freight transport model (SAMGODS) (Abate et al. 2018). Zhao et al. (2015) propose another approach to disaggregate zone-to-zone flows to firm group-to-firm group flows through a linear programing (LP) problem. They solve the market system optimum of commodity flows with the constraints on zone-to-zone flows, obtained from Freight Analysis Framework Version 3 (FAF3) data, for California, U.S.
Regarding fully disaggregate approaches, Boerkamps et al. (2000) propose the conceptual structure of Goodtrip model, one of the earliest urban freight microsimulation modeling systems. In the Goodtrip model, the commodity flows are estimated at an actor-to-actor level. Activity type (such as “consumers, supermarkets, stores, offices, distribution centers of retailers, and producers”) is determined for taking the differences in flows by shipper and receiver types (type of “linkage”) into account. However, the choice of the linkage type is not considered and the use of intermediate facilities is not modelled. An urban freight microsimulation model proposed by Wisetjindawat et al. (2005) includes “purchasing decision module” that consists of three components: distribution channel choice, (supplier) location choice, and supplier choice, all proposed to be multinomial logit models, for estimating commodity flows. In “distribution channel choice” model, the distribution channel is defined by supplier industry type (e.g. warehousing industry and manufactures), but not by function type (e.g. warehouse and factory). Although the work of Wisetjindawat et al. is pioneering, they do not fully describe the model estimation method and the implications from the estimation. Roorda et al. (2010) propose another conceptual framework for an agent-based logistics microsimulation. The proposed “commodity contract formulation” process is corresponding to the commodity flow estimation. In the model, a customer chooses a supplier from a choice set that can fulfill the requirements on order size and frequency. Similarly, Liedtke (2009) proposes “sourcing module” in which suppliers are chosen based on production size, commodity usefulness, and distance, for INTERLOG, a national level freight simulator. Both Roorda et al. and Liedtke do not explicitly consider distribution channels and logistics chain structures. There are also a couple of novel practices of the commodity flow estimation in the disaggregate freight modeling, taking deterministic modeling approaches. Gliebe et al. (2015) propose the use of a Bayesian game-based approach for connecting buyers and sellers. The proposed procurement market game (PMG) buyer–seller matching model was developed as a part of the meso-scale freight forecasting model for the Chicago Region (RSG 2015). Furthermore, Livshits et al. (2017) propose an agent-based computational economics (ACE) approach for the market-clearing process that matches buyers and suppliers in an agent-based behavioral freight model for the Arizona Sun Corridor Megaregion.
Despite the recent developments of disaggregate models for the commodity flow estimation, there is room for improving the consideration of the choice of distribution channel, particularly for urban freight modeling systems. In the existing urban freight modeling systems, the function type of an agent is underrepresented and often associated with industry type. However, it is fair to hypothesize that factories, warehouses and offices have quite different behavioral characteristics even if all those belong to manufacturing industry. Consideration of logistics facilities (such as warehouses and distribution centers) is especially important in simulating commodity flows. Huber et al. (2015) review more than a hundred freight models and find that only a small number of models consider the use of logistics facilities. Proposing one of such models, Davydenko and Tavasszy (2013) apply a unique approach to address the use of intermediate facilities, by extending the SMILE model lineage. The SMILE model is an aggregate, national level freight model developed by Tavasszy et al. (1998). The proposed logistics chain model, which has a multinomial logit structure, chooses intermediate locations for Production-Consumption (P–C) flows, and estimates commodity flows (i.e. shipment ODs). The above-mentioned model of RSG (2015) for the Chicago Region also considers the decisions of indirect/direct shipments (in their “distribution channel model”) and, for an indirect shipment, a local warehouse in the study area is assigned as the first or last transfer stop; however, the warehouse location is simply based on the random selection. The similar structure with the RSG’s distribution channel model is proposed for the Arizona Sun Corridor Megaregion, although the model was not estimated due to the data limitation (Livshits et al. 2017). Focusing on the logistics chains that go through intermediate facilities within a metropolitan area, Sakai et al. (2017) propose a logistics chain model, which pairs freight demand generating locations with logistics facilities, which become the origins or destinations of shipments. They estimate the models by commodity type and the type of demand locations. The estimated models are used for estimating indirect commodity flows. Alternatively, rule-based and/or optimization methods that consider the use of warehouses can be applied to estimate commodity flows (e.g. Friedrich 2010). However, the required data for such models is not compatible with the extension of the approach to replicate the entire urban commodity flows in a metropolitan area.
In this paper, we improve and expand the framework of Wisetjindawat et al. (2005) and Sakai et al. (2017) for the estimation of the commodity flows within a metropolitan area, covering various distribution channel types. We contribute to the state-of-the-art urban freight models by proposing a method to model the multi-level decision of supplier function choice (i.e. distribution channel) and supplier choice. The model is particularly innovative by considering the distribution channels based on business function for the urban commodity distribution and aggregately reproducing the parts of logistics chains that are within the study area. It should be noted that our approach does not replicate the entire logistics chains that go beyond the scale of a metropolitan area. In fact, the data for the entire logistics chains are extremely difficult to obtain through a survey. However, the proposed approach in this paper just requires the shipment and supplier records, both of which are usually covered in a standard establishment survey for urban freight.
Model structure and calibration data
Analytical settings
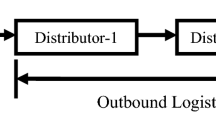
In this paper, we define a shipment as a quantity of goods shipped together from one location to another without transshipment. A shipment based on this definition is also called a “leg”. Logistics chains that connect producers and consumers consist of legs as shown in an illustrative logistics chain (Fig. 1). We use “daily attraction” (DA) as the unit of the data points for the analysis. A DA is defined as a daily freight attraction associated with a receiver facility that has specific function and location, which should be supplied by one of potential suppliers. In the simulation context, DAs, or freight attraction at another time scale, should be estimated by a freight attraction model. We consider five receiver function types: office/store/restaurant (OSRR), logistics facility (LFR), factory (FCR), cultural and educational facility (CEFR), and residential facility (RFR). The superscript “R” indicates that those are receiver establishments. We define a supplier as an establishment, categorized into one of three function types: office/store (OSS), logistics facility (LFS), or factory (FCS). As with receiver functions, the superscript “S” indicates that those are suppliers. Each supplier is associated with a geographical location and every supplier handling a required commodity type is a potential origin of a shipment for a receiver demanding goods.
The aim of the proposed model is to select a supplier, which is associated with one of three function types, for a DA at a receiver, who also has its own function type, for estimating intra-metropolitan commodity flows. In other words, the model estimates the shipment OD (or commodity flows) along with the “leg type”, which is defined by the functions of the upper and lower ends of the leg. Given the receiver function type, the “leg type” is equivalent to “distribution channel” (Boerkamps et al. 2000; Wisetjindawat et al. 2005). Leg type is important to replicate freight traffic in an urban freight simulation model. For example, shipment size, vehicle type used, and delivery tour pattern, are all tied to the leg type; a shipment from a factory to a logistics facility and that from a logistics facility to a store can be different in these aspects and, if any, such differences must be considered.
The model is designed so that a receiver, to whom a DA is associated, selects a supplier. It does not necessarily reflect the reality in which the origin of the shipment is determined in the course of the complex interactions between both receivers and suppliers. However, this is a reasonable premise applied in previous freight modeling efforts (Wisetjindawat et al. 2005, 2006; Liedtke 2009; Roorda et al. 2010). This is further justified as, in general, the need for goods movement is associated with the receiver (i.e. demand) side and the receiver directly/indirectly has an influence on the location of the shipment origin through the effort of minimizing the total cost.
The connections between the receivers and suppliers established by the model are to be used for generating shipments. A carrier operation model, which is included in SimMobility (Alho et al. 2017) (and, also, in other disaggregate urban freight simulators), takes these shipments as inputs and generates goods vehicle tours and trips, which are, in turn, the inputs for a traffic simulation. The type of the distribution channel can be considered at each of the steps that follows the commodity flow estimation. Regarding the framework of the SimMobility, the feedback structure is considered so that the outputs of the traffic simulation, for example travel time, are returned to the other “upstream” simulation components that include the commodity flow estimation.
Data
We use the data of the 2013 TMFS. The TMFS is an urban freight establishment survey conducted by the Transport Planning Commission of the Tokyo Metropolitan Region (TPCTMR) for the Tokyo Metropolitan Area (TMA), currently the most populous metropolitan area in the world. An area of 23 km2 was covered and the responses were collected from 43,131 establishments (a response rate of 31.6%) in various industry sectors such as manufacturing, wholesale, transportation, service, retail and restaurant. The TMFS collected both establishment information and shipment records through a paper-based survey. The establishment information includes location (address), industry and function types, commodity types handled, employment size, floor area, and the year of establishment. The shipment records were collected for a typical day. Commodity type, weight, and the information of origins and destinations including their locations at the municipality level (315 municipalities in the survey area) and function types are covered. Each data point (i.e. establishment) has an expansion factor, which is calculated by the TPCTMR based on industry type, employment size, and geographic location, for taking extraction rates into account. The average expansion factor is 4.61. We use these expansion factors to reproduce the population of supplier establishments, which are considered as alternatives in the choice model, and also to expand the shipment records for parameter estimations. It should be noted that, in the shipment records in the TMFS data, “offices and stores” with distribution functions, such as those of wholesalers, are labeled as “offices and stores”, as with those without distribution functions.
We estimate the models for nine commodity types shown in Table 1. This paper will focus the discussion on one commodity type (“household/light manufacturing goods”) for demonstrating the modeling approach and interpretation. It covers sundry items, clothing and textiles, products of paper, rubber, wood, and furniture. The numbers of the associated shipments and supplier establishments are summarized in Table 2. It should be noted that these shipments do not include external shipments, i.e. the shipments sent to or received from outside of the study area. As indicated by Sakai et al. (2017), the supplier choice mechanisms for intra-metropolitan and inter-regional shipments are quite different. For considering the external shipments in a simulation, one must define the external productions and consumptions and connect these external locations with the establishments in the study area using another set of models, which can be estimated with the similar framework proposed in this paper. Most of the urban freight movements in the TMA are by goods vehicles; therefore, the models in the present research are for the shipments transported by goods vehicles.
Model specification and estimation
Specification
The proposed structure of the supplier choice consists of two levels and we apply the logit mixture model with error components (Fig. 2) that allows us to capture the complex correlation structure among alternatives. The upper and lower levels are defined by supplier function types and individual suppliers, respectively. This structure is selected as the suppliers within the same function category (i.e. OSS, LFS or FCS) are expected to correlate with each other. Also, the cross-nested structure is considered as the suppliers from two different function categories may correlate. For example, in some case, a commodity is highly likely supplied to a receiver by either of a OSS or a LFS but not by a FCS. In Fig. 2, “downstream” (DWS) is the nest that includes both OSS and LFS and “upstream” (UPS) is that including LFS and FCS. This arrangement mimics the three-level nested logit model in which, the choice from UPS and DWS is at the first level, the one from OSS, LFS and FCS is at the second level, and the individual supplier choice is at the third level. The proposed explanatory variables for the utility of a supplier for a receiver (Table 3) are the travel time between a supplier and a receiver, the freight production (i.e. the total weight of outbound shipments) of a supplier, and the weight of the shipment (i.e. DA). We decided to use travel time, not travel distance, because the travel time can capture traffic conditions, although these two variables are highly correlated to each other. Overall, we assume a supplier that is located closer and has a larger capacity than others should have a higher potential to be selected by a receiver. In addition, depending on the size of demand, a supplier with a specific function type would be more likely to be chosen. In general, a larger demand is more likely to be catered by a logistics facility or a factory than an office/store.
Each model is specific to a combination of receiver function \(rf\) (OSR, LF, FC, CEF, or RF) and commodity type \(c\). For the simplicity of notification, \(rf\) and \(\it {\text{c}}\) are omitted in the following model specification.
The utility of a supplier with supplier function \(sf\) (\(sf\) = 1: office/store; \(sf\) = 2: logistics facility; \(sf\) = 3: factory), \(S^{ sf}\), for a daily attraction DA is:
where \(V_{{DA,S^{sf} }}\): Deterministic component of the utility. \(M_{{DA,S^{sf} }}\): Random component that captures the correlation structure among alternatives. \(\varepsilon_{{DA,S^{sf} }}\): Identically and independently Gumbel distributed random component (normalized: scale = 1, location = 0).
The deterministic component is given by the following equation:
where \(lnTIME_{{DA,S^{sf} }}\): The natural log of travel time between supplier \(S^{sf}\) and daily attraction \(DA\). \(ln FP_{{S^{sf} }}\): The natural log of freight production (i.e. total weight of outbound shipments) by supplier \(S^{sf}\). \(ln WEIGHT_{DA}\): The natural log of the weight of daily attraction \(DA\). \({Dum_{OS}}_{S^{sf}}\): Dummy variable. 1 if \(sf = 1\) (OS); 0 otherwise. \({Dum_{LF}}_{S^{sf}}\): Dummy variable. 1 if \(sf = 2\) (LF); 0 otherwise. \({Dum_{FC}}_{S^{sf}}\): Dummy variable. 1 if \(sf = 3\) (FC); 0 otherwise. \(\beta_{TIME}^{OS}\), \(\beta_{TIME}^{LF}\), \(\beta_{TIME}^{FC}\), \(\beta_{FP}^{OS}\), \(\beta_{FP}^{LF}\), \(\beta_{FP}^{FC}\), \(\beta_{Const}^{LF}\), \(\beta_{Const}^{FC}\), \(\beta_{Weight}^{LF}\), \(\beta_{Weight}^{FC}\): Parameters to be estimated.
The continuous variables are log-transformed as it significantly improves the significance of the variables and the fit of the models. We do not directly include the costs that are incurred upon the formulation of the receiver-supplier relationship as the explanatory variables. However, the deterministic component of the utility shown above could be regarded as consisting of the terms that represent transportation cost, which depends on the “impedance” between a supplier and a receiver, the scale of a supplier, and the relative purchasing price of commodity. We assume the followings: (i) the average transportation cost increases monotonically with travel time and the weight of goods; (ii) the scale is represented by freight production (i.e. total weight of outbound shipments); (iii) for a certain commodity type, the average price of the commodity monotonically increases with the weight of goods and differs by the function type of suppliers. For example, (2) can be rewritten for LFS as:
where
and;
The terms in (3) represent the effects of transportation cost, the scale of a supplier, and the relative purchasing price (against OSS), respectively. Note that \(\beta_{{Weight_{1} }}^{LF}\) and \(\beta_{{Weight_{2} }}^{LF}\), i.e. the coefficients relevant to the interaction and main effects of the weight of DA, cannot be estimated separately. The heterogeneity within the suppliers that are the same in terms of the three explanatory variables (Table 3) is captured as a part of the random component.
The identification of the parameters to be estimated within \(M_{{DA,S^{sf} }}\) is required to obtain definite estimations. We followed the procedure proposed by Walker et al. (2007), ensuring that the Order Condition, the Rank Condition, and the Equality Condition are satisfied, and determined the two nests, FC and UPS, for which the covariance, \(\sigma^{FC}\) and \(\sigma^{UPS}\), are fixed as 0. Thus, \(M_{{DA,S^{sf} }}\) is given by the following equation:
where \(\eta_{DA}^{OS}\), \(\eta_{DA}^{LF}\), \(\eta_{DA}^{DWS}\): Random terms following the normal distribution with zero mean and one standard deviation. \(\sigma^{OS}\), \(\sigma^{LF}\), \(\sigma^{DWS}\): Parameters to be estimated.
Given some values for \(\eta_{DA}^{OS}\), \(\eta_{DA}^{LF}\) and \(\eta_{DA}^{DWS}\), the conditional probability for \(S^{sf} \varvec{'}\) to be chosen by a receiver for DA is:
Unconditional probability is given by the following equation, using the multivariate density function of \(\eta\)s, f():
Estimation
The computational burden becomes an issue in estimating an error components logit mixture model with a large choice set. For example, we consider 13,152 potential suppliers that handle household/light manufacturing goods as the alternatives. Different approaches to select the choice set have been tested and discussed in the past research (Lemp and Kockelman 2012; Guevara and Ben-Akiva 2013). Guevara and Ben-Akiva compare three methods for sampling alternatives, i.e. population shares method, 1_0 method and Naïve method, and show that Naïve method, i.e. the random selection from all of the potential alternatives, is suitable and practical for logit mixture models. Furthermore, the draws of the random terms, ηs, must be specified. After testing various combinations of choice set size and the size of Halton draws, we decided to use 50 Naïve choices of alternatives with 1000 Halton draws as the estimated parameters are stable under such setting. We use PythonBiogeme (Bierlaire 2016) for the model estimation based on the maximum simulated likelihood method.
Estimation results and discussion
Models for household/light manufacturing goods
Table 4 shows the estimation results of five models for different receiver types. The adjusted Rho-square is the highest for CEFR, 0.651, and the lowest for LFR, 0.225. Most explanatory variables are significant for a 95% confidence interval, with the exception of DumFC in FCR model, ln FPLF in CEFR model, and DumLF and ln Weight × DumFC in RFR model. We first focus on the covariance parameters, as we will later discuss the effects of variables based on elasticities.
Compared with the covariance parameters in the other models, SigmaDWS in the models for CEFR and RFR are very high, 6.03 and 14.3, respectively. This indicates there are two uncorrelated categories identified for supplier function, i.e. non-factory and factory, while the suppliers in OSS and LFS (i.e. within non-factory category) are highly correlated. What is common between the two receiver types is that they are end-consumers of goods, not intermediate facilities or producers. On the other hand, the models for LFR and FCR shows the significant SigmaOS and SigmaLF (2.46 and 1.13, and 0.83 and 0.91, respectively) but not SigmaDWS. This indicates that the correlations exist mainly within each supplier function category for these facility groups. Lastly, all three covariance parameters are significant in the model for OSRR, corroborating the complex correlation structure within and across supplier function types. The estimated models for other commodity types are shown in the “Appendix”.
Elasticities
To compare the magnitude of the effects of the variables, we compute elasticity effects for the pairs of receiver and supplier function types. The average elasticities are defined by the following equations:
For travel time/freight production:
For weight:
where \({\text{P}}_{{{\text{DA}},{\text{S}}^{\text{sf}} }}\): Probability for a supplier \({\text{S}}^{\text{sf}}\) to be selected for a daily attraction \({\text{DA}}\). \({\text{x}}_{{{\text{DA}},{\text{S}}^{\text{sf}} }}\), \({\text{x}}_{\text{DA}}\): An explanatory variable (Travel Time, Freight Production, or Weight) without log transformation. \({\text{N}}_{{{\text{S}}^{\text{sf}} }}\): Number of alternatives (potential suppliers). \({\text{N}}_{\text{DA}}\): Number of observations (i.e. DA).
We compute the elasticities with respect to travel time/freight production for all receiver and supplier pairs and then calculate their average. As for weight, a DA specific variable, we first compute the elasticities of the probability of selecting a supplier function group for each DA and then calculate the average. For taking the error structures into account, we use Monte Carlo method. The random values are generated for \(\eta_{\text{DA}}^{OS}\), \(\eta_{\text{DA}}^{LF}\), \(\eta_{\text{DA}}^{DWS}\) and the average elasticities (defined above) are computed 1,000 times. The means of the simulated average elasticities are calculated.
Household/light manufacturing goods
The results are shown in Table 5. Travel time has a very strong effect on supplier choice, regardless supplier–receiver function pair. Especially, the effect is strong for CEFR and RFR, which indicates that suppliers that are closely located are highly likely to be selected for the needs of end-consumers. On the other hand, the effects are relatively weak for LFR, with the elasticities ranging between − 1.47 and − 1.10. The effect is the smallest when the supplier is also a logistics facility (LFS), which is due to the fact that logistics facilities often function as intermediate points for long logistics chains. Another interesting finding is that, for FCR, the travel time from LFS is more important than from the other supplier types (i.e. OSS and FCS), indicating logistics facilities should be located close to factories (FCR) for being selected as suppliers.
The scale of production is also a contributing factor to be selected as a supplier. Production has no effect only for one receiver-supplier functions pair, CEFR–LFS. In general, the elasticities associated with LFS are small. For the shipments from intermediate facilities, the volume of goods handled has only limited effects.
Lastly, the weight of DA relates to the decisions on supplier function. As naturally expected, a larger demand is less likely to be supplied by OSS. The choice of LFS or FCS for a heavier demand depends on the receiver function; as for FCR and CEFR, a heavier demand is more likely to be supplied by a FCS, while as for OSRR, LFR and RFR, a LFS is more likely to handle such demand.
Commodities other than household/light manufacturing goods
The average elasticities of other commodities are computed as shown in Table 6. Some features are common across commodity types. For example, excluding mixed goods and parcel, the effects of travel time tend to be low for LFR (between − 1.61 and − 0.93 for LFR-ALLS), while high for RFR (between − 3.37 and − 1.60). The travel time is least influential when the LFR receive from FCS (between − 1.06 and − 0.66). There are also some differences on the elasticity effect of travel time by commodity type; by receiver type, the commodity type that shows the smallest absolute elasticity effect (with ALLS) is different. On the other hand, the travel time is critical for mixed goods and parcel, having much larger absolute elasticity effects than other commodities in many cases.
As for freight production, like household/light manufacturing goods, the elasticity effects tend to be smaller when the suppliers are LFS, although in some cases, such as FCR–LFS and LFR–LFS pairs for food products and mixed goods and parcel, the effects are large. For agricultural product received by OSRR, LFR, FCR, and CEFR, the freight production is most sensitive when the suppliers are OSS, showing the elasticity effects of 0.50, 0.51, 0.48 and 0.58, respectively. For wood and paper products, the freight production has large effects for the pairs of OSRR–FCS (0.53), LFR–OSS (0.67), LFR–FCS (0.52), and FCR–FCS (0.44).
Lastly, a smaller DA is more likely to be catered by OSS and a larger DA by LFS. There are some cases where this characteristic does not apply; for instance, when a OSRR receives minerals, ore, stone, cement, ceramics or glass, a larger demand is less likely to be handled by LFS.
Observed versus estimated OD flows
We compare the estimated OD flows using the estimated models, against the observed OD flows. The purpose of this exercise is to test the reproducibility of the model at the OD level. Note that the process of comparing the simulation results against the data we used for the model estimation is different from the process of model validation, which requires a validation data set that is not used for the model estimation. For computing the OD flows, the TMA is divided into 18 zones. The OD flow is compared for each of 324 (18 × 18 zones) OD pairs. The Monte Carlo method is used for the OD flow estimation; the simulation for supplier choices is repeated 20 times and the averages are computed. We calculate \(R^{2}\) as the measure of the reproducibility; \(R^{2}\) is defined as:
where \(y_{i,j}\): Observed number of shipments for an OD pair i, j. \(\widehat{{y_{i,j} }}\): Estimated number of shipments for an OD pair i, j. \(\bar{y}\): Average observed number of shipments for all OD pairs.
Figures 3 and 4 show the comparison of each OD flow for all shipments and for the shipments from each receiver function type. Figure 3 considers the shipments of household/light manufacturing goods only and Fig. 4 covers all commodity types.
Figure 3 shows the high overall reproducibility of the model for household/light manufacturing goods with \(R^{2}\) of 0.70 (top-left). On the other hand, the reproducibility for the shipments that LFRs receive is low, showing \(R^{2}\) of 0.35 (middle-left). Also, the shipments to OSRRs show relatively low \(R^{2}\) (0.54, top-right). Both LFRs and OSRRs, especially LFRs, are the potential intermediate locations of logistics chains. The result highlights the difficulty of estimating the flows of the shipments sent to those facilities for household/light manufacturing goods. In contrast, the shipments to FCRs and RFRs, which are likely to be the consumers of goods received (in case of FCRs, goods are “consumed” to produce other goods), show relatively high R2s (0.73, middle-right, and 0.86, bottom-right, respectively), indicating this type of the shipment flows can be well-captured with the proposed model framework. The reason for the relatively low R2 for the shipments to CEFRs, which is also 0.54 (bottom-left), is unclear. As the underestimation for the two OD pairs which are the largest in terms of the observed shipment counts greatly lowers the R2, there may be some large-scale suppliers for CEFRs (e.g. schools) and the model may not properly capture the decisions of choosing them. Figure 4 shows the even higher reproducibility of the model when all commodity types are considered (\(R^{2}\) is 0.80; top-left). The models for LFR also achieve much higher \(R^{2}\) (0.77, middle-left) than the case only for household/light manufacturing goods; the errors for different commodity types are canceled out when all commodities are aggregated.
Additionally, we calculate R2 in terms of weight, instead of shipment counts, for the shipments of all commodity and receiver types. The computed weight-based R2 is 0.46, which is lower than the R2 based on the number of shipments. The weight distribution of the intra-metropolitan shipments is highly skewed. The analysis using the 2013 TMFS indicates that about 5% of the heaviest shipments account for 80% of the total shipment weight. Such high skewness makes it challenging to reproduce the observed OD flows in terms of weight using a disaggregate model. It is worth noting that, if the data is segmented into small groups (e.g. the groups by OD pair), the highly skewed distribution of shipment weight population may impair the representativeness of the sample sets for the groups, even with a large-scale survey data. For example, Sakai et al. (2015b) show that the highly skewed distribution of establishment-level freight generations causes a large error in the estimation of the average freight generation rate based on sample data.
Conclusions
Despite the fact that the type of distribution channel is relevant to the decisions on various aspects in logistics operations, the selection of distribution channel was not considered in most of the existing urban commodity flow models. Leveraging establishment and shipment records, which become increasingly more available for cities around the world, we propose a framework of the error component logit mixture model that considers the choices at two levels, the supplier function choice and the supplier choice. Given the function of the receiver, the supplier function choice is equivalent to the selection of distribution channel. We tested the model framework using the data obtained from the 2013 TMFS, a large-scale establishment survey.
The estimated model allows us to analyze the relationships among the distribution channels. The covariance parameters indicate that the correlations among the distribution channels are different by the function type of a receiver. For example, non-factory suppliers are highly correlated when a receiver is an end-consumer. Furthermore, the estimated model provides valuable insights about the relationship between the choice of the supplier/supplier function and the variables, i.e. distance (travel time), freight production, and the weight of demand by the receiver function and the commodity type. For instance, regarding household/light manufacturing goods, when a logistics facility supplies goods to a factory, the distance to the demand is crucial for an establishment to be a competitive supplier. The model also captures the fact that a large-size demand is more likely met by a supply from logistics facilities and factories. It also indicates that travel time is valued more highly for mixed goods and parcel than the other commodity types. Lastly, \(R^{2}\) obtained from the comparison of the simulated versus observed shipment counts motivates us to further use the proposed modeling framework in urban freight modeling systems, although it requires caution to interpret the estimated weight-based flows if the demand weight distribution is highly skewed.
The 2013 TMFS data we use has some limitation in differentiating the establishments that have only office functions from those serving both as office and distribution facilities. The business function information is valuable for urban freight modeling and we encourage to collect accurate records for it in future surveys. The receiver/supplier functions are also relevant to modeling other aspects of urban freight including carrier selection and goods vehicle tours. The development of new modeling/simulation approaches to deal with such elements is a future work. The integration of the simulations for the different decision-making processes in urban freight is especially important because it allows the feedbacks on the key decision parameters, especially those related to costs. For example, the accurate estimation of travel time through traffic simulations is important for a realistic simulation of mixed goods and parcel flows and a policy test focusing on this commodity type.
References
Abate, M., Vierth, I., Karlsson, R., de Jong, G., Baak, J.: A disaggregate stochastic freight transport model for Sweden. Transportation. (2018). https://doi.org/10.1007/s11116-018-9856-9
Adnan, M., Pereira, F. C., Azevedo, C.M.L., Basak, K., Lovric, M., Feliu, S.R., Yi, Z., Joseph, F., Christopher, Z. Ben-Akiva, M.: SimMobility: a multi-scale integrated agent-based simulation platform. In: 95th Annual Meeting of the Transportation Research Board, Washington, DC (2016)
Alho, A., Bhavathrathan, B.K., Stinson, M., Gopalakrishnan, R., Le, D.T., Ben-Akiva, M.: A multi-scale agent-based modelling framework for urban freight distribution. Trans. Res. Proc. 27, 188–196 (2017)
Alho, A., e Silva, J.D.A.: Lisbon’s establishment-based freight survey: revealing retail establishments’ characteristics, goods ordering and delivery processes. Eur. Transp. Res. Rev. 7(2), 16 (2015)
Ben-Akiva, M., de Jong, G.: The aggregate-disaggregate-aggregate (ADA) freight model system. In: Ben-Akiva, M., Meersman, H., Van de Voorde, E. (eds.) Freight Transport Modelling, pp. 69–90. Emerald Group Publishing Limited, Bingley (2013)
Bierlaire, M.: PythonBiogeme: a short introduction. Report TRANSP-OR 160706, Series on Biogeme. Transport and Mobility Laboratory, School of Architecture, Civil and Environmental Engineering, Ecole Polytechnique Fédérale de Lausanne, Switzerland (2016)
Boerkamps, J., van Binsbergen, A., Bovy, P.: Modeling behavioral aspects of urban freight movement in supply chains. Transp. Res. Rec. 1725, 17–25 (2000)
Cheah, L., Zhao, F., Stinson, M., Lu, F., Ding-Mastera, J., Marzano, V., Ben-Akiva, M. Next-generation commodity flow survey: a pilot in Singapore. In: 10th International Conference on City Logistics, Phuket, Thailand (2017)
Chow, J.Y., Yang, C.H., Regan, A.C.: State-of-the art of freight forecast modeling: lessons learned and the road ahead. Transportation 37(6), 1011–1030 (2010)
Comi, A., Delle Site, P., Filippi, F., Nuzzolo, A.: Urban freight transport demand modelling: a state of the art. Eur. Transp. (2012). http://hdl.handle.net/10077/6123
Dablanc, L., Rakotonarivo, D.: The impacts of logistics sprawl: how does the location of parcel transport terminals affect the energy efficiency of goods’ movements in Paris and what can we do about it? Proc. Soc. Behav. Sci. 2(3), 6087–6096 (2010)
Davydenko, I., Tavasszy, L.: Estimation of warehouse throughput in freight transport demand model for the Netherlands. Transp. Res. Rec. 2379, 9–17 (2013)
De Jong, G., Vierth, I., Tavasszy, L., Ben-Akiva, M.: Recent developments in national and international freight transport models within Europe. Transportation 40(2), 347–371 (2013)
Fischer, M., Outwater, M., Cheng, L., Ahanotu, D., Calix, R.: Innovative framework for modeling freight transportation in Los Angeles County, California. Transp. Res. Rec. 1906, 105–112 (2005)
Friedrich, H.: Simulation of logistics in food retailing for freight transportation analysis. Karlsruher Institut für Technoligie (KIT), Karlsruhe (2010)
Gliebe, J., Smith, C., Wies, K., Heither, C., Doyle, J., Outwater, M.: An agent-based gaming approach to simulating the evolution of commodity flows. In: Urban Freight and Behavior Change (URBE) Conference, Rome (2015)
Guevara, C.A., Ben-Akiva, M.E.: Sampling of alternatives in logit mixture models. Transp. Res. Part B Methodol. 58, 185–198 (2013)
Huber, S., Klauenberg, J., Thaller, C.: Consideration of transport logistics hubs in freight transport demand models. Eur. Transp. Res. Rev. 7(4), 32 (2015)
Hunt, J., Stefan, K., Brownlee, A.: Establishment-based survey of urban commercial vehicle movements in Alberta, Canada: survey design, implementation, and results. Transp. Res. Rec. 1957, 75–83 (2006)
Hunt, J.D., Stefan, K.J.: Tour-based microsimulation of urban commercial movements. Transp. Res. Part B Methodol. 41(9), 981–1013 (2007)
Lemp, J.D., Kockelman, K.M.: Strategic sampling for large choice sets in estimation and application. Transp. Res. Part A Policy Pract. 46(3), 602–613 (2012)
Liedtke, G.: Principles of micro-behavior commodity transport modeling. Transp. Res. Part E Logist. Transp. Rev. 45(5), 795–809 (2009)
Livshits, V., You, D., Zhu, H., Jeon, K., Vallabhaneni, L., Camargo, P., Pourabdollahi, Z.: Mega-regional multi-modal agent-based behavioral freight model. Final report. Strategic Highway Research Program 2 (SHRP2 C20 IAP Grant). http://www.azmag.gov/Portals/0/Documents/MagContent/TRANS_2017-02-13_SHRP2-TRANS_2017-06-06-C20-MAG-Next-Generation-Freight-Demand-Model-Update.pdf. (2018)
Moeckel, R., Donnelly, R.: A model for national freight flows, distribution centers, empty trucks and urban truck movements. Transp. Plan. Technol. 39(7), 693–711 (2016)
Nuzzolo, A., Comi, A.: Urban freight demand forecasting: a mixed quantity/delivery/vehicle-based model. Transp. Res. Part E Logist. Transp. Rev. 65, 84–98 (2014)
Oka, H., Hagino, Y., Kenmochi, T., Tani, R., Nishi, R., Endo, K., Fukuda, D.: Predicting travel pattern changes of freight trucks in the Tokyo Metropolitan area based on the latest large-scale urban freight survey and route choice modeling. Transp. Res. Part E Logist. Transp. Rev. (2018). https://doi.org/10.1016/j.tre.2017.12.011
Resource Systems Group, Inc.: User’s guide and model documentation: agent-based supply chain modeling tool. The report for Chicago Metropolitan Agency for Planning. http://www.cmap.illinois.gov/data/transportation/modeling (2015)
Roorda, M.J., Cavalcante, R., McCabe, S., Kwan, H.: A conceptual framework for agent-based modelling of logistics services. Transp. Res. Part E Logist. Transp. Rev. 46(1), 18–31 (2010)
Sakai, T., Kawamura, K., Hyodo, T.: Locational dynamics of logistics facilities: evidence from Tokyo. J. Transp. Geogr. 46, 10–19 (2015)
Sakai, T., Kawamura, K., Hyodo, T.: Urban freight survey sampling: challenges and strategies. In: 94th Annual Meeting of the Transportation Research Board, Washington DC (2015b)
Sakai, T., Kawamura, K., Hyodo, T.: Logistics chain modeling for urban freight: pairing truck trip ends with logistics facilities. Transp. Res. Rec. 2609, 55–66 (2017)
Tavasszy, L.A., Smeenk, B., Ruijgrok, C.J.: A DSS for modelling logistic chains in freight transport policy analysis. Int. Trans. Oper. Res. 5(6), 447–459 (1998)
Toilier, F., Serouge, M., Routhier, J.L., Patier, D., Gardrat, M.: How can urban goods movements be surveyed in a megacity? The case of the Paris region. Transp. Res. Proc. 12, 570–583 (2016)
Walker, J.L., Ben-Akiva, M., Bolduc, D.: Identification of parameters in normal error component logit-mixture (NECLM) models. J. Appl. Econom. 22(6), 1095–1125 (2007)
Wisetjindawat, W., Sano, K., Matsumoto, S.: Supply chain simulation for modeling the interactions in freight movement. J. East. Asia Soc. Transp. Stud. 6, 2991–3004 (2005)
Wisetjindawat, W., Sano, K., Matsumoto, S.: Commodity distribution model incorporating spatial interactions for urban freight movement. Transp. Res. Rec. 1966, 41–50 (2006)
Zhao, M., Chow, J.Y., Ritchie, S.G.: An inventory-based simulation model for annual-to-daily temporal freight assignment. Transp. Res. Part E Logist. Transp. Rev. 79, 83–101 (2015)
Acknowledgements
We would like to thank the Transportation Planning Commission of the Tokyo Metropolitan Region for sharing the data for this research. This research is supported in part by the Singapore Ministry of National Development and the National Research Foundation, Prime Minister’s Office under the Land and Liveability National Innovation Challenge (L2 NIC) Research Programme (L2 NIC Award No L2 NICTDF1-2016-1.). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not reflect the views of the Singapore Ministry of National Development and National Research Foundation, Prime Minister’s Office, Singapore. We thank the Urban Redevelopment Authority of Singapore, JTC Corporation and Land Transport Authority of Singapore for their support.
Author information
Authors and Affiliations
Contributions
TS Research Design, Literature Review, Model Specification, Analysis, and Manuscript Writing. BKB Model Specification and Analysis. AA Model Specification, Manuscript Writing and Editing. T Hyodo: Data Preparation and Analysis. MBA Research Design, Model Specification and Analysis.
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendix: Error component logit mixture models
Appendix: Error component logit mixture models
Tables 7, 8, 9, 10 show the estimated models for commodity types other than household/light manufacturing goods.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sakai, T., Bhavathrathan, B.K., Alho, A. et al. Commodity flow estimation for a metropolitan scale freight modeling system: supplier selection considering distribution channel using an error component logit mixture model. Transportation 47, 997–1025 (2020). https://doi.org/10.1007/s11116-018-9932-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-018-9932-1