Abstract
In the pursuit of sustainable mobility policy makers are giving more attention to cycling. The potential of cycling is shown in countries like the Netherlands, where cycling covers 25 % of all person trips. However, the effect of policy interventions on cycling demand is difficult to measure, not least caused by difficulties to control for changing context variables like weather conditions. According to several authors weather has a strong influence on cycling demand, but quantitative studies about the relationship are scarce. We therefore further explored this relationship, with the aim of contributing to the development of a generic demand model with which trend and coincidence in bicycle flows might be unraveled. The study is based on time-series between 1987 and 2003 of daily bicycle flows, collected on 16 cycle paths near two cities in the Netherlands. The regression analyses show that, not surprisingly, recreational demand is much more sensitive to weather than utilitarian demand. Most daily fluctuations (80 %) are described by weather conditions, and no less than 70 % of the remaining variation is locally constrained. The regression can therefore mainly be improved by incorporating path specific, as yet unknown, variables. We used the regression results to calculate weather-inclusive bicycle flow predictions and found indications of a downward trend in recreational demand. This trend has been off-set in the observed flows by more favorable weather conditions over the years considered.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cycling is an important mode of transport in the Netherlands. According to the Dutch National Travel Survey more than 25 % of all person trips are made by bicycle. This percentage also applies to work trips and recreational trips separately (V&W/DVS (Ministry of Transport) 2009). In 2009 in the Netherlands 0.8 trips per person per day were made by bicycle, more than in most other European countries, whereas the total number of trips (3.0) was more comparable to other countries (e.g. 2.7 in Great Britain, see www2.dft.gov.uk). Cycling delivers considerable benefits to society. It is healthy, sustainable, and inexpensive, it increases social participation and it also may reduce the number of short car trips in urban areas and so even has the potential to reduce congestion (Heinen et al. 2010). It is therefore not surprising that cycling is supported by governments, and that several measures are taken to increase its demand. To determine to which extent the increase aimed for is realized, cycling demand has to be measured. Complicating factors, however, are spatial and temporal variations that are not at all related to policy measures.
Several authors have used aggregated models to describe spatial variation in cycling demand according to census data. This was done in the US, e.g. Baltes (1996) and Dill and Carr (2003), in the UK, e.g. Parkin et al. (2008) and Waldman (1977), and in the Netherlands, e.g. Rietveld and Daniel (2004). Parkin et al. (2008) showed that hilliness, temperature and rain have a large influence on demand in the UK. Rietveld and Daniel (2004) found that cycling demand in Dutch cities depends on demographics such as ethnic composition, and policy-related variables like safety and modal competitiveness.
Although these studies give insight in spatial variation in cycling demand, they do not focus on temporal variation. Temporal variations consist of short-term (hourly/daily), seasonal and long-term variation. The patterns are thought to depend largely on differences in weather conditions and differ between utilitarian and recreational cyclists. Compared to car traffic, for bicycle flows this variation is relatively large (Emmerson et al. 1998). This may even cause differences on the level of yearly average flows (Jaarsma and Wijnstra 1995), especially for recreational areas (Beunen et al. 2004). As a consequence, developments on specific cycle paths are not directly interpretable from measured flows. Instead, these flows need to be corrected for weather conditions.
Weather is therefore an important factor when monitoring cycling demand over time and investigating developments in actual use of infrastructure. This paper aims to further explore the relationship between weather and bicycle flows, by deploying regression and residual analyses on data over a relatively long time-period (4–11 years). This study is also meant as a contribution to the development of a generic demand model that can account for a large part of the day-to-day bicycle flow variation. Such a model can ultimately be very useful to provide corrections for studies focusing on demand developments over a longer period of time, for example for evaluating policy measures to increase cycling demand. It may also be used as part of a benchmarking tool, when comparing cycling demand in different regions with different weather conditions. Corrected bicycle flows are also worthwhile when constructing a transport model calibration set. Another application is to clarify developments in traffic victims among cyclists, by relating (daily) weather conditions to differences in exposure (Bijleveld and Churchill 2009).
This paper is structured as follows. In Data we describe the data that are used. Method describes the methodology. In Development of the regression function, the functional form of the non-linear regression is determined, and in The influence of weather on bicycle flow, the results of the regression analysis are analyzed. Analysis of the remaining variation describes the remaining variation with respect to the regression. In Evaluation of trends over the years as an application, we applied the regression model to evaluate long term time-series of bicycle flows. Conclusions and further research is the discussion section, ending with conclusions.
Data
This section describes the observational data used in this study. It concerns daily bicycle counts (Bicycle counts) and weather data (Meteorological data). Data selection deals with the selection criteria for the data used in the regression analyses.
Bicycle counts
Since the late 1980s, the Wageningen University gathered cycle flows, measured by pneumatic tubes, on cycle paths in the countryside throughout the Netherlands. From this large data set we selected daily (24 h totals) data from 16 cycle paths, eight of them located near the city of Gouda (in the west) and another eight near the city of Ede (in the centre of The Netherlands).
Three types of cycle paths were distinguished: utilitarian, mixed and recreational. The utilitarian paths are connecting municipalities, playing an important role for mandatory trips, whereas recreational paths open up the country side for pursuing leisure activities by citizens. Mixed paths combine these functions. The allocation to the three classes is based on knowledge of the local situation.
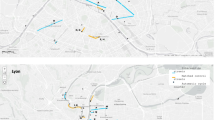
In Fig. 1 we give an overview of the data set of 24 hour total bicycle traffic counts. The period of the observations varies between 4 years (2 sites) and 11 years (7 sites) and covers partly different years from 1987 to 1993 (in Gouda) and from 1990 to 2003 (in Ede). All sites were measured in 1993. At the top of Fig. 1 the measuring points in both areas are presented geographically. We numbered the sites E1–E8 for the Ede region and G1–G8 for the Gouda region. If relevant, the site number is followed by u for utilitarian paths, by m for paths with a mixed character and by r for recreational paths.
In Fig. 2 and 3 we show the flow time-series for the recreational path E6-r (upper panel) and for the utilitarian path G1-u (lower panel). This is done for the whole measurement period (Fig. 2), and for the year 1993 (Fig. 3), as an example. Both cycle paths are judged to be typical for their sets.
The time-series of Fig. 2 show similar patterns over the years for each of the two paths. Within the years, as Fig. 3 shows more clearly, there are characteristic differences between the recreational and utilitarian time-series. Both patterns rise over spring and fall over wintertime, but differences are much larger in the recreational time-series. Also the difference in the summer period (around day 200) is remarkable: a rise in the recreational time-series versus a considerable dip in the utilitarian one. Within the weeks the variation between workdays and weekends is considerable, again in a different direction for both paths. The utilitarian path shows a repetition of dips which coincide with the weekends, as would be expected in the case of mandatory trips. The recreational path shows peaks in the weekends, as would be expected, since recreational trips are dominant in the weekends. Also, some strong peaks coincide with the Dutch bank holidays.
A problem related to counting with pneumatic tubes (and indeed with several other instruments as well) concerns the failure to detect the number of bicycles when cyclists cross the tube at the same time. However, we had no additional information on these occurrences and adopted the common assumption that in low flow regimes as is the case in our study these occurrences are not really selective in time.
Meteorological data
The weather ‘observables’ we used in the study were provided by the Dutch National Meteorological Institute (KNMI 2009), and can be downloaded free of charge from their website. We only used data from station “De Bilt”, because this station is in the proximity of both Ede and Gouda (about 35 km) and there are no local stations available. Therefore, the weather data do not necessarily present the local weather conditions. Moreover, at the time of conducting the research only 24 h aggregates were provided on the website, which leads to more uncertainties (e.g. a wet night followed by a sunny day might have the same total precipitation duration as a dry night followed by a wet day).
We investigated all daily meteorological data provided by the KNMI, except wind direction. These are: temperature (in °C), precipitation (in millimetres and hours), sunshine (amount in J/cm2 and duration in hours), wind velocity (in m/s), mean cloud cover (in octants), visibility (in metres) and humidity (%). For temperature, wind velocity, humidity and visibility, we could use minimum, maximum and average values. However, the correlations between the minima, maxima and averages were found to be very strong (correlation coefficients larger than 0.9). In addition, the amount and duration of precipitation are also strongly correlated, with a correlation coefficient of 0.8. The same applies for the amount and duration of sunshine. For correlation coefficients larger than 0.6, we choose one observable in the regression analysis. As a result, we minimize the effect of multicollinearity in the regression analysis. The results are described in Development of the regression function.
Data selection
Because of their distinctive character, bank holidays were taken out of the sample, including the school holiday weeks with Christmas and New Year. The remaining school holiday days (2 weeks during spring, 8 weeks during summer, and 1 week during autumn) were grouped together in a subsample. These holidays are also distinctive, but at the same time cover extensive periods in the year. We therefore evaluated the regression for these holidays separately. We took into account that the dates of these holidays slightly change year by year.
In order to reject (a large part of) possible false measurements, we excluded all cases with five bicycle counts per day or less. The most common cause of a false measurement is a temporally malfunctioning of the tube. In some cases, the measurement may be valid due to very low demand. However, such a low demand is rare, and normally demand exceeds 10 counts per day in our dataset. By adopting this selection criterion, we excluded less than 1 % of all measurements.
After determining the regression function, described in Method and Development of the regression function, we compared the measurements with the regression results. We then detected some weeks in which the observed utilitarian flows on workdays were much lower (more than 30 %) than in other weeks. We found four of such weeks in four different years. This bias might be explained by the fact that we failed to identify all school holidays, due to incomplete logging for the first few years. More likely, however, are false measurements, caused by a punctured tube. Although we could not retrieve the cause of the deviating demand during these weeks, we decided to exclude these weeks from the sample. By doing so, we rejected another 1 % of the measurements.
Method
Relatively little is known about the relation between weather and cycling demand. The few studies on this topic do show a strong influence of weather on cycling demand, e.g. Hanson and Hanson (1977); Emmerson et al. (1998); Jaarsma (1990); Nankervis (1999). From a correlation and regression analysis on a household survey over a 39 day period in Sweden, Hanson and Hanson (1977) showed that both temperature and cloud coverage are related to the proportion of daily cycling demand. In another Swedish study Bergström and Magnusson (2003) examined the attitudes towards cycling during winter in general, and in relation to winter maintenance of cycle paths in particular. Emmerson et al. (1998) used long-term counts and meteorological data to investigate the relative effects on cycle use of weather and other factors. Their data suggest that cycle flows are more influenced by maximum temperatures than by rainfall.
Jaarsma (1990) used a similar approach, by applying site-specific log linear multiple regression models to data collected over the years 1984–1988 at 14 sites, covering recreational as well as utilitarian cycle paths in the Netherlands. He found that most of the variation in demand was explained by the models, but that still quite a large fraction was unaccounted for. Jaarsma and Wijnstra (1995) and Hendriks (2002) made some changes to these models, like different models for workdays and weekends and incorporating a memory term to give extra impact to ‘sunny’ weather conditions after a cloudy period, but these changes did not reduce the remaining variation much.
Our study can be regarded as an extension of these previous studies, although our approach is slightly different. Instead, we took new data that cover a much longer time-period to find a more generic regression form that fits all data. Also, contrary to many studies, we did not determine the functional form of the regression in advance. For example, one could use a multiple linear regression analysis to relate the weather observables, like temperature and precipitation, to cycle use. The coefficients of this linear regression can then be estimated by a least-square fit. However, it is not known a priori whether the relation between cycle use and weather observables is linear. By inspecting the observations and by using logic arguments, one can estimate a realistic functional form, which may or may not be linear. We adopted the latter approach in the following way. First, we applied a linear multiple regression, deciding which weather observables should be included. Secondly, we evaluated the average residuals of the linear regression to arrive at the final (non-linear) functional form and calibrated regression coefficients. Finally, we analysed the remaining variation and studied long term trends.
The generic regression function
We start by expressing the regression in a very general form:
In Eq. 1, q est is the estimated daily flow, which is a function f of the weather observables W obs i , such as average temperature or the duration of precipitation. We use the natural logarithm (ln) in Eq. 1, because we assume that an absolute improvement in weather will uniformly lead to the same relative increase in demand.
The function f can be any function. To simplify the problem, we applied the restriction that the function f is a linear combination of weather parameters W i , whereas each weather parameter is regarded as a (non-linear) function of the corresponding weather observable.
To ease the interpretation of the relative contribution of each weather parameter, we chose to apply a normalization procedure. The normalization was carried out as follows. For each weather parameter we estimated the average and standard deviation over the total measurement period (1987–2003). From the parameter value per day we then subtracted the average and divided the result by the standard deviation. Each normalized parameter thus has an average equal to 0 and a standard deviation equal to 1. Equation 2 can then be rewritten as follows:
where c i = ba i , and \( \sum \limits ^{m}_{i \; = \; 1} a_{i}^2 \; = \; 1. \)
The variable q 0 in Eqs. 2 and 4 is the standardized flow, which is the flow corrected for weather influences. In Eq. 4, we call the coefficients a i the weather coefficients, W the weather construct, and the coefficient b the slope. The weather construct W can be regarded as an estimation on how (potential) cyclists experience the weather conditions. A high value corresponds to weather conditions that favor cycling. Just like the weather parameters, W also has an average of 0, and a standard deviation of about 1. The slope b describes how the rate of relative increase of bicycle flow depends on W. Different travelers may experience the weather in the same way, but their inclination to make a trip may have a rather different dependence on W. The slope is expected to be high for recreational paths, because the choice to make a trip for leisure is expected to depend strongly on weather conditions. The influence of weather is expected to be less severe for utilitarian paths. In the extreme case, parameter b might be close to 0, if the path is mainly used by captives (e.g. school children).
We did not explicitly include the variables area (Ede or Gouda) and path type (recreational or utilitarian) in the multiple regression analysis. The relation between weather and cycling demand may not only depend on area or path type, but can also depend on other (hidden) path specific characteristics such as dominant trip length. We therefore chose to carry out separate regressions for each individual cycle path, and day of the week. Note that some of these hidden characteristics may be correlated with weather. As a consequence the effect of weather might be somewhat overstated.
Linear and non-linear regression
According to Eqs. 2 and 4, we only need to solve linear equations, which can be done with a multiple linear regression analysis. However, the weather parameters of the weather construct W can still have complicated forms, because they can be non-linear functions of the weather observables. In the simplest form, the weather parameters are equal to the weather observables.
This functional form is therefore linear. We developed the linear regression as follows. We used all weather observables from the Dutch National Meteorological Institute for a least squares fit, and constructed a first linear regression model. We then excluded observables that did not show a statistically significant contribution, i.e. observables for which the coefficients c i in Eq. 2 are not significantly different from 0. We also excluded observables that showed a strong correlation (correlation coefficient >0.6) with one or more other observables that had a larger contribution in the regression. In this way, we tried to minimize the effect of multicollinearity in the fit, although we can never completely eliminate it.
This is the simplest functional form, but may not provide an optimal fit. To check this, we studied the residuals. The residuals are defined as the differences between observations and regression estimates: Δln q = ln q obs −ln q est . For each weather observable that was included in the regression, we defined (small) ranges in which we aggregated the observations. Then, for each aggregate we determined the average value of the residuals, i.e. the mean of Δln q. In some situations, the average residuals may show a clear trend (being different from 0), indicating a systematic difference between observations and regression estimates. By using non-linear terms in the weather parameters (Eq. 3) such systematic differences can be reduced.
For the non-linear regression, we only considered weather observables that were already included in the linear regression. We tested several non-linear functions for each of these weather observables, applying a least squares fit, in order to arrive to average residuals of about 0.
The goodness of fit was evaluated by R 2, which is a standard measure in multiple regression analysis, and which indicates how much of the total variation is explained by the regression model. A large R 2 indicates that the model fits the observations quite well. However, one should be careful with interpreting R 2 values, because they are sensitive to the way the measurements of the ‘independent’ variables are dispersed. A few outliers in the independent variables may influence the fit quite strongly, and also may lead to an artificial increase in R 2. We therefore also adopted the root-mean-square (RMS) of the residuals as a measure for the quality of the model. A low RMS indicates that the model fits the observations quite well.
In the next section we elaborate on the functional form of the regression model.
Development of the regression function
We applied a linear regression per cycle path and day of the week to determine the main weather determinants of bicycle flows (Selection of relevant weather observables). From an evaluation of the systematic variation in the residuals (Systematic variation in the residuals) we improved the regression function by using the non-linear weather parameters (Non-linear relationships) instead of the original ones.
We excluded the school holidays from the analysis, because, as we will see in School holidays, the school holidays have their own standardized flows, q0, which is in general much lower compared to the standardized flows outside the school holidays for the utilitarian paths, but much higher for the recreational paths. These variations and seasonal variations in general will be separately evaluated in Analysis of the remaining variation.
Selection of relevant weather observables
From similar, important weather observables we chose the ones with the strongest correlation with cycle flows. For temperature and wind velocity, these were the daily averages. For precipitation, this was the duration of precipitation (in hours). We can also justify these choices with regards to cycling, because cyclists make their trips over the whole day, including the morning during which the temperature is actually close to the minimum. Similarly, cyclists are put off by a long period of moderate rainfall, whereas one short, heavy thunderstorm will only have a temporary effect.
The same applies for the duration of sunshine, which also shows a strong correlation with cycle flows. The other observables did not show explanatory power and their corresponding coefficients were almost never significantly different from 0 (i.e. humidity and visibility), or they showed a strong (negative) correlation with the amount of sunshine (i.e. humidity and cloudiness). These observables were therefore not included in the further regression analysis.
Hence, we have the weather parameters for temperature, W T , for duration of sunshine, W S , for duration of precipitation W P , and for wind velocity, W V . According to Eq. 5, for the linear model, W T = T, W S = S, W P = P, and W V = V. The results of the least squares fit are quite straightforward. Rises in temperature and duration of sunshine have a positive effect on cycling, while precipitation and an increase in wind velocity have negative effects. If we average the R 2 for all cycle paths, we find an average R 2 of 0.79. We find the same R 2 when we include the other weather observables. From this, we conclude that the reduction to four weather observables in our model is justified.
Systematic variation in the residuals
As stated in Linear and non-linear regression, the linear model may not be the optimal model. We conclude this from an inspection of the (mean) residuals, of which the procedure is described in that section. The results for the linear model are shown by the open squared symbols in Fig. 4. From upper left to lower right, we show the mean residuals for temperature, duration of sunshine, duration of precipitation and wind velocity respectively. We found no large differences between utilitarian, mixed and recreational cycle paths, and therefore show the aggregate of all paths together.
From the Figure we conclude that the residuals show systematic deviations from 0. The linear regression under and over estimates the flows (positive and negative residuals respectively) for T < 3 and T > 18 °C respectively. These average temperatures correspond with respectively minimum temperatures below 0 and a maximum temperature exceeding 25 °C on a day. This is in line with the hypothesis that below and beyond a certain temperature, cycle flows are not that sensitive to respectively a drop or rise in temperature anymore. For the high temperatures, it may even hold that “too” hot temperatures make it less attractive to cycle. Also, residuals decrease and increase with increasing duration of sunshine and precipitation respectively. This non-linearity can be explained by the idea that a difference between zero and one hour of sunshine or precipitation is experienced as a larger difference than a difference between for example 10 and 11 h. Because sunshine has a positive effect on demand, the linear regression over estimates demand (negative residuals) for large S. Similarly, because precipitation has a negative effect on demand, the linear regression underestimates the flows (positive residuals) for large P.
For wind velocity, we also found systematic effects. When the wind velocity is low, the model over estimates the demand (negative residuals). This also appears to be the case when the wind velocity is high. This suggests that beyond a certain velocity, wind has a negative effect on cycling, and that this effect will become disproportional larger for strong winds. This can be explained by the fact that a small breeze can be felt as not really unpleasant, while strong winds make it hard to cycle.
Non-linear relationships
To take these systematic effects into account, we adapted the linear model by testing different non-linear relationships and parameter values. We arrived at the following formulas and parameter values:
The above formulas cannot be regarded as independent from each other, since some observables are correlated. There are two important correlations. The first one is the positive correlation between temperature and the duration of sunshine. Both observables are also related to the period of the year. The second one is for obvious reasons the negative correlation between the duration of sunshine and precipitation. Both correlations have exactly the same strength (0.39 and −0.39 respectively). We therefore decided to include all observables as if they were independent of each other. However, due to these correlations, the non-linear corrections are also correlated. For example, high temperatures are found on sunny days in the summer. Equations 6c and 7 should therefore not been seen as independent from each other.
After normalizing the weather parameters, as described in the previous section, we finally applied a least squares fit to obtain the model coefficients of the model described by Eq. 10.
The mean residuals for this non-linear regression are shown by the filled circles in Fig. 4. These symbols show that the large deviations, shown by the open squares, have disappeared. We therefore conclude that a non-linear model provides better results. However, the average R 2 of the non-linear model is 0.80, which means that it increased only with slightly more than 0.01 compared to the linear model. Clear systematic effects are accounted for by the non-linear model, but these effects only apply to certain temperature ranges, and certain durations of sunshine and precipitation, and certain wind velocities. In addition, as we will show in the next sections, still quite a large amount of variation cannot be explained by the model. This variation is much larger than that accounted for by the non-linear model. Yet, notwithstanding the remaining variation, we may argue that the non-linear model is a clear improvement and that in this respect, it is important to carefully interpret R 2 values.
The influence of weather on bicycle flow
In this section, we discuss the results from the regression which is described by Eq. 10 in Development of the regression function. We used the weather parameters of the non-linear model described by Eqs. 6a–9 in Development of the regression function. We applied a least squares fit of the non linear weather model (excluding the school holidays). For each cycle path and day of the week, we thus obtained the standardized flow q 0 , the slope b, the weather coefficients a i , the R 2 value, and the RMS in the residuals.
The average values of the weather coefficients for all cycle paths and all days are a T = 0.78, a S = 0.39, a P = −0.32 and a V = −0.38. Temperature thus has the largest effect which is also in agreement with results found by Emmerson et al. (1998). It is surprising that the effect of precipitation is quite small. It is however important to stress that the weather parameters are still correlated, in particular there is a correlation between season, temperature and sunshine on the one hand, and between sunshine and precipitation on the other hand. Multicollinearity may lead to an under estimation of the effect of precipitation. It is also possible that the effect of precipitation is under estimated, by the fact that we used 24 h instead of day-time figures. However, in Analysis of the remaining variation, we will argue that this under estimation cannot be very large.
The R 2 value (average for all paths and days of the week) for the aforementioned average values of the weather coefficients is 0.80. The R 2 value hardly changes (<0.01) when we consider the individual coefficients (per path and per day of the week). However, as mentioned before, a small change in R 2 value can still be statistically significant, even when it appears small compared to the total (remaining) variation. In fact, we find a small, but statistically significant, difference between the fits for utilitarian paths during workdays, that have an average a T = 0.80, a S = 0.32, a P = −0.32 and a V = −0.40, and the fits for all other paths and/or days, that have an average a T = 0.75, a S = 0.46, a P = −0.31 and a V = −0.36. However, this is the only statistically significant difference we find. Within these two groups of paths and days, the variation in the individual coefficients is quite small, i.e. the standard deviation is about 0.04 and 0.07 per weather parameter for the first and second group respectively. The result indicates that the amount of sunshine is the most important weather parameter that distinguishes utilitarian from recreational paths. Hence, sunshine seems relatively more important for travelers that make recreational trips than for travelers that make utilitarian trips.
In contrast to the weather coefficients, the coefficients q 0 and b are much more variable. The standardized demand q 0 depends on the strength of local OD flows, and is therefore less relevant for this study. The slope b can be seen as the most relevant coefficient of this regression, because it describes how sensitive demand is to weather variations. In Fig. 5 we illustrate the results for a recreational path (E6-r, upper panel) and a utilitarian path (G1-u, lower panel) for Thursdays (left) and Sundays (right). The Figure shows large differences in the slope b. The slope is very shallow for the utilitarian path on a Thursday (bottom left). The slope becomes steeper for recreational paths and for Sundays. The results in Fig. 5 are illustrative for all paths outside the holiday periods.
In Table 1, we show the results for all paths on workdays, Saturdays and Sundays. For each path, the table provides the slope b and R 2 value for each of the days. For the utilitarian paths, the average slope b is 0.18 (in the range between 0.14 and 0.22) for workdays. The slope is on average 0.36 (in the range between 0.31 and 0.46) for Saturdays and 0.53 (in the range between 0.46 and 0.66) for Sundays. For recreational paths, the variation in b is larger, which can be explained by the fact that paths with the same classification can still serve somewhat different heterogeneous cycle flows. For recreational paths, b is on average 0.74 for workdays, 0.77 for Saturdays, and 0.79 for Sundays. However, the slopes are somewhat steeper for the recreational paths in Ede (with an average slope above 0.8) than for those in Gouda. We found no statistically significant differences between workdays.
The mixed paths show mixed results. This can be attributed to the fact that these paths combine functions of recreational and utilitarian paths, but not always in the same proportion. We therefore decided to exclude them from further analysis.
We interpret the results as follows. The utilitarian paths mainly serve school and work trips during workdays. Contrary to recreational trips, these trips are less influenced by weather, because they are obligatory, and therefore cannot easily be canceled. Also, school pupils cannot easily substitute another mode for the bicycle. During weekends, utilitarian paths show quite a steep slope, because demand is then dominated by the less obligatory trips. The steepest slopes, however, were found for recreational paths in Ede, for which cyclists appear to be the most sensitive to weather. An explanation may be that the recreational paths in Ede are used by long-stay tourists. These people, contrary to for example people who use the bicycle for a sports or shopping motive, make the least obligatory trips of all. Their trips have no other purpose, but to enjoy the environment and the good weather.
The R 2 values are creditably high for modeling of this kind. They are slightly larger for the weekends than for the workdays, i.e. 0.82 versus 0.79 on average. The relative variation in the residuals compared to the total variation is thus similar for the different fits. The total variation in demand, and thus also the variation in the residuals, increases from utilitarian trips to recreational trips. The RMS of the residuals is on average 0.11 for utilitarian paths during workdays. The RMS is on average 0.20 for Saturdays and 0.26 for Sundays. For recreational paths, the RMS of the residuals is on average 0.44 for workdays, 0.45 for Saturdays, and 0.44 for Sundays.
Analysis of the remaining variation
In this section, we analyze the remaining variation described by the residuals. First, we study seasonal variation (Seasonal variation). Then, we evaluate the variation of cycle flows during school holidays (School holidays). Finally, we investigate the remaining variation that is unaccounted for (Unaccounted variation).
Seasonal variation
We used the regression function, described in the previous sections, to estimate the model flows q est . With these flows, the weekly residuals can be determined. Per week, we determined the average weekly residual for workdays and weekends over the years. In Figs. 6 and 7 we show the results for utilitarian and recreational cycle paths respectively.
The Figures show that seasonal variations are rather similar for paths in Gouda and Ede, especially for utilitarian paths. For workdays outside the school holidays, seasonal variations are small on utilitarian paths, while for recreational paths some seasonal trend is visible. Volumes appear to be somewhat higher than expected during the spring, and lower than expected at the end of the year. A similar trend we find for all paths during the weekend. This seasonal effect can be attributed to recreational traffic, which is dominant on recreational paths and on utilitarian paths during the weekend. This result might be related to a higher appreciation of the first good weather days after wintertime.
We correct for seasonal effects by adding the weekly residuals to the natural logarithm of the estimated daily flows. If we only consider the non-holiday periods, we expect that the RMS of the residuals will hardly change for utilitarian paths, because seasonal variations are quite small for these paths. This is indeed the case. The RMS of the residuals is 0.11 and 0.22 for workdays and weekends respectively, compared with 0.11 and 0.23 for the situation without seasonal corrections. For recreational paths, the RMS of the residuals decreases when we correct for the weekly residual, but the decreases are also small, i.e. from 0.44 to 0.43 for the workdays, and from 0.45 to 0.43 for weekends. Although there is clearly seasonal variation, its effect on the remaining variation is apparently quite small.
School holidays
For the school holidays, excluded so far, the daily flows were initially estimated with the same regression function that was fitted for the non-holiday periods in the previous section. In Figs. 6 and 7, the holiday residuals are denoted with filled symbols. The Figures show strong deviations for workdays (upper panels) during school holidays, when demand is lower than normal for utilitarian paths and higher than normal for recreational paths. This is the result of a shift from utilitarian (school and commuting) trips to recreational trips in the school holidays. For weekends (lower panels), the differences between the holiday and non-holiday periods are much smaller. This result is also not unexpected, because in the Netherlands recreational traffic is always dominant during weekends.
The weekly residuals are much larger during the holidays, and they would certainly have an effect on the RMS of the residuals. However, when we correct for the weekly residuals, we find that for recreational paths and for utilitarian paths during the weekends, the RMS of the residuals are the same or even slightly smaller for holiday periods than for non-holiday periods. From this, we conclude that the coefficients of the model are also well suited for recreational traffic during holidays. The only difference is that the total demand changes during holidays.
We cannot draw the same conclusion for utilitarian traffic, i.e. for utilitarian paths during workdays. Even after a correction for weekly residuals, the RMS of the residuals is much larger for the holiday period (RMS = 0.28) than for the non-holiday period (RMS = 0.11). We therefore fitted the regression function again for the daily flows on workdays on utilitarian paths, corrected for the weekly residuals (subtracting these residuals from the observations), during the holiday period. We decided not to include the weather coefficients (a T , a S , a P , a V ) in the fit, but to use the same coefficients as for the non-holiday period. This was done because of the limited number of days, and because the model results are much more sensitive to the slope b than to the weather coefficients. This procedure is justified by the results. The RMS of the residuals for the new fit is 0.11, which is the same as for the non-holiday period.
With the adapted model, the average slope is 0.32 compared to 0.18 for the non-holiday period. The slopes are thus steeper, which implies that the influence of weather is somewhat stronger during the holiday period. This result is expected. Due to the drop of utilitarian trips, these paths serve relatively more recreational trips during the holiday period, albeit still a relatively small number. This can also explain the large variation in slopes from path to path. We find a slope of 0.25 for the path with presumably the smallest drop in utilitarian trips, and a slope of 0.52 for the path with a large drop in utilitarian trips.
Interestingly for utilitarian paths, the average R 2 value is 0.9 for the holidays compared to 0.8 for the non-holidays. The fact that the RMS values are similar shows that one should be careful with interpreting R 2 values. The holidays mark distinct periods in the year for which the average weather patterns are quite different. As a result, the holidays are represented by data points that are clustered in different groups. Such a distribution of data points typically leads to higher R 2 values.
Unaccounted variation
In the previous sections, we showed that most variation in flows on rural cycle paths in the Netherlands can be attributed to weather. However, the remaining variation is still large. At first sight, it is not clear what causes this variation. We concluded that the inclusion of other weather parameters will not lead to better demand estimates, and that the residuals of the non-linear model do not show weather-related systematic variation. Furthermore, seasonal variation only has a marginal effect on the regression results.
Some of the variation may be caused by the aggregate nature of the weather observables. As mentioned before, we used 24 h aggregates, that are not necessarily representative for local conditions. Inaccuracies in weather measurements could be reflected in a positive correlation between the residuals of nearby cycle paths, since demand estimates of nearby cycle paths are influenced by the same weather conditions.
For workdays, we find evidence of such a correlation between paths in the same town, but only when they are of the same type. The correlation coefficient is more or less the same for utilitarian and recreational paths, i.e. 0.5 during workdays, and 0.6 during weekends. However, we also find similar correlations for paths of the same type which are not located in the same town. Although the correlations are statistically significant, they are not very strong. Outside the school holidays, still about 70 % of the RMS in the residuals is uncorrelated. We suggest that this variation is caused by local fluctuations that are not weather related. This variation is considered to be random, and cannot be predicted by generic variables. The remaining 30 % of the variation is systematic.
The nature of the systematic variation is illustrated in Fig. 8. The Figure shows the weekly variation of the residuals (not corrected for seasonal variation) for workdays for the year 1993, excluding school holidays. The solid symbols represent the averages over the utilitarian paths in Gouda (upper panel) and the recreational paths in Ede (lower panel). For comparison, the corresponding seasonal variation of the residuals for all years (Figs. 6 and 7, excluding holidays) is shown by the solid lines. The error-bars in the figure indicate the variation in the daily residuals within a workweek, due to day-to-day variation. The figure illustrates that the error-bars are smaller than the week-to-week variation, which reveals some quite distinct features. In the last two months of 1993, for example, the residuals were structurally higher than normal for the recreational paths. A large fraction of the remaining systematic variation thus has time-scales of weeks, but it is not seasonal, because its structure changes from year-to-year. We find that the RMS of this systematic week-to-week variation accounts for about 70 % of the total systematic variation. Most of the systematic variation therefore does not only have time-scales longer than one day, but even time-scales longer than one week. This is also confirmed by the auto-correlation of the time-series of weekly residuals corrected for seasonal variation. The correlation between residuals of successive weeks has a statistically significant correlation coefficient of 0.3, and we even find evidence for a weak correlation when the residuals are separated by as much as 7 weeks.
The cause of the systematic variation is far from clear. It is different for utilitarian and recreational paths. In addition, correlations are found between paths in different towns (when they are of the same type) and between residuals of successive weeks. These results suggest that it is not very likely that (most of) this variation can be explained by the aggregated nature of daily weather measurements.
We conclude that most of the variation in the residuals is caused by local fluctuations in demand, which we consider as noise. The remaining systematic variation is not locally constrained. These non-local demand fluctuations, which have time-scales of weeks, may be included in a generic model, but more research is needed to find the causes for these fluctuations.
Evaluation of trends over the years as an application
One of the objectives of policy makers for monitoring cycle flows is to recognize developments in demand. It is however difficult to disentangle long term trends from shorter-term, weather related, fluctuations. With our regression model we have estimated expected flows. We can compare their annual averages with those of the observed flows in order to recover long term trends. In Fig. 9 we illustrate how this can be done. The Figure shows the annual average for the observations (symbols) and regression estimates (solid lines). This was done for the aggregates of utilitarian paths in Gouda (upper panel) and recreational paths in Ede (bottom panel), that comprise the largest part of our sample. Because of their distinct characteristics, we excluded the school holidays in this analysis.
Figure 9 shows that the model follows the shorter-term fluctuations in the observations quite well. Possible trends are revealed from the deviations between observed and estimated annual flows. For the utilitarian paths in Gouda, no trend appears to be present. For the recreational paths in Ede, a downward trend seems to be existing. The observations do not directly show a downward trend, but according to the estimates, this downward trend may be concealed by better weather conditions during the last few years (from 2000 onwards).
We illustrated that it is possible to detect long term trends in cycling patterns. However, studies of long term trends are far more meaningful when a large number of cycle paths in different areas can be analyzed, which is not the case in our study.
Conclusions and further research
The impact of weather on traffic flows has been investigated with rather different scopes, such as impact on traffic activity and on accident exposure (Al Hassan and Barker 1999), management of urban road networks (Keay and Simmonds 2005; Lam et al. 2008), the potential modal shift from car to bicycle, especially for short car trips (Bergström and Magnusson 2003), a contribution to reducing congestion (Heinen et al. 2010) and visitor flows to outdoor recreation sites (Brandenburg and Ploner 2002). Most studies focus on car traffic. Studies specifically on bicycle flows are scarce.
From the different studies on the impact of weather on bicycle flows we find air temperature (either the daily average or the maximum), precipitation (either amount or duration), hours of sunshine (or equivalents such as cloud cover) and wind speeds as most relevant explaining variables for day-to-day variations, additional to cyclical progress through the year, by day of the week and by school holiday. The regression analyses in these studies are applied to one site at a time, either for one year or for a series of years. The regression coefficients show to be site-specific, and not transferable from one site to another (Emmerson et al. 1998; Jaarsma 1990; Jaarsma and Wijnstra 1995; Hendriks 2002). Therefore, in this study a slightly alternative approach was chosen, in which a series of sites with (partly) different years of observation was analyzed as one common set of input-data. With this approach we were able to draw the following conclusions:
-
(1)
The weather parameters in order of importance are: average 24 h temperature, the duration of sunshine, the duration of precipitation, and the average wind velocity.
-
(2)
Different user groups (utilitarian and recreational) appear to experience the weather in more or less the same way. However, the influence of weather on demand is very different for both user groups.
-
(3)
About 80 % of the variations in our flow time-series can be explained by the regression model. Most of the remaining variation is caused by local fluctuations in demand, and cannot be described by adding more generic variables.
The approach allows for the development of a generic ‘weather model’, with which flows can be standardized and long-term trends in demand can be disentangled from shorter-term, weather related, variations. Such an application is very relevant to practitioners and policy makers, for instance in the context of evaluating cycle policy interventions on a local and regional scale. For example, we found no apparent trend for cycle paths in Gouda, while for paths in Ede a possible negative trend in demand is concealed by a positive trend in weather conditions. According to our limited sample, there is no evidence for a positive long-term trend in volumes of bicycle traffic, despite considerable policy interventions to promote cycling.
Another relevant application for a weather model concerns the assessment of trends in visitor flows to recreational areas. Insight into the number of visitors and a distinction between systematic and random variation of visitor flows is required for ecologically and economically sustainable management of national parks and specific destinations for outdoor recreation (Loomis 2000). In this context, the interrelationship between cars and bicycles needs specific attention. In a further study we therefore also want to investigate the hypothesis that the model enables us to describe fluctuations in day-to-day traffic and visitor flows by car and bicycle to such sites. A model might be able to also exclude weather effects from car flows, since there is evidence that car and bicycle mode might be interrelated Bergström and Magnusson (2003).
However, further steps need to be taken before aforementioned applications can be implemented. First, a substantial amount of variation is left ‘unexplained’. More research is needed to find the causes for these fluctuations. Other non-weather variables should therefore be studied in relation with cycling demand, and may eventually be included in a more generic model. Second, this analysis is based on a limited number of cycle paths in only rural surroundings, and it is yet unknown how the weather model will perform in other spatial contexts. At the moment, it is not clear if these results can be transferred to other paths, for example to paths in city centres with a lot of cover by buildings. However, this regression analysis can be seen as an important step to the development of such a comprehensive model.
References
Al Hassan, Y., Barker, D.J.: The impact of unseasonable or extreme weather on traffic activity within Lothian region, Scotland. J. Transp. Geogr. 7(3), 209–213 (1999)
Baltes, M.: Factors influencing nondiscretionary work trips by bicycle determined from 1990 US metropolitan statistical area data. Transp. Res. Rec. 1538, 96–101 (1996)
Bergström, A., Magnusson, R.: Potential of transferring car trips to bicycle during winter. Transp. Res. A 37(8), 649–666 (2003)
Bijleveld, F., Churchill, T.: The influence of weather conditions on road safety. An assessment of the effect of precipitation and temperature. SWOV-report R-2009-9, Leidschendam (2009)
Beunen, R., Jaarsma, C.F., Kramer, R.J.: Counting of visitors in the Meijendel dunes, The Netherlands. J. Coast. Conserv. 10, 109–118 (2004)
Brandenburg, C., Ploner, A.: Models to predict visitor attendence levels and the presence of specific user groups. In: Arnberger, A., Brandenburg, C., Muhar, A. (eds.) Monitoring and management of visitor flows in recreational and protected areas. Conference proceedings, pp. 166–172. Bodenkultur University Vienna, Austria (2002)
Dill, J., Carr, T.: Bicycle commuting and facilities in major US cities. Transp. Res. Rec. 1828, 116–123 (2003)
Emmerson, P., Ryley, T.J., Davies, D.G.: The impact of weather on cycle flows. Traffic Eng. Control 39(4), 238–243 (1998)
Hanson, S., Hanson, P.: Evaluating the impact of weather on bicycle use. Transp. Res. Rec. 629, 43–48 (1977)
Heinen, E., Van Wee, B., Maat, K.: Commuting by bicycle: an overview of the literature. Transp. Rev. 30(1), 59–96 (2010)
Hendriks, A.: After raining, the sun will shine again. MSc-thesis, Wageningen University, The Netherlands (in Dutch) (2002)
Jaarsma, C.F.,: Temporal variations of bicycle traffic flows in the Netherlands. Transportation and Traffic Theory. Proceedings of the eleventh international symposium on transportation and traffic theory, Yokohama, Japan. pp. 443–459. Elsevier, New York (1990)
Jaarsma, C.F., Wijnstra, F.J.: Coincidence or trend? A method for analysis of temporal variation of daily bicycle traffic flows. Paper presented at the seventh world congress on transportation research, Sydney, 1995
Keay, K., Simmonds, I.: The association of rainfall and other weather variables with road traffic volume in Melbourne, Australia. Accid. Anal. Prev. 37, 109–124 (2005)
KNMI (Koninklijk Nederlands Meteorologisch Instituut) Daggegevens KNMI-stations (2009). http://www.knmi.nl/klimatologie/daggegevens/download.cgi, Accessed 2009
Lam, W.H.K., Shao, H., Sumalee, A.: Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply. Transp. Res. B 42(10), 890–910 (2008)
Loomis, J.B.: Counting on recreation use data: a call for long-term monitoring. J. Leis. Res. 32, 93–96 (2000)
Nankervis, M.: The effect of weather and climate on bicycling commuting. Transp. Res. A 33(6), 417–431 (1999)
Parkin, J., Wardman, M., Page, M.: Estimation of the determinants of bicycle mode share for the journey to work using census data. Transportation 35(1), 93–109 (2008)
Rietveld, P., Daniel, V.: Determinants of bicycle use: do municipal policies matter? Transp. Res. A 38(7), 531–550 (2004)
V&W/DVS (Ministry of Transport).: Kerncijfers MON 2009, The Hague (2009)
Waldman, J.A.: Cycling in towns: a quantitative investigation. LTR1 Working paper 3. Department for Transport, London (1977)
Acknowledgment
The authors would like to thank three anonymous reviewers for their comments for improving this paper.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Thomas, T., Jaarsma, R. & Tutert, B. Exploring temporal fluctuations of daily cycling demand on Dutch cycle paths: the influence of weather on cycling. Transportation 40, 1–22 (2013). https://doi.org/10.1007/s11116-012-9398-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11116-012-9398-5