Abstract
Purpose
Simultaneously interacting rhizosphere processes determine emergent plant behaviour, including growth, transpiration, nutrient uptake, soil carbon storage and transformation by microorganisms. However, these processes occur on multiple scales, challenging modelling of rhizosphere and plant behaviour. Current advances in modelling and experimental methods open the path to unravel the importance and interconnectedness of those processes across scales.
Methods
We present a series of case studies of state-of-the art simulations addressing this multi-scale, multi-process problem from a modelling point of view, as well as from the point of view of integrating newly available rhizosphere data and images.
Results
Each case study includes a model that links scales and experimental data to explain and predict spatial and temporal distribution of rhizosphere components. We exemplify the state-of-the-art modelling tools in this field: image-based modelling, pore-scale modelling, continuum scale modelling, and functional-structural plant modelling. We show how to link the pore scale to the continuum scale by homogenisation or by deriving effective physical parameters like viscosity from nano-scale chemical properties. Furthermore, we demonstrate ways of modelling the links between rhizodeposition and plant nutrient uptake or soil microbial activity.
Conclusion
Modelling allows to integrate new experimental data across different rhizosphere processes and scales and to explore more variables than is possible with experiments. Described models are tools to test hypotheses and consequently improve our mechanistic understanding of how rhizosphere processes impact plant-scale behaviour. Linking multiple scales and processes including the dynamics of root growth is the logical next step for future research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The rhizosphere is one of the most complex and vital interfaces on earth (Hinsinger et al. 2009). It hosts myriads of microorganisms, and its properties affect terrestrial fluxes of water and various elements including carbon and nitrogen. Since soil water and nutrients have to traverse the rhizosphere before being taken up by the plant, the rhizosphere is considered to be the critical interface governing plant productivity and consequently food, fuel and fibre production. Understanding and engineering rhizosphere properties may then well be the key to promoting sustainable agriculture and mitigating the effects of climate change (Ahkami et al. 2017; Ryan et al. 2009). Engineering rhizosphere properties may open new avenues for crop production management and contribute to limiting the input of mineral fertilization or increase the water use efficiency of crops (Ahmed et al. 2018). The application of the acquired knowledge in the field of rhizosphere research for practical management purposes is however still in its infancy.
Rhizosphere properties are the result of manifold biological, physical, and chemical processes that ultimately impact plant growth and soil properties. These processes include water and nutrient uptake, rhizodeposition and microbial activity (Paterson et al. 2007), and rearrangement of soil particles by the root as it grows (Lucas et al. 2019; Phalempin et al. 2021). These processes interactively affect each other and dynamically determine the rhizosphere properties. They act on scales which span more than six orders of magnitude—from the scale at which rhizosphere processes take place (typically between 1 µm and 1 mm) to the management scale (> 1 m). This imposes challenges not only in the measurements of corresponding quantities but also in the appropriate description and conceptualisation of these processes, on the modelling, parametrization and linking of the scales.
Novel technologies and experimental approaches have been developed recently, which allow one to image or characterize rhizosphere-scale processes with an unprecedented spatial resolution (Roose et al. 2016; Vetterlein et al. 2020). These technologies open new opportunities to understand the complexity but provide fragmented information on rhizosphere architecture and functions. In addition, new models have been developed during the last decade, which allow to integrate biological, chemical and physical processes at different scales, from pore (microbial or soil pore models) to plant scale. These models can help (i) integrate different processes, (ii) explore more variables than is possible with experiments, (iii) scale up from local, or small-scale observations to the whole system, or the reverse if only bulk information is available and local information is of interest, (iv) provide high temporal resolution even if measurements could only be provided for a limited number of time steps and finally (v) test if hypothesised co-occurring mechanisms/processes could bring about spatial or temporal patterns observed, in particular if they are non-linear in nature. Note that observed behaviours at larger scales are more than the average or sum of small-scale processes due to the functional complexity of the system—this phenomenon is termed emergent behaviour in the theory of complex systems (Camazine et al. 2001; Thurner et al. 2018; Vetterlein et al. 2020).
There are a number of excellent recent reviews on challenges in imaging and predictive modelling of rhizosphere processes (Pot et al. 2021; Roose et al. 2016), challenges in modelling soil processes (Vereecken et al. 2016), or plant-soil modelling (Ruiz et al. 2020b). The objective of this opinion paper is to present a series of modelling scenarios, which integrate detailed rhizosphere processes into a plant-scale and soil profile-scale modelling concept. It results from research that has been funded in the priority program “Rhizosphere Spatiotemporal Organisation – a Key to Rhizosphere Functions” (PP 2089 of the German Research Foundation DFG).
The working hypothesis of the proposed approach is that the emergent behaviour at the plant scale is determined by the combined interaction of rhizosphere processes (Vetterlein et al. 2020). The emergent behaviour includes plant growth (e.g. biomass), bulk soil properties (e.g. permeability), transpiration, carbon fluxes, nutrient uptake, plant health, soil aggregation, and carbon storage and transformation.
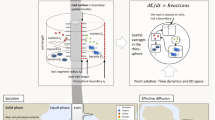
Rhizosphere processes include for instance root exudation, microbial transformation and biodiversity, water and nutrient uptake. We further distinguish between effective properties, which result from upscaling small-scale properties to larger scales, and emergent behaviour, which develops from the interactions between multiple small-scale processes and their responses to local soil and rhizosphere conditions. We focus on three spatial scales, namely the plant scale > single root scale > pore scale (see Fig. 1).
One aspect of our approach is to combine time-series images down to the pore scale with detailed models to define effective properties to be included in single root scale and plant scale models. Another aspect proposes to feed information from a larger scale models into the smaller scale models addressing longer temporal scales. Doing so, we propose a cross-talk between detailed processes and emerging behaviour, with both up- and down-scaling. A sketch of the scales and related processes we aim to address is shown in Fig. 1. The objective of upscaling multiple small-scale processes is to determine effective properties and emergent behaviours and to predict behaviours and trends. The objective of downscaling is to set boundary conditions for small-scale models, which are used to resolve smaller scale structures and evaluate their effect on emergent behaviours at larger scales.
Examples of case studies of linking mechanistic models and data across scales
The common theme of the five case studies in this paper is plant-derived soil organic carbon, its spatial and temporal pattern and effects on plant resource acquisition as well as microbial activity and biodiversity. The different presented modelling approaches involve processes taking place from pore to plant spatial scales (ranging from nm-µm to dm-m scales) and from second to week temporal scales. They all address how existing data could be integrated into the respective models. Figure 1 summarises these case studies, provides their specific scales and investigated processes (in colour). Some of the case studies are based on published data sets while others use yet unpublished work and are intended to serve as showcases.
Case study 1 couples a 3D dynamic root architecture simulation with root exudation of individual roots. The goal is to compute the rhizodeposition patterns at the plant scale during plant development as driven by multiple single root growth and rhizodeposition properties. It shows how plant root development might affect mm-scale carbon distribution.
Case study 2 quantifies the impact of root exudation by multiple growing roots of a plant to root phosphorus uptake. The overall plant phosphorus uptake and carbon investment emerge from the interaction between the rhizosphere processes on the single root scales. Again, this example bridges the gap between plant-scale development and the rhizosphere release of compounds and uptake processes. Case studies 1 and 2 require information on the diffusion coefficient in the rhizosphere. Case study 3 and 4 show how this diffusion coefficient is influenced by root hairs and mucilage, respectively.
Case study 3, for a given snapshot in root architecture development, zooms in to simulate the rhizodeposition around a single root affected by root hairs. This example demonstrates the use of µCT images for image-based modelling to investigate how root scale processes (at mm scale) impact micro-distribution of carbon in the rhizosphere at (sub-) mm scale in the rhizosphere and define the boundary and initial conditions for molecular and pore scale studies considered in case studies 4 and 5.
With case study 4, we explore pore scale processes in the range between nm and µm. In this example, we analyse the impact of the physico-chemical properties of mucilage on pore scale water dynamics. An effective diffusion coefficient is derived based on µCT pore scale images. The resulting diffusion coefficient can be included in models such as those of study 1 and 2.
Case study 5 focuses also on the pore scale and illustrates how microbe-driven processes emerge from interactions among the biotic and abiotic component using an individual-based approach describing microbial dynamics with an explicit description of the 3D soil structure, water, and carbon distributions.
Table 1 summarises the origins of the inputs needed for the different case studies. Most of the detailed 3D information can be provided through imaging, but some may also originate from the output of another model simulation.
All case studies are developed hereafter with the same basic structure: question, scales, approach, results, challenges, and open questions.
Models considering 3D root architecture and root growth
Case study 1: Rhizodeposition by a growing root system
Question What is the effect of root architecture development and exudate properties on the 3D distribution of rhizodeposits in soil?
Scale mm-cm, days-weeks.
Approach
The mathematical model behind this example is explained in Landl et al. (2021). Briefly, the 3D root architecture model CPlantBox (Schnepf et al. 2018) was coupled with a rhizodeposition model to investigate the spatio-temporal distribution patterns of rhizodeposits in the soil as affected by root architecture development and rhizodeposit properties. To simulate the 3D dynamic patterns of rhizodeposits in the soil, each growing root was considered to be a moving point source or a moving line source. Roots are considered moving point sources when rhizodeposition occurs mainly at the root tip (e.g. mucilage) and moving line sources when rhizodeposits are released over a certain length behind the root tip (e.g. citrate). In the soil, rhizodeposits were subject to diffusion, sorption and decomposition. Microorganisms were not considered explicitly, but degradation of rhizodeposits was included in form of linear first order decay (Kirk et al. 1999).
Analytical solutions for moving point or line sources in an infinite domain have long been available (Carslaw and Jaeger 1959). Thus, for any point in time or space, the analytical solution for rhizodeposit concentration around a growing root can be computed analytically. Since the underlying partial differential equation is linear, the concentration attributable to multiple roots of a growing root system was calculated as the sum of the concentrations attributable to each root using the superposition principle. However, the fact that the solution is based on analytical solutions does not imply a small computational time, since it involves the evaluation of integrals. Unless approximations are made that allow these integrals to be solved analytically, they must be evaluated numerically as many times as the spatial and temporal resolution requires. In this example, the simulation time was set to 21 days, simulation outputs were generated every day. The size of the soil domain was 20 × 20 × 45 cm3, and concentrations were computed at every mm3. Simulations were performed for two rhizodeposits, mucilage and citrate, and the example root system Vicia faba. Details can be found in Landl et al. (2021).
Parameterisation of the root architecture model
For the simulation of root architectures, CPlantBox requires a set of appropriate model input parameters. In this example, root architecture parameters were derived from µCT images of Vicia faba plants from a lab experiment (Gao et al. 2019). In this experiment, six replicates of Vicia faba plants were grown and each of them scanned at 7, 11, and 15 days after sowing. The roots on the µCT images were manually traced in the 3D virtual reality system of the Supercomputing Centre of Forschungszentrum Jülich, resulting in a data structure called root system markup language (RSML) (Lobet et al. 2015). It stores the 3D coordinates of the nodes along the center line of the root system and their connections, as well as various properties for the edges (root segments) connecting two nodes, such as the radius or the age of the root segment. The age of each root segment was linearly interpolated between the root tip (age = 0) and the root collar (age = time of measurement). Many model parameters could be calculated directly from the RSML files, such as the mean values and standard deviations of the radii, the lengths of the apical and basal zone, the intermodal distances and the branching angles. The remaining parameters, such as the emergence time of basal roots, were obtained by an inverse estimation that minimized the difference between the observed and the simulated total root length at the different measurement time points.
Rhizodeposit parameters
Rhizodeposition rates of mucilage and citrate from the roots of Vicia faba were derived from literature (Rangel et al. 2010; Zickenrott et al. 2016). We assumed that mucilage was released at the root tips, while citrate exudation occurred at a length of 4 cm behind the root tips. The diffusion coefficients in water for mucilage and citrate were taken from (Watt et al. 2006), the impedance factor from Olesen et al. (2001), the soil buffer power for citrate from Oburger et al. (2011) and the decomposition rate constants for mucilage and citrate from Kirk et al. (1999) and Nguyen et al. (2008). All values can be found in Table 1 of Landl et al. (2021).
Figure 2 outlines the workflow of case study 1. An important step in this case study was the development of a model that can simultaneously simulate root architecture development and root exudation as well as the fate of root exudate within the soil. Data acquisition included a plant growth experiment in which.
soil columns containing root systems were scanned with µCT. The roots on the µCT images were segmented and traced to derive the parameters of the root architecture model CPlantBox. The output of this case study is the 3D dynamic pattern of rhizodeposition concentration for different rhizodeposits around the growing root system of Vicia faba.
Results
Figure 3(a, b) shows the distribution of citrate and mucilage concentrations around the 3-week-old root system of Vicia faba. Due to the differences in rhizodeposit properties, the maximum mucilage concentrations were larger than the maximum citrate concentrations, while the extent of the mucilage enrichment zone was smaller than the extent of the citrate enrichment zone. Figure 3(c, d) shows the distribution of rhizodeposit hotspots, in which the rhizodeposit concentration is above a defined threshold. For mucilage, we chose a value at which the mucilage concentration is high enough to significantly alter soil hydraulic properties, i.e., 0.33 mg g−1 dry soil (Carminati et al. 2016). For citrate, we chose a concentration that is high enough to significantly mobilise phosphate, i.e., 5 µmol g−1 soil (Gerke 2015). We demonstrated that root growth rate had a significant effect on the volume of rhizodeposit hotspots and that the volume of rhizodeposit hotspots was greatest at intermediate root growth rates. At slow root growth rates, rhizodeposit concentrations were high, but the soil volume containing these high concentrations was low. At rapid root growth rates, the soil volume containing rhizodeposits was high, but rhizodeposit concentrations were mainly below the threshold concentration. Analysis also showed that the rhizodeposit hotspot volume around the 3-week-old root system of Vicia faba was significantly larger for citrate than for mucilage. Due to the different release behaviour of the rhizodeposits, high mucilage concentrations were mainly located at the root tip, while high citrate concentrations were found closer to the root base. As a result, additional hotspots were created for citrate by overlapping the rhizospheres of individual roots. Our analysis showed that rhizosphere overlap accounted for more than half of the total citrate hotspot volume, whereas only about 10% of the total mucilage hotspot volume was due to rhizosphere overlap. In addition, we showed that long duration of rhizodeposition hotspots is also strongly influenced by the overlap of rhizospheres, which is why long duration rhizodeposition hotspots occurred mainly in the root branching zone. This example demonstrates how the interaction between plant scale processes like root architecture development with single root processes like rhizodeposition defines the emergent spatial and temporal distribution of these rhizodeposits. Such a distribution could then be used to define time-varying boundary conditions for smaller scale models, e.g. in case study 5.
Vertical cut through the distribution of the rhizodeposit concentrations around 3-week-old root systems of Vicia faba (citrate (a), mucilage (b)); note that the colours are in logarithmic scale (from Landl et al., 2021). Distribution of rhizodeposit hotspots (pink patches) of citrate and mucilage around a 21-day-old root system of Vicia faba (citrate (c), mucilage (d))
The importance of root growth for the radial extension of the rhizosphere
Kim and Silk (1999) demonstrated the importance of root elongation rate for the extension of the radial concentration profiles around roots. They defined a root-related version of the Péclet number, a dimensionless number usually used to quantify the importance of diffusive relative to convective transport. Replacing convection with root elongation, the “rhizosphere Péclet number” Perhizo can be written as
where v is the root elongation rate, L is the characteristic length and D is the diffusion coefficient in soil.
The rhizosphere Péclet number in soils is usually greater than one, indicating that the elongation rate has an important effect on the rhizosphere gradients. In the above case study, the Perhizo values for citrate and mucilage are 192.68 and 1.17, respectively, for a root with a radius of 1 mm and growing at 2 cm/d. Thus, we can already predict that the rhizosphere will be considerably narrower for mucilage than for citrate, and this will vary with elongation rate. In the case of mucilage, root elongation is dominantly affecting the rhizosphere extent while for citrate, root elongation and diffusion both have an equally strong affect. Also, in this case, root elongation may not be neglected! This is illustrated in Fig. 4 that shows for mucilage and citrate how the extent of the zone of influence decreases with increasing root elongation rate. Thus, root growth dynamics are important for the investigation and analysis of rhizosphere gradients around individual roots. This may have implications on experimental designs such as the choice of sampling locations.
Challenges and open questions
The combined effects of root architecture development and rhizodeposition in turn affect multiple other relevant processes such as soil carbon turnover (Hütsch et al. 2002) and microbial activity (Paterson 2003) or plant water and nutrient uptake (Carminati et al. 2016; McKay Fletcher et al. 2020). Modelling those interactions will enable us to assess the impact of rhizodeposition on these processes at the root system scale. Little information exists on changes in the diurnal rhizodeposition and its dependence on light quality and quantity (Kuzyakov 2002; Melnitchouck et al. 2005). New experimental data sets on the distribution of rhizodeposits in soil are now available, including zymography or co-registered Magnetic Resonance Imaging and Positron Emission Tomography (Koller et al. 2018; Spohn and Kuzyakov 2014). Integrating those data into our model, we will be able to increase our process understanding as well as gain additional information on the location, intensity and temporal dynamics of rhizodeposition rates using inverse modelling. In case study 1, we have considered the root tip as a point. For detailed analysis within the elongation zone, its spatial (in the order of mm) and temporal (in the order of < 1 h) scales are relevant (Baskin 2013; Silk 1984).
Case study 2: Phosphate uptake by a growing root architecture as affected by citrate exudation
Question How is overall phosphate solubility and consequently uptake affected by root exudates released from a growing root system? How well are diffusion, transport and reaction of nutrients in the rhizosphere of a growing root architecture understood?
Scale: mm-cm, days-weeks.
Approach
In this case study, the dynamic root architecture model CPlantBox, formerly RootBox (Leitner et al. 2010a), was coupled with a model of phosphate transport in soil and rhizosphere that takes into account competitive sorption of phosphate and citrate in soil. In particular, the sink term for phosphate uptake by roots from soil was developed in a way to recognize the dynamic development of the rhizosphere gradients around each individual root segment. For each root segment of the root system, a 1D radially symmetric rhizosphere model was solved in each time step and coupled to the macroscopic plant-scale model in a mass-conservative way. Contrary to Case study 1, the rhizosphere domain recognises the physical presence of the roots. The inner boundary of the radially symmetric domain is at radius r = r0 while the outer boundary is at radius r = r1, where r0 is the root radius and r1 is the half mean inter-root distance which is computed from the root length density RLD as \({r}_{1}=\frac{1}{\sqrt{RLD\bullet \pi }}\). The model setup was a virtual representation of a rhizobox experiment with oilseed rape (Brassica napus L.) (see Schnepf et al. 2012 for details). Briefly, oilseed rape was grown in a rhizotron for 16 days and kept at an inclination of 49°. The simulations mimicked this experiment such that simulated root growth was confined inside the rhizotron boundaries and had the same root length as observed, namely 734 cm. The root architectural parameters were obtained by inverse estimation such that the difference of observed and simulated root length densities was minimized. Root exudation was assumed to occur at the whole root length with an exudation rate of 3 × 10–6 µmol cm−2 s−1 (Kirk et al. 1999). The water content was set constant at 0.3 cm3 cm−3; the effective diffusion coefficient in soil was computed based on the Millington-Quirk model (Millington and Quirk 1961). A competitive Langmuir sorption isotherm for citrate and phosphate was used to simulate phosphate mobilisation due to citrate exudation. The sorption parameters, microbial decomposition rate constant for citrate, and Michaelis Menten P uptake parameters were derived from literature (see Tables 1 and 2 in Schnepf et al. 2012). Initially, the soil had a homogeneous initial P concentration and zero citrate concentration. At the boundaries of the rhizotron, no-flux boundary conditions were prescribed, so that the only changes in citrate and phosphate concentration in the rhizotron occurred through the root activities, citrate exudation and P uptake. The Perhizo values for P and citrate individually are 0.15 and 0.22, respectively. The relatively smaller values compared to the previous example are due to the fact that root radii of oilseed rape in case study 2 are one order of magnitude smaller than those of bean in case study 1; i.e., the smaller the root radii, the smaller the rhizosphere Péclet number. As the values are only slightly smaller than one, still both root elongation and diffusion affect the radial extension of the concentration profiles, with diffusion being the dominant process.
Figure 5 outlines the workflow of case study 2. Model development resulted in a model that could simultaneously simulate root growth, root exudation and its effect on nutrient availability and uptake. Data acquisition involved a plant growth experiment where roots were washed from the soil, scanned, and the root length determined with WinRhizo. This data was used to inversely estimate root architectural parameters for the CPlantBox model. Together with transport properties and reaction rate parameters, the simulation results in the 3D dynamic pattern of phosphate and citrate concentration as well as cumulative nutrient uptake and exudation.
Results
This model quantifies how two traits, root system growth and exudation, affect plant phosphate uptake. Figure 6 shows the simulated root age distribution of roots grown inside the rhizotron, as well as the total phosphate and citrate concentrations in soil as affected by root exudation and phosphate uptake. The highest citrate concentration and phosphate depletion occurred in the region where the root system was oldest. In this case study, performed for a soil with medium sorption capacity, the model showed that cumulative phosphate uptake was more than doubled through root exudation of citrate (see Schnepf et al. 2012). This value would vary for soils with different sorption behaviours. The case study shown here is based on the assumption that root exudation occurs over the whole root length, so that the citrate concentration would be higher around older roots. This is different if the root exudation occurs only near the root tips as we have seen in case study 1, as then concentrations are highest near the root tips. In both cases, overlapping accumulation zones would further induce hotspot formation.
Challenges and open questions
Functional-structural models of root water and nutrient uptake may help to understand what the optimal coordination would be between root growth and rhizodeposition of different substances to obtain optimal water and nutrient uptake by the root system. The simulation results presented here made some assumptions about the location and dynamics of exudate release along the root axes. Based on available experimental data, a more accurate parameterisation would be possible. Alternatively, whole-plant structural functional models are now being developed that can model the flow of carbon from photosynthesis to the different plant organs and release into the soil (Zhou et al. 2020). Those model results may be used as input for the model presented in case study 1.
As shown in case study 4, it is now possible to derive an effective diffusion coefficient as a function of radial distance from the root surface using mathematical homogenisation based on µCT-derived soil structure and mucilage information. This is a chance to test where the standard Millington-Quirk model is valid and where new approaches to derive the effective diffusion coefficient in soils and rhizosphere are needed. By image based models it is also possible to investigate the effect of root hairs on element distribution (case study 3).
Another challenge is to compare the simulated nutrient gradients to the gradients found through chemical imaging methods at different positions within the root system and to evaluate whether the model can reproduce those observed gradients. If this is established, then observed element distributions could serve as input for inverse simulations for nutrient uptake and transport parameters.
Models computing the effect of root hairs and mucilage on effective diffusion
The following case studies 3–5 are examples of image-based modelling with a fixed soil and root geometry as captured by µCT images. This is either a limitation that could be accepted for the sake of simplicity or limited to slowly growing or thin roots (case studies 3 and 4), or required boundary conditions are made dynamic, e.g. from outputs of a larger scale model (as outlined in case study 5).
Case study 3: Root exudation and the role of root hairs on the single root scale
Question How do root hairs and the contact between the root surface and the soil matrix affect rhizodeposition and the spatial distribution of root exudates from the root surface?
Scales Spatial scale: < 1 mm, temporal scale: < 1 day.
Approach
Data acquisition and processing
Maize plants (Zea mays L.) were grown in seedling holder microcosms (Keyes et al., 2013; Koebernick et al., 2017) which were filled with a sieved and fertilized loamy substrate (Vetterlein et al. 2021). For image acquisition, roots of the 14 days old plants were scanned non-destructively at an actual voxel size of 0.653µm3 using a synchrotron radiation X-ray CT (TOMCAT, Paul Scherrer Institute Villigen, Switzerland). In order to segment the scanned roots as well as soil aggregates, image processing was performed in Avizo (Thermo Fisher Scientific). 3D finite element meshes consisting of the soil matrix and the root-soil contact, where the exudation boundary conditions are defined, were generated in Gmsh. A more detailed description of the experimental setup and data processing are available in the supplementary information.
Modelling
To assess the effect of root hairs on the spatial distribution of root exudates, image-based modelling on the pre-processed CT data was performed. Diffusion simulations of carbon released by a root segment of approx. 1.4 mm length into the rhizosphere were carried out for two cases on one exemplary sample – a root with and without hairs. We considered the root as well as its’ hairs to release carbon (Holz et al. 2017) treating their contact surface to soil aggregates as inlet at a constant concentration. Carbon diffusion was calculated in the partially saturated soil micropore region with a no-flow boundary condition at the surface of the soil aggregates. There was no carbon diffusion in the air-filled macropores. For a root growing at 2 cm/d, the root radius measured in our images of 300 µm, and a diffusion coefficient of carbon in soil of \(0.025 {\mathrm{cm}}^{2}{\mathrm{d}}^{-1}\), the rhizosphere Péclet number in this case study is \({\mathrm{Pe}}_{\mathrm{rhizo}}=\frac{2\cdot 0.03}{2.88\bullet {10}^{-7}}=2.41.\) Thus, both root elongation and diffusion affect the radial extent of the rhizosphere.
However, the aim of our model was to illustrate the effect of carbon released from root hairs on the carbon distribution at the time scale of 1 h using image-based modelling where adding root growth would add too much complexity. Therefore, we neglect root and root hair elongation and other dynamics such as shrinkage of roots and root hairs. We justify our assumption with the following considerations: root hairs grow at an elongation rate of 0.144 cm d−1 (Grierson and Schiefelbein 2002). Applying the same concept of rhizosphere Péclet number to a growing root hair (instead of a growing root), the Péclet number is \({Pe}_{hair,radial}=\frac{0.0018\bullet 0.144}{0.025}=0.01\ll 1\) due to the small root hair radius of only 18 µm. Thus, we can neglect the effect of root hair growth on the radial extend of the carbon concentration around the individual root hairs. However, it is also relevant to compare the characteristic time of root hair growth with the diffusion time scale from the main root. Considering a characteristic length of the root radius plus the root hair length of approximately 500 µm, we obtain that hair growth and diffusion from the main root are in the same order of magnitude. This means that the root hair growth affects the radial extent of the rhizosphere, and its role becomes increasingly more important when the diffusion coefficient decreases, for instance due to soil drying. It is therefore important to include root hairs in the estimation of exudate distribution as a function of distance from the root surface. These considerations are based on the implicit assumption that all root surface exudes into the soil (i.e., perfect contact between root and soil matrix) and that the diffusion coefficient in the soil is homogeneous. However, at the root hair scale, the soil matrix as well as the root-soil contact are not homogeneous and their specific geometry needs to be explicitly accounted for. For simplicity, our simulations are built on a static and image-based geometry, representing already grown root hairs.
Mathematically, the underlying problem is described by the diffusion equation—a second order parabolic partial differential equation:
where \(c\left(\overrightarrow{r}, t\right)\) denotes the concentration of the diffusing material at location \(\overrightarrow{r}=(x,y,z)\) and time \(t.D\left(c\left(\overrightarrow{r}, t\right), \overrightarrow{r}\right)\) represents the diffusion coefficient for a concentration \(c\) at a location \(\overrightarrow{r}\) and \(\overrightarrow{\nabla }\) the nabla operator.
Assuming a constant diffusion coefficient, our model is formulated as follows:
with
The domain obtained from CT images is denoted by\(\Omega\), \(\Sigma =[0 , 3600s]\) is the simulated time interval. \(\nu\) represents the unit outer normal and \(\Delta\) the Laplacian operator. The inlet carbon concentration \({c}_{in}\) was taken to be a fixed value from Holz et al. (2018) and it is imposed as constant boundary condition. The diffusion equation was discretized and solved by the “scalarTransportFoam” solver of OpenFoam – an open source CFD software package (Weller et al. 1998). Further details are provided in the supplementary information.
Figure 7 outlines the workflow of case study 3. Data acquisition includes conducting an experiment of plant growth in a soil column and the imaging of this soil column in a synchrotron facility. The raw images are processes in a way that results in a 3D finite element mesh of the soil domain on which diffusion of root-derived exudates was performed using image-based modelling techniques. The outcome is the spatio-temporal pattern of exudate concentration.
Results
We simulated the diffusion of root exudates, in particular carbon, into soil for one hour and one illustrative sample. The selected region of interest of approx. \(1.8\mathrm{ mm x }1.3\mathrm{ mm x }1.4\mathrm{ mm}\) contained a soil aggregate volume of \(1.3\mathrm{ m}{\mathrm{m}}^{3}\), an air-filled macropore volume of \(1.1\mathrm{ m}{\mathrm{m}}^{3}\), a root volume of \(0.4\mathrm{ m}{\mathrm{m}}^{3}\) and an air volume of \(0.4\mathrm{ m}{\mathrm{m}}^{3}\) that surrounded the sample tube (see Fig. 8a). The epidermis surface area was \(3.9\mathrm{ m}{\mathrm{m}}^{2}\) and a fraction of \(6.1\mathrm{\%}\) was in contact to soil. The corresponding soil contact fraction of the root including hairs was approximately three times bigger (17.7%).
Figure 8b shows the simulated carbon concentration in the soil surrounding a hairless root (left) and a root with hairs (right). Regarding the hairless root, a total carbon mass of \(0.067 \mathrm{\mu g}\) diffused into the soil after 1 h, whereas this value was three times higher for the root with hair (\(0.204\mathrm{ \mu g}\)). The comparison of carbon distributions within the rhizosphere revealed a lower radial concentration gradient for the hair case resulting in a right shift of the concentration data (Fig. 8c). In the hairless case, carbon concentration dropped below 1% at a distance of 0.29 mm from the root surface whereas the same value was reached in the hair-case at 0.74 mm.
CT sample consisting of the root with its elongated hairs in yellow and soil particles in grey; scale bar = 500 µm. (b) Illustrative comparison of the simulated carbon diffusion within the soil domain for the hairless root (left) and the root with hair (right) after a simulation time of 1 h. (c) Spatial carbon distribution within the rhizosphere represented by the carbon concentration regarding the radial distance from the root-surface.
Challenges and open questions
This illustrative case study shows how root hairs can increase the total amount of root exudates and their diffusional distance into the soil when we assume a constant concentration at the root and root hair surfaces. Explicit image-based simulations of root exudation including information of root-soil contact and the spatial distribution of root hairs allows estimating the importance of root hairs for rhizodeposition. This case study shows good agreement with experimental measurements by Holz et al. (2017).
Note that we assumed the same constant exudate concentration boundary condition for the two genotypes. Our simulations are based on the grid of a single wild-type sample before and after removing its’ root hairs. As demonstrated before, in order to capture system dynamics, root growth needs to be taken into account. However, the focus of this case study lies on exudate diffusion from a static (non-growing) root. Nevertheless, the outcome of our simulation provides value to more complex simulations considering a root elongation rate. Particularly, the results can be used to define the boundary conditions of the simulations performed in case study 5 that is described below.
One open question is how to implicitly account for hairs when their spatial distribution, and in particular as the fraction of their contact with the soil matrix surrounding the root, are not known and how to include such implementations in root system models. The problem of the partial contact between roots and soil has been solved for the case of a single roots by de Willigen et al. (2018). The solution should be extended to the case of a single root with hairs possibly having different fraction of contact with the soil matrix. The outcome of our simulation may be used to define the boundary conditions of the simulations performed in case study 5. An additional open question is the representativity of the selected volume. Indeed, soil porosity and root hair density might be highly variable in space (at the scale of 1 mm3) and time. Temporal information is needed to cover the lifetime of root hairs. Additionally, rhizosphere bacteria were shown to contribute to mucilage production, forming jointly with root mucilage a rhizosheath in maize whose extent is determined by soil moisture (Watt et al. 1994, 1993). Therefore different soil water contents and soil textures should be simulated in order to have a representative picture of the role of root hairs on rhizodeposition for variable conditions. Finally, we did not consider microbial degradation of exudates, which is discussed in case study 5.
In summary, the biggest challenges are related to the representativity of the imaged soil volume and how to integrate these simulations in models that consider root growth and other interacting processes, such as root water uptake (affecting soil water and the contacts) and microbial degradation of the rhizodeposits.
Case study 4: Mucilage and hydraulic properties
Question How does mucilage affect pore scale distribution and dynamics of water when soil dries? How does the altered liquid configuration affect effective diffusion?
Scales Spatial scale: from molecular to nm, µm and to mm, temporal scale: < 1 day.
Approach
Background
In the previous studies we evaluated the impact of root architecture and growth and of the impact of root hairs on the spatio-temporal distribution of mucilage, and on phosphate uptake. Although both approaches represent excellent tools to study rhizosphere dynamics, their predictive power depends on the quality of provided input parameters. While the effect of mucilage on soil properties has been observed and discussed multiple times, little is known about how it affects relevant pore-scale mechanisms.
In the following study, we examine how mucilage alters the physicochemical properties of the soil solution, how this modification affects liquid connectivity at the pore scale and show how its potential impact on nutrient diffusion can be evaluated by mathematical homogenization based on high resolution images. For the sake of simplicity, we neglect temporal changes of mucilage properties resulting from processes like microbial degradation or aging of the polymer network and focus on liquid distribution in a simplified rhizosphere.
Root mucilage is primarily released at root tips and mainly composed of polysaccharides, proteins and some lipids. In contact with water, these polymeric blends swell and form a 3D gel network. Gels possess specific properties, such as water holding capacity, the ability to swell and shrink, and viscoelasticity, which affect soil functions, such as water retention (Ahmed et al. 2014; Benard et al. 2019; Kroener et al. 2018; Naveed et al. 2019). In contrast to pure water whose distribution in soil is primarily controlled by surface tension and capillary forces, the liquid configuration of mucilage is affected by its chemical hydrogel properties and its physical stability, which depend on structure and arrangement of contained polysaccharide units.
Gel properties vary for mucilage located in soil pores in contrast to “free” mucilage (Brax et al. 2020, 2019; van Veelen et al. 2018). The polymers grip to the soil particle surface and the network has thus an increased strength compared to the “free” gel. The confinement by the pore walls leads to an inhomogeneous distribution of the polymer network in the pore during swelling and shrinking (Marcombe et al. 2010) and to pore-size specific organization of the polymeric network.
Upon drying, the concentration of polysaccharides within the liquid phase increases and the internal structural units of mucilage become more and more important in controlling its physical properties. Thereby, mucilage goes through a glassy transition, passing from a liquid to a hydrogel and finally to a rather solid structure (Carminati et al. 2017; Williams et al. 2021).
This leads to characteristic mucilage drying patterns that depend on intrinsic physical mucilage properties like viscosity and surface tension. Note that chemical properties of mucilage vary with plant species (Brax et al. 2020; Naveed et al. 2019, 2017) and environmental conditions (pH, ionic strength, cations, surfactants). For instance, viscosity of maize root mucilage is higher than that of wheat.
The different viscosities of wheat and maize mucilage explain different patterns formed at the nano-scale by the respective mucilage upon drying on a flat surface (Fig. 9a,b). For wheat, the nanostructure appears as a network characterized by thin branches smaller than 30 nm in width. Maize mucilage builds a more connected coating with larger hole-structures. The thin threads of wheat mucilage suggest less and weaker interactions between polymers in wheat compared to maize mucilage, which is consistent with the differences in viscosity (Fig. 9c).
a Atomic force microscopy height image of (a) wheat and (b) maize root mucilage dried on flat mineral surface taken in Peak-Force Quantitative Nanoscale Mechanical (PFQNM) mode; (c) flow curves of maize and wheat root mucilage at 7 mg/mL measured for three replicates; (d) mucilage (red) from maize nodal roots let dry in glass beads (100–200 µm in diameter; blue) imaged via X-ray CT and segmented. The content of mucilage was 8 mg g−1 (weight of dry mucilage per weight of dry particles). An interconnected 2D surface of dry mucilage was deposited through multiple pores upon drying (Benard et al. 2019)
Analogue pictures are visible in 3D porous media. Figure 9d shows that upon drying in a porous medium mucilage forms an interconnected surface that spans through multiple pores, maintaining the liquid phase connected during the drying process. This configuration of the liquid phase upon severe drying is very distinct from that of water, whose comparably high surface tension and low viscosity causes the breakup of liquid bridges (Carminati et al. 2017; Ohnesorge 1936; Williams et al. 2021). Improved liquid connectivity on the pore scale was proposed as a mechanism utilized by soil organisms to maintain and enhance nutrient diffusion in dry soil (Benard et al. 2019). In fact, addition of different kinds of mucilage lead to an increase in diffusion coefficient by a factor 3 under dry soil conditions for both glucose (Chenu and Roberson 1996) and 137Cs (Zarebanadkouki et al. 2019). Nevertheless, the impact of liquid connectivity at the pore scale on effective diffusion has not been evaluated systematically and remains unclear. Conventional models, as e.g., in Millington and Quirk (1961), relate diffusivity to the porosity or the water content, see e.g., (Chou et al. 2012) for a comparison. However, they do not take into account anisotropies, different tortuosities, or the explicit connected pathways as can be done by mathematical homogenization (see, e.g., (Ray et al. 2018). For this reason, we chose to evaluate the impact of liquid connectivity at the pore scale on diffusion using two simple examples. First, we illustrate the effect of mucilage on connectivity by simulating the drying of a liquid bridge between two spherical particles. Second, we demonstrate how the impact of increased liquid connectivity observed in dry sand on the effective diffusion coefficient can be quantified.
Spatial configuration
To simulate the interplay between molecules of the polymer network and water, modelling tools are needed that can describe both, dynamics of the polymer network and the liquid within. Lattice-Boltzmann methods are common tools to simulate pore scale dynamics of liquids (Pot et al. 2015; Richefeu et al. 2016; Sukop and Or 2004; Tuller and Or 2005). Discrete element methods are tools to describe deformation and rupture processes of solids (Bobet et al. 2009) and have been used to simulate fracture of hydrogels (Kimber et al. 2012; Yang et al. 2018). While most hydrogel simulations consider free hydrogels, here, we study hydrogel deformation confined by the pore space and attached to soil particle surfaces.
Transport properties
Both, phase distributions and connectivity as well as intrinsic mucilage properties will finally affect hydraulic properties, gas diffusion and nutrient transport. Macroscale models cannot take into account the explicit geometries and properties of phase distributions at the pore scale. The pore scale model however is not amenable to large-scale computations because of its high complexity. Information from the microscale can be incorporated to the single root scale using mathematical upscaling or homogenisation techniques (Hornung 1996). These methods allow, e.g., for the computation of, potentially anisotropic, effective diffusion coefficient tensors requiring only the geometric information on the microscale within representative elementary volumes. They have been used, e.g., for nutrient diffusion with regular geometries (Leitner et al. 2010b), but have been extended recently to irregular, evolving structures (Ray et al. 2018). Although the setting is periodic at the boundaries of the investigated domain, the underlying geometries can be arbitrarily complex, and are not restricted to idealised settings. This means that the effect of concrete phase distributions of water and mucilage in a realistic pore space can be quantified given the respective diffusivities, and a sufficiently large domain on the microscale. Compared to artificially constructed regular domains, CT images are now being used to obtain the real micro-structure of a given soil and serve as unit cell for the homogenisation approach. We obtain the periodicity inherent in the method of homogenisation (Hornung 1996) by translation, i.e. the considered domain is surrounded by identical samples (Guibert et al. 2016; Whitaker 1986). This method does not affect the geometrical features of the domain, however, in particular in 2D and unsaturated situations may decrease the connectivity of the fluid phase (Guibert et al. 2016). Another common approach is periodisation by symmetry (e.g., applied to CT images in Tracy et al. 2015), which mirrors the domain in all directions. This increases the computational domain and changes the properties of the medium. In particular, it removes anisotropies and therefore has been criticised as being unphysical for pore scale flow properties in comparative studies of different boundary conditions (Gerke et al. 2019). We present results for both approaches on one exemplary CT image (for details on the original image see Benard et al. 2019)being aware that the presented 2D problem may be too small for representative conclusions. We do not claim that this one CT image represents the real soil as there is a need to determine the size of the soil’s REV in relation to the CT image size (Auriault et al. 2010), and the connectivity is most likely too low due to the 2D representation and the discontinuities across boundaries. Note that connectivity in CT images is related to resolution. With smaller samples sizes there is a gain in resolution and hence pore sizes which can be analysed, resulting in higher connectivity. However, the soil volume analysed might become so small that larger structures are not adequately represented any more. For a detailed discussion see Lucas et al. (2020).
However, this CT image allowed to directly observe the distribution of mucilage structures (see Fig. 11b) and to evaluate the impact of increased liquid connectivity on effective diffusion at the same water content. Liquid distribution was simulated without (water only) and with observed mucilage structures to illustrate the impact of the presence of mucilage at the microscale – which can reduce or enhance the effective diffusion coefficient depending on the pore scale configuration and water (and mucilage) content.
Figure 10 outlines the workflow of case study 4. It is based on the same experimental setup as case study 3, but uses additional modelling approaches to (a) simulate the water distribution at the pore scale for different water contents and mucilage concentrations using Lattice-Boltzmann and Discrete Element methods, and (b) use amended images for mathematical homogenisation to compute effective diffusion tensors of a specific sample. Systematically evaluated on a larger data base those may be used in continuum-scale simulations such as case studies 1 and 2.
Results
Spatial configuration
Simulations based on Lattice Boltzmann methods and discrete element methods, respectively, show the deformation of a liquid bridge between two soil particles upon drying (Fig. 11a). In the case of highly concentrated mucilage, hollow structures can form that have also been observed in experiments (Benard et al. 2018). Due to internal polymeric structural units, hydrated mucilage structures can remain connected at a water content at which water bridges would break. Similar results were obtained in a theoretical study (Carminati et al. 2017) where the increased viscosity of mucilage was held responsible for the damping effect on motion.
a Simulation of drying dynamics of a liquid bridge between two soil particles (modified from Haupenthal et al. 2021). Top: pure water simulated using Lattice Boltzmann methods. Bottom: mucilage at high concentration simulated using the discrete element method; (b) 2D geometry used for the evaluation of the effective diffusion. Derived from X-ray computed tomography [courtesy of M. Zarebanadkouki, University of Bayreuth, and P. Benard, A. Carminati, ETH Zurich] of a sandy soil with porosity 41%. Artificial water distribution with water content of 0.19 cm−3 cm3 without (left) and with mucilage (right). Sand particles (brown); air (grey); water (light blue); hydrated mucilage (dark blue). The arrows represent the eigenvectors and eigenvalues (length) of the effective diffusion tensor of the “periodicity by translation” case, showing, in each case, the main directions of diffusion
Transport properties
Here we show how small changes in the spatial configuration of the liquid phase induced by mucilage can affect the effective diffusion of solutes (e.g. nutrients) across the rhizosphere. We deal with the effect of mucilage on the effective diffusion coefficient, assuming that the presence of mucilage locally decreases the diffusion coefficient of a given chemical species. The species does not diffuse in the gas nor in the solid phases. The diffusion in water is set to a reference value of 1. In the mucilage, the diffusion is assumed to be Dmuc/Dref = 0.5, exemplarily.
We present a scenario in a sandy soil with a volumetric water content of 0.19 cm3cm−3. Figure 11b shows the 2D solid phase geometries of particles derived from a cross-section of an X-ray CT used for two different scenarios. In the first scenario, the liquid phase consists of pure water whereas the second scenario includes pure water and liquid bridges induced by drying mucilage, which have been identified.
on images of a dry soil. In this particular case, the mucilage makes up only 10% of the liquid phase. The computed effective diffusion tensors differ significantly for the “periodisation by translation” case and read:
where \(\overline{{D }_{1}}\) and \(\overline{{D }_{2}}\) correspond to the matrices in the scenarios without and with mucilage respectively. The corresponding tensor for the fully saturated situation is \(\overline{{D }_{sat}}\).
For both scenarios, the first diagonal entry is non-zero implying that the diffusion is achievable in the domain horizontally. However, in the vertical direction, we notice that the diffusion is impeded though not impossible in the first scenario (≈ 10–11). In the second scenario the mucilage bridges keep the liquid phase more connected, creating new paths for the species to diffuse in the vertical direction. Note in particular the bridges (dark blue) at the top left and bottom left part of the right image in Fig. 11b that connect previously disconnected areas. For each case, the main directions of diffusion are plotted in Fig. 11. For comparison, we also calculated the effective diffusion tensors for the mirrored domain \(\overline{{D }_{1,sym}}\) and \(\overline{{D }_{2,sym}}\). There every path at the boundary is perfectly continued, which may be an overestimation of the real situation. Nevertheless we also see an enhanced diffusivity due to mucilage in one direction.
The Millington-Quirk approximation which is a function of water content and porosity only would result in scalar values of\({2.2628\cdot 10}^{-1}\) for the saturated case, and \(2.3457\cdot {10}^{-2}\)for the unsaturated case. It has been reported e.g. in Chou et al. (2012) that it overestimates the diffusivity in various soils.
In this numerical experiment, the presence of mucilage affects the diffusion paths and hence increases the effective diffusion despite the reduced solute diffusion in mucilage. Although this is a 2D numerical study, it demonstrates that small changes in the connectivity of the liquid phase can imply large changes in the effective diffusivity, and thus 3D pore scale information needs to be evaluated systematically in many samples and configurations to quantify the effect of mucilage on solute diffusion.
Challenges and open questions
We have demonstrated that the interaction between the mucilage polymer networks, water and soil particles increases the connectivity of the liquid phase across the rhizosphere. Upon drying, mucilage may be deposited as two-dimensional surfaces forming hollow cylinders or interconnected surfaces across the pore space. Although the solute diffusion coefficient in mucilage is smaller than in pure water, the positive impact of mucilage on liquid connectivity can result in an enhanced effective diffusion coefficient in dry soils.
These physical mechanisms, which have been addressed by the models and the experimental observations, qualitatively match. However, several parameters and processes are still not yet considered in these models. Physical mucilage properties affecting the contribution of mucilage to the maintenance of liquid connectivity in drying soil comprise its water holding capacity and its viscosity, which are properties that are methodically challenging to measure on the relevant pore scale. They are determined by chemical properties such as content of high molecular weight material and the length and ramification of the polymers, and can vary in the chemical environment, e.g. with pH, absence or presence of mono- and multivalent cations or of organic surfactants in soil solution. As soil texture, structure, and drying rate are likely to affect the spatial distribution of mucilage in soils, measurements of mucilage deposition for varying soil particle size and shape and drying rate are needed to improve our understanding of mechanistic pore scale mucilage drying processes. When combined with measured model input parameters, such as viscosity, surface tension and elasticity of the polymeric structure, it may help to advance pore scale modelling of spatial liquid distributions. Concerning the transport properties, simulations need to be extended from two to three dimensions where the effect of connectivity on the diffusion coefficient is qualitatively similar, but quantitatively different. A challenge is the difficulty to image mucilage in soils while it still contains a significant amount of water. In Benard et al. (2019), the samples were scanned air-dry and only the final mucilage distribution was imaged. Scanning wet samples damaged the polymer network while imaging dry mucilage structures is restricted to comparably coarse soil due to the high resolution required (a few micrometre). Nevertheless, improved diffusion reported by Chenu and Roberson (1996) in xanthan-amended kaolinite can hardly be compared to the observations of Zarebanadkouki et al. (2019) in chia mucilage-amended sand as both used different polymeric substances and concentrations. Overall, the impact of particle size and specific soil surface on liquid connectivity and other soil hydraulic properties remains indistinct. Image-based models and simulations can nevertheless help to quantify possible pore scale effects and bridge the scales in these cases (Roose et al. 2016).
From a computational point of view, dynamic interactions between mucilage deformation, drying and solute transport within the network need to be implemented. Finally, the impact of ageing, microbial degradation and transformation of mucilage (see case study 5) and the impact of mucilage on microbial activity need to be interconnected. Beside the complexity of such computational challenges, the experimental knowledge of such feedback between mucilage properties, transport processes and microbial activity is still in its infancy.
Case study 5: Microbial activity based on C-distributions: using modelling to integrate rhizosphere processes
Question Can we identify the key drivers of microbial activity and C distribution in the rhizosphere considering a holistic approach?
Scale from nm to cm; seconds to days/weeks.
Approach
A modelling framework is proposed that can predict microbial dynamics and processes resulting from interactions in the soil surrounding roots.
We conjecture that the rhizosphere as we measure it emerges from interactions occurring at the pore-scale around roots. The complexity of the rhizosphere demonstrated by the case studies may appear overwhelming at first sight, but we propose that it is possible to fully embrace this by a new generation of mechanistic, spatially explicit pore-scale models, building on recent advances in this area. For instance, using a mechanistic pore-scale fungal model, it has been shown that fungal growth in soil is non-linear and that, for a given volume and a given nutrient content, it depends on the micrometre scale distribution of nutrients and microbes (Falconer et al. 2015a). These micro-scale heterogeneities explain nonlinearities in the temporal evolution of fungal biomass, carbon degradation and CO2 flux observed experimentally. Focusing on soil bacterial dynamics, recently, it has been demonstrated how heterogeneity at the micro-scale can favour poor bacterial competitors, suggesting that pore geometry is a driver of soil biodiversity (Portell et al. 2018). These results indicate that mechanistic (first-principle) models are essential for upscaling microbial driven processes and that this approach can help to bridge the gap between pore-scale and the continuum-scale description of the system (Vetterlein et al. 2020). In this section, we propose the modification of an existing pore-scale microbial soil model as a first step to integrate rhizosphere experimental data and highlight the benefits and limitations of this approach and the path ahead for further work.
Proposed modelling framework for rhizosphere behaviour: an individual based approach.
Our starting point can be a spatially explicit, pore-scale model accounting for the activity of soil bacteria (Portell et al. 2018). Briefly, Portell et al. (2018) assumes a cubic lattice describing explicitly the soil architecture where particulate organic matter (POM) and microorganisms are located. POM hydrolyses over time creates dissolved organic carbon (DOC) that is released to the water phase where it becomes available for bacterial growth or diffuses away to more distant areas as determined by a lattice-Boltzmann model component. Bacterial position and physiology are controlled by an individual-based approach accounting for single bacteria that divide when the cell attain a critical mass.
In the rhizosphere, organic matter distribution can be seen as the result of the distribution of two main components that can already be mapped to organic matter pools considered by Portell et al. (2018). The dominating fraction is a large and dynamic C fraction that is continuously exuded to the soil from the region between root tip and root hair zone and that can be mapped to the DOC pool of the model. The distribution of “dynamic C” (i.e., root-exuded C) follows a gradient into the soil and can be traced using stable C isotope labelling. Labelled C exuded by the plant root can be followed and quantified on the millimetre-scale using an adequate sampling technique and can be visualized in 2D at the micro-scale when using resin embedded root-soil sections and nano-scale secondary ion mass spectrometry (NanoSIMS) (Vidal et al. 2018) or laser ablation-isotope ratio mass spectrometry (LA-IRMS) (Rodionov et al. 2019). This information can be used following two different approaches. In the first approach, a boundary condition is placed on the root surface of the living roots obtained from CT images (Ruiz et al. 2020a) to account for the exudation of carbon from the root. Following this approach, the gradients measured will be used to calibrate the exudation parameter of the model or, alternatively, use the boundary conditions obtained from models such as the one of case study 1. In a second approach when experimental information is available, we assume a spatially static gradient of exuded C.
The second fraction of C in the rhizosphere is a rather static, discontinuous fraction made of dead plant residues and microbial necromass and mineral-associated organic matter (MAOM) (e.g., Liang et al. 2019) that can be mapped to the POM considered by Portell et al. (2018). This fraction, which we can expect to be located more irregularly in areas with decreased accessibility by the microorganisms (Rodionov et al. 2019; Totsche et al. 2018) can also be estimated using NanoSIMS and LA-IRMS.
In bulk soil, bacteria invest energy to produce enzymes that hydrolyse POM over time, thereby releasing DOC to the water phase where it becomes available for bacterial growth or diffuses away to more distant areas (as dictated by the lattice-Boltzmann component of the model). It must be noted that most soil microorganisms has limited access to available carbon and resides in a dormant state most of the time. In the immediate vicinity of the growing root tip however, the release of DOC via exudation transiently lifts the carbon limitation of microbial growth in soil and favours fast-growing copiotrophic taxa (Bonkowski et al. 2021; Rüger et al. 2021). Modelling these processes requires accounting explicitly for trade-offs associated with the release of enzymes by microorganism, a function currently assumed ubiquitous in the model, as well as the diffusion of released enzymes through the water phase from where they can reach and control hydrolysis of distant volumes, where it might initiate a priming effect on POM.
Experimentally it has been observed that the microbial growth rate is a function of the availability of C-containing exudates, whose diffusion rates differ among molecule classes (Jones et al. 2004), therefore showing effects dependent on the distance and location of the root surface in relation to the point in space considered. As a first approximation, models could be based on a uniform source of DOC. At suboptimal DOC levels, carbon has been shown to be respired without any microbial growth (Anderson and Domsch 1985), while higher DOC levels, especially in the close vicinity of roots stimulate microbial growth. High DOC levels may also favour microbial enzyme production that subsequently leads to enhanced hydrolysis of carbon and nutrients from POM, a self-enhancing positive feedback mechanism on microbial growth, known as priming effect (Kumar et al. 2016; Mo et al. 2021). Assuming the individual-based model approach, this can be simulated with the implementation of appropriate rules ensuring that the growth and enzyme production is only possible when microbial maintenance requirements are covered. In addition, current root growth models suggest that microbial attachment to roots is a key strategy to gain maximum access to rhizodeposition (Dupuy and Silk 2016). Therefore, next to the growth rate, future models must consider microbial motility. Microbial motility is disregarded in the work of Portell et al. (2018), although the model structure is designed to allow the implementation of such modification.
Recently, Dupuy and Silk (2016) studied the colonisation of root surfaces resulting from the growth of root tips in bulk soil. These authors modelled root growing through a homogeneous (continuous) soil fraction and used a population-based approach to account for microbial growth and colonization dynamics. Dupuy and Silk (2016) found that the root elongation rate was a key trait for successful establishment of bacteria on the root surface. This suggest that in addition to microbial growth and motility, future models should consider root growth in order to reflect more realistic colonisation dynamics. When structural information of the solid, water and air phases of the soil are taken into account, as we are suggesting here, the introduction of growing roots in these models is challenging. In certain situations, time-lapse imaging could be used to follow root growth and its modifications of soil structure in order to implement this into complementary modelling scenarios. To our knowledge, this has not been achieved to date. Instead, root (or root hair) growth is tackled by introducing time dependent boundary conditions. In this approach, a common technique is to use a fully grown geometry and to activate the appropriate boundary conditions according to a (measured) growth rate (e.g. McKay Fletcher et al. 2020). Given the impossibility of following root growth in the field, we advocate the use of an equilibrium approach and static roots as a first approximation. Given the complexity of the rhizosphere, this is also advisable. We need to understand rhizosphere mechanisms around static (or slowly growing roots) before embracing the full complexity of the system.
Simulation scenarios and model initialisation
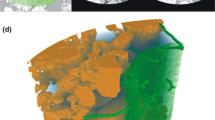
Structural information supplemented with existing knowledge will describe the physico-chemical state of the soil microhabitats around roots and be used as initial condition to conduct spatially explicit simulations with the pore-scale model Fig. 12a).
Scheme of the simulation scenarios (a) and detail of a 1283 sub-domain showing segmented roots (green) and the water (cyan) and air (grey) phases computed using the lattice-Boltzmann model described by Genty and Pot (2013) assuming a water saturation level of 50% (b)
A number of steps are required to set the physical environment surrounding roots. The soil architecture of the rhizosphere, including root positions, will be obtained with segmented X-ray CT images. Smaller sub-domains (e.g., 1283 voxel size) will be obtained from different distances from the root surface (Fig. 12b). The first challenge is to simulate the distribution of water and air within the pore space of the subdomains as described in the case study 4 above.
Root derived C has been shown to be distributed at least 100 µm distant from the root plane (Rodionov et al. 2019), but more likely extends in the mm range (Jones et al. 2004). Our first working assumption will be to assimilate 13-C labelled C to diffusible dissolved organic matter (DOC, i.e., readily available C for microorganisms) and all non-labelled C within a 100–1000 µm-rhizosphere-range as particulate organic matter (POM, that can be mineralized under the action of microbial enzymes).
The initial physico-chemical environment described so far will be the set up where the microorganisms evolve as controlled by the individual-based bacterial model. The 3D distribution of microorganisms has been obtained in bare soil (Eickhorst and Tippkötter 2008; Juyal et al. 2019; Nunan et al. 2001), but is largely unknown to date for the rhizosphere. To account for this lack of experimental data, our approach will use a preliminary simulation initialised using the bacterial numbers and distributions found in the bare soils. Since the microbial biomass and activity is modulated by microbial traits and the carbon available in the media, the microbial numbers reached in the preliminary simulation will depend on the biochemical conditions of the media. Spatial distributions of bacteria in soil thin sections have been approached using a 2D spatial statistical model (Raynaud and Nunan 2014) that can be expanded to a 3D soil structure. Bacterial biomass and respiration will be monitored in all spatial grid elements and plotted as a function of the distance to the root plane. The microbial model can be calibrated using quantitative measures of microbial respiration (i.e., mineralization) of different quantities of root exudates on bare soil such as the measurements shown in Fig. 13.
Microbial respiration in soil amended with increasing quantities of exudates (Ex 1- Ex 4). Note that the lowest exudate quantities (Ex1, Ex 2) only led to a short-term stimulation of microbial respiration (but not growth), while respiration curves with higher concentrations (Ex 3, Ex 4) show typical microbial growth dynamics
Model outputs will be qualitatively validated using microbial biomass and respiration measured at 3 mm intervals from the rhizosphere plane (Alphei et al. 1996).
A flow chart outlining steps from experimentation to the generation of model outputs can be found in Fig. 14. It combines the workflow of case study 4 (resulting in water distribution in 3D pore space) with carbon distribution as measured from resin-impregnated soil samples derived from the same experimental setup and the initial bacterial spatial distribution as simulated from a bacterial spatial statistical model. Together with the appropriate boundary conditions, transport properties and microbial behaviours and properties the simulation results in a 3D dynamic system where biotic and abiotic components interact. Results can be aggregated to provide continuum-scale properties such as bacterial mass or respiration per soil control element as a function of time.
Diagrammatic flow chart of case study 5. In the figure, CT stands for Computed Tomography, LBM stands for lattice-Boltzmann model, µIbM stands for microbial individual-based model, LA-IRMS stands for laser ablation-isotope ratio monitoring, and NanoSIMS stands for nanoscale secondary ion mass spectrometry. The oval shapes illustrate start and end points of the workflow, the rectangular boxes describe activities and the rhombs include outputs of intermediate steps that serve as inputs for the next step in the workflow
Results
The approach highlighted here is a first step towards the development of mechanistic models accounting for C distribution, and C transformation by microbial activity around roots. Assuming an equilibrium approach and one static root allows us to integrate the various experimental data collected and use them to predict the shape and distribution of the microbial activity in the soil surrounding roots and, more importantly, allows identification of the abiotic components or gradients measured driving the rhizosphere shape and extend. The approach is also a steppingstone towards the development of the much needed, fully fletched pore-scale rhizosphere model (see challenges and open questions section below).
The approach discussed in this section offers spatially explicit information of the bacterial biomass, the carbon decomposition, and the evolution of bacterial respiration over time. This allows estimating microbial activity namely biomass, respiration and spread rate as a function of the distance from the root surface. The use of an individual-based approach allows also to tackle fundamental and applied question related to the maintenance and development of microbial diversity in the rhizosphere.
Challenges and open questions
Rhizosphere complexity requires accounting for more reactive chemical species. For instance, recent publications highlight the important role of volatile carbon signals that expand the rhizosphere in the cm range (de la Porte et al. 2020). In addition to dissolved organic carbon (e.g., glucose), inclusion of nitrogen containing organic compounds (peptides, amino acids), CO2, O2, and signalling with phytochemicals such as lipo-chitooligosacharides (Venturi and Keel 2016) would allow to study a number of important mechanisms underlying microbial colonisation and establishment in the rhizosphere.
Further differentiation of DOM into specific root exudates, microbial biomass, microbial necromass and POM (Angst et al. 2016; Baumert et al. 2021) can be envisaged and tackled with the same modelling approach for an increased accuracy of the model outputs. This approach may even allow the characterization of priming effects in different aggregate size classes in the rhizosphere based on microbial stoichiometry (Mo et al. 2021; Wang et al. 2020). Molecular marker analyses including a suite of exudate-, bacteria- and fungi-specific substances has high potential to shed more light on rhizosphere gradients and hot spots of OM enrichment (time-integrated signals/stable on medium-term in contrast to microbiological parameters) (Baumert et al. 2021). As a first step 13C labelled carbon fraction which can be imaged in 2D with NanoSims or LA-IRMS is used to represent the soluble root derived carbon pool (exudates) and complement the C initialisation described and/or to assist validation of experimental results, especially in view of stoichiometric constraints for plant and microbial processes (Clode et al. 2009; Gorka et al. 2019; Vidal et al. 2018).
This first adaptation of existing spatial-explicit mechanistic models for the rhizosphere follows an equilibrium approach and one static root. A fully fletched pore-scale rhizosphere model requires the explicit representation of a dynamic root capable of simulating uptake and release of water and elements from (to) the soil. In addition to a static water flow scheme, water dynamic can be also taken into account using LBM approaches in both saturated and unsaturated porous media (Ginzburg 2008; Zhang et al. 2016).
Another fundamental issue comes from the huge, and largely unknown, microbial variability existing in soil. We advocate for the use of individual-based modelling of soil microorganisms in conjunction with a trait-based approach coupling bacterial (Portell et al. 2018) and fungal (Falconer et al. 2015a) models. Bacteria and fungi act at different scales and prefer different soil phases (i.e., water against air filled porosity), which suggest the need of this first division. Although the whole soil biodiversity is intractable using a species-centric approach, a trait-based approach can be used to identify trade-offs in microbial traits and strategies that lead to an improved rhizosphere colonisation. Such information has practical implications by extrapolation to specific species. For bacteria, we suggest accounting for the following minimum set of individual traits: lag phase length, specific growth rate, ability to grow anaerobically, mortality rate (by predators), motility, antibiotic production, root attachment behaviour, and C specificity (DOC, Mucilage, and plant signalling molecule –e.g., malic acid like). The consideration at the single-cell level of these traits would provide insights on beneficial traits and trait combinations for rhizosphere colonisation and establishment on root surfaces. For fungi, physiological trait combinations representative of functional groups proposed for arbuscular mycorrhizal fungi (Chagnon et al. 2013): competitors, stress tolerators, and ruderals, can be adopted. The first challenge is the identification of model parameters describing these experimentally unknown behaviours. Relevant questions are: what are the C costs vs. nutrient and/or water gains associated with the establishment and maintenance of mycorrhiza by roots? The adoption of an approach describing individual fungi with different properties and behaviours (Falconer et al. 2015b) will also allow to model interactions between fungal species such as the competition among symbionts (benefiting from root C) and necrotrophic pathogens that gain access to plant C only after killing parts of the root (Sarkar et al. 2019).
Synthesis and Outlook
Detailed pore scale and single root scale information to predict plant scale emerging behaviour
We have presented a series of case studies illustrating the effect of rhizosphere scale properties affecting transport across the root-soil interface and microbial activity. We have chosen the overall theme of rhizodeposition because of its relevance for water and nutrient uptake and microbial activity. We have presented two case studies, one in which we have calculated the spatial extent of different rhizodeposits across the rhizosphere and along the root system, and one in which we simulated the effect of root exudation on root nutrient uptake. For both examples, it became apparent that for growing roots, the elongation rate was important for the radial extent of the rhizosphere and the formation of hotspot volumes, with rhizosphere Péclet numbers larger or only slightly smaller than one. This should be considered in experimental designs such as the choice of sampling locations. Using image-based modelling for a non-growing root, we have illustrated how root hairs, at a given exudation rate, can increase the total exudation as well as the spatial extent of rhizodeposits into the soil. We have then discussed the mechanisms by which the polymers present in mucilage increase the viscosity of the soil solution and thus alter the spatial configuration of the liquid phase. Specifically, the high viscosity mucilage prevents the break-up of liquid bridges between soil particles and maintains the diffuse pathway for solute across the rhizosphere. The effect of root hairs and mucilage on solute transport across the rhizosphere could then be implicitly described with effective diffusion coefficients, as we have shown for the case of mucilage. Such effective diffusion coefficients can be implemented in root architecture models, where the effect of local rhizosphere properties (defined at the scale of root segments) can be investigated at the root system case. Finally, we have presented a pore-scale case study of a model of microbial activity, which takes explicitly into account the spatial distribution of soil particles, water, carbon, and microorganisms. Such a model allows accounting for emergent microbial driven processes emerging from large number of biotic and abiotic interactions occurring at the microscale, informing models using coarser spatial resolutions. At the same time, this model would benefit from the other case studies described as it depends on the connectivity of the liquid and gas phases as well as on the spatial distribution of rhizodeposits. The potential links between the different case studies are outlined in Fig. 15.
Our objective was not to present a complete and integrated multi-scale, multi-process model, but rather to show what ingredients (constitutive equations, parameters and boundary conditions) should be implemented in such model. The case studies described in this contribution show how rhizosphere traits (such as root hairs and mucilage) impact the properties (e.g. diffusion) of the rhizosphere at the single root scale, and how such properties could be implemented into a root architecture model to investigate root system scale output (e.g. total uptake of nutrients). This is an example of a bottom-up approach. Such upscaling is done by means of defining effective properties, as we have illustrated for mucilage, and as can be done for root hairs using the homogenization method (Leitner et al. 2010b; Zygalakis et al. 2011). Effective properties depend on the spatial arrangement of soil particles and of the liquid phase, which could be imaged in situ, for instance using X-ray CT. The price to reach a spatial resolution needed to resolve the pore space is that the field of view of such images is limited and might be below the REV (representative elementary volume) needed to define properties (such as diffusion) at the continuous scale. However, we argue that the spatial extent of some rhizosphere properties, for instance the spreading of mucilage in soils is smaller than the REV – i.e. it might cover only a few layers of soil particles. Therefore, it is allowed to define effective properties for such processes while having in mind that such transport properties cannot be used for longer distance transport. We illustrate this concept with an example related to water flow. Consider a 2D heterogeneous medium composed of elements with varying conductivity distributed randomly and with the conductivity lognormally distributed. If the medium is large enough compared to the size of its elements, the effective conductivity of the discrete medium is the geometric mean of the conductivities of the elements. However, if the domain is thin, or the flow process takes place only in a thin section of the domain, then the effective conductivity that should be taken converges to the arithmetic mean of the conductivities (von Jeetze et al. 2020). For the rhizosphere, different effective diffusion properties should then be defined depending on the spatial extent of the process. To our knowledge, this problem has not been addressed. Next to the REV, the non-periodic nature of CT images of the pore space requires extended homogenization methods on 3D rather than 2D images that are able to study the influence of potential boundary effects.
Beside the complexity of defining and determining effective properties, the advantage of such properties is that they can then be implemented in larger scale continuous models in which root architecture and root growth can be explicitly modelled. This bottom-up approach allows testing scenarios and qualitative behaviours. For instance, it can be used to investigate in what conditions and for what emergent behaviour (e.g., water uptake, P uptake, etc.) processes that affect the local transport properties in the rhizosphere are relevant on the plant scale. Such analysis can be done only at the plant scale where the appropriate boundary conditions and vertical gradients in soil variables are explicitly simulated. A problem with posing this question is that the meaning of ‘relevant’ needs to be defined. An at-hand definition would be that using bulk soil properties instead of considering the rhizosphere properties for predicting processes at the plant level might lead to incorrect estimates. This means that plant system scale processes are sensitive to rhizosphere properties. These sensitivities may also be dependent on the environmental conditions. For instance, in wet soils, the impact of mucilage on water uptake is not important whereas it is in dry soils. If some roots of the root system still have access to wet soil, root water uptake by the entire root system will hardly be affected by the impact of the mucilage around roots in the drier soil layers. When the sensitivity question is answered positively, the next question is whether the same prediction of processes at the entire plant system scale could be obtained by using different bulk soil properties or using different root system properties. If the answer to this question is yes, then an improper representation of rhizosphere processes or properties could be simply ‘compensated’ by adjusting root or soil properties. The question translates to whether sensitivities of the behaviour at the plant scale to rhizosphere properties, root system properties, and soil properties are correlated or not. It implies that when processes are observed at the plant system scale, rhizosphere properties cannot be derived (e.g., by inverse modelling) without knowing the other correlated properties. In order to unravel the ‘relevance’ of rhizosphere properties and processes for plant system scale processes, sensitivity analyses with multiscale models could be carried out and used to identify interaction effects (i.e., when the change in the larger scale process is larger than the sum of the changes due to changes in rhizosphere properties, bulk soil properties and root properties). Conditions when such interaction effects occur could then be used to infer rhizosphere properties from the observed emergent behaviour at the larger scale.
However, upscaled simulations require not only the effective properties in the rhizosphere at a given point in space, but also information on how these properties evolve over time and along the root system. This requires then a top-down approach and a general cross talk of models at different scales: the large scale to define the boundary conditions and state variables for the small-scale process, and the small-scale to estimate the effective properties for the large scale model. The behaviour of the system emerges from the interactions between the scales.
The importance of interactions between different processes
In addition to the interactions between scales, the emerging rhizosphere behaviour is also the result of the interactions between different simultaneously occurring processes. Here we have focussed on the example of rhizodeposition, and its interaction with root growth, soil water flow, nutrient uptake, and microbial growth and respiration. However, these are still limited examples that could be extended. More generally, nutrient uptake affects the plant status and most likely the quality and quantity of exudation, resulting in a feedback loop. Root water uptake takes also part to such feedback, due to convective fluxes affecting solute distribution and to the gradients in soil water potential and soil moisture around the roots, which in turn affect diffusion. De Bauw et al. (2020) illustrated that interactions between water uptake and nutrient uptake at the plant level scale could be linked to a combination of rhizosphere transport and root system scale water uptake. Understanding and properly implementing into models interactions between these processes, and their feedback with plant growth is a key to predict the emergent effect of rhizosphere properties on the plant scale. While there is an understanding on the effects of certain drivers such as drought on individual rhizosphere processes, the effects of these drivers on multiple, simultaneously occurring processes are still poorly understood. This requires the extension of existing models to a larger number of rhizosphere components.
How can measurements be used in modelling? State of the art and challenges
In the frame of a current priority program focusing on rhizosphere spatiotemporal organization (PP 2089, https://www.ufz.de/spp-rhizosphere/) it was hypothesized that spatiotemporal patterns in the rhizosphere are formed as a result of local interactions and numerous feed-back loops (self-organisation processes) and that these patterns result in emerging system properties for the soil–plant system. Scientist were encouraged to work with the same experimental platforms with a very reduced number of drivers (two textures, two genotypes, four growth stages, few compartments) in order to provide as many inputs for the different models operating at different scales. Can this be a successful strategy? The following sub-sections will tackle this question.
Parameters for bottom-up as well as top-down modelling approaches
The focus on joint experimental platforms with a few drivers only, provides for the same system information at a range of scales. If we take carbon flow as an example, the experimental data range from changes in standing above and below ground biomass in the field during the whole growth season, to root system exudation rates and their change with growth stage, to spatial distribution of recently assimilated carbon in the vicinity of roots at the µm scale. Thus, data from different scales can be used as input parameters and for validation, respectively. For all these scales, spatially resolved, quantitative and qualitative information is available; however, the level of detail changes with the scale and the units cannot always be converted directly into each other.
Experimenter can never provide all the required data – bottom-up
In describing the rhizosphere, we are forced into high-resolution data acquisition because some of the players are very small and some of the gradients are very steep. This is complicated by the fact that the closer we look, the more complex things can become. While we move from the continuum scale to the pore scale for soil, we must move from the single root scale down to the tissue scale for roots, and seemingly well-established knowledge, such as smooth gradients extending from the root surface into the root (what is happening in the plant), are challenged by questions such as where along the radial gradient is uptake or release actually taking place within the root (Sakurai et al. 2015), where along the root do we have to measure, which is the tissue concentration relevant for calculating 13C diffusion into the soil – 13C concentration of tangential walls of the endodermis or rather the mean 13C concentration of grind up root tissue from the whole root system? What adds to the experimenter's dilemma is that the higher the resolution, the more cumbersome it is to work with a reasonable number of replicates. That is, while we can now derive very detailed information, the modeller and experimenter must jointly develop strategies to test representativeness or plausibility. From a modelling point of view, the need of accounting for what happens in the plant suggest that strategies to couple rhizosphere pore-scale models to single-cell models of the root physiology and development (e.g., Dupuy et al. 2008) should be investigated in the future.
Labelling experiments with radioactive 11C carbon (or 14C) provide information where recent assimilates are transported in relation to root type and position along the root (Schulte et al., in preparation; Holz et al. 2018), but such information is only available for distinct time points and for very young plants. Likewise, stable carbon isotopes (13C) can be used as a tracer for recent assimilates and the radial spread of 13C across the root tissue into the soil can be mapped in relation to tissue type and particle distribution, however, only for a small number of samples. Chemical quality of rhizodeposits can also be mapped and quantified with a resolution of 20 µm as recently shown for individual disaccharides (Lohse et al. 2021). With similar resolution, radial gradients of elements around roots can be mapped in soil using different microscopy techniques (Vetterlein et al. 2020). Only a few of these techniques, e.g., µXRF, have so far shown the potential to process a larger number of replicates (Lippold et al. in preparation). Methods to measure exudation rates from soil-grown plants (Oburger and Jones 2018) are available and have great potential also for model parameterisation (see case studies 1 and 2).
For structural gradients the available tools are already more powerful. With a spatial resolution in the range of 10–20 µm bulk density gradients around roots were investigated and statistically evaluated in relation to a range of different drivers (Phalempin et al. 2021).
It is a major advance that approaches have now been developed for chemical and structural parameters that truly measure the magnitude of radial gradients, in contrast to measurements in linearized (compartmentalized) or pseudo-linearized (rhizoboxes) systems. That we tend to see narrower zones with these methods (Lohse et al. 2021, Lippold et al. in preparation) is consistent with model predictions (Vetterlein et al. 2020, Fig. 4).
Microbiota in models
A very special case are the data on rhizosphere microbiota, the very tiny amounts of sample required for sequencing studies enables investigation of community composition down to the single aggregate level(Szoboszlay and Tebbe 2021) and network analyses provides details on the interaction of the different species and how sensitively this is controlled by external drivers. Yet we lack quantitative data on functional properties or activities at the same resolution. There is a scarcity of data regarding the explicit distribution of microbes in general and of active ones in particular. Likewise, their habitat demands in relation to soil structure and resulting water, air filled pore space and carbon distribution can be addressed by modelling approaches, but validation of model output is challenging. Given the complexity and difficulty of obtaining non-destructive measures, confidence in models can be increased using simultaneously many measurable outputs related to the process(es) of interest as advocated by the so called pattern-oriented modelling approach (Grimm et al. 2005). In our opinion, validation using data from different levels of organisation such as emerging properties like respiration, change of C content and alike, or less available spatially explicit data (e.g., distribution of microorganisms on the root surface) can effectively test the assumptions included in the models, even when the data are not measured in the same experiment. Direct imaging of microbes in the pore space is possible with unspecific stains or Card-FISH (Catalysed Reporter Deposition-Fluorescence in situ Hybridisation), combined with stable isotope labelling, but the procedures are so tedious that it will be long until large datasets will be available. In view of the dynamic changes of microbiota along roots as they grow (Bonkowski et al. 2021) it is an open question whether focussing on specific microbes (CARD-FISH) or rather unspecific approaches are more promising for a given purpose. Each approach is able to tackle different questions. Targeted approaches can deal with biodiversity related questions or to focus on species with practical interest. An unspecific approach is more amenable to address question where the biodiversity is not the target but rather questions of CO2 release or total microbial biomass around roots.
The art of choosing the right drivers
Allowing for a few drivers only (in the priority program texture and genotype) bears the risk that important ones are missed out, or the chosen ones prove to be of no importance for the parameter in question. It turned out that both the soil- and the plant-oriented driver led to very interesting, sometimes surprising results. Two such opposing drivers have also served the function of motivating representatives of different disciplines to work together: i.e. plant scientists and microbiologist realized that their results are strongly dependent on texture, while physicists were challenged by the fact that plant’s feedback mechanisms are so smart that irrespective of substrate properties resources were exploited completely (Jorda et al. in preparation, Vetterlein et al. in preparation).
Core messages
To summarise the results of this opinion paper, we formulated the following core messages:
-
Rhizosphere processes occur at multiple spatial and temporal scales. There is a large potential that models at different scales inform each other.
-
Despite increasing complexity of rhizosphere models, feedback loops are still underrepresented.
-
Modelling reveals that 3D architecture of roots, root hairs and soil (soil structure) and mucilage and their temporal dynamics have a strong impact on emerging properties/efficiency of processes.
-
Pore-scale modelling has the potential to capture system behaviours emerging from the myriad of microscale biotic and abiotic interactions, complementing existing continuous models.
-
Continuum-scale models can be informed about pore-scale processes through the derivation of effective parameters or through more complex upscaling approaches.
-
For the first time, an approach combining modelling at different scales and multimodal imaging of the rhizosphere allowing to integrate outputs from the microscale to the whole root system has been outlined. Thereby, the modeller and experimenter must jointly develop strategies to test representativeness or plausibility.
Further challenges and path ahead
Linking between more than two spatial scales or processes is still a challenge. Linking multiple scales and processes is the logical next step for future research and needs the combined use of experimental and modelling approaches.
So far, the impact of rhizosphere properties and processes have been discussed from the soil perspective. Except for water flow, a link between processes within the plant and how these react to or are coordinated with rhizosphere processes is still missing. Understanding which within-plant mechanisms control C-exudation is important to understand interactions between exudation and rhizosphere conditions. How local conditions influence growth such as mechanical rhizosphere properties but also transport properties that influence transport of signalling substances, e.g. ethylene, and thereby growth are examples of two-way feedbacks between growth and rhizosphere properties and processes.
Another aspect is the temporal scale of the rhizosphere organisation. In this paper (and the priority program), we focussed on the dynamics around a growing root system of an annual plant (maize). Whether such a rhizosphere system has a legacy after the plant died off that is of benefit for subsequent generations or whether it rather has negative effects requires further research. This would call for investigating multi-annual self-organisation effects of the rhizosphere in annual cropping systems. Understanding these effects is important to design and manage crop rotations and no-till systems.
Data availability
All data are available on request from the authors.
Code availability
Code is available on request from the authors.
References
Ahkami AH, Allen White R, Handakumbura PP, Jansson C (2017) Rhizosphere engineering: Enhancing sustainable plant ecosystem productivity. Rhizosphere 3:233–243. https://doi.org/10.1016/j.rhisph.2017.04.012
Ahmed MA, Kroener E, Holz M, Zarebanadkouki M, Carminati A (2014) Mucilage exudation facilitates root water uptake in dry soils. Funct Plant Biol 41:1129–1137. https://doi.org/10.1071/FP13330
Ahmed MA, Zarebanadkouki M, Ahmadi K, Kroener E, Kostka S, Kaestner A, Carminati A (2018) Engineering Rhizosphere Hydraulics: Pathways to Improve Plant Adaptation to Drought. Vadose Zone Journal 17:160090. https://doi.org/10.2136/vzj2016.09.0090
Alphei J, Bonkowski M, Scheu S (1996) Protozoa, Nematoda and Lumbricidae in the rhizosphere of Hordelymus europeaus (Poaceae): faunal interactions, response of microorganisms and effects on plant growth. Oecologia 106:111–126. https://doi.org/10.1007/BF00334413
Anderson T-H, Domsch KH (1985) Maintenance carbon requirements of actively-metabolizing microbial populations under in situ conditions. Soil Biol Biochem 17:197–203. https://doi.org/10.1016/0038-0717(85)90115-4
Angst G, Kögel-Knabner I, Kirfel K, Hertel D, Mueller CW (2016) Spatial distribution and chemical composition of soil organic matter fractions in rhizosphere and non-rhizosphere soil under European beech (Fagus sylvatica L.). Geoderma 264:179–187. https://doi.org/10.1016/j.geoderma.2015.10.016
Auriault JL, Boutin C, Geindreau C (2010) Homogenization by multiple scale asymptotic expansions. In: Homogenization of Coupled Phenomena in Heterogenous Media. https://doi.org/10.1002/9780470612033.ch3
Baskin TI (2013) Patterns of root growth acclimation: constant processes, changing boundaries. Wires Dev Biol 2:65–73. https://doi.org/10.1002/wdev.94
Baumert VL, Forstner SJ, Zethof JHT, Vogel C, Heitkötter J, Schulz S, Kögel-Knabner I, Mueller CW (2021) Root-induced fungal growth triggers macroaggregation in forest subsoils. Soil Biol Biochem 157:108244. https://doi.org/10.1016/j.soilbio.2021.108244
Benard P, Zarebanadkouki M, Hedwig C, Holz M, Ahmed MA, Carminati A (2018) Pore-Scale Distribution of Mucilage Affecting Water Repellency in the Rhizosphere. Vadose Zone Journal 17:170013. https://doi.org/10.2136/vzj2017.01.0013
Benard P, Zarebanadkouki M, Brax M, Kaltenbach R, Jerjen I, Marone F, Couradeau E, Felde VJMNL, Kaestner A, Carminati A (2019) Microhydrological Niches in Soils: How Mucilage and EPS Alter the Biophysical Properties of the Rhizosphere and Other Biological Hotspots. Vadose Zone Journal 18:180211. https://doi.org/10.2136/vzj2018.12.0211
Bobet A, Fakhimi A, Johnson S, Morris J, Tonon F, Ronald Yeung M (2009) Numerical Models in Discontinuous Media: Review of Advances for Rock Mechanics Applications. J Geotech Geoenviron Eng 135:1547–1561. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000133
Bonkowski M, Tarkka MT, Razavi BS, Schmidt H, Blagodatskaya E, Koller R, Yu P, Knief C, Hochholdinger F, Vetterlein D (2021) Spatiotemporal Dynamics of Maize (Zea mays L.) Root Growth and Its Potential Consequences for the Assembly of the Rhizosphere Microbiota. Front Microbiol. https://doi.org/10.3389/fmicb.2021.619499
Brax M, Köhne M, Kroener E, Schaumann GE (2019) Potential of NMR relaxometry to unravel the properties of mucilage in several pore sizes. Geoderma 340:269–278. https://doi.org/10.1016/j.geoderma.2019.01.013
Brax M, Buchmann C, Kenngott K, Schaumann G, Diehl D (2020) Influence of the physico-chemical properties of root mucilage and model substances on the microstructural stability of sand. Biogeochemistry 147:35–52. https://doi.org/10.1007/s10533-019-00626-w
Camazine S, Deneubourg J-L, Franks NR, Sneyd J, Theraula G, Bonabeau E (2001) Self-Organization in Biological Systems Princeton University Press, Princeton, New Jersey.
Carminati A, Kroener E, Ahmed MA, Zarebanadkouki M, Holz M, Ghezzehei T (2016) Water for carbon, carbon for water. Vadose Zone Journal 15: vzj2015.2004.0060. https://doi.org/10.2136/vzj2015.04.0060
Carminati A, Benard P, Ahmed MA, Zarebanadkouki M (2017) Liquid bridges at the root-soil interface. Plant Soil 417:1–15. https://doi.org/10.1007/s11104-017-3227-8
Carslaw HS, Jaeger JC (1959) Conduction of Heat in Solids. Oxford University Press, Oxford, UK
Chagnon P-L, Bradley RL, Maherali H, Klironomos JN (2013) A trait-based framework to understand life history of mycorrhizal fungi. Trends Plant Sci 18:484–491. https://doi.org/10.1016/j.tplants.2013.05.001
Chenu C, Roberson EB (1996) Diffusion of glucose in microbial extracellular polysaccharide as affected by water potential. Soil Biol Biochem 28:877–884. https://doi.org/10.1016/0038-0717(96)00070-3
Chou H, Wu L, Zeng L, Chang A (2012) Evaluation of solute diffusion tortuosity factor models for variously saturated soils. Water Resources Research 48https://doi.org/10.1029/2011WR011653
Clode PL, Kilburn MR, Jones DL, Stockdale EA, Cliff JB III, Herrmann AM, Murphy DV (2009) In Situ Mapping of Nutrient Uptake in the Rhizosphere Using Nanoscale Secondary Ion Mass Spectrometry. Plant Physiol 151:1751–1757. https://doi.org/10.1104/pp.109.141499
De Bauw P, Mai TH, Schnepf A, Merckx R, Smolders E, Vanderborght J (2020) A functional-structural model of upland rice root systems reveals the importance of laterals and growing root tips for phosphate uptake from wet and dry soils. Ann Bot 126:789–806. https://doi.org/10.1093/aob/mcaa120
de la Porte A, Schmidt R, Yergeau É, Constant P (2020) A Gaseous Milieu: Extending the Boundaries of the Rhizosphere. Trends Microbiol 28:536–542. https://doi.org/10.1016/j.tim.2020.02.016
de Willigen P, Heinen M, van Noordwijk M (2018) Roots Partially in Contact with Soil: Analytical Solutions and Approximation in Models of Nutrient and Water Uptake. Vadose Zone J 17:170060. https://doi.org/10.2136/vzj2017.03.0060
Dupuy L, Mackenzie J, Rudge T, Haseloff J (2008) A system for modelling cell-cell interactions during plant morphogenesis. Ann Bot 101:1255–1265. https://doi.org/10.1093/aob/mcm235
Dupuy LX, Silk WK (2016) Mechanisms of Early Microbial Establishment on Growing Root Surfaces. Vadose Zone J 15https://doi.org/10.2136/vzj2015.06.0094
Eickhorst T, Tippkötter R (2008) Detection of microorganisms in undisturbed soil by combining fluorescence in situ hybridization (FISH) and micropedological methods. Soil Biol Biochem 40:1284–1293. https://doi.org/10.1016/j.soilbio.2007.06.019
Falconer RE, Battaia G, Schmidt S, Baveye P, Chenu C, Otten W (2015a) Microscale heterogeneity explains experimental variability and non-linearity in soil organic matter mineralisation. PLoS ONE 10:e0123774–e0123774. https://doi.org/10.1371/journal.pone.0123774
Falconer RE, Otten W, White NA (2015b) Chapter One - Toward Modeling the Resistance and Resilience of “Below-ground” Fungal Communities: A Mechanistic and Trait-Based Approach. In: S Sariaslani, GM Gadd (eds) Advances in Applied Microbiology. Academic Press
Gao W, Blaser SRGA, Schlüter S, Shen J, Vetterlein D (2019) Effect of localised phosphorus application on root growth and soil nutrient dynamics in situ – comparison of maize (Zea mays) and faba bean (Vicia faba) at the seedling stage. Plant Soil 441:469–483. https://doi.org/10.1007/s11104-019-04138-2
Genty A, Pot V (2013) Numerical Simulation of 3D Liquid-Gas Distribution in Porous Media by a Two-Phase TRT Lattice Boltzmann Method. Transp Porous Media 96:271–294. https://doi.org/10.1007/s11242-012-0087-9
Gerke J (2015) The acquisition of phosphate by higher plants: Effect of carboxylate release by the roots. A critical review. J Plant Nutr Soil Sci 178:351–364. https://doi.org/10.1002/jpln.201400590
Gerke KM, Karsanina MV, Katsman R (2019) Calculation of tensorial flow properties on pore level: Exploring the influence of boundary conditions on the permeability of three-dimensional stochastic reconstructions. Phys Rev E 100:053312. https://doi.org/10.1103/PhysRevE.100.053312
Ginzburg I (2008) Consistent lattice Boltzmann schemes for the Brinkman model of porous flow and infinite Chapman-Enskog expansion. Phys Rev E 77:066704. https://doi.org/10.1103/PhysRevE.77.066704
Gorka S, Dietrich M, Mayerhofer W, Gabriel R, Wiesenbauer J, Martin V, Zheng Q, Imai B, Prommer J, Weidinger M, Schweiger P, Eichorst SA, Wagner M, Richter A, Schintlmeister A, Woebken D, Kaiser C (2019) Rapid Transfer of Plant Photosynthates to Soil Bacteria via Ectomycorrhizal Hyphae and Its Interaction With Nitrogen Availability. Front Microbiol 10https://doi.org/10.3389/fmicb.2019.00168
Grierson C, Schiefelbein J (2002) Root Hairs. In: The Arabidopsis Book. American Society of Plant Biologists, Rockville, MD, http://www.aspb.org/publications/arabidopsis/
Grimm V, Revilla E, Berger U, Jeltsch F, Mooij WM, Railsback SF, Thulke H-H, Weiner J, Wiegand T, DeAngelis DL (2005) Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from Ecology. Science 310:987. https://doi.org/10.1126/science.1116681
Guibert R, Horgue P, Debenest G, Quintard M (2016) A Comparison of Various Methods for the Numerical Evaluation of Porous Media Permeability Tensors from Pore-Scale Geometry. Math Geosci 48:329–347. https://doi.org/10.1007/s11004-015-9587-9
Haupenthal A, Brax M, Bentz J, Jungkunst HF, Schützenmeister K, Kroener E (2021) Plants control soil gas exchanges possibly via mucilage. J Plant Nutr Soil Sci 184:320–328. https://doi.org/10.1002/jpln.202000496
Hinsinger P, Bengough AG, Vetterlein D, Young IM (2009) Rhizosphere: biophysics, biogeochemistry and ecological relevance. Plant Soil 321:117–152. https://doi.org/10.1007/s11104-008-9885-9
Holz M, Zarebanadkouki M, Kuzyakov Y, Pausch J, Carminati A (2017) Root hairs increase rhizosphere extension and carbon input to soil. Ann Bot 121:61–69. https://doi.org/10.1093/aob/mcx127
Holz M, Zarebanadkouki M, Kaestner A, Kuzyakov Y, Carminati A (2018) Rhizodeposition under drought is controlled by root growth rate and rhizosphere water content. Plant Soil 423:429–442. https://doi.org/10.1007/s11104-017-3522-4
Hornung U (1996) Homogenization and Porous Media. Springer Verlag, Berlin, Heidelberg
Hütsch BW, Augustin J, Merbach W (2002) Plant rhizodeposition — an important source for carbon turnover in soils. J Plant Nutr Soil Sci 165:397–407. https://doi.org/10.1002/1522-2624(200208)165:4%3c397::AID-JPLN397%3e3.0.CO;2-C
Jones DL, Hodge A, Kuzyakov Y (2004) Plant and mycorrhizal regulation of rhizodeposition. New Phytol 163:459–480. https://doi.org/10.1111/j.1469-8137.2004.01130.x
Juyal A, Otten W, Falconer R, Hapca S, Schmidt H, Baveye PC, Eickhorst T (2019) Combination of techniques to quantify the distribution of bacteria in their soil microhabitats at different spatial scales. Geoderma 334:165–174. https://doi.org/10.1016/j.geoderma.2018.07.031
Kim TK, Silk WK (1999) A mathematical model for pH patterns in the rhizospheres of growth zones. Plant, Cell Environ 22:1527–1538. https://doi.org/10.1046/j.1365-3040.1999.00512.x
Kimber JA, Kazarian SG, Štěpánek F (2012) Modelling of pharmaceutical tablet swelling and dissolution using discrete element method. Chem Eng Sci 69:394–403. https://doi.org/10.1016/j.ces.2011.10.066
Kirk GJD, Santos EE, Findenegg GR (1999) Phosphate solubilization by organic anion excretion from rice (Oryza sativa L.) growing in aerobic soil. Plant Soil 211:11–18. https://doi.org/10.1023/A:1004539212083
Koller R, Metzner R, van Dusschoten D, Pflugfelder D, Bühler J, Huber G, Chlubek A, Jahnke S (2018) Phenotyping spatial and temporal dynamics of roots by Magnetic Resonance Imaging and Positron Emission Tomography. 5th International Plant Phenotyping Symposium, 2 Oct 2018 - 5 Oct 2018, Adelaide (Australia)
Kroener E, Holz M, Zarebanadkouki M, Ahmed M, Carminati A (2018) Effects of Mucilage on Rhizosphere Hydraulic Functions Depend on Soil Particle Size. Vadose Zone J 17:170056. https://doi.org/10.2136/vzj2017.03.0056
Kumar A, Kuzyakov Y, Pausch J (2016) Maize rhizosphere priming: field estimates using 13C natural abundance. Plant Soil 409:87–97. https://doi.org/10.1007/s11104-016-2958-2
Kuzyakov Y (2002) Review: Factors affecting rhizosphere priming effects. J Plant Nutr Soil Sci 165:382–396. https://doi.org/10.1002/1522-2624(200208)165:4%3c382::AID-JPLN382%3e3.0.CO;2-#
Landl M, Haupenthal A, Leitner D, Kroener E, Vetterlein D, Bol R, Vereecken H, Vanderborght J, Schnepf A (2021) Simulating rhizodeposition patterns around growing and exuding root systems in silico. Plants 3. https://doi.org/10.1093/insilicoplants/diab028
Leitner D, Klepsch S, Bodner G, Schnepf A (2010a) A dynamic root system growth model based on L-Systems. Plant Soil 332:177–192. https://doi.org/10.1007/s11104-010-0284-7
Leitner D, Klepsch S, Ptashnyk M, Marchant A, Kirk GJD, Schnepf A, Roose T (2010b) A dynamic model of nutrient uptake by root hairs. New Phytol 185:792–802. https://doi.org/10.1111/j.1469-8137.2009.03128.x
Liang C, Amelung W, Lehmann J, Kästner M (2019) Quantitative assessment of microbial necromass contribution to soil organic matter. Glob Change Biol 25:3578–3590. https://doi.org/10.1111/gcb.14781
Lobet G, Pound MP, Diener J, Pradal C, Draye X, Godin C, Javaux M, Leitner D, Meunier F, Nacry P, Pridmore TP, Schnepf A (2015) Root System Markup Language: Toward a Unified Root Architecture Description Language. Plant Physiol 167:617. https://doi.org/10.1104/pp.114.253625
Lohse M, Haag R, Lippold E, Vetterlein D, Reemtsma T, Lechtenfeld OJ (2021) Direct Imaging of Plant Metabolites in the Rhizosphere Using Laser Desorption Ionization Ultra-High Resolution Mass Spectrometry. Frontiers in Plant Science 12https://doi.org/10.3389/fpls.2021.753812
Lucas M, Schlüter S, Vogel H-J, Vetterlein D (2019) Roots compact the surrounding soil depending on the structures they encounter. Sci Rep 9:16236. https://doi.org/10.1038/s41598-019-52665-w
Lucas M, Vetterlein D, Vogel H-J, Schlüter S (2020) Revealing pore connectivity across scales and resolutions with X-ray CT. Eur J Soil Sci 72https://doi.org/10.1111/ejss.12961
Marcombe R, Cai S, Hong W, Zhao X, Lapusta Y, Suo Z (2010) A theory of constrained swelling of a pH-sensitive hydrogel. Soft Matter 6:784–793. https://doi.org/10.1039/B917211D
McKay Fletcher DM, Ruiz S, Dias T, Petroselli C, Roose T (2020) Linking root structure to functionality: the impact of root system architecture on citrate-enhanced phosphate uptake. New Phytol 227:376–391. https://doi.org/10.1111/nph.16554
Melnitchouck A, Leinweber P, Eckhardt KU, Beese R (2005) Qualitative differences between day- and night-time rhizodeposition in maize (Zea mays L.) as investigated by pyrolysis-field ionization mass spectrometry. Soil Biol Biochem 37:155–162. https://doi.org/10.1016/j.soilbio.2004.06.017
Millington RJ, Quirk JP (1961) Permeability of porous solids. Trans Faraday Soc 57:1200–1207. https://doi.org/10.1039/TF9615701200
Mo C, Jiang Z, Chen P, Cui H, Yang J (2021) Microbial metabolic efficiency functions as a mediator to regulate rhizosphere priming effects. Sci Total Environ 759:143488. https://doi.org/10.1016/j.scitotenv.2020.143488
Naveed M, Brown LK, Raffan AC, George TS, Bengough AG, Roose T, Sinclair I, Koebernick N, Cooper L, Hackett CA, Hallett PD (2017) Plant exudates may stabilize or weaken soil depending on species, origin and time. Eur J Soil Sci 68:806–816. https://doi.org/10.1111/ejss.12487
Naveed M, Ahmed MA, Benard P, Brown LK, George TS, Bengough AG, Roose T, Koebernick N, Hallett PD (2019) Surface tension, rheology and hydrophobicity of rhizodeposits and seed mucilage influence soil water retention and hysteresis. Plant Soil 437:65–81. https://doi.org/10.1007/s11104-019-03939-9
Nguyen C, Froux F, Recous S, Morvan T, Robin C (2008) Net N immobilisation during the biodegradation of mucilage in soil as affected by repeated mineral and organic fertilisation. Nutr Cycl Agroecosyst 80:39–47. https://doi.org/10.1007/s10705-007-9119-1
Nunan N, Ritz K, Crabb D, Harris K, Wu K, Crawford JW, Young IM (2001) Quantification of the in situ distribution of soil bacteria by large-scale imaging of thin sections of undisturbed soil. FEMS Microbiol Ecol 37:67–77. https://doi.org/10.1111/j.1574-6941.2001.tb00854.x
Oburger E, Jones DL (2018) Sampling root exudates – Mission impossible? Rhizosphere 6:116–133. https://doi.org/10.1016/j.rhisph.2018.06.004
Oburger E, Jones DL, Wenzel WW (2011) Phosphorus saturation and pH differentially regulate the efficiency of organic acid anion-mediated P solubilization mechanisms in soil. Plant Soil 341:363–382. https://doi.org/10.1007/s11104-010-0650-5
Ohnesorge WV (1936) Die Bildung von Tropfen an Düsen und die Auflösung flüssiger Strahlen. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift Für Angewandte Mathematik Und Mechanik 16:355–358. https://doi.org/10.1002/zamm.19360160611
Olesen T, Moldrup P, Yamaguchi T, Rolston DE (2001) Constant slope impedance factor model for predicting the solute diffusion coefficient in unsaturated soil. Soil Sci 166:89–96
Paterson E (2003) Importance of rhizodeposition in the coupling of plant and microbial productivity. Eur J Soil Sci 54:741–750. https://doi.org/10.1046/j.1351-0754.2003.0557.x
Paterson E, Gebbing T, Abel C, Sim A, Telfer G (2007) Rhizodeposition shapes rhizosphere microbial community structure in organic soil. New Phytol 173:600–610. https://doi.org/10.1111/j.1469-8137.2006.01931.x
Phalempin M, Lippold E, Vetterlein D, Schlüter S (2021) Soil texture and structure heterogeneity predominantly governs bulk density gradients around roots. Vadose Zone J 20:e20147. https://doi.org/10.1002/vzj2.20147
Portell X, Pot V, Garnier P, Otten W, Baveye PC (2018) Microscale Heterogeneity of the Spatial Distribution of Organic Matter Can Promote Bacterial Biodiversity in Soils: Insights From Computer Simulations. Front Microbiol 9:1583. https://doi.org/10.3389/fmicb.2018.01583
Pot V, Peth S, Monga O, Vogel LE, Genty A, Garnier P, Vieublé-Gonod L, Ogurreck M, Beckmann F, Baveye PC (2015) Three-dimensional distribution of water and air in soil pores: Comparison of two-phase two-relaxation-times lattice-Boltzmann and morphological model outputs with synchrotron X-ray computed tomography data. Adv Water Resour 84:87–102. https://doi.org/10.1016/j.advwatres.2015.08.006
Pot V, Portell X, Otten W, Garnier P, Monga O, Baveye PC (2021) Accounting for soil architecture and microbial dynamics in microscale models: Current practices in soil science and the path ahead. Eur J Soil Sci. https://doi.org/10.1111/ejss.13142
Rangel AF, Rao IM, Braun HP, Horst WJ (2010) Aluminum resistance in common bean (Phaseolus vulgaris) involves induction and maintenance of citrate exudation from root apices. Physiol Plant 138:176–190. https://doi.org/10.1111/j.1399-3054.2009.01303.x
Ray N, Rupp A, Schulz R, Knabner P (2018) Old and New Approaches Predicting the Diffusion in Porous Media. Transp Porous Media 124:803–824. https://doi.org/10.1007/s11242-018-1099-x
Raynaud X, Nunan N (2014) Spatial ecology of bacteria at the microscale in soil. PLoS ONE 9:e87217. https://doi.org/10.1371/journal.pone.0087217
Richefeu V, Radjai F, Delenne J-Y (2016) Lattice Boltzmann modelling of liquid distribution in unsaturated granular media. Comput Geotech 80:353–359. https://doi.org/10.1016/j.compgeo.2016.02.017
Rodionov A, Lehndorff E, Stremtan CC, Brand WA, Königshoven H-P, Amelung W (2019) Spatial Microanalysis of Natural 13C/12C Abundance in Environmental Samples Using Laser Ablation-Isotope Ratio Mass Spectrometry. Anal Chem 91:6225–6232. https://doi.org/10.1021/acs.analchem.9b00892
Roose T, Keyes SD, Daly KR, Carminati A, Otten W, Vetterlein D, Peth S (2016) Challenges in imaging and predictive modeling of rhizosphere processes. Plant Soil 407:9–38. https://doi.org/10.1007/s11104-016-2872-7
Rüger L, Feng K, Dumack K, Freudenthal J, Chen Y, Sun R, Wilson M, Yu P, Sun B, Deng Y, Hochholdinger F, Vetterlein D, Bonkowski M (2021) Assembly Patterns of the Rhizosphere Microbiome Along the Longitudinal Root Axis of Maize (Zea mays L.). Front Microbiol 12:614501–614501. https://doi.org/10.3389/fmicb.2021.614501
Ruiz S, Koebernick N, Duncan S et al (2020a) Significance of root hairs at the field scale – modelling root water and phosphorus uptake under different field conditions. Plant Soil 447:281–304. https://doi.org/10.1007/s11104-019-04308-2
Ruiz S, Fletcher DM, Williams K, Roose T (2020b) Review of plant-soil modelling: root growth, nutrient and water transport/uptake, and mechanics. In: Annual Plant Reviews online. Wiley
Ryan PR, Dessaux Y, Thomashow LS, Weller DM (2009) Rhizosphere engineering and management for sustainable agriculture. Plant Soil 321:363–383. https://doi.org/10.1007/s11104-009-0001-6
Sakurai G, Satake A, Yamaji N, Mitani-Ueno N, Yokozawa M, Feugier FG, Ma JF (2015) In Silico Simulation Modeling Reveals the Importance of the Casparian Strip for Efficient Silicon Uptake in Rice Roots. Plant Cell Physiol 56:631–639. https://doi.org/10.1093/pcp/pcv017
Sarkar D, Rovenich H, Jeena G, Nizam S, Tissier A, Balcke GU, Mahdi LK, Bonkowski M, Langen G, Zuccaro A (2019) The inconspicuous gatekeeper: endophytic Serendipita vermifera acts as extended plant protection barrier in the rhizosphere. New Phytol 224:886–901. https://doi.org/10.1111/nph.15904
Schnepf A, Leitner D, Klepsch S (2012) Modeling Phosphorus Uptake by a Growing and Exuding Root System. Vadose Zone Journal 11(vzj2012):0001. https://doi.org/10.2136/vzj2012.0001
Schnepf A, Leitner D, Landl M, Lobet G, Mai TH, Morandage S, Sheng C, Zörner M, Vanderborght J, Vereecken H (2018) CRootBox: a structural–functional modelling framework for root systems. Ann Bot 121:1033–1053. https://doi.org/10.1093/aob/mcx221
Silk WK (1984) Quantitative Descriptions of Development. Annu Rev Plant Physiol 35:479–518. https://doi.org/10.1146/annurev.pp.35.060184.002403
Spohn M, Kuzyakov Y (2014) Spatial and temporal dynamics of hotspots of enzyme activity in soil as affected by living and dead roots—a soil zymography analysis. Plant Soil 379:67–77. https://doi.org/10.1007/s11104-014-2041-9
Sukop MC, Or D (2004) Lattice Boltzmann method for modeling liquid-vapor interface configurations in porous media. Water Resour Res 40https://doi.org/10.1029/2003WR002333
Szoboszlay M, Tebbe CC (2021) Hidden heterogeneity and co-occurrence networks of soil prokaryotic communities revealed at the scale of individual soil aggregates. MicrobiologyOpen 10:e1144. https://doi.org/10.1002/mbo3.1144
Thurner S, Klimek P, Hanel R (2018) Introduction to the Theory of Complex Systems. Oxford University Press, Oxford
Totsche KU, Amelung W, Gerzabek MH, Guggenberger G, Klumpp E, Knief C, Lehndorff E, Mikutta R, Peth S, Prechtel A, Ray N, Kögel-Knabner I (2018) Microaggregates in soils. J Plant Nutr Soil Sci 181:104–136. https://doi.org/10.1002/jpln.201600451
Tracy SR, Daly KR, Sturrock CJ, Crout NMJ, Mooney SJ, Roose T (2015) Three-dimensional quantification of soil hydraulic properties using X-ray Computed Tomography and image-based modeling. Water Resour Res 51:1006–1022. https://doi.org/10.1002/2014WR016020
Tuller M, Or D (2005) Water retention and characteristic curve. In: D Hillel (ed) Encyclopedia of Soils in the Environment. Elsevier, Oxford.
van Veelen A, Tourell MC, Koebernick N, Pileio G, Roose T (2018) Correlative Visualization of Root Mucilage Degradation Using X-ray CT and MRI. Front Environ Sci 6https://doi.org/10.3389/fenvs.2018.00032
Venturi V, Keel C (2016) Signaling in the Rhizosphere. Trends Plant Sci 21:187–198. https://doi.org/10.1016/j.tplants.2016.01.005
Vereecken H, Schnepf A, Hopmans J, Javaux M, Or D, Roose T, Vanderborght J, Young M, Amelung W, Aitkenhead M, Allison S, Assouline S, Baveye P, Berli M, Brüggemann N, Finke P, Flury M, Gaiser T, Govers G, Ghezzehei T, Hallett P, Hendricks Franssen H, Heppell J, Horn R, Huisman J, Jacques D, Jonard F, Kollet S, Lafolie F, Lamorski K, Leitner D, McBratney A, Minasny B, Montzka C, Nowak W, Pachepsky Y, Padarian J, Romano N, Roth K, Rothfuss Y, Rowe E, Schwen A, Šimůnek J, Tiktak A, Van Dam J, van der Zee S, Vogel H, Vrugt J, Wöhling T, Young I (2016) Modeling soil processes: review, key challenges, and new perspectives. Vadose Zone Journal 15:1–57. https://doi.org/10.2136/vzj2015.09.0131
Vetterlein D, Carminati A, Kögel-Knabner I, Bienert GP, Smalla K, Oburger E, Schnepf A, Banitz T, Tarkka MT, Schlüter S (2020) Rhizosphere Spatiotemporal Organization–A Key to Rhizosphere Functions. Front Agron 2https://doi.org/10.3389/fagro.2020.00008
Vetterlein D, Lippold E, Schreiter S, Phalempin M, Fahrenkampf T, Hochholdinger F, Marcon C, Tarkka M, Oburger E, Ahmed M, Javaux M, Schlüter S (2021) Experimental platforms for the investigation of spatiotemporal patterns in the rhizosphere—Laboratory and field scale. J Plant Nutr Soil Sci 184:35–50. https://doi.org/10.1002/jpln.202000079
Vidal A, Hirte J, Bender SF, Mayer J, Gattinger A, Höschen C, Schädler S, Iqbal TM, Mueller CW (2018) Linking 3D Soil Structure and Plant-Microbe-Soil Carbon Transfer in the Rhizosphere. Front Environ Sci 6https://doi.org/10.3389/fenvs.2018.00009
von Jeetze PJ, Zarebanadkouki M, Carminati A (2020) Spatial Heterogeneity Enables Higher Root Water Uptake in Dry Soil but Protracts Water Stress After Transpiration Decline: A Numerical Study. Water Resour Res 56:e2019WR025501. https://doi.org/10.1029/2019WR025501
Wang X, Dijkstra FA, Yin L, Sun D, Cheng W (2020) Rhizosphere priming effects in soil aggregates with different size classes. Ecosphere 11:e03027. https://doi.org/10.1002/ecs2.3027
Watt M, McCully ME, Jeffree CE (1993) Plant and bacterial mucilages of the maize rhizosphere: Comparison of their soil binding properties and histochemistry in a model system. Plant Soil 151:151–165. https://doi.org/10.1007/BF00016280
Watt M, McCully ME, Canny MJ (1994) Formation and Stabilization of Rhizosheaths of Zea mays L. (Effect of Soil Water Content). Plant Physiol 106:179–186. https://doi.org/10.1104/pp.106.1.179
Watt M, Silk WK, Passioura JB (2006) Rates of Root and Organism Growth, Soil Conditions, and Temporal and Spatial Development of the Rhizosphere. Ann Bot 97:839–855. https://doi.org/10.1093/aob/mcl028
Weller HG, Tabor G, Jasak H, Fureby C (1998) A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput Phys 12:620–631. https://doi.org/10.1063/1.168744
Whitaker S (1986) Flow in porous media I: A theoretical derivation of Darcy’s law. Transp Porous Media 1:3–25. https://doi.org/10.1007/BF01036523
Williams KA, Ruiz SA, Petroselli C, Walker N, McKay Fletcher DM, Pileio G, Roose T (2021) Physical characterisation of chia mucilage polymeric gel and its implications on rhizosphere science - Integrating imaging, MRI, and modelling to gain insights into plant and microbial amended soils. Soil Biol Biochem 162:108404. https://doi.org/10.1016/j.soilbio.2021.108404
Yang R, Gao T, Li D, Liang H, Xu Q (2018) Simulation of fracture behaviour of hydrogel by discrete element method. Micro & Nano Letters 13:743–746. https://doi.org/10.1049/mnl.2017.0844
Zarebanadkouki M, Fink T, Benard P, Banfield CC (2019) Mucilage Facilitates Nutrient Diffusion in the Drying Rhizosphere. Vadose Zone J 18:190021. https://doi.org/10.2136/vzj2019.02.0021
Zhang X, Crawford JW, Young IM (2016) A Lattice Boltzmann model for simulating water flow at pore scale in unsaturated soils. J Hydrol 538:152–160. https://doi.org/10.1016/j.jhydrol.2016.04.013
Zhou X-R, Schnepf A, Vanderborght J, Leitner D, Lacointe A, Vereecken H, Lobet G (2020) CPlantBox, a whole-plant modelling framework for the simulation of water- and carbon-related processes. in silico Plants 2. https://doi.org/10.1093/insilicoplants/diaa001
Zickenrott I-M, Woche SK, Bachmann J, Ahmed MA, Vetterlein D (2016) An efficient method for the collection of root mucilage from different plant species—A case study on the effect of mucilage on soil water repellency. J Plant Nutr Soil Sci 179:294–302. https://doi.org/10.1002/jpln.201500511
Zygalakis KC, Kirk GJD, Jones DL, Wissuwa M, Roose T (2011) A dual porosity model of nutrient uptake by root hairs. New Phytol 192:676–688. https://doi.org/10.1111/j.1469-8137.2011.03840.x
Funding
Open Access funding enabled and organized by Projekt DEAL. This project was carried out in the framework of the priority programme 2089 Rhizosphere spatiotemporal organization-a key to rhizosphere functions funded by the German Research Foundation DFG under the project numbers 403633986, 403635931, 403640293, 403640522, 403641034, 403668613, 403660839, 403670197, 403670844, 403801423, 403803214. This work has partially been funded by the German Research Foundation under Germany’s Excellence Strategy, EXC-2070 – 390732324 – PhenoRob. XP and WO acknowledge funding from the Natural Environment Research Council (NE/S004920/1).
Author information
Authors and Affiliations
Contributions
Our opinion is the result of many discussions we have had during meetings and workshops within the framework of the German priority program “Rhizosphere Spatiotemporal Organisation – a Key to Rhizosphere Functions”.
Corresponding authors
Ethics declarations
Additional declarations for articles in life science journals that report the results of studies involving humans and/or animals
Not applicable.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
All authors agreed with the content and gave consent to submit this manuscript.
Conflicts of interest/Competing interests (include appropriate disclosures)
There are no conflicts of interest.
Additional information
Responsible Editor: Philip John White
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schnepf, A., Carminati, A., Ahmed, M.A. et al. Linking rhizosphere processes across scales: Opinion. Plant Soil 478, 5–42 (2022). https://doi.org/10.1007/s11104-022-05306-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11104-022-05306-7