Rhizosphere models: their concepts and application to plant-soil ecosystems

Abstract

Background

The rhizosphere is the influence-sphere of the root. It is a local ecosystem with complex functions that determine nutrient uptake, cycling of resources, and plant health. Mathematical models can quantitatively explain and help to understand rhizosphere complexity. To interpret model predictions and relevance of processes, we require understanding of the underlying concepts. Conceptualization of rhizosphere processes bridges mathematical modeling and experimental work and thus is key to understanding the rhizosphere.

Scope

We review concepts and assumptions foundational to the modeling of soil-plant-microorganism processes in the rhizosphere. Rhizosphere models are designed to simulate a plurality of components (solutes, substrates, and microorganisms). They specify components and interactions, drawing from the disciplines of soil science, botany, microbiology, and ecology. Solute transport models are applied to describe bioavailability in the rhizosphere. The root is typically a sink (e.g. nutrient uptake) or source (e.g. exudation) for one or more solutes. Microorganisms are usually described in time only, neglecting possible spatial movement. Interactions between components, e.g. chemical reactions and substrate-dependent bacterial growth rates, are usually described by coupling via reaction terms.

Conclusions

Rhizosphere models share concepts that we organized in a collective framework. This collective framework facilitates the development of new models. The interdisciplinary approach in which knowledge from soil ecology, botany, and soil physics are combined in rhizosphere models has proven fruitful for applications in plant and soil systems. We advocate multi-component-multi-interaction ecosystems around the root, with each component represented by an advection-diffusion-motility-reaction equation.

Introduction

Plants form the rhizosphere through soil exploration by root growth. Abstractly, roots are sinks and sources altering the properties of the surrounding soil (e.g. Hinsinger et al. 2005; Sasse et al. 2018). Conversely, the root itself is influenced by the surrounding physical processes, chemical reactions, and microorganisms (Watt et al. 2006a). The rhizosphere is not only distinct from the bulk soil in its chemical and physical properties but also in its biological and ecological properties, including the activity of enzymes and microorganisms.

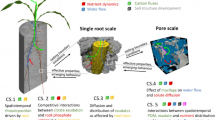
Rhizosphere research is interdisciplinary, bridging three traditional disciplines: soil science (including soil chemistry and soil physics), plant sciences, and soil microbial ecology (Fig. 1). Due to the complexity of the rhizosphere (Curl and Truelove 1986; Huang et al. 2014), its modeling is reductive and integrative. Rhizosphere modeling aims at a better understanding of temporal and spatial rhizosphere functioning and the underlying mechanisms of root traits and soil processes. The models serve as tools to explore the relative importance of such traits and processes. Thereby, rhizosphere models help to decide what plant-, soil-, and microbial properties to measure. Rhizosphere research is discovering ever more ways exudates, nutrients, water, and microbes interact. The models become more complex, aiming at a holistic description (York et al. 2016). The proposed mechanisms, however, are diverse, and there is a lack of mechanistic understanding when it comes to plant-microorganism interactions (Jacoby et al. 2017). An increasing number of components and proposed interactions leads to increasing diversity in rhizosphere models and their application.

Fig. 1

The rhizosphere is a micro-ecosystem formed around the root, and models draw on concepts in botany, soil science, and ecology. The classical models represent the rhizosphere as cylinder of unit length with the root as boundary condition. Microorganisms are modeled as a system of ordinary differential equations in time (0D space). Soil sorption and diffusion are important processes since they can limit crop production

The usefulness of a model is specific to its application. When comparing alternative models developed for the same application, it is important to verify assumptions and not only simulated outcomes. Despite the plurality, rhizosphere models share many common concepts. The models can thereby be categorized and summarized using a collective framework. A deeper understanding of the foundational concepts, assumptions, and commonalities leads to better designs of experiments with clear targets to test.

We review the diversity of published rhizosphere models, focusing on their concepts and underlying assumptions. Comparison of models is important to develop further mechanistic understanding. This review provides a framework for comparing and developing rhizosphere models.

Concepts in rhizosphere modeling

Physical and chemical soil properties strongly determine how nutrients are available to both plants and microorganisms. Hence, soil science has focused on solute transport towards the root surface and chemical reactions occuring in the rhizosphere (bioavailability, Barber 1995; Tinker and Nye 2000). Rhizosphere nutrient transport and uptake models date back to work from the 1960s (Bouldin 1961; Barber 1962; Olsen et al. 1962; Passioura 1963; Gardner 1965; Olsen and Kemper 1968; Nye and Marriott 1969), Fig. 2. The rate of transport is strongly influenced by sorption (desorption, adsorption, or absorption) and other reactions, as well as soil structure and water content.

Fig. 2

Milestones of the development of the classical rhizosphere model and spatial microorganism models (bottom part). All variants of the classical rhizosphere model consider transport in soil and root-soil interactions in the form of boundary conditions. Crank and others earlier applied the heat (transport) equation to porous media. Crank (1956) described the general (heat) diffusion referencing Henry (1939). Bouldin (1961) used diffusion to the root. Nye and Marriott (1969) used diffusion, advection, and Michaelis-Menten uptake kinetics. Barber and Cushman (1981) included efflux and zero-flux outer boundary. Barber (1962) wrote a concept paper about diffusion and mass flow in soil. Itoh and Barber (1983) combined root hair reaction using the formula in Baldwin et al. (1973) and Bhat et al. (1976). Today, 2021, there are many variations on the classical radial respectively cylindrical rhizosphere description published

Plant science has studied how the rhizosphere influences nutrient uptake and, more recently, the root phenotype, whereas soil microbial ecology has been concerned with population dynamics. Models of the rhizosphere combine concepts from these disciplines. We present mathematical descriptions of the concepts, at the same time merging the different formulations that can be found in literature into one collective framework.

Solute transport in soil

Rhizosphere models typically include transport of solutes as the sum of advection and diffusion. Advection is directed solute transport within the rhizosphere because of water flow (sometimes termed convection). It is often called mass flow (Passioura 1963; Nye and Marriott 1969; Bouldin 1989), despite diffusion also being a type of mass flow. Roots attract water along gradients in water potential induced by transpiration and osmotic potential differences. The differences in osmotic potentials can be caused by metabolites in the cells and not just by solutes themselves. Water flow causes the solutes to travel (i.e. by advection) to the root surface, where the root may take them up. The movement of soil nanoparticles (colloids) and the substances bound to them is usually not considered. It is assumed that advective transport only takes place in the liquid phase.

If the uptake is faster than the transport of a solute towards the root, depletion at the root surface occurs, forming a concentration gradient. This is also named the (nutrient-)depletion zone, in which the solute concentration gradient causes diffusion towards the root. If the uptake is slower than the transport of a solute, the solute concentrations increase at the root surface, causing diffusion away from the root.

Transport equation

The concentration of a single ion, C, in a given soil domain may be defined as the sum of the concentrations in the liquid, solid, and gas phases. The gas phase in soil, well described by Scanlon et al. (2001), has often been ignored in rhizosphere models as a common simplification for most plant nutrients. Thereby, the total concentration in soil is (Nye and Marriott 1969; Barber and Cushman 1981)

$$C:= \theta {C}_{\ell }+\rho {C}_s,$$

where C_ℓ [M] and C_s [mmol g^-1 soil] are the concentrations in liquid and solid phases respectively (subscripts ℓ and s), θ [cm³ cm^-3] is the volumetric water content, and ρ is the soil bulk density (dry solid soil mass per unit volume, g cm^-3).

In the following equations, we use the Nabla-operator, $\nabla$, to cover arbitrary (soil) dimensions and geometries for the sake of generality. A concrete specification of dimensions and coordinate systems is a modeling decision during the realization of the concept by a mathematical description. The change in the total concentration in soil is described by a diffusion-advection-reaction equation,

$$\begin{aligned}\frac{\partial C}{\partial t}=&\nabla\cdot D_e\nabla C+\nabla\cdot\boldsymbol vC_\ell+R,\end{aligned}$$

(1)

where v > 0 is the soil water flux towards the root surface, R is a reaction term (often a function of C, sink- and source terms), and D_e is the effective diffusion coefficient in terms of total C.

Equation (1) shows diffusion ($D_e\nabla C$) of total C. Here, C_s is in equilibrium and scales with C_ℓ. Hence, due to rapid de- and attachment of solutes from the solid, C diffuses in total. Eq. (1) does not describe diffusion through the solid or diffusion of slowly equilibrating soil fractions. The definition of D_e and the unit of C_ℓ are important to dismantle eq. (1).

The effective diffusion in soil is typically much slower than the diffusion constant of the solute in pure water (Fig. 1). With a diffusion coefficient that accounts for soil water content and tortuosity, D_f, the effective diffusion coefficient is typically estimated by D_e ≔ D_f dC_ℓ /dC, where dC_ℓ /dC is reciprocal to instant soil sorption.

Barber (1962) and Nye (1966a) added diffusive flux through the solid phase at first (intra-aggregate diffusion) but that was neglected after; thereby, the diffusion is approximately D_f ≔ D_ℓθτ (Nye 1966b), where D_ℓ is the diffusion coefficient in pure water. This estimation of the diffusion coefficient is concentration-dependent and holds for a certain range ΔC_ℓ (Nye 1966b). Soil pathways are not explicitly modeled but macroscopically accounted for by the soil-specific tortuosity (also called impedance) factor, τ < 1, which assumes that the average path for transport is longer and the diffusion is thereby slower (Porter et al. 1960). Because C_ℓ is the concentration in the soil solution (not soil volume), the volumetric water content θ scales C_ℓ but can be written together with the diffusion coefficient (Gardner 1965). Since these soil pathways contain sorption-sites, diffusion in soil is modeled to be additionally affected by equilibrium-sorption via dC/dC_ℓ. This term instantaneously adjusts the concentration in the solid phase to changes in the liquid phase.

With this definition of D_e, diffusion in the soil solution without sorption can be written as

$$\begin{aligned}\theta \frac{\partial {C}_{\ell }}{\partial t}& =\nabla \cdot {D}_{\ell}\theta \tau \nabla {C}_{\ell }.\end{aligned}$$

(2)

Soil sorption adds ρ∂C_s/∂t to the left-hand-side of eq. (2), rearranging gives again the diffusion part of eq. (1) (Olsen et al. 1962; Gardner 1965). Summarized, the physical (macro-)scale described here is a homogeneous mixture of liquid and solid phases in instant equilibrium.

The root system grows in all spatial directions, however, eq. (1) is commonly applied to a unit root segment on a radial symmetric plane. Hence, to specify the spatial dimensions of the described rhizosphere transport model, the 1D radial approach is used instead of higher dimensional alternatives. Sorption is described in the next section but is classically represented by the soil buffer power b ≔ ∂C/∂C_ℓ (Bouldin 1961; Olsen et al. 1962). Thus, the transport equation can be written in C_ℓ only as

$$\mathrm{b}\;\frac{\partial {C}_{\ell }}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left(r{D}_e\mathrm{b}\frac{\partial {C}_{\ell }}{\partial r}+{r}_0{v}_0{C}_{\ell}\right)+R,$$

(3)

where v₀r₀ is the inward flux of water (under steady-state water flux conditions 2πrv = 2πr₀v₀, Nye and Marriott 1969; Barber and Cushman 1981). To define a full model, however, initial and boundary conditions are required. Initial conditions are usually constant for the rhizosphere region, C_ℓ(r, t = 0) = C_ℓ,initial. The boundary conditions used in rhizosphere models are discussed in the following sections.

The 1D radial approach is the basis for many rhizosphere models and was, for example, applied to potassium and phosphate (Claassen et al. 1986; Leitner et al. 2010b). As such, eq. (3) may represent the ‘classical’ rhizosphere models that describe the transport and uptake of a single solute in (1D) radial coordinates around a root segment of unit length (Fig. 1). They are often named “Nye-Tinker”, “Barber-Cushman”, or “Nye-Tinker-Barber” models, even when they deviate from these classical works, for example, by specifying different uptake dynamics and constraints on the interface between the rhizosphere and bulk soil. In order to become more precise, we do not follow this naming but distinguish the classical models by the complexity of the transport equation, the rhizosphere boundary conditions at the root surface and rhizosphere distance, and the reaction term. For solute transport, we distinguish models that describe diffusion only (as in Bouldin 1961; Nye 1966b), from those that also include advection (Passioura and Frere 1967; Nye and Marriott 1969; Barley 1970). Solute uptake may be divided into categories concerning the concentration at the root surface: constant, linear, and non-linear. However, before we address the plant, we stay with the soil and review sorption in rhizosphere models.

Soil sorption and chemical reactions

Sorption is the exchange of concentrations in the soil solid and liquid phases: C_ℓ and C_s (Fig. 1). These concentrations may equilibrate rapidly or slowly, after weeks (Barrow 2008). Relative to the dynamics of the liquid phase, the solid phase can combine slow and fast processes,

$$\frac{\partial C}{\partial t}=\frac{\partial \theta {C}_{\ell }}{\partial t}+\frac{\partial \rho {C}_s}{\partial t}$$

(4)

with

$$\frac{\partial C_{s}}{ \partial t} :\,= \frac{\partial(C_{s,\text{fast}} + C_{s,\text{slow}})}{ \partial t} .$$

(5)

Slow sorption in rhizosphere models is described by ordinary differential equations (ODEs): ∂C_s,slow/∂t = g(C_ℓ, C_s,slow), where C_ℓ = (C_ℓ,1, …, C_ℓ, N) and C_s,slow = (C_s,slow,1, …, C_s,slow,N) are the interacting components (e.g. Darrah and Staunton 2000; Boghi et al. 2018; McKay Fletcher et al. 2020; Kuppe et al. 2022). The reaction term R of the transport equation would include the ad- and desorption kinetics relative to C_ℓ as function −g(C_ℓ, C_s,slow) (reversible reaction, Fig. 6). Additional ODEs need to be solved for C_s,slow. Because there are distinct ad- and desorption rates, at least one additional kinetic parameter is needed compared to the fast sorption (Fig. 3a). Each ODE needs an initial condition for C_s,slow, which is conveniently assumed to start in equilibrium with C_ℓ at t = 0, hence 0 = g(C_ℓ,initial, C_s,slow) gives the initial C_s,slow.

Fig. 3

Different ways to include sorption into the rhizosphere models. The equations also lead back to the applied assumptions. a The solid phase contains fast-, slow- or a combination of both processes. If the sorption reaction is not instant, a differential equation has to be solved. Remark: we did not write the θ and ρ for simplicity. b The soil buffer power can be interpreted as a “scaling” of the transport processes and determines the size of the instant equilibrating solid component. c Surface-plots of C_ℓ with b = 10⁷, 100, θ. Example parameters: Root radius r₀ = 0.05 cm, outer radius r₀ = 0.55 cm, Michaelis-Menten parameters, I_max = 2·10⁻⁷ μmol cm⁻² s⁻¹, K_m = 0.005 mM, C_min = 10⁻⁴ mM. Initial solute concentration 0.012 mM, diffusion in liquid D_ℓ = 10⁻⁷ cm² s⁻¹, θ = 0.3, soil tortuosity τ = 0.5, no advective water flux, v₀ = 0, no root hairs. Simulation over 14 days. d Cumulative uptake for constant soil buffer powers b. In this example, the uptake converged to its limit for b = 10⁷. The uptake, however, can be higher when including root hairs or higher I_max

Usually, solely fast sorption is assumed, i.e. C_s = C_s,fast. On the time-scale of C_ℓ, this is an instantaneous reaction. Steady-state (dC_s/dt = 0) is assumed and the sorbate concentration becomes an algebraic function of C_ℓ: the sorption isotherm C_s = f(C_ℓ) (Olsen and Kemper 1968). The derivative of the (steady-state) sorption isotherm is commonly substituted into the transport equation (see also Crank 1956),

$$\frac{\partial C}{\partial t}=\left(\theta +\rho \frac{d\;f\left({C}_{\ell}\right)}{d{C}_{\ell }}\right)\frac{\partial {C}_{\ell }}{\partial t}.$$

(6)

This method is unproblematic for the linear isotherm, but could be numerically problematic for non-linear isotherms. Most rhizosphere transport models, however, use a linear sorption isotherm with a slope dC_s/dC_ℓ = k, where k is the equilibrium constant (ratio of the ad- and desorption rate coefficients). Sometimes this equilibrium constant is called soil buffer power, hence, related to the concentration in the solid phase (Olsen et al. 1962; Olsen and Kemper 1968; Roose and Schnepf 2008; Roose and Kirk 2009). However, we use the definition of the soil buffer power related to total equilibrium concentration as b = dC/dC_ℓ (Nye 1966b; Nye and Marriott 1969; Barber and Cushman 1981; Kirk 1999).

Linear sorption is a reasonable approximation to simulate relatively low concentrations (Darrah 1991a) as it assumes that there are many unoccupied reacting sites. For example, Bhat and Nye (1973; Baldwin et al. 1973; Barber and Cushman 1981; Itoh and Barber 1983; Yanai 1994; Raynaud 2010) used the linear isotherm

$${C}_s=k{C}_{\ell },$$

(7)

where k = df(C_ℓ)/dC_ℓ is the equilibrium constant and obtained the expression,

$$\mathrm b=\theta+\rho k,$$

(8)

for the constant soil buffer power. This means that the soil buffer power determines the total concentration in the rhizosphere and plays an important role in replenishment and the shape of the solute concentration profile. If b > θ, the solid phase contributes to the total concentration. If b = θ, there is only liquid phase concentration (Fig. 3b), e.g. for nitrate (Darrah et al. 1983; Korsaeth et al. 2001; Kirk and Kronzucker 2005) or for non-adsorbed carbon (Darrah 1991b, 1991c).

Sometimes non-linear sorption isotherms may be a closer approximation, for example, when the sorption sites have been (partially) saturated by nutrients. Kirk and Nye (1985) used a Freundlich isotherm for sorption of phosphate fertilizer in a planar soil model, although, without a root. The Freundlich isotherm is a power-function, C_s = kC_ℓ^β, where β < 1 is a constant. It assumes that sorption is reduced at higher solute concentrations but does not cover extremely high solute concentrations at which all sorption sites are saturated. Kirk et al. (1999) fitted a Freundlich isotherm to a concentration profile of citrate but used a constant soil buffer power as an average of this sorption. The use of non-linear isotherms is often defended based on empirical observations but not mechanistically explained.

Microbial intra-cellular reactions are linked to solute transport in the soil through the uptake and release of substances by cells. In this way, microorganisms can affect local ion concentrations similarly to soil sorption. The soil buffer power constant and other implementations of sorption, therefore, might conveniently represent much more than just soil sorption. As such, sorption is effectively used as a fitting factor that encapsulates multiple abiotic and biotic soil processes.

Multiple solutes might compete, such that the adsorption is influenced by the occupation of sites. The saturation of one sorption site by a number (N) of adsorbates can be modeled by using the competitive Langmuir isotherm:

$${C}_{s,j} =\frac{k_j\;{\mathrm{s}}_j\;{C}_{\ell, j}}{1+\sum_{i=1}^N{k}_i\;{C}_{\ell, i}}\kern1em \text{for}\;\text{each}\;j$$

(9)

where C_s,j is the concentration in the solid phase j; s_j = n/n_j is the ratio of number of total available sorption sites per unit mass of soil, n, relative to the number of sorption sites one solute (of type j) occupies, n_j; and k_j is a Langmuir equilibrium constant (Schnepf et al. 2012). For each competing solute, a transport equation is solved. The transport equations of the solutes are then coupled via the sorption terms.

Solubilization is the desorption of an ion, C_s,1, by another solute, C_ℓ,2. It has been modeled by non-linear steady-state formulas of the type $C_{s,1} = k_1 C_{\ell,1} / \left( k_2 + k_3 C_{\ell,2} \right)$, where k₁, k₂, and k₃ are reaction rate coefficients. Examples include solubilization of zinc by deoxymugineic acid (Ptashnyk et al. 2011) and phosphate by citrate (Zygalakis and Roose 2012). Alternatively, a linear solubilization is sometimes used to model these (root-induced) solute interactions. A source (or sink) is added to ∂C₁/∂t of eq. (1), as a linear function of another interacting solute (see “diffusion of two interacting solutes”, Nye 1983). Thus, a solute concentration C_ℓ,1 increases instantaneously in response to a change in concentration of another solute C_ℓ,2. The total differential is used to specify an interaction coefficient (Nye 1983), which is then valid for a limited range of C_ℓ,2. This phenomenological approach was put into practice to model solubilization (Kirk 1999; Saleque and Kirk 1995). For example, phosphate may dissolve when the organic acid concentration (Kirk et al. 1999) or pH increases (Kuppe et al. 2022).

In contrast to the modeling of adsorption, described above, absorption as the accumulation of ions from solution into soil particles may be described by a so-called ‘dual-porosity’ model. It includes diffusion within soil particles (intra-aggregate diffusion), separate from diffusion among the surfaces of soil particles (Ptashnyk and Roose 2010; Ptashnyk et al. 2010; Zygalakis et al. 2011; Zygalakis and Roose 2012).

Chemical steady-state models have been coupled to transport equations (Geelhoed et al. 1999; Nietfeld and Prenzel 2015; Szegedi et al. 2008). For example, solubilization of phosphorus by citrate was realized by modeling the inner-sphere-complexations (Geelhoed et al. 1999) using a chemical steady-state model (Hiemstra and Van Riemsdijk 1996). Nietfeld and Prenzel (2015) modeled the root-induced pH and aluminum dynamics and the interaction of multiple ions to simulate the uptake of base cations by tree roots. Note that they estimated the diffusion coefficient ensuring electroneutrality (Nye 1966a). Espeleta et al. (2017) considered hydro-biogeochemical processes (water and solutes) for a non-growing single root without inter-root competition. They used the model MIN3P (Mayer et al. 2002) to include multiple chemical species in the rhizosphere for competitive soil cation exchange and diurnal plant-water rhythms. Gérard et al. (2017) also used MIN3P, but it was applied on a 2D soil column coupled to a root architecture model. The root-induced change in phosphate availability by change in pH and calcium concentrations has also been modeled as steady-state chemical reaction model without the coupling to transport equations (e.g. Devau et al. 2011). For an in-depth review of geochemical reactive transport models, we refer the reader to Nowack et al. (2006).

Application of the transport equation

Many rhizosphere models use the advection-diffusion-reaction equation to simulate various plants, soils, essential nutrients, and other solutes. These rhizosphere models can be grouped into models that only consider diffusion and those that include advection (Table 1). Barber (1962) stated that the dominant process in the rhizosphere is related to the ion concentration in the soil solution. Fried and Shapiro (1961) drew attention to the soil moisture content since, in dryer soil, advection might increase, whereas diffusion might decrease. Barber et al. (1963) stated that calcium, magnesium, and nitrogen are driven by advection while potassium and phosphate reach the root by diffusion. Diffusion is thought to drive phosphate transport, whereas advection was more important for calcium, magnesium, and potassium (Bouldin 1989; Williams and Yanai 1996). For widely spaced root segments, nitrate uptake was found to be sensitive to the rate of root water flux (McMurtrie and Näsholm 2018). However, this is a conclusion from a local, segment-based model that does not account for different root structures. Oyewole et al. (2017) studied the potential importance of advection experimentally in boreal forest soils. They conclude that there is a strong interaction between water and nitrogen availability where advection particularly contributes to nitrate transport to the root. We conclude that the concretization of eq. (3) varies for different soil types and solutes, and that the relative importance of diffusion versus advection is strongly dependent on the parameterization of the model.

Table 1 Rhizosphere model publications ordered by application and assumption on transport

Although often associated with phosphate uptake, the classical radial rhizosphere models have much broader applications. For example, Boghi et al. (2018) modeled plant uptake of uranium. The transport and consumption of dissolved oxygen was modeled (Højberg and Sørensen 1993) and later coupled to transport and uptake of nitrate (Kirk and Kronzucker 2005). Supply of oxygen (de Willigen and van Noordwijk 1984), and venting of carbon dioxide (Nye 1981; Kirk et al. 2019) and methane (Arah and Kirk 2000) by roots have been modeled. However, gases as sources or sinks in the rhizosphere system seem to be more common in ODE models without simulating transport (Blagodatsky and Richter 1998; Strigul and Kravchenko 2006; Faybishenko and Molz 2013).

To summarize this section, solute transport in the rhizosphere has been simulated by a diffusion-advection-reaction equation. Various published rhizosphere models, however, differ in (1) their diffusion coefficient, (2) inclusion or exclusion of the advection-term, (3) the way sorption and soil chemistry have been described, and (4) the number of solutes simulated.

The root in rhizosphere models

Most often, the root surface has been modeled as the inner boundary of the rhizosphere domain (rhizoplane). This is mathematically realized by a so-called ‘inner’ boundary condition (Fig. 1). The outer boundary is placed at the other end of the simulation domain and may not be equal to the width of the gradients formed and thereby the biological rhizosphere definition.

For rhizosphere models, the boundary conditions can be split into two groups. First (Dirichlet boundary conditions), concentrations prescribed on the boundary,

$${C}_{\ell}\left({r}_b,t\right)={C}_b,$$

(10)

and second (Neumann or Robin boundary conditions, respectively, when advection is included), fluxes prescribed (perpendicular) to the boundary,

$$D_e\mathrm b\frac{\partial C_\ell\left(r_b,t\right)}{\partial r}+\frac{v_0r_0}{r_b}C_\ell\left(r_b,t\right)=I_b.$$

(11)

where the subscript b denotes the inner or outer boundary, i.e. I_b is the flux across the boundary, and for the radial description as in eq. (3) r_b is either defined as the root surface r₀ or outer radius r₁.

In addition to the root surface forming the inner boundary condition, uptake or exudation can take place inside the simulated rhizosphere, for example, when root hairs are assumed to stick out into the rhizosphere domain (Bhat et al. 1976). In this case, the root is modeled as a sink or source reaction term (e.g. Gérard et al. 2017). Also, in non-spatial models (see the microbial section below), the root is often just a source or sink, e.g. of carbon (Table 3). Modeling the root as the inner boundary of the rhizosphere is most common, and therefore we next discuss different formulations and the associated assumptions.

Inner boundary conditions: Rhizodeposition and solute uptake by roots

For nutrient uptake, the inner boundary conditions can be: 1) fixed concentration (e.g. everything is taken up C_ℓ(r₀, t) = 0 or C_ℓ(r₀, t) = C_min at the root surface r₀); or 2) prescribed influx, I₀ > 0, or efflux, I₀ < 0, of the root at r_b = r₀ in eq. (11).

The so-called zero-sink condition, C_ℓ(r₀, t) = 0, is typically used for simulating phosphate uptake (e.g. Passioura and Frere 1967; Hoffland et al. 1990; de Willigen and van Noordwijk 1994b; Geelhoed et al. 1997). It is assumed that the root can take up the solute quickly and draw down the concentration at the root surface to a low (constant) level. Consequently, the uptake rate is limited by the transport of solutes to the root surface. Such models are numerically unfavorable since numerical errors can accumulate and the concentration can drift from the given value over time.

Alternative to the prescribed concentrations at the root surface is prescribed fluxes over the boundary. De Willigen and van Noordwijk (1994a) used a constant uptake rate, and Nye (1981) a constant release rate of protons at the root surface (and at the root hairs in this case). We further distinguish linear and non-linear functions of the solute concentration. In the earlier models (Bouldin 1961), solute uptake by a root, i.e. the inner boundary of the rhizosphere was assumed to be linear. Later it was assumed to be non-linear (Nye and Marriott 1969; Barber and Cushman 1981), see Fig. 2. Michaelis-Menten uptake kinetics, first introduced to the classical rhizosphere model by Nye and Marriott (1969), is arguably the most used non-linear inner boundary condition. Efflux was added to the Michaelis-Menten uptake a decade later (Claassen and Barber 1974, 1976; Barber and Cushman 1981), either by subtracting an efflux rate explicitly from the Michaelis-Menten influx or by setting a minimum concentration for uptake.

Michaelis-Menten kinetics are often considered to be mechanistic as it seems to mimic the workings of nutrient transporters in the cell membranes and thereby an upscaled version of micro-kinetic processes. The formulation fits data well (Nye and Marriott 1969; Claassen and Barber 1974; Van Rees 1994). This type of uptake kinetics is, however, empirical and not truly mechanistic since it does not describe apoplastic and symplastic pathways in the root cortex nor the summed kinetics of the various transporters, each with their own kinetics and membrane concentrations (Darrah et al. 2006). Upscaling from transporter density in a root surface area to the root segment uptake kinetics is still a knowledge gap and Michaelis-Menten kinetics remains the most used approach to model nutrient uptake (Griffiths and York 2020).

Outer boundary conditions: Inter-root competition and bulk soil interface

The rhizosphere first was described based on microorganisms that were more abundant close to the root than further away (Hiltner 1904). In contrast, classical rhizosphere models are based on a putative nutrient boundary or a mid-distance to nearby roots. If neighboring root segments have similar depleting strength, thereby influencing fluxes at this distance equally, inter-root competition is modeled by a zero-flux outer boundary condition, I₁ = 0 at r₁ in eq. (11), where no solute is flowing into or out of the modeled domain across the outer boundary (Cushman 1979a). The mid-distance to a neighboring root, r₁, is typically calculated from a local root length density, RLD = 1/(πr₁²) (Baldwin et al. 1973). This is geometrically not possible and thereby an approximation.

Furthermore, classical rhizosphere models assume no constraints on water fluxes (no root competition for water): over the rhizosphere distance, there is plenty of water, and there is no physical effect on the water flux, v, or the volumetric soil water content, θ. This results in a constant θ and effective diffusion coefficient, D_e. The water flux at radius r in the rhizosphere, 2πrv is equal to the water flux over the root surface, 2πr₀v₀ (conservation of water, Nye and Marriott 1969; Barber and Cushman 1981), whereas the nutrient flux is assumed to be zero over r₁ (Fig. 4). These are conflicting assumptions that are not easily resolved in a one-dimensional radial coordinate system, while in higher dimensions, there would be water influx from the sides or the top. Solutions for depletion of water in a radial rhizosphere exist, notably, the analytical solution by Schröder et al. (2008). However, this still provides no solution for the replenishment of water that typically occurs at a larger scale.

Fig. 4

a Schematic representation of the rhizosphere domain with symmetrical boundary and symmetric neighboring root. The green arrows illustrate the modeled advective solute flux that contradicts the actual physical flux, blue and red arrows. Assumption: $2\pi{r}_0{v}_0 = 2\pi rv$ (conservation of water), the water flux at r₀ is equal to the flux into the rhizosphere at r₁. b Diffusion only depletion profile of the classical rhizosphere model. c Advection-diffusion depletion profile, both with zero-flux outer boundary condition. d Simulated cumulative nutrient uptake of the root segment to illustrate how the uptake by the plant is influenced by the soil buffer power. Example parameters: Root radius r₀ = 0.05 cm, the outer distance is r₁ = 0.55 cm, Michaelis-Menten parameters, I_max = 2·10⁻⁷ μmol cm⁻² s⁻¹, K_m = 0.005 mM, C_min =  10⁻⁴ mM. Initial solute concentration 0.012 mM, root hair radius r_h = 0.0005 cm, root hair length l_h = 0.2 cm, the number of root hairs on the segment surface of unit length N_h = 1000, soil buffer power b = 25, liquid diffusion D = 10⁻⁷ cm² s⁻¹, θ = 0.3, soil tortuosity τ = 0.5, water flux velocity ${v}_0 = 0\;\text{or}\;{v}_0 = {10}^{-6}\;\text{cm}\;\mathrm{s}^{-1}$, respectively

Less conflicting with respect to water would be the use of a far-field boundary (Roose et al. 2001; Passioura and Frere 1967), where a constant solute concentration is given at the outer boundary, equal to the initial condition in bulk soil (C → C₀, r → ∞ for t > 0), i.e. a Dirichlet condition at a reasonably large outer radius, r₁, relative to the depletion zone, “far” away from the root surface. The far-field boundary approach, however, ignores root competition completely and gives similar results to placing the outer zero-flux boundary itself far away from the root. A Dirichlet condition (no inter-root competition) is applicable to one solute with relatively high soil buffer powers.

Root competition for nutrients, or facilitation by exudates, is more likely to occur when the actual depletion or exudation zones are relatively wide and occurs more rapidly for mobile components like nitrate, potassium, or protons and hydroxide ions (pH). Unless roots are very close together, (inter-)root competition may not influence phosphate uptake (Darrah et al. 2006) since phosphate travels slowly through the soil due to stronger sorption (e.g. Kuppe et al. 2022). Postma et al. (2014) computed from simulated 3D root system architecture that the overlap of phosphate depletion zones in a maize monoculture is less than 14%, of which the most overlap occurred among roots of the same plant at the branching points.

Solute uptake by root hairs

Root hairs are important for solute uptake as they increase the root surface. We consider four approaches to representing root hairs in models. Listed with increasing level of detail, the root hairs have been modeled by: (1) increasing the root radius (Passioura 1963; Nye 1966b); (2) including a reaction term using a steady-state depletion profile (Itoh and Barber 1983; Bhat et al. 1976); (3) using the homogenization theory (Leitner et al. 2010a; Zygalakis et al. 2011; Zygalakis and Roose 2012); and (4) describing their geometry spatially explicit (Geelhoed et al. 1997; Keyes et al. 2013).

Including root hairs as increased root radius (approach 1) assumes that the effective radius of uptake is the root radius plus an average root hair length and ignores the uptake from in-between the hairs. It assumes that the root hair tips are the primary way to achieve soil contact and that they do so at an average distance from the root surface. Passioura (1963; Nye and Tinker 1977) called this an “equivalent cylinder”. To approximate the total surface area, Passioura (1963) gave this new root radius twice the average root hair length. For example, Gardner et al. (1983) and Kirk (1999) just extended the inner boundary (root radius equals the length of root hairs). Imagine a root with such dense hairs that only the root hair tips can contribute to uptake, and no nutrients move in-between the hairs towards the root surface. Nye (1966b) and Huguenin-Elie et al. (2003) modeled the root hair effect on the solute concentration in a so-called ‘hairy zone around the root’ and calculated uptake for both hairy and non-hairy zones separately. Although simple, the approach is likely to underestimate uptake.

Including a reaction term using a steady-state depletion profile (approach 2) models a sink over the length of the root hairs (r = r₀ to l_h) in the transport equation. The uptake is calculated from the solute concentration at the root hair surface, C_rh. This C_rh is obtained by steady-state diffusive flux orthogonally between the root hair radius r_h and an average C_ℓ(r, t), as a Dirichlet boundary at the mid-distances, r_h1, to neighboring root hairs (Fig. 5). The reaction term thus becomes a function of C_ℓ(r, t) for r ≤ r₀ + l_h, where l_h is the length of the average root hairs. Note that in steady-state, the time gradient is zero, but spatial gradients can be present. The transport equation towards r₀ is still transient, and when numerically integrated, the uptake in steady-state by root hairs is updated per time- and spatial step.

Fig. 5

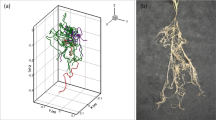
Root hairs. a Michaelis-Menten uptake, including efflux via $\displaystyle{C}_{\ell}^{\ast}:= {C}_{\ell }-{C}_{\min}$. Zero-flux at outer boundary r₁. The value ${r_{\mathrm h1}}$ is the mid-distance between root hairs, e.g. pairwise equidistant, ${r}_{\mathrm h1}=\sqrt{r\pi /\left(2{N}_\mathrm{h}\right)}$. For root hairs, the orthogonally radial steady-state diffusion can be used (derivation Baldwin et al. 1973), the flux over the root surface, at r₀, is transient. b Numerical discretization of the 1D radial coordinate system: a root segment of unit length gives the virtual cylinder. Hence, the discretization is often shown as hollow cylinders. c Example depletion profile of a nutrient in soil solution resulting from the model outlined in (a, b) after Itoh and Barber (1983). Parameters as in Fig. 4b but with b = 80. On the left: Pictures of wheat roots (from field) were taken by M. Watt at the CSIRO Black Mountain Microscopy Centre

The steady-state equations that are used are derived in Baldwin et al. (1973) with and without advection for a single root. Bhat et al. (1976) modeled linear uptake by root hairs and used the diffusion equation (v = 0) since it is commonly assumed that the root hairs do not take up water. Itoh and Barber (1983) included root hairs after Bhat et al. (1976) but replaced linear uptake by Michaelis-Menten kinetics.

The approach assumes there is no competition among hairs and that, consequently, the outer boundary concentration is constant and far away from the root hair surface (${r_{\text{h1}}}^{2} \gg {r_{\text{h}}}^{2}$). With this assumption, the solution of the steady-state integration (eq. iii, Baldwin et al. 1973) can be simplified by collecting terms because ${r_{\text{h1}}}^{2}/({r_{\text{h1}}}^{2} -{r_{\text{h}}}^{2}) \to 1$. These assumptions may be invalid for relatively densely spaced or thick root hairs. The inclusion of root hairs as a reaction term is macroscopic and couples different spatial scales while ignoring the hairs as a physical boundary in the soil. It avoids using C_ℓ for uptake by hairs directly and accounts for root hair depletion, C_rh < C_ℓ, and holds in the simplified version if r_h < r_h1/1.65. We suggest using the non-simplified version (eq. iii, Baldwin et al.1973) as applied by Kuppe et al. (2022).

The homogenization theory (approach 3) is used to average spatially heterogeneous equations for root and root hair geometries and has similarities to approach (2) because it computes a sink for hairs (model 1 in Leitner et al. 2010a). Both approaches (2) and (3) have a sink term in the macroscopic transport equation and no sink beyond the root hair zone. Finer coordinates are scaled by l/L to coarser coordinates: micro-structures at a microscopic scale l, the inter-hair-distance, are incorporated in the macro-structure at macroscopic scale L, the axial length of the cylindrical root segment ($l \ll L$ required). Leitner et al. (2010a) used Cartesian coordinates, and thus the distances between the root hairs, 2r_h1, do not increase further away from the root surface. Also, if the solute is rather diffusive and the depletion zone is not narrow, a radial coordinate system seems more applicable. In the Cartesian coordinates, the distance at the surface r₀ needs to assume to be comparable with the distance between the root hair tips at r₀ + l_h. That means the modeling error increases with root hair length. The method of homogenization was also applied to root hairs and diffusion of solutes within and between soil particles of sorbing soils (Zygalakis et al. 2011) and dense cluster roots (Zygalakis and Roose 2012).

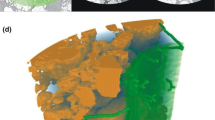
In describing geometry spatially explicit (approach 4), Geelhoed et al. (1997) address root hairs as the physical boundary in a 3D cylindrical simulation of the rhizosphere with root hairs. The root and root hairs were treated together as one geometry. However, the volume of the root hairs was neglected, and root hairs were still assumed straight with equal length. Geelhoed et al. (1997) assumed that roots and root hairs have zero-sink boundary conditions and phosphate transport by diffusion. They added root hairs to a model by Hoffland et al. (1990) and compared this zero-sink diffusion-reaction model in 1D radial coordinates with a 3D cylindrical version, (diffusion in r, φ, z direction) and concluded that the differences in cumulative uptake, simulated by the 1D and 3D models were usually less than 15%, with the largest deviations after the longest run times of scenarios with low soil buffer powers. More recently, a three-dimensional simulation of root hairs in the rhizosphere was implemented with even greater detail by including the pore-scale soil structure. Keyes et al. (2013) and Daly et al. (2016) applied a finite element method to real soil-root synchrotron images and calculated uptake by root hairs using Michaelis-Menten kinetics. They conclude that root hair uptake in macroscopic rhizosphere models might be overestimated and depends not only on root hair morphology but also soil structure.

Root growth and development

New root cells are formed at the root apex and from thereon develop over time. This development includes cell elongation and differentiation, notably the formation of anatomical structures such as xylem, phloem, endo- and epidermis, pericycle, and root hairs from the epidermal cells. Root growth and development have been introduced in various ways. Most models define an absolute space reference (so-called Eulerian representation), where age and activity of the root might be modeled as time-dependent functions, for example, time-dependent exudation rates (Zelenev et al. 2000).

Alternatively, a moving root tip (so-called Lagrangian representation) can be taken as a frame of reference. In this representation, the soil is quasi flowing through the domain as it moves with the root tip. This is achieved by an additional vertical advection term parallel to the growth direction. This advection term is not related to water flow but to the velocity of the root (2D, Kim and Silk 1999). Such a moving reference frame proved useful for simulating the activity of bacteria that attach to the root and ‘travel’ with the velocity of root elongation (1D, Dupuy and Silk 2016), as observed by Watt et al. (2003).

Besides longitudinal growth, radial thickening (secondary growth) may be considered. This results in a moving- or free inner boundary. Moving outer boundaries can be used to simulate changes in root length density (RLD) that occur over time as the root system grows (e.g. Reginato et al. 1990; Reginato et al. 1993; Huguenin-Elie et al. 2003; Crank and Gupta 1972). These moving boundaries become especially apparent in root architectural models, which do not make assumptions about homogeneous root length distribution. For example, Postma and Lynch (2011) implemented both a moving inner boundary, related to secondary thickening, as well as a moving outer boundary, related to the local RLD, computed from the simulated growing root architecture. Architectural root system simulations can be used to scale-up the rhizosphere models (assumed more or less locally independent), for example, by integrating the simulated nutrient uptake over the root system (Postma et al. 2017; Mai et al. 2019). The root system length, and its expansion, are often used to upscale rhizosphere models to compute whole plant or crop nutrient uptake. The upscaling methods are beyond the context here but are addressed shortly in a later section.

Modeling microorganism activity

Microorganisms can be modeled from the individual cell to the whole community using different model representations (Song et al. 2014). In the rhizosphere context, microorganisms are typically modeled as trait-based ecosystems, which lump functional properties together at the community level. Hence, microorganisms were modeled by time dynamics (decay, turnover, and release) of the substrates (solutes) they consume or produce (Toal et al. 2000). Population dynamics of each species were modeled by integrating growth and death rates over time, typically defined as a function of substrate concentrations and population size. In general, the motility of microorganisms is not considered in the rhizosphere modeling literature, with one exception (Dupuy and Silk 2016), where the aim was to investigate bacterial attachment and colonization on the root surface, as visualized and described by Watt et al. (2006a, 2006b). We discuss motility in a section below as it is more common in models of microorganisms outside the context of the rhizosphere but, in our opinion, should not be overlooked.

Substrate decay, release, or turnover

The change in population density over time of a network of components (C_ℓ,i in Fig. 6) used in microorganism models can be described as an ODE system, dC/dt = R(C) (vectors: C and R, Fig. 6), made up of growth and death rates, which are typically substrate-dependent. In a rhizosphere context, substrates might be root exudates, as carbon source of which the bacteria feed (Raynaud et al. 2006; Toal et al. 2000). The reactions of the cell metabolism are catalyzed by enzymes. Enzymes have maximal turnover rates and are often activated or inhibited by other effectors.

Fig. 6

Modeling framework. Steps to construct a rhizosphere model: a Models can be characterized by concepts of considered physical entities and their processes. b Mathematical models realize the conceptual model, with spatial change (dark blue), time dynamics (blue), and reaction terms (red). If present, chemotaxis is related to the gradient of an attractant or repellent, C_j, and can be substituted for V. The depicted diffusion is called motility in the case of microorganisms (a pseudo-component) and is the macroscopic formulation of random motion. c Full mathematical description: Define initial and boundary conditions, choose a coordinate system and dimension (implying assumptions). d Implementation of the mathematical model aims to find a solution within computational error bounds. Analytical solutions are often not available, and generally, a numerical solution is used. e Simulations are used to address research questions. f Model development becomes an iterative process if results lead to changes in earlier decision steps

Decay terms have been modeled as first-order rate equations (irreversible reaction, Fig. 6), e.g. as exponential decay (Raynaud 2010; Zhu et al. 2016). Non-rhizosphere models have developed the ideas of exponential decay further. For example, Yang and Janssen (2000); Sierra et al. (2012); Sierra and Müller (2015) modeled the decay of organic matter, also scaling the rate constants with temperature and moisture functions. Zelenev et al. (2006) stated that temperature and moisture fluctuations are particularly important for long-term predictions of mineralization. Water content is directly coupled to the decomposition of soil organic matter. The time scale is arguably longer than in the usual rhizosphere models predicting nutrient uptake (Manzoni and Porporato 2007, 2009). When including microbial activity, the gas phase or temperature dependencies may be important. Temperature is known to affect, among others, diffusion coefficients, growth rates, and kinetic parameters and, as such, seems important (Carter and Lathwell 1967; Michaletz 2018). However, to our knowledge, existing rhizosphere models did not allow for the effects of temperature, and hence, assume a time window with an average temperature, a short enough growth period, and no day-night temperature cycle.

Population dynamics of microorganisms in the rhizosphere

The population dynamics of microorganisms in the rhizosphere resulting from several organisms competing over carbon, oxygen, and root exudates have been modeled by non-linear ODE systems (Faybishenko and Molz 2013; Strigul and Kravchenko 2006; Kravchenko et al. 2004). To outline the structure and functionality of such models, we look at the model by Zelenev et al. (2000). Here, a system of two ODEs describes the time dynamics of bacteria, model component C₁ ≔ X [μg cm^-3 soil], and substrate, C₂ ≔ S [μg cm^-3 soil]. The growth and death rates of bacteria are non-linear functions, μ(S) and δ(S) [h^-1], of the substrate concentration. In this model, the substrate input rate, F_E, into the system is a time-dependent function. They assumed that the exudation rate declines exponentially along the length of the root. The mathematical formulation is,

$$\frac{\partial X(t)}{\partial t}=\left(\mu(S)-\delta(S)\right)X(t)$$

(12)

$$\frac{\partial S(t)}{\partial t} = -\left(\mu(S)/Y + K_{r} \delta(S) \right)X(t) + I(t),$$

(13)

with system input, I(t) ≔ BGF + F_E(t), where BGF defines a constant (background) substrate influx [μg h^-1 cm^-3], F_E(t) is the exudation rate [μg h^-1 cm^-3], K_r is the fraction of dead biomass recycling to substrate [−], Y is the yield coefficient for bacteria [μg carbon μg^-1 carbon], and 

$$\mu (S)={\mu}_{\max }\frac{S}{K_S\theta +S}$$

(14)

$$\delta(S)={\delta}_{\max }\frac{K_d\theta }{K_d\theta +S}$$

(15)

$${F}_E(t)={E}_{\max }\exp \left(-{E}_{\mathrm{T}}t\right)$$

(16)

where μ_max is the maximal relative growth rate of bacteria related to substrate concentration [h^-1], K_S its half-saturation constant [μg cm^-3 soil solution] (μ(K_S) = μ_max/2), θ the volumetric water content, δ_max is the maximal relative death rate of bacteria [h^-1], K_d its half-saturation constant [μg cm^-3 soil solution], E_max is the maximal exudation rate [μg h^-1 cm^-3] and E_T is the exudation time constant [h^-1]. Eqs. (14) and (15) are Monod equations, mathematically equal to Michaelis-Menten kinetics (Monod 1949; Liu 2007).

This model can be expanded by chaining the Monod equations for additional substrates. Thus the growth and death rates are functions of the environment. Zelenev et al. (2000, 2006) ignored diffusion and advection of the substrate and bacteria in the rhizosphere. Models that include the diffusion of substrate radially away from the root are presented by Newman and Watson (1977), Darrah (1991b), and Sung et al. (2006). The transport of the substrate is modeled analogously to the concept of solute transport in soil described in the previous section. A partial differential equation (PDE) describes the diffusing substrate and is coupled to an ODE for the bacteria living off that substrate. A spatial distribution (gradient) of bacteria is given owing to the substrate profile that gives local differences in growth rates. This model assumes bacteria do not move but only react with a certain point in space, which is tricky because, at an (infinitely small) point, there is practically no mass that can be absorbed as a substrate. The substrate is therefore always taken from a certain environment. Its concentration would have to be correctly described using Dirac distributions (Kondrat et al. 2016). Spatial discretization conveniently solves the volume issue but not the homogeneity within a volume.

Motility of microorganisms

Microorganisms in soil models refer, among other organisms, to bacteria (Keller and Segel 1971b; Lauffenburger et al. 1982; Dupuy and Silk 2016), amoebae (Keller and Segel 1970, 1971a), and even relatively large nematodes (Feltham et al. 2002). Few rhizosphere models consider the motility of microorganisms, but the broader literature on bacteria speaks about the motility of bacteria based on various mechanisms (Kearns 2010). Motility may be directed, especially through advection and chemotaxis, or with random direction if the microorganism cannot respond to chemo-gradients. At the cell level, this is described as tumbling. Macroscopically, the movement of the cells can be described by a model with a certain diffusion coefficient. Principally all cells can appear mobile as particles with D ≈ 10^-9 cm² s^-1 (assumed order, Lauffenburger et al. 1982). The free organisms move along gradients of chemo-attractants towards the root (chemotaxis, e.g. to carbon exudates). For the radial transport on the root surface, other than longitudinal movement, chemotaxis was found to be important (Dupuy and Silk 2016).

The motility of the cells is described by an equation similar to the transport equation for solutes, except for the additional chemotaxis. Adler and Dahl (1967) and Segel et al. (1977) described motility using an effective diffusivity parameter distinct from chemotaxis (motility coefficient, here D – we used their definition in Fig. 6).

Thus, although the simulation of microorganisms is largely developed in the literature separately from that of solutes in the soil, at the rhizosphere level, we can recognize very similar transport processes. We can thereby consider solutes, substrates, and microorganisms as components that may be summarized in a framework for categorizing rhizosphere models and simulated by a generalized transport equation.

Collective framework: A general mathematical structure encompassing concepts of rhizosphere models

Despite the plurality of the different rhizosphere models for various applications presented in the literature, the models draw on similar concepts (physical, biological, chemical) mechanistically and phenomenologically. They thereby share similar structures that fit into a general modeling template. Hence, new models can be developed using a typical four-step workflow in which the concept development, mathematical model, software implementation, and simulation studies proceed each other. Figure 6 synthesizes the previously reviewed rhizosphere models and other model components into a generalized mathematical framework. Experiments would suit the modeling according to this framework and vice versa (structure and parameters).

Conceptual model

The template in Fig. 6 highlights the commonalities among rhizosphere models as well as the simplifications by omissions of processes. It exposes prior implicit assumptions of zero gradients, zero parameters, or constant values. Expanding this general model increases complexity. Despite the similarities among the mathematical models, the generalized template leaves ample room for varying assumptions and concepts like different phases (e.g. adsorption, desorption) and chemical reactions (e.g. decay). This template shows N coupled solid and liquid phase components. Additional M components may specify microbial biomass in soil (e.g. gram carbon or cells), which are usually modeled as non-sorbed (e.g. Newman and Watson 1977; Darrah 1991b, 1991c; Zelenev et al. 2000; Dupuy and Silk 2016).

The establishment of the conceptual model (Fig. 6a) starts with selecting the components. That is, what solutes or microorganisms are assumed to be of importance to the processes of interest in the rhizosphere. Simplifications here might leave out, for example, advection or spatial change. Complications might specify coupling among the components. The number of components present in the rhizosphere is in reality very large and must be reduced drastically to have a sufficiently simple model for which the parameter values can be determined (Fig. 7).

Fig. 7

The selected references from Tables 2, 3, and 4 are the numbered dots, which are colored by their number of main components. The grid shows a space-complexity pattern, and visualizes the dimensional realizations

Mathematical model

We elaborate on parts (b) and (c) of the workflow in Fig. 6, where the hypotheses on involved components (C_ℓ,i, C_s,i) and processes (Fig. 6a) are realized in a mathematical model. In rhizosphere models, the space coordinate is usually r, along the radial axis orthogonal to the root surface. In some publications, the z-direction longitudinal to the root axis is considered (Darrah 1991c; Kim and Silk 1999; Dupuy and Silk 2016), and rarely all three space coordinates.

A mathematical model as a realization of concepts can be presented by a system of coupled equations with initial and boundary conditions and is thereby extensible. The classical rhizosphere models can be expanded to include interactions among rhizosphere components through the reaction terms. For example, Schnepf et al. (2011), Schnepf and Roose (2006) added mycorrhizal fungi via a sink term – similar to the inclusion of root hairs.

The reaction term in rhizosphere models is of special importance since coupling between various PDEs and ODEs is usually achieved with this term, which is arguably the most variable part (Fig. 6b). In rhizosphere modeling, the time dynamics of the bacteria becomes the reaction part in the associated substrate transport PDE. For example, growth and death may be functions of a substrate and population size. If only reaction terms are considered (rates), we obtain ODEs in time (D$\nabla$²C = 0, v$\nabla$C = 0). ODE models assume that the spatial derivatives are negligible or simply not of interest.

Different orders of magnitude of time scales are coupled when steady-state processes are included in the transient equation for C_ℓ. We gave examples of sorption, which either can be simulated as a slow process or assumed to equilibrate instantaneously. We reviewed sorption as an important example of a reaction term that by itself can be formulated as an ODE and reversible reaction (Fig. 3).

Besides realizing interactions among components by coupling via reaction terms, coupling of gradients is possible, which we can call direct coupling, as the state variable of one model (e.g. fluid velocity) directly enters the other without integration (e.g. in the advection term). A prominent example is water flow, simulated with the Richards equation (not part of this framework) and coupled to a PDE for solute transport via the water potential gradient-dependent flow rate. The soil water flux densities are used to compute the advective transport of solutes.

Inclusion of processes and components is not always achieved by including extra transport equations and coupling terms. As many processes appear similarly at the spatial and temporal macroscale, they might be implied in one term or parameter. For example, the soil buffer power, b, avoids having the adsorbed C_s as explicit model component by assuming C_s proportional to C_ℓ.

We summarize that the advection-diffusion-reaction-motility equation in its general form can encompass most rhizosphere models, and most future rhizosphere models may be represented by a coupled system of advection-diffusion-reaction-motility PDEs.

Software implementation

The common rhizosphere PDE is a parabolic initial-boundary-value-problem. Those general classifications help to choose the numerical method for solving the equation (Fig. 6d). The numerical method is important for accuracy of the solution, but often the method used is not mentioned or only minimally described in the literature on rhizosphere models (Tables 2, 3, and 4). Most of the classical non-modular 1D rhizosphere models are integrated with the Crank-Nicolson method (Crank and Nicolson 1947), which is neither the fastest nor the most accurate method, in particular when the equation is stiff (Kuppe et al. 2021). Stiff problems occur, for example, when the effective diffusion is rapid (e.g. for nitrate) as the gradients of the solute profile are smooth, but fluxes can still be high. Equation (1) is generally solved numerically by discretization of the rhizosphere domain (e.g. Figure 5b) but is sometimes treated approximately analytical (Cushman 1979a, 1979b, Cushman 1980a, 1980b; van Genuchten 1981; Roose et al. 2001; Roose and Kirk 2009; Ou 2019). We advocate the use of numerical software packages and the use of suitable solvers as they are available for many programming languages.

Table 2 PDE models

Table 3 ODE rhizosphere models

Table 4 Coupled PDE-ODE models

Simulation studies

Once implemented, the model might be applied to several studies using different parameters (Fig. 6e). Parameters may be estimated by direct measurements, literature values, or calibration (e.g. Kuzyakov and Xu 2013; Blagodatsky et al. 1998). A model can be evaluated, for example, by comparison against other versions or measured values to test a hypothesis (model selection). Kirk et al. (1999) compared rates of citrate secretion needed in their model to achieve a sufficient phosphate solubilization effect against measurements. Sensitivity analysis questions how sensitive the model results are to changes in the model parameters or input values. Thereby, it elucidates feasible simplifications and identifies key processes that describe most of the variance in the results. Mathematically, sensitivity to a variable requires differentiation of the model for the variable. However, in rhizosphere modeling, sensitivity analysis has been achieved by comparing simulation results for which the parameter was varied. For example, Kuppe et al. (2022) estimated the relative importance of model parameters for phosphate uptake by upland rice in strongly sorbing soil, where uptake became sensitive to r₁ when small enough (increasing RLD). Silberbush and Barber (1983) investigated phosphate uptake by maize, showing that uptake was insensitive to C_min, r₁, and v₀. Hence, in this case, uncertainty in these parameters was not of concern, and the model could be reduced by excluding advection and setting C_min = 0.

Connecting models to experimentation

Experimentation is needed for parameterization, validation, and verification of results (e.g. Claassen et al. 1986; Zelenev et al. 2000; Strigul and Kravchenko 2006). The model is calibrated and validated for a certain parameter range that is also determined by the applied assumptions, like the soil buffer power, which is constrained by soil conditions. Toal et al. (2000), for example, discussed the challenges in calibration of rhizosphere carbon flow models. They found that rhizodeposition is not well defined, experimental data sets are missing essential information, and often use non-comparable units.

Sometimes validation of models comes from experiments where the medium was stirred or rapidly diffused (roots in hydroponics or agar), such that spatial variation is negligible. Therefore, ODE models can be applied to that data. Model validation, however, is often understood as a demonstration that the model predictions are close to measurements, and this may provide circumstantial evidence that the model can be used for predicting and sensitivity analysis. This kind of model validation does not inform the researcher about the validity of the assumptions or concepts. A model represents a theory or hypothesis. Similar to the null hypothesis in statistics, we cannot exclude other processes or explanations just from matching the model output to data only. It is important to validate as many state variables as experimentation permits. For example, when citrate concentrations are simulated to predict phosphate transport and uptake, the predicted citrate concentrations can be validated. Predictive models can, however, help to expand mechanistic understanding. They are especially helpful in the falsification of hypotheses by excluding the importance of certain processes (‘loop back’ in the modeling cycle, Fig. 6).

Final remarks and future directions

Knowledge-gain by interpretation of experimental or in-silico results relies on the assumptions and concepts made. We reviewed how various rhizosphere processes have been modeled across the disciplines of soil science, botany, and microbial ecology. The classical rhizosphere models have their origins in the works of Bouldin, Barber, and Nye (Fig. 2). The majority of rhizosphere model publications are on the diffusion and uptake of phosphorus (Table 1). Many of the spatially explicit rhizosphere models ignore microorganisms and mycorrhizal fungi (Fig. 7). In contrast, the more ecological-oriented models generally ignore space: the motility of microorganisms and the structure of the root system (Fig. 1).

Limitations of the classical rhizosphere models

In the past, the radially symmetrical rhizosphere models ignored root morphology and focused on solute transport to the root. The root was represented as a cylinder, and root hairs were often not modeled. A boundary condition represented the root, and the soil was hitherto considered the most limiting factor for plant nutrition (see zero-sink boundary condition, i.e. transport in soil limits the uptake of nutrients and is not regulated by the root), and the endo-rhizosphere (inside the root) was ignored for reasons of simplification. Solute concentration is considered to act as a signal influencing the kinetic uptake parameters. For example, a Michaelis-Menten constant K_m of ion-carrier complexes in plant roots for different concentrations and types of solutes. The mechanisms are still poorly understood and constant kinetic parameters are assumed in time. Alternatives are discussed by Griffiths and York (2020).

The conventional segment-based rhizosphere models are local and consider a virtual root cylinder of unit length. This implies two assumptions about the larger root system and soil scale: (1) that the root only responds locally, and (2) that there are homogeneous soil conditions in the rhizosphere, including axial symmetry.

In the assumption (1) that the root responds locally, the inner boundary conditions are functions (e.g. Michaelis-Menten type) of the solute concentration at the root surface, C_ℓ(r₀, t). This allows for local responses but ignores systemic plant regulation to the local uptake. Different extensions of Michaelis-Menten type uptake according to their time scales and plant feedback mechanisms appear possible, e.g. nitrogen regulation on leaf photosynthesis (Le Bot et al. 1998).

Combining rhizosphere models to a growing root and whole root systems is addressed in functional-structural plant models. The homogeneous soil conditions do not have to apply root-system-wide if the classical models are implemented in a heterogeneous root architecture model. The single segment models, each with a local rhizosphere, are coupled to root architecture and, thereby, upscaled (Postma and Lynch 2011; Dunbabin et al. 2013). Integration of a growing root over time may estimate nutrient uptake. Three-dimensional root architectural models are used in combination with the one-dimensional radial transport models (e.g. Postma et al. 2017). However, simplified upscaling has also been achieved by integration of root growth functions (e.g. exponential or logistic, Cushman 1979a; Barber and Cushman 1981; Itoh and Barber 1983). This simple scaling up to the plant scale smooths the variation over time as root systems are at any moment in time populations of younger and older root segments (Kuppe et al. 2022). Modeling approaches for upscaling rhizosphere processes to the whole-plant scale were reviewed by Darrah et al. (2006).

With the assumption (2) that there are homogeneous soil conditions in the rhizosphere, including axial symmetry, rhizosphere models not only lack connection to the larger scale (assumption 1), they also assume homogeneity at lower scales, notably, the pore structure of the soil. Adjusting an analytical formulation of steady-state for nutrient and water uptake, de Willigen et al. (2018) addressed partial root-soil contact in the rhizosphere. Helliwell et al. (2019) observed an increase in soil porosity in the direct vicinity of a root, where the deformation of the rhizosphere was temporally and spatially heterogeneous due to root growth. The pore-scale soil-packing influences the geometry of root hairs, which may be important in low moisture conditions and for strongly sorbed nutrients (Keyes et al. 2017; Koebernick et al. 2017). Recent studies, however, show that macroscale averaging of diffusion was valid for most scenarios (Masum et al. 2016; Daly et al. 2018).

At the rhizosphere scale, water distribution and its flow rate are usually assumed homogeneous as well. A lot of the processes in the rhizosphere are influenced by water (see review by Vereecken et al. 2016). Macroscopic water flow and solute transport to the local scale have been modeled (Bar-Yosef et al. 1980; Roose and Fowler 2004; Tournier et al. 2015; Mai et al. 2019; Fang et al. 2019; Ruiz et al. 2020). However, gradients in water potential around roots are yet a challenging topic (Carminati et al. 2016; Schwartz et al. 2016). Some have simulated the effect of root exudates and soil pore structure on water distribution in the rhizosphere (Naveed et al. 2018; Cooper et al. 2018; Aravena et al. 2011, 2014). Recently, Landl et al. (2021) showed the effect of radial changes in bulk density and exudate concentration (mucilage) on rhizosphere water flow and root water uptake, and as such, the rhizosphere models may need updating. Root-induced feedback can be implemented into the suggested framework, for example, as coupling to diffusion or reaction rates. Nietfeld and Prenzel (2015) coupled the diffusion coefficient to ion concentrations in the soil solution, and Kuppe et al. (2022) coupled soil sorption rates to root-induced pH change.

Parameterization is challenging

The mechanistic modeling approach has led to potentially redundant processes. Therefore it is important to fix (using measured data) as many parameters as possible before fitting or estimating other unknown parameters. For example, the transport equation of the classical rhizosphere models, eq. (3) is over-parameterized for the solute concentration, C_ℓ. The same solute concentration profile can be obtained over the soil buffer power, with fixed effective diffusion coefficient and scaled maximal influx rate, I_max (in case of a Michaelis-Menten inner boundary), and v₀, respectively (Kuppe et al. 2021). Despite the depletion profiles of C_ℓ being the same in this case, the uptake is not. An increase in soil buffer power increases the total concentration if the solute concentration, C_ℓ, is kept constant, and despite the (1/b)-th slower transport rates, the root segment would have a higher cumulative uptake because of the instantaneous replenishment from solid phase to liquid phase (Fig. 3d). This implies higher total C and higher uptake eventually with the same C_ℓ. Similarly, functional redundancy among microbes is an important topic in soil ecology. If we want to have mechanistic models to understand plant nutrient acquisition by roots and its interactions in soils, over-parameterizing of the model seems inevitable. This means we need measurements that distinguish observed phenomena and provide a basis for parameterization of modeled processes as well as validation of intermediate outcomes.

Extending models

Rhizosphere modeling draws on concepts of transport developed for models at the larger agrosphere scale. Recently, hydro-biogeochemical modeling includes multiple important components, in particular soil hydraulics and chemical reactions. The coupled chemical complexation models are in steady-state, and therefore, the equilibrium constants from databases are approximations to rhizosphere conditions. However, the complexity of the rhizosphere and the coupling of models that are developed for different scales and validation by data remains challenging.

On a finer scale, there is the modeling of metabolic networks and microbial communities (Perez-Garcia et al. 2016), which eventually will be needed for a mechanistic understanding of the rhizosphere. As mechanisms are often poorly understood, there is a need for joint research of experiments in soil and in-silico. This is especially apparent for the emerging topic of plant growth-promoting bacteria (PGPR) (Strigul and Kravchenko 2006; Rosier et al. 2018). Okutani et al. (2020) demonstrate this nicely by modeling rhizosphere solute and water distribution, exudation of daidzein by a single cylindrical root, and combining the analysis with the extraction of bacterial DNA showing different community compositions. To our knowledge, there is no rhizosphere model about hormones, albeit experimental research. We suggest the bio-phase (e.g. bacteria) as a mostly overlooked rhizosphere model component. Future rhizosphere models may include both more ecto-rhizosphere factors and the biological endo-rhizosphere factors.

Conclusion

Concepts and foundations of rhizosphere modeling build a base for biologists and modelers in trait discovery and application to plant and soil ecosystems. Assumptions of the processes in the rhizosphere ecosystem are a crucial part of modeling and are shown in this review. We conclude that despite the large variation in rhizosphere models and model applications, most models can be represented as specific implementations of a more general rhizosphere modeling framework (Fig. 6). This general modeling framework may be used as a starting point for developing new rhizosphere models, which may address current gaps, including (1) a need for extended linking and coupling between soil ecology, physics, and chemistry; and (2) consideration of microorganisms, their motility and spatial relevance in soil ecology models. To connect experimental systems and theoretical concepts, we advocate a workflow for future rhizosphere model development in which researchers distinguish the conceptual model, the mathematical model, and model implementation from studies that apply models to particular research questions.

Glossary

Classical rhizosphere model(s)

The classical rhizosphere models consist of a 1D partial differential equation (PDE) for transport of a single solute radially symmetrical to a single root segment of unit length. They can differ in the applied boundary conditions.

Concepts (Conceptual Model)

Models do not need to be expressed mathematically in the beginning; they can be conceptualized first. The concepts can be communicated using mathematics.

Dynamics

A model considers dynamics when transient (physical, chemical, biological) processes are included, i.e. time-dependent phenomenons, dC/dt ≠ 0, in contrast to steady-state where dC/dt = 0.

Framework

Here, a collective and generalized mathematical outline for constructing rhizosphere models, including a mathematical template, Fig. 6.

Mechanism(s)

Mode of action(s) (of rhizosphere components) relative to the scale of interest.

Model

Here, deterministic mathematical model (e.g. as differential equation(s) including initial and boundary conditions): A simplified description of a system in nature.

Rhizosphere

The rhizosphere is the influence-sphere of the roots, Hiltner (1904), who considered nitrogen-fixing bacteria. The definition later extended to “endorhizosphere” (Balandreau and Knowles 1978), “rhizoplane” (Clark 1949), and “ectorhizosphere” (Lynch 1987; York et al. 2016). Classical rhizosphere models have the rhizoplane (root) as boundary conditions and the ectorhizosphere (soil) as simulation domain.

Validation

Validation is the method to compare model predictions against experimental data (‘fit for purpose’), whereas verification is associated with the correctness of the implementation or assumptions.