A generic form of fibre bundle models for root reinforcement of soil

Abstract

Purpose

The mechanical contribution of plant roots to the soil shear strength is commonly modelled using fibre bundle models (FBM), accounting for sequential breakage of roots. This study provides a generic framework, able to includes the many different existing approaches, to quantify the effect of various model assumptions.

Methods

The framework uses (1) a single model parameter determining how load is shared between all roots, (2) a continuous power-law distribution of root area ratio over a range of root diameters, and (3) power-law relationships between root diameters and biomechanical properties. A new load sharing parameter, closely resembling how roots mobilise strength under landslide conditions, is proposed. Exact analytical solutions were found for the peak root reinforcement, thus eliminating the current need for iterative algorithms. Model assumptions and results were validated against existing biomechanical and root reinforcement data.

Results

Root reinforcements proved very sensitive to the user-defined load sharing parameter. It is shown that the current method of discretising all roots in discrete diameter classes prior to reinforcement calculations leads to significant overestimations of reinforcement. Addition of a probabilistic distribution of root failure by means of Weibull survival functions, thus adding a second source of sequential mobilisation, further reduced predicted reinforcements, but only when the reduction due to load sharing was limited.

Conclusion

The presented solutions greatly simplify root reinforcement calculations while maintaining analytical exactness as well as clarity in the assumptions made. The proposed standardisation of fibre bundle-type models will greatly aid comparison and exchange of data.

Introduction

Plant roots reinforce shallow soil layers against mass movements through both extracting moisture and by mobilising their mechanical strength. The latter effect is however difficult to predict and many models have since been developed.

A simple and therefore commonly used root reinforcement model was developed by Waldron (1977) and Wu et al. (1979) (since called the ‘Wu/Waldron model’, or ‘WWM’), who proposed the peak root reinforcement is linearly correlated to the sum of root tensile resistances:

$$ c_{r,u,WWM} = k^{\prime} \underset{i}{\sum} \phi_{r,i} t_{r,u,i} $$

(1)

where t_r,u,i is the tensile strength of root i (subscript ‘r’ for ‘root’ and ‘u’ for ‘ultimate’, i.e. at root peak strength), ϕ_r,i the root area ratio of root i (i.e. the fraction of the soil cross-section occupied by this root) and $k^{\prime }$ an multiplication factor accounting the effect of root orientation at root failure, often assumed as $k^{\prime }=1.2$ (Wu et al. 1979).

Experiments by many authors have shown that this model tends to overestimate reinforcements due to the underlying assumption that all roots break simultaneously (e.g. Operstein and Frydman 2000, Loades et al.2010, Liang et al. 2017). More realistically, roots will mobilise their strength sequentially instead (some break before others), resulting in a reduction in reinforcement. Sequential root mobilisation may be affected by:

• 1. Variation in root diameters and associated differences in biomechanical properties (such as tensile strength and stiffness, e.g Loades et al. (2013) and Boldrin et al. (2017), among many others). This variation is related to differences in root topology and anatomy (Loades et al. 2013; Mao et al. 2018) and is henceforth referred to as ‘inter-diameter variation’ in root properties;

• 2. Variation in root biomechanical properties and topology between roots with the same diameter (no single root is the same) (Schwarz et al. 2013; Mao et al. 2018). This variation is henceforth called ‘intra-diameter variation’;

• 3. Variation in root architecture, e.g. root orientations (Thomas and Pollen-Bankhead 2010) or root branching (Mao et al. 2018; Meijer et al. 2019b);

• 4. Variation in root anchorage (Waldron 1977; Pollen 2007). Some roots may slip more easily than others, and some may never reach tensile failure if anchorage is insufficient.

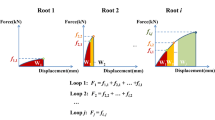
Fibre bundle models (FBM), developed by Daniels (1945) and introduced to root reinforcement research by Pollen and Simon (2005), are widely used to incorporate inter-diameter effects. The reduction in peak reinforcement due to sequential mobilisation can be captured by adding an additional reduction factor $k^{\prime \prime }$ (e.g. Bischetti et al. 2009, Thomas and Pollen-Bankhead 2010, Preti 2013):

$$ c_{r,u,FBM} = k^{\prime\prime} c_{r,u,WWM} $$

(2)

where c_r,u,FBM is the peak root reinforcement predicted by the fibre bundle model. Such models require a mechanism for how the total load is shared between all roots. Many mechanisms have been proposed (e.g. Pollen and Simon Pollen and Simon, Schwarz et al. 2010, Ji et al. 2020), which are discussed in more detail in this paper. It is however not clear what which mechanism most closely resembles the actual mobilisation behaviour of a bundle roots. Commonly conducted experiments such as shear box tests only provide information about the bulk behaviour of the rooted soil and not about the behaviour of individual roots within this soil. More advances models such as the RBMw model by Schwarz et al. (2013) in addition include intra-diameter variation by considering a probability of failure for each root depending on the current level of root displacement.

WWM and FBM-type models require that the diameter of each root or the diameter class it belongs to is known, both for calculation of the root area ratio and biomechanical properties. Measuring all diameters, either by trench wall (e.g. Moos et al. 2016) or (core) sampling methods (e.g. Genet et al. 2008) is however time-consuming. Commonly, root diameters are grouped into a finite number of root diameter classes (e.g. Genet et al. 2008, Ji et al. 2020). All roots within each class must be assigned a diameter (this may be the average diameter in the class, or may follow some other rule, see for example Thomas and Pollen-Bankhead 2010, Ji et al. 2020). All roots with the same assigned diameter are assigned the same root properties and will therefore break simultaneously. It is here hypothesised that this will result in an overestimation of root reinforcement, analogous to the WWM predicting larger reinforcements compared to the FBM.

Given the large number of roots involved in slope stability mechanisms, the distribution of roots diameter is likely to approximate a continuous distribution. Few studies have attempted to use continuous rather than discrete distributions of root diameters. Notably, Cohen et al. (2011) successfully used uniform, log-normal and Weibull distributions for modelling of root pullout tests. This study was limited to one species (Norway spruce) and 29 individual roots. There is therefore scope for a more thorough investigating of the use of continuous diameter distributions, covering a wider range of species and larger root samples, as well as integrating this approach into calculation models for root reinforcement of soil.

This study aimed to increase our understanding of the mechanical interaction between roots and soil and the accuracy of root reinforcement predictions. The specific objective were to:

• 1. Standardise existing fibre bundle-type models into a generic and coherent framework, incorporating both inter- and intra-diameter variation. This will facilitate easy comparison between models and reveal the merits and drawbacks of each model;

• 2. Incorporate continuous distributions of root diameters, rather than counts of individual roots with discrete diameters, to simplify both experimental and computational procedures.

This generic fibre bundle model framework was used to:

• 1. Study the effect of various load-sharing mechanisms and the relative contribution of inter-diameter and intra-diameter variation on soil reinforcement by plant roots;

• 2. Investigate the magnitude of the errors introduced by using a limited number of root diameter classes.

Existing experimental data for root biomechanical properties, root diameter distributions and measured root reinforcements was used to demonstrate the proposed approach.

Materials and methods

Fitting root biomechanical properties

The root tensile strength t_r,u was assumed to vary as function of root diameter d_r following the commonly-used power-law (e.g. Mao et al. 2012 among many others):

$$ t_{r,u} = t_{r,u,0} \left( \frac{d_{r}}{d_{r,0}} \right)^{\beta_{t}} $$

(3)

where t_r,u,0 is the tensile strength of a root with a diameter equal to reference diameter d_r,0, and β_t a dimensionless power-law coefficient. A reference diameter, usually set to d_r,0 = 1 mm and therefore often omitted in the literature, is required to make the system of units used fully consistent. d_r,0 = 1 mm is assumed throughout the remainder of this manuscript.

The tensile strain 𝜖_r,u required to reach root peak tensile strength may also follow a power law:

$$ \epsilon_{r,u} = \epsilon_{r,u,0} \left( \frac{d_{r}}{d_{r,0}} \right)^{\beta_{\epsilon}} $$

(4)

where 𝜖_r,u,0 is the tensile strain to peak of a root with a diameter equal to reference diameter d_r,0, and β_𝜖 a dimensionless power-law coefficient.

Assuming the roots behave linear elastic until failure, it follows that the root stiffness E_r also follows a power-law relation (as for example used by Loades et al. (2013) or Boldrin et al. (2017)), since:

$$ E_{r} = \frac{t_{r,u}}{\epsilon_{r,u}} = E_{r,0} \left( \frac{d_{r}}{d_{r,0}} \right)^{\beta_{E}} $$

(5)

where:

$$ E_{r,0} = \frac{t_{r,u,0}}{\epsilon_{r,u,0}} \qquad \beta_{E} = \beta_{t} - \beta_{\epsilon} $$

(6)

All power-law curves were fitted using the non-linear weighted squares method.

Root biomechanical properties vary widely, even between roots with similar diameters. This variation was captured using a Weibull distribution, characterised by a shape parameter κ and scale parameter λ. Assuming that the mean of the distribution is equal to t_r,u or 𝜖_r,u, it follows that the scale parameters for the distribution of tensile strength (λ_t) and strain to peak (λ_𝜖) satisfy:

$$ \lambda_{t} = \frac{t_{r,u}}{{{\varGamma}}\left( 1+\frac{1}{\kappa_{t}}\right)} \qquad \lambda_{\epsilon} = \frac{\epsilon_{r,u}}{{{\varGamma}}\left( 1+\frac{1}{\kappa_{\epsilon}}\right)} $$

(7)

where Γ() is the gamma-function and κ_t and κ_𝜖 the shape parameters for the distribution of tensile strength and tensile strain to peak, respectively. Essentially, strengths/strains were first normalised by the best power-law fit and subsequently a Weibull distribution with a mean of 1 was fitted, using the log-likelihood method, to obtain the shape of the distribution.

Continuous distributions of root area ratio over root diameters

When quantifying the root area ratio (for example using trench wall methods or root scanning methods), root diameters are generally discretised into a finite number of diameter classes. Thicker roots may still be counted individually. In typical cases where root reinforcement may be of importance, for example in the case of shallow landslides, the number of roots mobilised may however be very large and the distribution of root diameters may therefore approximate a continuous distribution over the root diameter range present.

In this study, it was assumed that all roots fall within a diameter range defined by a minimum (d_r,min) and a maximum (d_r,max) diameter. These limits can be easily established from a representative sample of roots. It was proposed to model the continuous distribution of the root area ratio ϕ_r (e.g. the fraction of cross-sectional area occupied by roots) over this continuous diameter range using a power law:

$$ \phi_{r} = \phi_{r,0} \left( \frac{d_{r}}{d_{r,0}} \right)^{\beta_{\phi}} $$

(8)

where ϕ_r,0 is the root area ratio contribution of roots with a diameter equal to reference diameter d_r, and β_ϕ a dimensionless power coefficient. When β_ϕ = 0, the root area ratio is equally split over all root diameters. When β_ϕ > 0, relatively many large roots are present, and when β_ϕ < 0, thin roots are relatively abundant.

The total root area ratio ϕ_r,t should satisfy:

$$ \phi_{r,t} = \overset{d_{r,max}}{\underset{x=d_{r,min}}{\int}} \phi_r dx $$

(9)

And therefore ϕ_r,0 can be expressed as:

$$ \phi_{r,0} = \left\{\begin{array}{ll} \frac{\phi_{r,t} \left( 1+\beta_{\phi} \right)} {d_{r,0} \left[\left( \frac{d_{r,max}}{d_{r,0}} \right)^{1+\beta_{\phi}} - \left( \frac{d_{r,min}}{d_{r,0}} \right)^{1+\beta_{\phi}} \right]} & \text{when } 1+\beta_{\phi} \neq 0 \\ \frac{\phi_{r,t}}{d_{r,0} \ln{\left( \frac{d_{r,max}}{d_{r,min}} \right)}} & \text{when } 1+\beta_{\phi}=0 \end{array}\right. $$

(10)

where $\ln ()$ is the natural logarithm function.

Load sharing in fibre bundle models

The fibre bundle model is often used to account for progressive root failure. An important modelling choice in this model is how to distribute the total tensile load over all unbroken roots. In root reinforcement literature, the load is typically split according to the root diameter:

$$ \frac{F_{i}}{F_{j}} = \left( \frac{d_{r,i}}{d_{r,j}} \right)^{\beta_{F}} $$

(11)

where F is the current tensile force in unbroken roots i and j, and β_F a dimensionless load sharing parameter.

Existing load sharing laws

All previously proposed FBMs are part of the same ‘family’; they can all be described in terms of the value of β_F assumed:

• β_F = 0: Load is split equally over all roots, regardless of root diameter (e.g. Thomas and Pollen-Bankhead2010, Mao et al. 2012);

• β_F = 1: Load is split proportionally to root diameter (e.g. Pollen and Simon 2005, Thomas and Pollen-Bankhead 2010, Mao et al. 2012);

• β_F = 2: Load is split proportionally to the root cross-sectional area (resulting in equal tensile stresses in each root) (e.g. Thomas and Pollen-Bankhead 2010, Mao et al. 2012);

• β_F = 2 + β_E − β_L (or β_F = 2 + β_t − β_𝜖 + β_L): This is the underlying assumption in the Root Bundle Model (RBMw) by Schwarz et al. (2013), in which an equal root elongation u_r is applied to each root. In this model, the length L_r of each root may vary with root diameter d_r according to a power law:

  $$ L_{r} = L_{r,0} \left( \frac{d_{r}}{d_{r,0}}\right)^{\beta_{L}} $$

  (12)

  where L_r,0 is the length of a root with a diameter equal to the reference diameter d_r = d_r,0, and β_L a dimensionless power coefficient. The tensile strain (𝜖_r) in each root is subsequently assumed constant along the entire root: 𝜖_r = u_r/L_r.

  The load sharing law can be demonstrated by looking at load sharing between two arbitrary linear elastic roots with diameters d_r,i and d_r,j and circular cross-sectional areas A_r,i and A_r,j:

  $$ \begin{array}{@{}rcl@{}} \frac{F_{i}}{F_{j}} & =& \frac{A_{r,i} E_{r,i} \epsilon_{r,i}}{A_{r,j} E_{r,j} \epsilon_{r,j}} \end{array} $$

  (13)
  $$ \begin{array}{@{}rcl@{}} & =& \frac{\left( \frac{\pi {d}_{r,i}^{2}}{4}\right) E_{r,0} \left( \frac{d_{r,i}}{d_{r,0}}\right)^{\beta_{E}} \left( \frac{u_{r}}{L_{r,0}}\right) \left( \frac{d_{r,i}}{d_{r,0}}\right)^{-\beta_{L}}}{\left( \frac{\pi {d}_{r,j}^{2}}{4}\right) E_{r,0} \left( \frac{d_{r,j}}{d_{r,0}}\right)^{\beta_{E}} \left( \frac{u_{r}}{L_{r,0}}\right) \left( \frac{d_{r,j}}{d_{r,0}}\right)^{-\beta_{L}}} \end{array} $$

  (14)
  $$ \begin{array}{@{}rcl@{}} & =& \left( \frac{d_{r,i}}{d_{r,j}}\right)^{2+\beta_{E}-\beta_{L}} \end{array} $$

  (15)

• $\beta _{F}=\left \{2 \text {, } 2.5 \text { or } 3\right \}+0.5\beta _{E}$ (or $\beta _{F}=\left \{2 \text {, } 2.5 \text { or } 3\right \}+0.5\beta _{t}-0.5\beta _{\epsilon }$): This is underlying assumption in the energy-based models (FBM-W) proposed by Ji et al. (2020), in the case of linear elastic roots. In these models, the tensile force is distributed according to the mechanical work (energy) per unit cross-sectional area of root (W_r) required to elongate a root with initial length L_gauge by a distance u_r in a uniaxial tension test:

  $$ W_{r} = \frac{1}{A_{r}} {\int}_{x=0}^{u_{r}} F(x) dx $$

  (16)

  where F(x) is the root tensile force given root elongation x. For linear elastic roots, W_r can be rewritten as:

  $$ W_{r} = \frac{F u_{r}}{2 A_{r}} $$

  (17)

  where F is the tensile force at elongation u_r, which for linear elastic roots equals:

  $$ F = A_{r} E_{r} \epsilon_{r} = A_{r} E_{r} \frac{u_{r}}{L_{gauge}} $$

  (18)

  Combining Eqs. 17 and 18, the current tensile force F can be written as function of the mechanical work W_r:

  $$ F = A_{r} \sqrt{\frac{2 E_{r} W_{r}}{L_{gauge}}} $$

  (19)

  Now consider two unbroken linear elastic roots with diameters d_r,i and d_r,j. Assuming the gauge length L_gauge is the same for both roots, the load sharing equals:

  $$ \begin{array}{@{}rcl@{}} \frac{F_{i}}{F_{j}} & =& \frac{A_{r,i} \sqrt{\frac{2 E_{r,i} W_{r,i}}{L_{gauge}}}}{A_{r,j} \sqrt{\frac{2 E_{r,j} W_{r,j}}{L_{gauge}}}} \end{array} $$

  (20)
  $$ \begin{array}{@{}rcl@{}} & =& \frac{\left( \frac{\pi {d}_{r,i}^{2}}{4}\right) \sqrt{\frac{2 E_{r,0} \left( \frac{d_{r,i}}{d_{r,0}}\right)^{\beta_{E}} W_{r,i}}{L_{gauge}}}} {\left( \frac{\pi {d}_{r,j}^{2}}{4}\right) \sqrt{\frac{2 E_{r,0} \left( \frac{d_{r,j}}{d_{r,0}}\right)^{\beta_{E}} W_{r,j}}{L_{gauge}}}} \end{array} $$

  (21)
  $$ \begin{array}{@{}rcl@{}} & =& \left( \frac{d_{r,i}}{d_{r,j}}\right)^{2+0.5\beta_{E}} \left( \frac{W_{r,i}}{W_{r,j}}\right)^{0.5} \end{array} $$

  (22)

  Ji et al. (2020) defined three different energy-based models. In the FBM-WN, the mechanical work is distributed evenly over all roots, so:

  $$ \frac{W_{r,i}}{W_{r,j}} = \left( \frac{d_{r,i}}{d_{r,j}}\right)^{0} = 1 $$

  (23)

  Substituting this into Eq. 22 reveals the load sharing law for the FBM-WN:

  $$ \frac{F_{i}}{F_{j}} = \left( \frac{d_{r,i}}{d_{r,j}}\right)^{2+0.5\beta_{E} + 0.5 \cdot 0} \longrightarrow \beta_{F} = 2 + 0.5 \beta_{E} $$

  (24)

  In the FBM-WDia, the mechanical work is distributed proportionally to the diameter of each unbroken root, so:

  $$ \frac{W_{r,i}}{W_{r,j}} = \left( \frac{d_{r,i}}{d_{r,j}}\right)^{1} \longrightarrow \beta_{F} = 2.5 + 0.5 \beta_{E} $$

  (25)

  In the FBM-WS, the mechanical work is distributed proportionally to the root cross-sectional area, so:

  $$ \frac{W_{r,i}}{W_{r,j}} = \left( \frac{d_{r,i}}{d_{r,j}}\right)^{2} \longrightarrow \beta_{F} = 3 + 0.5 \beta_{E} $$

  (26)

It should be emphasized that load sharing parameter β_F is not limited to any of these values. In fact, β_F may take any value $-\infty \leq \beta _{F} \leq \infty$. The influence of β_F on the predicted reinforcement will be explored later.

New load sharing mechanism based on mobilisation of root strength in direct shear conditions

The value of load sharing parameter β_F should ideally be based on the actual physics behind the mobilisation of root stress, rather than being a more arbitrary model assumption (such as assuming equal stress or equal strain in each root). A new load sharing rule is therefore proposed using a load sharing rule based on Waldron (1977)’s model for the tensile stress t_r in a root loaded in direct shear, accounting for the gradual mobilisation of root–soil interface friction along the root axis:

$$ t_{r} = \sqrt{\frac{4 \tau_{i} E_{r}}{d_{r}}} \sqrt{\sqrt{{u_{s}^{2}}+h^{2}}-h} $$

(27)

where τ_i is the shear resistance along the root–soil interface, u_s the direct shear displacement of the soil and h the shear zone thickness. This expression is also valid for a tensile crack, in which case h = 0 and u_s the width of the crack opening. Since E_r is a function of diameter d_r (Eq. 5), Eq. 27 can be rewritten as:

$$ t_{r} = {d}_{r}^{0.5\left( \beta_{E} - 1\right)} \sqrt{\frac{4\tau_{i} E_{r,0}}{{d}_{r,0}^{\beta_{E}}}} \sqrt{\sqrt{{{u}_{s}^{2}}+h^{2}}-h} $$

(28)

After converting from tensile stress to tensile force by multiplying by the root cross-sectional area, it follows that the corresponding FBM load sharing factor β_F associated with Waldron’s mobilisation mechanism equals:

$$ \beta_{F} = 2 + 0.5\left( \beta_{E}-1\right) = 1.5 + 0.5 \beta_{E} $$

(29)

Load sharing and the order of root breakage

There has been some debate about which load sharing mechanism is most accurate, based on observations on which root diameters break first (e.g. Schmidt et al. 2001, Comino et al. 2010, Thomas and Pollen-Bankhead 2010). This can be further investigated by looking at the tensile stresses during mobilisation.

The load sharing rule (Eq. 11) can be re-expressed in term of tensile stresses by dividing by the circular root cross-sectional area:

$$ \frac{t_{r,i}}{t_{r,j}} = \left( \frac{d_{r,i}}{d_{r,j}} \right)^{\beta_{F}-2} $$

(30)

The load sharing rule can equally be re-expressed in terms of the fraction of tensile strength mobilised by dividing the tensile stress in each root by its tensile strength (Eq. 3). After rewriting:

$$ \frac{t_{r,i}}{t_{r,u,i}} = \frac{t_{r,j}}{t_{r,u,j}} \left( \frac{d_{r,i}}{d_{r,j}} \right)^{\beta_{F}-2-\beta_{t}} $$

(31)

From this follow that all roots break simultaneously when β_F = 2 + β_t. When β_F < 2 + β_t, roots will break in the order from thin to thick. When β_F > 2 + β_t, roots will break in the order from thick to thin.

The order of breakage is therefore insufficient information for uniquely determining what the most suitable load sharing parameter β_F would be; it can only indicate a range of appropriate load-sharing parameters β_F at best.

Model derivations

Wu/Waldron Model with continuous root diameter distributions (WWMc)

The continuous root distribution (Eq. 8) can be used to calculate the peak root reinforcement according to the Wu/Waldron solution (Eq. 1) by integrating over all root diameters, rather than the usual summation over all root diameter classes:

$$ c_{r,u,WWMc} = k^{\prime} \overset{d_{r,max}}{\underset{x=d_{r,min}}{\int}} \phi_{r} t_{r,u} dx $$

(32)

where c_r,u,WWMc is the peak reinforcement according to the WWM with continuous root diamemeter distributions (‘c’ for ‘continuous’). Resolving the integral gives:

$$ c_{r,u,WWMc} = \left\{\begin{array}{ll} \frac{k^{\prime} \phi_{r,0} t_{r,u,0} d_{r,0}}{1+\beta_{\phi}+\beta_{t}} \left[ \left( \frac{d_{r,max}}{d_{r,0}}\right)^{1+\beta_{\phi}+\beta_{t}} - \left( \frac{d_{r,min}}{d_{r,0}}\right)^{1+\beta_{\phi}+\beta_{t}} \right] & \text{when } 1+\beta_{\phi}+\beta_{t} \neq 0 \\ k^{\prime} \phi_{r,0} t_{r,u,0} d_{r,0} \ln{\left( \frac{d_{r,max}}{d_{r,min}}\right)} & \text{when } 1+\beta_{\phi}+\beta_{t} = 0 \end{array}\right. $$

(33)

Fibre bundle models with continuous root diameter distributions (FMBc)

Most FBMs have typically been described as a force-controlled mechanism (apart from the RBMw, which is formulated in terms of displacement). The peak reinforcement is found by gradually increasing the load in an iterative process until all roots have broken.

All FBMs can however easily be expressed in an equivalent strain-controlled framework. Assume 𝜖_r,0 is the tensile strain in a root with reference diameter d_r,0. When unbroken, the tensile stress in this root is:

$$ t_{r,0} = E_{r,0} \epsilon_{r,0} = \left( \frac{t_{r,u,0}}{\epsilon_{r,u,0}}\right) \epsilon_{r,0} $$

(34)

Using the load sharing law in terms of stress (Eq. 30), the tensile stress t_r in a root with an arbitrary diameter x satisfies:

$$ t_{r} = t_{r,0} \left( \frac{x}{d_{0}}\right)^{\beta_{F}-2} $$

(35)

Substituting Eq. 34 into Eq. 35 gives the tensile stress in a root with diameter x given the current level of reference strain 𝜖_r,0:

$$ t_{r} = \frac{t_{r,u,0}}{\epsilon_{r,u,0}} \left( \frac{x}{d_{r,0}}\right)^{\beta_{F}-2} \epsilon_{r,0} $$

(36)

The current tensile strain in this root can be obtained by dividing the tensile stress by the root stiffness:

$$ \epsilon_{r} = \frac{t_{r}}{E_{r}} = \left( \frac{x}{d_{r,0}}\right)^{\beta_{F}-2-\beta_{t}+\beta_{\epsilon}} \epsilon_{r,0} $$

(37)

The breakage parameter f_b indicates whether a root is still unbroken (f_b = 1) or broken (f_b = 0):

$$ f_{b} = H \left( t_{r,u} - t_{r} \right) $$

(38)

where H is the Heaviside function (H(y < 0) = 0, H(y ≥ 0) = 1).

The (current) root reinforcement (c_r,FBMc) at a given value of strain 𝜖_r,0 can be established by integrating the contribution of each root diameter at this level of strain:

$$ c_{r,FBMc} = k^{\prime} {\int}_{x=d_{r,min}}^{d_{r,max}} \phi_{r} t_{r} f_{b} dx $$

(39)

It is more convenient to integrate only over the range of roots d₁ ≤ d_r ≤ d₂ that are still unbroken. Resolving the integral in Eq. 39:

$$ c_{r,FBMc} = \left\{\begin{array}{ll} \frac{k^{\prime} \phi_{r,0} t_{r,u,0} d_{r,0}}{\beta_{F}-1+\beta_{\phi}} \left[ \left( \frac{d_{2}}{d_{r,0}}\right)^{\beta_{F}-1+\beta_{\phi}} - \left( \frac{d_{1}}{d_{r,0}}\right)^{\beta_{F}-1+\beta_{\phi}} \right] \frac{\epsilon_{r,0}}{\epsilon_{r,u,0}} & \text{when } \beta_{F} \neq 1-\beta_{\phi} \\ k^{\prime} \phi_{r,0} t_{r,u,0} d_{r,0} \ln \left( \frac{d_{2}}{d_{1}}\right) \frac{\epsilon_{r,0}}{\epsilon_{r,u,0}} & \text{when } \beta_{F} = 1-\beta_{\phi} \end{array}\right. $$

(40)

𝜖_r,0,min and 𝜖_r,0,max are defined as the values of the reference strains 𝜖_r,0 at which the thinnest and thickest roots break. These can be found by solving t_r = t_r,u using Eq. 36:

$$ \epsilon_{r,0,min} = \epsilon_{r,u,0} \left( \frac{d_{r,min}}{d_{r,0}}\right)^{2-\beta_{F}+\beta_{t}} $$

(41)

$$ \epsilon_{r,0,max} = \epsilon_{r,u,0} \left( \frac{d_{r,max}}{d_{r,0}}\right)^{2-\beta_{F}+\beta_{t}} $$

(42)

The integration limits d₁ and d₂ required in Eq. 40 can be expressed as:

• when both 𝜖_r,0 ≤ 𝜖_r,0,min and 𝜖_r,0 ≤ 𝜖_r,0,max, all roots are still unbroken, so:

  $$ d_{1} = d_{r,min} \qquad d_{2} = d_{r,max} $$

  (43)

• when 𝜖_r,0,min < 𝜖_r,0 < 𝜖_r,0,max, some of the thinnest roots have already broken while thicker ones are still unbroken:

  $$ d_{1} = d_{r,0} \left( \frac{\epsilon_{r,u,0}}{\epsilon_{r,0}}\right)^{1/\left( \beta_{F}-2-\beta_{t}\right)} \qquad d_{2} = d_{r,max} $$

  (44)

• when 𝜖_r,0,min > 𝜖_r,0 > 𝜖_r,0,max, some of the thicker roots have already broken while thinner ones are still unbroken:

  $$ d_{1} = d_{r,min} \qquad d_{2} = d_{r,0} \left( \frac{\epsilon_{r,u,0}}{\epsilon_{r,0}}\right)^{1/\left( \beta_{F}-2-\beta_{t} \right)} $$

  (45)

• when 𝜖_r,0 ≥ 𝜖_r,0,min and 𝜖_r,0 ≥ 𝜖_r,0,max, all roots are broken and therefore:

  $$ c_{r,FBMc} = 0 $$

  (46)

With the full reinforcement versus strain behaviour now established, attention can be shifted to the peak root reinforcement c_r,u,FBMc, often of more interest for engineering applications. It is convenient to normalise this reinforcement by the WWMc solution defined previously:

$$ k^{\prime\prime} = \frac{c_{r,u,FBMc}}{c_{r,u,WWMc}} $$

(47)

An exact analytical solution for $k^{\prime \prime }$ was found, which is a function of just two dimensionless parameter groups ζ₁ and ζ₂:

$$ \zeta_{1} = \left( 2+\beta_{t}-\beta_{F} \right) \ln\left( \frac{d_{r,max}}{d_{r,min}}\right) $$

(48)

$$ \zeta_{2} = \left( 1+\beta_{t}+\beta_{\phi} \right) \ln\left( \frac{d_{r,max}}{d_{r,min}}\right) $$

(49)

ζ₁ is directly related to how the load is distributed among the range of root diameters (inter-diameter variation). ζ₂ is a measure for the skewness of available strength across the range of root diameters.

Exact analytical solutions for $k^{\prime \prime }$ are shown in Table 1. These can be used to directly calculate the peak root reinforcement for any combination of root parameters and load sharing rule adopted, without the need for any iterative computation algorithms.

Table 1 Ratio $k^{\prime \prime }$ between peak root reinforcements calculated using the continuous WWM and the FBM. Due to the asymptotic nature of the various power-law curves used, different solutions are required for various combinations of ζ₁ and ζ₂

Fibre bundle models with continuous root diameter distributions and Weibull survival functions (FMBcw)

Intra-diameter variation can be incorporated into the proposed generic fibre bundle model approach in a similar fashion to Schwarz et al. (2013). In their approach, the probability of a root still being unbroken given the current root elongation (u_r) equals:

$$ f_{b} = \exp\left[-\left( \frac{u_{r}}{\lambda}\right)^{\kappa}\right] $$

(50)

where κ and λ are the user-defined shape and scale parameter of a Weibull survival function.

The average displacement u_r,u at which a root breaks depends on the tensile strain to peak and the root length L_r:

$$ u_{r,u} = \epsilon_{r,u} {L_{r}} $$

(51)

The average displacement at root breakage (u_r,u) has be be equal to the mean of the Weibull distribution, and therefore scale parameter λ is given by:

$$ \lambda = \frac{\epsilon_{r,u} L_{r}}{{{\varGamma}}\left( 1+\frac{1}{\kappa}\right)} = \frac{\epsilon_{r,u,0}L_{r,0}}{{{\varGamma}}\left( 1+\frac{1}{\kappa}\right)} \left( \frac{d_{r}}{d_{r,0}}\right)^{\beta_{\epsilon}+\beta_{L}} $$

(52)

The current root elongation u_r in a root with diameter x can be found by multiplying the current tensile strain 𝜖_r (Eq. 37) by the root length L_r (Eq. 12):

$$ u_{r} = \epsilon_{r} L_{r} = L_{r,0} \left( \frac{x}{d_{r,0}}\right)^{\beta_{F}-2-\beta_{t}+\beta_{\epsilon}+\beta_{L}} \epsilon_{r,0} $$

(53)

Substituting Eqs. 52 and 53 into Eq. 50 gives an alternative expression for the breakage parameter f_b for a root with diameter x as function of the reference strain 𝜖_r,0:

$$ f_{b} = \exp\left[-\left( {{\varGamma}}\left( 1+\frac{1}{\kappa}\right) \frac{\epsilon_{r,0}}{\epsilon_{r,u,0}} \left( \frac{x}{d_{r,0}}\right)^{\beta_{F}-2-\beta_{t}} \right)^{\kappa}\right] $$

(54)

Assuming $\kappa =\infty$ corresponds with the breakage parameter definition in the FBMc solution.

The current reinforcement c_r,FBMcw (added subscript ‘w’ for ‘Weibull’), given reference strain 𝜖_r,0, can again be obtained by integration of the reinforcement contributions of all roots (similar to Eq. 39), now using the just derived expression for f_b (Eq. 54).

$$ c_{r,FBMcw} = k^{\prime} {\int}_{x=d_{r,min}}^{d_{r,max}} \phi_{r} t_{r} f_{b} dx $$

(55)

The peak reinforcement c_r,u,FBMcw is then obtained by finding the maximum value of c_r,FBMcw on the strain interval $0 \leq \epsilon _{r,0} \leq \infty$.

No exact analytical solution for c_r,u,FBMcw could be found and numerical solutions were obtained instead. These are further discussed in the results section. The results for reduction factor $k^{\prime \prime }$ can be expressed as a function of three parameters only: the same ζ₁ and ζ₂ as obtained in the FBMc, plus Weibull shape parameter κ.

For the special case ζ₁ = 0, in which case there is only intra- and no inter-diameter variation, an analytical solution for the peak reinforcement c_r,u,FBMcw does exist:

$$ k^{\prime\prime} \big\rvert_{\zeta_{1}=0} = \frac{\sqrt[\kappa]{\frac{1}{\kappa}} \exp\left( \frac{-1}{\kappa}\right)}{{{\varGamma}}\left( 1+\frac{1}{\kappa}\right)} $$

(56)

Experimental data sources

The validity of the assumed distributions for root biomechanical properties and the power-law distribution of root area ratio over the range of root diameters was tested against previously collected data. To prevent numerical problems associated with negative or zero diameters during root area ratio fitting, d_r,min ≥ 0.05 mm was enforced. This data was also used to compare experimentally measured peak root reinforcement to those predicted by the various models.

The first set of data consisted of laboratory direct shear tests on soil reinforced by juvenile willow, gorse and festulolium grass grown under laboratory conditions (Liang et al. 2017), Bull et al. (2020). In the following, first author initials ‘TL’ and ‘DB’ are used to differentiate tests conducted by Liang et al. and Bull et al.. Root area ratios were determined by measuring the diameter of each root crossing a shear plane.

A second set of data consisted of field cork screw extraction tests on blackcurrant shrubs (Meijer et al. 2018a) and mature Sitka spruce trees at two different field sites in Scotland: Halliburton Hill (’HH’, see Meijer et al.2018a) and the Queen Elizabeth Forest Park (’QEFP’, see Meijer et al. 2019a). Additional data was obtained from blade penetrometer tests on mature Pedunculate oak (Meijer et al. 2018b). Root area ratios were derived from WinRhizo root volume scans.

For all data sets, root biomechanical data was collected by means of uniaxial tensile testing in the laboratory.

Model simulations

A series of FBMc and FBMcw calculations was conducted to explore the effect of load sharing rules on the mobilisation of root reinforcement.

To systemically explore how root biomechanical properties, root diameter distributions and load sharing rules affect the peak root reinforcement predicted by both the FBMc and FBMcw, $k^{\prime \prime }$ was analysed for a large combination of dimensionless coefficients ζ₁, ζ₂ and κ.

The current practice of discretising root diameters into a finite number of root diameter classes prior to calculating reinforcements will result in two sources of errors when using fibre bundle models:

• 1. The tensile strength for the average diameter in a root diameter class is generally not equal to the average tensile strength of all roots within a diameter class;

• 2. Using a finite number of root diameter classes results in a sawtooth-like strain versus reinforcement response, corresponding with the (sudden) tensile failure of roots in each diameter class (for a graphic example of this, see Fig. 8 in the results section). This will result in overestimations of reinforcement.

These two types of errors can be mathematically separated. For the FBMc:

$$ \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Discrete diameter classes error}}}{\underbrace{\frac{c_{r,u,FBM}}{c_{r,u,FBMc}}}}= \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Tensile strength error}}}{\underbrace{\frac{c_{r,u,WWM}}{c_{r,u,WWMc}}}} \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Sawtooth strength error}}}{\underbrace{\frac{c_{r,u,FBM}/c_{r,u,WWM}}{c_{r,u,FBMc}/c_{r,u,WWMc}}}} $$

(57)

where c_r,u,FBM and c_r,u,WWM are the peak reinforcement predictions obtained by using the traditional fibre bundle model approach of first separating all root diameters into a discrete number of diameter classes n_c. Similarly, for the FBMcw:

$$ \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Discrete diameter classes error}}}{\underbrace{\frac{c_{r,u,FBMw}}{c_{r,u,FBMcw}}}}= \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Tensile strength error}}}{\underbrace{\frac{c_{r,u,WWM}}{c_{r,u,WWMc}}}} \underset{\underset{\text{(expressed as a fraction)}}{\text{1+Sawtooth strength error}}}{\underbrace{\frac{c_{r,u,FBMw}/c_{r,u,WWM}}{c_{r,u,FBMcw}/c_{r,u,WWMc}}}} $$

(58)

where c_r,u,FBMw is the peak reinforcement predictions obtained using a discrete number of root diameter classes and Weibull survival functions.

For each source of experimental data, these errors were quantified by varying the number of equal-width diameter classes between n_c = 1 and 200.

Model validation

Predictions for the peak root reinforcement were made for all experimental data sets, using both the FBMc and FBMcw solutions and the various existing and proposed load sharing rules.

A choice has to be made with respect to what shape parameter κ to use in the FBMcw solution to reflect the intra-diameter variation in root properties and architecture. This parameter was chosen based on the experimentally measured intra-diameter variation in root tensile strength (so κ = κ_t). These measurements are less susceptible to errors compared to tensile strain to peak measurements (κ_𝜖, which may be affected by root tortuosity or slippage in clamps, for example).

The RBMw load sharing rule requires a root length power coefficient β_L. Root lengths were unknown for the experimental data analysed, and therefore separate analyses were conducted assuming β_L = 0 (assuming all roots have the same length) or β_L = 0.575 (value for Norway spruce roots used by Schwarz et al. 2013).

Results

Fitting root biomechanical properties

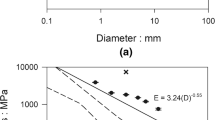
Biomechanical fitting parameters obtained for the experimental data are presented in Table 2. Tensile strength and tensile strain to peak fitting is presented in Figs. 1 and 2 respectively. As discussed in the original publications, most power-law trends are weak (power coefficients close to zero).

Table 2 Power law and Weibull fitting for the tensile strength and tensile strain to peak for various plant species. Reference diameter d_r,0 = 1 mm was assumed for all fits. R² indicates the coefficient of determination for the power-law fits and KS the Kolmogorov-Smirnov distance of Weibull fits (goodness-of-fit measure)

Fig. 1

Tensile strength (t_r,u) versus root diameter (d_r). First, a power law is fitted to all data (solid blue line). Subsequently, a Weibull distribution is fitted to the normalised data (t_r,u/t_r,u,fit). Gray, dashed lines indicate the proportion of (fitted) root strengths that fall below each line (5%, 25%, 50%, 75% and 95%)

Fig. 2

Tensile strain to peak (𝜖_r,u) versus root diameter (d_r). First, a power law is fitted to all data (solid blue line). Subsequently, a Weibull distribution is fitted to the normalised data (𝜖_r,u/𝜖_r,u,fit). Gray, dashed lines indicate the proportion of (fitted) tensile strain to peak values that fall below each line (5%, 25%, 50%, 75% and 95%)

Continuous distributions of root area ratio over root diameters

Curve fitting results for the cumulative root area ratio versus root diameter data verified the feasibility of power-law fitting (Fig. 3).

Fig. 3

Example experimental and fitted root diameter distribution data for various species at different depths. Cumulative root area ratios are normalised by the total root area ratio measured. Red points indicate experimental data, and blue lines the best fit according to Eq. 8

For most data series, the fitted power law coefficient β_ϕ was negative, indicating that smaller diameter roots contribute more to the root area ratio than larger diameter roots. However, a significant positive relation (p < 0.001) between the width of the root diameter range (expressed as the ratio d_r,max/d_r,min) and β_ϕ was found (Fig. 4). This suggests that when thicker roots are present (e.g. in the case of oak), their contributions become increasingly important and should not be ignored.

Fig. 4

All results for root diameter distribution parameter β_ϕ as function of species and width of the root diameter range

Model simulations

Example plots of the predicted reference strain versus root reinforcement traces (Fig. 5) graphically show how the load sharing parameter β_F substantially changes both the mobilisation and magnitude of the peak root reinforcement in both the FBMc and FBMcw models.

Fig. 5

Example of different mobilisation of root reinforcement as function of strain 𝜖_r,0, depending on load sharing parameter 2 + β_t − β_F. The reinforcement is normalised by the peak reinforcement according to the (continuous) WWM model. Example generated using parameters for gorse measured at 400 mm depth. Weibull survival parameter κ was assumed equal to κ_t = 2.13, the fitted Weibull shape parameter for tensile strength for gorse

The exact analytical solution for the peak root reinforcement predicted by the FBMc (Table 1) is visualised in Fig. 6.

Fig. 6

FBMc peak root reinforcement reduction factor $k^{\prime \prime }$ due to sequential mobilisation, as function of load sharing parameter β_F, root diameter range d_r,min ≤ d_r ≤ d_r,max, tensile strength power coefficient β_t and root area ratio distribution power coefficient β_ϕ

These solutions shows some interesting features of the general behaviour of fibre bundle models:

• Fibre bundle models are very sensitive to the choice of load sharing parameter β_F. Theoretically, any value $0 < k^{\prime \prime } \leq 1$ can be achieved depending on the choice of β_F;

• The closer β_F is to 2 + β_t, the closer the FBMc solution approximates the WWMc solution (ζ₁ approaches zero, and therefore $k^{\prime \prime }$ approaches 1);

• Larger diameter ranges (larger values of d_r,max/d_r,min, and therefore larger values of ζ₁ and ζ₂) always result in a decrease in reinforcement. The narrower the diameter range, the closer the the FBMc solution approximates the WWMc solution ($k^{\prime \prime }$ approaches 1);

• More skewed distributions of root strength towards either thin roots (ζ₂ moves towards $-\infty$) or thick roots (ζ₂ moves towards $\infty$) increases the magnitude of $k^{\prime \prime }$. This effect is less pronounced than the influence of load sharing factor β_F.

Figure 7 provides solutions for the peak reinforcement calculated with the FBMcw for a large number of combinations of ζ₁, ζ₂ and κ. It shows that the addition of intra-diameter variation (by means of a Weibull survival function) further reduces the predicted reinforcement, especially if there is no or little inter-diameter variation (i.e. ζ₁ is near 0). With increasing values of ζ₁ the inter-diameter sequential mobilisation becomes dominant and the effect of adding intra-diameter variation diminishes rapidly.

Fig. 7

FBMcw peak root reinforcement reduction factor $k^{\prime \prime }$ due to sequential mobilisation, as function of Weibull surival function shape parameter κ and FBMc parameter groups ζ₁ and ζ₂. $\kappa =\infty$ corresponds with the FBMc solution. When ζ₂ < 0, the correct value for $k^{\prime \prime }$ can be obtained by assuming ζ₁ = −ζ₁ and ζ₂ = −ζ₂

Figures 6 and 7 can be used to rapidly estimate $k^{\prime \prime }$ without the need for any additional computations when root strength, root diameter distributions and load sharing parameters are known.

The sawtooth error — the error introduced by binning roots into a finite number of diameter classes prior to root reinforcement calculations — can be reduced by increasing the number of classes (Fig. 8). Sawtooth-type errors were smaller when also incorporating intra-diameter variation (FBMw) rather than inter-diameter variation only (FBM). Using Weibull survival functions provides additional smoothing of the strain–root reinforcement response, but significant sawtooth-type errors still remain (Fig. 8b).

Fig. 8

Example of the effect of using a finite number of root diameter classes n_c on root reinforcement in models with (FBMw) or without Weibull survival functions (FBM). The dashed lines indicate the continuous FBMc and FBMcw solutions respectively. Results are normalised by the WWM solution using the same root diameter classes. Note that even when 20 diameter classes were used, a significant overestimation was made compared to the continuous solutions. Example generated using parameters for blackcurrant measured at 60 mm depth with Waldron load sharing. For FBMw/FBMcw predictions, κ = κ_t was assumed

Analysing these errors for the experimental data shows that, for most species apart from festulolium grass, the tensile strength error was relatively small (Fig. 9c) as values of β_t were close to zero. Sawtooth-type errors were substantial, especially when values of $k^{\prime \prime }$ were small, i.e. when sequential mobilisation has a large effect on the predicted reinforcement. Using the FBM (Fig. 9a), when 5 root classes, the sawtooth effect caused an overestimation of 14 (festulolium grass) to 66% (blackcurrant). When using 10 classes, errors were reduced to 9 to 45% respectively. Adding Weibull survival functions (FMBw) reduced but not removed the sawtooth errors (n_c = 5: 1% (festulolium grass) and 22% (blackcurrant); n_c = 10: 1% (festulolium grass); 12% (blackcurrant); see Fig. 9b).

Fig. 9

Sawtooth and tensile strength error when using fibre bundle models with a discrete number of root diameter classes, either without (FBM) or with Weibull survival functions (FBMw). Lines indicate the average error for each species while shaded areas indicate the range in errors measured at different depths for each species

To reduce the sawtooth error to below 5% in the FBM, at least 24 (festulolium grass) to 135 (blackcurrant) diameter classes were required. In the FBMw, these numbers were are reduced to 1 and 22, respectively.

Model validation

Evaluation of load sharing parameters β_F for each species in the experimental data set showed a wide range (− 0.55 ≤ β_F ≤ 2.36), see Table 3. This wide range in load sharing corresponds with widely ranging predictions for the peak root reinforcement (Fig. 10). On average, root reinforcement predictions using the load sharing rule resulting in the largest predictions were 4.59 times larger than those using the load sharing rule resulting in the smallest prediction when using the FBMc, and 2.80 times larger when using the FBMcw.

Table 3 Load sharing parameters β_F associated with various proposed load sharing mechanisms for each species in the experimental data set

Fig. 10

Comparison between experimental results and model predictions for the reinforcement reduction factor $k^{\prime \prime }$ associated with sequential mobilisation. Large black hollow bars indicate experimental results while coloured bars indicate model results with varying load sharing assumptions. Experimental reinforcement data for gorse, festulolium grass and willow originally measured by Liang et al. (2017) were re-analysed as part of this study. No shear tests were performed on Pedunculate oak

These results confirm that the predicted reinforcement is very sensitive to the load sharing rule adopted. Addition of Weibull survival functions reduced the predicted reinforcement but only when predictions for $k^{\prime \prime }$ were not already small before adding the survival functions.

The developed models performed well for gorse, festulolium grass and willow. These specimens were grown in tall tubes in lab conditions, thus forcing the roots to grow primarily vertically and cross the shear plane at right angles. In contrast, tests on all other species were conducted under field conditions where root orientations will have varied more widely, providing an explanation for why experimentally measured reinforcements are lower than model predictions.

Discussion

Figure 11 shows a schematic representation of each model, graphically showing the different assumptions in each model as well as the effect of using continuous diameter distribution and/or Weibull survival functions.

Fig. 11

Schematic representation of the various root reinforcement models, as function the (reference) strain 𝜖_r,0. Each fill colour indicates the reinforcement contribution by a particular root diameter class. ‘c’ indicates inclusion of continuous root diameter distributions, in which case the fill colours form a smooth gradient since a continuous distribution corresponds with using an infinite number of diameter classes. ‘w’ indicates intra-diameter variation by means of Weibull survival functions was included

This study showed that all existing root reinforcement calculation procedures that rely on a fibre bundle approach are part of the same ‘family’, with different assumptions for load sharing parameter β_F, despite the different names used to identify these models. While previously recognised by Meijer et al. (2018a) for FBMs assuming β_F = 0, β_F = 1 and β_F = 2, this has now been proven in systematic fashion.

This systematic investigation of fibre bundle-type models raises a fundamental question: given that load sharing parameter β_F has such a strong effect on the root reinforcement calculated (as previously observed by Mao et al. (2012) and others) but may can take any value, which value for β_F is most appropriate? The validity of the mechanisms behind existing FBM approaches, such as equal force (β_F = 0), equal stress (β_F = 2) or equal displacement in each root (RBMw), have not been proven by dedicated experiments that investigate the individual responses of roots within a block of rooted soil, and therefore the choice of β_F currently involves a degree of arbitrariness.

This study proposed to base load sharing on the root reinforcement mobilisation mechanism proposed by Waldron (1977), which has been validated by experiments, by using β_F = 1.5 + 0.5β_E. Selecting a physics-based value for β_F results in a testable hypothesis for future experiments, and prevents the pitfall of manipulating a model to fit the data. Dedicated experiments to validate this, and in fact any, load sharing rule are however required.

Sequential mobilisation was shown to be driven by both inter-diameter variation (governed by load sharing parameter β_F) and intra-diameter variation (governed by Weibull shape parameter κ). Both reduced the peak-reinforcement compared to the WWM. Both effects however do not stack: intra-diameter variation is primarily reducing reinforcements when reductions in predicted reinforcement due to inter-diameter effects are small.

Even with our best assumptions (Waldron load sharing, adding intra-diameter variation based on experimentally measured variations in root strength), predicted reinforcements still overestimated experimentally measured values for some species. This highlights some of the limits of FBM-type models, which only account for two sources of sequential mobilisation (inter- and intra-diameter effects) but not for any sequential mobilisation due to root slippage or — perhaps more importantly — root orientation effects. It may be perhaps be possible to incorporate (some of) these effect through careful adjustment of the Weibull parameter κ. Future research should aim to explicitly account for these effects in order to obtain more accurate models.

The models developed in this study assumes the root tensile strength, stiffness and root area ratio distribution all vary as function of root diameter according to a power law. They may be less suitable if experimental data substantially deviates from these assumptions. Validation against a wider range of root data is therefore necessary.

The proposed power-law relationship describing how the root area ratio is distributed across the range of root diameters will greatly simplify existing root reinforcement calculations. The range of root diameters can be captured simply by establishing the diameter of the smallest and thickest root (easily established from a representative sample), estimating the total root area ratio ϕ_r,t (e.g. by using correlations with total root mass) and assuming or measuring β_ϕ. Thus the cumbersome process of measuring the diameter of every single root may be avoided. The only additional parameters required for subsequent predictions of peak root reinforcement are the root diameter–tensile strength power law coefficients (t_r,u,0 and β_t, which can be obtained by tensile testing), a choice for load sharing parameter β_F, and an optional Weibull survival function shape parameter κ in case intra-diameter variation is considered.

The power-law fitting of the root area ratio as function of root diameter was suitable for the large range of plant types investigated (including grass, shrubs and tree species). Future work should aim to establish β_ϕ parameters for a larger number of species and growing conditions to see whether it is feasible to obtain ‘averaged’ values for power coefficient β_ϕ, in a similar fashion to those established by Mao et al. (2012) for the tensile strength power law coefficients β_t.

Using continuous root diameters furthermore eliminates any errors caused by discretising root diameters into a limited number of root classes (e.g. the `sawtooth’ effect). Given that in this study for some species over a 100 diameter classes were required to push the error below 5%. This `sawtooth’ effect may be partially responsible for FBMs overestimating experimentally-measured root reinforcement as the number of classes used in practice is relatively small, e.g. 4 (Genet et al. 2008; Mao et al. 2012; Ji et al. 2020), 15 (Schwarz et al. 2010; Moos et al. 2016) or 20 (Comino et al. 2010). Adding Weibull survival functions reduces but not eradicates this error. This error may also be reduced by artificially distributing the root diameters within each class, for example by using probabilistic functions (e.g. Ji et al. 2020). Using the continuous approach eliminates the need for iterative calculation algorithms which may a source of additional (numerical) errors.

The proposed generic fibre bundle framework reduces rather than increases the number of root reinforcement models. It greatly simplifies calculations, exchange of data and comparisons between models without losing exactness or losing sight of underlying model assumptions as it contains no ‘fudge factors’ that may be site or species-specific. This standardisation will greatly help the root reinforcement community.

Conclusions

This paper set out to formulate a generic form for fibre bundle models. It systematically investigated the effect of various mechanisms for load sharing between roots on root reinforcement calculations. A continuous distribution of root diameter was implemented, allowing investigation of the effect of discretising root diameters into diameters classes prior to root reinforcement calculations. Key conclusions are:

• All existing fibre bundle models (including the Root Bundle Model) are essentially iterations of the same generic FBM but with different assumptions for load sharing parameter β_F;

• A new, physics-based load sharing law was proposed based on Waldron (1977)’s model for mobilisation of root stresses;

• The distribution of the root area ratio over the range of root diameters can be accurately captured using a continuous distribution based on the smallest and largest root diameter and a power law coefficient. Once these are known, the time-consuming process of measuring the diameter of every root may no longer be required;

• An exact, analytical solution for the peak root reinforcement was derived for any combination of root parameters and load sharing rule (FBMc). When Weibull survival functions are added to this model, values for the peak reinforcement can directly be determined using a simple design chart (FBMcw, Fig. 7);

• Including Weibull survival functions only substantially reduced the predicted reinforcement when the effect of inter-diameter load sharing is limited. Otherwise, the influence of load sharing β_F is dominant;

• The common practice of using discrete root diameter classes in traditional fibre bundle model calculations may result in a substantial overestimation of peak root reinforcement. These are caused by sawtooth-like effects associated with (sudden) failure of discrete roots. These can be avoided by using continuous root diameter distributions;

• The generic fibre bundle model approach provides clear insight into how these models operate, allows to make a rapid estimation of peak reinforcements w ithout the need for iterative procedures, and simplifies comparison between models in future work.