Two notions of fusion and the landscape of extensionality

Abstract

There are two main ways in which the notion of mereological fusion is usually defined in the current literature in mereology which have been labelled ‘Leśniewski fusion’ and ‘Goodman fusion’. It is well-known that, with Minimal Mereology as the background theory, every Leśniewski fusion also qualifies as a Goodman fusion. However, the converse does not hold unless stronger mereological principles are assumed. In this paper I will discuss how the gap between the two notions can be filled, focussing in particular on two specific sets of principles that appear to be of particular philosophical interest. The first way to make the two notions equivalent can be used to shed some interesting light on the kind of intuition both notions seem to articulate. The second shows the importance of a little-known mereological principle which I will call ‘Mild Supplementation’. As I will show, the mereology obtained by adding Mild Supplementation to Minimal Mereology occupies an interesting position in the landscape of theories that are stronger than Minimal Mereology but weaker than what Achille Varzi and Roberto Casati have labelled ‘Extensional Mereology’.

1 Introduction

The notion of mereological fusion is central to many debates in contemporary metaphysics. Two main definitions of this notion have been proposed in the literature which, following Cotnoir (2018), we can call ‘Leśniewski’ and ‘Goodman’ fusion, respectively.^,12 Let ‘$<$’ stand for the relation of proper parthood (which I will be assuming to be a primitive notion), and let us stipulate that x is part of y just in case x is either a proper part of y or identical to y, and that x and y overlap just in case they have a common part:

$$\left( {{\text{Parthood}}} \right)\quad x \le y =_{df} x < y \vee x = y$$

$$\left( {{\text{Overlap}}} \right)\quad Oxy =_{df} \exists z\left( {z \le x \wedge z \le y} \right)$$

By adopting the following abbreviations for ease of exposition (where ‘$yy$’ is a plural variable and ‘$\prec$’ is the one-many ‘one of’ relation)

$$xOyy =_{df} \exists z\left( {z \prec yy \wedge Oxz} \right)$$

$$xx \le y =_{df} \forall z\left( {z \prec xx \to z \le y} \right)$$

(‘$xOyy$’ and ‘$xx\le y$’ can be read as ‘x overlaps the yy’, and ‘all the xx are part of y’, respectively) the notions of Leśniewski fusion and Goodman fusion can be defined as follows:

$$\left( {{\text{L}} \text{-} {\text{def}}} \right)\quad xF^{L} yy =_{df} yy \le x \wedge \forall z\left( {z \le x \to zOyy} \right)$$

$$\left( {{\text{G}} \text{-} {\text{def}}} \right)\quad xF^{G} yy =_{df} \forall z\left( {Ozx \leftrightarrow zOyy} \right)$$

The mereological theory known in the literature as ‘Minimal Mereology’ (henceforth ‘MM’) can be axiomatized by means of the following two principles—transitivity of proper parthood and Weak Supplementation:

$$(<\text{-Transitivity})\quad \forall x\forall y\forall z\left( {\left( {x < y \wedge y < z} \right) \to x < z} \right)$$

$$\left( {{\text{WSP}}} \right)\quad \forall x\forall y\left( {x < y \to \exists z\left( {z \le y \wedge \sim Ozx} \right)} \right)$$

(notice that MM entails that proper parthood is a strict partial order, and so it is not only transitive but also irreflexive and asymmetric). As is well-known (see, for instance, Pietruszczak 2005: 216), in the presence of ($<$-Transitivity) every Leśniewski-fusion (or ‘L-fusion’ for short) qualifies as a Goodman-fusion (or ‘G-fusion’ for short):³

$$\left( {{\text{L}} \text{-} {\text{to}} \text{-} {\text{G}}} \right)\quad \forall x\forall yy\left( {xF^{L} yy \to xF^{G} yy} \right)$$

However, even under the assumption of MM, we don’t have that every G-fusion qualifies as an L-fusion, as one can easily appreciate from the model depicted in Fig. 1. In fact, as noted by Pietruszczak (2018: 147), Hovda (2009: 64–65) and Varzi (2009: 602), in Fig. 1 many pluralities of entities have a G-fusion without having an L-fusion. For instance, the plurality $[a,b,c,d]$ (that is, the plurality of entities that are identical to either a, b, c, or d)⁴ is G-fused by both a and b, and yet there is no entity that is their L-fusion, given that no entity has all of them as parts (as required by the first conjunct of (L-def)). It follows, therefore, that the following principle—stating that something is an L-fusion if and only if it is a G-fusion—is not a theorem of MM:

$$\left( {{\text{EqLG}}} \right)\quad \forall x\forall yy\left( {xF^{L} yy \leftrightarrow xF^{G} yy} \right)$$

Fig. 1

Not every G-fusion is an L-fusion

This naturally raises the question as to which pluralities of pairwise logically independent principles jointly entail (EqLG)—with MM in the background—and are entailed by it. In other words: let say that a plurality ${S}_{1},\dots ,{S}_{n}$ of sentences (taken together) are a way of expressing (or, more simply, express) the difference between L-fusions and G-fusions just in case the following is true:

$$\begin{array}{*{20}l} {\left( {{\text{Diff}}} \right)} \hfill & {\left( {\text{i}} \right)} \hfill & {{\text{for}}\;{\text{every}}\; m {\text{ and }}o \;(1 \le m/o \le n),\;\;{\text{if}},\;m \ne o\;{\text{then}}\;\;{\mathbf{MM}},S_{m} { \nvdash }S_{o} } \hfill \\ {} \hfill & {({\text{ii}})} \hfill & {{\mathbf{MM}},S_{1} , \ldots ,S_{n} { \vdash }\left( {{\text{EqLG}}} \right)\;\;{\text{and}},\;{\text{for}}\;{\text{every}}\;m\;(1 \le m \le n),\;\;{\mathbf{MM}},\left( {{\text{EqLG}}} \right){ \vdash }S_{m} } \hfill \\ \end{array}$$

The question raised by the considerations just made is, thus, the following: which pluralities of sentences comply with (Diff) and, thus, ‘express the difference’ between L-fusions and G-fusions?

The aim of this paper is not to list all the possible ways to express the difference between L-fusions and G-fusions. Rather, I will only discuss two ways to do so that appear to be of particular interest. In the literature, it is a well-known fact that, assuming ($<$-Transitivity), (EqLG) is equivalent to Strong Supplementation (and, thus, that (SSP) complies with (Diff)):

$$\left( {{\text{SSP}}} \right)\quad \forall x\forall y\left( {x{ \nleqslant }y \to \exists z\left( {z \le x \wedge \sim Ozy} \right)} \right)$$

(Pietruszczak 2005: 218, 2018: 142; Gruszczyński 2013: 140; Varzi 2016: section 4.3). As I will argue in Sect. 2, however, there is a way to reach this result which shows how (L-def) and (G-def) can be seen as articulating the same, highly plausible intuition concerning the notion of mereological fusion. In Sect. 3, I will argue that there is a second way of articulating the difference between L-fusions and G-fusions on the background of MM which reveals the importance of a little-known mereological principle that I will label ‘Mild Supplementation’. As I will show, Mild Supplementation will allow us to unearth a theory which appears to occupy an interesting position in the logical space lying between MM and the theory that Casati and Varzi (1999) call ‘Extensional Mereology’.

2 L-fusions, G-fusions and strong supplementation

According to the definition of L-fusion, an entity x is an L-fusion of a plurality yy of entities just in case all the yy are part of x and every part of x overlaps at least one of the yy. Instead, according to the definition of G-fusion, an entity x is a G-fusion of a plurality yy of entities just in case something overlaps x if and only if it overlaps one of the yy:

$$\left( {{\text{L}} \text{-} {\text{def}}} \right)\quad xF^{L} yy =_{df} yy \le x \wedge \forall z\left( {z \le x \to zOyy} \right)$$

$$\left( {{\text{G}} \text{-} {\text{def}}} \right)\quad xF^{G} yy =_{df} \forall z\left( {Ozx \leftrightarrow zOyy} \right)$$

Consider, then, the second conjunct of (L-def).

(1)	$\forall z\left(z\le x\to zOyy\right)$

Notice that, under the assumption of MM, (1) is equivalent to⁵:

(2)	$\forall z\left(Ozx\to zOyy\right)$

But (2) is just the left-to-right direction of (G-def). Consider, then, the right-to-left direction of (G-def):

(3)	$\forall z\left(zOyy\to Ozx\right)$

(3) can be unpacked as:

(4)	$\forall z\left(\exists w\left(w\prec yy\wedge Owz\right)\to Ozx\right)$

In turn, (4) is logically equivalent to:

(5)	$\forall z\left(z\prec yy\to \forall w\left(Owz\to Owx\right)\right)$

Let, then, an entity x be covered by an entity y (‘$x\sqsubseteq\,y$’) if and only if everything that overlaps x also overlaps y:

(6)	$x\sqsubseteq y=_{df}\forall z\left(Ozx\to Ozy\right)$

The right-to-left direction of (G-def) can, then, be rewritten as follows:

(7)	$\forall z\left(z\prec yy\to z\sqsubseteq\,x\right)$

Putting everything together, we have that, under the assumption of MM, (L-def) and (G-def) are equivalent to the following two definitions:

$$\left( {{\text{L}} \text{-} {\text{def}} + } \right)\quad xF^{L} yy =_{df} \forall z\left( {z \prec yy \to z \le x} \right) \wedge \forall z\left( {z \le x \to zOyy} \right)$$

$$\left( {{\text{G}} \text{-} {\text{def}} + } \right)\quad xF^{G} yy =_{df} \forall z\left( {z \prec yy \to z{ \sqsubseteq }x} \right) \wedge \forall z\left( {z \le x \to zOyy} \right)$$

Consider the following principle employing pre-theoretic notions of ‘containment’ and ‘covering’ (and in which ‘fusion’ can be taken to be a dummy term for an object that is made from a plurality of entities):

(Fusion) A an entity x is a fusion of a plurality yy of entities just in case (i) x ‘contains’ all the yy, and (ii) the yy ‘cover’ all of x.

(Fusion) strikes me as a highly intuitive principle. If x didn’t ‘contain’ z and z was one of the yy, how could one say that x a fusion of them? At the same time, if some part of x wasn’t completely ‘covered’ by the yy—if some part of x was free of the yy, so to speak—how could a fusion of the yy be identical to x? (L-def+) and (G-def+) allow one to appreciate at a glance how close the two definitions are. Both (L-def+) and (G-def+) consist, in fact, in a conjunction which can be seen as formulating the two conditions expressed by (Fusion). The ‘covering condition’ is expressed in the second conjunct of (L-def+) and (G-def+) in the same way: x is covered by the yy in the sense that every part of x overlaps at least one of the yy, so that no part of x is disjoint from—and, in this sense, ‘free of’—all of them. We can call this sense of covering plural covering (or many-one covering). The difference between (L-def+) and (G-def+) concerns the way in which the ‘containment condition’ is expressed in their first conjunct. According to (L-def+), to contain an entity is to have it as a part, so that x can contain all the yy only if it has all of them as parts. Instead, according to (G-def+), to contain an entity is to cover it, in the sense of overlapping everything it overlaps (we can call this sense of covering singular covering, or one–one covering, for disambiguation). Therefore, (L-def+) and (G-def+) can be seen as disagreeing on how the pre-theoretical notion of (mereological) ‘containment’ should be properly expressed.⁶

Before moving further, notice that a third definition of the notion of fusion can be found in the literature, which following Cotnoir (2018) we can call ‘Algebraic’ fusion:

$\left( {{\text{A}} \text{-} {\text{def}}} \right)\quad xF^{A} yy =_{df} \forall z\left( {z \prec yy \to z \le x} \right) \wedge \forall z\left( {\forall w\left( {w \prec yy \to w \le z} \right) \to x \le z} \right)$

(A-def) gets the ‘containment part’ of (Fusion) right (or, at least, in a way that is at least prima facie legitimate). The problem with (A-def) is the way it gets the ‘covering part’ of (Fusion). Consider, for instance, the model depicted in Fig. 2. In Fig. 2a counts as an A-fusion of $[b,d]$. Yet there is clearly more to a than just b and d taken together, namely, c. b and d taken together clearly fail to cover all of a. Therefore, as long as we follow (Fusion) as our guiding intuition, the notion of A-fusion appears to fall short of being a live option to define the notion of mereological fusion.⁷

Fig. 2

a is an A-fusion of [b,d]

Also the notion of G-fusion may be subjected to some criticism. Consider, in fact, the model depicted in Fig. 1. a is a fusion of $[a,b,c,d]$ and yet it doesn’t have b as a part. However, as Varzi (2009) claims, it may seem that

[…] no matter how exactly one defines the word, one should always expect a fusion to include, among its parts, all the things it fuses. (Varzi 2009: 602)

Even worse, a is a fusion of [b]—the ‘improper’ plurality of the things that are identical to b—without having it a part. Yet, it may seem plausible to object that

surely a fusion is supposed to include, among its parts, at least some of the things it fuses. (Varzi 2009: 603)

Notice, first, that G-mereologists endorsing a notion of ‘containment-as-covering’ agree that a fusion must contain all the entities it fuses. What they deny is that, in order to be contained by their fusion, the entities fused must be part of the fusion. Therefore, simply replying that a fusion must contain all the entities it fuses as parts seems to be dialectically ineffective in this case. Second, G-mereologists appear to have an independent way to argue that in Fig. 1a and b do contain each other, namely, by appealing to the idea that a fusion is ‘nothing over and above’ the plurality of its proper parts. This argument can be presented as follows:

(A1)	For every x and y and zz, if x contains the zz and y is nothing over and above the zz, then x also contains y
(A2)	In Fig. 1, a contains [c,d]
(A3)	b is nothing over and above [c,d]
(A4)	Therefore, a contains b

1. (A2) is something that also containment-as-parthood theorists like Varzi (2009) accept. Therefore, whether or not this argument is successful depends on whether G-theorists can appeal to a notion of nothing-over-and-aboveness that is both compatible with anti-extensionalism and such as to make (A1) and (A3) true.

Many philosophers share the intuition that a whole is nothing over and above the parts it fuses⁸: if I buy separately the four parts composing a certain lot of land, I don’t need to also buy the lot they compose. Similarly, if I buy six cans of beer, I don’t need to spend extra money to also buy the six-pack (Baxter 1988). Several ways to cash out the slippery notion of nothing-over-and-aboveness have been proposed in the literature.⁹ However, many of them appear to be incompatible with anti-extensionalist models like the one depicted in Fig. 1. For instance, G-theorists cannot take a whole to be nothing over and above its parts in the sense that it is literally identical to its parts taken together (a thesis commonly known as ‘Strong Composition as Identity’).¹⁰ In fact, if both a and b in Fig. 1 were identical to the plurality of their proper parts then (by symmetry and transitivity of identity) they themselves would be identical. Similarly, G-mereologists cannot take a composite entity to be nothing over and above its parts in the sense that it is the only object that is composed of those parts (Smid 2017: 2; 12, fn 2), as that would also be straightforwardly inconsistent with Fig. 1. More generally, the idea that anti-extensionalists cannot claim that entities sharing the same proper parts are nothing over and above them may indeed seem to have the ring of intuitiveness to it:

if some Xs compose two things, then wholes could not be “nothing over and above their parts.” How could distinct things each be nothing over and above the same parts? (Sider 2007: 70; my italics)

Gilmore (2010: 181) formulates the principle that appears to be behind Sider’s (2007) intuition as follows:

‘P1 For any Xs, any y, and any z, if y is nothing over and above the Xs, and z is nothing over and above the Xs, then y = z’ (Gilmore 2010: 181)

As Gilmore argues, as intuitive as P1 may initially sound, there seem to be good reasons to doubt it. Consider, in fact, the following principle P1+ which extends P1 to pluralities of entities:

‘P1+ For any Xs, any Ys, and any Zs, if [the Ys are nothing over and above the Xs, the Zs are nothing over and above the Xs, and there are exactly as many of the Ys as there are of the Zs], then the Ys = the Zs.’ (Gilmore 2010: 181)

If being nothing over and above is ‘identity-like’ as P1 suggests, it seems that also P1+ should be accepted as true. However, P1+ is intuitively false: both the rows and the columns in my chessboard (which are equal in number) are nothing over and above the squares of my chessboard, and yet they are not identical (the rows run horizontally, the columns vertically). It seems, therefore, that if we are ‘free to endorse the nonidentity of pluralities […] each of which [are] nothing over the same things’ we should also be ‘free to endorse the nonidentity of single individuals [that are] nothing over and above the same things’ (Gilmore 2010: 182).

Furthermore, there seems to be at least one possible way to account for the notion of ‘being nothing over and above’ that is both consistent with anti-extensionalist models like the one of Fig. 1 and with premises (A1) and (A3). The general idea behind this account can be briefly sketched as follows. Intuitively, certain entities seem to depend for their existence on other entities. In particular, composite entities are often claimed to depend for their existence on their proper parts. This notion of existential dependence can be understood by means of the notion of metaphysical grounding, in at least two ways.¹¹ The first one, proposed by Correia (2005) and Schnieder (2006), is that of taking an entity x to depend existentially on a plurality yy of entities if and only if the fact that x exists is grounded in some facts concerning the yy. Alternatively, one could follow Schaffer (2009) and identify this notion of dependence with a primitive, cross-categorical relation of grounding.^{12, 13} In both cases, there seems to be at least some intuitive appeal to the idea that, if x’s existence is grounded in the yy, then x owes its existence to the yy, so that x and the yy are really the same ‘portion of reality’, or the same ‘amount of being’, so to speak.¹⁴ This suggests the possibility of the following kind of grounding-based account of nothing-over-and-aboveness:

(NOA) The xx are nothing over and above the yy if and only if either (i) the xx depend for their existence on the yy, (ii) the yy depend for their existence on the xx, or (iii) for some zz, both the xx and the yy depend for their existence on the zz.

According to (NOA), in order for the xx to really ‘add something’ to the yy in the required sense, the portion of reality in which the xx consist must not be completely contained in the portion of reality in which the yy consist. Therefore, in order to be something over and above the yy the xx cannot stand in a grounding relation to the yy or share a common ground with them. Given (NOA), (A3) follows directly from the assumption that b is grounded in [c,d], while (A1) appears to have at least the ring of plausibility to it. Suppose, in fact, that an entity x contains the zz and that the existence of a certain other entity y is grounded in the zz. In this case, it seems plausible to say that—in virtue of containing the ‘ontological root’ of y (as we may call it)—x also contains y.¹⁵

Both this kind of account of the notion of being nothing over and above in terms of grounding and the general idea that anti-extensionalism is compatible with nothing-over-and-aboveness may, of course, be challenged. Be that as it may, however, the foregoing considerations seem to show at least that the case against the notion of G-fusion is not as tight as it may appear at first sight and certainly not as straightforward as the case against the notion of A-fusion. Therefore, we seem to have at least some prima facie reason to conclude that, pace Sider (2007) and Varzi (2009), both the notion of L-fusion and the notion of G-fusion can be taken to be admissible notions of fusion.

Let us now return to the issue concerning the difference between L-fusions and G-fusions. It is a theorem of MM that parthood entails covering¹⁶:

(8)	$\forall x\forall y\left(x\le y\to x\sqsubseteq\,y\right)$

It is, thus, straightforward to observe from the first conjuncts of (L-def+) and (G-def+) that (assuming MM) if something is an L-fusion (of a certain plurality of entities) it is also a G-fusion (of those entities):

(9)	$\forall x\forall yy\left(x{F}^{L}yy\to x{F}^{G}yy\right)$

In the same way, it is also straightforward to see what principle can fill by itself the gap between the two notions. In fact, if an entity x is a G-fusion of some entities yy, then although the yy cover all of x (as required by the second conjunct of (L-def+)) we only have that if something is one of the yy, it is only guaranteed to be covered by x and not to be part of it. It is, thus, sufficient to add to the mix the principle according to which if x is covered by y, then x is part of y—

(10)	$\forall x\forall y\left(x\sqsubseteq\,y\to x\le y\right)$

—in order to guarantee that every G-fusion is also an L-fusion:

(11)	$\forall x\forall yy\left(x{F}^{G}yy\to x{F}^{L}yy\right)$

Notice that if we unpack (10) we get.

(12)	$\forall x\forall y\left(\forall z\left(Ozx\to Ozy\right)\to x\le y\right)$

which, given MM, is equivalent to the Strong Supplementation principle¹⁷

$$\left( {{\text{SSP}}} \right)\quad \forall x\forall y\left( {x{ \nleqslant }y \to \exists z\left( {z \le x \wedge \sim Ozy} \right)} \right)$$

Therefore, MM and (SSP) jointly entail (EqLG):

(13)	$\mathbf{M}\mathbf{M},(\mathrm{SSP})\vdash(\mathrm{EqLG})$

Similarly, it can be proved that (EqLG) and MM jointly entail (SSP).

(14)	$\mathbf{M}\mathbf{M},(\mathrm{EqLG})\vdash(\mathrm{SSP})$

Proof

Suppose that x is covered by y. Clearly, y covers itself. Therefore, each of the $[x,y]$ (that is, the plurality of x and y taken together) is covered by y. On the other hand, every part of y overlaps at least some of the $[x,y]$, since $y$ clearly overlaps itself. Therefore y is a G-fusion of $[x,y]$. From (EqLG) it follows that $y$ is also an L-fusion of the $[x,y]$, so that $x$ is a part of $y$. We have, thus, proved (10), and namely that, for every $x$ and every $y$, if x is covered by y, then $x$ is a part of $y$. As we have just seen above, given MM (10) is equivalent to (SSP). ■

We can, thus, conclude that (SSP) is a way to express the difference between L-fusions and G-fusions on the background of MM:

(Difference 1)

$\mathbf{M}\mathbf{M},(\mathrm{SSP})\vdash(\mathrm{EqLG})$ and $\mathbf{M}\mathbf{M},(\mathrm{EqLG})\vdash(\mathrm{SSP})$

This result shouldn’t come as a surprise: the fact that, in the presence of (SSP), (L-def) and (G-def) are equivalent is well-known in the literature.¹⁸ It is, however, the way in which we reached this result that is particularly interesting. In fact, what we have done in this section is to unpack both definitions of mereological fusion so as to make a ‘containment’ part (requiring the fusion to ‘contain’ in some sense all the things it fuses) and a ‘covering’ part (requiring the things fused to completely ‘cover’ the fusion) explicit. This allowed us to interpret the difference between the two notions of fusion as a different way of articulating the notion of containment at play in the definition of fusion: containment-as-parthood and containment-as-covering. At that point, the ‘gap’ between the two notions emerged very naturally as the requirement that covering entail parthood, which is just a different way to express (SSP). Therefore, in this section we haven’t just proved that (SSP) is a way to express the difference between L-fusions and G-fusions. We have also provided a seemingly intuitive explanation as to why that is the case, namely because (SSP) functions as a bridge principle between the two different notions of containment in play.

3 Mild Supplementation and Extensionality

The model of Fig. 1 was used to show that, if MM is the only mereological assumption in the background, then not every G-fusion is an L-fusion. Figure 1 is a counterexample to Extensionality of Proper Parthood:

$$\left( {{\text{EPP}}} \right) \forall x\forall y\left( {\exists z\left( {z < x} \right) \to \left( {\forall z\left( {z < x \leftrightarrow z < y} \right) \to x = y} \right)} \right)$$

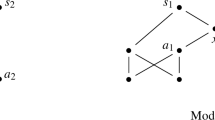
This may lead one to suppose that (EPP) is another way to express the difference between the two notion of fusions. However, the model depicted in Fig. 3 clearly shows that this is not the case. Consider, in fact, the plurality [${b}_{1}$,${b}_{2}$,${b}_{3}$] (the ‘bs’). a is clearly a G-fusion of the bs, as it covers all of them and it is covered by them (taken together). However, no entity in Fig. 3 is an L-fusion of the bs, as no entity in Fig. 3—not even a—has all the bs as parts. Figure 3 is a model of (EPP). Therefore, (EPP) is not enough to fill the gap between L-fusions and G-fusions.

Fig. 3

A model of (EPP) that is not a model of (EqLG)

In Fig. 3a would qualify as a fusion of the bs if it had all of the bs as parts. In that case each of the bs would be a proper part of a. This is, thus, what may appear to be odd about Fig. 3¹⁹: a covers each of the bs, none of the bs covers a, and yet none of the bs is a proper part of a. Therefore, it is sufficient to add the following principle to MM (which I will label ‘Mild Supplementation’) to ensure that in Fig. 3a is also an L-fusion of the bs²⁰:

$$\left( {{\text{MSP}}} \right)\quad \forall x\forall y\left( {\left( {x{ \sqsubseteq }y \wedge y\not\sqsubseteq\,x} \right) \to x < y} \right)$$

or, in its contrapositive form

$$\left( {{\text{MSPc}}} \right)\quad \forall x\forall y\left( {x{ \nless }y \to \left( {x\not\sqsubseteq\,y \vee y{ \sqsubseteq }x} \right)} \right)$$

which is equivalent to the following formulation:

$$\left( {{\text{MSPc2}}} \right)\quad \forall x\forall y\left( {x{ \nless }y \to \left( {x{ \sqsubseteq }y \to y{ \sqsubseteq }x} \right)} \right)$$

Notice that, given MM, (SSP) is equivalent to the following principle:

$$\left( {{\text{SSP2}}} \right)\quad \forall x\forall y\left( {x{ \nless }y \to \left( {x{ \sqsubseteq }y \to x = y} \right)} \right)$$

Therefore, for every x and y such that x is not a proper part of y and yet it is covered by y we have that, while (SSP2) demands that x be identical to y (thus excluding both models like the one depicted in Figs. 1 and in 3), (MSPc2) requires only that x cover y (thus excluding only models like the one in Fig. 3 and leaving the door open to failure of extensionality).

(MSP) and (EPP) are independent principles. Figure 1 is a model of (MSP) but not of (EPP), while Fig. 3 is a model of (EPP) but not of (MSP). Furthermore, as Figs. 1 and 3 witness, both (MSP) and (EPP) are weaker than (SSP). However, (under the assumption of MM) (SSP) entails both (MSP) and (EPP), while (MSP) and (EPP) jointly entail (SSP):

(15)	a.	$\mathbf{M}\mathbf{M},(\mathrm{SSP})\vdash(\mathrm{MSP})$
	b.	$\mathbf{M}\mathbf{M},(\mathrm{SSP})\vdash(\mathrm{EPP})$
	c.	$\mathbf{M}\mathbf{M},(\mathrm{MSP}),(\mathrm{EPP})\vdash(\mathrm{SSP})$

The proofs of both (15a) and (15b) are straightforward.²¹ The proof of (15c) can be presented as follows. First, we prove that MM and (MSP) jointly entail the principle ‘(OPP)’ according to which entities overlapping the same entities have the same proper parts

$$\left( {{\text{OPP}}} \right)\quad \forall z\left( {Ozx \leftrightarrow Ozy} \right) \to \forall z\left( {z < y \leftrightarrow z < x} \right)$$

(16)	$\mathbf{M}\mathbf{M},(\mathrm{MSP})\vdash(\mathrm{OPP})$

Proof

Suppose that x and y overlap the same entities. Suppose, for reductio, that some entity w is a proper part of only one of them (say, of x). w is not a proper part of y. It follows from (MSP) that either w is not covered by y or y is covered by w. Since w is a proper part of x, everything that overlaps w also overlaps x (by the transitivity of parthood). But we are assuming that everything that overlaps x also overlaps y. Therefore, everything that overlaps w overlaps y so that w is covered by y. Therefore, y is covered by w, so that everything that overlaps y also overlaps w. w is a proper part of x. It follows by (WSP) that some entity k is part of x and doesn’t overlap w. Therefore, k doesn’t overlap y. But we are assuming that x and y overlap the same entities, so that k doesn’t overlap x either. Yet, k is a proper part of x and so it overlaps x. Contradiction! Therefore, for every x and y, if x and y overlap the same entities they have the same proper parts. ■

Second, we show that MM, (MSP), and (EPP) jointly entail (SSP):

(17)	$\mathbf{M}\mathbf{M},(\mathrm{MSP}),(\mathrm{EPP})\vdash(\mathrm{SSP})$

Proof

Suppose that x is not part of y and that yet every part of x overlaps y. It follows by the transitivity of parthood that everything that overlaps x also overlaps y or, in other words, that x is covered by y. Since x is not a part of y, x is not a proper part of y. By (MSP) we have that either x is not covered by y or y is covered by x. y is, thus, covered by x. x and y cover each other. By (OPP) they have the same proper parts. Suppose that x is an atom (the reasoning being similar in the case of y). x is, thus, a part of y that is different from y. Therefore, x is a proper part of y. But x and y have the same proper parts, so that x is a proper part of itself, contra the irreflexivity of proper parthood. Therefore, x and y are two different composite entities with the same proper parts. By (EPP), they are identical. Contradiction! Therefore, some part of x doesn’t overlap y. By generalization it follows that, for every x and y, if x is not a part of y, then some part of x doesn’t overlap y. ■

From (15) and (Difference-1) it follows, thus, that (MSP) and (EPP) taken together are a further way to express the difference between L-fusions and G-fusions:

(Difference 2)	$\mathbf{M}\mathbf{M},(\mathrm{MSP})\nvdash(\mathrm{EPP})$ and $\mathbf{M}\mathbf{M},(\mathrm{EPP})\nvdash(\mathrm{MSP})$
	$\mathbf{M}\mathbf{M},(\mathrm{MSP}),(\mathrm{EPP})\vdash(\mathrm{EqLG})$
	$\mathbf{M}\mathbf{M},(\mathrm{EqLG})\vdash(\mathrm{MSP})$ and $\mathbf{M}\mathbf{M},(\mathrm{EqLG})\vdash(\mathrm{EPP})$

4 Between minimal mereology and extensional mereology

Casati and Varzi (1999) call ‘Extensional Mereology’ (‘EM’) a theory that is equivalent to MM+(SSP) (and, thus, to MM+(EPP)+(MSP)). They justify the label ‘extensional’ with the fact that EM rules out countermodels to (EPP) (Casati and Varzi 1999: 40). Other extensionality principles that can be found in the literature are the principles ‘Extensionality of Overlap’, ‘Uniqueness of G-Fusion’, and ‘Uniqueness of L-Fusion’:

$$\left( {{\text{EO}}} \right)\quad \forall x\forall y\left( {\forall z\left( {Ozx \leftrightarrow Ozy} \right) \to x = y} \right)$$

$$\left( {{\text{UGF}}} \right)\quad \forall x\forall y\left( {\exists zz\left( {xF^{G} zz \wedge yF^{G} zz} \right) \to x = y} \right)$$

$$\left( {{\text{ULF}}} \right)\quad \forall x\forall y\left( {\exists zz\left( {xF^{L} zz \wedge yF^{L} zz} \right) \to x = y} \right)$$

In addition we also have the principle that Varzi (2008) calls ‘Extensionality of Composition’:

(EC)	‘If x and y are composed of the same things, then x = y’ (Varzi 2008: 109).

where

(C)	‘x is composed of the zs = df x is a [fusion] of the zs and the zs are pairwise disjoint (i.e., no two of them have any parts in common)’ (Varzi 2008: 109; see also van Inwagen 1990: 29)

Letting ‘${\mathbb{D}}xx$’ stand for ‘the xx are pairwise disjoint’

$$\left( {{\mathbb{D}} \text{-} {\text{def}}} \right)\quad {\mathbb{D}}xx =_{df} \forall x\forall y\left( {\left( {x \prec xx \wedge y \prec xx \wedge x \ne y} \right) \to \sim Oxy} \right)$$

we can define two notions of composition in this sense, namely, Goodman-composition (or G-composition) and Leśniewski-composition (or L-composition):

$$\left( {{\text{GC}}} \right)\quad xxC^{G} y =_{df} yF^{G} xx \wedge {\mathbb{D}}xx$$

$$\left( {{\text{LC}}} \right)\quad xxC^{L} y =_{df} yF^{L} xx \wedge {\mathbb{D}}xx$$

In turn, (GC) and (LC) allow us to state two different versions of Varzi’s principle (EC):

$$\left( {{\text{EGC}}} \right)\quad \forall x\forall y\left( {\exists zz\left( {zzC^{G} x \wedge zzC^{G} y} \right) \to x = y} \right)$$

$$\left( {{\text{ELC}}} \right)\quad \forall x\forall y\left( {\exists zz\left( {zzC^{L} x \wedge zzC^{L} y} \right) \to x = y} \right)$$

Most of the ways in which (with MM in the background) (SSP), (EPP), (EO), (UGF), (ULF), (EGC), and (ELC) relate to each other are well-known in the literature. It may be useful to briefly review them in turn²²:

• (a) (EPP) doesn’t entail any of the other principles. For instance, the model depicted in Fig. 4 is a model of (EPP) but not a model of either (EO), (UGF), (ULF), (EGC), or (ELC). In fact, although a₁ and a₂ are different, they (i) overlap the same entities (contra (EO) and (ii) are both G-fusions and L-fusions of the cs (contra (UGF), (ULF), (EGC), and (ELC)).

  Fig. 4

  

  A model of (EPP) that is not a model of either (EO), (UGF), (ULF), (EGC), or (ELC)

• (b) MM and (EO) jointly entail (EPP)²³:

  (18)	$\mathbf{M}\mathbf{M},(\mathrm{EO})\vdash\left(\mathrm{EPP}\right)$

• (c) MM+(EO), MM+(UGF), and MM+(ULF) are logically equivalent. One elegant way to prove this is due to Pietruszczak (2018: 85–86, 144) and can be briefly reformulated within this framework as follows.²⁴ First, it is proved from ($<$-Transitivity) that if every part of x overlaps y, then x is an L-fusion of the plurality of entities that are parts of both x and y:²⁵²⁶

  (19)	$\forall z\left(z\le x\to Ozy\right)\to x{F}^{L}(\iota xx.\forall z\left(z\prec xx\leftrightarrow \left(z\le x\wedge z\le y\right)\right)$

Given (19), (EO) can be shown to be equivalent to (ULF), under the assumption of MM²⁷:

(20)	a. $\mathbf{M}\mathbf{M},$ (EO) $\vdash$ (ULF)
	b. $\mathbf{M}\mathbf{M},$ (ULF) $\vdash$ (EO)

Finally, (20) can be used to prove that, given MM, (UGF) and (ULF) are equivalent²⁸:

(21)	$\mathbf{M}\mathbf{M},$(UGF) $\vdash$ (ULF) and $\mathbf{M}\mathbf{M},$ (ULF) $\vdash$ (UGF)

• (d) EM isn’t entailed by either MM+(EO) or MM+(ELC):

  (22) $\mathbf{M}\mathbf{M},(\mathrm{EO})\nvdash\mathbf{E}\mathbf{M}$ and $\mathbf{M}\mathbf{M},(\mathrm{ELC})\nvdash\mathbf{E}\mathbf{M}$

  For instance, the model depicted in Fig. 3—which is a counter-model to EM —is a model of both MM+(EO) and MM+(ELC).

• (e) Finally, EM entails (EO)²⁹:

  (23)	$\mathbf{E}\mathbf{M}\vdash(\mathrm{EO})$

  In addition to (a)-(e) we clearly have that MM+(ULF) entails both (ELC) and (EGC):

  (24)	$\mathbf{M}\mathbf{M},(\mathrm{ULF})\vdash(\mathrm{ELC})$ and $\mathbf{M}\mathbf{M},(\mathrm{UGF})\vdash(\mathrm{EGC})$

Also, it follows directly from the fact that MM entails (L-to-G) (see Sect. 1) that (EGC) and MM jointly entail (ELC):

(25)	$\mathbf{M}\mathbf{M},\left(\mathrm{EGC}\right)\vdash\left(\mathrm{ELC}\right)$

Interestingly, given the axiom of choice it can also be proved that (ELC) and MM jointly entail (UGF):

(26)	$\mathbf{M}\mathbf{M},\left(\mathrm{ELC}\right)\vdash\left(\mathrm{UGF}\right)$

Proof

Part I. Suppose a and b are both G-fusions of the zz (which may or may not be pairwise disjoint). Let W be the non-empty set of parts that a and b have in common,³⁰$R$ be a well-order on W,³¹${e}_{1}$ be the least element of W under $R$, and ${\mathbb{S}}$ be a subset of W that is defined as follows:

• (i) ${e}_{1}\in {\mathbb{S}}$;

• (ii) $\forall x\left(\left(x\in W\wedge \left(\forall y\left(yRx\wedge y\in {\mathbb{S}}\right)\to Dxy\right)\right)\to x\in {\mathbb{S}}\right)$(an item in W is in ${\mathbb{S}}$ whenever every R-smaller item in ${\mathbb{S}}$ is disjoint from it);

• (iii) nothing else is a member of ${\mathbb{S}}$.³²

We have, thus, the following: (a) ${e}_{1}$ is disjoint from any other member of ${\mathbb{S}}$³³; (b) any two other members c and d of ${\mathbb{S}}$ are disjoint.³⁴ Therefore, the members of ${\mathbb{S}}$ are pairwise disjoint.³⁵

Part II. Suppose that z is a part of a. If z is a member of ${\mathbb{S}}$, then it clearly overlaps some member of ${\mathbb{S}}$ (by $\le$-reflexivity). Suppose that z is not a member of ${\mathbb{S}}$. Since a and b are G-fusions of the same plurality of entities it follows from (G-def) that they overlap the same entities. By the reflexivity of parthood, z overlaps a. Therefore, z also overlaps b and has, thus, a part v in common with b. By the transitivity of parthood v is a member of W (namely, the set of entities that are parts of both a and b; see Part I). If v is also a member of ${\mathbb{S}}$, then z clearly overlaps some member of ${\mathbb{S}}$ (by $\le$-reflexivity). If v is not a member of ${\mathbb{S}}$, it follows from the definition of ${\mathbb{S}}$ that some member w of ${\mathbb{S}}$ is such that $wRv$ and v overlaps w. Since v is part of z, the part that v has in common with w is also part of z (by $\le$-transitivity) so that z overlaps w. Therefore, in each of these cases z overlaps some member of ${\mathbb{S}}$. By generalization, we have that every part of a overlaps some member of ${\mathbb{S}}$. By symmetry of reasoning, we can also conclude that every part of b overlaps some member of ${\mathbb{S}}$.

Part III. Let the cc be the plurality of entities that are in ${\mathbb{S}}$. Each of the cc is part of both a and b. As we just proved in Part II, every part of either a or b overlaps the cc. Therefore, both a and b are an L-fusion of the cc. The cc are pairwise disjoint. It follows, thus, from (ELC) that a and b are identical.³⁶ ■

It follows from (21), (24), and (26) that (pace Varzi 2008: 110–111),³⁷ given MM, (EO), (ELC), (EGC), (UGF), and (ULF) are all equivalent:

(27)	MM+(EO)=MM+(ELC)=MM+(EGC)=MM+(UGF)=MM+(ULF)

Notice, finally, that MM+(EO) doesn’t entail MM+(MSP):

(28)	$\mathbf{M}\mathbf{M},\left(\mathrm{EO}\right)\nvdash\mathbf{M}\mathbf{M}$+(MSP)

For instance, the model depicted in Fig. 3 is a model of MM+(EO) but not of MM+(MSP).

Therefore, it can be concluded that that MM+(MSP) appears to occupy an interesting place among the theories under consideration (see Fig. 5).³⁸ In fact, while MM+(MSP) is a non-extensional mereology that is stronger than MM,³⁹ the only extensional mereology (among those under consideration) that is stronger than MM+(MSP) is EM.

Fig. 5

Some of the theories between MM and EM

5 Conclusion

In this paper I have addressed the question concerning the ‘difference’—with MM in the background—between the notion of Leśniewski fusion and the notion of Goodman fusion. Although it is well known that the Strong Supplementation principle is sufficient to fill this gap, I have argued that this fact can be proved in a way that sheds some interesting light on the relationship between the two notions of fusion. I have also shown how the difference between Leśniewski fusions and Goodman fusions can be broken down into two logically independent components, namely, the well-known principle Extensionality of Proper Parthood and the lesser-known Mild Supplementation. Finally, the theory combining Minimal Mereology and Mild Supplementation has also emerged as a non-extensional theory that occupies an interesting position in the logical space of theories that are stronger than Minimal Mereology but weaker than Casati and Varzi’s (1999) Extensional Mereology.⁴⁰