Abstract
International comparative assessments of student achievement are constructed to assess country-level differences and change over time. A coherent understanding of the international trends in educational outcomes is strongly needed as suggested by numerous previous studies. Investigating these trends requires long-term analysis, as substantial changes on the system level are rarely observed regarding student outcomes in short periods (i.e., between adjacent international assessment cycles). The present study aims to link recent and older studies conducted by the International Association for the Evaluation of Educational Achievement (IEA) onto a common scale to study long-term trends within and across countries. It explores the comparability of the achievement tests of the Trends in International Mathematics and Science Study and previous IEA studies on mathematics in grade eight. Employing item response theory, we perform a concurrent calibration of item parameters to link the eight studies onto a common scale spanning the period from 1964 to 2015 using data from England, Israel, Japan, and the USA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For more than half a century, international large-scale assessments (ILSAs) have provided a large body of data on student achievement from a vast number of educational systems all over the world. ILSAs are constructed to compare educational systems and assess country-level change (Strietholt and Rosén 2016). The results of ILSAs are presented in different ways outside the research community, fueling political discussion on for example school reforms (e.g., Braun and Singer 2019). Without a doubt, the country rankings based on ILSA results have gained considerable attention in many countries. Klemenčič and Mirazchiyski (2018) argue that league tables should not be perceived as the ultimate product of ILSAs and the responsibility for interpretation lies with the researchers’ working on the ILSA data. While the results of ILSAs may be used as snapshots for countries’ performances, the longitudinal component on the country level warrant analyses with a larger scope. However, to facilitate analyses of quasi-longitudinal designs (e.g., fixed effects) for causal inference as well as adequate cross-country comparisons, data must be made comparable both within and between countries.
Data gathered by the IEA provides a rich source for further secondary analyses. Many countries lack sufficient national evaluation or monitoring systems that facilitate comparisons over time. Such countries may use international trend data to evaluate whether certain national educational reforms were effective or not because it is possible to track changes in student achievement on the national level from a longitudinal perspective. Furthermore, international trend data are of great value for comparative studies. Because many features of educational systems and policies vary only at the country level, international comparative studies provide a unique approach to analyze the impact of specific educational policies on educational outcomes (Hanushek and Wößmann 2011). For example, comparative studies can be used to investigate global phenomena, such as trends towards a “world curriculum” (Rutkowski and Rutkowski 2009; Johansson and Strietholt 2019) or the longitudinal examinations of the “socioeconomic achievement gap” (Broer et al. 2019; Chmielewski 2019).
2 Background
There is extensive research on linking cognitive outcomes in ILSAs (e.g., Afrassa 2005; Altinok et al. 2018; Chmielewski 2019; Hanushek and Wößmann 2012; Strietholt and Rosén 2016; Johansson and Strietholt 2019). For example, Strietholt and Rosén (2016) demonstrated how to link the achievement tests from recent and older IEA studies of reading literacy onto the same measurement scale with item response theory (IRT) modeling. Johansson and Strietholt (2019) used overlaps in the assessment material to equate five cycles of the Trends in International Mathematics and Science Study (TIMSS). They applied a common-item nonequivalent group design and IRT modeling. An attempt to link older and recent IEA studies on mathematics has been made by Afrassa (2005), who used the Rasch model equating procedures on data from the first three IEA studies (between 1964 and 1995) of students in Australia. We extend the scope of the above examples by discussing the degree of similarity across the IEA assessments on mathematics, including more educational systems, and proposing a different linking method. In all, the above examples are similar to our approach in terms of using IRT linking methods, which require item-by-item overlap across tests among other preconditions. There are several attempts to link test scores from different regional, national, or international assessments over a long period that rely on IRT within the studies and classical test theory across them because of the limited amount of overlapping items (e.g., Altinok et al. 2018; Chmielewski 2019; Hanushek and Wößmann 2012).
Chmielewski (2019) combined 30 international large-scale assessments over 50 years, including 100 countries and about 5.8 million students. She used standardized scores of a mean of 0 and a standard deviation of 1 within each country-study-year-subject to calculate the socioeconomic achievement gap. Hanushek and Wößmann (2012) presented a longitudinal analysis of changes in cognitive skills and growth rates. They also directly calculated standardized scores for all countries on all assessments by combining the adjustments in levels based on the US National Assessment of Educational Progress (NAEP) scores and the adjustment in variances based on the Organization for Economic Co-operation and Development (OECD) Standardization Group. Altinok et al. (2018) present a large panel database of 163 countries and regions, 32 of which are from Sub-Saharan Africa, over 1965–2015. They constructed the outcomes by linking standardized international and regional achievement tests, using multiple linking methods, including pseudo-linear linking (a fusion of mean and linear linking) and equipercentile linking of test scores.
2.1 The TIMSS scale
The metric of the TIMSS reporting scales for mathematics achievement was established in 1995 by setting the mean of the national average scores for all participating countries to 500 and the standard deviation to 100 (Foy and Yin 2016). To enable measurement of trends over time, achievement data from successive TIMSS assessments were transformed to these same metrics by concurrently scaling the data from each successive assessment with the data from the previous assessment and applying linear transformations to place the results on the same scale. This procedure enables TIMSS to measure trends across all six assessment cycles to present.
2.2 The present study
Linking the first two international mathematics studies with the TIMSS studies has a number of challenges. First, the documentation of the old studies is more difficult to access and to study than the documentation of the recent assessments. Second, changes in the target populations and sampling imply comparability issues. Third, sample weights are not available for all assessments. Another challenge is the number of anchor items between the first three studies. There were 37 items out of 70 in the First International Mathematics Study (FIMS) that were repeated in the Second International Mathematics Study (SIMS), nine of which were repeated in TIMSS 1995, and 18 items in SIMS out of a pool of 199 items that were repeated in TIMSS 1995. According to Wingersky and Lord (1984), good linking may be achieved with as few as five common items or less with concurrent calibration. They studied the sampling errors of maximum likelihood estimates of IRT parameters in the case when both people and item parameters are estimated simultaneously. Furthermore, they investigated the effect of varying sample size, test length, the shape of the ability distribution, and the effect of anchor-test length on the standard error of item. These results encouraged the use of concurrent calibration in the present study.
We believe that despite the above challenges, the first two international mathematics studies provide rich data for secondary analyses and that it is relevant to evaluate the possibilities of linking these studies with the recent ones. It is important to highlight that the present undertaking is exploratory. Arguably, comparing studies administered decades apart is challenging, and involving multiple countries “is in several aspects an exercise in comparing the incomparable” (Husén 1983, as cited by Kaiser 1999, p. 3). Even if the maxim “to measure change do not change the measure” introduced by Beaton (1990, p. 10) is fulfilled, it is questionable whether, for instance, the measured constructs carry the same meaning over several decades. In our attempt to tackle these challenges, we take the following steps.
We investigate the degrees of similarity of ILSAs in mathematics from FIMS administered in 1964 to the most recent cycle of TIMSS in 2015. Meaningful comparisons across different assessments require comparable data. Kolen and Brennan (2014) proposed four criteria to evaluate the degree of similarity between tests: inferences, populations, constructs, and measurement characteristics. First, we use this scheme to explore similarities and differences in the assessment material of the studies before discussing the consequences of linking the tests. Second, the results of the evaluation of similarity guide the concurrent calibration of test items onto a common scale. The scores estimated with the use of linking models provide an empirical basis for investigations of long-term trends in mathematics achievement to study the long-term effects of educational policy and policy-related issues on educational outcomes.
3 Method
3.1 Data
The present study focuses on grade eight (or equivalent) student achievement data in eight IEA studies on mathematics, thus, all (six) cycles of TIMSS from 1995 to 2015 and the two older studies administered in 1964 and 1980. Data are drawn from achievement tests completed by students. The data of FIMS and SIMS were gathered from the Center for Comparative Analyses of Educational Achievement website (COMPEATFootnote 1). Data and documentation ofthe TIMSS studies from 1995 to 2015 were downloaded from the IEA Study Data Repository.Footnote 2
3.2 Selected countries
All participating educational systems in the selected populations are shown in Table 7, Appendix A. Eighty-three countries have participated in at least one study, with an average of 36 educational systems per time point. It is worth noting that participation is much lower in FIMS and SIMS than in the TIMSS cycles. Due to the large sample size (N = 1,550,261) but also a considerable amount of missing information due to non-participation, in the present study, we decided to focus on the four educational systems that participated in all studies: England, Israel, Japan, and the USA. The sample sizes of these countries by years of schooling are shown in Table 1. The mean age and their standard deviations were not considerably different over time. The US FIMS sample consisted of less than 2% extreme values of the age variable, hence the large standard deviations. It is difficult to trace back whether those are coding errors or not, therefore we kept those cases in the analysis.
The overall number of cases used for score estimation was N = 175,939. It is noticeable how the shift from age-based sampling (FIMS) to grade-based sampling (SIMS) affected the data. For comparability reasons, we kept data of students who were attending the 7th–9th year of schooling at the time of testing in all time points. The FIMS data varied across countries, the samples of England and the US contained cases indicating to be studying in other years of schooling than 7–9, whereas those of Israel and Japan did not. Therefore, this step was only necessary in the case of England and the USA, and involved excluding 5.85 and 5.36% of the samples, respectively. We discuss the implications of this heterogeneity in the next sections. What follows is the evaluation of the preconditions for linking the studies by investigating the degrees of similarity across the assessments.
3.3 Preconditions for the analyses
The following analytic steps were employed to evaluate the preconditions for linking. First, document analysis was conducted using the international reports of the respective studies to evaluate the degrees of similarity by employing the previously mentioned scheme of Kolen and Brennan (2014). Second, we explored overlaps in the instruments by identifying anchor items of the student achievement tests.
Inferences
According to Robitaille (1990), “FIMS was not, strictly speaking, a study of mathematics education, but rather a study of schools and schooling, with mathematics serving as a surrogate for achievement” (p. 396). Husén (1967) lists several reasons for choosing mathematics as the subject matter of the first international comparative assessment. The countries involved agreed that learning mathematics is the basis of improving their scientific and technical education and the “New Mathematics” represented an international agreement upon aims, contents, and methods of teaching mathematics. Criticisms of FIMS pointed out problems with the measurement of opportunity to learn and the involvement of mathematicians and mathematics teachers as well as the lack of operationalizing curriculum (Robitaille 1990). Such critiques led to structural changes in SIMS and the development of contextual variables such as curricular emphases, pedagogical practices, and school organization (Robitaille 1990).
The types of inferences that can be drawn from the different mathematics studies are essentially the same. All mathematics studies are effectively low-stake assessments, even though this might have changed at the country level, for example, due to the increasing number of international studies, as well as an intensified policy discussion around these. Overall, the studies have had the same purpose over time, to compare the performance of different educational systems.
Populations
Several different populations have been tested across the years, i.e., primary school, secondary school, and upper secondary school. We have selected the populations that were attending secondary school in our study, typically in the 7-9th year of schooling, i.e., 13–14 year-olds. One reason for this is that these grades/ages participated in all the conducted assessments. Thereby, the selected assessments addressed students in the secondary school years. Thus, the target population is quite similar across all studies. However, in ILSAs, it is not possible to define the target population in such a way that both age and grade are balanced across all countries because of their different school entry ages. A comparison of the target sample definitions presented in Table 2 shows that the study designers employed different approaches but there is a possibility for adjustment given the samples of adjacent grades in 1995. In the report of the changes in achievement between the FIMS and SIMS studies, Robitaille and Taylor (1989) argue that the populations targeted in FIMS and SIMS should be considered equivalent because all students in the assessed educational systems around the age of 13 would be studying the same levels of mathematics.
In the 1980s, IEA changed the definition of target populations from an age-based to a grade-based definition for all their studies of student achievement (Strietholt et al. 2013). Arguably, any sampling strategy changes result in a violation of the assumption of comparable samples. Strietholt et al. (2013) developed a correction model to improve comparability across countries and IEA studies on reading in terms of age and schooling. They hypothesized that grade-based sampling strategies result in more comparable samples across countries. In the present study, we do not develop extensive corrections for the sampling composition differences. As mentioned earlier, we have decided to keep the years of schooling in the FIMS datasets corresponding to the further cycles, i.e., 7–9 years, to improve comparability.
Constructs
Mathematics consists of several different content areas that together form the construct of mathematics. These domains are, for instance, arithmetic, algebra, and probability. In the mathematics studies of IEA, the content domains have varied slightly between the different studies. Tables 3 and 4 overview the assessment cycles in terms of the proportion of items in the different mathematical content areas as well as the terminology applied for the processes of comprehension. It is noticeable that the studies used different terms for the processes and contents. However, often such differences are not substantive but rather terminological.
For instance, the content area Statistics in SIMS was refined to Data representation, analysis, and probability in the early TIMSS cycles and in 2015, Data and chance have been used since 2007. The cognitive domains were described in more detail in the old studies and early TIMSS cycles, whereas three domains: knowing, applying, and reasoning have been used consistently since 2007.
Concerning the proportion of items from the various content areas, it is noticeable that in the most recent cycles of TIMSS, the terminology and the proportion of the items in the different content areas are more aligned. However, the differences in the earlier studies are rather small and in most cases are a result of restructuring the areas based on curricula analyses of the participating education systems. Given the extent of overlaps in the content areas, we conclude that the tests were intended to measure the same construct over time.
Measurement characteristics
In all studies, several mathematics tests were administered to the students, who completed these in a given time. The studies investigated in the present study used a matrix sampling design except for FIMS. In FIMS, the 13-year-olds received three booklets with 70 items in total and a complete range of content areas varying in difficulty level in each of them (Thorndike 1967), and 60 min were given for each of these tests (see Tables 3 and 4 for more details). In SIMS, the mathematics test consisted of five different tests. A scheme of matrix sampling was applied with a core test and four rotated tests (Schmidt et al. 1992). The core test was the same for all students and comprised 40 items. The other four tests (A-D) were comprised of 34 tasks each and were constructed through stratified randomization of the remaining items.
In TIMSS 1995, the test conditions were somewhat different from the previous assessments in that students also took a test consisting of science items. Another difference was that TIMSS 1995 used a complex matrix sampling. The test items were allocated to 26 different clusters, labeled A through Z. Then the 26 clusters were assembled into eight booklets. Each student completed one booklet, for which students were given 90 min. Of the 26 clusters, eight take 12 min, 10 take 22 min, and eight take 10 min. All students took the core cluster (cluster A), comprising six mathematics and six science multiple-choice items. The seven focus clusters appear in at least three booklets, and the ten breadth clusters appear in only one booklet. The eight free-response clusters, each containing 10 min of short-answer and extended-response items, were each assigned to two booklets. The overall pool of items contained 151 mathematics items, including 125 multiple-choice items, 19 short-answer items, and 7 extended-response items. In total 198 unique testing minutes were needed for mathematics.
In further TIMSS studies, the test approach was similar to that used in 1995. TIMSS uses a matrix-sampling approach that involves packaging the entire assessment pool of mathematics and science items at each grade level into sets of student achievement booklets, with each student completing just one booklet. The number of booklets has varied slightly over the years. Each item appears in two booklets, providing a mechanism for linking together the student responses from the various booklets. Booklets are distributed among students in participating classrooms so that the groups of students completing each booklet are approximately equivalent in terms of student ability. To assemble a comprehensive picture of the achievement for the entire student population, TIMSS uses IRT scaling methods which allow for taking advantage of individual students’ responses to the booklets that they are assigned. This approach reduces the testing time that would otherwise be an impossible student burden.
Finding anchor items
For FIMS, data were downloaded from the study websiteFootnote 3 to determine the item IDs, while the test documentation available was used to study the specific questions comprising the items. The datasets alongside the test instrument of SIMS were gathered from the study website.Footnote 4 To obtain information about the TIMSS studies the available datasets, as well as the accompanying documentation, were downloaded from the IEA Study Data Repository.Footnote 5
Each item has an associated content category (e.g., Algebra), and sometimes a more specific topic (e.g., Equations and formulas), and a cognitive domain (e.g., Reasoning). For every item, there might be several of these categories, as every study employed different sets of categories. Items in SIMS are listed in Travers and Westbury (1989). To find the linked items, however, for each item of the FIMS study, a short description was used to map it to the items in the SPSS file of the SIMS study. To verify the validity of the links in some cases the original phrasing of the items was used to compare the items. To find the links between the items used in SIMS and TIMSS 1995, SPSS item descriptions of the TIMSS studies were used. Furthermore, the item descriptions of the already published items were used to check single items for overlap. The TIMSS studies employ a unified set of variable IDs for the items in the SPSS files. It was therefore easy to map the anchoring items.
For every item, we checked its type: multiple-choice or constructed-response, the maximally reachable points, and in the case of multiple-choice items, the number of response categories. Four items used in both FIMS and SIMS required a constructed response in FIMS but were multiple choice-items in SIMS. These items have been treated as different items in further analysis. To conclude, we have found that there were 37 items out of 70 in FIMS that were repeated in SIMS, nine of which were repeated in TIMSS 1995, and 18 items in SIMS out of a pool of 199 items that were repeated in TIMSS 1995.
3.4 Missing data
It is useful to distinguish three types of missing responses in the respective datasets: not-administrated, omitted, and not-reached items. In the datasets of the older studies, the various types of missing data were not distinguished. The average omission rate per item was below 10% in all the four countries in FIMS, with Israel having the highest average of 9%. According to the documentation of the study, the omission rate in SIMS was less than 5% in England, Japan, and the USA; however, in Israel, the average omission rate per item was 19% (Robitaille 1989). Detailed item statistics for all TIMSS cycles are reported in the documentation of the respective studies.Footnote 6 Table 5 shows the proportion of students who did not finish the respective TIMSS mathematics tests, which varied considerably between countries and studies.
Not-administrated answers were treated as missing responses, while omitted responses were treated as incorrect answers both when estimating item parameters and scoring. We have chosen to treat the not-reached items at the end of the tests as if they were not administrated, i.e., missing for item calibration to avoid comparability issues between the assessment cycles (see Gustafsson and Rosén 2006). In contrast, not-reached items were treated as incorrect responses when student proficiency scores were generated. This approach is in line with the procedures of handling missing responses in the TIMSS studies (see, e.g., Foy and Yin 2016). Cases and items with all missing responses were excluded from the calibration.
3.5 Design
The present study uses a nonequivalent groups with anchor test (NEAT; Von Davier and Von Davier 2007) design for linking. The NEAT design is based on three assumptions. First, there are different populations of examinees, each of which can take one of the tests and the anchor test. Second, the samples are independently and randomly drawn from the populations. Third, the tests to be linked are all unidimensional and the local independence assumption holds (Hambleton et al. 1991). These assumptions are assumed to be fulfilled based on the procedures described in the documentation of the respective studies.Footnote 7
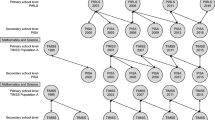
The item parameter estimation was conducted by concurrent calibration (Wingersky and Lord 1984) of all items in all studies, thus the parameters for all tests are automatically put on the same scale, and therefore, no linear transformation is necessary. We have chosen the concurrent procedure for three main reasons. This method provides smaller standard errors and involves fewer assumptions than other IRT procedures, and good linking may be achieved with as few as five common items or less (Wingersky and Lord 1984). The third benefit was particularly important because of the relatively small number of anchor items (18) between SIMS and TIMSS 1995. Kolen and Brennan (2014) have reviewed a number of simulation studies for comparing IRT scale transformation methods. They concluded that the concurrent calibration procedure was more accurate than separate estimation when the data fit the IRT model but it might be less robust to violations of the IRT assumptions than separate estimation methods. Moreover, in contrast to the TIMSS concurrent calibration procedure, we pooled all data from all cycles and performed the item calibration. Hence, we used more information, i.e., responses for anchor items that typically span over more than two cycles as shown in Fig. 1.
Item parameters were estimated simultaneously while the parameters of the anchor items were assumed identical in each sample. We used Angoff’s delta plot method (Angoff and Ford 1973) for the detection of differential item functioning (DIF) to investigate the fulfillment of this assumption, i.e., the item parameter drift between cycles using the deltaPlotR package (Magis and Facon 2014). It is a score-based and relative DIF method that compares the proportions of correct responses in the reference group and the focal group and DIF items are flagged concerning the set of all items in the test (Magis and Facon 2014). Magis and Facon (2014) argue that the main benefit of relative DIF methods is that the identification of DIF items relies on the particular items themselves, in contrast with traditional DIF methods, which use fixed detection thresholds arising only from asymptotic statistical distributions.
Data management was done with SPSS 25; IRT analyses were performed with the R package TAM (Robitzsch et al. 2019), employing an expectation-maximization algorithm to achieve marginal maximum likelihood estimates of the item parameters outlined by Bock and Aitkin (1981). The latent normal distribution of student proficiency was assumed.
3.6 IRT modeling
First, we compared three models, in which different IRT models were used for different item types. In model 1, dichotomous items, i.e., multiple-choice items and constructed-response items that were scored as either correct or incorrect were modeled using the Rasch model that gives the probability that a student s with the unobserved mathematics ability θs gives the correct answer to item i as follows:
in which
-
xis is the response of student s to item i (0 or 1 if correct),
-
θs is the ability of student s, and
-
bi is the location/difficulty parameter of item i.
For polytomous items, i.e., constructed response items requiring an extended response were scored for partial credit, with 0, 1, and 2 as the possible score levels, and were scaled using the partial credit model (pcm; Masters 1982) that gives the probability that a student with proficiency θs will have, for item i, a response xis that is scored in the lth of mi ordered score categories as:
in which
-
mi is the number of response categories for item i, and
-
di, l is the category l threshold parameter of item i.
In model 2, for dichotomous items, we used a 2-parameter logistic (2PL) model that gives the probability that a student s with the unobserved mathematics ability θs gives the correct answer to item i as follows:
in which ai is the slope/discrimination parameter of item i.
Polytomous items were calibrated using a generalized partial credit model (gpcm; Muraki 1992). The fundamental equation of this model gives the probability that a student with proficiency θs will have, for item i, a response xis that is scored in the lth of mi ordered score categories as:
in which
-
mi is the number of response categories for item i, and
-
di, l is the category l threshold parameter of item i.
In model 3, we followed a similar modeling approach to that in modern IEA studies, i.e., for multiple-choice items, we used the 3-parameter logistic (3PL) model, which accommodates guessing by adding a lower-asymptote parameter (Eq. 5), and for dichotomous constructed response items the 2PL model, and for polytomous items the gpcm model (see Eq. 4).
in which ci is the lower asymptote/guessing parameter of item i.
We assessed the fit of the above-described three models. Based on model fit and model comparison results, we selected one of the models for item calibration and person scoring.
3.7 Concurrent calibration
The calibration of the item parameters and the estimation of students’ abilities were done in two steps. First, we calibrated the item parameters according to the chosen model onto the same IRT scale using data from all studies and countries using senate weights, thus, each country contributed equally. Senate weights that sum to 500 for each country’s student data were applied (stratum weights in SIMS were rescaled to sum to 500). There were no weight variables in the FIMS 1964 datasets; therefore, individuals within a country were weighted equally, to sum up to 500. Where two grades were sampled, senate weights were rescaled so that each grade weighted equally within a country. The second step was to use the estimated item parameter estimates with the recoded dataset for person scoring. The recoding concerned the not reached items as described previously.
Based on the item parameter estimates, we fitted the model on the recoded dataset and computed students’ mathematics ability scores by drawing five plausible values (PVs) using the expected a-posteriori method. The estimated abilities were converted to scale scores; thus, we transformed each PV on a metric with a mean of 500 and a standard deviation of 100 points across time. We used the transformed scores to compute the mean mathematics achievement for the respective country per study following Rubin’s (1987) rules.
4 Results
4.1 Linking
The number of common and bridging mathematics items of the achievement scales is shown in Fig. 1. Travers and Westbury (1989) list 41 items in SIMS that have been used in FIMS, whereas Robitaille (1990) refers to 35 anchor items. The anchor items between FIMS and SIMS are also listed in the Swedish report on SIMS with a total number of 40 (Murray and Liljefors 1983). We identified 37 items for bridging these studies (i.e., first bridge). The 199 SIMS items listed by Travers and Westbury (1989) were successfully identified. However, not every educational system used all 199 items: England used 185, Israel 186, Japan 185, and the USA 189. Eighteen items are common in SIMS and TIMSS 1995 (i.e., second bridge). Seven out of these items were repeated in TIMSS 2003.
We applied the delta plot method on all seven bridges between adjacent time points. As shown in Fig. 2, a total number of three items were flagged for DIF in the first two bridges, i.e., from FIMS to SIMS, and from SIMS to TIMSS 1995, respectively. No DIF items were detected in the rest of the bridges. We have decided to exclude these items from the calibration. Twelve non-anchor items were excluded due to missing answers in all countries. Overall, we used 893 items in the concurrent calibration. The descriptive statistics of the anchor items are shown in Table 8, Appendix B. We can observe that the proportion of correct answers ranges from 0.11 to 0.92; thus, the anchor items have a wide range of difficulty among test-taker across time.
Model fit and comparison results are presented in Table 6. First, the standardized root mean square root of squared residuals (SRMSR; Maydeu-Olivares 2013), which is based on comparing residual correlations of item pairs were calculated for each model. Second, the Akaike information criteria (AIC; Akaike 1974) and the Bayesian information criteria (BIC; Schwarz 1978) were calculated alongside the pairwise likelihood ratio tests. The smaller criteria measures are preferred. In addition, for item fit, root mean square deviance (RMSD) statistics were calculated. RMSD ranges from 0 to 1, with larger values representing poorer item fit. The results range between 0.005 and 0.170 for model 1, between 0.002 and 0.096 for model 2, and between 0.004 and 0.103 for model 3. We conclude that model 2 fits the data better than model 1 and well enough to choose it over the more complicated model 3.Footnote 8 Therefore, we have chosen the 2PL model for the purpose of parsimony i.e. the 3PL model did not provide considerable improvement in fitting the data.
4.2 Trends
Trends of the mean achievement of the educational systems are represented in Fig. 3. We compared the results within countries using the z statistic. The z statistic to test whether the means differ can be calculated as follows:
where \( {\overline{\theta}}_{S2} \) and \( {\overline{\theta}}_{S1} \) are the country means, seS2 and seS1 are the standard errors of the means in two adjacent studies/cycles. The comparisons revealed that the average performance between adjacent cycles in England significantly changed over time, except in 1999 and 2003. In Japan, the average performance change was significant across time except in 1999, 2007, and 2011. In the USA, the average performance changed significantly only in the assessment cycles between 1995 and 2003. In the case of Israel, according to the accompanying documentation of TIMSS 2015, the data is only comparable for measuring trends from 2011 to 2015, due to changes in translations and increasing population coverage. Therefore, we cannot compare the whole trend line with those reported by the IEA (Mullis et al. 2016). In our analyses, the change between the average levels of performance was not significant from 2011 to 2015, while all the other changes were statistically significant.
We compared the trends of the new IRT scores with those of the original tests, hereinafter referred to as old scores and scale. The reports of these two studies contained number-correct scores overall but noticeably more emphasis was put on reporting by content areas. Therefore, we constructed the scales of FIMS and SIMS by standardizing the number-correct scores and scaling them to a metric with a mean of 500 and a standard deviation of 100 points. The TIMSS scales were obtained using the original PVs.
The country performance changes over time showed similar trends as observed with the newly estimated scale described above. There are quite substantial country differences in changes from FIMS to SIMS as shown in Fig. 3. Robitaille (1990) analyzed the achievement change from FIMS to SIMS and reported the country’s average percent correct by three major areas of the curriculum: arithmetic, algebra, and geometry and measurement (p. 403). We calculated the average achievement across these content areas and the decline in the case of England and Israel was similar to each other, 8 and 9%, respectively, while Japan’s average achievement increased by 1%, and there was a 1% decrease in the US. Our results are in line with this comparison in terms of magnitude. In the more recent studies, we found small deviations in the trends on three occasions, England in 2003 and 2011, and the US in 2015, i.e., the statistical significance of the mean changes between adjacent cycles differed from those in the new scale. The combined trend lines by country are shown in Fig. 4.
Concerning the position of the countries in the rank orders by year, we can observe minor deviations between the old and the newly estimated scales in the first two studies. The only case, where this deviation is significant, is Israel’s position in SIMS. A possible explanation is that both the omission rate and the proportion of students who did not finish the test was considerably higher in Israel than in the other countries. Country means of the average achievement of the old scales are shown in Fig. 5.
5 Discussion and conclusions
The main purpose of the present study was to construct comparable trend measures of mathematics achievement as assessed by IEA, i.e., TIMSS and its predecessors. In order to achieve this aim, we investigated the degree of similarity of all eight studies on mathematics from the First International Mathematics Study (FIMS) administered in 1964 to the most recent cycle of TIMSS in 2015. In contrast to a previous attempt by Afrassa (2005), we used a different linking method to explore the old IEA studies on mathematics in relation to the TIMSS cycles. We were able to link mathematics achievement for the population of grade 8 students for the four countries that participated in all ILSAs. Thereby we achieved scores that can be compared from 1964 up to 2015. The trends revealed in the present study are largely in line with the originally reported trends with the advantage of being put on the same scale.
We evaluated the stability of this scale with respect to four criteria: (1) trends are not influenced by different purposes of the various assessments because the respective assessments were designed to compare the performance of different educational entities; and (2) comparable target samples exist for secondary and upper secondary schools but not in primary school. With respect to the test conditions (3) and the constructs (4), our review revealed a high degree of similarity as the earlier studies served as a model for the later studies. Overall, our analyses indicate a sufficient degree of similarity across the assessments.
Several challenges were encountered and further research is needed to explore the robustness of the linking. A possible limitation of the study lies in the within-country comparability because of the populations sampled in FIMS and subsequent studies. The IEA shifted from age-based to grade-based sampling with TIMSS. In contrast, the OECD applies an age-based sampling method in the Programme for International Student Assessment (PISA; Adams and Wu 2003) of 15-year-old students. These differences show that attempts to achieve comparability in terms of age and schooling have been approached differently. Between-country comparability difficulties add further complexity because of school entry age differences. It is not possible to define the target population in such a way that both age and grade are balanced across all countries. The IEA sampling strategy change is an unsolvable issue but we tried to tackle it with as good approximations of homogenous samples over time as possible.
Another limitation of our study is that we did not take sample characteristics into account in person scoring. As reported in the documentation of the TIMSS studies (see, e.g., Martin and Mullis 2000), to enhance the reliability of the student scores, their scaling approach uses a process known as conditioning. Thus, all available background data are included in the model, thereby accounting for the relationships between background variables, such as gender and ethnicity, to provide an accurate representation of these underlying relationships.
Finally, further research including more countries could reveal more trend information, as well as more possibilities to investigate cross-cultural differences. A possibility for expanding to more countries is to scale the data from all countries in each assessment separately and link the results onto the scale estimated in the present study.
Notes
Item parameter estimates are available along with the documentation upon request from the corresponding author.
References
Adams, R., & Wu, M. (Eds.). (2003). Programme for international student assessment (PISA): PISA 2000 technical report. Paris: PISA, OECD Publishing. https://doi.org/10.1787/9789264199521-en .
Afrassa, T. M. (2005). Monitoring mathematics achievement over time. In S. Alagumalai, D. D. Curtis, & N. Hungi (Eds.), Applied Rasch measurement: A book of exemplars (pp. 61–77). Dordrecht: Springer.
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. https://doi.org/10.1109/TAC.1974.1100705 .
Altinok, N., Angrist, N., & Patrinos, H. (2018). Global data set on education quality (1965-2015). Policy research working paper, no. WPS 8314. Washington, D.C.: World Bank Group http://documents.worldbank.org/curated/en/706141516721172989/Global-data-set-on-education-quality-1965-2015. Accessed 25 Nov 2019.
Angoff, W., & Ford, S. (1973). Item-race interaction on a test of scholastic aptitude. Journal of Educational Measurement, 10(2), 95–106.
Beaton, A. E. (1990). Introduction. In A. E. Beaton & R. Zwick (Eds.), The effect of changes in the national assessment: Disentangling the NAEP 1985–86 reading anomaly (NAEP Report No. 17–TR–21 (pp. 1–13). Princeton: Educational Testing Service.
Bock, R., & Aitkin, D. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46(4), 443–459. https://doi.org/10.1007/BF02293801 .
Braun, H. I., & Singer, J. D. (2019). Assessment for monitoring of education systems: International comparisons. The Annals of the American Academy of Political and Social Science, 683(1), 75–92. https://doi.org/10.1177/0002716219843804 .
Broer, M., Bai, Y., & Fonseca, F. (2019). Socioeconomic inequality and educational outcomes: Evidence from twenty years of TIMSS. IEA Research for Education, A Series of In-depth Analyses Based on Data of the International Association for the Evaluation of Educational Achievement (Vol. 5). Cham, Switzerland: Springer. https://doi.org/10.1007/978-3-030-11991-1 .
Chmielewski, A. K. (2019). The global increase in the socioeconomic achievement gap, 1964 to 2015. American Sociological Review, 84(3), 517–544. https://doi.org/10.1177/0003122419847165 .
Foy, O., & Yin, L. (2016). Scaling the TIMSS 2015 achievement data. In M. O. Martin, I. V. S. Mullis, & M. Hooper (Eds.), Methods and procedures in TIMSS 2015 (pp. 13.1–13.62). Chestnut Hill: Boston College.
Garden, R. A. (1987). Second IEA mathematics study. Sampling report. http://www4.gu.se/compeat/SIMS/Design/Gardner_SIMS_SamplingReport.pdf. Accessed 25 Nov 2019.
Gustafsson, J.-E., & Rosén, M. (2006). The dimensional structure of reading assessment tasks in the IEA reading literacy study 1991 and the Progress in International Reading Literacy Study 2001. Educational Research and Evaluation, 12(5), 445–468. https://doi.org/10.1080/13803610600697179 .
Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of item response theory. Newbury Park: SAGE Publications, Inc..
Hanushek, E. A., & Wößmann, L. (2011). The economics of international differences in educational achievement. In E. A. Hanushek, S. Machin, & L. Wößmann (Eds.), Handbook of the Economics of Education (Vol. 3, pp. 89–200). Amsterdam: Elsevier.
Hanushek, E. A., & Wößmann, L. (2012). Do better schools lead to more growth? Cognitive skills, economic outcomes, and causation. Journal of Economic Growth, 17(4), 267–321. https://doi.org/10.1007/s10887-012-9081-x .
Husén, T. (1967). Intentions and background of the project. In T. Husén (Ed.), International study of achievement in mathematics: A comparison of twelve countries (Vol. 1, pp. 25–34). Stockholm: Almqvist & Wiksell.
Husén, T. (1983). Are standards in U.S. schools really lagging behind those in other countries? Phi Delta Kappan, 64(7), 455–461.
Johansson, S., & Strietholt, R. (2019). Globalised student achievement? A longitudinal and cross-country analysis of convergence in mathematics performance. Comparative Education, 55(4), 536–556. https://doi.org/10.1080/03050068.2019.1657711 .
Kaiser, G. (1999). International comparisons in mathematics education under the perspective of comparative education. In G. Kaiser, E. Luna, & I. Huntley (Eds.), International Comparisons in Mathematics Education (pp. 3–15). London, Philadelphia: Falmer Press.
Klemenčič, E., & Mirazchiyski, P. V. (2018). League tables in educational evidence-based policy-making: Can we stop the horse race, please? Comparative Education, 54(3), 309–324. https://doi.org/10.1080/03050068.2017.1383082 .
Kolen, M. J., & Brennan, R. L. (2014). Test equating, scaling, and linking: Methods and practices (3rd ed.). New York: Springer.
Magis, D., & Facon, B. (2014). deltaPlotR: An R package for differential item functioning analysis with Angoff's delta plot. Journal of Statistical Software, 59(code snippet 1). https://doi.org/10.18637/jss.v059.c01 .
Martin, M. O., & Kelly, D. L (Eds.). (1996). Third International Mathematics and Science Study (TIMSS) Technical Report, Volume I: Design and Development. Chestnut Hill, MA: Boston College.
Martin, M. O., Gregory, K. D., & Stemler, S. E. (Eds.). (2000). TIMSS 1999 Technical Report. Chestnut Hill, MA: Boston College.
Martin, M. O., Mullis, I. V. S., & Chrostowski, S. J. (Eds.).(2004). TIMSS 2003 Technical Report. Chestnut Hill, MA: Boston College.
Martin, M. O., & Mullis, I.V.S. (Eds.). (2012). Methods and Procedures in TIMSS and PIRLS 2011. Chestnut Hill, MA: Boston College.
Masters, G. N. (1982). A Rasch model for partial credit scoring. Psychometrika, 47(2), 149–174.
Maydeu-Olivares, A. (2013). Goodness-of-fit assessment of item response theory models. Measurement: Interdisciplinary Research and Perspectives, 11(3), 71–101. https://doi.org/10.1080/15366367.2013.831680 .
Mullis, I. V. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 international results in mathematics. Chestnut Hill: Boston College.
Mullis, I. V. S., Martin, M. O., Hooper, M. (Eds.). (2016). Methods and Procedures in TIMSS 2015. Chestnut Hill, MA: Boston College.
Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16(2), 159–176. https://doi.org/10.1177/014662169201600206 .
Murray, A., & Liljefors, R. (1983). Matematik i svensk skola. Stockholm: Skolöverstyrelsen.
Oldham, E. E., Russel, H. H., Weinzweig, A. I., & Garden, R. A. (1989). The international grid and item pool. In K. J. Travers & I. Westbury (Eds.), The IEA Study of Mathematics I: Analysis of Mathematics Curricula (pp. 15–53). Oxford: Pergamon Press.
Olson, J. F., Martin, M. O., & Mullis, I. V. S. (Eds.). (2008). TIMSS 2007 Technical Report. Chestnut Hill, MA: Boston College.
Robitaille, D. F. (1989). Students’ achievements: Population A. In D. Robitaille & R. A. Garden (Eds.), The IEA study of mathematics II: Contexts and outcomes of school mathematics (pp. 102–125). Oxford: Pergamon.
Robitaille, D. F. (1990). Achievement comparisons between the first and second IEA studies of mathematics. Educational Studies in Mathematics, 21(5), 395–414. https://doi.org/10.1007/BF00398860 .
Robitaille, D. F., & Taylor, A. R. (1989). Changes in patterns of achievement between the first and second mathematics studies. In D. Robitaille & R. A. Garden (Eds.), The IEA study of mathematics II: Contexts and outcomes of school mathematics (pp. 153–177). Oxford: Pergamon.
Robitzsch, A., Kiefer, T., Wu, M. (2019). TAM: Test Analysis Modules, version 3.3-10. https://CRAN.R-project.org/package=TAM. Accessed 25 Nov 2019.
Rubin, D. (1987). Multiple imputation for nonresponse in sample surveys. Hoboken, NJ: John Wiley.
Rutkowski, L., & Rutkowski, D. (2009). Trends in TIMSS responses over time: Evidence of global forces in education? Educational Research and Evaluation, 15(2), 137–152. https://doi.org/10.1080/13803610902784352 .
Schmidt, W. H., Wolfe, R. G., & Kifer, E. (1992). The identification and description of student growth in mathematics achievement. In L. Burstein (Ed.), The IEA study of mathematics III: Student growth and classroom processes. Oxford: Pergamon.
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6(2), 461–464. https://doi.org/10.1214/aos/1176344136 .
Strietholt, R., & Rosén, M. (2016). Linking large-scale reading assessments: Measuring international trends over 40 years. Measurement: Interdisciplinary Research and Perspectives, 14(1), 1–26. https://doi.org/10.1080/15366367.2015.1112711 .
Strietholt, R., Rosén, M., & Bos, W. (2013). A correction model for differences in the sample compositions: The degree of comparability as a function of age and schooling. Large-Scale Assessments in Education, 1(1), 1. https://doi.org/10.1186/2196-0739-1-1 .
Thorndike, R. L. (1967). The mathematics test. In T. Husén (Ed.), International study of achievement in mathematics: A comparison of twelve countries (Vol. 1, pp. 90–108). Stockholm: Almqvist & Wiksell.
Travers, K. J., & Westbury, I. (1989). Supplement to the IEA Study of Mathematics I: Analysis of Mathematics Curricula. http://www4.gu.se/compeat/SIMS/Design/Travers_Westbury_Supplement.pdf. Accessed 25 Nov 2019.
Von Davier, M., & Von Davier, A. A. (2007). A unified approach to IRT scale linking and scale transformations. Methodology European Journal of Research Methods for the Behavioral and Social Sciences, 3(3), 115–124. https://doi.org/10.1027/1614-2241.3.3.115 .
Wingersky, M., & Lord, F. (1984). An investigation of methods for reducing sampling error in certain IRT procedures. Applied Psychological Measurement, 8(3), 347–364. https://doi.org/10.1177/014662168400800312 .
Acknowledgments
We are grateful for the helpful input of Eugenio J. Gonzalez from Educational Testing Service, Princeton, NJ, USA. Erika Majoros, Monica Rosén, and Jan-Eric Gustafsson are part of the European Training Network OCCAM. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 765400.
Funding
Open Access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1. Participating educational systems
Appendix 2. Descriptive statistics of the anchor items
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Majoros, E., Rosén, M., Johansson, S. et al. Measures of long-term trends in mathematics: linking large-scale assessments over 50 years. Educ Asse Eval Acc 33, 71–103 (2021). https://doi.org/10.1007/s11092-021-09353-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11092-021-09353-z