Combination of DBD and Catalysts for CH₄ and CO₂ Conversion: Basics and Applications

Abstract

This paper describes dielectric barrier discharge and catalyst combination technology which is applied for dry methane reforming (DMR: CH₄ + CO₂ = 2CO + 2H₂) and reverse water gas shift reaction (RWGS: CO₂ + H₂ = CO + H₂O). The purpose of this paper is not to discuss the efficiency of plasma catalytic conversion of CH₄ and CO₂, catalyst synthesis method, or diagnostics of surface reactions; it focuses on the macroscopic characterization of DBD and catalyst hybrid reactions for a reactor design and appropriate parameter setting. DBD is characterized by the discharge sustain voltage and the mean discharge current which are readily obtainable from the Lissajous diagram and is further correlated with a power density (W/m³) via Manley's equation. Meantime, power density is decoupled into specific energy density (SEI) and gaseous space velocity (GHSV). SEI provides a guideline for the energy efficiency of the plasma catalytic process, and GHSV is an important measure of residence time or productivity of the process. The DBD-catalyst hybrid reaction is superior to warm discharge alone when it is generated by a high-frequency power source, which is discussed based on the lifetime of vibrationally excited CH₄; not only cumulative population of a fundamental mode of vibrationally excited CH₄, but also overtone vibrational states of CH₄ is anticipated by multiple electron collision at high-frequency operation. The importance of overtone vibrational molecules on surface reaction is proven by molecular beam study, and distinguished from the ladder-climbing mechanism in gas phase plasma chemistry; catalytic reactions would further promote without unavoidable trade-off relationship between reactant conversion rate and energy efficiency. Finally, nonequilibrium product distribution by plasma catalysis is discussed based on the surface reaction model in connection with vibrationally excited molecules.

Introduction

Plasma processing has emerged in the last several decades as a viable and robust technology in materials science and electronic device fabrication, finding applications in microfabrication, thin film deposition, surface modification/cleaning, etc. The first application of plasmas in the chemical synthesis dates back to the ozone synthesis in 1857 which was invented by Ernst Werner von Siemens [1]. The discovery of ozone was about 20 years earlier, in 1839, by Christian Friedrich Schönbein. Siemens developed a highly transient and localized nonthermal plasma at atmospheric pressure, and called it a “silent discharge”, which is currently known as a dielectric barrier discharge (DBD). As a result of these studies, much of the basic chemistry and physics in DBD has been learned through ozone-related research. Later, various applications of DBD have been developed which are described in the legendary review article by Ulrich Kogelschatz [2]. Other chemical applications of DBD were developed for pollution control such as diesel exhaust treatment and abatement of volatile organic compounds [3]. These technologies were further advanced by combining supported metal catalysts. DBD is used exclusively for this purpose. With the growing concern of energy and environmental issues, as well as the necessity for future decarbonatization in our society, DBD-based plasma catalysis and related technologies are highlighted as an emerging type electrification technology [4]. The combination technology of plasma and catalysts receives special attention in greenhouse gas conversion, nitrogen fixation, and hydrocarbon chemistry. Currently, combining nonthermal plasmas and catalysts has enabled a new frontier field of research [5, 6] and an urgent need for fundamental research to provide better insight into interfacial phenomena.

This review article focuses exclusively on DBD and heterogenous catalyst combination that is applied to dry methane reforming (DMR: CH₄ + CO₂ = 2CO + 2H₂, ΔH° = 247 kJ/mol) and reverse water gas shift reaction (RWGS: CO₂ + H₂ = CO + H₂O, ΔH° = 41 kJ/mol). In thermal catalysis, the temperature difference is the driving force of the endothermic reactions. At the inlet of the reactor, the conversion of reactants increases abruptly which accompanies a large temperature drop. As the reaction rate decelerates toward downstream of the reactor, the temperature difference between the external heat source and catalyst layer decreases (Chapter 8 in ref [6]). Finally, the reaction is terminated at the point where the temperature establishes the equilibrium. The point of discussion is whether the product distribution is in thermal equilibrium at the given catalyst temperature. If the conversion is not satisfactory, the temperature of the external heat source needs to be increased which is not desired for energy penalty as well as for the materials used for the catalyst and reactor. In contrast, nonthermal plasma chemistry occurs without temperature difference because electron impact dissociation of molecules initiates catalytic reactions, while catalyst temperature is maintained constant. Meantime, the energy necessary for the endothermic reaction is supplied from nonthermal plasma. As a result, the conversion of reactants beyond thermal equilibrium is readily established. However, in such a situation, energy consumption becomes incredibly large which is measured by specific energy input (SEI). For the case of DMR, SEI < 125 kJ/mol (equivalent to 100 W and 1200 cm³/min at STP: Standard temperature and pressure. Hereafter it represents 25 °C and 101.3 kPa) needs to be satisfied for the efficient CH₄ and CO₂ conversion. Therefore, before knowing the molecular scale insight into the mechanism, we have to design a plasma-catalyst hybrid reactor appropriately so that energy efficiency, as well as productivity of the chemical processes, are attractive from the industrial point of view. For this purpose, this paper focuses on the macroscopic characterization of the DBD and catalyst hybrid reaction, reactor design, and appropriate parameter setting. Vibrational chemistry in DMR is further discussed based on the electron energy loss fraction, electron impact rate coefficient, and the lifetime of vibrationally excited CH₄, leading to the conclusion that DBD is one of the best plasma sources for the generation and utilization of vibrationally excited molecules under the presence of heterogeneous catalysts. Moreover, DBD-catalyst hybrid reaction was applied to reverse water gas shift (RWGS) reaction where CO₂ conversion increased by DBD beyond thermal equilibrium. Comparative discussion between plasma-enhanced DMR and RWGS in terms of surface reaction mechanisms would provide better insight into the new concept of catalyst design, yielding non-equilibrium product distribution. Finally, concluding remarks are presented.

Classification of Process Plasmas

DBD is known to be an atmospheric pressure nonthermal plasma where the gas temperature is close to the room temperature, while mean electron energy reaches 1–10 eV. DBD is studied frequently in plasma catalysis, together with microwave and gliding arc discharges, which are known as warm discharge where gas temperature elevated to higher than 2000 K. Figure 1 shows various plasmas mapped on electron density and electron energy coordinates [7]. Gliding arc discharge (GAD) was added to the original figure [8,9,10,11]. The solid line diagonally crossing Fig. 1 expresses constant Debye length (λ_D) calculated by Eq. 1.

$${\uplambda }_{{\text{D}}} = \sqrt {\frac{{{\upvarepsilon }_{0} {\kappa T}_{{\text{e}}} }}{{{N}_{{\text{e}}} {{e}}^{2} }}} = 7.43 \times 10^{3} \sqrt {\frac{{{T}_{{\text{e}}} }}{{{N}_{{\text{e}}} }}}$$

(1)

Fig. 1

Classification of atmospheric pressure nonthermal plasmas (modified by the authors) [7]. AAPJ, atmospheric pressure plasma jet; DBD, dielectric barrier discharge; MPJ, microwave plasma jet; MPT, microwave plasma torch; MTD, microwave torch discharge; TIA, torche à injection axiale (plasma torch with axial plasma injection); GAD, gliding arc discharge was added by authors [8,9,10,11]. Reproduced from Ref. [7] with permission from the Elsevier

The Debye length is a physical quantity calculated from the electron energy T_e (eV) and the electron density N_e (m⁻³), and is one of the representative parameters describing the plasma characteristics. Equation 1 does not take into consideration the deviation of the electron energy distribution from the Maxwellian, but the Debye length can be obtained conveniently using the mean electron energy. Various process plasmas can be classified into three regions with respect to the Debye length.

λ_D > 100 μm (Low pressure nonthermal plasma): Nonthermal plasmas formed in a reduced pressure of 100 Pa or less is classified as λ_D > 100 μm, assuming an electron density of 10¹⁵ m⁻³ and an electron energy of 1 eV or higher. The degree of ionization is low, and most of the particles in plasma are neutral atoms and molecules. Due to the low electron density, the frequency of electron-molecule collision as well as electron–electron collision is low, and the electron energy distribution deviates greatly from the Maxwellian. Electrons, ions, and radicals generated by electron collision cause chemical reactions in the reactor walls and substrates rather than in the gas phase, so they are used for thin film deposition, etching, microfabrication, and surface modification.

100 > λ_D > 1 μm (Atmospheric pressure nonthermal plasma): It is characterized by the formation of plasma with locally high electron density, such as corona discharge and dielectric barrier discharge, and is classified into a different regime from nonthermal and thermal plasmas. Although the gas temperature is relatively low and satisfies the condition of “electron temperature >  > gas temperature”, the collision frequency between particles is high; the gas temperature tends to be higher than nonthermal plasma formed in a low pressure. Many plasma sources used in the energy and environmental field, such as ozone synthesis and CH₄ reforming, fall into this regime.

λ_D < 1 μm (High temperature thermal plasma): A thermal plasma with a high electron density and low electron energy corresponds to this regime. It has a high energy density and a high mass throughput (e.g. kg/s). Interestingly, it is not much different from nonthermal plasma when compared with the power per mass throughput ((J/s)/(kg/s) = J/kg), which can be measured by specific energy input (SEI, kJ/mol). They are often not energy efficient as much of the power is lost to the cooling water. Heat recovery from hot process gas is also an important technology for high efficiency. Gutsol denotes atmospheric pressure nonthermal plasma in which the gas temperature rises to above 2000 K as warm discharge and distinguishes it from other atmospheric pressure plasmas [12]. It is important for endothermic reactions such as fuel reforming because radicals and heat are supplied simultaneously. Warm discharge is classified in the boundary region (λ_D≈ 1 μm) between thermal plasma and atmospheric pressure nonthermal plasma.

Atmospheric pressure nonthermal plasma is clearly distinguished from thermal plasma and nonthermal plasma in low pressure, and is classified as a reactive plasma formed in a new parameter region. By overviewing Fig. 1, plasma is not plotted in the region where the electron energy is below 1 eV at λ_D > 1 μm. It indicates that gas molecules must be ionized to form plasma and that the mean electron energy must be at least 1 eV. On the other hand, plasma with a lower electron energy is preferable for vibrational excitation of gas molecules, and its effectiveness has been verified for CO₂ conversion to CO [13, 14] and N₂ oxidation (NO_x) [15, 16] and reduction (NH₃) [17, 18]. The development of new plasma sources in such unexplored regions is an important subject of research.

Basic Properties of DBD in Packed Bed

Packed-Bed DBD Reactor

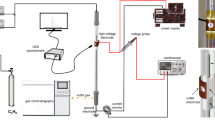
Coaxial packed-bed configuration is commonly used for DBD and catalyst combination [6]. Figure 2 shows the schematic diagram of packed-bed DBD (PB-DBD) reactor used for DMR [19]. Quartz tube (i.d. 20 mm, o.d. 23 mm) was filled with Lanthanum-modified Ni/Al₂O₃ catalyst pellets (La 3 wt%, Ni 11 wt%) over 40 mm length. High-voltage electrode is located coaxially in the reactor (3 mm diameter). The power source generates quasi-sinusoidal high-voltage output. Online gas analysis was employed by a quadrupole mass spectrometer (QMS, PrismaPlus; Pfeiffer Vacuum GmbH). Temperature of the catalyst bed was measured by the infrared camera (TH5104; NEC Sanei Instrument Ltd.). The measured data was calibrated by the thermocouples in advance, and further correlated with the rotational temperature of CO Angstrom system [20], showing the gas (rotational) temperature of corresponding emission region (i.e. streamers) and the catalyst temperature are equilibrated.

Fig. 2

Schematic diagram of PB-DBD reactor [19]. Inset pictures show DBD generated by 12 kHz high-voltage power source (Logy Electric) at 5 kPa and a corresponding thermo-image of the catalyst bed. Catalyst pellets (Raschig ring): 3 × 3 mm (diameter × height) having 1 mm hole

Streamer Generation in Packed-Bed Reactor

DBD is characterized as a swarm of filamentary microdischarges (known as streamers) with nanosecond duration (1–10 ns), which is recognized as a number of nanosecond current pulses [2]. Dynamic behavior of streamer propagation in a packed-bed DBD reactor has been studied by Kim et al. [21]. Figure 3 shows the streamers generated by the nanosecond high-voltage pulse on Ag/Al₂O₃ catalyst pellets in air. Streamers propagate in close contact with catalyst pellets, enabling better interaction of reactive species with the pellet surface. However, due to highly transient and localized nature of DBD, interaction of reactive species and catalysts are not always efficient. First, the plasma promotion effect would be limited for a short duration (1–10 ns) where the individual streamer is in contact with the catalyst surface. Moreover, there may be no plasma effect over the dark areas where streamers are absent. Gas breakdown occurs every half cycle of applied voltage, indicating the thermal reaction dominates during discharge-off period. The facts indicate clearly what we observe for DBD and catalyst interaction is a mixture of purely thermal reaction and DBD-induced plasma reaction. In order to decouple the plasma promotion effect and thermal catalysis, we need careful kinetic analysis which will be discussed using Arrhenius plot in “Kinetic Analysis” section.

Fig. 3

Time-resolved images of surface streamers propagating on the surface of γ-Al₂O₃ pellet (50 scans) (9.3 kV, 5 ns gate-time, NIR lens). Reproduced from Ref. [21] with permission from the IOP Publishing

Analysis of Lissajous Diagram

Figure 4 shows the voltage-charge diagram, known as the Lissajous diagram. The data was obtained using 12 kHz and 100 kHz power sources in packed-bed DBD reactor shown in Fig. 2. The Lissajous diagram exhibits a quasi-parallelogram; gas breakdown occurs with multiple streamer generation between points B–C and D–A, respectively. The gas breakdown does not occur between A–B and C–D, showing thermal reaction dominates during discharge-off periods. Also, considering Fig. 3, thermal and plasma reactions are not decoupled.

Fig. 4

Lissajous diagram for 12 kHz and 100 kHz DBD [19]. Total pressure = 5 kPa; CH₄/CO₂ = 0.8; Power = 90 W

The discharge power is estimated by the integral of the Lissajous diagram multiplied by frequency.

$$P_{L} = f\oint {QdV} \left( W \right)$$

(2)

The discharge power is also given by Manley’s equation for the parallel-plate electrode configuration without packing materials between the gap [22]. Manley derived Eq. 3 assuming the Lissajous diagram in a parallelogram.

$$P_{M} = 4fV^{*} C_{d} \left( {V_{p} - \left( {1 + \frac{{C_{g} }}{{C_{d} }}} \right)V^{*} } \right) \left( W \right)$$

(3)

The f represents frequency; C_g and C_d respectively denote the capacitance of the gas gap and the dielectric material; V_p is the applied peak voltage and V^* expresses the effective gas breakdown voltage (refer to Fig. 4). Because V^* is equivalent to the voltage acting across the gas gap; it is preferably defined as the discharge sustain voltage rather than the gas breakdown voltage. Assume C_d >  > C_g, Eq. 3 reduces to Eq. 4 showing the power density (W/m³):

$$\begin{aligned} \frac{{P_{M} }}{A \times d} & \approx 4f\left( {\frac{{V^{*} }}{d}} \right)\left( {\frac{{C_{d} }}{A}} \right)\left( {V_{p} - V^{*} } \right) = 4\left( {\frac{{V^{*} }}{d}} \right)\left( {\frac{{I_{p} }}{A}} \right) \left( {{\text{W/m}}^{3} } \right) \\ I_{p} & = fC_{d} \left( {V_{p} - V^{*} } \right) \\ \end{aligned}$$

(4)

Here, V^*/d represents the mean electric field strength between the gas gap (V/m); I_p/A is the apparent current density (A/m²). I_p does not represent the intensity of the current spike due to streamer formation, but it is correlated with the sum of charges (Q_p) during the half cycle of applied voltage. Our concern is to make a correlation between a Lissajous diagram observed in parallel plate empty electrodes and packed-bed co-axial electrodes. Figure 5 compares P_L and P_M with and without catalyst pellets at different frequencies. Interestingly, all data points are plotted on a single line: there is no dependence on packed materials or frequency. Similarly, packed materials do not influence discharge properties such as V^* and I_p [19]. P_M slightly overestimates P_L because Eq. 3 was derived by assuming an ideal parallelogram, while the actual Lissajous diagram is deformed. Obviously, the area of the measured Lissajous diagram is smaller than the corresponding parallelogram (Fig. 4). Disregarding such a small deviation, Eq. 4 implies that power in PB-DBD is characterized by V^* and I_p.

Fig. 5

The relationship between P_M and P_L [19]. □ 100 kHz Empty-DBD; ■ 100 kHz PB-DBD; ○ 12 kHz Empty-DBD; ● 12 kHz PB-DBD. CH₄/CO₂ = 0.8; Power = 6–90 W; catalyst temperature = ca. 600 °C

The discharge power is determined by the number of streamers generated per unit area and unit time; a typical number density of streamers in air DBD is 10⁶ cm⁻² s⁻¹ [23]. Manley's equation does not display parameters indicating electron density and electron energy in a streamer, and streamer number density. All these important properties of DBD are included in V^*, and hardly decoupled. In many cases, we do not tailor V^*; we merely measure V^* which is determined as a consequence of complex discharge events. Because V^* does not change to a large extent with respect to the increase of V_p, power density is controllable by a lone tuning knob, i.e. I_p. It must be mentioned that the total number of streamers per half cycle, or Q_p, increases with V_p: however, electron energy and electron density in streamers are essentially unchanged. Meanwhile, frequency (f) has a much greater impact on discharge properties than V_p; frequency is associated with I_p (Eq. 4), but it also influences V^* as shown in Fig. 4. Such peculiar characteristics of DBD has reported by Kogelschatz in relation to ozone synthesis [2]. Later, Nozaki et al. demonstrated similar characteristics in CH₄-DBD by the comprehensive energy balance analysis [24, 25].

Because there is no clear difference between PB- and empty-DBD, we assumed that V^* divided by gas gap (d) would express the representative value of electric field in PB-DBD. It must be mentioned that there is a limitation of Lissajous analysis, although it is a powerful diagnostic tool for DBD. Assuming a parallel plate empty DBD configuration, the average electric field estimated by this method (V^*/d) does not represent the local electric field of the advancing streamer head, which is several times larger than the average electric field [26]. Similarly, the local electric field created at the pellet contacts may not be measured clearly by the Lissajous diagram. Other inconsistencies may arise in terms of gas conversion experiments. In the case of DMR, the discharge property at the inlet (e.g. CH₄/CO₂) and the outlet (e.g. CH₄/CO₂/H₂/CO/H₂O) of the reactor is different to a large extent. Meanwhile, SEI, GHSV, and the power density (i.e. V^* and I_p) represent the overall averaged properties of PB-DBD reactor. By knowing the limitation of Lissajous analysis, we should not discard any possible discharge characteristics which may be hidden behind the macroscopic measured data; an overly detailed interpretation of plasma chemistry with macroscopic parameters might lead to inconsistent inferences.

Catalyst Effectiveness Factor: Does DBD Interact with Micropores?

Catalyst effective factor must be considered when porous pellet was used. In the thermal reaction, when the catalyst pellet temperature is low, the reaction rate is slow thus gas molecules are able to diffuse into micropores. Because catalytic reactions occur over the entire micropores, the catalyst effectiveness factor is defined as “1”. Meantime, as the catalyst temperature increases, the reaction rate increases exponentially, and the reaction is terminated near the outermost surface of pellets: in this case, the catalyst effectiveness factor becomes much smaller than “1” [27, 28].

Catalyst effectiveness factor is formulated using a non-dimensional parameter, known as the Thiele modulus [28]. In the case of plasma catalysis, the reaction is terminated near the outer surface regardless of catalyst temperature because the reactivity of plasma-activated species is high. Spherical Ni/Al₂O₃ pellets (3 mm diameter) are exposed to either CO₂ (thermal reaction) or CO₂-DBD [29]. Figure 6 shows the catalyst color change clearly when CO₂-DBD is applied, but only over the outer surface. Cross-sectional Raman spectroscopy identifies that the whitish materials was nickel oxide with a thickness of about 20 μm. The fact implies gas breakdown does not occur in micropores due to the limitation of Paschen's law [30]. Moreover, electrons and ions do not diffuse into micropores, which is limited by the Debye length (see also Fig. 1). Because not all gases are excited into vibrational or electronic states, ground state molecules diffuse into micropores that induce thermal reaction over the cross-section of pellets. Especially, when the catalyst temperature is low, it is hard to decouple the plasma promotion effect from thermal reaction.

Fig. 6

Cross-sectional view of hemispherical catalyst pellets (Ni/Al₂O₃) a Thermal reaction, b DBD reaction, and c Nickel oxide distribution after plasma reaction in CO₂

The criterion for interaction between nonthermal plasma and the porous catalyst was discussed by Kim et al. [31]. They estimated the lifetime of reactive species such as O(¹D); 10 ns, O(3P); 50 μs and OH; 100 μs, and assumed one-dimensional diffusion length of 0.7–65 μm. If reactive species are adsorbed or trapped on the active sites, the diffusivity of these species is weakened by orders of magnitude. However, an apparent lifetime of reactive species is extended as an active surface species, which would promote plasma-induced surface reactions. It is a particularly important mechanism for the weakly ionized plasma. Although radical concentration in the gas phase is low, they are accumulated on the catalyst surface which would promote gross conversion of reactants.

One may expect the generation of nonthermal plasma in the micropores. Following the standard Paschen’s law, gas breakdown hardly occurs in porous media with less than 10 μm due to the limited number of electron-molecule collisions. Gas breakdown in the micropores might be possible by the modified Paschen’s mechanism where sufficient secondary electrons are supplied by the field emission from the metallic electrode [32], which is presumably not possible in the dielectric micropores. Zhang et al. investigated gas breakdown behavior numerically in the atmospheric pressure helium, showing the increased electric potential when the pore size was larger than 100 μm, followed by intensified electron energy to generate reactive species [33]. They concluded gas breakdown would be possible with pores larger than 10 μm. It was validated experimentally by Hensel et al. that gas breakdown occurred in a porous ceramic with 15 μm pores: no discharge was possible in 0.8 μm pores [34]. In conclusion, the standard Paschen-type gas breakdown is not possible in micropores on the order of 1 nm, or under the situation where the Knudsen diffusion dominates the mass transport.

Evaluation of Operational Parameters

Specific Energy Input and Energy Efficiency

Energy efficiency is one of the most important parameters for energy and environmental applications. In this section, we discuss how to evaluate energy efficiency. Examples of CH₄ reforming reactions are listed in Table 1. The energy efficiency of the endothermic reforming reaction is expressed by the following formulae:

$$SEI = \frac{{P \left( {{\text{kJ}}/{\text{s}}} \right)}}{{F_{total} \left( {{\text{mol}}/{\text{s}}} \right)}} \left( {{\text{kJ}}/{\text{mol}}} \right)$$

(5)

$$\begin{aligned} \eta & = \frac{{{\Delta }H^{^\circ } { }\left( {{\text{kJ}}/{\text{mol}}} \right) \times \chi_{{CH_{4} }} \left( {\text{\% }} \right) \times F_{{{\text{CH}}_{4} }} { }\left( {{\text{mol}}/{\text{s}}} \right)}}{{P{ }\left( {{\text{kJ}}/{\text{s}}} \right)}} = \frac{{\Delta H^{^\circ } }}{SEI} \times \chi_{{CH_{4} }} \times \phi = \frac{{\Delta H^{^\circ } }}{SEI/\phi } \times \chi_{{CH_{4} }} { }\left( {\text{\% }} \right) \\ \phi & = \frac{{F_{{{\text{CH}}_{4} }} }}{{F_{{{\text{total}}}} }}{ }\left( - \right) \\ \end{aligned}$$

(6)

Table 1 Relationship between standard enthalpy of formation (ΔH°) and SEI

ΔH° (kJ/mol) denotes standard enthalpy of formation of each reaction, ${\chi }_{{CH}_{4}}$ (%) expresses CH₄ conversion, F (mol/s) shows flow rate of gas. P (kJ/s) refers to the discharge power which is determined by the Lissajous diagram. The Lissajous analysis provides a macroscopic insight, and discharge behavior on a streamer basis is not accessible. Nevertheless, it is obviously a key parameter for the reactor design. The SEI is calculated unambiguously by the discharge power (P) and the total flow rate of feed gas (F_total) no matter what the reaction conditions would be. Therefore, performance levels of different conditions as well as different plasma reactors can be classified on an SEI basis [35]. Relationship between energy efficiency and SEI must be evaluated carefully because ΔH° is defined by the reaction, but SEI is calculated by the total flow rate of the feed gas: the energy efficiency becomes 100% when ΔH° = SEI/ϕ is satisfied (Table 1). Energy efficiency is smaller than 100% when SEI = ΔH°. Obviously, diluting the feed gas with argon, helium, nitrogen, etc. is detrimental for the energy efficiency because of ϕ << 1. Similarly, if the S/C (Steam/Carbon) ratio is set above stoichiometric ratio to prevent coking in steam reforming, the SEI must be decreased accordingly; otherwise, energy efficiency decreases due to ϕ << 1 even if CH₄ conversion reached 100%. Therefore, when comparing different reaction conditions by SEI basis, both SEI and ϕ (Eqs. 5, 6) must be considered appropriately; if not, an evaluation of the energy efficiency of the plasma catalysis may lead to an unexpected misunderstanding.

At least the energy equivalent to ΔH° must be added to the reactor so that the conservation of energy is satisfied. Preferably, reaction conditions are tuned so that SEI < ΔH° × ϕ is fulfilled: for DMR, SEI < ΔH° × ϕ = 123.7 kJ/mol. Assume plasma catalysis of DMR is operated at SEI = 100 kJ/mol (equivalent to P = 100 W and ca. Q_total = 1500 cm³/min at STP); about 81% (= 100/123.7 × 100) of energy required for DMR is supplied from plasma and 19% is from ambient thermal energy. When SEI > ΔH × ϕ, energy efficiency is inevitably below 100% and such condition must be avoided. For an exothermic reaction system, the definition of energy efficiency and relationship with SEI is discussed in ref [36].

Space Velocity and Residence Time

The Gaseous Hourly Space Velocity (GHSV) is used commonly to express contact time, representing how many times of volumetric gaseous materials are processed with respect to the total volume of the reactor per unit time (h⁻¹) at STP. In many cases, superficial volume, or empty reactor, is considered for the calculation of GHSV, which is equivalent to the inverse of apparent residence time. For simplicity, we defined GHSV using the empty reactor volume (V) as an alternative parameter of residence time.

$$GHSV = \left( {Residence\;time} \right)^{ - 1} = \frac{{60 \times Q_{total} \left( {{\text{cm}}^{3} {\text{/min}}} \right)}}{{V \left( {{\text{cm}}^{3} } \right)}} \left( {h^{ - 1} } \right)$$

(7)

The product of GHSV and SEI is equivalent to the power density; Eq. 8 is correlated with Manley’s equation (Eq. 4).

$$GHSV \times SEI \propto \frac{P}{V} \left( {{\text{W/cm}}^{3} } \right)$$

(8)

Alternatively, Weight Hourly Space Velocity (WHSV) is used which is calculated from the total mass flow rate of feed gas (g/h) divided by the total weight (g) of catalysts loaded in a reactor. WHSV becomes important parameter, especially when the experiments are conducted with different catalyst loading weight. Also, in a fluidized-bed DBD reactor (“Fluidized-Bed DBD Reactor” section), it is hard to define the superficial reactor volume because the reactor volume occupied by fluidized powder is varying dynamic and complex. Although GHSV and WHSV have the same unit (h⁻¹), the inverse of WHSV is not correlated with residence time. For simplicity, WHSV is expressed commonly in the unit cm³/g/h.

Power density (P/V, W/cm³) is obtained by the discharge power and the reactor volume independently of the total gas flow rate. Assume a total gas flow rate is doubled; SEI and residence time (i.e. GHSV⁻¹) are halved simultaneously. Therefore, the conversion of reactants may decrease by less than half; while power density is kept unchanged when discharge power is constant. Such reaction behavior cannot be discussed by a power density basis. The individual contribution of SEI and GHSV must be taken into account so that the operating conditions are optimized in a rational manner. Power density (W/cm³) becomes the important parameter when designing a dimension of the reactor (length and diameter) including the performance of the power source. Refer to Eq. 4 which describes a power density in relation to Manley's equation.

Dry Methane Reforming

As an example of DBD and catalyst hybrid reaction, DMR is discussed in relation to parameter setting such as SEI and GHSV. Kinetic analysis of packed-bed DBD (PB-DBD) revealed the thermal and DBD reactions occur simultaneously when DBD is operated at 12 kHz power source, which is called mixed catalysis [19]: such reaction behavior is correlated with catalyst effectiveness factor (“Catalyst Effectiveness Factor: Does DBD Interact with Micropores?” section). In contrast, plasma-induced reaction dominates over thermal catalysis when the power source frequency increases to 100 kHz. To overcome mass transport resistance through micropores, fluidized-bed DBD (FB-DBD) is introduced in which the performance of DMR is enhanced dramatically. Discharge behavior in PB- and FB-DBD reactors is discussed from a macroscopic viewpoint by Lissajous diagram analysis.

Kinetic Analysis

Dry methane reforming was studied using DBD packed with La–Ni/Al₂O₃ pellets. Refer to “Packed-Bed DBD Reactor” section for detailed information of PB-DBD reactor configuration. CH₄ and CO₂ conversion increased by DBD (12 kHz), which was further promoted when high frequency DBD (100 kHz) was applied. In order to discuss plasma promotion effect quantitatively, activation energy for the overall DMR reaction was measured.

Figure 7 shows the Arrhenius plot for three conditions which are listed in Table 2 together with discharge properties (V^* and I_p–p). In thermal catalysis, DMR is characterized by the reaction-limited regime at low temperatures, where the slope of the line expresses the activation energy of the forward CH₄ reaction rate. Activation energy for thermal catalysis yielded E_t = 91.0 kJ/mol which agrees well with reported value for DMR [37]. In high temperatures, the activation energy is almost halved (E_t = 53.4 kJ/mol); the apparent activation energy is determined by the combined effect of surface reactions and the diffusion of molecules through micropores of pellets [27, 28]. Reaction rate is proportional to the square root of reaction rate constant, yielding E_app = E_t/2 as formulated in Eq. 9. Such reaction behavior agrees well with the experimental observation. Here, D denotes the diffusion coefficient of feed gas molecules in the porous medium.

$$r_{app} \propto \sqrt {\frac{{k_{f} }}{D}} \propto e^{{ - \frac{{E_{t} /2}}{RT}}}$$

(9)

Fig. 7

Arrhenius plot for thermal (●), mixed (■), and plasma catalysis (▲) [19]

Table 2 Experimental conditions for Arrhenius plot analysis

Similar to thermal catalysis, 12 kHz DBD hybrid reaction exhibits a convex Arrhenius behavior where the reaction regime is separated at the same break temperature of T_B = 510 °C. Because of highly transient nature of DBD as discussed in “Streamer Generation in Packed–Bed Reactor” sections, 12 kHz DBD hybrid reaction is characterized as mixed catalysis in which thermal and DBD reactions are not decoupled. Convex behavior is explained by the mass transfer resistance in the micropores, or thermal catalysis occurs predominantly in 12 kHz case. The additional CH₄ conversion via vibrationally excited CH₄ occurs in parallel over the outermost surface of pellets, yielding a larger reaction rate constant compared to the thermal catalysis. Correspondingly, apparent activation energy is measured as slightly smaller value than thermal catalysis (83.2 kJ/mol [19]).

Similar Arrhenius behavior was observed in our previous study on DBD-assisted CH₄ steam reforming [25, 38]. Spherical 12 wt%-Ni/Al₂O₃ catalyst pellets (3 mm diameter) were applied and DBD was generated using 1–5 kHz bipolar pulsed high voltage. The activation energy for the thermal catalysis was measured as E_t = 102 kJ/mol; CH₄ chemisorption is the rate-determining step and this value agrees well with the literature [39]. The activation energy was halved from 102 to 53 kJ/mol with the same as Fig. 7 at the break temperature of T_B = 420 °C. The Arrhenius plot for DBD hybrid reaction shifts toward a larger reaction rate constant having slightly smaller activation energy than the thermal reaction (90 kJ/mol), indicating the DBD hybrid reaction at low frequency is mixed catalysis.

Arrhenius plot in 100 kHz DBD is unique. First, the break temperature at T_B = 510 °C is no longer observed. The observation implies that the overall reaction is dominated by the vibrationally excited CH₄ which increases reaction rate constant dramatically compared to thermal reaction. Electron collision rate coefficients for vibrational excitation of CH₄ do not change to a large extent between 12 and 100 kHz DBD [19]; however, the mean discharge current is doubled in 100 kHz DBD, producing more vibrationally excited CH₄ than 12 kHz DBD does. Vibrationally excited CH₄ is consumed most likely in the 20 µm thin layer of the outer surface of pellets [29]. Although, the effect of internal diffusion of ground-state molecule is not fully ruled out in 100 kHz case, we could rationally conclude that overall reaction is dominated by DBD with minimum contribution of thermal catalysis in micropores: the activation energy (E_p = 44.7 kJ/mol) expresses the pure plasma catalysis in the case of 100 kHz DBD. Note, Arrhenius plot shows convex behavior at 580 °C at 100 kHz DBD. This is not related to the internal mass transfer resistance, but it is due to the excessive CH₄ and CO₂ conversion which approaches the thermal equilibrium [37, 39].

Fluidized-Bed DBD Reactor

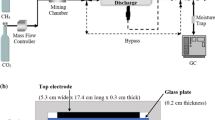
We constructed a fluidized-bed DBD (FB-DBD) reactor which exhibited excellent heat and mass transport properties, enabling enhanced plasma catalysis performance. Figure 8 shows the schematic diagram of FB-DBD reactor. The quartz reactor (20 mm i.d. × 23 mm o.d.) was supported vertically, and the ground electrode and the electric heater were in close contact, while the high-voltage electrode (stainless steel tube, 6 mm o.d.) was coaxially placed in the quartz reactor, creating 7 mm gas gap in the radial direction [40]. The La–Ni/Al₂O₃ catalyst powder (La 3 wt%, Ni 11 wt%), the identical catalyst used for Fig. 7, was applied for the reforming reaction. La–Ni/Al₂O₃ catalysts were grounded by mechanical milling, then grain size was graded by sieving between 180 and 300 μm. 4 g of catalyst particles were loaded into the reactor. The catalysts were reduced prior to the reforming experiments in H₂(10%)/Ar flow at 700 °C for 60 min using annealing equipment. A feed gas was supplied through the high-voltage tubular electrode. The feed gas blows off the catalyst powders which initiate self-sustaining fluidization motion. Fluidization behavior is shown in the supplementary movies in ref [40].

Fig. 8

Schematic diagram of FB-DBD and experimental system [40]. The inset thermograph corresponds to the hybrid reaction with a catalyst temperature of 404 ℃. Movies of fluidized-bed DBD are provided in supplementary data of ref [40]

Operating conditions are not as flexible as PB-DBD because gas flow rate, catalyst powder loading, temperature, and pressure need to be tuned so that stable fluidization of catalyst powder is secured. Table 3 compares experimental conditions for PB- and FB-DBD. Note, dilution gas was not used throughout the experiments. Because the catalyst loading weight decreases three times less to secure the bubble fluidization [41], WHSV was adjusted to be the close value for PB-DBD. As a result, the total gas flow rate in the FB reactor must be reduced by one-third. Correspondingly, discharge power decreased by one-third so that the SEI is adjusted to be a similar value.

Table 3 Experimental conditions (^*1 STP)

Figure 9a and b compare the CH₄ conversion in FB and PB reactors, respectively. In Fig. 9a, the results of thermal reaction for PB and FB reactors are shown to better comparison of reactor performance. When the catalyst temperature is lower than ca. 500 °C, there is no clear difference between FB and PB reactors (● and ○). As shown in the Arrhenius plot (Fig. 7), mass transfer is not the rate-determining step below 500 °C, thus FB reactor does not increase the CH₄ conversion with respect to PB reactor. However, when the catalyst temperature is higher than 500 °C, the FB reactor demonstrates higher CH₄ conversion in the thermal catalysis. Because mass transport resistance through micropores is reduced by small particle size in FB reactor. When DBD is generated in the FB reactor, CH₄ conversion reaches the thermal equilibrium in both 12 kHz and 100 kHz: plasma promotion effect in 12 kHz DBD is much greater than that of PB-DBD (12 kHz) (Fig. 9b). Results imply the plasma promotion effect at 12 kHz DBD is intrinsically excellent, but it is suppressed due to the mass transport through micropores when a packed-bed reactor is used.

Fig. 9

CH₄ conversion and energy efficiency in DMR [41]. a Fluidized-bed reactor (● thermal, ▲ 12 kHz DBD, ■ 100 kHz DBD, dashed line represents DBD only (without catalyst), ○ thermal for packed-bed reactor); b Packed-bed reactor (○ thermal, ∆ 12 kHz DBD, □ 100 kHz DBD); c Energy efficiency

Figure 9c displays the energy efficiency (η) which is calculated by Eq. 6. Because the power consumption and gas flow rate were kept constant for PB and FB-DBD, respectively, the energy efficiency and CH₄ conversion were in similar trends. In PB-DBD, 100 kHz operation is superior to 12 kHz because more vibrationally excited molecules are produced than 12 kHz case. As a result, energy efficiency for 100 kHz PB-DBD (□) is clearly higher than 12 kHz PB-DBD (∆). The same principle is applicable to FB-DBD. However, CH₄ conversion is suppressed by the equilibrium limitation; the superiority of 100 kHz operation is not seen in FB-DBD. In FB-DBD, CH₄ conversion reached equilibrium over the entire temperature range at both frequencies and the maximum energy efficiency of 70% was confirmed at a catalyst temperature of 650 °C. In addition to the plasma power consumption, thermal energy also affects the endothermic reforming reaction. Therefore, Fig. 9c can be used as a guide for improving energy efficiency. It is necessary to develop new catalysts to drive the CH₄ conversion beyond the thermal equilibrium to achieve high energy efficiency at low temperatures. This critical issue is discussed in the application to reverse water gas shift reaction (“Reverse Water Gas Shift Reaction” section) where CO₂ conversion increased more than the thermal equilibrium limit. Nonequilibrium product distribution is discussed further in terms of surface reaction mechanisms (“Surface Reaction Mechanisms” section).

Figure 10 shows the Lissajous diagram for FB- and PB-DBD at different frequencies. The discharge power was kept constant at 30 W (FB-DBD) and 90 W (PB-DBD), respectively. Similar to standard DBD where packing material is absent, the discharge and non-discharge phases are distinguished during one cycle. The charge transferred in FB-DBD is approximately one-third of the PB-DBD simply because the discharge power was decreased from 90 W (PB-DBD) to 30 W (FB-DBD). Correspondingly, the mean discharge current in FB-DBD decreased by threefold. Interestingly, the discharge sustain voltage (V^*) was kept unchanged between FB- and PB-DBD at fixed frequency [40]; macroscopic discharge behavior is not distinguished by either pellet catalysts or powdered catalysts. This is the same trend as Fig. 5 that the discharge properties of PB-DBD and empty DBD reactor are not distinguished. However, it is hard to correlate the discharge sustain voltage (V^*) and the local reduced electric field (E/N) directly because a complex interaction of fluidized catalyst particles and streamers is not analyzed by the Lissajous diagram.

Fig. 10

Lissajous diagram for a FB-DBD and b PB-DBD, respectively [40]. Catalyst temperature was ca. 480 °C in all cases

DBD Versus Warm Discharge

Electron Energy Loss Fraction Versus Rate Coefficient

Figure 11 shows energy distribution to the excited states of CO₂ with respect to E/N (Td) [35]. A similar diagram is obtained for N₂ plasma [42]. It is generally accepted that microwave (MW) and gliding arc (GA) discharge are suitable for the generation of vibrationally excited molecules because the MW and GA are characterized as low E/N plasma sources. In contrast, DBD is generated at higher E/N and is not superior to MW or GA in terms of vibrational excitation of molecules. Meantime, the gas temperature of MW and GA would increase above 1000 K which would be detrimental to the plasma promotion effect via vibrationally excited molecules. First, thermal catalysis due to plasma heating would dominate the overall reaction. Therefore, vibrational excitation may not arise a profound effect when MW or GA is coupled with heterogeneous catalysts. Second, vibrational deactivation is fast at elevated temperatures. Finally, catalyst degradation is anticipated under a high-temperature plasma environment. Because DBD is one of the best plasma sources for the combination with catalysts, the role of vibrationally excited molecules in DBD-type plasma is discussed further.

Fig. 11

Energy distribution to the excited states of CO₂ with the E/N regions of DBD, microwave (MW), and gliding arc (GA) discharges. Reproduced from Ref. [35] with permission from the Royal Society of Chemistry

Fractions of electron energy loss to the respective excited states of CH₄ and CO₂ were calculated for CH₄ and CO₂ mixture at CH₄/CO₂ = 1 and 873 K. Analysis was performed using BOLSIG + (version 03/2016) [43] with the electron collision cross-section data [44, 45] which were adapted in our past study for kinetic analysis of CH₄ and CO₂ plasma [19, 46]. The results are shown in Fig. 12 which is the equivalent to Fig. 11. Meantime, the E/N (Td) in 100 kHz DBD (250–400 Td) and 12 kHz DBD (600–1200 Td) was confirmed by the experiment [19].

Fig. 12

Fraction of electron energy to the excited states of a CH₄ and b CO₂, respectively. Calculation performed by BOLSIG + (version 03/2016) at CH₄/CO₂ = 1 and 873 K

In Fig. 12, electron energy loss fractions to vibrational excitation of CH₄ and CO₂ are smaller than 10% respectively within the scope of DBD (E/N > 200 Td). The result may lead to an inappropriate interpretation that the contribution of vibrationally excited species to the plasma promotion effect is minor in DBD. Such inconsistency arises due to a significant difference in excitation threshold energy between dissociation and vibrational excitation. For example, the excitation threshold energy for C-H dissociation (e.g. CH₄ + e = CH₃ + H + e) is 9.0 eV, while CH₄ bending vibrational excitation energy (CH₄ + e = CH₄(ν_B) + e) is 0.16 eV: energy loss for C–H dissociation per single electron collision is 56-fold larger than that of bending vibration.

Electron collision rate coefficients are more important than the energy loss fraction because rate coefficients determine how many and what types of active species are produced per unit time. For this reason, electron-impact rate coefficients of CH₄ and CO₂ mixture were estimated with the same cross-section data set and conditions in Fig. 12. Results are summarized in Fig. 13, showing the production of vibrationally excited CH₄ and CO₂ is the dominant reaction pathway at E/N < 700 Td, which is equivalent to 100 kHz DBD case. Although dissociation and ionization rates increase sharply at E/N > 200 Td, vibrational excitation still plays a key role until E/N = 1000 Td; this condition is equivalent to 12 kHz DBD case. Generation of vibrationally excited molecules is the dominant reaction path in DBD up to about 1000 Td. 100 kHz DBD is more beneficial than 12 kHz DBD for vibrational excitation, leading to a higher plasma promotion effect of catalysis.

Fig. 13

Electron collision rate coefficients and mean electron energy calculated by BOLSIG + (version 03/2016) at CH₄/CO₂ = 1 and 873 K. Momentum transfer and electron attachment coefficients are not shown

Lifetime of Vibrationally Excited CH₄

For the better understanding of vibrational chemistry in DBD, the lifetime of vibrational excited CH₄ is estimated by solving the rate equation. Analysis of vibrationally excited CO₂ has not been performed due to its excessively complex gas phase vibrational chemistry [47]. For simplicity, three state system is assumed to estimate the V–V and V–T transition decay of vibrationally excited CH₄ (Fig. 14) [19]. Two stretching and two bending modes were combined respectively as single ν_S and ν_B due to the fast V-V transition between ν₃ and ν₁ (k_3,1) and ν₂ and ν₄ (k_2,4). Hereafter, stretching and bending mode CH₄ are designated respectively as CH₄(ν_S) and CH₄(ν_B). Electron impact excitation rate coefficients to bending (k_eB) and stretching (k_eS) vibration was estimated by the electron Boltzmann equation solver (BOLSIG + ver. 03/2016) [43] with an appropriate electron-CH₄ cross-section data [44, 45]. Quenching rate coefficients for stretching to bending vibration (k_SB) and bending vibration to ground state (k_BG) were obtained from literature, showing the lifetime of CH₄(ν_S) and CH₄(ν_B) is expressed respectively as τ_SB and τ_BG [19]:

$$\tau_{SB} = \frac{1}{{2k_{SB} N}} = 0.1\;\upmu {\text{s}}\quad \tau_{BG} = \frac{1}{{2k_{BG} N}} = 31\;\upmu {\text{s}}$$

(10)

Fig. 14

Schematic representation of the three-state excitation and quenching model [19]

N refers to the gas density determined by gas temperature (873 K) and pressure (5 kPa). Quenching from bending vibration to the ground state is relatively slow process. In 100 kHz DBD, gas breakdown occurs at 5 μs intervals (0.5/100 kHz = 5 μs), implying 6 discharge events are possible during the lifetime of bending vibration (τ_BG = 31 μs). As a result, CH₄(ν_B) would populate to high density. In 12 kHz DBD, the gas breakdown interval is 42 μs (0.5/12 kHz = 42 μs) which is comparable to the lifetime of CH₄(ν_B). CH₄(ν_B) is fully consumed every half-cycle of applied voltage and the cumulative population of CH₄(ν_B) over several cycles is difficult. Although decent interaction of CH₄(ν_B) to the catalyst is possible, contribution to the plasma promotion effect is obviously weaker than 100 kHz DBD. It is noteworthy that the plasma promotion effect of 12 kHz DBD is comparable to 100 kHz DBD in fluidized-bed DBD reactor (Fig. 9a). FB-DBD enhances heat and mass transport that maximizes the plasma-catalyst coupling even if no cumulative population of CH₄(ν_B) is absent in 12 kHz DBD. Meantime, CH₄ conversion is suppressed by the thermodynamic equilibrium in both 12 kHz and 100 kHz DBD. Therefore, as discussed in “Surface Reaction Mechanisms” section, the development of new catalysts enabling nonequilibrium product distribution is a key thrust subject of plasma catalysis research.

Electron impact excitation rate coefficients (k_eB and k_eS) are in the same order in both 12 kHz and 100 kHz DBD [19]. The point is high-frequency operation can generate vibrationally excited CH₄ which is more frequent than a vibrational quenching. Moreover, the high-frequency operation would generate overtone vibrational CH₄ because vibrationally excited CH₄ is further excited by multiple electron collisions, which is different from the vibrational ladder-climbing process. Because the reactivity of overtone vibrational CH₄ is higher than the fundamental vibration mode [48], 100 kHz operation is critically important and not achieved by 12 kHz DBD. A higher frequency DBD may be even more beneficial unless excess gas heating occurs.

Reverse Water Gas Shift Reaction

To further verify the effectiveness of DBD and catalyst hybrid reaction, reverse water gas shift (RWGS) reaction (CO₂ + H₂ = CO + H₂O) was studied in fluidized-bed DBD using Pd₂Ga/SiO₂ alloy catalyst [49]. The configuration of FB-DBD reactor is similar to Fig. 8 and detailed conditions and catalyst characterization are available in ref [49]. Because DMR and RWGS reactions occur in the different reaction mechanisms as discussed in “Surface Reaction Mechanisms” section, RWGS can be a good model reaction for the validation of the plasma promotion effect in DBD.

Figure 15 shows the CO₂ conversion and corresponding Arrhenius plot for the RWGS reaction [49]. Because the Pd₂Ga loading weight varies, the vertical axis of the Arrhenius plot represents the reaction rate constant per unit catalyst weight. For the thermal reaction, the CO₂ conversion was higher at 10 wt% than at 3 wt%. In both cases, hybridization with DBD approximately doubled the CO₂ conversion. In particular, with 10 wt% catalyst and a frequency of 100 kHz, the CO₂ conversion exceeded the equilibrium conversion. The thermal and plasma reactions can be clearly distinguished in the Arrhenius plots (Fig. 15b), which show a drastic decrease in the activation energy by DBD. 100 kHz FB-DBD yielded higher CO₂ conversion than that of 12 kHz FB-DBD because 100 kHz operation is suitable for the generation of vibrationally excited CO₂. However, the reaction mechanism is considered unchanged by the catalyst loading and frequency. Because apparent activation energy for plasma catalysis is 43 kJ/mol regardless of conditions. According to the in situ FTIR and DFT combined analysis, there are two rate determining steps for RWGS reactions: one is HCOO formation which is promoted by vibrationally excited CO₂. The other is the decomposition of HCOO (HCOO + H = HCO + OH) with increased surface hydrogen by DBD [49]. In both DMR and RWGS reactions, 100 kHz operation is beneficial that yields higher concentration of vibrationally excited molecules. One essential difference between DMR and RWGS is whether the conversion of feed gas is beyond the thermal equilibrium or not. This phenomenon is discussed further in “Surface Reaction Mechanisms” section.

Fig. 15

Kinetic studies of reverse water gas shift (RWGS) reaction in the fluidized-bed DBD reactor [49]. a CO₂ conversion and b Arrhenius plot. ■ 10 wt% (100 kHz), ▲ 10 wt% (12 kHz), □ 3 wt% (100 kHz), ∆ 3 wt% (12 kHz), ● 10 wt% (Thermal), ○ 3 wt% (Thermal). Conditions: Total flow rate = 200 cm³/min (STP), Power = 30 W, H₂/CO₂ = 3, WHSV = 3000 cm³/g/h (STP), Total pressure = 15 kPa, SEI = 220 kJ/mol

Surface Reaction Mechanisms

The surface reaction mechanism is categorized into three types: (1) Langmuir–Hinshelwood (L–H), (2) Eley–Rideal (E–R), and (3) Mars–van Krevelen (MvK) as schematically shown in Fig. 16. DMR on La–Ni/Al₂O₃ is explained by the L–H mechanism [19] where both CH₄ and CO₂ are adsorbed on a catalyst to produce intermediate species such as CH_i and CO₃, followed by surface reactions to produce CO and H₂. In contrast, RWGS reaction on Pd₂Ga/SiO₂ is explained by the E–R mechanism [49], in which gas phase CO₂ reacts directly with adsorbed hydrogen to form intermediate species (HCOO) toward final products (CO and H₂O).

Fig. 16

Schematic representation of surface reaction mechanisms

It is inevitable that both forward and backward reactions are promoted by DBD because all molecules are vibrationally excited randomly by electron impact. The elementary reaction of mode-selective vibrationally excited CH₄ was investigated by molecular beam study. In the case of CH₄ chemisorption, as a rate-determining step, vibrationally excited CH₄ accelerates chemisorption of the order of magnitude [48]. However, saturated surface coverage by CH₃ is not influenced by vibrational excitation [50]. The fact implies the overall reaction is dominated by the surface coverage of intermediate species or the adsorption/desorption equilibrium. Therefore, the reaction rate of CH₄ is accelerated dramatically by vibrational excitation; however, its conversion seems to be hard to overcome beyond the thermal equilibrium. In the E–R mechanism, surface coverage by hydrogen atoms would be suppressed by the adsorption equilibrium; however, direct interaction of vibrationally excited CO₂ with adsorbed hydrogen is possible without the limitation of CO₂ adsorption equilibrium (or CO₂ coverage on the catalyst surface). Meantime, the backward reaction of RWGS occurs via the L–H pathway that is governed by the adsorption equilibrium of CO and H₂O. In other words, the forward reaction of RWGS is promoted selectively by DBD than the backward reaction. This is presumably the reason that product distribution is governed by the thermodynamic equilibrium in the L–H mechanism (DMR), but non-equilibrium product distribution is possible in the E-R mechanism (RWGS).

If the catalyst is designed so that the forward DMR occurs via the E–R mechanism, the conversion of CH₄ and CO₂ might exceed the equilibrium by DBD. It is also worth mentioning that the MvK mechanism may overcome the equilibrium limit. Because vibrationally excited species interact directly with the lattice oxygen to create oxygen vacancy on the surface, which in turn becomes active sites for the subsequent surface reaction. Such a reaction has been proven experimentally in room-temperature CO oxidation on ZnO catalyst [51]. Perovskite-type catalysts or metal oxide semiconductors, such as TiO₂, ZnO, CeO₂, are potential candidates for plasma-enhanced MvK mechanism. It is hard to establish a universal guideline for the catalyst design and emerging plasma promotion effect; however, the above discussion would provide better insight into the new concept of catalyst design which is suitable for plasma catalysis, yielding non-equilibrium product distribution.

Concluding Remarks

A combination of DBD and catalyst technology is reviewed based on our previous studies. Major conclusions are derived as follows.

• 1. DBD is one of the best plasma sources when combining heterogeneous catalysts. The gas heating is suppressed, thus reaction promotion by vibrationally excited molecules at low temperatures is possible. Although warm discharges, such as microwave and gliding arc discharges, are known to be a suitable plasma source for the generation of vibrationally excited species, a combination of heterogeneous catalysts is rarely studied probably because thermal catalysis would dominate due to high gas temperatures.

• 2. DBD and catalyst combination reaction is characterized as mixed catalysis, where thermal and plasma reactions are essentially not decoupled. Because DBD consists of highly transient and localized streamers. Moreover, there is a plasma-off period at every half cycle where thermal reaction plays a major role. High-frequency operation is beneficial (e.g. 100 kHz) because vibrationally excited molecules are produced faster than quenching. In addition, the high-frequency operation would generate overtone vibrational molecules which are even more reactive than in fundamental vibration mode. Such a situation depends on the lifetime of vibrationally excited molecules.

• 3. The Lissajous analysis is a powerful diagnostic tool for DBD from a macroscopic viewpoint. Discharge properties of empty-, PB-, and FB-DBD are characterized by the discharge sustain voltage (V^*) and the mean discharge current (I_p). However, V^* is not correlated with the local electric field of the advancing streamer head. Moreover, V^* does not represent the electric field concentration at the pellet contacts or fluidized catalyst powders. As for I_p, it is derived from total charges during the half cycle of applied voltage, which is not associated with nanosecond current pulses due to streamer formation. A high-frequency operation generates DBD having low V^* and large I_p, which is beneficial for the generation of vibrationally excited molecules.

• 4. Vibrationally excited molecules are consumed on the outermost surface of catalyst pellets, of the order of 20 μm. Therefore, the catalyst effectiveness factor is much smaller than 1 no matter what the catalyst temperature would be. Neither gas breakdown nor plasma diffusion occurs in dielectric micropores.

• 5. Fluidized-bed DBD enhances the interaction of reactive species and catalysts which is more effective than packed-bed DBD. Because plasma-catalyst interaction increases by decreasing the primary particle size. Also, heat and mass transport in the plasma reaction field is promoted. In endothermic reactions (such as DMR and RWGS), the reaction is promoted dramatically by DBD which in turn leads to a drastic temperature drop. Eventually, the reaction is terminated due to low-temperature situation and DBD becomes the equivalent of the heating device. The generation of vibrational species is not enough, but high heat flux must be ensured simultaneously.

• 6. Warm discharges are more suitable for the generation of vibrationally excited species than DBD. The fact does not imply that DBD does not promote vibrational chemistry in plasma catalysis. In the case of CH₄ and CO₂ mixtures, the production of vibrationally excited species is the dominant electronic reaction path up to about E/N = 1000 Td. High-frequency DBD (e.g. 100 kHz) generates low E/N and large I_p nonthermal plasma, thus more beneficial for the generation of vibrationally excited molecules than low-frequency DBD (e.g. 12 kHz).