Introduction

Afterglows of N2 flowing microwave discharges have been previously studied at medium gas pressures (1–20 Torr) for sterilization of medical instruments by N-atoms [1, 2]. The effect of the introduction of a low percentage of H2 into N2 on the paper surface wettability was also previously investigated in the early afterglow [3]. A slight maximum of the N-atom density in the N2/0.4%H2 afterglow at 2 Torr, 1 slpm, 100 Watt was correlated to an increase of surface wettability.

In the present study, the early afterglow flowing from N2/(0–2.5%) H2 microwave plasmas is studied with two different experimental configurations, the first set up is the same as the one already reported in [4]. The second set up is having a new experimental arrangement [5] in which a direct connection with the microwave flowing plasma to the reactor chamber is achieved. With this new set-up, the time necessary for the gas to flow between the discharge and the reactor (post-discharge time) was reduced from 2 × 10–2 s to (1–3) × 10–3 s at 2 Torr, 0.5–1.0 slpm.

For this second configuration, it was expected to add to N-atoms other N2 active species: N2(A), N2 (X,v > 13) metastable molecules, N2+ ions, NH radicals and H-atoms in the post-discharge chamber. The importance of two configurations i.e. different afterglow residence times which play a crucial role in the generated species were made in evidence.

Intensities emitted by the N2 1st positive system at 580 nm (N2(B,11) → N2(A,7) vibrational band) and by the N2 2nd positive system at 316 nm (N2(C,1) → N2(B,0) vibrational band) are measured to obtain the N–atoms, N2(A), N2(X,v > 13) metastable molecules and N2+ ions absolute densities after NO titration to calibrate the N-atom densities [3]. From the NH(A → X) bands at 336 nm, the possibility to evaluate the NH radical and H-atom densities is analyzed by choosing the appropriated kinetic reactions at the origin of NH 336 nm emission.

Experimental Setup

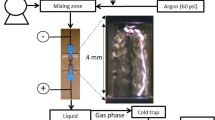
The first experimental setup is reported in previous works [1,2,3, 5]. It is reproduced in Fig. 1.

Fig. 1
figure 1

Microwave discharge in a tube of diameter 5 mm, length 20 cm and in a post-discharge bent tube of diameter 18 mm, length 30 cm connected to a 5 L reactor

Full size image

The discharge is located inside a 5 mm diameter tube and a length of 20 cm after the surfatron gap. The discharge tube is connected to a bent tube of 18 mm diameter and 50 cm length before a 5 L reactor where the previous surface treatments occurred [1,2,3]. The residence time of the afterglow in the 18 mm tube diameter before the 5 L reactor is in the range of 10–3–10–2 s.

A pink afterglow is observed in the bent part of the 18 mm tube with pure N2 at 0.5 slpm, p = 5 Torr and 100 Watt. The NO titration of N-atoms in the late afterglows was performed by introducing an Ar-1.5%NO flow after the pink afterglow. At 8 Torr, 0.5 slpm and 100 Watt, z = 3 cm, a N-atom density of 1.0 × 1015 cm−3 was previously obtained [5].

The experimental setup of Fig. 1 has been modified as shown in Fig. 2 to directly introduce the 5 mm int. diameter discharge tube inside the 5 L reactor. The afterglow residence time at the entrance of the 5 L reactor was then reduced to (1–3) × 10–3 s [6, 7] as for the early afterglow at z = 3 cm in Fig. 1.

Fig. 2
figure 2

Microwave discharge in a tube of diameter 5 mm, length 20 cm directly connected to a 5 L reactor

Full size image

The aim of the present study is to compare the density of the N2-H2 active species, firstly in conditions of the same afterglow times (10–3 s) and secondly with two afterglow times: 10–3 s and 10–2 s to check the capacity of the setup shown in Fig. 2 to treat surfaces in the reactor. The importance of the two configurations is to extend the afterglow residence time which plays a crucial role in the generated species, as seen in Table 2.

The N2-H2 microwave plasma is produced by a surfatron cavity at 2450 MHz, 100–200 Watt, 0.5–2 slpm at pressure from 2 to 8 Torr. At 2 Torr, a satisfactory diffusion of the afterglow is produced inside the whole 5 L reactor.

The optical emission spectroscopy across the reactor is performed by means of an optical fiber connected to an Acton Spectra Pro 2500i spectrometer (grating 600 g/mm) equipped with a Pixis 256E CCD detector (front illuminated 1024 × 256 pixels).

The N–atom density is obtained from the I580 measured intensity after calibration by NO titration with a mixed gas of Ar and NO(1.5%) introduced across the 18 mm diameter tube as shown in Fig. 1.

Kinetic Equations of Active Species in the Mixed Gas of N2 and H2(0–2.5%) Early Afterglow

N-Atom Density

The pure late afterglow emission is produced by a dominant N + N recombination.

The N2 580 nm band head intensity (I580), in arbitrary unit, was measured for constant parameters of the Acton spectrometer (grating 600 gr/mm, entrance slit width of 150 μm and integrating time of 1 s).

I580 is related to the N-atom density [N] as follows:

$$I_{{{58}0}} = k_{{1}} \cdot \left[ {\text{N}} \right]^{{2}}$$
(1)
$${\text{with}}\,k_{{1}} = c\left( {{58}0} \right) \cdot V \cdot (h \cdot c/{58}0) \cdot A\left( {{58}0} \right) \cdot k_{a} \cdot \left[ {\text{M}} \right]/\left( {\upsilon^{{\text{R}}}_{{{\text{B}},{11}}} + \, \left[ {{\text{N}}_{{2}} } \right] \cdot k^{{{\text{N2}}}}_{{{\text{B}},{11}}} } \right)$$
(2)

As mentioned in [6, 7], it is expressed in k1:

The spectral response c(580) of spectrometer (ratio of measured and true intensities at λ = 580 nm of tungsten lamp), h and c are respectively the constant of Planck and the light velocity, 580 is for λ = 580 nm, V the afterglow volume observed by the optical fiber of the spectrometer, A(580) the Einstein coefficient of the N2 (580 nm) transition. The term c(580)\(.\) h·c/580 is in arbitrary unit.

υRB,11 and kN2B,11 are respectively the radiative frequency and the quenching rate constant of N2 (B,11) by N2.

The ka coefficient is for the following recombination reaction:

$${\text{N }} + {\text{ N }} + {\text{ N}}_{2} \to {\text{ N}}_{2} ({\text{B}},{\text{v}}^{\prime} = 11) \, + {\text{ N}}_{2}$$
(3)

In k1, c(580) is the spectral response of the used spectrometer, A(580) = (7.8–9.6) × 104 s−1 [8, 9], ka = 4.4 × 10–33 cm6s−1 [10], υRB,11 = (2–2.4) × 105 s−1 [8, 9] and kN2B,11 = 3 × 10–11 cm3s−1 [11].

The fraction aN+N of the N + N recombination in the I580 intensity has been determined in [6, 7] with the conditions of mixed pink and late afterglows (aN+N = 1 in pure late afterglow with a dominant reaction (3) and aN+N = 0 in pure pink afterglow with a minor reaction (3)). Therefore, Eq. (1) becomes:

$$a_{{{\text{N}} + {\text{N}}}} \cdot {\text{I}}_{{{58}0}} = k_{{1}} \cdot \left[ {\text{N}} \right]^{{2}}$$
(4)

With aN+N·I580 is the fraction aN+N of the measured intensity I580 at emission of the early afterglow.

The N-atom absolute density was calibrated by NO titration and was determined from Eq. (4) by measuring aN+N·I580 with constant spectrometer parameters.

The uncertainty on the N-atom density determination is estimated to be 30%.

By introducing directly the discharge tube of diameter 5 mm in the post-discharge reactor of 5 L (Fig. 2), an afterglow jet is produced along the whole reactor chamber at pressures of 6–8 Torr, flow rates 0.5–1.0 slpm and injected microwave power of 200 Watt.

The jet disappeared when the gas pressure was reduced to 2 Torr in N2/2.5%H2 for the 0.5 slpm flow rate and power of 200 Watt. These plasma conditions were taken in the following for an afterglow diffusion in the whole 5 L chamber.

At 2 Torr, 0.5 slpm, N2/1%H2, 200 Watt, it is found that aN+N = 0.85 and [N] = 6 × 1014 cm−3 from Eq. (4). With aN+N = 0.85, it can be considered that the afterglow was a nearly pure late afterglow (at 85%).

Densities of N2(A), N2(X,v > 13) and N2 +

The line intensity ratio method [4, 12] is applied to determine the density of N2(A) ([A]) from that of N-atoms, by comparing the I316 and aN+N·I580 intensities,

where I316 is the intensity emitted from the N2(C,v = 1) radiative state. In the afterglow, the following dominant reaction is considered:

$${\text{N}}_{{2}} \left( {\text{A}} \right) \, + {\text{ N}}_{{2}} \left( {\text{A}} \right) \, \to {\text{ N}}_{{2}} ({\text{C}},{\text{v}} = {1}) \, + {\text{ N}}_{{2}} \left( {\text{X}} \right)$$
(5)

As reported in [13], the aN+N·I580 / I316 intensity ratio is as follows:

$$a_{{{\text{N}} + {\text{N}}}} .I_{{{58}0}} /I_{{{316}}} = k_{{3}} .\left( {\left[ {\text{N}} \right]/\left[ {\text{A}} \right]} \right)^{{2}}$$
(6)

The value of k3 is 2.5 × 10–7 taken from [13].

The density of all N2(X,v > 13) molecules ([X, v > 13]) has been obtained by comparing the fractions of late and pink afterglows in the I580 intensity: as reported in [13], aN+N·I580 for the late (Eq. (4)) and (1-aN+N)·I580 for the pink where it is considered the following dominant reaction:

$${\text{N}}_{{2}} \left( {\text{A}} \right) \, + {\text{ N}}_{{2}} \left( {{\text{X}},{\text{v}} > {13}} \right) \, \to {\text{ N}}_{{2}} ({\text{B}},{\text{v}} = {11}) \, + {\text{ N}}_{{2}} \left( {\text{X}} \right)$$
(7)

It comes:

$$a_{{{\text{N}} + {\text{N}}}} /\left( {{1} - a_{{{\text{N}} + {\text{N}}}} } \right) \, = k_{{4}} \cdot \left[ {\text{N}} \right]^{{2}} /\left[ {\text{A}} \right] \cdot \left[ {{\text{X}},{\text{ v}} > {13}} \right]$$
(8)

The value of k4 is 4–5 × 10–6 determined from [11].

The N2+ ions density ([N2+]) is determined by comparing the I316 intensity from reaction (5) with the I391 intensity coming from the N2+(B,v = 0) radiative state excited by the following reaction [13]:

$${\text{N}}_{{2}}^{ + } \left( {\text{X}} \right) \, + {\text{ N}}_{{2}} \left( {{\text{X}},{\text{v}} > {12}} \right) \to {\text{ N}}_{{2}}^{ + } \left( {{\text{B}},{\text{v}} = 0 \, } \right) \, + {\text{ N}}_{{2}} \left( {\text{X}} \right)$$
(9)

The I391 / I316 intensity ratio is defined as follows:

$$I_{{{391}}} /I_{{{316}}} = k_{{5}} .\left( {\left[ {{\text{N}}_{{2}}^{ + } } \right]\left[ {{\text{X}},{\text{ v}} > {13}} \right]} \right)/\left[ {\text{A}} \right]^{{2}}$$
(10)

where it is taken the same value for the [X, v > 12] and [X, v > 13] densities.

The value of k5 is 1.6 × 10–2 defined in [11].

From the N-atom density of 6 × 1014 cm−3, at 2 Torr, 0.5 slpm, for an afterglow time of (1–3) × 10–3 s in the 5 L reactor, with N2-1%H2, 200 Watt, the following densities: [A] = 4 × 1010 cm−3, [X, v > 13] = 1 1013 cm−3 and [N2+] = 3 ×109 cm−3 are obtained from Eqs. (6, 8 and 10).

Densities of NH Radicals and H-atoms

The kinetics reactions at the origin of the NH(A) emission shown in Fig. 3 are analyzed.

Fig. 3
figure 3

Spectrum of the N2-1%H2 afterglow in the 5 L reactor (Fig. 2) at 10–3 s, 2 Torr, 0.5 slpm and 200 Watt

Full size image

It is first considered that the NH(A) radiative states in N2–H2 afterglows can be produced by the recombination of N and H atoms. However, the reaction coefficient producing the NH(A) state is unknown. Only the coefficient ke of the following full reaction:

$${\text{N }} + {\text{ H }} + {\text{ M }} \to {\text{ NH }} + {\text{ M}}$$
(11)

where M = N2 as reported in [14], with ke = 5(± 3)10–32 cm6 s−1.

By considering the NH potential curves [15], the NH(A,v = 0) vibrational level is almost at the same N + H dissociation energy (3.8–4.0 eV). Moreover, a NH(5Σ−) repulsive curve is crossing NH(A2П) at 4.2 eV. As a consequence, there is a potential barrier which inhibits the production of NH(A,v = 0) by the N + H recombination.

By comparing with the N2/O2 gas mixtures, the NO(B,0) level being 0.9 eV is lower than the N + O dissociation (6.5 eV), the reaction N + O + M → NO(B,0) + M is exothermic with a rate coefficient of 3 × 10–34 cm6 s−1 [6, 7].

By taking into account now the N2(X,v) + NH → N2 + NH(A,v = 0) reaction, it is observed that the excitation of the NH(A,0) level from NH(X,0) needing 3.8–4.0 eV will be excited by the N2(X,v = 14–15) energy levels.

Then the following reaction will be exothermic:

$${\text{N}}_{{2}} \left( {{\text{X}},{\text{v}} > {13}} \right) \, + {\text{ NH}} \to {\text{ N}}_{{2}} + {\text{ NH }}\left( {{\text{A}},{\text{v}} = 0} \right)$$
(12)

The rate coefficient of reaction (12) is unknown. kf = 4 × 10–11 cm3 s−1 is chosen as for the two exothermic reactions: N2(X, v > 13) + N2(A) → N2 + N2(B,11) and N2(X, v > 13) + N2+  → N2 + N2+(B) [6, 7] 12].

The I336 intensity is then written as follows:

$$I_{{{336}}} = c\left( {{336}} \right) \cdot \left( {hc/{336}} \right)A\left( {{336}} \right) \cdot \left[ {{\text{X}},{\text{v}} > {13}} \right] \cdot \left[ {{\text{NH}}} \right].k_{{\text{f}}} /\left( {\upsilon^{{\text{R}}}_{{{\text{NH}},{\text{A}}}} + \, \left[ {\text{M}} \right] \cdot k^{{\text{M}}}_{{{\text{NH}},{\text{A}}}} } \right)$$
(13)

where c(336) is the spectral response of the used monochromator, A(336) = νRNH,A = 2 × 106 s−1 [16], kf = 4 × 10–11 cm3 s−1 and kMNH,A is the quenching rate of the NH(A) state by the M molecules. In [16], it is reported that kN2NH,A < 5 × 10–14 cm3s1 and kH2NH,A = 5 × 10–11 cm3 s−1.

The line ratio method is applied to determine the NH radical relative density from the following aN+N·I580/I336 intensity ratio, calculated with eqs. (4) and (13) at 2 Torr [13]:

$$a_{{{\text{N}} + {\text{N}}}} \cdot I_{{{58}0}} /I_{{{336}}} = { 7}.{5} \times {1}0^{{ - {7}}} \left[ {{\text{N}}^{{2}} } \right]/\left[ {{\text{X}},{\text{ v}} > {13}} \right] \cdot \left[ {{\text{NH}}} \right]$$
(14)

The H-atoms are related to NH by the reaction (11) and the following relationships see [17]:

$${\text{N }} + {\text{ NH }} \to {\text{ H }} + {\text{ N}}_{2} ,{\text{ with k}}_{{\text{g}}} { = }5 \times 10^{ - 11} {\text{cm}}^{{3}{}} {\text{s}}^{ - 1}$$
(15)
$${\text{N}}\left( {^{{2}} {\text{D}}} \right) \, + {\text{ H}}_{{2}} \to {\text{ H }} + {\text{ NH}}$$
(16)
$${\text{H }} + {\text{ NH }} \to {\text{ H}}_{{2}} + {\text{ N}}$$
(17)

It comes:

$$\left[ {{\text{NH}}} \right] = (k_{{\text{e}}} \cdot \left[ {\text{H}} \right] \cdot \left[ {\text{N}} \right] \cdot \left[ {{\text{N}}_{{2}} } \right] + k_{{\text{h}}} \cdot \left[ {{\text{H}}_{{2}} } \right] \cdot \left[ {{\text{N}}\left( {^{{2}} {\text{D}}} \right]} \right)/\left( {k_{{\text{g}}} \cdot \left[ {\text{N}} \right] + k_{{\text{i}}} \cdot \left[ {\text{H}} \right]} \right)$$
(18)

with [H2] = [H20] − 1/2[H].

The NH(0–0)-(1–1) bands at 336–337 nm are intense as shown in Fig. 3. The NH(1–1) band at 337 is mixed with the N2(0–0) band at 337 nm. Consequently, the I336 intensity is chosen alone to detect the NH radical. It is measured from the middle of the I336 and I337 junction.

Gas Temperature

The gas temperature Tg in the discharges and afterglows was estimated by the P1/P2 intensity ratio of the first two rotational bands of the 1st positive emission at 775 nm [18]. If a hot temperature was found in the N2 discharge (Tg = 500–600 K at 8 Torr, 1 slpm [19]), the room gas temperature (300 K) was measured in the present afterglows. Consequently, the rate coefficients above are taken at 300 K as for reaction (3) which is depending on gas temperature [10].

The Experimental Results

In Table 1, the first and second lines show the results of active species density in mixed gas of N2 and H2(0–2.5%) with the Figs. 1 and 2 setups for the same plasma and afterglow conditions (10–3 s, 0.5 Slpm, 200 Watt).

Table 1 A aN+N factors (from the I11/9 band ratio) and active species densities along the 5 L diameter in the afterglows of N2-x%H2 with x = 0–2.5%, p = 2 Torr, Qtot = 0.5 slpm and 200 Watt
Full size table

The N(2D) and H atom densities reported in Table 1 are deduced from Eq. 18 calculations as being the upper density limits to obtain a positive value of H and N(2D) densities.

In the two N2- < 2.5%H2 early afterglows of Figs.  1 and 2, identical values of N-atom densities which increased up to 0.4%H2 from 5 to a maximum value of 7 × 1014 cm−3 were found. While between 0.4 and 1.0% of H2, the density of the N-atoms slowly decreased. These results are similar to that of Ref. [3]. The weak maximum of the N-atom density at x(H2) = 0.4% has been previously correlated to a best surface wettability.

For the other active species, lower densities were found with the Fig. 2 setup except for NH and H in N2-1%H2.

By comparing the results obtained with the setup of Fig. 1 at z = 3 cm and of Fig. 2 in the 5 L reactor at the same afterglow times of 10–3 s (lines 1 and 2), it was observed with the setup of Fig. 2 an increase of the late afterglow condition by the aN+N factor. Keeping the same densities of N-atoms, a decrease of N2(X, v > 13) density with H2 and a reduction of 10 times of N2+ ions density was noticed. The H-atom density was the same with 1%H2 into N2. Thus the Fig. 1 setup at z = 3 cm was in favour of N2+ ions.

Table 2 shows the comparison of the results in pure N2 at 2 Torr, obtained with the setups of Fig. 1 at 10–3 s (z = 3 cm—line 1) and at 10–2 s (across the 5 L reactor—line 2).

Table 2 A aN+N factors and active species densities in the N2 afterglows of Fig. 1 at times 10–3 s and 10−2 s at p = 2 Torr, Qtot = 0.5 slpm and 100 Watt
Full size table

In the Fig. 1 setup a constant N-atom density is kept from an afterglow time of 10–3 s and 10–2 s in that a huge reduction, at time 10–2 s by a factor 10 for N2(X,v > 13) and 102 for N2+ active species density, were observed. A long afterglow time in the Fig. 1 setup (10–2 s) is thus detrimental to high N2(X, v > 13) and N2+ active species density in the 5 L reactor. Such a result comes from the very low destruction probability of N-atoms on the tube wall (γ = 10–4–10–5) in comparison to those of N2(X, v > 13): γ = 10–2–10–3 for N2(X,v > 13) [4] and a full wall recombination for N2+.

For a surface treatment with high densities of N2(X, v > 13) and N2+ added to constant N and H atoms, the Fig. 2 setup, with an afterglow time of 10–3 s, appears to be the most appropriate setup. Still higher N2+ ions density should be obtained inside the 18 mm diameter tube, before the 5 L reactor, where a sample could be introduced.

To increase the H2 dissociation rate, the afterglows of Ar-N2-H2 gas mixtures of Ar-N2-H2 gas mixtures specifically the Ar-2%(N2-5%H2) has been studied [13, 20, 21]. The plasma length increased from 4 cm with N2–xH2 to 20 cm with a 98%Ar dilution. Then a jet was observed at 2 Torr inside the 5 L reactor. The present optical measurement was performed 2 cm above the jet, expecting a full afterglow diffusion inside the 5 L reactor.

In N2 at 4 Torr, 1 slpm, 100 Watt, an afterglow time of 3 10–3 s, a N/N2 ratio higher than 10% has been previously observed [5].

In the Ar-2%N2-10–3 H2 gas mixture at 2 Torr, 1 Slpm, 150 Watt, afterglow time of 1 10–3 s, it has been measured with the Fig. 2 setup in the 5 L reactor: [N] = 2 × 1014 cm−3, [N2, v > 13] = 0.4 × 1013 cm−3, [N2(A)] = 1.7 1010 cm−3, [N2+] = 2 × 109 cm−3, [NH] = 0.2 × 109 cm−3, [H] ≤ 0.4 × 1013 cm−3. The corresponding [N]/[N2] and [H]/[H02] ratios were 15% and ≤ 6% respectively. By comparison in N2-(0.4–1)%H2, 2 Torr, 0.5 slpm, 200 Watt (Table 1), there is thus a sensitive increase of the [N]/[N2] and [H]/[H02] ratios with the 98%Ar dilution.

Conclusion

By connecting the diameter 5 mm discharge tube directly to the 5 L reactor, an homogenous short afterglow (SA of 10–3 s) in the whole 5 L reactor with the mixed gas of N2 and H2(0–2.5%) at 2 Torr, 0.5 slpm, 200 Watt was obtained. By comparison with a 1.8 cm diameter early afterglow in the same plasma and afterglow time condition of 10–3 s, the part of the N + N recombination in the 5 L afterglow increased, with a N-atom density unchanged and a dissociation rate N/2N2 = (5–7) × 10–3. By considering a rate coefficient kc = 4 × 10–11 cm3 s−1 for the N2(X,v > 13) + NH reaction, the H/2H02 dissociation rates were found to be ≤ (1–4) × 10–3 in the same range for the two considered setup.

The purpose of using a direct connection of 5 mm diameter discharge tube to the 5 L reactor was to obtain a more efficient surface treatment in a short afterglow (SA of 10–3 s) with more N2(X, v > 13) and N2+ active species than in a long afterglow (LA of 10–2 s). For the experimental conditions of N2-1%H2 at 2 Torr, 0.5 slpm, the N/N2 and H/N ratios had constant values of 1% and 0.3% respectively.

To increase the N and H atom densities, an Ar-2% N2-10−3H2 gas mixture was experimented, giving in the 5 L reactor N/N2 and H/N ratios of 7.5% and 2%, nearly one order of magnitude higher than in N2-(0.4–1)%H2.