Introduction

During a combination of high temperature, long exposure times and under certain atmospheres, there can be a transition from corrosion protection function of oxidized surface of Cr–Ni austenitic steels to intensive surface degradation, and this transition is accelerated by transient thermal cycling. In the protection regime, growth of the oxide layer was decreased with time and such conditions are preferable for the majority of high temperature applications. The formation of the dense, stable, and adherent external oxide scale prevents the metal matrix from being attacked by corrosive species such as O2 and H2O, which are commonly present during most in-service environments and especially at high temperature applications. However, transitioning to the second regime accelerates surface degradation which can lead to detrimental consequences during the life-time of in-service applications. Surface degradation can be classified as intensive oxidation due to the formed micro-structural defectives within the scale, decohesion, swallowing, and spallation of external oxide layer, vaporization of hydroxides of alloying elements. In addition, there can be changes related to the interface processes, such as grain boundary corrosion, dissolution or precipitation of strengthening phases, depletion of alloying elements, which could result in a local solid-state phase transformation. These and the other high temperature degradation processes, which could occur in different alloys, are described in the recent review [1].

When oxidation followed by parabolic-oxidation trend in pure iron and carbon steel, the developed scale consists of an extremely thin outermost hematite layer, followed by a thin intermediate magnetite layer, along with a thick inner wustite layer. The proportion of oxide phases reflects the fact that the diffusion coefficient of iron in wustite is much greater than in magnetite and that the diffusion of oxygen and iron through the hematite layer is extremely slow [2]. The isothermal-oxidation kinetics of pure iron and steels in air or oxygen during steady-state reaction conditions typically expressed by the parabolic equation:

$$x^{2} = k_{x} t$$
(1)

where: x is the scale thickness, t is the oxidation time, and kx is the parabolic rate constant, usually measured in cm2/sec.

The parabolic rate constant is exponentially dependent on temperature:

$$k_{x} = \, k_{0} \exp \left( { - Q/RT} \right)$$
(2)

where: k0, is a constant, Q (J/mol) is the activation energy of oxidation, T is absolute temperature, and R (J/Kmol) is the gas constant.

For a multilayered oxide scale in pure iron and plane steels, the activation energy of oxidation is equivalent to the activation energy of iron diffusion in wüstite [3]. It was found that during isothermal oxidation of iron between 700 and 1250 °C, the thickness ratio of hematite, magnetite, and wustite layers within the scale were nearly constant 1:4:95, and the overall activation energy for scaling rate constant was 170 kJ/mol [4]. In most experimental studies, the oxidation kinetics have been described by the weight gain as a function of oxidation time and the obtained parabolic constant (kp, g2cm−4 s−1) and can be converted to kx considering scale structure, composition, and density [2]:

$$k_{p} \left( {{\text{g}}^{2} {\text{cm}}^{ - 4} \sec^{ - 1} } \right) = \left( {1.7 - 1.8} \right)k_{x} \left( {{\text{cm}}^{2} \sec^{ - 1} } \right)$$
(3)

Typically, experimental oxidation kinetics below 700 °C in carbon steels fit the parabolic law; however, the oxidation behavior could be different at higher temperatures. Variation from the parabolic law was also observed in austenitic stainless steels exposed in air above 800 °C [5,6,7,8,9]. In this case, to fit the experimental results, a combination of linear and parabolic law was considered. For example, weight gain at 400 °C in 316L stainless steel follows a parabolic law, while it deviates from a parabolic law for 600 and 800 °C [10]. There are several reasons for such deviations, including the different diffusion coefficient of O, Cr, Fe and Ni through the oxide films at different oxidation temperatures as well as changing thermodynamic stability of formed oxides which have the potential to modify the multilayered oxide structure. These considerations assume that the formed oxide layer has a dense structure and is well adhered to the metal matrix, which typically takes place at relatively moderate oxidation temperatures during the static thermal condition without thermal cycling.

However, increasing micro-defectiveness (void and crack) and macro-detachment of oxide layer from the matrix (blistering and spallation) occurred at elevated temperatures. The interface detachment of the oxide layer will create a fresh surface to develop newly formed oxides, which will lead to an increase in the rate of oxidation and intensify of the diffusion flux of metal ion outward of and oxygen cation inward during the oxidation process [11]. Cracks and any porous regions within the scale structures will promote the diffusion rate of Cr, Fe and O in austenitic steels. Therefore, oxidation kinetics deviates from the parabolic law at 800 °C in the studied austenitic steel [10] and experimentally measured weight gain during oxidation cannot be directly used to calculate a “true” oxidation constant. A review article [2] summarized published experimental results on deviation in oxidation kinetics resulting from blistering and spallation. They stated that the average scale thickness in 316L austenitic steel after oxidation in air at a temperature around 980–1010 °C reached a maximum after several hours and did not increase during longer exposure times; moreover, above this temperature range, the average scale thickness decreased with increasing oxidation temperature. Scale blistering is thought to be responsible for such behavior.

Blistering is thought to occur during several distinct stages: nucleation, growth, coalescence, shrinkage, and collapse. Findings from the previous studies show that several conditions must be met for the blisters to form: (i) stress is generated in the scale by the outward diffusion of iron and the inward diffusion of vacancies, (ii) different thermal-expansion coefficients of the scales and the substrate, (iii) by forming gas build-up at the scale–steel interface because of carbon oxidizing. The scale plasticity promotes blistering; however, the brittleness could cause spallation and complete detachment of the layers. Using fracture mechanics, the parameter of critical strain in the scale needed to form oxide layer spallation was suggested [12]. During cooling of the oxidized metal, the external oxide layers usually experience compression. The buckling and wedging processes of decohesion of the oxide layer in this situation were considered [13].

There are several other macro-mechanical models suggested to describe scale spallation [14]. Adhesion of the oxide layer to the steel substrate depends on various parameters; among them are the thickness of the scale, its growth rate, the stress state, the interfacial energy, and the elastic properties of the oxide [15, 16]. The oxidation and oxide spallation behavior of austenitic and ferritic heat resistant cast steels were investigated under isothermal and cyclic conditions. It was shown that ferritic steel appeared to be more resistant to oxide spallation as compared to the austenitic alloys which was related to aggregation of interface defects [17]. In that study, strain energy models considering the fracture energy at the interface substrate/oxide were employed to discriminate the various routes of spallation depending on the oxide thickness. Using the values of the critical temperature drop, the initiated spallation size was estimated and compared to the image analysis. It was shown that wedging and buckling modes of spallation preferentially develop for thin and thick oxides. This modeling approach is based on the parameter related to the ratio of critical strain of the scale failure to the oxide scale thickness. The other approach uses a comprehensive operational parameter wo that summarizes a multi-level treatment of all contributing factors, e.g., physical defect size, interface roughness, scale thickness, Young’s modulus, fracture toughness, etc., that can influence the failure strain. [18].

There is a significant gap between the proposed micro-models and phenomenological macro-models which describe overall oxidation kinetics, such as using Eq. 1. A macro-approach is typically used in life-time prediction models. Because experimental oxidation kinetics do not always follow the parabolic law, multiple polynomial equations which combined first, second and higher orders were considered to simplify and approximate to the experimental data [2]. To solve this problem, a parabolic law was incorporated into more complicated macro-models considering several experimentally observed micro-effects, such as a local scale spallation. For example, the effect of spallation and additional surface renovation on overall parabolic oxidation kinetics was considered within the spallation model (COSP) designed for cyclic oxidation [19]. In this model, an iterative approach to oxide spallation included subtraction of spalled oxide and the weight after each spallation event from the weight of oxide to calculate the retained oxide weight during that time step. It was assumed that the weight of spalled oxide is proportional to the retained oxide weight in power two. A time step between spallation events also was considered as a function of retained oxide weight. Some parameters of these relationships could be quantified from experiments or predicted from above-described micro- thermo-mechanical models of spallation. A deterministic interfacial cyclic oxidation spallation model (DICOSM) treated loss of individual oxide segments as events occurring after every thermal cycle [20]. The other developed analytical approach [21] was based on the DICOSM model and fitted to two parameters, including a parabolic rate constant and a discrete oxide spallation probability at each cycle (between 0 and 1). These models were successfully used to quantify oxidation and spallation during frequent thermal cycling, such as gas turbine components, when the probability of spallation event could be linked to a thermal cycle frequency.

Spallation of scale is accelerated by frequent thermal cycling; however, it also takes place during static and low cycle near quasi-static oxidation. In former conditions, locally buckled scales could be partially attached to metal surfaces and after that did not prevent oxidant penetration into the interface; however, vibration and other mechanical stress can promote later full detachment of the buckled scale. Such conditions take place in components of automotive gas exhaust systems, which are exposed to low frequency thermal cycling during each on/off engine cycle. For such applications, it is important to simulate topological properties of fallen scale in addition to the overall oxidation kinetics because the detached oxidation products could be contaminated by particulates in an exhaust gas treatment system. The goal of this article was to develop a stochastic oxidation model which included a frequency of spallation event and geometrical topology which was fitted to experimentally determined statistics of spalled spots on oxidized surface.

Procedures

Stochastic Simulation

In order to simulate the process of oxidation with effects of timing and geometrical parameters of scale spallation, it was assumed that the growth of the oxide layer follows the parabolic Eq. (1), and the stochastic process of spallation occurs in the oxide layer. It was also assumed that this stochastic process is a compound Poisson process with piecewise constant intensity per unit of area. For each step of constant intensity, jump size distribution is given by the finite table. This table expresses experimental frequencies of the diameters of spallation spots. This distribution could be time dependent, reflecting the possibility of changing spallation topology during oxidation. After each simulated spallation event, the thickness of the oxide layer is adjusted, and the decrease of the remaining layer leads to the accelerated oxidation. To make the simulation results more realistic, the model also used several topological restrictions, such as L-ratio of spalled layer thickness (lsp) to form scale thickness (lsc). Because a typical scale structure in studied austenitic steels consisted of a relatively dense complex chromium-containing oxide internal layer and a more defected iron-based oxide external layer, cracking and spallation often occurred at the boundary between these layers and L-ratio could be estimated from cross-sectional analysis.

Input into simulation includes a variable oxidation constant and an intensity of spallation for experimentally determined or estimated from thermo-mechanical micro-model topology of spalled scale (Table 1). The program is also enabled to change spalled scale distribution probability during simulated oxidation progress if there are such experimental results completed for simulation. The actual spallation frequency and oxidation constant for a specific oxidation condition could be determined to compare simulated prediction with the experimental results, which includes the weight change of the oxidized specimen and the weight of spalled scale. The rate change of these parameters could be obtained in either interrupted static or transient oxidation experiments. Simulation output contained timing step results of generated spalled particle topology and the thickness of residual oxide layer, frequency of spallation event and evaluated oxidation constant. The simulation of spallation is based on the usage of the random number generator provided by JavaScript global function Math.random [22]. Algorithm for spallation simulation is given below.

Table 1 Input parameters and output results
Full size table

Experimental

A heat resistant Cr/Ni austenitic steel with the addition of N and Mn to stabilize austenite, Si to improve oxidation resistance, and Nb for creep resistance was used in this study (Table 2). This type of steel is commonly being used for exhaust system cast components. The steel was melted in 100 kg capacity induction furnace and poured into no-bake sand molds to produce 18-mm wall thickness plate castings.

Table 2 Composition of studied austenitic steel (wt.%)
Full size table

Samples were machined from plate castings into rectangular specimens 35 × 15 × 5 mm. Each of the samples was finished using wet grinding with 60 grit silicon carbide, and the surface quality was measured to have Ra of 0.27 µm using 3D optical profiler (Nanovea, Model PS50 Micro Photonic Inc.). To prevent rusting prior to testing, sample surfaces were preserved by immersion in ethanol and air dried. Static oxidation test was performed in still air at 950 °C for 400 h. The samples were put into a thermally stabilized cylindrical alumina crucible 50-mm tall and 20-mm internal diameter, which were placed into a shallow rectangular crucible to contain the spalled scale. The test temperature represents the upper working temperature of an exhaust component, and test time was sufficient to simulate service condition. Oxidation tests were interrupted after 50, 100, 300 h of thermal exposure to measure the specimen weight and collect spalled scale. SEM/EDX (Vega 3, Tecscan with Bruker spectrometer) analysis was performed on as oxidized surfaces to estimate spallation geometry and to evaluate the cross section of the scale structure and steel structure. The spalled scale was evaluated using two techniques for chemical composition: ICP (Inductively Coupled Plasma) method to quantify the metallic elements and LECO combustion in a tin container for total oxygen.

Thermodynamic Simulation

Experimentally observed multilayered-scale structure was simulated using FactSage 7.2 thermodynamic software under the local equilibrium conditions [23]. The database used included FSsteel, FToxid and FasctPS. The local equilibrium condition was examined by making stepwise oxygen additions into the simulated streams developed from previous step which assumed irreversible reactions. The formed oxides were “extracted” at each time step. This method allows one to predict different phases that form at low (inner layer) and high (outer layer) added oxygen levels. The thermodynamic simulations were performed assuming that the local equilibrium conditions were reached between gas components, the formed oxide phases, and the steel.

Results

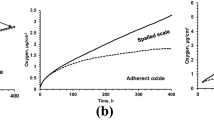
The weight change of a thermally exposed specimen with a stable adherent oxide layer and the weight of the spalled scale during 400 h test at 950 °C are shown in Fig. 1. The data are represented as per area unit in µg/cm2. The data show that there is only a slight weight change of the specimen with adherent oxide until 100 h at 400 °C; however, after 100 h, there is a significant decline. In addition, a substantial amount of spalled scale was collected. The total weight change in the specimen-spalled scale system near parabolic increased with increasing test time (solid line in Fig. 1).

Fig. 1
figure 1

Experimental data collected during 400 h oxidation test at 950 °C, including weight change of a specimen with oxide layer, weight of spalled scale and total weight change

Full size image

This total weight change in a specimen/spalled scale system was influenced by the amount of oxygen which reacted with the specimen and formed both adhered oxide layer and spalled scale. To determine the specific amount of oxygen which occurred on the oxidation reaction products, the amount of oxygen in spalled scale was estimated based upon its weight (Fig. 1) and a defined oxygen concentration from a Leco combustion test (33 wt.% average from three tests). The amount of oxygen in adherent to the specimen was calculated by subtracting the amount of oxygen in the spalled scale from the total weight change. The results are shown in Fig. 2 and illustrate that even though there was a negative weight change in the specimen, the adherent oxide layer existed on the surface. These two values could be determined from a thermo-gravimetric test with separate collecting of both reaction products. The negative weight change of a specimen in the experiment resulted from the total amount of metallic components, which were transferred from the matrix to spalled scale. The metallic composition of the spalled scale from ICP analysis (oxygen was excluded) is shown in Table 3. The analysis showed that the spalled scale contained significantly less Cr and more Fe as compared to base steel composition (Table 2), which indicated strong chromium partitioning between spalled scale and adherent to the matrix oxide layer.

Fig. 2
figure 2

Experimentally determined amount of oxygen reacted during oxidation at 950 °C with forming strong adherent to a specimen surface oxide and spalled scale (markers). The simulated results are presented by solid lines

Full size image
Table 3 Metallic composition of the spalled scale (wt.%) from ICP analysis after excluding oxygen
Full size table

SEM/EDX analysis of the Cr–Ni austenitic steel microstructure in as-cast condition and after 400 h holding at 950 °C is shown in Fig. 3. The as-cast microstructure consisted of an austenitic metal matrix (FCC) with interdendritic Nb(CN) particles which formed during the last region to solidify and decorated austenite dendrites. The grain boundary (insert in Fig. 3a) also contained (Cr,Fe)23C6 type carbides which resulted from Cr segregation during solidification. After a long time of high holding temperature, there were no visible changes in the shape of Nb(CN) phase indicating thermal stability, while small chromium carbides precipitated near the grain boundary and adjusted metal matrix (Fig. 3b).

Fig. 3
figure 3

SEM images of as-cast (a) and after 400 h holding at 950 °C (b) austenitic steel

Full size image

Adherent scale structure was observed in cross section after testing. Figure 4 and Table 4 showed multilayered scale with different compositions: (i) silica at metal/scale boundary (point 4), (ii) mostly chromium oxide internal layer (3) and (iii) mixed Cr, Mn, Fe oxide external layer with multiple lateral cracks. Element mapping in Fig. 5 illustrates layered scale composition.

Fig. 4
figure 4

Cross section of adherent scale with point for EDX analysis given in Table 3

Full size image
Table 4 EDX analysis of chemical composition (wt.%) of multilayered scale (point from Fig. 4)
Full size table
Fig. 5
figure 5

EDX element maps of formed scale

Full size image

The multilayered-scale structure observed during the experimentation verified by the thermodynamic simulations (Fig. 6), when equilibrium was simulated at different oxygen/steel ratios. The data appeared to mimic the situation from near matrix/scale interface (low ratio) to outer scale/atmosphere boundary (high ratio). The sequential formation of silica film, followed by chromium oxide, (Cr-Fe) spinel, and outer Mn and Fe oxides was predicted in the same order as the experimental results (Figs. 4 and 5).

Fig. 6
figure 6

Thermodynamically simulated multilayered scale composition formed on Cr–Ni austenitic steel at different oxygen/steel ratios which corresponded to the different oxygen accessibility from outer to inner layers

Full size image

The described multilayered scale with various compositions of the internal and external layers was responsible for local spallation by detaching these layers during high temperature oxidation. As the outer high Fe and Mn scale spalled, the high chromium layer was exposed, and oxidized surface mapping could be used for evaluation of spalled scale topology. Figure 7a presents an example of multi-elemental map, which was used to estimate spalled spots diameter distribution (Fig. 7b), and obtained data wereimplemented as input into a stochastic simulation.

Fig. 7
figure 7

Multi-element map of oxidized surface (a) used for experimental determination of spalled (detached) scale diameter distribution (b)

Full size image

Discussion

A simulated oxidation kinetics, considering parabolic law in adherent oxide layer (Eq. 1) and frequency of spallation, presented in Fig. 2 by solid lines and well fitted to the experimental amount of oxygen spent to form adherent layer and spalled scale (markers). The true oxidation constant was determined in this case as a kp = 2.5e-6 mg2cm−4 s−1, and the frequency of spallation was predicted at 0.4 events per hour in each unit of area (1 cm2). The predicted distribution of spalled spot diameter was in agreement with the experimental observation which was obtained from the EDS mapping of oxidized surface (Fig. 7). Therefore, the model simulated spallation events at given frequency, considering experimental topology of spalled scale. The simulated thickness of adherent layer after spallation followed by parabolic law considering diffusion-controlled kinetics. Optimization of these two parameters (spallation frequency and true oxidation constant) requires an experimentally measured specimen weight change and weight of spalled scale during oxidation test.

Parametric analysis of the spallation parameters was performed to illustrate the effect of spalling geometry and frequency of spallation event on oxidation kinetics. Assuming the same value of the true oxidation constant which was obtained from the described above experiment. The five different spallation diameter distributions, from fine, with average 100 µm diameter to above 1 mm, were considered (Fig. 8). The real distribution in this experiment was between #3 and #4.

Fig. 8
figure 8

Sets of spallation distribution diameters used for parametric analysis

Full size image

Simulation predicted three possible scenarios for oxidation kinetics assisted by scale spallation, depending on variations in spallation diameter and spallation intensity, characterized by event frequency (Fig. 9). These graphs show the amount of oxygen in the adherent layer, assuming a strong attachment to the oxidized surface scale (dashed line), and the total amount of oxygen which reacted with the surface (solid line) to form the adherent and spalled scale during the 400 h oxidation with a defined oxidation constant. The area between these curves presents the spallation kinetics. The first type of kinetics (Fig. 9a), with signs of adherent layer to a specimen surface, followed by parabolic law which resulted in the case of limited spallation (small diameter distribution #1 and low, less than 0.1 h−1 cm−2 spallation event frequency). In the other extreme cases, (Fig. 9c) with a large spallation diameter #5 and high spallation frequency above 1 h−1 cm−2, the short initial period of increasing adherent scale followed such intensive spallation that all newly formed scale was practically removed from the interface leaving only a tiny adherent layer on the surface. There are a variety of possible oxidation kinetics, which could be formally fitted to a combination of linear and parabolic trends which existed for different spalled diameter distributions of event frequency (Fig. 9b).

Fig. 9
figure 9

Three types of predicted oxidation kinetics with variation in spalled diameter distribution and spallation frequency: a oxidation with restricted spallation, b oxidation assisted by spallation, and c intensive spallation of formed scale. Dashed line presented the amount of strongly adherent scale, solid line represents the total amount of oxygen which reacted to the specimen unit area, and a region between these lines presents the amount of oxygen in spalled scale

Full size image

Parametric simulation illustrates a potential complex effect of two spallation parameters (spallation diameter distribution and spallation event frequency) on the test results after 400 h of oxidation, which assumed the same oxidation constant for all cases. In these simulations, the amount of reacted oxygen was recalculated to predict a specimen weight change, which is typically monitored in thermo-gravimetric experiments. Increasing spallation diameter and spallation intensity dramatically increased the weight of the spalled oxide after 400 h during the virtual test, which was presented in log scale in Fig. 10. However, the actual weight change of the specimen after the test could be positive (gain) or negative (loss) depending on spallation parameters. The specimen weight with strongly adherent scale could be increased at low spallation intensity or decreased at high spallation rates because the spalled scale removed some amount of metallic elements from the reaction surface.

Fig. 10
figure 10

Parametric analysis of the oxidation with spallation for virtual thermal gravimetric analysis (TGA) experiments, assuming different spallation intensities and detached scale topology: a simulated weight of spalled scale and b weight gain or loss of specimen with strongly adhered to alloy surface oxide

Full size image

These simulations clearly illustrated the necessity of full analysis of reaction products from TGA experiment, including the weight change of a specimen as well as the weight of spalled scale. In many cases, only the specimen weight change could not only provide the wrong kinetical constant value but also mislead the alloy comparison. The image analysis is also used for evaluation of oxidation kinetics together or separately from the TGA [1]. Simulation illustrates that the image results interpretation will depend on spallation intensity, and it is recommended that additional data may be needed to get a reliable oxidation constant. Figure 11 illustrates a potential for discrepancy of the test result when only the thickness of the adherent layer was used to evaluate oxidation kinetics. To make this simulation comparable, the predicted thickness of the adherent scale was recalculated by using the oxygen weight per unit area based on the scale density and element concentration (Table 3). At a low spallation intensity, the image results accurately predict the oxidation constant in weight units (Eq. 3). This condition depends on a combination of the spalled diameter along with an intensity, which is shown by the shaded area. However, the imaging interpretation may provide a large difference in the true oxidation kinetics when a high spallation intensity takes place within a sample, because the data did not include spallation characteristics. There could be an order of magnitude difference. Therefore, the described methodology includes the stochastic simulation of spallation along with incorporated experimental topological parameters enabling one to accurately represent such complicated oxidation processes.

Fig. 11
figure 11

taken from measured thickness

Potential effect of spallation intensity and topology of estimated oxygen in adherent scale

Full size image

Conclusions

The scale spallation which occurred above the critical oxidation conditions (temperature, atmosphere, thermal cycling) significantly affected the oxidation kinetics. To accurately predict the effect of scale spallation on the oxidation constant, a simulation was performed using a proposed stochastic model. The model considers topological parameters along with the intensity of spallation events while delivering a true oxidation constant. The model's input included experimentally determined spalled scale topology. A suggested experimental approach for oxidized austenitic Cr/Ni steel was based on element mapping of a surface because both external and internal scale layers are composed of different types of oxides and delamination often takes place between these layers. Simulation of experimental oxidation kinetics showed a potential to deliver a true oxidation constant as well as the spallation intensity.

Performed parametric analysis for the same value of true oxidation kinetics showed that depending on the intensity and topology of spallation, there can be a large variety of predicted trends for development of the adhered oxide layers. The oxidation could follow the parabolic law with low spallation intensity, or it could be formally fitted to a combination of linear and parabolic trends or in some cases a newly formed scale could practically be removed from the interface leaving only a tiny adherent layer with a constant thickness when intensive spallation occurs. The proposed model provides boundary conditions between these trends.

The described methodology, which is based on stochastic simulation of spallation with incorporated experimental topological parameters, gives the potential to accurately describe such complicated oxidation processes. The practical results for implementation of the suggested methodology for studying the oxidation-resistant austenitic steels will be done in the separate article.

figure a