Introduction

The problem of chiral symmetry breaking during formation of life on Earth has been puzzling researchers for over 150 years starting from the discovery of enantiomers by L. Pasteur. The number of works in this area could be made a subject of a separate research. Vast number of models of chiral symmetry breaking were proposed over the years and numerous experiments were performed, for example (Frank 1953; Avetisov and Goldanskii 1996; Plasson et al. 2004, 2007; Saito and Hyuga 2004; Weissbuch et al. 2005; Brandenburg et al. 2007; van der Meijden et al. 2009; Noorduin et al. 2010; Blackmond 2011; Coveney et al. 2012; Hein et al. 2012; Ribó et al. 2013; Konstantinov and Konstantinova 2013, 2014), and many others. However, most, if not all, theories and experiments related to chiral symmetry breaking during formation of life on Earth considered only a very limited number of substances and reactions, whereas the actual number of possible substances and reactions among them must have been extremely large, as we will soon discuss. Therefore, it is a variety of both substances and reactions that substantially alters the picture.

There are only three possible ways how enantiomeric content of a closed chemical system can change over time. The chiral molecules can be created, destroyed, or converted into each other. Pass-through systems also allow eliminating some “waste” products. Mathematically, such an elimination is equivalent to “destroying” the “waste”. Subsequently all models of chiral symmetry breaking have to utilize one or several of these channels. The models based on creation and destruction utilize reversible autocatalytic or catalytic synthesis of amino acids (Avetisov and Goldanskii 1996; Plasson et al. 2007) and in addition often require a “mutual antagonism” as was originally proposed by Frank (1953). Alternative models of chiral symmetry breaking are based on inter-conversion of enantiomers. These models can be grouped into two classes: the models based on epimerization (Plasson et al. 2004, 2007; Weissbuch et al. 2005; Brandenburg et al. 2007) and the models based on the deracemization process (Hein et al. 2012; van der Meijden et al. 2009; Noorduin et al. 2010).

In order to have chiral symmetry breaking, autocatalytic models (Avetisov and Goldanskii 1996) require substantial enantioselectivity of a catalyst. This can be called “fine-tuning” or described as needing a “robust system”. However, the abundance of various substances on a prebiotic Earth means effective averaging of the rates of catalytic reactions over all available catalysts for a given reaction and having the large value of enantioselectivity of the averaged rates seems questionable due to the law of large numbers. We will consider this in more detail below. In addition, it is often argued that amino acids do not possess autocatalytic properties. However, there are known catalysts for asymmetric synthesis of amino acids already at the dipeptide level (Iyer et al. 1996) and therefore it is important to extend catalytic models to longer peptide chains.

However, what is even more important is that some of the autocatalytic models mentioned above utilized incorrect assumptions about how catalysts change the reaction. Due to thermodynamic reasons (because the catalyst is not consumed), the presence of a catalyst cannot change thermodynamic equilibrium. Only the speed at which the equilibrium is reached is increased. This fact imposes very strict constraints on some of the parameters of catalytic reactions: total enantioselectivity, which is defined as a sum of forward and backward enantioselectivities, must be identically zero. This effectively eliminates all the models, which require any non-zero value of total enantioselectivity in order to result in chiral symmetry breaking. We will also consider this in more detail below.

Current epimerization based models (Activation, Polymerization, Epimerization, Depolymerization – APED) also have some fine-tuning requirements, which are similar to fine-tuning in catalytic and autocatalytic models. Certain parameters in such models must be placed far away from the expected average values (Plasson et al. 2004, 2007).

On the opposite side, deracemization utilizes a phase transition process of crystallization and nonlinearity due to the rate of crystallization being proportional to the surface area of the crystals (Hein et al. 2012; van der Meijden et al. 2009; Noorduin et al. 2010). In contrast to basic chemical reactions, which are polynomial functions of concentrations, a phase transition, if viewed as a mathematical function, exhibits some discontinuity. It is therefore not subject to the averaging considerations above, because a small change in the parameters near a phase transition point results in substantial changes in the output. However, deracemization requires a high racemization rate in the solution and enantiopure substance(s) accumulate in the sediment. While it is relatively easy to imagine how this process could have been realized on a geological scale, it poses some difficulties to chiral symmetry breaking on a prebiotic Earth. A high racemization rate in the solution means that most, if not all, complex molecules, which could have been formed in the solution, would have had a racemic content. Rather, an enantiopure sediment must be taken away and only then could complex enantiopure substances be formed. In addition, deracemization also requires that the enantiomer substances crystallize as conglomerates, and there is only about 5–10% of amino acids, which exhibit that property. That means that, if the number of substances in the solution is very large, then a substantial number of substances will not form conglomerates. Subsequently, that results in sediment containing an enantiopure mixture of some substances and a racemic mixture of a far more substantial amounts of some other substances.

From the third side, it was experimentally shown in (Blackmond 2011 that different properties of enantiomers and, in particular, formation of sediment of insoluble diastereomeric pairs may result in substantial enantiomeric excess (sometimes called chiral polarization) even in the absence of any autocatalysis. The application of this process to autocatalytic reactions was studied theoretically in (Konstantinov and Konstantinova 2013) where it was shown how the differences between physical properties of diastereomers may result in additional enantioselective factors. However, that is not sufficient due to the absence of autocatalytic properties of amino acids.

In addition, Earth is not a thermodynamically closed system as it constantly receives light (high frequency photons) from the Sun and emits heat (low frequency photons) into the outside space. This is most likely the most important factor influencing chiral symmetry breaking on Earth, as it places its chemical system into far from equilibrium state. The importance of far from thermodynamic equilibrium states for chiral symmetry breaking was considered previously in (Plasson et al. 2007) and they require a constant inflow of energy to operate.

It is therefore important to consider if there are models, which correctly treat thermodynamic constraints on the properties of catalysts, do not encounter fine-tuning issues in case of a very large number of substances, consider far from thermodynamic equilibrium systems, and take into account that amino acids may form longer peptide chains.

Definitions

Current work considers large number of complex models, which, in turn, have substantial number of parameters and / or various definitions. The main parameters and definitions used throughout the article are as follows:

  • ρ X is the concentration of a substance X.

  • We consider models with only one achiral “food” substance, which we denote as Y and its concentration as ρ Y and only one left amino acid, which we denote as A and its enantiomer as a (the letter is not related to standard one letter amino acid coding).

  • Letter C is used to denote a catalyst.

  • \( \widehat{E}(X) \) is the enantiomer of some chiral substance X. So, for example:

$$ \widehat{E}(AAaA)= aaAa $$
(1)

  • θ X and Δ X variables. For any chiral substance X we denote its enantiomer as \( \widehat{E}(X) \), their concentrations as ρ X and \( {\rho}_{\widehat{E}(X)} \) correspondingly, and introduce a change of variables:

$$ {\displaystyle \begin{array}{c}{\theta}_X={\rho}_X+{\rho}_{\widehat{E}(X)}\\ {}{\varDelta}_X={\rho}_X-{\rho}_{\widehat{E}(X)}\end{array}} $$
(2)

  • For any peptide chain P, for example, P = AAaA, we denote \( \widehat{I}(P) \) as an inverse of P, which is a peptide chain in a reverse order, for example:

$$ \widehat{I}(AAaA)= AaAA $$
(3)

Some of the models, which we considered, are invariant to this inversion transformation of the equations.

  • \( {\rho}_A^{tot}=\sum \limits_s{n}_A(s){\rho}_s,\kern0.5em {\rho}_a^{tot}=\sum \limits_s{n}_a(s){\rho}_s \), where n A (s) is a number of left amino acids in a given substance s, n a (s) is a number of right amino acids in a given substance s, ρ s is the final concentration of substance s, are the total equivalent concentrations of left and right amino acids,

  • \( \eta =\left|\frac{\rho_A^{tot}-{\rho}_a^{tot}}{\rho_A^{tot}+{\rho}_a^{tot}}\right| \) is the enantiomeric excess,

  • \( {\rho}_0={\rho}_Y+{\rho}_A^{tot}+{\rho}_a^{tot} \) is the integral of motion and it describes the total amount of matter (per unit of volume) present in the system.

  • For any reaction R we denote k(R) as the rate of such a reaction, for example k(A + C → Y + C) is the rate of forward part of reaction Y + C ⇌ A + C.

  • c + = k(Y → A) = k(Y → a), c − = k(A → Y) = k(a → Y) are the rates of forward and backward amino acid synthesis reactions.

  • a + = k(A → A ∗) = k(a → a ∗), a − = k(A ∗ → A) = k(a ∗ → a) are the rates of forward and backward activation reactions (when used).

  • \( {\Gamma}_{+}=\left(k\left(Y+C\to A+C\right)+k\left(Y+\widehat{E}(C)\to A+\widehat{E}(C)\right)\right) \) is the total rate of forward catalytic synthesis of amino acid reaction in the presence of catalyst C and its enantiomer \( \widehat{E}(C) \).

  • \( {\Gamma}_{-}=\left(k\left(A+\widehat{E}(C)\to Y+\widehat{E}(C)\right)+k\left(A+C\to Y+C\right)\right) \) is the total rate of backward catalytic synthesis of amino reaction acid in the presence of catalyst C and its enantiomer \( \widehat{E}(C) \)

  • \( {\upgamma}_{+}=\frac{k\left(Y+C\to A+C\right)-k\left(Y+\widehat{E}(C)\to A+\widehat{E}(C)\right)}{k\left(Y+C\to A+C\right)+k\left(Y+\widehat{E}(C)\to A+\widehat{E}(C)\right)} \) is the enantioselectivity of forward catalytic synthesis of amino acid.

  • \( {\upgamma}_{-}=\frac{k\left(A+\widehat{E}(C)\to Y+\widehat{E}(C)\right)-k\left(A+C\to Y+C\right)}{k\left(A+\widehat{E}(C)\to Y+\widehat{E}(C)\right)+k\left(A+C\to Y+C\right)} \) is the enantioselectivity of backward catalytic synthesis of amino acid.

  • Λ+ is the rate of polymerization (forward ligation) reactions, for example: A + aa → Aaa. The same value of Λ+ was used regardless enantiomeric content and length of peptides.

  • Λ− is the rate of depolymerization (backward ligation) reactions, for example: Aaa → A + aa. The same value of Λ− was used regardless enantiomeric content and length of peptides.

  • ε − = k(P 1 + P 2 → nY), where P 1 and P 2 are the substances (peptides), which form an insoluble pair, and n is their combined length, is the rate of sedimentation of insoluble pair. Please, refer below to the discussion below why such “reactions” were used.

  • a = k(A → A ∗) ≡ a +, b = k(A ∗ → A) ≡ a −, e = k(Aa → aa), h = k(AA → A + A) ≡ Λ−, and p = k(A ∗ + A → AA) are parameters of activation, polymerization, epimerization, depolymerization (APED) model. Letters a, b, e, h were chosen for describing the rates of reactions to match the terminology used in APED model.

“Closure” of Models

Consider some general isotropic and homogeneous model of chemical reactions. Suppose that we have N different chemical substances (S 1, …S N ) and K possible reactions among them (R 1, …R K ). The state of the system is determined by the number of molecules of each substance: X(t) = (X 1(t), …X N (t)) at a given time, or equivalently by their concentrations:

$$ \boldsymbol{\rho} (t)=\left({\rho}_1(t),\dots {\rho}_N(t)\right) $$
(4)

where \( {\rho}_{\alpha }(t)=\frac{1}{\varOmega }{X}_{\alpha }(t) \) and Ω is a volume of the system and α = 1, 2, …N. Evolution of such a system under the assumption that X i  ≫ 1 can be written as a system of ordinary differential equations (Andrews et al. 2009):

$$ \frac{d{\rho}_{\alpha }(t)}{dt}=\sum \limits_{i=1}^K{\nu}_{\alpha i}\ {a}_i\left(\boldsymbol{\rho} (t)\right), $$
(5)

where ν αi is a stoichiometric matrix and a i is the rate of i-th reaction. In the general case a i could be some complicated functions of ρ(t).

A system of Eq. (5) expressed in ρ Y , θ X , and Δ X variables will be called a full system. A reduced system is defined as a system (5) with all Δ X  ≡ 0 for all chiral X. Studying a symmetry breaking in a full system (or a bifurcation from a racemic steady-state) is equivalent to studying the eigenvalues of a matrix of coefficients of all Δ X . This matrix is obtained by linearizing a full system near stable fixed point(s) of a reduced system. This linearization effectively makes many models (for example, pass-through models and cyclic models) equivalent or nearly equivalent to each other, provided that the steady state concentrations do not change under such closing. For example, consider a pass-through model where some achiral substances flow into the system at some rate and some substances flow out of the system. A good example is a system of a geological scale, in which a sediment constantly forms and falls to the ocean floor, thus effectively leaving the reaction area. Suppose that the system is in some stable fixed point of a reduced system and we are interested in the symmetry breaking in a full system. We can “close” such a pass-through model and make it a cyclic model by adding fictitious irreversible decay reactions with the properly chosen rate coefficients, so that all output (and effectively non-chiral) substances decay into input (non-chiral) substances. The linearized matrix of coefficients of Δ X for such a completed cyclic model will be the same as for a pass-through model, from which we started. This can be illustrated by the following example. Consider two irreversible reactions, which terminate a pass-through model with some rate coefficient k:

$$ {\displaystyle \begin{array}{c}A+B\to Z\\ {}\widehat{E}(A)+\widehat{E}(B)\to Z\end{array}} $$
(6)

where A and B are some chiral substances and Z is some discarded substance. We can view Z as an achiral substance because it leaves the reaction area. Then in θ and Δ variables we will have:

$$ \frac{d{\rho}_Z}{dt}=k{\rho}_A\ {\rho}_B+k{\rho}_a\ {\rho}_b=\frac{k}{2}\left({\theta}_A{\theta}_B+{\varDelta}_A{\varDelta}_B\right)\approx \frac{k{\theta}_A{\theta}_B}{2} $$
(7)

because we ignore quadratic term Δ A Δ B in the linearized model. The requirement that the steady state concentrations do not change under closing requires that some of the rate coefficients need to be adjusted in order to fulfill that under closing. It is important to note that both pass-through models and “closed” cyclic models are open systems: pass-through models require constant inflow of “food” matter and a “sink” to remove waste products and “closed” cyclic models require constant inflow of energy to “recycle” the waste products.

Averaging of Enantioselectivity in Catalytic Models

We would like first to consider how averaging of various rates of reactions due to large number of substances may affect enantioselectivity of different types of reactions. Consider some reversible reaction:

$$ A+B\rightleftharpoons D $$
(8)

and its catalytic version:

$$ A+B+C\rightleftharpoons D+C $$
(9)

where C is a catalyst and A, B, and D are some substances (not necessarily amino acids in these equations). Such reactions or their autocatalytic versions are usually a basis of analysis for chiral symmetry breaking (Avetisov and Goldanskii 1996; Saito and Hyuga 2004; Plasson et al. 2007). Forward (R +) and backward (R −) reaction rates for Eq. (9) are then:

$$ {\displaystyle \begin{array}{c}{R}^{+}={k}^{+}\ {\rho}_A\ {\rho}_B\ {\rho}_C\\ {}{R}^{-}=-{k}^{-}\ {\rho}_D\ {\rho}_C\end{array}} $$
(10)

where ρ i is a concentration of the i-th substance, k + and k − are forward and backward rate coefficients. However, if the number of catalysts is very large (which must be the case if the number of substances is very large), then at each moment of time forward and backward rates effectively become weighted averages of the rates of reactions with all relevant catalysts:

$$ {\displaystyle \begin{array}{c}{R}^{+}={\rho}_A{\rho}_B\sum \limits_{\left\{C\right\}}{k}_C^{+}{\rho}_C\equiv {k}_{eff}^{+}{\rho}_A{\rho}_B{\rho}_{tot}\\ {}{R}^{-}=-{\rho}_D\sum \limits_{\left\{C\right\}}{k}_C^{-}{\rho}_C\equiv -{k}_{eff}^{-}{\rho}_D{\rho}_{tot}\end{array}} $$
(11)

where {C} is a set of all possible catalysts for a given reaction at a given time and:

$$ {\displaystyle \begin{array}{c}{\rho}_{tot}\sum \limits_{\left\{C\right\}}{\rho}_C\\ {}{k}_{eff}^{+}=\sum \limits_{\left\{C\right\}}{k}_C^{+}\frac{\rho_C}{\rho_{tot}}\end{array}} $$
(12)

If catalyst C is chiral, then its enantiomer \( \widehat{E}(C) \) is also a catalyst.

$$ A+B+\widehat{E}(C)\rightleftharpoons D+\widehat{E}(C) $$
(13)

and, therefore, both will contribute to averaged reaction rates as expressed by Eq. (11). In the current work, we are only interested in the analysis of the stability of the symmetric state. Subsequently, we ignore any possible asymmetry between enantiomers, for example, global asymmetry due to weak interaction (Rein 1974; Letokhov 1975). Therefore, we consider that the rates of reaction (9) and its equivalent for all enantiomers:

$$ \widehat{E}(A)+\widehat{E}(B)+\widehat{E}(C)\rightleftharpoons \widehat{E}(D)+\widehat{E}(C) $$
(14)

are exactly the same.

In addition, thermodynamic considerations require that the equilibrium state is unchanged for Eqs. (9) and (13) in comparison to Eq. (8). This well-known fact means that forward and backward rates of the reaction (8) are equally affected by the catalyst and, therefore, forward and backward rates (in the presence of catalyst) must just be multiplied by exactly the same number. Subsequently, that means that total enantioselectivity, which is defined by Eq. (21) below, must be identically zero for any catalyst / enantiomer pair. Surprisingly, total enantioselectivity was “allowed” to deviate from that identically zero value in a substantial number of models and for quite a large number of years. However, since current work is not about the analysis of the previous mistakes, we will not perform any further review of that matter.

Apart from some very exotic cases, like some specifically constructed cyclic peptides, which are invariant under simultaneous application of operator \( \widehat{E} \) and some nontrivial rotation around the cycle, the enantiomer \( \widehat{E}(C) \) is a different substance and, in general, will have different catalytic properties when applied to reaction (8). Therefore, multiplication factors could be different for Eqs. (9) and (13) and that will result in non-zero enantioselectivities of forward and backward reactions. It is then interesting that some of the well-known catalysts for chiral separation, asymmetric synthesis, or even ligation (Fujima et al. 2006; Sczepanski and Joyce 2014) have more stereo centers of opposite chirality in comparison to the substances on which they operate.

Models with Peptides up to Length 5, Catalytic Synthesis, and Crystallization of Insoluble Pair

Modeling system with a large number of amino acids and long peptides is an NP-complete problem (Cook 1971) because the number of possible peptides and reactions grows exponentially as the number of amino acids and length of peptides increases. Therefore, it is important to understand if there are models, which can produce chiral symmetry breaking with a substantially limited number of amino acids and short peptides, but without fine-tuning. Models with autocatalytic synthesis of a single amino acid (which could be called a “peptide” of length one) were considered in great detail in the last 60 years (Frank 1953; Avetisov and Goldanskii 1996) and APED-like models considered peptides of length two but without catalytic synthesis of amino acids. Therefore, the minimum interesting length of peptides is three. From one side, further increase in peptide length and / or number of amino acids in the model will result in exponentially increasing difficulties. From the other side, if peptide formation is reversible, which is applicable in this case because we will be considering polymerization and depolymerization reactions, then it is straightforward to illustrate that the distribution of concentration of peptides by length forms decreasing geometric progression with some common ratio α < 1. Therefore, the longer the peptide lengths, the smaller concentration they will have and therefore the smaller their contribution will be. As such, we would like now to limit our consideration to just one amino acid, which we denote here as A for left enantiomer and as a for right enantiomer. We combine several well-known models described in the literature (Frank 1953; Avetisov and Goldanskii 1996; Plasson et al. 2004, 2007; Saito and Hyuga 2004; Weissbuch et al. 2005; Brandenburg et al. 2007; van der Meijden et al. 2009; Noorduin et al. 2010; Blackmond 2011; Coveney et al. 2012; Hein et al. 2012; Ribó et al. 2013; Konstantinov and Konstantinova 2013, 2014) and then study which combinations can possibly result in the symmetry breaking under the conditions of weak enantioselectivity of all relevant reactions. Even though the minimum interesting peptide length is three, we consider peptide chains up to length five in order to study how the increase in peptide length influences the symmetry breaking. Therefore, the possible substances are:

$$ {\displaystyle \begin{array}{l}Y,{A}^{\ast },{a}^{\ast },A,a, AA, Aa, aA, aa, AA A, AA a, Aa A, aA A, Aa a, aA a, aa A, aa a, AA A A, AA A a, AA a A,\\ {} AaAA, aA A A, AA a a, Aa A a, Aa a A, aA A a, aA a A, aa A A, Aa a a, aA a a, aa A a, aa a A, aa a a, AA A A A,\\ {} AAAAa, AA A a A, AA a A A, Aa A A A, aA A A A, AA A a a, AA a A a, AA a a A, Aa A A a, Aa A a A, Aa a A A, aA A A a,\\ {} aAAaA, aA a A A, aa A A A, AA a a a, Aa A a a, Aa a A a, Aa a a A, aA A a a, aA a A a, aA a a A, aa A A a, aa A a A,\\ {} aaaAA, Aa a a a, aA a a a, aa A a a, aa a A a, aa a a A, aa a a a\end{array}} $$
(15)

where A ∗, a ∗ are activated left and right amino acids as used in some models. We would like to study all possible variants when no more than one substance (and its enantiomer) are catalysts with low forward enantioselectivity and exactly one pair of substances (and their enantiomers) forms some insoluble substances. If we have many substances in the solution, then as the amount of solvent decreases and concentrations increase, there is always the least soluble substance, which will be the first to start forming sediment. In the current simplified model, we assume that the least soluble substance is insoluble. However, a more realistic model must take into account non-zero solubilities of all substances in the system and their influence on each other.

It is important to note that, while sedimentation / dissolution is, of course, a reversible process, there are certain conditions under which it could be viewed as irreversible. For example, a sediment could fall into the ocean floor where the temperature is much lower. Thus, it will effectively leave the reaction area. We consider here sedimentation as an effectively irreversible process and that imposes a cycle of how chiral matter moves in the system. The following reactions are included in our consideration:

Reversible Synthesis of Amino Acids

$$ Y\rightleftharpoons A,\kern0.5em Y\rightleftharpoons a $$
(16)

It was shown (Avetisov and Goldanskii 1996) that the coefficients k(Y → A) and k(A → Y) must be small in comparison to the rate of catalytic synthesis. However, the maximum of \( \frac{1}{k\left(Y\to A\right)} \) and \( \frac{1}{k\left(A\to Y\right)} \) determines time, which is needed for the system to reach equilibrium if only these two reactions are considered. Therefore, the evolution time must be \( t\gg \mathit{\max}\left(\frac{1}{k\left(Y\to A\right)},\frac{1}{k\left(Y\to A\right)}\right) \). If these coefficients are chosen too small, then the evolution time will be very large and subsequently the calculation time will increase drastically. We used the values k(Y → A) = k(Y → a) = c + = 10−2 and k(A → Y) = k(a → Y) = c − = 10−3 in our calculations.

Catalytic Synthesis of Amino Acids

$$ {\displaystyle \begin{array}{cc}Y+C\rightleftharpoons A+C,& Y+\widehat{E}\rightleftharpoons A+\widehat{E}(C)\\ {}Y+C\rightleftharpoons a+C,& Y+\widehat{E}\rightleftharpoons a+\widehat{E}(C)\end{array}} $$
(17)

where C is a catalyst (any one of A, a, AA, Aa, aA, aa, AAA, AAa, AaA, Aaa, aAA, aAa, aaA, aaa, …, aaaaa).

We are interested in the scenario when the forward coefficient is much larger than the backward one. However, backward coefficients must be also chosen so that the characteristic evolution time is not too large. Given that the estimated minimum concentration of a potential catalyst in the models, which we considered, is ~10−3 and the used evolution time, backward coefficient should not less than 0.1. If catalytic reactions were used, then given a catalyst C, we used the following values of the parameters:

$$ {\Gamma}_{+}=10,\kern0.5em {\Gamma}_{-}=0.1 $$
(18)

Alternatively, if catalysis was not used, then we used:

$$ {\Gamma}_{+}={\Gamma}_{-}\equiv 0 $$
(19)

As discussed above, thermodynamic considerations require that the catalyst does not change the equilibrium. This condition means that coefficients of enantioselectivity of forward and inverse catalysis satisfy the following condition:

$$ {\upgamma}_{+}\equiv -{\upgamma}_{-} $$
(20)

Subsequently that means that total enantioselectivity of a catalyst, γ, is identically zero:

$$ \upgamma ={\upgamma}_{+}+{\upgamma}_{-}\equiv 0 $$
(21)

For the cases when Γ+ > 0 and Γ− > 0 we considered two distinct variants of enantioselectivity:

$$ {\displaystyle \begin{array}{c}\kern1.00em {\gamma}_{+}\equiv -{\gamma}_{-}=0\kern1.00em \\ {}\kern1.00em {\gamma}_{+}\equiv -{\gamma}_{-}=\pm {\delta}_{\gamma}\kern1.00em \end{array}} $$
(22)

We used the value δ γ  = 0.1 in our calculations.

Activation

It is important to note that two primary scenarios can be realized experimentally in regards to the formation of peptides: peptides can be considered as growing only in one direction by adding one amino acid at only one end of the peptide or arbitrary reactions of peptide formation can be considered. That loosely corresponds to two distinct classes of models: the models with activation and the models without activation. The first scenario was considered in (Plasson et al. 2004; Brandenburg et al. 2007) and therefore we consider the class of models where an amino acid must first be activated before it can attach to another amino acid of a peptide chain, as well as the models when the peptides can grow from both sides. The activation reaction (if used) can be written as follows:

$$ A\rightleftharpoons {A}^{\ast },\kern0.5em a\rightleftharpoons {a}^{\ast } $$
(23)

We used the values k(A → A ∗) = k(a → a ∗) = a + = 1 and k(A ∗ → A) = k(a ∗ → a) = a − = 10−3 in our calculations. This corresponds to the situation when most of the amino acids are in an activated state.

Polymerization / Depolymerization

If activation was taken into account, then we consider the models where the peptide chains can only grow to the left:

$$ {\displaystyle \begin{array}{cc}{A}^{\ast }+X\to AX,& {a}^{\ast }+X\to aX\\ {} AX\to A+X,& aX\to a+X\end{array}} $$
(24)

where X is any of the allowed by the model substances (A, a, AA, Aa, aA, aa, …, aaaa).

If activation was not considered, then the following reactions are used:

$$ {\displaystyle \begin{array}{cccc}A+X\rightleftharpoons AX,& a+X\rightleftharpoons aX,& X+A\rightleftharpoons XA& X+a\rightleftharpoons Xa\\ {} AX\rightleftharpoons A+X,& aX\rightleftharpoons a+X& XA\rightleftharpoons X+A& Xa\rightleftharpoons X+a\end{array}} $$
(25)

where X is any of the allowed by the model substances (A, a, AA, Aa, aA, aa, …, aaaa).

The following reactions were also considered for the models with peptides longer than three and when activation was not used:

$$ {P}_1+{P}_2\rightleftharpoons {P}_1{P}_2, $$
(26)

where P 1 and P 2 are some peptide chains with a combined length not exceeding five. With the exception of APED-like models coefficients for all forward polymerization reactions were considered to have the same value Λ + = 1. Similarly, all depolymerization reactions were also considered as having the same coefficient with the value Λ − for all models except APED-like ones. We considered several values of Λ − in order to study how it affects the symmetry breaking.

Sedimentation of Insoluble Pairs

As discussed above, any pass-through models, including models with sedimentation can be “closed” by short-circuiting them back to the beginning of the models (synthesis of amino acids). As we are interested only in the symmetry breaking, we can utilize this to short-circuit pair formations with subsequent sedimentation. That allows us to use a simplified model of irreversible sedimentation:

$$ {P}_1+{P}_2\to nY,\kern0.5em \widehat{E}\left({P}_1\right)+\widehat{E}\left({P}_2\right)\to nY $$
(27)

where P 1 and P 2 are the substances (peptides), which form an insoluble pair, and n is their combined length. Given two substances P 1 and P 2 there are two other possible combinations, which may form insoluble pairs:

$$ {P}_1+\widehat{E}\left({P}_2\right)\to nY,\kern0.5em \widehat{E}\left({P}_1\right)+{P}_2\to nY $$
(28)

In a simplified model of sedimentation, we assume that only one of the reactions Eqs. (27) or (28) holds, while the other pair is soluble.

While the computational complexity substantially decreases in such a case, it is important to compare the results with a more realistic model. If we assume that a pair of peptides may form a temporary (not peptide) bond and then subsequently some of such pairs are insoluble, then we have to consider all possible combinations. That creates additional reaction channels:

$$ {P}_1+{P}_2\rightleftharpoons \left({P}_1\right)\left({P}_2\right), $$
(29)

which are different from peptide formation reaction (26), and then some of these pairs form a sediment. In addition, we can no longer consider only one combination Eqs. (27) or (28). Rather, it is important to take both into account and also consider possible mutual influence on the solubility: if we have many substances in the solvent, then it becomes a very complicated process. Moreover, the sedimentation process \( {C}_{\rho_i\rightleftharpoons {\rho}_{C_i}}\left({\rho}_i,{\rho}_{C_i}\right) \), even in its simplest form, is a discontinuous function of two variables ρ i (the concentration of the substance in the solution) and \( {\rho}_{C_i} \) (the total amount of the sediment divided by the total volume of the system):

$$ {C}_{\rho_i\rightleftharpoons {\rho}_{C_i}}\left({\rho}_i,{\rho}_{C_i}\right)=\left\{\begin{array}{c}0,\kern0.5em {\rho}_i\le {\rho_i}^{\left(\mathit{\max}\right)}\kern0.5em and\kern0.5em {\rho}_{C_i}=0\\ {}{k}_{sol}\left({\rho}_i-{\rho_i}^{\left(\mathit{\max}\right)}\right),{\rho}_i\le {\rho_i}^{\left(\mathit{\max}\right)}\kern0.5em and\kern0.5em {\rho}_{C_i}>0,\\ {}\begin{array}{cc}{k}_{cryst}\left({\rho}_i-{\rho_i}^{\left(\mathit{\max}\right)}\right),& {\rho}_i>{\rho_i}^{\left(\mathit{\max}\right)}\end{array}\end{array}\right. $$
(30)

where ρ i (max) is a maximum solubility, k cryst is the rate of sedimentation if the concentration exceeds the maximum solubility, k sol is the rate at which the sediment dissolves if the concentration is less than the maximum solubility and there is some sediment present, and a simplified Noyes - Whitney equation (Dokoumetzidis and Macheras 2006) was assumed. The fact that function \( {C}_{\rho_i\rightleftharpoons {\rho}_{C_i}}\left({\rho}_i,{\rho}_{C_i}\right) \) is a discontinuous function results in significant difficulties in numerical simulations. The major one is that the solver engine will routinely overshoot when approaching zero and will calculate some concentrations as negative. While Filippov’s continuation (Filippov 1988) could be used to remedy the situation, it will require creating some artificial constraints for non-physical negative concentrations. A simpler solution is to smooth out the function \( {C}_{\rho_i\rightleftharpoons {\rho}_{C_i}}\left({\rho}_i,{\rho}_{C_i}\right) \) near discontinuities and also wrap all concentrations into Heaviside theta functions to ensure that unphysical negative concentrations (if they occurred due to the solver’s overshooting) will be treated as zeros. While the solution method then becomes stable and does not produce unphysical results, it also slows down very significantly. Therefore, we compare the simplified model described by Eq. (27) and the more realistic model described by Eqs. (29) and (30) for the models with peptides up to length three and use only simplified equations for the models with peptides up to length five.

Classes of Considered Models

Table 1 below contains classification of the models, which we considered.

Table 1 Classes of considered models
Full size table

where column Max Peptide Length contains the maximum length of the peptides allowed in the model, column Activation indicates whether activation was considered or not, column Catalysis contains types of considered catalytic synthesis of amino acids (No – no catalytic synthesis, NE – catalytic synthesis is not enantioselective γ+ = γ− = 0, WE – catalytic synthesis is weakly enantioselective: 0 < |γ+| = |γ−| = δ γ  ≪ 1) column APED indicates whether the model is APED-like, and column Sedimentation contains type of sedimentation considered (No uses no sedimentation, Noyes – Whitney uses Eqs. (29) and (30) and Simplified uses Eq. (27)).

Solution Method

The solution method is as follows. First, we choose a class of model from Table 1. Then for each combination of the catalyst and insoluble pair we generate a system of ordinary differential equations which describes such a model. The initial conditions were set to have slightly larger amounts of left amino acids in the system. Then the system of ordinary differential equations was solved for some period of time (t = 105) and we recorded the final enantiomeric excess η.

The algorithm was written in Wolfram and it runs under Mathematica 10 or above. The source code is provided under GNU GPLv3 license or any later version (GNU General Public License 2007) and is available on GitHub at https://github.com/kkkmail/CLM/.

Symmetry Breaking in the Models with Peptides up to Length 5, Catalytic Synthesis of Amino Acids and Simplified Sedimentation

We first start with the models with peptide length up to five with or without activation and simplified sedimentation. These models are described by lines one and two of Table 1. We study the models with catalytic synthesis in three steps. First, we consider the models, in which catalytic synthesis is completely turned off, then we add catalytic synthesis, which has no enantioselectivity γ+ = γ− = 0 for exactly one pair of enantiomers, and then we study the models with weak forward enantioselectivity of catalytic synthesis: γ+ =  − γ− =  ± δ γ (δ γ  > 0). The value γ+ = δ γ corresponds to the slightly positively enantioselective forward reaction Y + C → A + C and the value γ+ =  − δ γ corresponds to the slightly positively enantioselective forward reaction \( Y+\widehat{E}(C)\to A+\widehat{E}(C) \). Therefore, there are a total of 62 possible catalysts for the peptides of length up to five.

We considered that exactly two substances (and their enantiomers) form insoluble substances. Given two substances F and G and their enantiomers the following distinct cases are possible. We can choose either pairs F + G and \( \widehat{E}(F)+\widehat{E}(G) \) or pairs \( F+\widehat{E}(G) \) and \( \widehat{E}(F)+G \) as insoluble. Even though there are 62 × 62 = 3844 pairs, there are only 992 possible unordered distinct pairs for peptides of length up to five. Therefore, all possible combinations of catalysts and pairs form a 62 × 992 matrix. We will call the models with no sedimentation and no catalytic synthesis as base models.

As mentioned earlier, the distribution of concentration of peptides by length for all base models forms a geometric progression with some scale factor, which we denote as ρ 1, and some common ratio, which we denote as α. It is difficult to directly compare the models without activation (NA) and with activation (A) because they have some differences in the equations. In particular, given the chosen coefficients of activation and deactivation, most of the amino acids in the considered models with activation are in an activated state (A ∗). Nevertheless, if we add a concentration of not-activated and activated molecules then the geometric progression still holds. In order to compare such models, we chose to adjust coefficients ρ 0 and Λ− for relevant models with activation, so that the base models with and without activation have the same values of ρ 1 and α. Table 2 summarizes the values of Λ+, Λ−, and ρ 0, which we considered, as well as the resulting values of ρ 1 and α. The model name was introduced for convenience and is used in subsequent results.

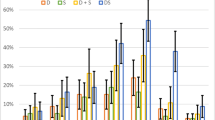
Table 2 Considered values of Λ +, Λ −, ρ 0, ρ A0, and α
Full size table

The base model NA030 has a larger common ratio (α = 0.788) than model NA100 (α = 0.519). As the total concentration is the same for both models, this results in model NA030 having a larger concentration of peptides at length 4 and 5, approximately the same at length 3, and a smaller concentration at lengths 1 and 2 in comparison to model NA100. This is illustrated on Fig. 1. Therefore, the influence of longer peptides should increase and the influence of shorter peptides should decrease in model NA030 in comparison to model NA100. Similar results should be expected in comparing models A100 and A044. Nevertheless, it is important to note that such an adjustment introduced some extra matter into the systems described by models A100 and A044 and, therefore, this may affect some output values of these models.

Fig. 1
figure 1

Total concentration of peptides of different length for the models NA100 and NA030

Full size image

There is still some ambiguity left in comparing models with different common ratios of geometric progression while limiting the length of considered peptides up to 5. The problem is that by limiting our consideration to peptides of length 5 we effectively cut the tail of longer peptides. If the common ratio is larger, then the ignored tail is bigger. Therefore, it could be argued that the models NA030 and A044 have a larger effective total concentration ρ 0 if it were adjusted for that missing tail.

Taking into account that the models that we considered are symmetric under permutation of the elements of the pairs that form a sediment, all models with sedimentation and no catalytic synthesis can be described either by 62 × 62 matrix of values of output enantiomeric excess η for each combination of two possible peptides, which form insoluble pairs in the model, or by 1 × 992 column if only unique variants are considered. Similarly, the models with sedimentation and catalytic synthesis can be described either by a 62 × 62 × 62 cube of values of output enantiomeric excess η for each combination of a catalyst and an insoluble pair or by a 62 × 992 matrix if only unique insoluble pairs are considered.

Symmetry Breaking without Catalytic Synthesis

We start from the analysis of the results of the models with sedimentation and no catalytic synthesis. All non-zero results are summarized in Table 3. The table utilizes 3-color gradient color coding (red-yellow-green) to assist in identifying the pairs that result in a substantial symmetry breaking: the greener is the cell, the larger is the output enantiomeric excess and subsequently the redder is the sell, the lower is the output enantiomeric excess. Yellow cells mark pairs with intermediate enantiomeric excess output and white cells correspond to the pairs that produce no symmetry breaking at all.

Table 3 Enantiomeric excess in the absence of catalytic synthesis
Full size table

There are several interesting facts that can be observed from that table:

  1. 1.

    Total number of left enantiomers is never equal to total number of right enantiomers in the pairs that produce symmetry breaking. This is subtle but very crucial. It is due to the following fact. Consider two peptides, P 1 and P 2, which form insoluble pairs, and which have symmetric state concentrations:

$$ \rho \left({P}_1\right)=\rho \left(\widehat{E}\left({P}_1\right)\right)=\frac{\theta_1}{2},\kern0.5em \rho \left({P}_2\right)=\rho \left(\widehat{E}\left({P}_2\right)\right)=\frac{\theta_2}{2} $$
(31)

and consider that total numbers of left and right amino acids in P 1 and P 2 are:

$$ {N}_A^{tot}=\sum \limits_{s=1,2}{n}_A(s),\kern0.5em {N}_a^{tot}=\sum \limits_{s=1,2}{n}_a(s) $$
(32)

where n A (s) is a number of left amino acids in a given substance s, n a (s) is a number of right amino acids in a given substance s. And then consider a variation:

$$ {\displaystyle \begin{array}{cc}\kern1.00em \rho \left({P}_1\right)\to \frac{\theta_1+{\varDelta}_1}{2},\kern1.00em & \kern1.00em \rho \left(\hat{E}\left({P}_1\right)\right)\to \frac{\theta_1-{\varDelta}_1}{2}\kern1.00em \\ {}\kern1.00em \rho \left({P}_2\right)\to \frac{\theta_2+{\varDelta}_2}{2},\kern1.00em & \kern1.00em \rho \left(\hat{E}\left({P}_2\right)\right)\to \frac{\theta_2-{\varDelta}_2}{2}\kern1.00em \end{array}} $$
(33)

The variation in the difference between the number of left and right amino acids turns out to be proportional to \( \left({N}_A^{tot}-{N}_a^{tot}\right) \) and, therefore, when this quantity is zero, symmetry breaking cannot possibly occur in the considered models.

  1. 2.

    Minimum total combined length of pairs, which produce symmetry breaking, is 5, for example, AA + Aaa. There are no pairs consisting of peptides of length one or two, and which could result in chiral symmetry breaking in the absence of catalytic synthesis. There are very interesting pairs at length 3 (AA + Aaa, AA + aAa, AA + aaA), which result in substantial enantiomeric excess both for models with and without activation. Similar pairs appear at length 4 (AAA + aaaA, AAA + aaAa, AAA + aAaa, AAA + Aaaa) and length 5 (AA + aaaAA, AA + aaAaA, AA + aaAAa, AA + aAaaA, AA + aAaAa, AA + aAAaa, AA + AaaaA, AA + AaaAa, AA + AaAaa, AA + AAaaa).

  2. 3.

    It is then interesting to look in more details at the shortest possible combinations, which produce the symmetry breaking: AA + Aaa, AA + aAa, AA + aaA. They all share the same property: a “perfect”; dipeptide (AA) “eliminates” a “non-perfect” tri-peptide of “competing” amino acid (Aaa, aAa, aaA). Such dipeptides are routinely used for chiral resolution on a commercial scale.

  3. 4.

    The question then becomes why shorter pair combinations don’t work. The models with peptides with length up to two can be considered analytically. Consider, for example, a model with the following insoluble pair: A + Aa. Using θ X and Δ X variables and performing a variation around the fixed point, the following matrix of coefficients can be obtained for Δ A , Δ AA , Δ Aa :

$$ M=\left(\begin{array}{ccc}-\frac{\theta_A{\varLambda}_{+}\left(5{\varepsilon}_{-}{\theta}_A+8{\varLambda}_{-}\right)}{4\left({\varepsilon}_{-}{\theta}_A+2{\varLambda}_{-}\right)}& {\varLambda}_{-}& -\frac{\varepsilon_{-}{\theta}_A}{2}\\ {}\frac{\theta_A{\varLambda}_{+}}{2}& -\frac{\varLambda_{-}}{2}& \kern0.84em 0\\ {}-\frac{\varepsilon_{-}{\theta}_A^2{\varLambda}_{+}}{4\left({\varepsilon}_{-}{\theta}_A+2{\varLambda}_{-}\right)}& \kern0.36em 0& -\frac{\varepsilon_{-}{\theta}_A+2{\varLambda}_{-}}{4}\end{array}\right) $$
(34)

Performing analysis of the roots of characteristic equation, it is straightforward to show that all roots have negative real part for any values of parameters and, therefore, no symmetry breaking can occur in such model.

  1. 5.

    Models NA100 and A100 have much less possible insoluble pairs which can produce a symmetry breaking without any catalytic synthesis, in comparison to models NA030 and A044. This is due to the fact that models NA030 and A044 have larger concentrations of longer peptides and, therefore, longer peptides can have larger possible contribution to the symmetry breaking in these models.

  2. 6.

    It appears that model A100 has more possible pairs, which produce a symmetry breaking in the absence of any catalytic synthesis, than model NA100. Similarly, model A044 seems to have more possible pairs, which produce such symmetry breaking in comparison to model NA030. While it might be tempting to say that models with activation can produce symmetry breaking for the larger number of possible pairs, this discrepancy could be attributed to the higher total concentration ρ 0 in models A100 and A044 in comparison to models NA100 and NA030.

  3. 7.

    Models without activation (NA100, NA030) are invariant to inversion transformation: the values of the output enantiomeric excess for the pairs F + G and \( \widehat{I}(F)+\widehat{I}(G) \) are the same. On the opposite side, models with activation are not invariant to inversion transformation. As a result, the values of output enantiomeric excess may be different for the pairs F + G and \( \widehat{I}(F)+\widehat{I}(G) \).

  4. 8.

    The models with and without activation are nearly identical if sedimentation occurs at peptide length no more than 3. However, as the length of the peptides increases, the models with activation start to differ more and more from the models without activation. Again, this should be attributed to the invariance / non-invariance of the equations to the inversion transformation for models without / with activation.

Symmetry Breaking in the Presence of Weakly Enantioselective Forward Catalytic Synthesis

We now “turn on” slightly enantioselective forward catalytic synthesis and compare the differences with the models without any catalytic synthesis. In particular, we are interested if there are any insoluble pairs which will result in significant symmetry breaking in the presence of catalytic synthesis but did not work without it.

If forward catalytic synthesis is not enantioselective at all (γ+ = γ− = 0) then it mostly does not result in any additional pairs, which can result in symmetry breaking. There are a few pairs, which produce weak output enantioselectivity: AA + AaaA, Aaaa + aAAAa, and AAAa + AaaaA. Only the first pair (AA + AaaA) produces a reasonably large output of enantiomeric excess (η = 0.36–0.46) for some catalysts and some models and the other two produce an insignificant output of enantiomeric excess. We do not consider models with non-enantioselective forward catalytic synthesis further, as they do not produce significant chiral symmetry breaking beyond what is produced by the models without catalytic synthesis. Some catalysts may actually work against symmetry breaking and therefore some combinations do not produce symmetry breaking in the presence of catalysts in comparison to models without catalytic synthesis.

If forward catalysis is weakly enantioselective (γ+ ≠ 0, but, as mentioned earlier, γ+ + γ− ≡ 0) then additional variants of symmetry breaking occur in comparison to base models. The first question is what happens with the pairs that produced symmetry breaking without any catalytic synthesis, as specified in Table 3. It turns out that the “strong” pairs, which produce substantial symmetry breaking, are mostly unaffected by the catalysts, even by the ones that inhibit symmetry breaking rather than amplify it. We will not consider that in details as it does not add anything interesting to the results described above. Much more interesting question is if there are pairs, which did not produce a symmetry breaking without catalytic synthesis but produce it in its presence. The number of combinations where this happens is still quite large. Therefore, we only look at a subset where enantiomeric excess η ≥ 0.6 and the number of catalysts, which works for at least one of the models, is also sufficiently large. Given that only 31 catalyst at maximum can potentially increase the symmetry breaking (the remaining 31 are their enantiomers and, therefore, they inhibit the symmetry breaking), we only looked at combinations where at least half of potential catalysts (15 or more) could work for at least one of the models. Table 4 shows all such pairs along with the number of catalysts that work for a particular model / pair combination. This table also utilizes 3-color gradient color coding (red-yellow-green) to assist in identifying the pairs that work with a substantial number of catalysts: the greener is the cell, the larger is the number of catalysts, which produce symmetry breaking, and subsequently the redder is the sell, the smaller is the number of such catalysts. Yellow cells mark pairs with intermediate number of catalysts and white cells correspond to the pairs that produce no symmetry breaking at all for any catalysts.

Table 4 Number of catalysts producing symmetry breaking with η ≥ 0.6
Full size table

The results are very interesting (some of them are not possible to show in the table above but follow from the analysis of all data):

  1. 1.

    Out of 104 pairs in Table 4, 89 have equal total number of right and left amino acids. Such pairs cannot possibly produce symmetry breaking without catalytic synthesis, as discussed above. What happens is that the catalyst is responsible for symmetry breaking in such models and sedimentation “assists” the catalyst by eliminating either the “competing” catalyst directly or some peptides, from which it could be assembled.

  2. 2.

    All catalysts, which work with a substantial number of insoluble pairs for models without and with activation, share the same property. They have either zero or one amino acid of the opposite chirality: A, aA, Aa, AA, aAA, AaA, Aaa, AAA, aAAA, AaAA, AAaA, AAAa, AAAA, aAAAA, AaAAA, AAaAA, AAAaA, AAAAa, AAAAA.

  3. 3.

    The catalysts with length 1 and 2 work only with a very limited number of possible insoluble pairs.

  4. 4.

    The catalysts with length 3 to 5 work almost with the same pairs for the models without activation. The catalysts with length 3 work with a slightly smaller number of pairs for the models with activation.

  5. 5.

    All the models considered in the current article are far from equilibrium. Given that considered models enforce a unidirectional flow of matter, this effectively “turns off” the effect of enantioselectivity of reverse catalysis. Subsequently it is only the value of γ+ that affects symmetry breaking, whereas models in thermodynamic equilibrium are governed by the value of total enantioselectivity γ = (γ+ + γ−) ≡ 0 for catalytic models.

Symmetry Breaking in Epimerization Based Models

The models based on activation, polymerization, epimerization, depolymerization cycle and peptides up to length 2 (APED-2) (Plasson et al. 2004, 2007; Weissbuch et al. 2005; Brandenburg et al. 2007) are based on the following set of reactions:

$$ {\displaystyle \begin{array}{cccc}A\to {A}^{\ast },& a\to {a}^{\ast },& {A}^{\ast}\to A,& {a}^{\ast}\to a\\ {}{A}^{\ast }+A\to AA,& {A}^{\ast }+a\to Aa& {a}^{\ast }+A\to aA,& {a}^{\ast }+a\to aa\\ {} AA\to a\to, & Aa\to aa,& aA\to AA,& aa\to Aa\\ {} AA\to A+A,& Aa\to A+a,& aA\to a+A,& aa\to a+a\end{array}} $$
(35)

where A and a are left and right enantiomers of some amino acid and A ∗ and a ∗ are activated amino acids. The APED-2 model utilizes parameters α, β, and γ to measure enantioselectivity of polymerization, depolymerization, and epimerization correspondingly:

$$ a=\frac{k\left({A}^{\ast }+a\to Aa\right)}{k\left({A}^{\ast }+A\to AA\right)},\kern0.5em \beta =\frac{k\left( Aa\to A+a\right)}{k\left( AA\to A+A\right)},\kern0.5em \gamma =\frac{k\left( AA\to aA\right)}{k\left( Aa\to aa\right)} $$
(36)

In order to compare the APED-2 model with the APED-like model for peptides up to length three (APED-3) we need to express both models using the same parameters. Starting from the APED-2 model and transforming to θ X , and Δ X variables, it is straightforward to obtain the system of equations for a reduced system:

$$ \left\{\begin{array}{c}{\rho}_Y+{\theta}_A+{\theta}_{A^{\ast }}+2\left({\theta}_{Aa}+{\theta}_{AA}\right)=0\\ {}a{\theta}_A-\frac{1}{2}\left(2b+p\left(1+\alpha \right){\theta}_A\right){\theta}_{A^{\ast }}=0\\ {}\frac{1}{2}\left(2e{\theta}_{Aa}-2\left(h+ e\gamma \right){\theta}_{AA}+p{\theta}_A{\theta}_{A\ast}\right)=0\\ {}\frac{1}{2}\left(-2\left(e+ h\beta \right){\theta}_{Aa}+2e{\gamma \theta}_{AA}+ pa{\theta}_A{\theta}_{A\ast}\right)=0\end{array}\right. $$
(37)

where a = k(A → A ∗), b = k(A ∗ → A), e = k(Aa → aa), h = k(AA → A + A), and p = k(A ∗ + A → AA) are parameters of the APED model. The equations are linear in ρ Y , θ A , θ Aa , and θ AA . Therefore, they can be solved to express these variables via \( {\theta}_{A^{\ast }} \):

$$ {\theta}_A=\frac{2b{\theta}_{A^{\ast }}}{C_2},\kern0.5em {\theta}_{AA}=\frac{bpD{\theta_{A^{\ast}}}^2}{hBC_2},\kern0.5em {\theta}_{Aa}=\frac{bpE{\theta_{A^{\ast}}}^2}{hBC_2}, $$
(38)

where:

$$ {\displaystyle \begin{array}{c}B=e\left(1+\beta \gamma \right)+ h\beta \\ {}{C}_2=2a-\left(1+\alpha \right)p{\theta}_{A^{\ast }}\\ {}D=e\left(1+\alpha \right)+ h\beta \\ {}E= h\alpha +e\left(1+\alpha \right)\gamma \end{array}} $$
(39)

Condition C 2 > 0 imposes a constraint on the maximum possible value of dimensionless quantity \( \epsilon =\left(\frac{p\ {\theta}_{A^{\ast }}}{a}\right) \) in such a system:

$$ {\epsilon}^{max}={\left(\frac{p\ {\theta}_{A^{\ast }}}{a}\right)}^{max}=\frac{2}{\left(1+\alpha \right)} $$
(40)

Linearizing near the fixed point of a reduced system produces the following 4 × 4 matrix M of coefficients of small variations \( {\Delta}_A=\left({\Delta}_A,{\Delta}_{A^{\ast }},{\Delta}_{AA},{\Delta}_{Aa}\right) \) around the fixed point:

$$ M=\left(\begin{array}{cccc}-a-\frac{1}{2}p\left(1+\alpha \right){\theta}_{A^{\ast }}& b-\frac{1}{2}p\left(1-\alpha \right){\theta}_A& 2h& 0\\ {}a-\frac{1}{2}p\left(1-\alpha \right){\theta}_{A^{\ast }}& -b-\frac{1}{2}p\left(1+\alpha \right){\theta}_A& 0& 0\\ {}\frac{p{\theta}_{A^{\ast }}}{2}& \frac{p{\theta}_A}{2}& -h- e\gamma & -e\\ {}-\frac{1}{2}p{\alpha \theta}_{A^{\ast }}& \frac{p{\alpha \theta}_A}{2}& - e\gamma & -e- h\beta \end{array}\right) $$
(41)

We only need the determinant of matrix M to determine the boundary conditions for α, β, and γ. The boundary is determined when the value of the determinant crosses zero. The following equation describes the boundary:

$$ \beta\ \gamma =\frac{\left(1-\alpha \right)p{\theta}_{A^{\ast }}}{4a-\left(1-\alpha \right)p{\theta}_{A^{\ast }}}\equiv \frac{\alpha \left(1-\alpha \right)}{p\left(1+3\alpha \right)+\left(\frac{b}{p{\theta}_A}\right)} $$
(42)

The case when there is no enantioselectivity in the APED-2 model corresponds to values α = β = γ = 1. For the values β = γ, the maximum value of (β γ) is reached at \( \alpha =\beta =\gamma =\frac{1}{3} \). The reported experimental value α ≈ 0.35 (Plasson 2003) for some amino acids is close to the optimal and estimated value for γ ≈ 0.3 interestingly points to a systematic shift (Plasson et al. 2004; Saint-Martin and Julg 1991). However, there seems to be no solid experimental data on the value of parameter β. Therefore, fine-tuning in APED-like models may also require specific values of enantioselectivity of polymerization, epimerization, and depolymerization reactions.

If the number of amino acids is very large, then instead of, for example, reaction A ∗ + A → AA we will have many reactions like A ∗ + B → AB where B is any of the available in the solution amino acids. We can therefore view the enantioselectivity of polymerization:

$$ {\tilde{\lambda}}_{A,B}^{+}=\frac{1}{4}\left(\frac{k\left({A}^{\ast }+B\to AB\ \right)}{k\left({A}^{\ast }+b\to Ab\right)}-\frac{k\left({A}^{\ast }+b\to Ab\right)}{k\left({A}^{\ast }+B\to AB\ \right)}\right) $$
(43)

as a function of two discrete variables, A and B. Consider first \( {\tilde{\lambda}}_{A,A}^{+} \). Measured for some amino acids value of α ≈ 0.35 corresponds to a value of \( {\tilde{\lambda}}_{A,A}^{+}\approx 0.63 \), which is far enough from zero. Consider now some amino acid A, for which \( {\tilde{\lambda}}_{A,A}^{+} \) has appropriate for APED value and consider what are the values of \( {\tilde{\lambda}}_{A,B}^{+} \) when we look at many different B values. Two extreme cases are as follows. In one case, the value of \( {\tilde{\lambda}}_{A,B}^{+} \) depends solely on A amino acid. In this case weighted averaging over B does not change the effective averaged value of \( {\tilde{\lambda}}_{A,B}^{+} \) and it will be equal to \( {\tilde{\lambda}}_{A,A}^{+} \). Thus, an APED-like model may result in the symmetry breaking for amino acid A in this case. In another case the value of \( {\tilde{\lambda}}_{A,B}^{+} \) depends solely on B amino acid (values of \( {\tilde{\lambda}}_{B,B}^{+} \) for all B). In this case weighted averaging over B will produce a value, which is close to the mean value of distribution of \( {\tilde{\lambda}}_{B,B}^{+} \). Therefore, if the mean is close to zero, then an APED-like model will not work in this case. The same considerations apply to epimerization and depolymerization. Therefore, experimental measurements of enantioselectivity of polymerization, epimerization, and depolymerization of a large number of pairs of amino acids are needed in order to make a conclusion on applicability of APED-like models to chiral symmetry breaking in complex chemical systems.

We now consider the APED-3 model. Similar to the APED-2, we consider that interconversion between A and a enantiomers occurs only on N-terminal residue of the peptides (Plasson et al. 2004) and therefore the following epimerization reactions are included in APED-3 model:

$$ {\displaystyle \begin{array}{cc} AA\rightleftharpoons aA,& aa\rightleftharpoons Aa\\ {} AA A\rightleftharpoons aA A,& aa a\rightleftharpoons Aa a\\ {} AA a\rightleftharpoons aA a,& aa A\rightleftharpoons Aa A\end{array}} $$
(44)

The equations in θ variables for a reduced system in the APED-3 model and expressed in APED-model parameters (Eq. (36)) are as follows:

$$ \left\{\begin{array}{c}{\theta}_A+{\theta}_{A^{\ast }}+2\left({\theta}_{Aa}+{\theta}_{AA}\right)+3\left({\theta}_{Aa a}+{\theta}_{Aa A}+{\theta}_{AA a}+{\theta}_{AA A}\right)={\rho}^{tot}\\ {}-{\alpha \theta}_A+\left(\frac{p\left(1+\alpha \right){\theta}_A}{2}\right){\theta}_{A^{\ast }}+h\left(2{\theta}_{Aa}+\beta \left(2{\theta}_{Aa}+{\theta}_{Aa a}+{\theta}_{Aa A}\right)+{\theta}_{AA a}+{\theta}_{AA A}\right)=0\\ {}{\alpha \theta}_A-{\theta}_{A^{\ast }}\left(b+\frac{p\left(1+\alpha \right)\left({\theta}_A+{\theta}_{Aa}+{\theta}_{AA}\right)}{2}\right)=0\\ {}\frac{p{\theta}_{A^{\ast }}\left({\theta}_A-\left(1+\alpha \right){\theta}_{AA}\right)}{2}+e\left({\theta}_{Aa}-{\gamma \theta}_{AA}\right)+h\left({\beta \theta}_{Aa a}+{\theta}_{AA A}-{\theta}_{AA}\right)=0\\ {}\frac{p{\theta}_{A^{\ast }}\left({\alpha \theta}_A-\left(1+\alpha \right){\theta}_{Aa}\right)}{2}+e\left({\gamma \theta}_{AA}-{\theta}_{Aa}\right)+h\left({\beta \theta}_{Aa A}+{\theta}_{AA a}-{\theta}_{Aa}\right)=0\\ {}\frac{p{\theta}_{A^{\ast }}{\theta}_{AA}}{2}+e{\theta}_{Aa a}-h{\theta}_{AA A}-e{\gamma \theta}_{AA A}=0\\ {}\frac{p{\theta}_{A^{\ast }}{\theta}_{Aa}}{2}+e{\theta}_{Aa A}-h{\theta}_{AA a}-e{\gamma \theta}_{AA a}=0\\ {}\frac{p{\alpha \theta}_{A^{\ast }}{\theta}_{Aa}}{2}+e{\theta}_{Aa A}-h{\beta \theta}_{Aa A}+e{\gamma \theta}_{AA a}=0\\ {}\frac{p{\alpha \theta}_{A^{\ast }}{\theta}_{AA}}{2}+e{\theta}_{Aa a}-h{\beta \theta}_{Aa a}+e{\gamma \theta}_{AA A}=0\end{array}\right. $$
(45)

The equations are linear in θ A , θ AA , θ Aa , θ AAA , θ AAa , θ AaA , θ Aaa and the solution is:

$$ {\displaystyle \begin{array}{c}{\theta}_A=\frac{4 bhB{\theta}_{A^{\ast }}}{C_3},\kern0.5em {\theta}_{AA}=\frac{2 bpD{\theta_{A^{\ast}}}^2}{C_3},\kern0.5em {\theta}_{Aa}=\frac{2 bpE{\theta_{A^{\ast}}}^2}{C_3},\\ {}\begin{array}{cccc}{\theta}_{AA A}=\frac{bp^2{D}^2{\theta_{A^{\ast}}}^3}{hBC_3},& {\theta}_{AA a}=\frac{bp^2 DE{\theta_{A^{\ast}}}^3}{hBC_3},& {\theta}_{Aa A}=\frac{bp^2{E}^2{\theta_{A^{\ast}}}^3}{hBC_3},& {\theta}_{Aa a}=\frac{bp^2 DE{\theta_{A^{\ast}}}^3}{hBC_3}\end{array}\end{array}} $$
(46)

where:

$$ {\displaystyle \begin{array}{c}B=e\left(1+\beta \gamma \right)+ h\beta \\ {}{C}_3=4\alpha hB-p\left(1+\alpha \right){\theta}_{A^{\ast }}\left(2h\left(e\left(1+\beta \gamma \right)+ h\beta \right)+p\left(h\left(\alpha +\beta \right)+e\left(1+\alpha \right)\left(1+\gamma \right)\right){\theta}_{A^{\ast }}\right)\\ {}D=e\left(1+\alpha \right)+ h\beta \\ {}E= h\alpha +e\left(1+\alpha \right)\gamma \end{array}} $$
(47)

Condition ρ tot → ∞ is equivalent to condition C 3 → 0 and that determines the maximum possible value of dimensionless quantity \( \epsilon =\left(\frac{p\ {\theta}_{A^{\ast }}}{a}\right) \) in such a system:

$$ {\epsilon}^{max}={\left(\frac{p\ {\theta}_{A^{\ast }}}{a}\right)}^{max}=\frac{4}{\left(1+\alpha \right)\left(1+\sqrt{1+\delta}\right)} $$
(48)

where \( \delta =\left(\frac{4a\left(D+E\right)}{hB\left(1+\alpha \right)}\right) \). The value of \( {\epsilon}^{max}\approx \frac{2}{\left(1+\alpha \right)} \) for small values of δ and ϵ max decreases \( \sim \frac{1}{\sqrt{\delta }} \) for large values of δ. Comparing this expression with a similar expression for APED-2 model (Eq. (40)), we can note that ϵ max for the APED-3 model is smaller than that for the APED-2 model by a factor of \( \left(\frac{1+\sqrt{1+\delta }}{2}\right)>1 \). Linearizing near the fixed point of a reduced system produces the following 8 × 8 matrix M of coefficients of small variations \( {\Delta}_X=\left\{{\Delta}_A,{\Delta}_{A^{\ast }},{\Delta}_{AA},{\Delta}_{Aa},{\Delta}_{AA A},{\Delta}_{AA a},{\Delta}_{Aa A},{\Delta}_{Aa a}\right\} \) around the fixed point:

$$ M=\left\{\begin{array}{cccccccc}\frac{p+{\theta}_{A^{\ast }}}{2}+\alpha & -b+\frac{p-{\theta}_A}{2}& -2h& 0& -h& -h& - h\beta & - h\beta \\ {}\frac{p_{-}{\theta}_{A^{\ast }}}{2}-\alpha & b+\frac{p+\left({\theta}_A+{\theta}_{Aa}{\theta}_{AA}\right)}{2}& \frac{p_{-}{\theta}_{A^{\ast }}}{2}& \frac{p_{-}{\theta}_{A^{\ast }}}{2}& 0& 0& 0& 0\\ {}-\frac{p{\theta}_{A^{\ast }}}{2}& \frac{-p\left({\theta}_A\left(1-\alpha \right){\theta}_{AA}\right)}{2}& h+ e\gamma +\frac{p+{\theta}_{A^{\ast }}}{2}& e& -h& 0& 0& h\beta \\ {}\frac{p\alpha +{\theta}_{A^{\ast }}}{2}& \frac{1}{2}p\left({\theta}_{Aa}-\alpha \left({\theta}_A+{\theta}_{Aa}\right)\right)& e\gamma & e+ h\beta +\frac{p+{\theta}_{A^{\ast }}}{2}& 0& -h& h\beta & 0\\ {}0& -\frac{p{\theta}_{AA}}{2}& -\frac{p{\theta}_{A^{\ast }}}{2}& 0& h+ e\gamma & 0& 0& e\\ {}0& -\frac{p{\theta}_{Aa}}{2}& 0& -\frac{p{\theta}_{A^{\ast }}}{2}& 0& h+ e\gamma & e& 0\\ {}0& -\frac{p{\alpha \theta}_{Aa}}{2}& 0& \frac{p{\alpha \theta}_{A^{\ast }}}{2}& 0& e\gamma & e+ h\beta & 0\\ {}0& -\frac{p{\alpha \theta}_{AA}}{2}& \frac{p{\alpha \theta}_{A^{\ast }}}{2}& 0& e\gamma & 0& 0& e+ h\beta \end{array}\right\} $$
(49)

where p + = p(1 + α) and p − = p(1 − α). Similar to the APED-2 model, the boundary conditions for α, β, and γ is determined when the value of the determinant of matrix M crosses zero. However, the resulting expression for the APED-3 model is substantially more complicated than that for the APED-2 model:

$$ {\displaystyle \begin{array}{l}p{\theta}_{A^{\ast }}\left(-1+\alpha \right)\left(\alpha +\beta \gamma \right)\left(h\left(-p{\theta}_{A^{\ast }}\ast \alpha +2 h\beta +p{\theta}_{A^{\ast }}\beta \right)\right.\\ {}\begin{array}{ccc}& & \end{array}\kern1.50em +e\left.\left(-p{\theta}_{A^{\ast }}\left(1+\alpha \right)\left(-1+\gamma \right)+2\left(h+ h\beta \gamma \right)\right)\right)\left(h\left(2 h\beta +p{\theta}_{A^{\ast }}\left(\alpha +\beta \right)\right)\right.\\ {}\begin{array}{cccc}\begin{array}{ccc}& & \end{array}& & & +e\left.\left(-p{\theta}_{A^{\ast }}\left(1+\alpha \right)\left(-1+\gamma \right)+2\left(h+ h\beta \gamma \right)\right)\right)\end{array}\\ {}\begin{array}{cccc}\begin{array}{ccc}& & \end{array}& & & +4\alpha h\left(e+ h\beta + e\beta \gamma \right)\left(h\right.\end{array}p{\theta}_{A^{\ast }}\alpha \left(\alpha -\beta \right)+ h\beta \left(4 h\beta +p{\theta}_{A^{\ast }}\left(\alpha +3\beta \right)\right)\gamma \\ {}\begin{array}{cccc}\begin{array}{ccc}& & \end{array}& & & +e\left.\left(4 h\beta \gamma \left(1+\beta \gamma \right)+p{\theta}_{A^{\ast }}\left(\left(-1+\alpha \right)\alpha +\left(3+\alpha \right)\left(\alpha +\beta \right)\gamma +\left(-1+\alpha \right){\beta \gamma}^2\right)\right)\right)=0\end{array}\end{array}} $$
(50)

The equation can be solved numerically, for example, for γ as a function of α and β, and it determines the boundary, provided that the constraint \( \frac{p\ {\theta}_{A^{\ast }}}{a}\le {\epsilon}^{max} \) is satisfied. Figures 2 and 3 illustrate the values of γ for the values \( p{\theta}_{A^{\ast }}=a=e=h=1 \) for the APED-2 and the APED-3 models correspondingly.

Fig. 2
figure 2

Boundary of symmetry breaking in the APED-2 model

Full size image
Fig. 3
figure 3

Boundary of symmetry breaking in the APED-3 model

Full size image

That edge of the graph as α goes toward one on Fig. 3 illustrates the end of possible values due to violation of the \( \frac{p\ {\theta}_{A^{\ast }}}{a}\le {\epsilon}^{max} \) constraint (the value \( p{\theta}_{A^{\ast }}=1 \) cannot be achieved in the area where the graph is absent). As the Figs. 2 and 3 illustrate, the area, where the symmetry breaking can occur, shrinks in αβγ parameter space when we go from the APED-2 to the APED-3 model. In addition, the situation of weak enantioselectivity in APED models corresponds to the area near point α = β = γ = 1. Neither the APED-2, nor the APED-3 could produce a symmetry breaking near that point.

Symmetry Breaking in APED Models in the Presence of Sedimentation

According to our calculations, adding sedimentation of an insoluble pair to APED-2 and APED-3 models unfortunately did not produce any substantial extension of the symmetry breaking area toward weak enantioselectivity values for α, β, and γ. We calculated several dependencies of maximum real part of all eigenvalues of linearized matrix of coefficients for the model APED-3 near the fixed point of the system and in the presence of sedimentation of the most promising pair (AA + Aaa). That pair produces symmetry breaking with η ≈ 0.90 in model A100 without any catalytic synthesis. It appears that the combination of systems A100 and APED-3 produces symmetry breaking in some disjoint areas in the space of parameters, so that in one area the system must be like the A100 model with almost no APED-related enantioselectivity of α, β, and γ parameters and no epimerization, and in another area the system must be like the APED-3 with large enantioselectivity of α, β, and γ parameters and epimerization but indifferent to sedimentation in a certain window of sedimentation rates. We do not present the figures as they seem to provide no additional useful information.

Symmetry Breaking in the Models with Peptides up to Length 3, Catalytic Synthesis of Amino Acids, Pair Formation and Noyes – Whitney Sedimentation

We now want to consider a more realistic scenario when any pair of peptides may form a temporary (not peptide) bond as described by Eq. (29) and subsequently where some of the pairs are insoluble. We also would like to apply a more realistic reversible sedimentation process as described by Eq. (30). While it could be argued that formation of temporary pairs is proportional to collision probability and therefore the larger the peptide molecule the higher is the probability of its collision with some other peptide molecule, we did not want to take this into account in the current work. Rather we assumed that all the rates for temporary pair formations are the same. A model is fixed by assuming that a certain pair of substances is insoluble. However, following the discussion above we consider both Eqs. (27) and (28) and set the parameters so that one combination is nearly insoluble and the other has good solubility. Nevertheless, it is important to note that the more realistic model of sedimentation process where there are many substances involved is needed before more precise results can be produced.

The results are as follows. First, the pairs (up to length three), which can produce the symmetry breaking in the absence of any catalytic synthesis, in these models are the same as in the models with simplified sedimentation and peptides up to length 5 (AA + aaA, AA + aAa, AA + aaA). Second, if both Eqs. (27) and (28) are taken into account, then the symmetry breaking can occur only within a certain window of concentrations. A similar result was obtained in (Konstantinov and Konstantinova 2013) for the model with peptide length up to two. We did not want to pursue this research further in the current work because more precise model of sedimentation of solution of many substances is needed in order to produce meaningful results.

It is also important to contrast the difference between fine tuning of some chemical rate coefficients, as required in some models, and adjusting the concentrations. The rate coefficients are what they are and as such they cannot be changed. Requiring that they have some specific values for the model to operate is fine-tuning. The concentrations, on the other side, can be easily adjusted by adding or removing solvent and, therefore, there is no fine-tuning in such models. For example, a standard attrition-enhanced deracemization also has some constraints on concentrations: if we add too much solvent, then there will be no sediment at all and attrition-enhanced deracemization will not work.

Proposed Experiment

Given the calculations above, it would be interesting to devise an experiment, which would attempt to study chiral symmetry breaking along the considered models. Figure 4 shows the sketch of a proposed experiment of chiral symmetry breaking.

Fig. 4
figure 4

Layout of proposed experiment of chiral symmetry breaking

Full size image

As discussed in (Avetisov and Goldanskii 1996), the rate of non-catalytic synthesis must be small in comparison to the rate of catalytic synthesis. Otherwise, non-catalytic synthesis will substantially dampen symmetry breaking. Therefore, a one-time non-catalytic synthesis of amino acids might be necessary in order to start the cycle. There are three major blocks in the main cycle of proposed experiment.

The first step is the catalytic synthesis of amino acids with some constant inflow of achiral matter ΔY and in the presence of a mixture of various peptides, some of which may be catalysts. It is crucial that non-catalytic synthesis is severely limited on this step.

The second step is the reversible synthesis of peptides. Control parameters on this step include forward and backward reaction rates (which affect the common ratio of geometric progression in the base model) as well as whether or not activation is used. We can look at the equivalent total concentration of amino acids in peptides of length n. If we consider that the total amount of amino acids in the system is the same (ρ 0) then Λ+ and Λ− determine ρ 1 and α. The total amount of amino acids in peptides of length n is ρ n  = n ρ 1 α n and then:

$$ \sum \limits_{n=1}^{\infty }{\rho}_n=\sum \limits_{n=1}^{\infty }n\ {\rho}_1\ {\alpha}^n={\rho}_0 $$
(51)

Therefore:

$$ \frac{\rho_n}{\rho_0}=n\ {\alpha}^{n-1}\ {\left(1-\alpha \right)}^2 $$
(52)

Figure 5 shows the distribution of \( \frac{\rho_n}{\rho_0} \) for various n and α with the same color corresponding to the same value of α.

Fig. 5
figure 5

Total amount of amino acids in peptides of different length

Full size image

Following the result above, since there are no insoluble pairs, which can produce symmetry breaking for “peptides” of length one in the absence of catalytic synthesis, we can see from Fig. 5 that the maximum amount of amino acids for peptides of length two and three is in the range α ≈ 0.3 − 0.6 and for peptides with length four and five is in the range α ≈ 0.4 − 0.7. Concentrations of individual peptides are even smaller by a factor of 2−n. In addition, if there are many possible amino acids in the solution, then concentrations of individual peptides of length n further decrease by approximately ~M −n where M is the number of amino acids, which are present in the solution in substantial amounts. However, we would expect that there will be many similar pairs and catalysts with various amino acid content in that case. It is therefore our view that parameter α should first be probed experimentally in the range α ≈ 0.3 − 0.7.

The third step is sedimentation process. It is very easy to discard the sediment both from experimental and geological points of views. For example, a device with much lower temperature at the bottom may allow continuous operation of the sedimentation step of the system. In this case the bottom layer with much lower temperature could be slowly washed away whereas the ingredients from the previous step are flowing to the much warmer top layer. As discussed in (Konstantinov and Konstantinova 2013), if more than one substance can form a sediment then it is possible that there is a certain window of concentrations in which the sedimentation may work as an additional enantioselective factor. Therefore, the control parameters of this step are the factors which affect the solubility, like temperature, total amount of solvent, some additives which may affect the overall solubility, etc.

The control parameters of the feedback are the percentages of what is recycled back to the catalytic synthesis block and what is considered as output ΔP.

Conclusion

It was argued that the number of substances and possible reactions among them must have been very large on prebiotic Earth and, therefore, that resulted in effective averaging over similar reaction channels, including the reactions related to chiral symmetry breaking in amino acids. Effective averaging for catalytic synthesis of amino acids, epimerization, polymerization, depolymerization, and sedimentation was considered. It was shown that such averaging results in weak effective enantioselectivity of forward catalytic synthesis, does not affect sedimentation, and needs additional research to assess the effect on epimerization, polymerization, and depolymerization.

Classes of models with formation of peptides up to length five, catalytic synthesis of amino acids, and a pair of substances, which form an insoluble substance, were considered. The Wolfram Mathematica program, which is capable of solving an arbitrary system of homogeneous chemical equations, was created. Using the program, all the matrix of 62 possible catalysts by 992 possible unique insoluble pairs was analyzed and all combinations, which result in substantial chiral symmetry breaking in the presence of very weak enantioselectivity of catalytic synthesis, were found:

  • The models with sedimentation of insoluble pair and no catalytic synthesis require that minimum total combined length of pairs, which produce symmetry breaking, is 5, for example, AA + Aaa. Shorter pairs simply cannot work for any values of parameters.

  • The models with sedimentation of insoluble pair and no catalytic synthesis require that total number of left enantiomers is never equal to total number of right enantiomers in the pairs that produce symmetry breaking.

  • The models, which produce substantial symmetry breaking where sedimentation alone does not work, and which utilize sedimentation of insoluble pair and slightly enantioselective forward catalytic synthesis, mostly have equal total number or left and right enantiomers in the pair that form a sediment. It is important to note that the models, which worked without any catalytic synthesis, mostly continue to work in its presence. And, therefore adding slightly enantioselective catalytic synthesis increases the number of sediment forming pairs, which can result in the symmetry breaking. It was discussed that the catalyst is responsible for symmetry breaking in such models and sedimentation “assists” the catalyst by eliminating either the catalyst directly or some peptides, from which it could be assembled.

  • It was shown that catalysts, which result in significant chiral symmetry breaking in the large number of possible insoluble pair combinations, have either zero or one amino acid of the opposite chirality: A, aA, Aa, AA, aAA, AaA, Aaa, AAA, aAAA, AaAA, AAaA, AAAa, AAAA, aAAAA, AaAAA, AAaAA, AAAaA, AAAAa, AAAAA. It was shown that catalysts with length one and two work only with very limited number of possible insoluble pairs and therefore it was shown that the minimum interesting length of potential catalysts is three.

  • It was shown that the models with higher concentrations of longer peptides have more longer pairs / catalysts, which result in the symmetry breaking, in comparison to models with lower concentration of longer peptides.

  • The difference between fine tuning of some chemical rate coefficients, as required in some models, and adjusting the concentrations was discussed. It was argued that the rate coefficients are what they are and as such they cannot be changed. Requiring that they have some specific values for some model to operate is fine-tuning. The concentrations, on the other side, can be easily adjusted by adding or removing solvent and, therefore, there is no fine-tuning in such models.

  • It was shown that an increase in peptide length from two to three in models based on activation, polymerization, epimerization depolymerization (APED) cycle results in a decrease of area in parameter space where chiral symmetry breaking can occur.

An experiment of chiral symmetry breaking was proposed. The experiment consists of a three-step cycle where the first step is catalytic synthesis of amino acids, the second step is reversible synthesis of peptides, and the third step is sedimentation of substances. Control parameters of the experiments were discussed and the ranges where to probe some of the parameters were proposed.