1 Introduction

Ternary semiconducting chalcogenides are three-element materials that often include one or more chalcogens such as sulfur, selenium, or tellurium coupled with other elements, i.e., metals or metalloids (Sujith et al. 2022; Jawad et al. 2024; Azam et al. 2019). These compounds have drawn much attention because of their distinct electrical, optical, and sometimes magnetic characteristics, making them ideal choices for several technological applications (Hoang and Mahanti 2016; Mbilo and Musembi 2022; Kormath et al. 2018; McKeever et al. 2023; Shen et al. 2023; Wang et al. 2022). They are intensively researched for use in electronics, optoelectronics, and energy-related sectors like photovoltaics and thermoelectric devices. Further, each ternary chalcogenide has diverse features and possible uses, and ongoing scientific works investigate their potential in different innovative technology sectors. Among the ternary semiconducting chalcogenides, the family with the formula A2BX3 (A = Li, Na, K, Rb, Cs, and Cu with 1 + cation; B = Ti, Zr, C, Si, Ge, Sn, Pb with 4+ cation and X = O, S and Se with 2-anion) has become especially popular during the past half-decade due to their switchable polarizations like solid-state ferroelectrics and antiferroelectrics which make them functional materials for recent solar energy applications (Gorai et al. 2019; Khan et al. 2022). On the other hand, although several experimental and theoretical works were overlooked for the diverse physical viewpoints of A2BX3 ternary sulfur chalcogens, e.g., Na2CS3, Cu2SiS3, K2TiS3 (Bennett 2020) and Cs2ZrS3, Rb2ZrS3 (Khan et al. 2022), there is still not any theoretical work reported for the Rb2XS3 (X = Si, Ge, Sn) ternary sulfur chalcogens. Therefore, in this work, we have performed DFT calculations not only to answer the questionable electronic, elastic, mechanical, phonon, and optic features of Rb2XS3 (X = Si, Ge, Sn) compounds but also contribute to the future experimental and theoretical literature of these technologically crucial ternary sulfur chalcogens.

2 Computational concept

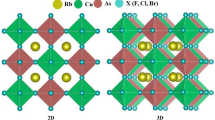
CASTEP plane-wave DFT code was handled (Clark et al. 2005; Segall et al. 2002, 1996) for all computations. Figure 1a–c indicates the crystal views of presently examined Rb2XS3 (X = Si, Ge, Sn) chalcogens under the symmetry of C2/M (C2H-3) with accompanying space group number 12. Further, Table 1. lists the lattice information of Rb2XS3 (X = Si, Ge, Sn) compounds with existing literature results. The generalized-gradient approximation (GGA) of DFT within the Perdew-Burke-Ernzerhof (PBE) exchange correlation was applied carefully (Perdew et al. 1996, 1998). A robust BFGS optimization algorithm (Güler and Güler 2013) was effectually applied to the alloys to reduce the constraints of geometry optimization procedures. For the electron–ion interactions of the studied compounds, OTFG-norm conserving pseudopotentials (Lejaeghere et al. 2013) were selected within Rb: [5s1], Si: [3s23p2], Ge: [3d104s24p2], Sn: [4d105s25p2] and S: [3s2 3p4] the pseudo atomic configurations. The limit for energy cut-off was 600 eV for all compounds. Also, sampling of the Brillouin zone was done with the Monkhorst–Pack standard (Monkhorst and Pack 1976) with 3 × 5 × 4 k points. The converged energy limit was 5 × 10–6 eV/atom, whereas the maximum Hellmann–Feynman force value was kept at 0.01 eV/Å with an SCF tolerance of 5 × 10–6 eV/atom. During computations, displacements between the atoms were set to be 5 × 10−4 Å, where the atoms were exposed 0.02 GPa to external stress values. To resolve the optical characteristics, the highest incident energy was counted as 25 eV, which covers the infrared region (IR < 1.59 eV), visible (1.65–3.26 eV) scale, and the ultraviolet fragments (~ 4–123 eV) of the entire electromagnetic spectrum under [100] polarization vector. Dynamical stabilities were enlightened from the phonon dispersions of each compound from the linear response method, where elastic constants calculations were derived from the stress–strain method implemented in the CASTEP (Clark et al. 2005; Segall et al. 2002, 1996).

Fig. 1
figure 1

Crystal views of Rb2SiS3 (a), Rb2GeS3 (b), and Rb2SnS3 (c) along with the y-axis

Full size image
Table 1 Lattice information of Rb2XS3 (X = Si, Ge, Sn)
Full size table

3 Results and discussion

3.1 Comparing the electronic bands of Rb2XS3 (X = Si, Ge, Sn) compounds

Figures 2, 3, and 4 portray each computed electronic band structure of Rb2XS3 (X = Si, Ge, Sn) compounds, with matching total density of states (TDOS) and partial density of states (PDOS) distributions, respectively. As is feasible within all band plots, Rb2XS3 (X = Si, Ge, Sn) compounds forbidden energy band gap formations peculiar to the semiconductors arise amongst the top edge of the valance bands (VB) and the bottom edge of the conduction bands (CB) of the considered compounds. Again, from Figs. 2, 3, and 4, all the band gaps display a direct nature where their values hold at 2.806 eV for Rb2SiS3, 2.206 eV for Rb2GeS3, and 2.156 eV for Rb2SnS3, around Fermi energy (EF) levels those set to zero. In other words, the direct band gap order of Rb2XS3 (X = Si, Ge, Sn) compounds follows the Rb2SiS3 > Rb2GeS3 > Rb2SnS3 range. Further, all PDOS curves for each Rb2XS3 (X = Si, Ge, Sn) compound suggest the dominant contributions of the p-orbitals to the existing semiconducting behavior of these compounds where the p orbital of Rb2SnS3 has the highest contribution compared to Rb2SiS3 and Rb2GeS3.

Fig. 2
figure 2

Electronic band structure, total density of states, and partial density of state of Rb2SiS3

Full size image
Fig. 3
figure 3

Electronic band structure, total density of states, and partial density of state of Rb2GeS3

Full size image
Fig. 4
figure 4

Electronic band structure, total density of states, and partial density of state of Rb2SnS3

Full size image

3.2 Computed optical parameters for Rb2XS3 (X = Si, Ge, Sn) compounds

For recent technology, comprehensive evaluation of the optical properties is significant to produce novel optoelectronic devices. So, we concentrated on several distinct optical features of the examined compounds, i.e., optical absorptions, reflections, dielectric constants, refractions, photo conductivities, and loss functions. By the way, if a material is exposed to an outer energy of incident photons, the optical response of this material can be ascertained from the frequency-dependent Kramers–Kronig rule of ε(ω) = ε1(ω) + iε2(ω). Here, ε1(ω) indicates the real part (Re) that is sensible to energy storages, and iε2(ω) denotes the imaginary part (Im) of the complex dielectric function ε(ω) associated with the energy loss (Uğur et al. 2022; Güler et al. 2021a, 2021b, 2021c, 2023a). Also, the Kramers–Kronig rule allows us to attain other critical optical factors, i.e., optical absorption constants, reflection characteristics, refractivity indexes, and loss function (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a).

Figures 5, 6, and 7 demonstrate the obtained optical factors of Rb2XS3 (X = Si, Ge, Sn) compounds via the considered incident photon energy. In Fig. 5, all ε1(ω) parts of surveyed Rb2XS3 (X = Si, Ge, Sn) compounds, which also determines the refractive of these compounds, begin over the scalar magnitude 6 and are identical to each other with little peaking differences. Due to their approaching limit of high-k dielectrics (ε1(ω) > 7) and overestimating limit of low-k dielectrics (ε1(ω) < 3.9), all Rb2XS3 (X = Si, Ge, Sn) compounds can be readily considered as high-k dielectric replacement materials of recent silicon dioxide gate dielectric materials often used in modern semiconductor manufacturing and many practical fields of microelectronics (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). Also, all Im parts of Rb2XS3 (X = Si, Ge, Sn) compounds signified with ε2(ω) those cooperated to the optical absorption response initiates from zero energy values and track a similar photon energy raise, and then drop to zero energy points around 25 eV where they further stick to the unity.

Fig. 5
figure 5

Dielectric function of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image
Fig. 6
figure 6

Optical conductivity of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image
Fig. 7
figure 7

Refractive index of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image

The optical conductivity (photo-conductivity) expressed with σ (ω) signifies and implies the existence of thermal conduction in the presence of sufficient incoming photon energy (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). In Fig. 6, the Rb2XS3 (X = Si, Ge, Sn) compounds display robust optical conductivities. Also, both real (Re) and Im (imaginary) components of Rb2XS3 (X = Si, Ge, Sn) compounds show the sharpest peaks at about 8 eV incident photon energies. So, this result supports their practical uses in functional UV applications (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). In addition, refraction (n) and extinction(k) coefficients are two typical optic agents for applied optoelectronic technology. Figure 7 exhibits the (n) and (k) peaks of Rb2XS3 (X = Si, Ge, Sn) compounds deduced from: n (ω) = [(ε12+ε22)1/2 + ε1)/2]1/2 and k (ω) = [(ε12+ε22)1/2-ε1)/2]1/2. In general, materials with n > 1.5 are presumed to be high-refractors for manufacturing light-emitting diodes (LEDs) or organic light-emitting diodes (OLEDs) of contemporary optoelectronic tools. The calculated refractive indices (n) of Rb2XS3 (X = Si, Ge, Sn) compounds in Fig. 7, are over the value of 2 and lie through the IR segment of the whole energy scale. Thus, Rb2XS3 (X = Si, Ge, Sn) compounds can be supposed to be new high-refractor alternatives for efficient IR purposes.

Figure 8 yields the absorption plots of Rb2XS3 (X = Si, Ge, Sn) compounds extracted from the equation α(ω) = [\(\sqrt{2}\upomega \)(ε12+ε22)2−ε1)1/2]. Strong light absorptions and oppositely weak optical reflections arise in semiconductors when the incoming energy of photons exceeds the bandgap energy values of the corresponding material. (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). This trend is also valid for the studied Rb2XS3 (X = Si, Ge, Sn) compounds where the maximum absorptions for each compound remarkably emerge between 5 and 20 eV points of the UV in the range of Rb2SiS3 > Rb2GeS3 > Rb2SnS3 (Fig. 8). As another outcome, Rb2XS3 (X = Si, Ge, Sn) compounds may be regarded as capable absorbers and optical windows devices for feasible UV intents (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a).

Fig. 8
figure 8

Absorption plots of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image

Figure 9 also exposes the optical reflectance response of Rb2XS3 (X = Si, Ge, Sn) compounds concerning incident energy derived from the expression of R (ω) = [{(n-1)2 + k2/(n + 1)2 + k2}] (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). In Fig. 9, the reflection curves of Rb2XS3 (X = Si, Ge, Sn) compounds parade somewhat trivial reflectivity due to their strong absorption as described in the optical absorbance (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a).

Fig. 9
figure 9

Reflectivity of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image

The loss function parameter, acquired mostly from photon absorptions, stipulates knowledge of the energy loss of rapid inner electrons of materials (Bellil et al. 2021; Güler et al. 2021d, 2023b; Baaziz et al. 2022; Uğur et al. 2021a). The low-loss energy scales commonly occur amongst zero eV and 100 eV energy values, and characteristic sharp plasmon (joint vibrations of VB electrons) peaks exist at these energies. The loss plots in Fig. 10 depict the loss function behavior of Rb2XS3 (X = Si, Ge, Sn) compounds within the adjusted photon energy pathway. As explicit in Fig. 10, it is possible to notice some energy loss in the small-scale energies around 12 eV for all compounds. Moreover, a specific plasmon peak releases at 23 eV for Rb2SiS3, where other compounds (Rb2GeS3 and Rb2SnS3) do not show the same characteristics. However, above 25 eV, loss function peaks of all surveyed compounds slightly decline to zero energy and conclusively reach the unity.

Fig. 10
figure 10

Loss function of Rb2SiS3, Rb2GeS3 and Rb2SnS3

Full size image

3.3 Obtained phonon dispersions and stability of Rb2XS3 (X = Si, Ge, Sn) compounds

The dynamic stability of materials is a significant issue for experimental synthesis and reliable production (Mouhat and Coudert 2014; Ye et al. 2018). So, it is worth checking the dynamical stability of any new material and deciding whether it is dynamically stable or not. At this point, phonon dispersions provide valuable knowledge about the stability of the materials of concern (Güler et al. 2022a, 2023c; Uğur et al. 2021b, 2023). For this reason, phonon dispersion curves of Rb2XS3 (X = Si, Ge, Sn) compounds were also addressed as an additional part of the present work to gain a piece of prior knowledge about the dynamical natures of Rb2XS3 (X = Si, Ge, Sn) compounds. Figure 11 renders the phonon dispersion plots of Rb2XS3 (X = Si, Ge, Sn) compounds obtained during this work. As detectible in Fig. 11, all phonon dispersion curves of Rb2XS3 (X = Si, Ge, Sn) compounds have positive (above zero) and definite frequency modes proving the evident dynamical stability (Güler et al. 2022a, 2023c; Uğur et al. 2021b, 2023) of the Rb2XS3 (X = Si, Ge, Sn) compounds. In other words, the presence of none imaginary phonon frequencies strongly underlines the dynamical stability of Rb2XS3 (X = Si, Ge, Sn) compounds, and these compounds can be easily synthesized from experiments to serve as alternative novel optoelectronic materials in demanding fields of the emergent technology.

Fig. 11
figure 11

Phonon dispersions and total density of states for Rb2XS3 (X = Si, Ge, Sn)

Full size image

3.4 Elastic properties and linking mechanical data of Rb2XS3 (X = Si, Ge, Sn) compounds

Clarifying elastic and interrelated mechanic data provides an in-depth understanding of a given material and handy predictions about the elastic and mechanical nature before production (Güler et al. 2022b; Güler and Güler 2014, 2015; Benmekideche et al. 2018; Živković et al. 2019; Naceur et al. 2022). So, as a result of these former predictions, it is possible to determine whether the examined material corresponds to the desired elastic and mechanical features. Under this focus, various elastic and connected mechanical data of Rb2XS3 (X = Si, Ge, Sn) compounds were also addressed and evaluated for the present work.

Elastic stiffness constants (Cij) of materials are the most representative data of materials that decide the overall elastic and mechanical aspects of related materials. In this manner, since Rb2XS3 (X = Si, Ge, Sn) compounds monoclinic crystal structure, they yield 13 independent elastic constants due to their crystal symmetry (Güler et al. 2022b; Güler and Güler 2015, 2014; Benmekideche et al. 2018; Živković et al. 2019; Naceur et al. 2022), as readily summarized in Table 2. On the other hand, according to Born's mechanical stability norms, Cij of the monoclinic systems must fulfill the requirements like; C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0, C44C66 − 2C46 > 0, C11 + C22 + C33 + 2(C12 + C13 + C23) > 0, C22 + C33 − 2C23 > 0 (Güler et al. 2022b; Güler and Güler 2014, 2015; Benmekideche et al. 2018; Živković et al. 2019; Naceur et al. 2022). So, from a mechanical stability outlook, currently computed Rb2XS3 (X = Si, Ge, Sn) compounds perform reliable mechanical stability due to the obtained corresponding data in Table 3. Several additional mechanical parameters derived from the elastic stiffness constants were also considered. For instance, the bulk modulus (B), shear (rigidity) modulus (G), and Young modulus (E) were also reported in Table 3 with Voigt-Reuss-Hill notations. From a mechanical aspect, B represents the internal resistance of materials to external deformations, whereas G denotes the response of the materials to the shear deformations. A material's Young modulus (E) (the modulus of elasticity), on the other hand, explains the material's stiffness subjected to a deformation along an axis when opposing forces are employed by this axis (Güler et al. 2022b; Güler and Güler 2015, 2014; Benmekideche et al. 2018; Živković et al. 2019; Naceur et al. 2022). As can be noticed in Table 3. the average Hill magnitudes of the bulk moduli of Rb2XS3 (X = Si, Ge, Sn) compounds track the Rb2SiS3 > Rb2GeS3 > Rb2SnS3 order where the same order is valid for the shear moduli and Young moduli of the investigated compounds. As another mechanical aspect, brittleness and ductility hold for two distinct and fundamental mechanical characteristics, particularly for the materials production process. Notably, easily broken brittle materials cannot be deformed much compared to more deformable and hardly broken ductile materials. At this stage, the Pugh ratio (B/G) is an important indicator of whether a material is brittle or ductile (Pingak et al. 2023; Joshi et al. 2021; Senkov and Miracle 2021). If B/G > 1.75, the material is ductile; otherwise, it is brittle (Pingak et al. 2023; Joshi et al. 2021; Senkov and Miracle 2021). Again, from Table 3, since all Pugh ratio values of the Rb2XS3 (X = Si, Ge, Sn) compounds are larger than the critical limit of 1.75, it is easy to conclude that all the surveyed compounds are ductile in nature where the highest value belongs to Rb2SnS3 with 3.55. As an additional mechanical parameter, Poisson's ratio (ν) shows how the cross-section of a deformable material varies under lengthwise stretching or compression. (Shah et al. 2023; Yoo et al. 2018; Zhang et al. 2023). It can also propose precious info about the brittle or ductile abilities of the relevant materials (Pius et al. 2023; Mott and Roland 2009). For example, ν < 0. 26 signifies the brittle materials, and ν > 0. 26 indicates the ductile capacity of regarding material (Pius et al. 2023; Mott and Roland 2009). The stated ν values of Rb2XS3 (X = Si, Ge, Sn) compounds in Table 3. with 0.31, 0.32, and 0.37, once more underline the ductile performance of Rb2XS3 (X = Si, Ge, Sn) compounds and confirms mutually the presently obtained Pugh ratio results (Table 3).

Table 2 Calculated elastic constants Cij (in GPa) of Rb2XS3 (X = Si, Ge, Sn)
Full size table
Table 3 Calculated bulk modulus B (all in GPa), shear modulus G (all in GPa), Young's modulus E (all in GPa), Poisson's ratio v and the B/G ratio of Rb2XS3 (X = Si, Ge, Sn)
Full size table

On the whole, compared to former theoretical work performed only for the bandgaps of Rb2SiS3 with 2.83 eV and Rb2GeS3 with 2.33 eV (Gorai et al. 2019), our results reported in this work for the same parameters for Rb2SiS3 with 2.806 eV and Rb2GeS3 with 2.206 eV are reasonable. Remarkably, although this work addresses a complimentary outlook including elastic, phonon and mechanical parameters of Rb2XS3 (X = Si, Ge, Sn) compounds, unfortunately there is no available data reported for the elastic, phonon and mechanical properties to conduct a complete comparison.

4 Conclusions

Hitherto, unreported electronic, optical, phonon, elastic, and mechanical features of Rb2XS3 (X = Si, Ge, Sn) semiconducting chalcogen compounds were analyzed and evaluated thanks to DFT computations. The main conclusions of the work can be given point by point as in the following:

  • Obtained electronic band gaps with 2.806 eV for Rb2SiS3, 2.206 eV for Rb2GeS3 and 2.156 eV for Rb2SnS3 proves the semiconducting nature of these compounds.

  • According to presently obtained optical dielectric constants data, all Rb2XS3 (X = Si, Ge, Sn) compounds can be good alternatives as high-k dielectric replacement materials of recent silicon dioxide gate dielectrics frequently used in semiconductor technology and microelectronics.

  • High optical conductivities make Rb2XS3 (X = Si, Ge, Sn) compounds ideal candidates for functional UV applications.

  • Due to their materials with n > 1.5 are presumed to be high-refractors for manufacturing light-emitting diodes (LEDs) or organic light-emitting diodes (OLEDs) of contemporary optoelectronic tools.

  • Because of their high refractive indexes over 2 along the IR region, Rb2XS3 (X = Si, Ge, Sn) compounds can also be promising materials for manufacturing light-emitting diodes (LEDs) or organic light-emitting diodes (OLEDs) and new high-refractor alternatives of efficient IR purposes.

  • Since they have satisfactory optical absorbance characteristics, Rb2XS3 (X = Si, Ge, Sn) compounds may be regarded as capable absorbers and optical windows devices for feasible UV intents.

  • All phonon dispersions for Rb2XS3 (X = Si, Ge, Sn) compounds yield positive frequencies denoting dynamical stability, suggesting the easy experimental synthesis of compounds. In addition, thermodynamic potentials of the reactions and their kinetic parameters of Rb2XS3 (X = Si, Ge, Sn) compounds should be also considered during further experiments to concretize this theoretical foresight obtained from the present phonon dispersions.

  • Computed elastic stiffness constants prove the mechanical stability of all compounds.

  • All compounds have a ductile nature attained from the mutual agreement of Pugh ratio analyses and calculated Poisson ratio values.