1 Introduction

The study of optical wave solutions for complex nonlinear evolution equations is highly important in many areas of science, technology, and engineering (Song and Wu 2023; Ghayad et al. 2023; Gao et al. 2022; Li et al. 2023; Osman et al. 2020). The optical wave pattern of a complex nonlinear equation offers a potent tool for investigating the behavior of complex physical structures. They enable us to gain insights into the behavior of such systems and make predictions about their behavior in various situations. Additionally, these solutions can be used to guide the design of various optical systems, both for engineering and scientific purposes. For example, they can help inform the design of optical waveguides and imaging systems, as well as the design of optical components for communication, imaging, and sensing applications (Hussain et al. 2019; Nisar et al. 2021; Zhou 2022; Zhou et al. 2022; Malik et al. 2023). Furthermore, the study of optical wave solutions for complex nonlinear evolution equations can provide insights into a variety of scientific phenomena, including the evolution of optical waves in space and time and the behavior of optical systems in various environments. Finally, optical wave solutions to complex nonlinear evolution equations can be used to develop algorithms and numerical methods for solving such equations in a computationally efficient manner. These methods include the modified Hirota method (Yan and Liu 2021), modified deformation algorithm (Lou et al. 2023), bilinear method (Wang et al. 2022; Ma et al. 2021), NMSE technique (Roshid et al. 2022a), Tanh method (Roshid et al. 2021), simplest equation method (Roshid and Bashar 2019), extended direct algebraic method (Karmina et al. 2024), extended direct algebraic technique and modified auxiliary equation method (Al Alwan et al. 2023), GREMM and q-HATM approaches (Akinyemi et al. 2022), EMSE method (Islam et al. 2020), MSE technique (Roshid et al. 2022b), \({\varphi }^{6}\)-model expansion approach (Faridi et al. 2022), AEE method (Bashar and Roshid 2020), sine–Gordon expansion approach (Fahim et al. 2022), Lie symmetry approach (Faridi et al. 2023; Ullah et al. 2024), modified auxiliary expansion method (Gao et al. 2020), (G’/G)-expansion method (Ali et al. 2024; Alam et al. 2024a, 2024b, 2023; Talib et al. 2024) and so on.

2 Governing model

The space–time truncated M-proportional paraxial wave (s-tM-fPW) model is considered to be:

$$i{{\text{D}}}_{{\text{M}},x}^{{\text{p}},\mathrm{ n}}u+\frac{a}{2}{{\text{D}}}_{{\text{M}},{\text{t}}}^{2{\text{p}},\mathrm{ n}}u+\frac{b}{2}{{\text{D}}}_{{\text{M}},y}^{2{\text{p}},\mathrm{ n}}u+\epsilon {\left|u\right|}^{2}u=0.$$
(1)

The space–time beta fractional paraxial wave (s-tb-fPW) model is considered to be:

$$i{}_{0}{}^{A}{D}_{x}^{p}u+\frac{a}{2}{}_{0}{}^{A}{D}_{t}^{2p}u+\frac{b}{2}{}_{0}{}^{A}{D}_{y}^{2p}u+\epsilon {\left|u\right|}^{2}u=0.$$
(2)

The space–time conformable fractional paraxial wave (s-t cfPW) model is considered to be:

$$i\frac{{\partial }^{p}(u)}{{\partial {\text{x}}}^{p}}+\frac{a}{2}\frac{{\partial }^{2p}(u)}{{\partial t}^{p}}+\frac{b}{2}\frac{{\partial }^{2p}(u)}{{\partial y}^{p}}+\epsilon {\left|u\right|}^{2}u=0.$$
(3)

The classical form of the paraxial wave (PWM) model is considered.

$$i\frac{\partial u}{\partial x}+\frac{a}{2}\frac{{\partial }^{2}u}{{\partial t}^{2}}+\frac{b}{2}\frac{{\partial }^{2}u}{{\partial y}^{2}}+\epsilon {\left|u\right|}^{2}u=0.$$
(4)

where \({\text{a}},{\text{b}},\upepsilon \) are real constants, \(a\) is the dispersal effect, \({\text{b}}\) is the diffraction effect and \(\epsilon \) is the Kerr nonlinearity effect. Mathematically, the PWM for a monochromatic beam is equivalent to the Schrödinger equation of a free quantum particle. The variable \({\text{x}},{\text{y}},\mathrm{ t}\) represents the longitudinal, transverse and temporal propagations. For the special case, \(ab<0\) represents the hyperbolic nonlinear Schrodinger equation, and for the case where \(ab>0\), Eq. (1) represents the elliptic nonlinear Schrodinger equation. Several methods have recently been used to find numerous optical wave structures for PW simulations, such as W. Gao, who tested the modulation instability and obtained some optical solitons for the PW model by using the MAE technique (Gao et al. 2020); M.A. Al Sharif, who used the Sardar subequation method (Rasool et al. 2023) for the time-truncated M-proportional PW equation and obtained several periodic solutions; Hamood Ur Rehman, who found the exact solution of the PW equation by using the \({\varphi }^{6}\)-expansion technique (Rehman et al. 2022); M. Arshad, who solved the PW model by using the ISE, \(exp(-\Phi (\zeta ))\)-expansion and MEDA techniques (Arshad et al. 2020); M.M. Roshid, who applied a unified technique (Roshid et al. 2023) to the time M-fractional PW equation; N. Ullah, who generated exact solutions from the PW model by using an analytic method (Ullah 2023); and V.R. Chinni, who tested accurate solutions of the paraxial wave equation using Richardson extrapolation (Chinni 1994). The motivation of this study is to investigate novel optical soliton solutions of a space–time M-fractional paraxial wave dynamical model with the Kerr law by applying the simplest equation techniques. Our solutions include periodic waves, kink types, rogue types, and several novel periodic waves by providing the proper parametric values, which have significant applications in nonlinear physics and engineering. The physical properties of the obtained solutions are well defined, and the results demonstrate the influence and effectiveness of these techniques. The following sections compose the manuscript. The introduction is offered in the initial section. The second section provides a brief summary of the Simplest equation procedures. In the third section, "The execution of the presented technique" illustrates multiple outcomes that were accomplished, including trigonometric, rational, exponential, and hyperbolic function solutions. 3D contour plot graphs and comparisons of diverse fractions in 2D plots of some of the newly observed solutions are presented in section four, "Results and Discussion". An overview of this article has been added to the last section.

3 Preliminaries of method

3.1 The truncated M-proportional derivative concept, along with certain of its unique features.

Theorem: Let us consider a mapping \(\mathrm{\wp }:\left(0,\mathrm{ \infty }\right)\to {\mathbb{R}}\). The \(p\)-order truncated M-derivative (Roshid et al. 2023; Akram et al. 2023) of \(\mathrm{\wp }\) is expressed as:

$$ {\text{D}}_{{{\text{M}},{\text{t}}}}^{{{\text{p}},{\text{ n}}}} \wp \left( {\text{x}} \right) = \mathop {\lim }\limits_{{{\text{h}} \to 0}} \frac{{\wp \left( {{\text{xH}}_{{\text{d}}} \left( {{\text{hx}}^{{1 - {\text{n}}}} } \right)} \right) - \wp \left( {\text{x}} \right)}}{{\text{h}}};\,{\text{d}} > 0,{ }0 < {\text{p}} < 1 .$$

Here, \({{\text{H}}}_{{\text{d}}}\left({\text{x}}\right).\) is a one-parameter truncated Mittag–Leffler function that is well defined as (Roshid et al. 2023; Ahmad et al. 2023):

$${{\text{H}}}_{{\text{d}}}\left({\text{x}}\right)=\sum_{{\text{j}}=0}^{{\text{i}}}\frac{{{\text{x}}}^{{\text{j}}}}{\Gamma \left({\text{dj}}+1\right)}$$

Mannerisms:

Assume that \({\text{n}}>0, 0<{\text{p}}<1,\mathrm{ g},{\text{h}}\in \mathfrak{R}\) and \(\mathfrak{\wp },\mathfrak{I},{\text{p}}-\) are differentiable at point \({\text{x}}>0,\); then,

$${{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\left(\mathrm{g\wp }\left({\text{x}}\right)+{\text{h}}\mathfrak{I}\left({\text{x}}\right)\right)={{\text{gD}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathrm{\wp }\left({\text{x}}\right)+{{\text{hD}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathfrak{I}\left({\text{x}}\right).$$
$${{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\left(\mathrm{\wp }\left({\text{x}}\right)\mathfrak{I}\left({\text{x}}\right)\right)=\mathrm{\wp }\left({\text{x}}\right){{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathfrak{I}\left({\text{x}}\right)+\mathfrak{I}\left({\text{x}}\right){{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathrm{\wp }\left({\text{x}}\right).$$
$${{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\left(\frac{\mathrm{\wp }\left({\text{x}}\right)}{\mathcal{g}\left({\text{x}}\right)}\right)=\frac{\mathfrak{I}\left({\text{x}}\right){{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ d}}\mathrm{\wp }\left({\text{x}}\right)-{\mathrm{\wp }\left({\text{x}}\right)\mathrm{ D}}_{{\text{M}},{\text{t}}}^{{\text{p}},,\mathrm{ d}}\mathfrak{I}\left({\text{x}}\right)}{{\mathfrak{I}\left({\text{x}}\right)}^{2}}.$$
$${{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathrm{\wp }\left({\text{x}}\right)=0\;\mathrm{Where\;\wp }\left({\text{x}}\right)={\text{a}}.$$
$${{\text{D}}}_{{\text{M}},{\text{t}}}^{{\text{p}},\mathrm{ n}}\mathrm{\wp }\left({\text{x}}\right)=\frac{{{\text{t}}}^{1-{\text{p}}}}{\Gamma \left({\text{d}}+1\right)}\frac{\mathrm{d\wp }\left({\text{x}}\right)}{{\text{dx}}}.$$

3.2 Simplest equation scheme for solving the nonlinear model

This subdivision provides a short explanation of the simplest equation (Taghizadeh et al. 2013) technique for solving a fractional nonlinear problem. For this purpose, we consider a general space–time M-fractional NLEE:

$${\text{g}}\left({{\text{D}}}_{{\text{M}},x}^{2{\text{p}},\mathrm{ n}}\upchi ,{{\text{D}}}_{{\text{M}},t}^{{\text{p}},\mathrm{ n}}\upchi ,\uptau {{\text{D}}}_{{\text{M}},x}^{{\text{p}},\mathrm{ n}}\upchi ,{{\text{D}}}_{{\text{M}},x}^{3{\text{p}},\mathrm{ n}}\upchi ,{\upchi }^{{\text{n}}},.............\right)=0.$$
(5)

Now, we instigate \(\upzeta ={\text{k}}\frac{\Gamma \left(n+1\right)}{p}{x}^{p}-\upomega \frac{\Gamma \left(n+1\right)}{p}{t}^{p}.\), where \(\upchi ({\text{x}},{\text{t}})={\text{u}}(\upzeta ),\), to obtain an ODE form of the given nonlinear model in Eq. (5). Then, we integrate it if possible.

$${{\text{g}}}_{1}({k}^{2}{u}_{\mathrm{\zeta \zeta }},-\upomega {{\text{u}}}_{\upzeta },\mathrm{\omega u}{{\text{u}}}_{\upzeta },{{\text{u}}}^{{\text{n}}},{k}^{3}{{\text{u}}}_{\mathrm{\zeta \zeta \zeta }},........)=0.$$
(6)

In this schema, we study the solution of Eq. (6) in the following form:

$${\text{u}}\left(\upzeta \right)={{\text{a}}}_{0}+{\sum }_{{\text{i}}=1}^{{\text{N}}}\left[{{\text{a}}}_{{\text{i}}}{\text{F}}{\left(\upzeta \right)}^{{\text{i}}}\right].$$
(7)

where \({{\text{a}}}_{{\text{i}}}\) and \(({\text{i}}=\mathrm{0,1},2,...,{\text{N}})\) are arbitrary quantities and \({{\text{a}}}_{{\text{N}}}\ne 0\), where \({\text{N}}\in {\mathfrak{R}}^{+}\) can be determined by balancing the nonlinear terms and the highest order in Eq. (6).

By inserting Eq. (7) with the help of two ordinary differential equations, Bernoulli and Riccati, into Eq. (6), we can obtain a polynomial \({\text{F}}\left(\upzeta \right)\). Now, we set the coefficient of the polynomial to zero. Using the computational software Maple, we then solve the system of algebraic equations. We develop the values of \({{\text{a}}}_{{\text{i}}}\) \(({\text{i}}=\mathrm{0,1},2,...,{\text{N}})\) and \({\text{k}},\upomega .\) By substituting \({{\text{a}}}_{{\text{i}}},\) \({\text{k}}\) and \(\upomega \) into Eq. (7), we obtain explicit solutions of Eq. (5).

Here, we describe the different types of solutions for different conditions of the two differential equations.

For the Bernoulli differential equation:

$${{\text{F}}}^{\mathrm{^{\prime}}}(\upzeta )={\text{rF}}(\upzeta )+{{\text{hF}}}^{2}(\upzeta ).$$
(8)

where \(c\) and \(d\) are arbitrary constants.

The solution of Eq. (8) is:

$${\text{F}}(\upeta )=\frac{-rE}{\left(E+{\text{cosh}}\left(r\left(\upzeta +E\right)\right)-{\text{sinh}}\left(r\left(\upzeta +E\right)\right)\right)}.$$
$${\text{F}}(\upeta )=\frac{{\text{cexp}}[{\text{c}}(\upzeta +E)]}{1-{\text{dexp}}[{\text{c}}(\upzeta +{\text{E}})]},{\text{h}}<0,{\text{r}}>0.$$

\(\mathrm{And\;F}(\upxi )=\frac{-{\text{cexp}}[{\text{c}}(\upzeta +E)]}{1+{\text{dexp}}[{\text{c}}(\upzeta +{\upzeta }_{0})]},{\text{h}}>0,{\text{r}}<0.\)where \({\upzeta }_{0}\) is the integration constant.

If \({\text{r}}={\text{l}}\) and \({\text{h}}=-1\), then another form of the Bernoulli equation is given:

$${{\text{F}}}^{\mathrm{^{\prime}}}(\upzeta )={\text{lF}}\left(\upzeta \right)-{{\text{F}}}^{2}(\upzeta ).$$

The solutions are:

$${\text{F}}(\upzeta )=\frac{{\text{l}}}{2}\left[1+{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +{\upzeta }_{0}\right)\right)\right];{\text{l}}>0.$$
$${\text{F}}(\upzeta )=\frac{{\text{l}}}{2}\left[1-{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +{\upzeta }_{0}\right)\right)\right];{\text{l}}<0$$

When \({\text{r}}=1\) and \({\text{h}}=-1\), then another form is

$${{\text{F}}}^{\mathrm{^{\prime}}}(\upzeta )={\text{F}}\left(\upzeta \right)-{{\text{F}}}^{2}(\upzeta ).$$

The solution is:

$${\text{F}}(\upzeta )=\frac{1}{2}\left(1+{\text{tanh}}\left(\frac{\upzeta }{2}\right)\right).$$

4 Formation of optical soliton solutions

Due to the fractional form of the paraxial wave equation, the pulse pattern can be represented by \(u(x,y,t)=u(\zeta ){e}^{i\xi }\) in Eq. (1):

For the truncated M- proportional derivative:

$$ \begin{gathered} \zeta = l_{1} \frac{{{\Gamma }\left( {n + 1} \right)}}{p}x^{p} + l_{2} \frac{{{\Gamma }\left( {n + 1} \right)}}{p}y^{p} + \frac{{{\Gamma }\left( {n + 1} \right)}}{p}\left( {\omega t^{p} } \right); \hfill \\ \xi = v_{1} \frac{{{\Gamma }\left( {n + 1} \right)}}{p}x^{p} + v_{2} \frac{{{\Gamma }\left( {n + 1} \right)}}{p}y^{p} + \frac{{{\Gamma }\left( {n + 1} \right)}}{p}\tau t^{p} + \delta. \hfill \\ \end{gathered} $$
(9)

For the beta fractional derivative:

$$ \begin{gathered} \zeta = l_{1} \frac{{\left( {x + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p} + l_{2} \frac{{\left( {y + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p} + \omega \frac{{\left( {t + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p}; \hfill \\ \xi = v_{1} \frac{{\left( {x + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p} + v_{2} \frac{{\left( {y + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p} + \tau \frac{{\left( {t + \frac{1}{{{\Gamma }\left( n \right)}}} \right)^{p} }}{p} + \delta. \hfill \\ \end{gathered} $$
(10)

The conformable fractional derivative.

$$ \zeta = l_{1} \frac{{x^{p} }}{p} + l_{2} \frac{{y^{p} }}{p} + \omega \frac{{t^{p} }}{p};\,\xi = v_{1} \frac{{x^{p} }}{p} + v_{2} \frac{{y^{p} }}{p} + \tau \frac{{t^{p} }}{p} + \delta . $$
(11)

For the classical form:

$$ \zeta = l_{1} x + l_{2} y + \omega t;\,\xi = v_{1} x + v_{2} y + \tau t + \delta. $$
(12)

By converting Eq. (9) into Eq. (1), Eq. (10) into Eq. (2), Eq. (11) into Eq. (3) and Eq. (12) into Eq. (4), The resultant shape is then divided into real and imaginary parts:

The real part is:

$$ \left( {a\omega^{2} + bl_{1}^{2} } \right)u^{\prime\prime} + \left( {a\tau^{2} + bv_{1}^{2} + 2v_{2} } \right)u - 2\gamma u^{3} = 0 .$$
(13)

and the imaginary part is.

$$\left(2a\tau \omega +2b{l}_{1}{v}_{1}+2{l}_{2}\right)u{\prime}=0.$$
(14)

As \(u{\prime}\ne 0\), so

$${l}_{2}=-a\tau \omega -b{l}_{1}{v}_{1}.$$

With \(m=1\) and a uniform equilibrium rule acting as support, the standard solution to problem (13) has the following form.

$$u={\mu }_{0}+{\mu }_{1}M(\zeta ).$$
(15)

By inserting Eq. (15) with Eq. (8) into Eq. (13), we obtain a polynomial of \(M\). By equating the coefficient of \(M\), the following system of equations can be obtained:

$${M}^{3}: 2{\mu }_{1}b{l}_{1 }^{2}{h}^{2}+ 2{\mu }_{1}a{\omega }^{2}{h}^{2}-2m{\mu }_{1}^{3} =0.$$
$${M}^{2}:3{\mu }_{1}a{\omega }^{2}rh -6m{\mu }_{0}{\mu }_{1}^{2} +3{\mu }_{1}b{l}_{1 }^{2}rh=0.$$
$$M:-b{v}_{1}^{2}{\mu }_{1}+{\mu }_{1}b{l}_{1 }^{2}{r}^{2}-6m{\mu }_{0}^{2}{\mu }_{1}-a{\tau }^{2}{\mu }_{1}+{\mu }_{1}a{\omega }^{2}{r}^{2}-2{v}_{1}{\mu }_{0}=0.$$
$${M}^{0}:-b{v}_{1}^{2}{\mu }_{0}-2m{\mu }_{0}^{3} -2{v}_{2}{\mu }_{0}=0.$$

Using the computational software Maple 18, we obtain the values of the parameters by solving the above system of equations.

Set-01 when \(\tau =\tau ,\omega =\frac{1}{h} \sqrt{\frac{-m{\mu }_{1}^{2} + b {l}_{1 }^{2}{h}^{2}}{-a}}, {l}_{1} = {l}_{1}, {\mu }_{0}= \frac{1}{2} \frac{{\mu }_{1 } r}{h}, {\mu }_{1}= {\mu }_{1}, {v}_{1}={v}_{1}, {v}_{2}=- \frac{1}{4} \frac{2 b{v}_{1}^{2}{h}^{2}+m{\mu }_{1}^{2} {r}^{2}+2\alpha {\tau }^{2}{h}^{2} }{{h}^{2}}.\), then the following solutions are obtained:

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)= \left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{-rE}{h(E+{\text{cosh}}\left(r\left(\upzeta +k\right)\right)-{\text{sinh}}\left(r\left(\upzeta +k\right)\right))}\right)\right){e}^{i\xi }.$$
(16)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{{\text{rexp}}[{\text{r}}(\upzeta +E)]}{1-{\text{hexp}}[{\text{r}}(\upzeta +{\text{E}})]}\right)\right){e}^{i\xi };h<0,r>0.$$
(17)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{-{\text{rexp}}[{\text{r}}(\upzeta +{\text{E}})]}{1+{\text{hexp}}[{\text{r}}(\upzeta +{\text{E}})]}\right)\right){e}^{i\xi };h>0, r<0.$$
(18)

If we set \(h=-1, r=r\), then the following solutions are attained.

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2}{\mu }_{1 }r+{\mu }_{1}\left(\frac{{\text{l}}}{2}\left[1+{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +E\right)\right)\right]\right)\right){e}^{i\xi }.$$
(19)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2}{\mu }_{1 }r+{\mu }_{1}\left(\frac{{\text{l}}}{2}\left[1-{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +E\right)\right)\right]\right)\right){e}^{i\xi }.$$
(20)

If we set \(h=-1, r=1\), then the following solutions are attained.

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{-{\mu }_{1 }}{2}+{\mu }_{1}\left(\frac{1}{2}\left(1+{\text{tanh}}\left(\frac{\upzeta }{2}\right)\right)\right)\right){e}^{i\xi }.$$
(21)

where \(\zeta ={l}_{1}\frac{\Gamma \left(n+1\right)}{p}{x}^{p}+{l}_{2}\frac{\Gamma \left(n+1\right)}{p}{y}^{p}+\frac{\Gamma \left(n+1\right)}{p}.\)(\(\omega {t}^{p}\)) and \(\xi ={v}_{1}\frac{\Gamma \left(n+1\right)}{p}{x}^{p}+{v}_{2}\frac{\Gamma \left(n+1\right)}{p}{y}^{p}+\frac{\Gamma \left(n+1\right)}{p}\tau {t}^{p}+\delta .\)

Set-02 when \({l}_{1}=\frac{1}{h}\sqrt{\frac{a{\omega }^{2}{h}^{2}-m {\mu }_{1}^{2}}{-b}}r, {\mu }_{0}=\frac{1}{2} \frac{{\mu }_{1 } r}{h}, {\mu }_{1}= {\mu }_{1}, {v}_{1}={v}_{1}, {v}_{2}=- \frac{1}{4} \frac{2 b{v}_{1}^{2}{h}^{2}+m{\mu }_{1}^{2} {r}^{2}+2\alpha {\tau }^{2}{h}^{2} }{{h}^{2}}.\).

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)= \left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{-rE}{h(E+{\text{cosh}}\left(r\left(\upzeta +k\right)\right)-{\text{sinh}}\left(r\left(\upzeta +k\right)\right))}\right)\right){e}^{i\xi }.$$
(22)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{{\text{rexp}}[{\text{r}}(\upzeta +E)]}{1-{\text{hexp}}[{\text{r}}(\upzeta +E)]}\right)\right){e}^{i\xi };h<0,r>0.$$
(23)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{1}{2} \frac{{\mu }_{1 } r}{h}+{\mu }_{1}\left(\frac{-{\text{rexp}}[{\text{r}}(\upzeta +E)]}{1+{\text{hexp}}[{\text{r}}(\upzeta +E)]}\right)\right){e}^{i\xi };h>0, r<0.$$
(24)

If we set \(h=-1, r=r\), then the following solutions are attained.

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(-\frac{1}{2}{\mu }_{1 }r+{\mu }_{1}\left(\frac{{\text{l}}}{2}\left[1+{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +E\right)\right)\right]\right)\right){e}^{i\xi }.$$
(25)
$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(-\frac{1}{2}{\mu }_{1 }r+{\mu }_{1}\left(\frac{{\text{l}}}{2}\left[1-{\text{tanh}}\left(\frac{{\text{l}}}{2}\left(\upzeta +E\right)\right)\right]\right)\right){e}^{i\xi }.$$
(26)

If we set \(h=-1, r=1\), then the following solutions are attained.

$${\text{u}}\left({\text{x}},{\text{y}},{\text{t}}\right)=\left(\frac{-{\mu }_{1 }}{2}+{\mu }_{1}\left(\frac{1}{2}\left(1+{\text{tanh}}\left(\frac{\upzeta }{2}\right)\right)\right)\right){e}^{i\xi }.$$
(27)

where \(\zeta ={l}_{1}\frac{\Gamma \left(n+1\right)}{p}{x}^{p}+{l}_{2}\frac{\Gamma \left(n+1\right)}{p}{y}^{p}+\frac{\Gamma \left(n+1\right)}{p}.\)(\(\omega {t}^{p}\)) and \(\xi ={v}_{1}\frac{\Gamma \left(n+1\right)}{p}{x}^{p}+{v}_{2}\frac{\Gamma \left(n+1\right)}{p}{y}^{p}+\frac{\Gamma \left(n+1\right)}{p}\tau {t}^{p}+\delta. \).

5 Graphical representation

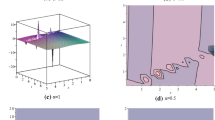
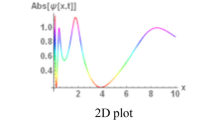
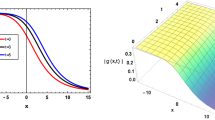
In this section, we observe diverse optical wave patterns by executing the simplest equation method. For the numerical form of the obtained solutions, we depicted diverse optical waves in three-dimensional plots with density and contour plots and compared the solutions in the truncated \(M\)-fractional (Roshid et al. 2023; Akram et al. 2023) form with the beta fraction (Akram et al. 2023), conformable fraction (Ahmad et al. 2023) and classical form. The comparative solutions are depicted with two-dimensional plots. It is essential to obtain analytical solutions for the paraxial model as well as the fractional paraxial model. These answers provide an in-depth understanding of light propagation by providing exact mathematical descriptions of intricate optical phenomena. They guarantee the accuracy of computational models by acting as essential benchmarks for numerical simulations and experimental validations. Furthermore, by serving as a basis for creative inquiry, these analytical solutions facilitate the creation of cutting-edge optical systems and technologies. By deciphering these answers, researchers and technologists can improve our knowledge of how light interacts with materials, advancing the fields of imaging, laser optics, and telecommunication. In three-dimensional plots, we show the effect of the truncated \(M\)-fractional parameter \(p;p=0.001, 0.1, 0.5, 0.75, 0.99\). Figure 1 shows the periodic wave soliton, whereas the fractional parameter increases, the soliton transforms to a periodic wave with a lump soliton. Two-dimensional plots comparing the three fractional derivatives to the classical form are shown in \(p=0.001, 0.1, 0.5, 0.75, 0.99\). If we increased the value of the fractional parameter in the solution to Eq. (16), then this solution gradually changed its shape from soliton to kink and finally became periodic. Figure 2 shows the effect of the \(M\)-fractional parameter at \(p=0.001, 0.1, 0.5, 0.75, 0.99\) in three-dimensional plots, and comparisons are also shown in two-dimensional plots. In Fig. 3, the periodic rogue wave soliton solutions are illustrated, where three-dimensional plots represent the effect of the \(M\)-fractional parameter at \(p=0.001, 0.1, 0.5, 0.75, 0.99\) and two-dimensional plots also represent the comparison of three fractions to the classical form. In Fig. 4, the solutions of Eq. (25) are periodic wave solutions, where three-dimensional plots represent the effect of the \(M\)-fractional parameter at \(p=0.001, 0.1, 0.5, 0.75, 0.99\) and two-dimensional plots compare the three fractions to the classical form. In Figs. 5 and 6, the real and imaginary portions of the solution to Eq. (25) are illustrated for several novel optical waveforms, where three-dimensional plots represent the effect of the \(M\)-fractional parameter at \(p=0.001, 0.1, 0.5, 0.75, 0.99\) and two-dimensional plots compare the three fractions to the classical form.

Fig. 1
figure 1

3D profile of Eq. (16) for \({\mu }_{1}=-0.1,{v}_{1}=0.5,y=1, \tau =1, m=1, \delta =-0.005,a=0.2, b=0.5, d=1,{l}_{1}=1,c=-2, E=-0.1, k=-1,n=0.5\)

Full size image
Fig. 2
figure 2figure 2

3D profile of Eq. (17) for \({\mu }_{1}=-1,{v}_{1}=-0.2,x=1, m=-0.5, \delta =0.005,a=-0.5, b=3, d=-3,{l}_{1}=1,c=0.5, E=3, n=0.5, \tau =-1\)

Full size image
Fig. 3
figure 3figure 3

3D profile of Eq. (20) for \({\mu }_{1}=0.5,{v}_{1}=-5,y=1, \tau =-1, m=-1.5, \delta =0.005,a=0.5, b=0.01, d=-1,{l}_{1}=1,c=1.5, E=-0.01, n=1\)

Full size image
Fig. 4
figure 4figure 4

3D profile of Eq. (25) for \({\mu }_{1}=1,{v}_{1}=-0.35,y=0, \tau =3, m=-3, \delta =-0.5,a=2, b=0.25, d=2, r=1, \omega =2,c=1,n=1.5\)

Full size image
Fig. 5
figure 5

3D profile of Eq. (25) for \({\mu }_{1}=-3,{v}_{1}=-0.35,y=0.1, \tau =-0.1, m=3, \delta =2,a=-3, b=-0.05, d=2,\omega =-0.5,c=1,n=0.5\)

Full size image
Fig. 6
figure 6

3D profile of Eq. (25) for \({\mu }_{1}=-3,{v}_{1}=-0.35,y=0.1, \tau =-0.1, m=3, \delta =2,a=-3, b=-0.05, d=2,\omega =-0.5,c=1,n=0.5\)

Full size image

6 Conclusion

In this manuscript, we successfully implemented the simplest equation method for the paraxial wave model; checked the stability of the obtained optical soliton solutions with a 3D truncated M-proportional derivative; and compared the results with the beta fraction, conformable fraction, and classical form of the obtained solution of the PW model. In the present case, the SE approach had the ability to offer a few new viewpoints on how the suggested systems behaved and resulted in the discovery of novel phenomena. For the numerical form of the obtained solutions, numerous types of optical soliton solutions, including counting periodic waves, kink types, rogue types, and novel periodic waves, can be obtained by providing the appropriate fractional parametric values. The governing model's solutions provide significant and dynamic interpretations for a variety of natural phenomena that occur in the real world. To show the physical dynamics of the governing model, several acquired soliton solutions are shown in 3D plots, related density plots, and contour plots. Additionally, the results show that the recommended approach is to identify wave solutions to a variety of nonlinear equations that arise in optics. In the future, we will apply the bilinear Hirota method to determine the multisoliton solution, lump wave, and interaction wave for the paraxial wave equation.