1 Introduction

In order to explore the properties and traits of nonlinear models found in nonlinear science, thorough investigation is necessary. Nonlinear science encompasses a vast array of disciplines, including chaos theory, fractals, complex systems, and nonlinear dynamics. These models exhibit behaviors that are not easily predictable or linearly related to their inputs, making them particularly intriguing and challenging to study. By delving into the intricacies of these nonlinear models, researchers can gain valuable insights into the complexity and interconnectedness of natural phenomena, leading to a deeper understanding of our world and its underlying dynamics. A crucial area of focus lies in the in-depth exploration of the propagation of nonlinear waves, particularly emphasizing their behavior within multilayered bodies. This subject is essential for a thorough analysis and understanding of the intricate dynamics and properties associated with the transmission of nonlinear waves in the context of layered materials. Through a meticulous examination of these phenomena, the goal is to furnish a comprehensive understanding of the distinctive challenges and complexities inherent in the propagation of nonlinear waves within multilayered structures. These investigations significantly contribute to the advancement of our knowledge in this field, offering insights into the subtle interactions and dynamics that govern the propagation of nonlinear waves across various material configurations. Nonlinear partial differential equations pose significant challenges when it comes to finding analytical solutions. These equations involve nonlinear terms that make it difficult to employ conventional methods for solving linear partial differential equations. As a result, researchers have developed various techniques to tackle these nonlinear equations, including numerical methods, perturbation methods, integral transforms, and more. While exact analytical solutions are often elusive for nonlinear partail differential equations (NPDEs), approximate solutions or qualitative insights can still be obtained through these methods. Nonlinear partial differential equations are challenging to solve analytically, and various methods have been developed to obtain exact or approximate solutions. Some commonly used techniques include the \(\phi ^6\)-model expansion technique (Ullah et al. 2023; Isah and Yokus 2022; Isah 2023; Yao et al. 2023; Ali et al. 2022; Sadaf et al. 2022), The Kudryashov method (Murad et al. 2023; Malik et al. 2023; Cinar et al. 2023; Esen et al. 2023), the Hirota bilinear method (Ismael et al. 2023; Yokus and Isah 2023; Mandal et al. 2023; Batool et al. 2023; Seadawy et al. 2021; Yokus and Isah 2022; Ismael and Sulaiman 2023; Ali et al. 2023), the extended simplest equation method (Murad et al. 2023; Zayed and Shohib 2019; Ahmed et al. 2021; El Sheikh et al. 2020; Hassan and Altwaty 2020), and other methods (Ali et al. 2023; Kamal Ali et al. 2022; Ismael et al. 2023, 2023; Ali et al. 2023, 2023; Zhu et al. 2021; Isah and YOKUS 2022; Günerhan et al. 2020; Zayed and El-Ganaini 2024; Al-Amr 2015; El-Ganaini et al. 2023; Mubaraki et al. 2024; Asif et al. 2023a, b; Mubaraki et al. 2023; Mahdy 2023, 2022; Mahdy et al. 2022; Al-Bugami et al. 2023; Mahdy et al. 2023, 2022; Mahdy and Mohamed 2022; Mahdy et al. 2023; Anaç 2023). In this study, we will employ the modified version of the Sardar sub-equation method (MSSEM) as our chosen approach. Extensive research has been conducted on this particular method, with numerous studies dedicated to its exploration and analysis. Akinyemi et al. conducted a comprehensive investigation of the unstable nonlinear Schrödinger equation when generalized to incorporate the mentioned method (Akinyemi et al. 2022). Another research endeavor focused on the examination of optical solitons utilizing the mentioned method (Cinar et al. 2022). The method was applied to the space-time fractional modified third-order Korteweg-de Vries equation to investigate soliton solutions in a research study (Rehman et al. 2022). Numerous studies have been conducted on this method, encompassing a wide range of equations and employing diverse approaches. These investigations have delved into various aspects and applications, contributing to a comprehensive understanding of the method’s effectiveness and versatility in different contexts (Ullah et al. 2023; Rehman et al. 2022; Asjad et al. 2022; Onder et al. 2023; Yao et al. 2023; Akinyemi et al. 2021; Yusuf et al. 2022; Faisal et al. 2023; Akinyemi 2021; Alia et al. 1402; Muhammad et al. 2022). In this particular study, our focus will be on utilizing the generalized Pochhammer–Chree equation as the primary equation of interest. We applied the modified Sardar sub-equation method to construct some novel solutions. The Pochhammer-Chree equation, introduced by Clarkson et al. in (1986), represents the propagation of longitudinal deformation waves in an elastic rod. It is mathematically described as follows:

$$\begin{aligned} u_{tt}-u_{ttxx}-\frac{1}{n}\left( u^n\right) _{xx}=0, \end{aligned}$$
(1)

where the function u(x, t) represents the longitudinal displacement at time t of a material point that was initially located at position x. It serves as a fundamental quantity for studying the behavior and dynamics of the deformation waves within the elastic rod (Clarkson et al. 1986). Bogolubsky successfully obtained soliton-type solutions by considering various values of n, specifically \(n = 2, 3, and 5\). These solutions offer valuable insights into the behavior and characteristics of solitons within the context of the Pochhammer–Chree equation (Bogolubsky 1977). Exact solutions have been acquired by Triki et al. for \(n = 6\) (Triki et al. 2015). The generalized Pochhammer–Chree equation is given by Yokus et al. (2022), Parand and Rad (2010)

$$\begin{aligned} u_{tt}-u_{ttxx}- \left( \mu u +\beta u^{n+1} + v u^{2n+1} \right) _{xx}=0, n\ge 1, \end{aligned}$$
(2)

where \(\mu \), \(\beta \) and v are constants. The Pochhammer-Chree equation has been extensively investigated using various methods, for obtaining solitary wave solutions, periodic solutions, kink shape solutions, singular solutions, complex rational function solutions, complex periodic solutions, and so Weiguo and Wenxiu (1999), Liu (1996), Wazwaz (2008), Li and Zhang (2002), Shawagfeh and Kaya (2004), El-Ganaini (2011), Mohebbi (2012), Parand and Rad (2010), Zuo (2010), Zhang (2005), Zhang et al. (2010), Jaradat et al. (2022). These different approaches have been employed to analyze the equation, explore its properties, and obtain meaningful solutions. Each method offers unique advantages and insights into the behavior and dynamics of the equation, contributing to a comprehensive understanding of its mathematical properties.

In this article, we provide an introduction in the previous section. Then, in the second section, we provide an overview of the MSSEM. Next, in the third section, we apply MSSEM to find new exact solutions for The generalized Pochhammer-Chree equation and present them using 3D, 2D, and counter plots. Finally, we conclude our work in the last section.

2 Description of the MSSEM

The Sardar sub-equation method is a powerful technique to obtain exact solutions of nonlinear PDEs (Akinyemi et al. 2022). A recent study proposed a modification version of this method, incorporating arbitrary functions into the trial solution ansatz. The NPDEs is expressed as:

$$\begin{aligned} F(u,u_{x},u_{t},u_{xx}, u_{xt}...)=0. \end{aligned}$$
(3)

If we consider the following transformation:

$$\begin{aligned} u(x,t)=\mathcal {U}(\chi ), \chi =k(x-r t). \end{aligned}$$
(4)

The new modification of the Sardar sub-equation method depends on the following function:

$$\begin{aligned} \mathcal {U}(\chi )=\lambda _{0}+\sum _{i=0}^{L}\lambda _{i}\mathcal {Q}^{i}(\chi ), \end{aligned}$$
(5)

where \(\lambda _{i}, (i=0,1,2,...,L)\) are coefficients of \(\mathcal {Q}^{i}(\chi )\) with \(\lambda _{N}\ne 0\) and the following equation exists for the \(\mathcal {Q}(\chi )\) function:

$$\begin{aligned} (\mathcal {Q}^{'}(\chi ))^2= \gamma _{2} \mathcal {Q}^4(\chi )+ \gamma _{1} \mathcal {Q}^2(\chi ) +\gamma _{0}, \end{aligned}$$
(6)

where \(\gamma _{0}\), \(\gamma _{1}\) and \(\gamma _{2}\) are constants. The general solutions Eq. (6) are outlined as follows:

  1. 1.

    When \(\gamma _{0}=0\), \(\gamma _{1}>0\), and \(\gamma _{2}\ne 0\), then

    $$\begin{aligned}{} & {} \mathcal {Q}_{1}(\chi )=\pm \sqrt{-\frac{\gamma _{1}}{\gamma _{2}}} \text {sech}[\sqrt{\gamma _{1}}(\chi + \rho )], \end{aligned}$$
    (7)
    $$\begin{aligned}{} & {} \mathcal {Q}_{2}(\chi )=\pm \sqrt{\frac{\gamma _{1}}{\gamma _{2}}} \text {csch}[\sqrt{\gamma _{1}}(\chi + \rho )]. \end{aligned}$$
    (8)
  2. 2.

    When \(\gamma _{0}=0\), \(\gamma _{1}>0\), and \(\gamma _{2}= \pm 4 \beta _{1} \beta _{2}\), then

    $$\begin{aligned} \mathcal {Q}_{3}(\chi )= \pm \frac{4 \beta _{1} \sqrt{\gamma _{1}}}{\left( 4 \beta _{1}^2 - \gamma _{2}\right) \text {cosh}[\sqrt{\gamma _{1}}(\chi + \chi _{0})]+\left( 4 \beta _{1}^2 + \gamma _{2}\right) \text {sinh}[\sqrt{\gamma _{1}}(\chi + \chi _{0})]}, \end{aligned}$$
    (9)

    where \(\beta _{1}\) and \( \beta _{2}\) are constants.

  3. 3.

    When \(\gamma _{0}=\frac{\gamma _{1}^2}{4 \gamma _{2}}\), \(\gamma _{1}<0\), and \(\gamma _{2}> 0 \), with constants \(A_{1}\) and \(A_{2}\), then

    $$\begin{aligned} \mathcal {Q}_{4}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{2 \gamma _{2}}} \text {tanh}\left[ \sqrt{-\frac{\gamma _{1}}{2}}(\chi + \rho )\right] , \end{aligned}$$
    (10)
    $$\begin{aligned} \mathcal {Q}_{5}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{2 \gamma _{2}}} \text {coth}\left[ \sqrt{-\frac{\gamma _{1}}{2}}(\chi + \rho )\right] , \end{aligned}$$
    (11)
    $$\begin{aligned} \mathcal {Q}_{6}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{2 \gamma _{2}}} \left( \text {tanh}[\sqrt{-2 \gamma _{1}}(\chi + \rho )] \pm i \text {sech}[\sqrt{-2 \gamma _{1}}(\chi + \rho )] \right) , \end{aligned}$$
    (12)
    $$\begin{aligned} \mathcal {Q}_{7}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{8 \gamma _{2}}} \left( \text {tanh}\left[ \sqrt{-\frac{\gamma _{1}}{8}}(\chi + \rho )\right] + \text {coth}\left[ \sqrt{-\frac{\gamma _{1}}{8}}(\chi + \rho )\right] \right) , \end{aligned}$$
    (13)
    $$\begin{aligned} \mathcal {Q}_{8}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{2 \gamma _{2}}} \left( \frac{\text {cosh}[\sqrt{-2\gamma _{1}}(\chi + \rho )]}{\text {sinh}[\sqrt{-2\gamma _{1}}(\chi + \rho )]\pm i}\right) . \end{aligned}$$
    (14)
  4. 4.

    When \(\gamma _{0}=0\), \(\gamma _{1}<0\), and \(\gamma _{2}\ne 0 \), then

    $$\begin{aligned} \mathcal {Q}_{9}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{ \gamma _{2}}} \text {sec}\left[ \sqrt{-\gamma _{1}}(\chi + \rho )\right] , \end{aligned}$$
    (15)
    $$\begin{aligned} \mathcal {Q}_{10}(\chi )= \pm \sqrt{-\frac{\gamma _{1}}{ \gamma _{2}}} \text {csc}\left[ \sqrt{-\gamma _{1}}(\chi + \rho )\right] . \end{aligned}$$
    (16)
  5. 5.

    When \(\gamma _{0}=\frac{\gamma _{1}^2}{4 \gamma _{2}}\), \(\gamma _{1}>0\), \(\gamma _{2}> 0 \), and \(A_{1}^2- A_{2}^2>0\), then

    $$\begin{aligned} \mathcal {Q}_{11}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 2 \gamma _{2}}} \text {tan}\left[ \sqrt{\frac{\gamma _{1}}{2}}(\chi + \rho )\right] , \end{aligned}$$
    (17)
    $$\begin{aligned} \mathcal {Q}_{12}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 2 \gamma _{2}}} \text {cot}\left[ \sqrt{\frac{\gamma _{1}}{2}}(\chi + \rho )\right] , \end{aligned}$$
    (18)
    $$\begin{aligned} \mathcal {Q}_{13}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 2 \gamma _{2}}} \left( \text {tan}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] \pm \text {sec}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] \right) , \end{aligned}$$
    (19)
    $$\begin{aligned} \mathcal {Q}_{14}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 8 \gamma _{2}}} \left( \text {tan}\left[ \sqrt{\frac{\gamma _{1}}{8}}(\chi + \rho )\right] - \text {cot}\left[ \sqrt{\frac{\gamma _{1}}{8}}(\chi + \rho )\right] \right) , \end{aligned}$$
    (20)
    $$\begin{aligned} \mathcal {Q}_{15}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 2 \gamma _{2}}} \left( \frac{\pm \sqrt{A_{1}^2-A_{2}^2}-A_{1}\text {cos}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] }{A_{1}\text {sin}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] \pm A_{2}}\right) , \end{aligned}$$
    (21)
    $$\begin{aligned} \mathcal {Q}_{16}(\chi )= \pm \sqrt{\frac{\gamma _{1}}{ 2 \gamma _{2}}} \left( \frac{\text {cos}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] }{\text {sin}\left[ \sqrt{2\gamma _{1}}(\chi + \rho )\right] \pm 1}\right) . \end{aligned}$$
    (22)
  6. 6.

    When \(\gamma _{0}=0\), \(\gamma _{1}>0\), then

    $$\begin{aligned} \mathcal {Q}_{17}(\chi )= \frac{4 \gamma _{1} e^{\sqrt{\gamma _{1}}(\chi + \rho )}}{e^{\pm 2\sqrt{\gamma _{1}}(\chi + \rho )}-4 \gamma _{1} \gamma _{2}}, \end{aligned}$$
    (23)
    $$\begin{aligned} \mathcal {Q}_{18}(\chi )= \frac{\pm 4 \gamma _{1} e^{\pm \sqrt{\gamma _{1}}(\chi + \rho )}}{1- 4 \gamma _{1} \gamma _{2} e^{\pm 2\sqrt{\gamma _{1}}(\chi + \rho )} }. \end{aligned}$$
    (24)

3 Applications of MSSEM

In this portion, the MSSEM is applied to Eq. (2). At first, by inserting the transformation Eq. (4) into Eq. (2), we have

$$\begin{aligned} {{k}^{2}}\left( {{r}^{2}}-\mu \right) \mathcal {U}\left( \chi \right) -{{k}^{2}}\beta \mathcal {U}{{\left( \chi \right) }^{1+n}}-{{k}^{2}}v\mathcal {U}{{\left( \chi \right) }^{1+2n}}-{{k}^{4}}{{r}^{2}}{{\mathcal {U}}^{\prime \prime }}\left( \chi \right) =0. \end{aligned}$$
(25)

By using the transformation \(\mathcal {U}(\chi )^n=\mathcal {V}(\chi )\),

$$\begin{aligned} {{k}^{2}}{{n}^{2}}\left( {{r}^{2}}-\mu \right) \mathcal {V}{{\left( \chi \right) }^{2}}-{{k}^{2}}{{n}^{2}}\beta \mathcal {V}{{\left( \chi \right) }^{3}}-{{k}^{2}}{{n}^{2}}v\mathcal {V}{{\left( \chi \right) }^{4}}-{{k}^{4}}\left( 1-n \right) {{r}^{2}}{\mathcal {V}}'{{\left( \chi \right) }^{2}}-{{k}^{4}}n{{r}^{2}}\mathcal {V}\left( \chi \right) {{\mathcal {V}}^{\prime \prime }}\left( \chi \right) \end{aligned}$$
(26)

is attain. In this study, our focus will be on searching for solutions specifically for the \(n=1\) case. By using balance principle to Eq. (26), yields \(L=1\) and substituting Eq. (5)

$$\begin{aligned} \mathcal {U}(\chi )= \lambda _{0}+ \lambda _{1} \mathcal {Q}(\chi ) \end{aligned}$$
(27)

is obtain. Substituting Eq. (26) in Eq. (27), a system of nonlinear equations is obtained. By utilizing the computer program to solve the obtained system, we will examine the solutions by considering the following result from the obtained results:

$$\begin{aligned} \begin{aligned} Case 1: \lambda _{0}=\frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }, \lambda _{1}=-\frac{3\sqrt{-{{\gamma }_{2}}}\left( {{r}^{2}}-\mu \right) }{\sqrt{2}\beta \sqrt{{{\gamma }_{1}}}}, v=-\frac{2{{\beta }^{2}}}{9\left( {{r}^{2}}-\mu \right) }, k=\frac{\sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}. \end{aligned} \end{aligned}$$
(28)

Considering Eqs. (4), (27) and (28), we find solutions of Eq. (2) for the following situations.

  1. 1.

    When \(\gamma _{0}=0\), \(\gamma _{1}>0\), and \(\gamma _{2} \ne 0\), considering Eqs. (7) and (8) respectively, so the solutions of Eq. (2) are given by

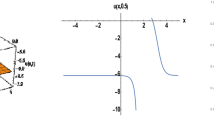
    $$\begin{aligned} u_{1}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) \left( 1-\sqrt{2}\text {sech}\left( \sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) \right) }{2\beta }, \end{aligned}$$
    (29)
    Fig. 1
    figure 1

    The graphics of Eq. (29) solution for \(\gamma _{1}=0.5\), \(r=-0.05\), \(\mu =-1.2\), \(\beta =0.04\), \(\gamma _{2}=2.5\), and \(\rho =1\)

    Full size image
    $$\begin{aligned} u_{2}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) \left( 1-\sqrt{-2}\text {csch}\left( \sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) \right) }{2\beta }. \end{aligned}$$
    (30)
    Fig. 2
    figure 2

    The graphics of Eq. (30) solution for \(\gamma _{1}=0.5\), \(r=0.05\), \(\mu =1.2\), \(\beta =0.04\), \(\gamma _{2}=-0.5\), and \(\rho =1\)

    Full size image
  2. 2.

    When \(\gamma _{0} = 0\), \(\gamma _{1} > 0\), and \(\gamma _{2} =\pm 4 \beta _{1} \beta _{2}\), considering Eq. (11), so the solution of Eq. (2) is given by

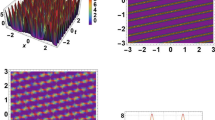
    $$\begin{aligned} \begin{aligned} u_{3}(x,t)=\frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -\frac{12\sqrt{-2{{\beta }_{1}}{{\beta }_{2}}}\left( {{r}^{2}}-\mu \right) }{\beta \left( \left( 4{{\beta }_{1}}-4{{\beta }_{2}} \right) \text {cosh} \left( \sqrt{{{\gamma }_{1}}}\left( {{\chi }_{0}}+\frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}} \right) \right) +\left( 4{{\beta }_{1}}+4{{\beta }_{2}} \right) \sinh \left( \sqrt{{{\gamma }_{1}}}\left( {{\chi }_{0}}+\frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}} \right) \right) \right) }.\\ \end{aligned} \end{aligned}$$
    (31)
    Fig. 3
    figure 3

    The graphics of Eq. (31) solution for \(\gamma _{1}=0.5\), \(r=1.75\), \(\mu =1.2\), \(\beta =4\), \(\eta _{0}=1\), \(\beta _{1} =2\) and \(\beta _{2} =3\)

    Full size image
  3. 3.

    When \(\gamma _{0} = \frac{\gamma _{1}^2}{4 \gamma _{2}}\), \(\gamma _{1} < 0\), and \(\gamma _{2} > 0\), considering Eqs. (10), (11), (12), (13) and (14) respectively, so the solutions of Eq. (2) are given by

    $$\begin{aligned} u_{4}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\left( {{r}^{2}}-\mu \right) \tanh \left( \frac{\sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) }{\sqrt{2}} \right) }{2\beta }. \end{aligned}$$
    (32)
    Fig. 4
    figure 4

    The graphics of Eq. (32) solution for \(\gamma _{1}=-0.2\), \(r=3\), \(\mu =1.2\), \(\beta =1.5\), \(\gamma _{2}=0.1\) and \(\rho =1\)

    Full size image
    $$\begin{aligned} u_{5}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\left( {{r}^{2}}-\mu \right) \coth \left[ \frac{\sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) }{\sqrt{2}} \right] }{2\beta } \end{aligned}$$
    (33)
    Fig. 5
    figure 5

    The graphics of (33) solution for \(\gamma _{1}=-0.5\), \(r=0.9\), \(\mu =2\), \(\beta =1.2\), \(\gamma _{2}=2\),, and \(\rho =1\)

    Full size image
    $$\begin{aligned} \begin{aligned} u_{6}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -\frac{3\left( {{r}^{2}}-\mu \right) \left( \text {i}\text {sech}\left( \sqrt{-2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) +\tanh \left( \sqrt{-2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) \right) }{2\beta }, \\ \end{aligned} \end{aligned}$$
    (34)
    $$\begin{aligned} \begin{aligned} u_{7}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta } \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -\frac{3\left( {{r}^{2}}-\mu \right) \left( \coth \left( \frac{\sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{2\sqrt{2}} \right) +\tanh \left( \frac{\sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{2\sqrt{2}} \right) \right) }{4\beta },\\ \end{aligned} \end{aligned}$$
    (35)
    $$\begin{aligned} u_{8}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\left( {{r}^{2}}-\mu \right) \cosh \left( \sqrt{-2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) }{2\beta \left( \text {i}+\sinh \left( \sqrt{-2\gamma 1}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) \right) }. \end{aligned}$$
    (36)
  4. 4.

    When \(\gamma _{0} = 0\), \(\gamma _{1} < 0\), and \(\gamma _{2} \ne 0\), considering Eqs. (15) and (16) respectively, so the solutions of Eq. (2) are given by

    $$\begin{aligned} u_{9}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\left( {{r}^{2}}-\mu \right) \sec \left( \sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) }{\sqrt{2}\beta }, \end{aligned}$$
    (37)
    $$\begin{aligned} u_{10}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\left( {{r}^{2}}-\mu \right) \csc \left( \sqrt{-{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) }{\sqrt{2}\beta }. \end{aligned}$$
    (38)
  5. 5.

    When \(\gamma _{0}=\frac{\gamma _{1}^2}{4 \gamma _{2}}\), \(\gamma _{1}>0\), and \(\gamma _{2}> 0 \), with constants \(A_{1}^2- A_{2}^2>0\), considering Eqs. (17), (18), (19), (20), (21), and (22) respectively, so the solutions of Eq. (2) are given by

    $$\begin{aligned} u_{11}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3i\left( {{r}^{2}}-\mu \right) \tan \left( \frac{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{\sqrt{2}} \right) }{2\beta }, \end{aligned}$$
    (39)
    Fig. 6
    figure 6

    The graphics of (39) solution for \(\gamma _{1}=2\), \(r=1.05\), \(\mu =1.7\), \(\beta =2.3\), \(\gamma _{2}=0.6\) and \(\rho =1\)

    Full size image
    $$\begin{aligned} u_{12}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\text {i}\left( {{r}^{2}}-\mu \right) \cot \left( \frac{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{\sqrt{2}} \right) }{2\beta } \end{aligned}$$
    (40)
    Fig. 7
    figure 7

    The graphics of (40) solution for \(\gamma _{1}=0.004\), \(r=0.1\), \(\mu =1.4\), \(\beta =1.25\), \(\gamma _{2}=2\) and \(\rho =1\)

    Full size image
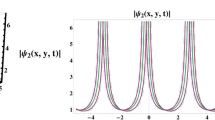
    $$\begin{aligned} \begin{aligned} u_{13}(x,t)=\frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,-\frac{3\text {i}\left( {{r}^{2}}-\mu \right) \left( \sec \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) +\tan \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) \right) }{2\beta },\\ \end{aligned} \end{aligned}$$
    (41)
    $$\begin{aligned} \begin{aligned} u_{14}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta } \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, -\frac{3\text {i}\left( {{r}^{2}}-\mu \right) \left( -\cot \left( \frac{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{2\sqrt{2}} \right) +\tan \left( \frac{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }{2\sqrt{2}} \right) \right) }{4\beta }, \\ \end{aligned} \end{aligned}$$
    (42)
    $$\begin{aligned} \begin{aligned} u_{15}(x,t)=\frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }\\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,-\frac{3\text {i}\left( {{r}^{2}}-\mu \right) \left( \sqrt{{{A}_{1}}^{2}-{{A}_{2}}^{2}}-{{A}_{1}}\cos \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) \right) }{2\beta \left( {{A}_{2}}+{{A}_{1}}\sin \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) \right) \right) }, \\ \end{aligned} \end{aligned}$$
    (43)
    Fig. 8
    figure 8

    The graphics of (43) solution for \(\gamma _{1}=0.5\), \(r=0.01\), \(\mu =0.2\), \(\beta =3\), \(\gamma _{2}=0.3\), \(A_{1}=0.1\), \(A_{2}=0.2\) and \(\rho =1\)

    Full size image
    $$\begin{aligned} u_{16}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{3\text {i}\left( {{r}^{2}}-\mu \right) \cos \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) }{2\beta \left( 1+\sin \left( \sqrt{2{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{r\sqrt{2{{\gamma }_{1}}}}+\rho \right) \right) \right) }. \end{aligned}$$
    (44)
    Fig. 9
    figure 9

    The graphics of (44) solution for \(\gamma _{1}=0.03\), \(r=2\), \(\mu =0.1\), \(\beta =1\), \(\gamma _{2}=0.01\) and \(\rho =1\)

    Full size image
  6. 6.

    When \(\gamma _{0}=0\), \(\gamma _{1}>0\), considering Eq. (23), and Eq. (24) respectively, so the solutions of Eq. (2) are given by

    $$\begin{aligned} u_{17}(x,t)= \frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{6\sqrt{2}{{\text {e}}^{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }}\sqrt{-{{\gamma }_{1}}{{\gamma }_{2}}}\left( {{r}^{2}}-\mu \right) }{\beta \left( {{\text {e}}^{2\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }}-4{{\gamma }_{1}}{{\gamma }_{2}} \right) }, \end{aligned}$$
    (45)
    $$\begin{aligned} u_{18}(x,t)=\frac{3\left( {{r}^{2}}-\mu \right) }{2\beta }-\frac{6\sqrt{2}{{\text {e}}^{\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }}\sqrt{-{{\gamma }_{1}}{{\gamma }_{2}}}\left( {{r}^{2}}-\mu \right) }{\beta \left( 1-4{{\text {e}}^{2\sqrt{{{\gamma }_{1}}}\left( \frac{\left( -rt+x \right) \sqrt{-{{r}^{2}}+\mu }}{\sqrt{2}r\sqrt{{{\gamma }_{1}}}}+\rho \right) }}{{\gamma }_{1}}{{\gamma }_{2}} \right) }. \end{aligned}$$
    (46)

4 Conclusions

This paper introduces a novel approach using MSSEM to analyze various solutions of the generalized Pochhammer Chree equation that describes the propagation of longitudinal deformation waves in an elastic rod. The generalized Pochhammer Chree equation is a fundamental equation in the field of solid mechanics. It characterizes the behavior of an elastic rod subjected to longitudinal forces or deformations. It takes into account the material properties of the rod, such as its elasticity and density, as well as the wave propagation characteristics, such as the wave speed. Through the solution of the equation, we gain the capability to analyze the behavior of the rod under diverse loading conditions. This enables a comprehensive study of the propagation of deformation waves along the length of the rod. By applying mathematical methods to address the equation, we unlock insights into how the rod responds to varying external forces or conditions, allowing for a detailed examination of the dynamic processes involved in the transmission of deformation waves. This analytical approach provides a valuable tool for understanding the intricate mechanics governing the rod’s response to different stimuli and contributes to a deeper comprehension of wave propagation phenomena in the context of structural materials. This equation is widely used in various fields, including structural engineering, mechanical engineering, and materials science, to understand and design structures and systems involving elastic rods. To provide a physical interpretation of the solutions and better understand this situation, we present them graphically in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9. Figures 1, 2, 3, 4, 5, 6, 7, 8, 9 shows how the settings have an influence. In addition, it can be interpreted from the figures that each solution is different and the solutions it belongs to have different structures.Muhammad et al. (yyy) Apart from this, it can be seen that the solutions found are different from studies such as solitary solutions (Yokus et al. 2022), periodic wave solutions (Parand and Rad 2010; Jaradat et al. 2022; Ali et al. 2020) and soliton solutions (Hussain et al. 2023). These figures visually depict the behavior and characteristics of the solutions, allowing for a clearer understanding of the propagation of longitudinal deformation waves in the elastic rod. Consequently, the solutions obtained are in the form of bright solutions for Eq. (29) as presented in Fig. 1, singular solutions for Eqs. (29), and (33) as shown in Figs. 2 and 5, trigonometric solutions for Eqs. (31), (43) and (44) as seen in Figs. 3,  8 and 8 , dark solutions for Eq. (32) as presented in Fig. 4, and periodic solutions for Eq. (39) and Eq. (40) as presented in Figs. 6 and Fig. 7. This diverse set of solution types provides valuable insights into the complex dynamics and phenomena associated with the propagation of longitudinal deformation waves in elastic rods. It showcases the effectiveness of these methods in capturing the rich complexity of nonlinear partial differential equations and their applications in fields such as physics, engineering, and applied mathematics.