1 Introduction

Optical applications of differential fractional approaches have been used for defining electric and magnetic phases in electromagnetic structures. These approaches generally are used to define the magnetic flux frequency circulations within the structures. Electromagnetic vector fields are presented by model and work of electromagnetic flow with fractional differential structures (de Andrade 2006; Maluf and Faria 2008; Körpinar and Körpinar 2021a, b; Körpınar et al. 2021a, b).

Associated curves bring important geometric definitions to fields of differential geometry, physics, and mathematics in explanation of the behavior of curves and surfaces and in work of particle motion in ordinary space. Also, concepts such as magnetic curves, Bertrand curves, spherical curves, and involute-evolute curve pairs have been widely investigated in fields of differential geometry (do Carmo 1976; Bishop 1975; Bukcu and Karacan 2008; Bükcü and Karacan 2009a; Karacan and Bukcu 2007a; Bükcü and Karacan 2009b; Karacan and Bukcu 2007b, 2008; Maluf and Faria 2008; Körpınar et al. 2021c).

There is no concrete calculation of entropy and energy in Minkowski spacetime in literature research. Diverse efforts have been made to define the energy using local-quasi concepts. But definitions of energy don’t match with each other all time and they are not suitable to spaces of anti de Sitter and de Sitter type (Hayward 1994; Martinez 1994; Epp 2000). It can be started with using local method to make any advancement on the notion of energy in this spacetime. Therefore, it can be said that one of most effective ways to achieve this method is to use geometric properties of particle moving in Minkowski spacetime. Moreover, it is examined that calculation of energy of a specific particle in many spacetimes has various applications (Körpinar 2014; Körpinar and Turhan 2015; Körpinar 2018; Körpinar and Demirkol 2017). Geometrical energy examined its ordinary optical geometric propriety for instances of geometrical physics. Also, diverse methods of geometric phases of energy and fractional magnetic flux for physical energy areas are presented and are computed F-W derivative on \({\mathbb {S}}_{1}^{2}\) by authors (Körpinar and Demirkol 2018; Körpinar 2022).

This work is organized as follows. Firstly, we have given basic definitions of Bishop frame equations for different type of spacelike magnetic curves in space. Then, we have presented a geometrical analysis of conformable energy for electromagnetic vector fields. In the following section, we have computed the conformable derivatives of the normalization and recursional electromagnetic vector fields. Finally, we have given conformable energies of normalization and recursional electromagnetic fields related to spacelike magnetic curves.

2 Preliminaries

Let \(\delta :I\rightarrow {\mathbb {E}}^{3}\) be unit speed magnetic curve. Thus, conformable derivatives according to \(\{\mathbf {t,{\textbf{n}}_{1}, {\textbf{n}}_{2}\}}\) Bishop frame are as

$$\begin{aligned} \nabla _{\delta ^{^{\prime }}}{\textbf{t}}= & {} v^{1-\sigma }k_{1}{\textbf{n}} _{1}+v^{1-\sigma }k_{2}{\textbf{n}}_{2}, \nonumber \\ \nabla _{\delta ^{^{\prime }}}{\textbf{n}}_{1}= & {} -v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{t}}, \nonumber \\ \nabla _{\delta ^{^{\prime }}}{\textbf{n}}_{2}= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{t}}. \end{aligned}$$
(1)

Here the vector product is as follows

$$\begin{aligned} \begin{array}{ccc} \epsilon _{{\textbf{t}}}{\textbf{t}}={\textbf{n}}_{1}\mathbf {\times {\textbf{n}}_{2}, }&\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {{\textbf{n}}_{1}}=\mathbf { {\textbf{n}}_{2}\mathbf {\times }t,}&\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {{\textbf{n}}_{2}}=\mathbf {t\times {\textbf{n}}_{1}.} \end{array} \end{aligned}$$

and where is \(\epsilon _{{\textbf{X}}}=g({\textbf{X}},{\textbf{X}}).\)

\(\blacklozenge ~\)Let \(\beta \) spacelike magnetic curves according to Bishop frame. Thus, Lorentz equations of magnetic fields are given as

$$\begin{aligned} \nabla _{\delta ^{{\prime }}}{\textbf{t}}= & {} \Pi \left( {\textbf{t}}\right) = {\textbf{G}} {\times }{\textbf{t}}, \nonumber \\ \nabla _{\delta ^{{\prime }}}{\textbf{n}}_{1}= & {} \Pi \left( {\textbf{n}} _{1}\right) ={\textbf{G}} {\times }{\textbf{n}}_{1}, \nonumber \\ \nabla _{\delta ^{{\prime }}}{\textbf{n}}_{2}= & {} \Pi \left( {\textbf{n}} _{2}\right) ={\textbf{G}} {\times }{\textbf{n}}_{2}. \end{aligned}$$
(2)

The first equation is named \({\textbf{t}}-spacelike\) magnetic curve;  the second equation is named \({\textbf{n}}_{1}-spacelike\) magnetic curve;  the third equation is named \({\textbf{n}} _{2}-spacelike\) magnetic curve.

\(~\blacklozenge ~\)Lorentz magnetic fields of \({\textbf{t}}-spacelike\) magnetic curve are given as

$$\begin{aligned} \begin{array}{c} \Pi ({\textbf{t}})=v^{1-\sigma }k_{1}{\textbf{n}}_{1}+v^{1-\sigma }k_{2}\textbf{n }_{2}, \\ \Pi ({\textbf{n}}_{1})=-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{t}}+\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ \Pi ({\textbf{n}}_{2})=-v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {t-}\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}, \\ \mathbf {G=}\rho \mathbf {t-}v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{n}}_{2}, \end{array} \end{aligned}$$
(3)

where \(\rho =g(\Pi \left( {\textbf{n}}_{1}\right) ,{\textbf{n}}_{2})\) is conformable differential potential.

\(\blacklozenge ~\)Lorentz magnetic fields of \({\textbf{n}}_{1}-spacelike\) magnetic curve are presented as

$$\begin{aligned} \Pi \left( {\textbf{t}}\right)= & {} v^{1-\sigma }k_{1}\epsilon _{\mathbf {\textbf{ n}_{1}}}{\textbf{n}}_{1}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu \mathbf {{\textbf{n}}_{2},} \\ \Pi \left( {\textbf{n}}_{1}\right)= & {} -v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}\textbf{t,} \\ \Pi \left( {\textbf{n}}_{2}\right)= & {} -\mu \textbf{t,} \\ {\textbf{G}}= & {} -\mu {\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {{\textbf{n}}_{2},} \end{aligned}$$

where \(\mu =g(\Pi \left( {\textbf{t}}\right) ,{\textbf{n}}_{2})\) is conformable differential potential.

\(\blacklozenge \) Lorentz magnetic fields of \({\textbf{n}}_{2}-spacelike\) magnetic curve are obtained as

$$\begin{aligned} \Pi \left( {\textbf{t}}\right)= & {} \gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{n}}_{1}+v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {{\textbf{n}}_{2},} \\ \Pi \left( {\textbf{n}}_{1}\right)= & {} -\gamma \textbf{t,} \\ \Pi \left( {\textbf{n}}_{2}\right)= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\textbf{t,} \\ {\textbf{G}}= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mathbf {{\textbf{n}}_{1}+}\gamma {\textbf{n}}_{2}, \end{aligned}$$

where \(\gamma =g(\Pi \left( {\textbf{t}}\right) ,{\textbf{n}}_{1})\) is conformable differential potential.

3 Conformable normalization and recursional functions of spacelike magnetic curves

Let\(\ \{\mathbf {t,{\textbf{n}}}_{1}\textbf{,n}_{2}\}\) be the Bishop frame, and conformable derivative system is

$$\begin{aligned} \ D_{\sigma }{\textbf{t}}= & {} v^{1-\sigma }k_{1}{\textbf{n}} _{1}+v^{1-\sigma }k_{2}{\textbf{n}}_{2}, \\ D_{\sigma }{\textbf{n}}_{1}= & {} -v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}}\textbf{t,} \\ D_{\sigma }{\textbf{n}}_{2}= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}\mathbf {t.} \end{aligned}$$

Here \(\mu =\det \left( \delta ,\textbf{t,}\nabla _{v}{\textbf{t}}\right) .\)

Normalization operator of \({\mathbb {V}}=a_{0}{\textbf{t}}+a_{1}{\textbf{n}} _{1}+a_{2}{\textbf{n}}_{2}\) is

$$\begin{aligned} {{\mathbb {N}}}{{\mathbb {V}}}={\textbf{I}}_{\sigma }^{a}(a_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}} }k_{1}v^{1-\sigma }+a_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2}v^{1-\sigma }){\textbf{t}}+a_{1}{\textbf{n}}_{1}+a_{2}{\textbf{n}}_{2}. \end{aligned}$$

Recursional operators \({\mathcal {R}}{\mathbb {V}}\) and \({\mathcal {R}}^{2}{\mathbb {V}}\) are

$$\begin{aligned} {\mathcal {R}}{\mathbb {V}}=-{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\mathbb {V }\right) , \end{aligned}$$

and

$$\begin{aligned} {\mathcal {R}}^{2}{\mathbb {V}}=-{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma } {\mathcal {R}}{\mathbb {V}}\right) . \end{aligned}$$

\(\mathbf {\spadesuit }\)The Lorentz magnetic fields of \({\textbf{t}} -spacelike\) magnetic curve are obtained as

$$\begin{aligned} \begin{array}{c} \Pi ({\textbf{t}})=v^{1-\sigma }k_{1}{\textbf{n}}_{1}+v^{1-\sigma }k_{2}\textbf{n }_{2}, \\ \Pi ({\textbf{n}}_{1})=-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{t}}+\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ \Pi ({\textbf{n}}_{2})=-v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {t-}\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}, \\ \mathbf {G=}\rho \mathbf {t-}v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{n}}_{2}. \end{array} \end{aligned}$$
(4)

Conformable derivatives of \({\textbf{t}}-spacelike\) magnetic curve Lorentz magnetic fields are

$$\begin{aligned} D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -((v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}+(v^{1-\sigma }k_{2})^{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}){\textbf{n}} _{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}){\textbf{n}}_{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} -(v^{1-\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma }k_{1})+\rho v^{1-\sigma }k_{2}){\textbf{t}} \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1})^{2}\textbf{ n}_{1}+(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}} })-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2}){\textbf{n}} _{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} (-v^{1-\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2})+\rho v^{1-\sigma }k_{1}){\textbf{t}} \\{} & {} -(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}})) {\textbf{n}}_{1}-\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2} {\textbf{n}}_{2}, \\ D_{\sigma }\textbf{G}= & {} v^{1-\sigma }\dfrac{d\rho }{dv}\mathbf {t+(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}} _{2}}}v^{1-\sigma }k_{2}))\textbf{n}_{1} \\{} & {} +\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))\textbf{n}_{2}. \end{aligned}$$

Normalization of these spacelike curves of Lorentz forces are

$$\begin{aligned} {\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} {\textbf{I}}_{\sigma }^{a}(\epsilon _{ \mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma })^{2}+\epsilon _{\mathbf { {\textbf{n}}_{2}}}(k_{2}v^{1-\sigma })^{2}){\textbf{t}} \\{} & {} +v^{1-\sigma }k_{1}{\textbf{n}}_{1}+v^{1-\sigma }k_{2}{\textbf{n}}_{2}, \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} {\textbf{I}}_{\sigma }^{a}(\rho k_{2}v^{1-\sigma }){\textbf{t}}+\rho \epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} -{\textbf{I}} _{\sigma }^{a}(\rho k_{1}v^{1-\sigma })\mathbf {t-}\rho \epsilon _{\mathbf { {\textbf{n}}_{1}}}{\textbf{n}}_{1}, \\ {\mathbb {N}}\textbf{G}= & {} c_{0}\mathbf {{\textbf{t}}-}v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}{\textbf{n}}_{2}, \end{aligned}$$

where \(c_{0}\) is constant of normalized function.

Thus, we get

$$\begin{aligned} D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -((v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}+(v^{1-\sigma }k_{2})^{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}){\textbf{n}} _{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}){\textbf{n}}_{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} -(v^{1-\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma }k_{1})+\rho v^{1-\sigma }k_{2}){\textbf{t}} \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1})^{2}\textbf{ n}_{1}+(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}} })-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2}){\textbf{n}} _{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} (-v^{1-\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2})+\rho v^{1-\sigma }k_{1}){\textbf{t}} \\{} & {} -(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}})) {\textbf{n}}_{1}-\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2} {\textbf{n}}_{2}, \\ D_{\sigma }\textbf{G}= & {} v^{1-\sigma }\dfrac{d\rho }{dv}\mathbf {t+(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}} _{2}}}v^{1-\sigma }k_{2}))\textbf{n}_{1} \\{} & {} +\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))\textbf{n}_{2}, \end{aligned}$$

and we have

$$\begin{aligned}{} & {} {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) =-v^{1-\sigma } \dfrac{d}{dv}(v^{1-\sigma }k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{n }_{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})\epsilon _{\mathbf { {\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\{} & {} {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right) =-(v^{1-\sigma } \dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}})-\epsilon _{\mathbf { {\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{n}}_{1}-\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\{} & {} {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right) =-\epsilon _{ \mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2}\epsilon _{\mathbf {{\textbf{n}} _{1}}}{\textbf{n}}_{1}+(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {\textbf{n }_{1}}}))\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\{} & {} {\textbf{t}}\times D_{\sigma }{\textbf{G}}=-\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}))\textbf{n}_{1}+\mathbf {(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }v^{1-\sigma }k_{2}))\textbf{n}_{2}, \end{aligned}$$

moreover, we have

$$\begin{aligned} {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right)= & {} {\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv} (v^{1-\sigma }k_{2}) \\{} & {} +v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1})){\textbf{t}}-v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{ n}_{1} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{1}\right) \right)= & {} -{\textbf{I}}_{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{ dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}}) \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})+v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}){\textbf{t}}-(v^{1-\sigma } \dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}}) \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})\epsilon _{ \mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-\epsilon _{\mathbf {{\textbf{n}} _{1}}}(v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}} _{2,} \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{2}\right) \right)= & {} {\textbf{I}}_{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} & {} +v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2} }}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}}))) {\textbf{t}} \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}} }))\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }{\textbf{G}}\right)= & {} {\textbf{I}} _{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf { (}\rho v^{1-\sigma }k_{2} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}}))+v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {(}\rho v^{1-\sigma }k_{1} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2})))\textbf{t}-\mathbf {(}v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\\{} & {} +\rho v^{1-\sigma }k_{2}))\textbf{n}_{1}+\mathbf {(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }v^{1-\sigma }k_{2}))\textbf{n}_{2}. \end{aligned}$$

Recursional operators of \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}} _{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) \) and \({\textbf{G}}\) magnetic fields are

$$\begin{aligned} {\mathcal {R}}\Pi \left( {\textbf{t}}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right) =-{\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv}(v^{1-\sigma }k_{2}) \\{} & {} +v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1})){\textbf{t}}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{ n}_{1} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right) \right) ={\textbf{I}} _{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf { {\textbf{n}}_{2}}}) \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})+v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}){\textbf{t}}+(v^{1-\sigma } \dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}}) \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})\epsilon _{ \mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+(v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right) \right) =-{\textbf{I}} _{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}} \\{} & {} +v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2} }}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}}}))) {\textbf{t}} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}} }))\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}{\textbf{G}}= & {} -{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }{\textbf{G}}\right) =-{\textbf{I}}_{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}\mathbf {(}\rho v^{1-\sigma }k_{2} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}}))+v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {(}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }v^{1-\sigma }k_{2}) \\{} & {} +\rho v^{1-\sigma }k_{1}))\textbf{t}+\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}))\textbf{n}_{1} \\{} & {} -\mathbf {(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{ \mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2}))\textbf{n}_{2}. \end{aligned}$$

\(\mathbf {\spadesuit }\) The Lorentz magnetic fields of \({\textbf{n}} _{1}-spacelike\) magnetic curve are

$$\begin{aligned} \Pi \left( {\textbf{t}}\right)= & {} v^{1-\sigma }k_{1}\epsilon _{\mathbf {\textbf{ n}_{1}}}{\textbf{n}}_{1}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu \mathbf {{\textbf{n}}_{2},} \\ \Pi \left( {\textbf{n}}_{1}\right)= & {} -v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}\textbf{t,} \\ \Pi \left( {\textbf{n}}_{2}\right)= & {} -\mu \textbf{t,} \\ {\textbf{G}}= & {} -\mu {\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {{\textbf{n}}_{2}.} \end{aligned}$$

Conformable derivatives of magnetic fields are

$$\begin{aligned} D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -((v^{1-\sigma }k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}})^{2}+\mu v^{1-\sigma }k_{2}){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}){\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{ \mathbf {{\textbf{n}}_{2}}}\mu ){\textbf{n}}_{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} -v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}){\textbf{t}} \\{} & {} -v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{n }_{1}-v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}} _{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} -v^{1-\sigma }\dfrac{d\mu }{dv} \mathbf {t-}\mu k_{1}v^{1-\sigma }{\textbf{n}}_{1}-\mu v^{1-\sigma }k_{2} {\textbf{n}}_{2}, \\ D_{\sigma }\textbf{G}= & {} (\mu \epsilon _{\mathbf {{\textbf{n}}_{1}} }k_{1}v^{2-2\sigma }-k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}v^{2-2\sigma }){\textbf{t}} \\{} & {} -v^{1-\sigma }\dfrac{d\mu }{dv}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv} (k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma }){\textbf{n}}_{2}. \end{aligned}$$

Normalizations of Lorentz fields are

$$\begin{aligned} {\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} {\textbf{I}}_{\sigma }^{a}((k_{1}v^{1-\sigma })^{2} \\{} & {} +\mu v^{1-\sigma }k_{2}){\textbf{t}} \\{} & {} +v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}\mathbf {+ }\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu \mathbf {{\textbf{n}}_{2},} \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} c_{1}\textbf{t,} \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} c_{2}{\textbf{t}}, \\ {\mathbb {N}}\textbf{G}= & {} {\textbf{I}}_{\sigma }^{a}\mathbf {(-}\mu \epsilon _{ \mathbf {{\textbf{n}}_{1}}}k_{1}v^{1-\sigma } \\{} & {} +v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}){\textbf{t}} \\{} & {} -\mu {\textbf{n}}_{1}+v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}}\mathbf {{\textbf{n}}_{2},} \end{aligned}$$

where \(c_{1},c_{2}\) are constants of normalized function.

Also, we have

$$\begin{aligned} {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -v^{1-\sigma } \dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )\epsilon _{\mathbf { {\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}} {\textbf{n}}_{2}, \\ {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}} _{1}}}{\textbf{n}}_{1}-v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf { {\textbf{n}}_{1}}}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} \mu v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}- \mu k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2} , \\ {\textbf{t}}\times D_{\sigma }{\textbf{G}}= & {} -v^{1-\sigma } \dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma })\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-v^{1-\sigma }\dfrac{d\mu }{dv} \epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \end{aligned}$$

and

$$\begin{aligned} {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right)= & {} \mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )+k_{2}v^{2-2\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))\mathbf {{\textbf{t}}} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf { {\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{1}\right) \right)= & {} \mathbf {{\textbf{I}}}_{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}-v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})\mathbf {{\textbf{t}}} \\{} & {} +v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{2}\right) \right)= & {} c_{3}\mathbf {{\textbf{t}}}+\mu v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-\mu k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }{\textbf{G}}\right)= & {} \mathbf { {\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}v^{1-\sigma })-v^{2-2\sigma }k_{2}\dfrac{d\mu }{dv}) \mathbf {{\textbf{t}}} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}} }v^{1-\sigma })\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-v^{1-\sigma }\dfrac{d\mu }{dv}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \end{aligned}$$

where is \(c_{3}\) recursion function.

Recursional \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) ,{\textbf{G}}\) magnetic fields are as following

$$\begin{aligned} {\mathcal {R}}\Pi \left( {\textbf{t}}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right) =-\mathbf {{\textbf{I}}} _{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {\textbf{n }_{2}}}\mu )+k_{2}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}))\mathbf {{\textbf{t}}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf { {\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right) \right) =-\mathbf {\textbf{ I}}_{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}-v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}) \mathbf {{\textbf{t}}} \\{} & {} -v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{\mathbf {{\textbf{n}} _{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right) \right) =c_{3}\mathbf { {\textbf{t}}}-\mu v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{ n}_{1}+\mu k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}} {\textbf{n}}_{2}, \\ {\mathcal {R}}\textbf{G}= & {} -{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\textbf{G }\right) =-\mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv }(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma })-v^{2-2\sigma }k_{2} \dfrac{d\mu }{dv})\mathbf {{\textbf{t}}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}} }v^{1-\sigma })\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d\mu }{dv}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}. \end{aligned}$$

\(\mathbf {\spadesuit }\)The Lorentz magnetic fields of \({\textbf{n}} _{2}-spacelike\) magnetic curve are

$$\begin{aligned} \Pi \left( {\textbf{t}}\right)= & {} \gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}} {\textbf{n}}_{1}+v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \mathbf {{\textbf{n}}_{2},} \\ \Pi \left( {\textbf{n}}_{1}\right)= & {} -\gamma \textbf{t,} \\ \Pi \left( {\textbf{n}}_{2}\right)= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\textbf{t,} \\ {\textbf{G}}= & {} -v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mathbf {{\textbf{n}}_{1}+}\gamma {\textbf{n}}_{2}. \end{aligned}$$

Conformable derivatives of Lorentz forces are

$$\begin{aligned} D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -((v^{1-\sigma }k_{2})^{2}+\gamma v^{1-\sigma }k_{1}){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1} }}){\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}){\textbf{n}}_{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} -v^{1-\sigma }\dfrac{d\gamma }{ dv}\mathbf {t-}\gamma k_{1}v^{1-\sigma }{\textbf{n}}_{1}-\gamma k_{2}v^{1-\sigma }{\textbf{n}}_{2}, \\ D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} -v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}){\textbf{t}} \\{} & {} -v^{2-2\sigma }k_{2}k_{1}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\textbf{ n}_{1}-v^{2-2\sigma }k_{2}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}} _{2}, \\ D_{\sigma }{\textbf{G}}= & {} (v^{2-2\sigma }\epsilon _{\mathbf {{\textbf{n}}_{1}} }\epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{1}k_{2}-\gamma k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }){\textbf{t}} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}){\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d\gamma }{dv}{\textbf{n}} _{2}. \end{aligned}$$

Normalizations of Lorentz fields are

$$\begin{aligned} {\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} {\textbf{I}}_{\sigma }^{a}(\gamma k_{1}v^{1-\sigma }+(k_{2}v^{1-\sigma })^{2}){\textbf{t}} \\{} & {} +\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+ v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {{\textbf{n}}_{2},} \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} c_{4}\textbf{t,} \\ {\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} c_{5}{\textbf{t}}, \\ {\mathbb {N}}\textbf{G}= & {} {\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}} _{1}}} \\{} & {} +v^{1-\sigma }\gamma \epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2})\textbf{t}- v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {{\textbf{n}}_{1}+} \gamma {\textbf{n}}_{2}, \end{aligned}$$

where \(c_{4,}\) \(c_{5}\) are constants of normalized function. Then, we get

$$\begin{aligned} {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right)= & {} -v^{1-\sigma } \dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}} {\textbf{n}}_{2}, \\ {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right)= & {} \gamma k_{2}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}- \gamma k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2} , \\ {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right)= & {} v^{2-2\sigma }k_{2}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}} _{1}}}{\textbf{n}}_{1}-v^{2-2\sigma }k_{2}k_{1}{\textbf{n}}_{2}, \\ {\textbf{t}}\times D_{\sigma }{\textbf{G}}= & {} v^{1-\sigma }\dfrac{d\gamma }{dv} \epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-v^{1-\sigma } \dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \end{aligned}$$

and

$$\begin{aligned} {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right)= & {} {\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})+k_{2}v^{2-2\sigma } \dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{t}} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}})\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{1-\sigma }\dfrac{ d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {\textbf{ n}_{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{1}\right) \right)= & {} c_{6}\mathbf {t+}\gamma k_{2}v^{1-\sigma }\epsilon _{ \mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1}-\gamma k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{n}} _{2}\right) \right)= & {} c_{7}\mathbf {t+}v^{2-2\sigma }k_{2}^{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1} -v^{2-2\sigma }k_{2}k_{1}{\textbf{n}}_{2}, \\ {\mathbb {N}}({\textbf{t}}\times D_{\sigma }\textbf{G})= & {} {\textbf{I}}_{\sigma }^{a}( \dfrac{d\gamma }{dv}v^{2-2\sigma }k_{1}-v^{2-2\sigma }k_{2}\dfrac{d}{dv} (v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d\gamma }{dv}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{ n}_{1}-v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \end{aligned}$$

where \(c_{6},\) \(c_{7}\) are constants of normalized potential.

Recursional operators of \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}} _{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) ,{\textbf{G}}\) magnetic fields are

$$\begin{aligned} {\mathcal {R}}\Pi \left( {\textbf{t}}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}}\times D_{\sigma }\Pi \left( {\textbf{t}}\right) \right) =-{\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}) \\{} & {} +k_{2}v^{2-2\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}} })){\textbf{t}}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}} _{1}-v^{1-\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}} })\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{1}\right) \right) =c_{6}\mathbf {t-} \gamma k_{2}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{1}}}{\textbf{n}}_{1} +\gamma k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}} {\textbf{n}}_{2}, \\ {\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= & {} -{\mathbb {N}}\left( {\textbf{t}} \times D_{\sigma }\Pi \left( {\textbf{n}}_{2}\right) \right) =c_{7}\mathbf {t-} v^{2-2\sigma }k_{2}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf { {\textbf{n}}_{1}}}{\textbf{n}}_{1}+v^{2-2\sigma }k_{2}k_{1}{\textbf{n}} _{2}, \\ {\mathcal {R}}{\textbf{G}}= & {} -\mathbb {N(}{\textbf{t}}\times D_{\sigma }\mathbf {G)}=- {\textbf{I}}_{\sigma }^{a}(\dfrac{d\gamma }{dv}v^{2-2\sigma }k_{1}-v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}})){\textbf{t}} \\{} & {} +v^{1-\sigma }\dfrac{d\gamma }{dv}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\textbf{ n}_{1}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}}{\textbf{n}}_{2}. \end{aligned}$$

4 Conformable energies of spacelike magnetic curves

In this section, we compute the conformable energy characterized by Sasaki metric of normalization and recursion operator of spacelike magnetic curves according to Bishop frame.

Let be Riemann manifolds \((M,\rho )\) and (s, h) magnetic energy of differentiable map \(q:(M,\rho )\rightarrow (s,h).\) Sasaki metric energy is characterized as the following

$$\begin{aligned} {\mathbb {E}}(q)=\dfrac{1}{2}\mathbf {\int }_{M}\sum h(dq(p_{a}),dq(p_{a}))\upsilon . \end{aligned}$$
(5)

Here \(\{p_{a}\}\) is base of ordinary space and \(\upsilon \) is canonical type in M.

4.1 Conformable energy of normalized electromagnetic fields

In this part, the conformable energy of normalized \(\Pi \left( {\textbf{t}} \right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) \) and \({\textbf{G}}\) electromagnetic fields are calculated. Also, geometrical and physical characterizations for energies of normalization operator of these electromagnetic fields are presented.

\(\mathbf {\spadesuit }\) The energy of normalized \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}} _{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{t}}-spacelike\)  magnetic curve are presented as following

$$\begin{aligned} D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} (v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\epsilon _{\mathbf {{\textbf{n}}_{1}} }(k_{1}v^{1-\sigma })^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}} }(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})){\textbf{n}}_{1} \\{} & {} +(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\epsilon _{\mathbf {{\textbf{n}} _{1}}}(k_{1}v^{1-\sigma })^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}} }(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} k_{1}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(\rho k_{2}v^{1-\sigma }){\textbf{n}} _{1}+(k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(\rho k_{2}v^{1-\sigma })+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2}}})) {\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} -(v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\rho k_{1}v^{1-\sigma })+v^{1-\sigma }\dfrac{d}{dv} (\rho \epsilon _{{\textbf{n}}_{1}})){\textbf{n}}_{1}-k_{2}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(\rho k_{1}v^{1-\sigma }){\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\textbf{G}= & {} (c_{0}v^{1-\sigma }k_{1}- v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}})){\textbf{n}}_{1}+\mathbf {(}c_{0}v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{ d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{2}, \end{aligned}$$

and we have conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\epsilon _{\mathbf {{\textbf{n}}_{1}} }(k_{1}v^{1-\sigma })^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}} }(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma }) ^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }) ^{2})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}))^{2}), \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(\rho k_{2}v^{1-\sigma }))^{2}+\epsilon _{\mathbf { {\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(\rho k_{2}v^{1-\sigma })+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf { {\textbf{n}}_{2}}}))^{2}), \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\rho k_{1}v^{1-\sigma })+v^{1-\sigma }\dfrac{d}{dv} (\rho \epsilon _{{\textbf{n}}_{1}}))^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}} }(k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(\rho k_{1}v^{1-\sigma }))^{2}), \\ {\mathbb {E}}({\mathbb {N}}\textbf{G})= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}c_{0}v^{1-\sigma }k_{1} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}))^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {(} c_{0}v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2}). \end{aligned}$$

\(\mathbf {\spadesuit }\) The energy of normalized \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}} _{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{n}} _{1}-spacelike\) magnetic curve are given as following

$$\begin{aligned} D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} (v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}((k_{1}v^{1-\sigma })^{2}+\mu v^{1-\sigma }k_{2}) \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}})){\textbf{n}}_{1}+(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}((k_{1}v^{1-\sigma })^{2} \\{} & {} +\mu v^{1-\sigma }k_{2})+v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mu )){\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} k_{1}v^{1-\sigma }c_{1}{\textbf{n}}_{1}+k_{2}v^{1-\sigma }c_{1}{\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} k_{1}v^{1-\sigma }c_{2}{\textbf{n}}_{1}+k_{2}v^{1-\sigma }c_{2}{\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\textbf{G}= & {} (v^{1-\sigma }k_{1}\mathbf {{\textbf{I}}} _{\sigma }^{a}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}} }\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} & {} -\mu \epsilon _{\mathbf {{\textbf{n}}_{1}}}k_{1}v^{1-\sigma })-v^{1-\sigma }\dfrac{d\mu }{dv}){\textbf{n}}_{1}+\mathbf {(}v^{1-\sigma }k_{2} \mathbf {{\textbf{I}}}_{\sigma }^{a}\mathbf {(-}\mu \epsilon _{\mathbf {{\textbf{n}} _{1}}}k_{1}v^{1-\sigma } \\{} & {} +v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{2}, \end{aligned}$$

and we obtain conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+(v^{1-\sigma }k_{1}{\textbf{I}}_{\sigma }^{a}((k_{1}v^{1-\sigma })^{2}+\mu v^{1-\sigma }k_{2})+v^{1-\sigma } \dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2} \\{} & {} +(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}((k_{1}v^{1-\sigma }) ^{2}+\mu v^{1-\sigma }k_{2})+v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mu ))^{2}, \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma }c_{1})^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }c_{1})^{2}), \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma }c_{2})^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }c_{2})^{2}) , \\ {\mathbb {E}}({\mathbb {N}}\mathbf {G)}= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}v^{1-\sigma }k_{1} \mathbf {{\textbf{I}}}_{\sigma }^{a}\mathbf {(-}\mu \epsilon _{\mathbf {{\textbf{n}} _{1}}}k_{1}v^{1-\sigma }+v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {\textbf{n }_{1}}}\epsilon _{\mathbf {{\textbf{n}}_{2}}})-v^{1-\sigma }\dfrac{d\mu }{dv} )^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {(}v^{1-\sigma }k_{2}\mathbf { {\textbf{I}}}_{\sigma }^{a}\mathbf {(-}\mu \epsilon _{\mathbf {{\textbf{n}}_{1}} }k_{1}v^{1-\sigma }+v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1} }}\epsilon _{\mathbf {{\textbf{n}}_{2}}})+v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2}). \end{aligned}$$

\(\mathbf {\spadesuit }\) The energy of normalized \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}} _{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{n}} _{2}-spacelike\) magnetic curve are presented as following

$$\begin{aligned} D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{t}}\right)= & {} (v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\gamma k_{1}v^{1-\sigma }+(k_{2}v^{1-\sigma })^{2}) \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})) {\textbf{n}}_{1}+(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\gamma k_{1}v^{1-\sigma } \\{} & {} +(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right)= & {} k_{1}v^{1-\sigma }c_{4}{\textbf{n}}_{1}+k_{2}v^{1-\sigma }c_{4}{\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right)= & {} k_{1}v^{1-\sigma }c_{5}{\textbf{n}}_{1}+k_{2}v^{1-\sigma }c_{5}{\textbf{n}}_{2}, \\ D_{\sigma }{\mathbb {N}}\textbf{G}= & {} (v^{1-\sigma }k_{1}\mathbf {{\textbf{I}}} _{\sigma }^{a}\mathbf {(-}v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {\textbf{n }_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}} \\{} & {} +v^{1-\sigma }\gamma \epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2}) -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}})){\textbf{n}}_{1} \\{} & {} +\mathbf {(}v^{1-\sigma }k_{2}\mathbf {{\textbf{I}}}_{\sigma }^{a}\mathbf {(-} v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{ \mathbf {{\textbf{n}}_{1}}} \\{} & {} +v^{1-\sigma }\gamma \epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2}) +v^{1-\sigma }\dfrac{d\gamma }{dv}){\textbf{n}}_{2}, \end{aligned}$$

and we obtain conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}((v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\gamma k_{1}v^{1-\sigma }+(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}} })))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\gamma k_{1}v^{1-\sigma }+(k_{2}v^{1-\sigma })^{2})+v^{1-\sigma } \dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}))^{2}) , \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma }c_{4})^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }c_{4})^{2}) , \\ {\mathbb {E}}({\mathbb {N}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{I }_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(k_{1}v^{1-\sigma }c_{5})^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}(k_{2}v^{1-\sigma }c_{5})^{2}) , \\ {\mathbb {E}}({\mathbb {N}}\mathbf {G)}= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}v^{1-\sigma }k_{1} \mathbf {{\textbf{I}}}_{\sigma }^{a}\mathbf {(-}v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}}+v^{1-\sigma }\gamma \epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2}) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}))^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {(}v^{1-\sigma }k_{2} \mathbf {{\textbf{I}}}_{\sigma }^{a}\mathbf {(-}v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}}+v^{1-\sigma }\gamma \epsilon _{\mathbf {{\textbf{n}}_{2}}}k_{2})+v^{1-\sigma } \dfrac{d\gamma }{dv})^{2}. \end{aligned}$$

4.2 Conformable energy of recursional electromagnetic fields

In this part, the conformable energy of recursional \(\Pi \left( {\textbf{t}} \right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) \) and \({\textbf{G}}\) electromagnetic fields are computed.

\(\mathbf {\spadesuit }\) The energy of recursional \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}} _{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{t}}-spacelike\)  magnetic curve are given as following

$$\begin{aligned} D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{t}}\right)= {} (-v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv}(v^{1-\sigma }k_{2})+v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1})) \\{} {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{1}+(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv}(v^{1-\sigma }k_{2}) \\{} {} +v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1}))-v^{1-\sigma }\dfrac{d }{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})\epsilon _{\mathbf { {\textbf{n}}_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= {} (k_{1}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{ \mathbf {{\textbf{n}}_{2}}})-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})+v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}} \\{} {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{ \mathbf {{\textbf{n}}_{2}}})-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})){\textbf{n}}_{1}+(k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{2} }}) \\{} {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})+v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})+v^{1-\sigma }\dfrac{d}{dv }((v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= {} -(v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}+v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf { {\textbf{n}}_{1}}})) \\+v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{1}-( k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}+v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} {} +v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}} }))+v^{1-\sigma }\dfrac{d}{dv}((v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {\textbf{n }_{1}}}))\epsilon _{\mathbf {{\textbf{n}}_{2}}}){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\textbf{G}= {} (v^{1-\sigma }k_{1}{\textbf{I}}_{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}\mathbf {))+}v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mathbf {(}\rho v^{1-\sigma }k_{1} \\{} {} -v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2}\mathbf {))+}v^{1-\sigma }\dfrac{d}{dv}(\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}})\mathbf {\mathbf {)})n}_{1} \\{} {} +\mathbf {(}v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}\mathbf {))+}v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}} _{2}}}\mathbf {(}\rho v^{1-\sigma }k_{1} \\{} {} -v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2}\mathbf {))-}v^{1-\sigma }\dfrac{d}{dv}\mathbf {(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }v^{1-\sigma }k_{2}\mathbf {)))n}_{2}, \end{aligned}$$

moreover, we have conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv}(v^{1-\sigma }k_{2})+v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1})) \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2})\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2}+\epsilon _{\mathbf {\textbf{n }_{2}}}(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1} \dfrac{d}{dv}(v^{1-\sigma }k_{2}) \\{} & {} +v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1}))-v^{1-\sigma }\dfrac{d }{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1})\epsilon _{\mathbf { {\textbf{n}}_{2}}}))^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}((k_{1}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{ \mathbf {{\textbf{n}}_{2}}})-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2}) \\{} & {} +v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}} _{2}}})-\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2}))^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}}}((k_{2}v^{1-\sigma } {\textbf{I}}_{\sigma }^{a}(k_{1}(v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{ \mathbf {{\textbf{n}}_{2}}}) \\{} & {} -\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{2-2\sigma }k_{1}k_{2})+v^{3-3\sigma }k_{2}k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})+v^{1-\sigma }\dfrac{d}{dv }((v^{1-\sigma }k_{1})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}))^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}+v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}} \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}} }))+v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }(v^{1-\sigma }k_{2})^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})^{2}+\epsilon _{ \mathbf {{\textbf{n}}_{2}}}(\mathcal {(}k_{2}v^{1-\sigma }{\textbf{I}}_{\sigma }^{a}(v^{3-3\sigma }k_{1}k_{2}{}^{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}} \\{} & {} +v^{1-\sigma }k_{2}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2} }}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {{\textbf{n}}_{1}} }))+v^{1-\sigma }\dfrac{d}{dv}((v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}+v^{1-\sigma }\dfrac{d}{dv}(\rho \epsilon _{\mathbf {\textbf{n }_{1}}}))\epsilon _{\mathbf {{\textbf{n}}_{2}}})^{2}), \\ {\mathbb {E}}({\mathcal {R}}\textbf{G})= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1}{\textbf{I}} _{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf { (}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})) \\{} & {} +v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mathbf {(} \rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf { {\textbf{n}}_{2}}}v^{1-\sigma }k_{2}))+v^{1-\sigma }\dfrac{d}{dv} (\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\mathbf {(}\rho v^{1-\sigma }k_{2}+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}))+v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mathbf {(}\rho v^{1-\sigma }k_{1} \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}v^{1-\sigma }k_{2}))-v^{1-\sigma }\dfrac{d}{dv}\mathbf {(}\rho v^{1-\sigma }k_{1}-v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}} }v^{1-\sigma }k_{2})))^{2}). \end{aligned}$$

\(\mathbf {\spadesuit }\) The energy of recursional \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{n}} _{1}-spacelike\) magnetic curve are presented as following

$$\begin{aligned} D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{t}}\right)= {} (-v^{1-\sigma }k_{1} \mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )+k_{2}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})) \\{} {} +v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf { {\textbf{n}}_{2}}}\mu )\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}} _{1}+(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{ d}{dv}(v^{1-\sigma }k_{2}) \\{} {} +v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1}))-v^{1-\sigma }\dfrac{d }{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}})\epsilon _{\mathbf {{\textbf{n}}_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= {} (v^{1-\sigma }\dfrac{ d}{dv}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}-k_{1}v^{1-\sigma }\mathbf {{\textbf{I}}}_{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }-v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})))\textbf{n}_{1} \\{} {} +(-k_{2}v^{1-\sigma }\mathbf {{\textbf{I}}}_{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}-v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}})+v^{1-\sigma }\dfrac{d}{dv }(v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}\epsilon _{ \mathbf {{\textbf{n}}_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= {} (v^{1-\sigma }k_{1}c_{3}-v^{1-\sigma }\dfrac{d}{dv}(\mu v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{1}+(v^{1-\sigma }k_{2}c_{3}+v^{1-\sigma }\dfrac{d}{dv}(\mu k_{1}v^{1-\sigma }\epsilon _{ \mathbf {{\textbf{n}}_{2}}}){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\textbf{G}= {} (-v^{1-\sigma }k_{1}\mathbf {{\textbf{I}}} _{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}v^{1-\sigma })-v^{2-2\sigma }k_{2}\dfrac{d\mu }{dv})\mathbf {+ }v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}v^{1-\sigma })))\textbf{n}_{1} \\{} {} +\mathbf {(-}v^{1-\sigma }k_{2}\mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}} _{1}}}v^{1-\sigma })-v^{2-2\sigma }k_{2}\dfrac{d\mu }{dv})+ v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d\mu }{dv}\epsilon _{\mathbf { {\textbf{n}}_{2}}})){\textbf{n}}_{2}, \end{aligned}$$

moreover, we have conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-v^{1-\sigma }k_{1} \mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu ) \\{} & {} +k_{2}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf { {\textbf{n}}_{1}}}))+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv} (\epsilon _{\mathbf {{\textbf{n}}_{2}}}\mu )\epsilon _{\mathbf {{\textbf{n}}_{1}} }))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-v^{2-2\sigma }k_{1}\dfrac{d}{dv}(v^{1-\sigma }k_{2})+v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{1})) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {{\textbf{n}}_{2}} }))^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-k_{1}v^{1-\sigma } \mathbf {{\textbf{I}}}_{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}} \\{} & {} -v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}} })+v^{1-\sigma }\dfrac{d}{dv}(v^{2-2\sigma }k_{1}k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(-k_{2}v^{1-\sigma }\mathbf {{\textbf{I}}} _{\sigma }^{a}(v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}} }-v^{2-2\sigma }k_{1}^{2}k_{2}\epsilon _{\mathbf {{\textbf{n}}_{1}}}) \\{} & {} +v^{1-\sigma }\dfrac{d}{dv}(v^{2-2\sigma }k_{1}^{2}\epsilon _{\mathbf { {\textbf{n}}_{1}}}\epsilon _{\mathbf {{\textbf{n}}_{2}}}))^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1}c_{3}-v^{1-\sigma }\dfrac{d}{dv}(\mu v^{1-\sigma }k_{2}\epsilon _{ \mathbf {{\textbf{n}}_{1}}})^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma } \dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma })))^{2}) , \\ {\mathbb {E}}({\mathcal {R}}\textbf{G})= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-v^{1-\sigma }k_{1} \mathbf {{\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv} (k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}}}v^{1-\sigma }) \\{} & {} -v^{2-2\sigma }k_{2}\dfrac{d\mu }{dv})+v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{\mathbf {{\textbf{n}}_{1}} }v^{1-\sigma })))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(-v^{1-\sigma }k_{2}\mathbf { {\textbf{I}}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(k_{1}\epsilon _{ \mathbf {{\textbf{n}}_{1}}}v^{1-\sigma }) \\{} & {} -v^{2-2\sigma }k_{2}\dfrac{d\mu }{dv})+v^{1-\sigma }\dfrac{d}{dv} (v^{1-\sigma }\dfrac{d\mu }{dv}\epsilon _{\mathbf {{\textbf{n}}_{2}}}))^{2}). \end{aligned}$$

\(\mathbf {\spadesuit }\) The energy of recursional \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}} _{2}\right) ,{\textbf{G}}\) magnetic fields for \({\textbf{n}} _{2}-spacelike\) magnetic curve are given as following

$$\begin{aligned} D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{t}}\right)= & {} (-v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}) \\{} & {} +k_{2}v^{2-2\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}} }))+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{1}} })){\textbf{n}}_{1} \\{} & {} +(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{ dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})+k_{2}v^{2-2\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d }{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {\textbf{n }_{2}}})){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right)= & {} (v^{1-\sigma }k_{1}c_{6}-v^{1-\sigma }\dfrac{d}{dv}(\gamma k_{2}v^{1-\sigma }\epsilon _{ \mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{1} \\{} & {} +(v^{1-\sigma }k_{2}c_{6}+v^{1-\sigma }\dfrac{d}{dv}(\gamma k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}}}){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right)= & {} (v^{1-\sigma }k_{1}c_{7}-v^{1-\sigma }\dfrac{d}{dv}(v^{2-2\sigma }k_{2}^{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}})){\textbf{n}}_{1} \\{} & {} +(v^{1-\sigma }k_{2}c_{7}+v^{1-\sigma }\dfrac{d}{dv}(v^{2-2\sigma }k_{2}k_{1}){\textbf{n}}_{2}, \\ D_{\sigma }{\mathcal {R}}\textbf{G}= & {} (-v^{1-\sigma }k_{1}{\textbf{I}}_{\sigma }^{a}(\dfrac{d\gamma }{dv}v^{2-2\sigma }k_{1}-v^{2-2\sigma }k_{2}\dfrac{d}{dv }(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d\gamma }{dv} \epsilon _{\mathbf {{\textbf{n}}_{1}}})))\textbf{n}_{1}+\mathbf {(-}v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\dfrac{d\gamma }{dv}v^{2-2\sigma }k_{1} \\{} & {} -v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}))+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d }{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{ \mathbf {{\textbf{n}}_{2}}})){\textbf{n}}_{2}, \end{aligned}$$

and we obtain conformable energy

$$\begin{aligned} {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{t}}\right) )= & {} \dfrac{1}{2}{\textbf{I}} _{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}}) \\{} & {} +k_{2}v^{2-2\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}} }))+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{\mathbf {{\textbf{n}}_{1}} }))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(-k_{1}v^{2-2\sigma }\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}})+k_{2}v^{2-2\sigma }\dfrac{d}{dv}(\gamma \epsilon _{\mathbf { {\textbf{n}}_{1}}})) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d }{dv}(\gamma \epsilon _{\mathbf {{\textbf{n}}_{1}}})\epsilon _{\mathbf {\textbf{n }_{2}}}))^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{1}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1}c_{6}-v^{1-\sigma }\dfrac{d}{dv}(\gamma k_{2}v^{1-\sigma }\epsilon _{ \mathbf {{\textbf{n}}_{1}}}))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2}c_{6}+v^{1-\sigma } \dfrac{d}{dv}(\gamma k_{1}v^{1-\sigma }\epsilon _{\mathbf {{\textbf{n}}_{2}} })^{2}), \\ {\mathbb {E}}({\mathcal {R}}\Pi \left( {\textbf{n}}_{2}\right) )= & {} \dfrac{1}{2}\textbf{ I}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(v^{1-\sigma }k_{1}c_{7}-v^{1-\sigma }\dfrac{d}{dv}(v^{2-2\sigma }k_{2}^{2}\epsilon _{ \mathbf {{\textbf{n}}_{2}}}\epsilon _{\mathbf {{\textbf{n}}_{1}}}))^{2} \\{} & {} +\epsilon _{\mathbf {{\textbf{n}}_{2}}}(v^{1-\sigma }k_{2}c_{7}+v^{1-\sigma } \dfrac{d}{dv}(v^{2-2\sigma }k_{2}k_{1})^{2}), \\ {\mathbb {E}}({\mathcal {R}}\textbf{G})= & {} \dfrac{1}{2}{\textbf{I}}_{\sigma }^{a}(1+\epsilon _{\mathbf {{\textbf{n}}_{1}}}(-v^{1-\sigma }k_{1} {\textbf{I}}_{\sigma }^{a}(\dfrac{d\gamma }{dv}v^{2-2\sigma }k_{1}-v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}})) \\{} & {} -v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d\gamma }{dv} \epsilon _{\mathbf {{\textbf{n}}_{1}}})))^{2}+\epsilon _{\mathbf {{\textbf{n}}_{2}} }(-v^{1-\sigma }k_{2}{\textbf{I}}_{\sigma }^{a}(\dfrac{d\gamma }{dv} v^{2-2\sigma }k_{1} \\{} & {} -v^{2-2\sigma }k_{2}\dfrac{d}{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf { {\textbf{n}}_{2}}}))+v^{1-\sigma }\dfrac{d}{dv}(v^{1-\sigma }\dfrac{d }{dv}(v^{1-\sigma }k_{2}\epsilon _{\mathbf {{\textbf{n}}_{2}}})\epsilon _{ \mathbf {{\textbf{n}}_{2}}})^{2}). \end{aligned}$$

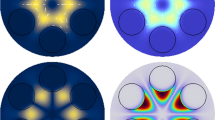
The application of recursional \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) \) enegies of the system can be evaluated with different volume fractions for different conformable permeability. The evaluation of energy is based in heat conformable transfer and potential of friction with viscosity and thermal conformable \(\Pi \left( {\textbf{t}}\right) ,\Pi \left( {\textbf{n}}_{1}\right) ,\Pi \left( {\textbf{n}}_{2}\right) \) conductivity in Figs. 1, 2 and 3.

Fig. 1
figure 1

Recursional\(\Pi \left( {\textbf{t}}\right) \) energy with conformable permeability

Full size image
Fig. 2
figure 2

Recursional\(\Pi \left( {\textbf{n}}_{1}\right) \) energy with conformable permeability

Full size image
Fig. 3
figure 3

Recursional\(\Pi \left( {\textbf{n}}_{2}\right) \) energy with conformable permeability

Full size image

5 Conclusions

In this paper, we have investigated spacelike magnetic curves according to Bishop frame. Firstly, we have presented conformable derivatives of Lorentz magnetic fields of these magnetic curves. Moreover, we have calculated the conformable derivatives of the normalization and recursional electromagnetic vector fields. Finally, we obtain conformable energy of the normalization and recursional operators for these electromagnetic fields associated with Bishop frame.