1 Introduction

Soliton theory is a branch of mathematics and physics that focuses on the study of solitons, specifically, the mathematical description, properties, and behavior of these solitary wave solutions to nonlinear partial differential equations (NLPDEs) (Kudryashov 2023a, b; Kudryashov and Nifontov 2023; Kudryashov et al. 2023; Rizvi et al. 2021; Rezazadeh et al. 2021; Triki et al. 2017; Iqbal et al. 2023; Cinar et al. 2023b; Peng et al. 2023; Onder et al. 2022; Ozdemir et al. 2022; Malik et al. 2022, 2023a; Yadav et al. 2023; Malik et al. 2023b; Akbar et al. 2022; Islam et al. 2022a, b, c, 2023b; Abdullah et al. 2023; ur Rehman et al. 2022; Ullah et al. 2022; Younis et al. 2014; Rehman et al. 2022a; Fahad et al. 2023; Rehman et al. 2022b, 2023a; Nasreen et al. 2023c; Seadawy et al. 2019; Nasreen et al. 2018). It plays a crucial role in understanding phenomena observed in various physical systems, including fluid dynamics (Shen et al. 2021; Ma et al. 2021; Islam et al. 2023c; Yokuş et al. 2022), water waves (Akbar et al. 2023), optics (Chen et al. 2012; Hasegawa 2000; Islam et al. 2023a; Boulaaras et al. 2023; Rehman et al. 2021, 2022c, 2023b; ur Rehman and Ahmad 2023; Akram et al. 2023), and plasma physics (Deng et al. 2020; Khalique and Adeyemo 2021). Soliton theory has practical applications in various fields. For example, solitons are essential in the field of fiber optics for long-distance data transmission (Kodama and Nozaki 1987; Ahmad et al. 2023; Nasreen et al. 2023a, b). They also serve a function in comprehending rogue waves in fluid dynamics and other phenomena in different working areas of physics (Ren et al. 2022; Ismael et al. 2023) and engineering. Overall, soliton theory provides a mathematical framework for understanding the behavior of solitons and has contributed to advancements in diverse scientific and technological areas. Researchers continue to explore new soliton equations and their applications, expanding our understanding of these intriguing nonlinear wave phenomena.

In many cases, the nonlinear Schrödinger equation (NLSE), which is a NLPDE that includes terms representing both dispersion and nonlinearity describes the dynamics of solitons. The NLSE is a fundamental equation in soliton theory and has solutions that describe the evolution of solitons over time and space. As is known to all, dozens forms of the NLSE have been attained and these forms have been subjected to perusal by many researchers. Some of these investigations are: the higher order NLSE with Kudryashov’s sextic power-law of nonlinear refractive index (Ozisik et al. 2023a; Samir et al. 2023), the NLSE with Kudryashov’s law arbitrary refractive index and generalized non-local laws of nonlinearity (Zayed et al. 2022), a generalized NLSE including dual power-law media (Triki et al. 2019), the perturbed NLSE with cubic-quartic dispersive including parabolic non-local combo law nonlinearity (Zayed et al. 2021a), the highly dispersive NLSE having cubic-quintic-septic law nonlinearity (Az-Zo’bi et al. 2022; Kohl et al. 2019), the higher-order NLSE with cubic and quintic nonlinearities (Triki and Kruglov 2022), the cubic-quartic NLSE with the parabolic law media in birefringent fibers (Li and Kai 2023), the resonant NLSE including Kerr, parabolic, power, dual-power, triple-power, parabolic law with non-local, polynomial, anti-cubic, quadratic-cubic, generalized anti-cubic, generalized quadratic-cubic nonlinearities in the presence of spatio-temporal dispersion (STD) and inter-modal dispersion (IMD) (Ozisik et al. 2023b), the NLSE with anti-cubic law nonlinearity (Ozisik et al. 2023c), the three-component coupled NLSE (Malik et al. 2023c), the NLSE with parabolic law and non-local law non-linearities (Yao et al. 2023), the stochastic (2+1)-dimensional chiral NLSE with multiplicative noise in the Itô sense (Rehman et al. 2023c).

In this paper, the third-order (1+1)-NLSE (Al-Kalbani et al. 2021) with power-law of self-phase modulation (SPM), STD and IMD in the absence of chromatic dispersion is given as:

$$\begin{aligned} i \left( \Theta _t+ \alpha \Theta _{xxx}\right) +\gamma \Theta _{xt}+\left( \beta \Theta +i\lambda \Theta _x\right) |\Theta |^{2p}+i\mu \Theta \left( |\Theta |^{2p}\right) _x=i\tau \Theta _{x}. \end{aligned}$$
(1)

Herein, \(\Theta =\Theta (x,t)\) refers to the complex soliton profile, x, t are the independent spatial and temporal variables, \(i\Theta _{t}\) stands for the general representation of evolution term, \(\alpha \), \(\gamma \) denote the coefficients of third-order dispersion, the STD terms, respectively. Besides, \(\beta \) is the coefficient of the power law media parameter that explicates SPM. The exponent p stands for the type of power law media and it is necessary that \(p \ne 0\). Furthermore, the coefficients of \(\lambda \) and \(\mu \) express the nonlinear dispersion effects, and \(\tau \) indicates the coefficient of the inter-modal dispersion term. Besides \(\alpha \), \(\gamma \), \(\beta \), \(\lambda \), \(\mu \) and \(\tau \) represent the real constants.

The third-order NLSE with power law nonlinearity in the absence of chromatic dispersion is a specific form of the NLSE that considers third-order nonlinearity with a power-law dependence on intensity and ignores the effects of chromatic dispersion. This type of model is often employed to study the behavior of optical pulses in fiber optics and other nonlinear optical systems. Researchers use such models to gain insights into the dynamics of optical wave propagation in media with specific nonlinear characteristics. The absence of chromatic dispersion means that the equation does not consider the spreading of different frequency components, focusing solely on the nonlinear effects on the pulse envelope as it propagates through the medium. Chromatic dispersion and self-phase modulation are often interconnected in optical communication systems. The dispersion-induced pulse broadening can increase the intensity of the optical pulse, leading to self-phase modulation. In turn, self-phase modulation can cause spectral broadening, which can exacerbate the effects of chromatic dispersion. The interplay between these two phenomena is a critical consideration in designing high-speed and long-distance optical communication systems. The absence of chromatic dispersion in an optical communication system is a desirable condition because chromatic dispersion can lead to signal degradation and limitations on the data-carrying capacity of the system. When chromatic dispersion is effectively eliminated or minimized, it allows for better signal quality and longer-distance communication without significant signal distortion. Why the absence of chromatic dispersion is important is explained in the cited studies (Younas et al. 2021; Zahran and Bekir 2022; Zayed et al. 2020; Rehman et al. 2022d; Yıldırım et al. 2020; Zayed et al. 2021b; Biswas et al. 2021). One of the sensitive points in soliton transmission is maintaining the balance between the chromatic dispersion and self-phase modulation. For this reason, the interaction between them is important. However, in 2016, it was shown in a laboratory study by Redondo et al. that the effect of the absence of the chromatic dispersion term on soliton transmission is not undeniably large (Blanco-Redondo et al. 2016). Such studies are generally referred to as pure quartic solitons in the literature. At the same time, pure cubic soliton studies containing third-order nonlinear terms have become the focus of attention of many researchers, especially recently. In this respect, the problem examined in the study includes the analysis of the power-law form of the pure cubic form, and many possible studies on the interaction of the cubic form with self-phase modulation are still waiting for researchers to focus on.

The study of solitons with power law media is crucial in understanding the behavior of optical pulses in nonlinear media. It has implementations in the optimization and envisagement of optical communication systems, where solitons can be employed for long-distance transmission of information. Researchers use mathematical methods, such as the inverse scattering transform and numerical simulations, to analyze and predict soliton behavior in systems with power law nonlinearity. Some examples of these studies such as the Biswas-Milovic equation (BME) with Kerr, parabolic and power laws (Altun et al. 2022), the perturbed NLSE including triple power and cubic-quintic-septic laws (Cinar et al. 2023a), the BME with dual-power and power laws (Eslami and Mirzazadeh 2016), the Korteweg-de Vries equation (KDV) (Biswas 2009), the nonlinear Zakharov-Kuznetsov equation (Baskonus et al. 2016), the Boussinesq equation (Ekici et al. 2016) with power law media.

The rest of the work is structured as: The NODE (nonlinear ordinary differential equation) form is acquired by making use of a complex transformation in Sect. 2. We sum up the new Kudryashov method (nKM) and give their implementations in Sect. 3. We tackle with the modulation instability analysis in Sect. 4. The acquired results are explicated in Sect. 5. The conclusion is given in Sect. 6.

2 Obtaining the NODE form of Eq. (1)

In order to acquire the NODE structure of Eq. (1), we take advantage of the following complex wave transformation:

$$\begin{aligned} \Theta (x,t)=\Theta (\zeta )\, e^{i\Psi \left( x,t\right) }, \,\,\, \Psi \left( x,t\right) =ax+\omega t+\varphi _{0}, \,\,\, \zeta =kx+vt. \end{aligned}$$
(2)

Herein, \(a,\omega , \varphi _{0}, k\) and v are real numbers. \(\Theta (\zeta )\) denotes the soliton pulse profile, \(\varphi _{0}\) is the phase constant, and \(a, \omega \) represent the wave number and the frequency, respectively. Besides, k refers to the width of the inverse pulse and v is the velocity. Let’s insert Eq. (2) to Eq. (1), then we derive the imaginary and real parts of the obtained equation in the following form, respectively:

$$\begin{aligned}{} & {} \Theta ^{\prime \prime \prime }+ \left( \frac{\left( 2 \mu p +\lambda \right) \Theta ^{2 p}}{\alpha \,k^{2}}+\frac{\left( \gamma \omega -3 a^{2} \alpha -\tau \right) k +\left( a \gamma +1\right) v}{\alpha \,k^{3}}\right) \Theta ^{\prime }=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \Theta ^{\prime \prime }+\frac{\left( a \lambda -\beta \right) }{3 a \alpha \,k^{2}-\gamma k v} \Theta ^{1+2p}-\frac{a^{3} \alpha +\left( \tau -\gamma \omega \right) a -\omega }{3 a \alpha \,k^{2}-\gamma k v} \Theta =0, \end{aligned}$$
(4)

where \(\Theta =\Theta (\zeta )\), \(\alpha ,k \ne 0\), \(3 a \alpha \,k^{2}-\gamma k v \ne 0\).

If we integrate Eq. (3) and assume the integration constant as zero, then we acquire:

$$\begin{aligned} \Theta ^{\prime \prime }+\frac{\left( 2 \mu p +\lambda \right) }{\alpha \,k^{2} \left( 1+2 p \right) }\Theta ^{1+2p}+\frac{\left( \gamma \omega -3 a^{2} \alpha -\tau \right) k +\left( a \gamma +1\right) v }{\alpha \,k^{3}}\Theta =0. \end{aligned}$$
(5)

Performing the homogeneous balance between the Eqs. (4), (5), the following ratios are ensured:

$$\begin{aligned}{} & {} \frac{2 \mu p +\lambda }{k^{2} \left( 1+2 p \right) \alpha } = \frac{a \lambda -\beta }{k \left( 3 a \alpha k -\gamma v \right) }, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \frac{\left( \gamma \omega -3 a^{2} \alpha -\tau \right) k +\left( a \gamma +1\right) v}{\alpha \,k^{3}}= \frac{\omega -a^{3} \alpha +\left( \gamma \omega -\tau \right) a }{3 a \alpha \,k^{2}-\gamma k v}. \end{aligned}$$
(7)

Solving the Eqs. (6), (7), we get the following constraint conditions:

$$\begin{aligned}{} & {} \beta =\frac{2 a \alpha k \lambda p -6 a \alpha k \mu p -2 a \alpha k \lambda +2 \gamma \mu p v +\gamma \lambda v}{\alpha k \left( 1+2 p \right) }, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \omega =-\frac{8 a^{3} \alpha ^{2} k^{2}-6 a^{2} \alpha \gamma k v +2 a \alpha \,k^{2} \tau +a \,\gamma ^{2} v^{2}-3 a \alpha k v -\gamma k \tau v +\gamma \,v^{2}}{k \left( -2 a \alpha \gamma k +\gamma ^{2} v +\alpha k \right) }. \end{aligned}$$
(9)

Paying regard to these constraint conditions, we can take into consideration Eqs. (4) or (5) as a ODE form of Eq. (1). Let’s suppose that Eq. (4) is ODE structure and perform the balance principle between the terms \(\Theta ^{\prime \prime }\), \(\Theta ^{1+2p}\), then we achieve the balance constant as \(B=\frac{1}{p}\). Because the balancing constant is identified as a positive integer, we need to set as follows:

$$\begin{aligned} \Theta (\zeta )= V^{1/p}(\zeta ). \end{aligned}$$
(10)

If we reconstitute Eq. (4) taking into consideration Eq. (10), we get the following expression:

$$\begin{aligned} \left( 1+2 p \right) \left( 2 k^{2} p \Upsilon _{1} V V^{\prime \prime }-2 k^{2} \left( p-1 \right) \Upsilon _{1} (V^{\prime })^{2}+\Upsilon _{2} V^{2}\right) \alpha +2p^{2} \left( 2 \mu p +\lambda \right) \Upsilon _{1} V^4=0, \end{aligned}$$
(11)

in which \(V=V\left( \zeta \right) \), \(\Upsilon _{1}=\frac{k \left( 2 a \gamma -1\right) \alpha -\gamma ^{2} v}{2}\) and \(\Upsilon _{2}=p^{2} \left( a^{2} k \left( 2 a \gamma +3\right) \alpha +k \tau -v \left( a \gamma +1\right) ^{2}\right) \).

As a result, performing the balance principle between \(VV^{\prime \prime }\) and \(V^4\), then we figure out the balance constant as \(B=1\).

3 Application

3.1 The nKM and its utilization

The nKM (Kudryashov 2020; Ozisik et al. 2022) suggests that Eq. (11) has a solution as the following truncated series form:

$$\begin{aligned} V(\zeta )=\sum _{J=0}^{B}\Lambda _{J}\Omega ^{J}(\zeta ), \,\, \Lambda _{B}\ne 0, \end{aligned}$$
(12)

where \(\Lambda _J\) are real constants, B is the balance constant which was determined as 1 in Sect. 2 and the function \(\Omega (\zeta )\) expresses the solution of the following equation:

$$\begin{aligned} (\Omega ^{\prime }(\zeta ))^2=\delta ^2\Omega ^2(\zeta )\left( 1-\chi \Omega ^2(\zeta )\right) ,\,\, \end{aligned}$$
(13)

in which \(\delta \), and \(\chi \) are nonzero real numbers to be specified later. One of the solutions for Eq. (13) is expressed with the following structure:

$$\begin{aligned} \Omega (\zeta )=\frac{4\Gamma }{4\Gamma ^{2} {\mathrm e}^{\delta \zeta }+\chi {\mathrm e}^{-\delta \zeta }}. \end{aligned}$$
(14)

Equation (14) contributes to the bright soliton and singular soliton for \(\chi =\mp 4\Gamma ^2\), respectively and also can be presented in the following hyperbolic forms:

$$\begin{aligned} \Omega (\zeta )=\frac{1}{2\Gamma } {{\,\textrm{sech}\,}}(\delta \zeta ), \end{aligned}$$
(15)

and

$$\begin{aligned} \Omega (\zeta )=\frac{1}{2\Gamma } \coth (\delta \zeta ), \end{aligned}$$
(16)

in which \(\Gamma \) is a real constant.

Owing to \(B=1\), Eq. (12) transforms the following structure:

$$\begin{aligned} V(\zeta )= \Lambda _0+\Lambda _1 \Omega (\zeta ),\,\, \Lambda _{1}\ne 0. \end{aligned}$$
(17)

Combination of the Eqs. (17), (13), (11) produces the following algebraic system:

\(\Omega ^{0} \) coefficient:

$$\begin{aligned}\begin{array}{l} {\Lambda _{0}^{2} p^{2} \left( \left( 2 a \gamma +3\right) \left( 2 p +1\right) a^{2} k \,\alpha ^{2}-\Lambda _{0}^{2} v \,\gamma ^{2} \left( 2 p \mu +\lambda \right) -\alpha v \left( 2 p +1\right) \left( a^{2} \gamma ^{2}+1\right) \right) }\\ {+\Lambda _{0}^{2} p^{2} \left( \left( 2 \Lambda _{0}^{2} \left( 2 p \mu +\lambda \right) k -2 v \left( 2 p +1\right) \right) a \gamma +\left( 2 \left( -\Lambda _{0}^{2} \mu +\tau \right) p -\Lambda _{0}^{2} \lambda +\tau \right) k \right) \alpha =0.} \end{array} \end{aligned}$$

\(\Omega ^{1} \) coefficient:

$$\begin{aligned} \begin{array}{l} {p \Lambda _{0} \Lambda _{1}\! \left( \left( 2 \left( 2 a^{3} \gamma +3 a^{2}\right) p +\Xi _1 k^{2} \delta ^{2}\right) \left( 2 p +1\right) k \,\alpha ^{2}-4 \Lambda _{0}^{2} p v \,\gamma ^{2} \left( 2 p \mu +\lambda \right) -k^{2} v \,\delta ^{2} \gamma ^{2} \alpha \right) }\\ {+p \Lambda _{0} \Lambda _{1} \left( \left( 4 \left( 2 \Lambda _{0}^{2} \mu \Xi _1+\tau \right) k -4 v \Xi _2\right) p^{2}+\left( -2 k^{2} v \,\delta ^{2} \gamma ^{2}+2 \left( 2 \lambda \Lambda _{0}^{2} \Xi _1+\tau \right) k -2 v \Xi _2\right) p \right) \alpha = 0.} \end{array} \end{aligned}$$

\(\Omega ^{2} \) coefficient:

$$\begin{aligned} \begin{array}{l} { \Lambda _{1}^{2} \left( \left( 2 p +1\right) \left( \left( 2 a^{3} \gamma +3 a^{2}\right) p^{2}+\Xi _1 k^{2} \delta ^{2}\right) k \,\alpha ^{2}-6 \Lambda _{0}^{2} p^{2} v \,\gamma ^{2} \left( 2 p \mu +\lambda \right) \right) }\\ {+ \Lambda _{1}^{2} \left( \left( 2 \left( 6 \Lambda _{0}^{2} \mu \Xi _1+\tau \right) k -2 v \Xi _2\right) p^{3}+\left( \left( 6 \lambda \Lambda _{0}^{2} \Xi _1+\tau \right) k -v \Xi _2\right) p^{2}-k^{2} v \,\delta ^{2} \gamma ^{2} \left( 2 p +1\right) \right) \alpha =0.} \end{array} \end{aligned}$$

\(\Omega ^{3} \) coefficient:

$$\begin{aligned} \begin{array}{l} {\Lambda _{0} \left( k \Xi _1 \alpha -\gamma ^{2} v \right) \left( -\chi \left( 2 p +1\right) k^{2} \delta ^{2} \alpha +2 \Lambda _{1}^{2} p \left( 2 p \mu +\lambda \right) \right) p \Lambda _{1}= 0.} \end{array} \end{aligned}$$

\(\Omega ^{4} \) coefficient:

$$\begin{aligned} \begin{array}{l} {\Lambda _{1}^{2} \left( -\chi \left( 2 p +1\right) k^{2} \left( p +1\right) \delta ^{2} \alpha +\Lambda _{1}^{2} p^{2} \left( 2 p \mu +\lambda \right) \right) \left( k \Xi _1 \alpha -\gamma ^{2} v \right) = 0.} \end{array} \end{aligned}$$

Herein, \(\Xi _1=2 a \gamma -1\) and \(\Xi _2=\left( a \gamma +1\right) ^{2}\).

The solution of the above system derives the following set:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {\delta =\delta ,v = \frac{k \left( \left( \alpha \,a^{2} \left( 2 a \gamma +3\right) +\tau \right) p^{2}+k^{2} \alpha \,\delta ^{2} \left( 2 a \gamma -1\right) \right) }{\left( a \gamma +1\right) ^{2} p^{2}+\delta ^{2} \gamma ^{2} k^{2}}} \\ {k=k,{\Lambda _0}=0,{\Lambda _{1}} = \frac{\sqrt{\left( 2 p \mu +\lambda \right) \alpha \chi \left( 2 p^{2}+3 p +1\right) }\, \delta k}{\left( 2 p \mu +\lambda \right) p} } \end{array}\right\} . \end{aligned}$$
(18)

where \(\left( 2 p \mu +\lambda \right) p \ne 0\), \(\left( a \gamma +1\right) ^{2} p^{2}+\delta ^{2} \gamma ^{2} k^{2} \ne 0\).

Regarding Eq. (17) with Eqs. (2), (10), (14), the following solution is derived:

$$\begin{aligned} \Theta _1\left( x,t\right) = \left( \frac{4 \Lambda _{1} \Gamma }{4 \Gamma ^{2} {\mathrm e}^{\delta \left( k x +v t \right) }+\chi \,{\mathrm e}^{-\delta \left( k x +v t \right) }}\right) ^{\frac{1}{p}}{\mathrm e}^{\textrm{i} \left( a x +\omega t +\varphi _{0}\right) }, \end{aligned}$$
(19)

For \(\chi =\mp 4\Gamma ^2\), Eq. (19) permits us to reach bright and singular soliton solutions:

$$\begin{aligned} \Theta _{2,3}\left( x,t\right) = \left( \frac{ \Lambda _{1} }{\Gamma \left( {\mathrm e}^{\delta \left( k x +v t \right) } \mp \,{\mathrm e}^{-\delta \left( k x +v t \right) }\right) }\right) ^{\frac{1}{p}}{\mathrm e}^{\textrm{i} \left( a x +\omega t +\varphi _{0}\right) }, \end{aligned}$$
(20)

Besides, Eq. (19) can be given in the following hyperbolic forms by benefiting from Eqs. (15) and (16):

$$\begin{aligned}{} & {} \Theta _4(x,t)= \left( \frac{ \Lambda _{1} \textrm{sech}\! \left( \delta \left( k x +v t\right) \right) }{2 \Gamma }\right) ^\frac{1}{p} {\mathrm e}^{\textrm{i} \left( a x +\omega t +\varphi _{0}\right) }, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \Theta _5(x,t)= \left( \frac{ \Lambda _{1} \textrm{coth}\! \left( \delta \left( k x +v t\right) \right) }{2 \Gamma }\right) ^\frac{1}{p} {\mathrm e}^{\textrm{i} \left( a x +\omega t +\varphi _{0}\right) }, \end{aligned}$$
(22)

in which, \(\Lambda _1, \delta , k,v,\omega \) are figured out in Eqs. (9), (18).

4 Modulation instability analysis

In this part, the modulation instability Eq. (1) with the help of the standard linear stability analysis (Zakharov and Ostrovsky 2009; Guo et al. 2018; Yue and Huang 2022) is contemplated to be examined in detail. So, we assume that the Eq. (1) has the next steady-state (SS) solution:

$$\begin{aligned} \Theta (x,t)=\left( \sqrt{\kappa }+\varrho (x,t)\right) e^{i\kappa t}, \end{aligned}$$
(23)

in which \(\kappa \) is defined as the normalized optical power. \(\varrho (x,t)\) is also a small perturbation which satifies the expression \(\varrho (x,t)\ll \sqrt{\kappa }\). In this part, we regard the various values of p as \(p=1,2,3\).

Case 1: (p=1)

Unifiying Eq. (23) with Eq. (1) and selecting linear terms with respect to the \(\varrho (x,t)\), we get,

$$\begin{aligned} i \alpha \varrho _{xxx} + \gamma \varrho _{xt} +i ((\mu + \gamma + \lambda ) \kappa - \tau ) \varrho _{x} + i\mu \kappa \varrho _{x}^* +i \varrho _{t} + (2 \beta - 1) \kappa \varrho + \beta \kappa \varrho ^*=0, \end{aligned}$$
(24)

in which (\(^*\)) expresses the complex conjugate of \(\varrho =\varrho (x, t)\). Consider that the solution of Eq. (24) is stated as:

$$\begin{aligned}&\varrho (x,t)=A_1 e^{i \left( \Delta x -\sigma t\right) }+A_2 e^{-i \left( \Delta x -\sigma t\right) }, \end{aligned}$$
(25)

where \(A_1, A_2\) are real-valued coefficients, \(\sigma \) and \(\Delta \) are defined as the frequency of perturbation and wave number. Combining Eq. (25) with Eq. (24), considering separately the coefficients of \(e^{i \left( \Delta x -\sigma t\right) }\) and \(e^{-i \left( \Delta x -\sigma t\right) }\), we acquire a coefficient matrix which constitutes of the coefficients of \(A_1, A_2\). Then, the determinant of the resulted matrix for \(\sigma \) gives the following relation:

$$\begin{aligned} \sigma =\frac{\eta _{11}-\sqrt{\eta _{12}+ \eta _{13}+\eta _{14}}}{\Delta ^{2} \gamma ^{2}-1}, \,\,\, \Delta ^{2} \gamma ^{2} \ne 1, \end{aligned}$$
(26)

in which

$$\begin{aligned}{} & {} \eta _{11}=\alpha \,\Delta ^{3}-\left( \left( 2 \beta \gamma +\lambda +\mu \right) \kappa -\tau \right) \Delta , \\{} & {} \eta _{12}=\Delta ^{4} \gamma ^{4} \kappa ^{2}+2 \kappa \left( \left( \mu +\lambda \right) \kappa -\Delta ^{2} \alpha -\tau \right) \Delta ^{4} \gamma ^{3}, \\{} & {} \eta _{13}=\left( \left( 4 \beta +\beta ^{2}+2\mu \,\Delta ^{2} \lambda + \Delta ^{2} \lambda ^{2}-2\right) \kappa ^{2}-2\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) \left( \mu +\lambda \right) \kappa +\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) ^{2}\right) \Delta ^{2} \gamma ^{2}, \\{} & {} \eta _{14}=4 \kappa \left( \left( \mu +\lambda \right) \kappa -\Delta ^{2} \alpha -\tau \right) \left( \beta -\frac{1}{2}\right) \Delta ^{2} \gamma +\kappa ^{2} \left( \Delta ^{2} \mu ^{2}+3 \beta ^{2}-4 \beta +1\right) . \end{aligned}$$

The modulation instability arises when \(\eta _{12}+\eta _{13}+\eta _{14}<0\).

Case 2: (p=2)

Combining Eq. (23) with Eq. (1) and selecting linear terms with respect to the \(\varrho (x,t)\), we get,

$$\begin{aligned} i \alpha \varrho _{xxx} + \gamma \varrho _{xt} +i ((2 \mu +\lambda ) \kappa ^2+\gamma \kappa - \tau ) \varrho _{x} + i2\mu \kappa ^2 \varrho _{x}^* +i \varrho _{t} + (3 \beta \kappa - 1)\kappa \varrho + 2\beta \kappa ^2 \varrho ^*=0. \end{aligned}$$
(27)

Combination of Eq. (25) with Eq. (27), considering separately the coefficients of \(e^{i \left( \Delta x -\sigma t\right) }\) and \(e^{-i \left( \Delta x -\sigma t\right) }\), a coefficient matrix which constitutes of the coefficients of \(A_1, A_2\) is obtained. Computing the determinant of the matrix for \(\sigma \), the following equation is gained:

$$\begin{aligned} \sigma =\frac{\eta _{21}-\sqrt{\eta _{22}+\eta _{23}+\eta _{24}}}{\Delta ^{2} \gamma ^{2}-1},\,\,\, \Delta ^{2} \gamma ^{2} \ne 1, \end{aligned}$$
(28)

where

$$\begin{aligned}{} & {} \eta _{21}=\alpha \,\Delta ^{3}+\left( \left( -3 \beta \gamma -\lambda -2 \mu \right) \kappa ^{2}+\tau \right) \Delta , \\{} & {} \eta _{22}=\Delta ^{4} \gamma ^{4} \kappa ^{2}+2 \kappa \left( \left( 2\mu +{\lambda }\right) \kappa ^{2}-{\Delta ^{2} \alpha }-{\tau }\right) \Delta ^{4} \gamma ^{3}+\left( 4\mu \,\Delta ^{2} \lambda + \Delta ^{2} \lambda ^{2}+4\beta ^{2}\right) \kappa ^{4}\Delta ^2\gamma ^2, \\{} & {} \eta _{23}= \left( {6 \beta \,\kappa ^{3}}-2\left( {\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) \lambda }+1+2\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) \mu \right) \kappa ^{2}+{\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) ^{2}}\right) \Delta ^{2} \gamma ^{2}, \\{} & {} \eta _{24}=2\left( 3\beta \kappa -1\right) \kappa \left( \left( 2\mu +{\lambda }\right) \kappa ^{2}-{\Delta ^{2} \alpha }-{\tau }\right) \Delta ^{2} \gamma +\left( 4 \Delta ^{2} \mu ^{2}+5 \beta ^{2}\right) \kappa ^{4}-6 \beta \,\kappa ^{3}+\kappa ^{2}. \end{aligned}$$

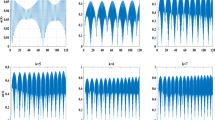
The modulation instability emerges if \(\eta _{22}+\eta _{23}+\eta _{24}<0\) (Fig. 1).

Case 3: (p=3)

Combining Eq. (23) with Eq. (1) for \(p=3\) and selecting linear terms with respect to the \(\varrho (x,t)\), we get,

$$\begin{aligned} i \alpha \varrho _{xxx} + \gamma \varrho _{xt} +i ((3\mu +\lambda ) \kappa ^3+\gamma \kappa - \tau ) \varrho _{x} + i3\mu \kappa ^3 \varrho _{x}^* +i \varrho _{t} + (4 \beta \kappa ^3 - \kappa ) \varrho + 3\beta \kappa ^3 \varrho ^*=0. \end{aligned}$$
(29)

Combination of Eq. (25) with Eq. (29), considering separately the coefficients of \(e^{i \left( \Delta x -\sigma t\right) }\) and \(e^{-i \left( \Delta x -\sigma t\right) }\), a coefficient matrix which constitutes of the coefficients of \(A_1, A_2\) is obtained. Computing the determinant of the matrix for \(\sigma \), the following equation is gained:

$$\begin{aligned} \sigma =\frac{\eta _{31}-\sqrt{\eta _{32}+\eta _{33}+\eta _{34}}}{\Delta ^{2} \gamma ^{2}-1},\,\,\, \Delta ^{2} \gamma ^{2} \ne 1, \end{aligned}$$
(30)

where

$$\begin{aligned}{} & {} \eta _{31}=\alpha \,\Delta ^{3}+\left( \left( -4 \beta \gamma -\lambda -3 \mu \right) \kappa ^{3}+\tau \right) \Delta , \\{} & {} \eta _{32}=\Delta ^{4} \gamma ^{4} \kappa ^{2}+2 \Delta ^{4} \left( \left( \mu +{\lambda }\right) \kappa ^{3}-{\Delta ^{2} \alpha }-{\tau }\right) \kappa \,\gamma ^{3}, \\{} & {} \eta _{33}= \Delta ^{2} \left( \left( 6\mu \,\Delta ^{2} \lambda +\Delta ^{2} \lambda ^{2}+9 \beta ^{2}\right) \kappa ^{6}+{8 \beta \,\kappa ^{4}}+2\left( 3\mu +{\lambda }\right) \left( \Delta ^{2} \alpha +\tau \right) \Delta ^{2} \kappa ^{3}+2{\kappa ^{2}}+{\Delta ^{2} \left( \Delta ^{2} \alpha +\tau \right) ^{2}}\right) \gamma ^{2},\\{} & {} \eta _{34}=2 \Delta ^{2} \left( 4\beta \,\kappa ^{2}-1\right) \left( \left( \mu +{\lambda }\right) \kappa ^{3}-{\Delta ^{2} \alpha }-{\tau }\right) \kappa \gamma +\left( 9 \Delta ^{2} \mu ^{2}+7 \beta ^{2}\right) \kappa ^{6}-8 \beta \,\kappa ^{4}+\kappa ^{2}. \end{aligned}$$

The modulation instability emerges if \(\eta _{32}+\eta _{33}+\eta _{34}<0\).

Fig. 1
figure 1

Gain spectrum of \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) for \(\gamma = 0.2, \tau = 0.5, \alpha = 1, \mu = 0.5, \beta = 1.6, \lambda = 0.3\)

Full size image

5 Results and discussion

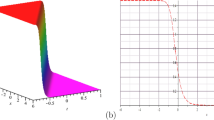
In this section, we have supported the bright optical soliton solutions of the third-order NLSE with the power law media attained in the relevant sections with graphical presentations by taking advantage of Maple and Matlab symbolic computing software. The 2D, contour, and 3D diagrams of the bright soliton solution have been visualized to demonstrate the soliton dynamics of the attained solution with Matlab. Figure 2 represents the bright soliton solution function attained by Eq. (19) and the graphic is structured by choosing the parameters such as \(\varphi _0=1.21, \gamma =2.2, \delta =0.56, \chi =0.78, \Gamma =1.4, k=0.98,p=1, a=1.2, \alpha =-0.65, \tau =1.4, \lambda =1.6, \mu =-0.98\). One of the important points is how and on what basis the parameters are chosen. The limitations of both the problem and the proposed technique are the binding and limiting point here. In Fig. 2a–c, 3D views of \(|\Theta _1(x,t)|^2\), \(Im(\Theta _1(x,t))\), \(Re(\Theta _1(x,t))\) are given, respectively. The contour view of \(|\Theta _1(x,t)|^2\) is depicted in Fig. 2d. In addition, the diagrams of \(|\Theta _1(x,t)|^2\) for \(t=1,2,3,4,5\) and \(Im(\Theta _1(x,t))\), \(Re(\Theta _1(x,t))\) for \(t=1,2,3\) in 2D are shown in Fig. 2e and f, respectively. On the other side, as can be seen from the Fig. 2a and f, these graphs stand for the bright soliton character, which has wave properties moving towards the right (from blue line to pink line) for \(|\Theta _1(x,t)|^2\).

Now, we show Fig. 3 which is a variety of representations of Eq. (19) to demonstrate the impact of \(\alpha , \lambda , p\) and \(\mu \). Figure 3a graph is allocated to investigating the impact of \(\alpha \). Here, the impact is beholden by deciding on the parameter \(\alpha \) as the values of \(-2.5,-1.5,-0.5,0.5,1.5,2.5\), respectively. When the graphic is analyzed carefully, it can be clearly stated that the soliton sustains its form, that is to say, there is no deformation in the overall structure of the bright soliton. As a whole, the soliton reflects a symmetrical view with respect to the perpendicular axis for positive and negative values of \(\alpha \). Here, \(\alpha \) denotes the third-order dispersion term. This term helps to account for how the pulse shape changes over time due to variations in the group velocity dispersion with frequency. For positive values of \(\alpha \), as \(\alpha \) approaches zero, while the perpendicular highness of the soliton step-by-step declines and its horizontal amplitude increases, the horizontal distance between the soliton skirts widens outward. Similarly, for negative values of \(\alpha \), it gives a similar result as \(\alpha \) approaches zero. Therefore, the soliton is exposed to deterioration both perpendicularly and horizontally. This means that it is very difficult to ensure the effect and control of the refractive index terms added to the problem. Third-order dispersion becomes important in the design and optimization of optical communication systems, especially when dealing with ultrashort pulses or broadband signals. Understanding and managing dispersion effects are crucial for minimizing pulse distortion and maintaining signal integrity over long-distance optical fiber communication links. Fig. 3b and c graphs are allocated to perusing the influence of \(\lambda , \mu \). Herein, this impact is beholden by choosing the parameter \(\lambda \) as the values of 0.25, 0.5, 0.75, 1.25, 1.5, \(\mu \) as the values of \(-2.75,-2.25,-1.75,-1.25,-1\), respectively. When Fig. 3b is examined, it can be seen that as the positive values of \(\lambda \) increase, the perpendicular height of the soliton increases, while its horizontal amplitude decreases and is subject to contraction. When Fig. 3c is investigated, a similar result is seen for increasing negative values of \(\mu \). Figure 3d shows us that as p parameter values increase, soliton sustains its bright soliton character, but the peaks of the soliton slide down perpendicularly. This means that while the horizontal amplitude of the soliton increases, its perpendicular height decreases. While it is observed that the alteration in perpendicular amplitude is extremely sharp in the transition from \(p=1\) to \(p=2\), this alteration does not proceed in the same line after p changes by the same increasing amount. The exponent p stands for the type of power law media. The power-law dependence on the intensity provides a more generalized description of how the pulse intensity influences the refractive index of the medium. Different values of p can represent various nonlinear effects, and the specific choice of p depends on the characteristics of the medium.

Fig. 2
figure 2

Some schematics of \(\Theta _1(x,t)\) when \( \varphi _0 = 1.21, \gamma =2.2, \delta =0.56, \chi =0.78, \Gamma = 1.4, k = 0.98,p = 1, a = 1.2, \alpha =-0.65, \tau =1.4, \lambda =1.6, \mu =-0.98\)

Full size image
Fig. 3
figure 3

2D plots of \(\Theta _1(x,t)\) when \(\varphi _0 = 1.21, \gamma =2.2, \delta =0.56, \chi =0.78, \Gamma = 1.4, k = 0.98, a = 1.2, \tau =1.4\)

Full size image

6 Conclusion

In this article, the bright optical soliton solutions were acquired by analyzing the thirdorder (1+1)-NLSE including power law nonlinearity with inter-modal and spatio-temporal dispersions in the absence of chromatic dispersion via the nKM. This equation describes the interplay between the effects of dispersion, nonlinearity, and power-law nonlinearity on the propagation of optical pulses in a medium. Solutions to this equation can provide insights into the behavior of optical pulses under these conditions. The proposed algorithm is easy to use and highly effective and produce efficient outcomes. Acquiring the bright solitons is one of the targets of the study, and the second objective is to peruse the influences of the parameters of power law nonlinearity, nonlinear dispersion and third-order dispersion terms on soliton attitude. The equation has not been studied with the power law nonlinearity in the absence of chromatic dispersion and for the first time, the modulation instability analysis has been examined for this form of the equation in this article. Furthermore, the parameter values stated in the graphical presentations were specified in consequence of long efforts, and one of the most important examination points was whether the bright soliton maintained its shape under the effect of these parameter values. In this respect, we believe that the attained results will contribute to the researches to be made for the solution of this and similar nonlinear problems. Moreover, considering the different self-phase modulation forms and their interactions with the third-order nonlinear term, there are many problems that can be studied in this field. Considering the fields of study such as multi soliton solution, fractional, stochastic, bifurcation analysis, it can be seen how wide this range can be spread.