1 Introduction

The majority of dynamical phenomena in nature are intrinsically nonlinear and are characterized by nonlinear partial differential equations (NLPDEs), which can be either continuous or discontinuous. Knowing their accurate or reasonable results is critical for comprehending most natural events. They are generally divided into two types: integrable and non integrable structures. While integrable problems can be easily analyzed analytically using well-known approaches such as the Inverse Scattering Transform (Ablowitz et al. 1974), the Hirota method (Hirota 2004), and the Darboux transformation method (Matveev and Salle 1991), non integrable systems can only be examined in general situations through numerical simulations (Hoffman and Frankel 2018; Imkeller and Monahan 2002). The NLPDEs have traveling wave solutions, which have become a fundamental aspect of research in nonlinear wave dynamics and have been explored in various disciplines such as optical fibers, plasma, fluid dynamics, elastic media, and so on. Numerous strategies for obtaining various soliton solutions to these NLPDEs have been discovered in the literature. Among these are the square operator approach (Wang et al. 2022), the unified technique (Vivas-Cortez et al. 2023), Hirota’s bilinear approach (Geng et al. 2023, Geng et al. 2023), the neural network approach (Xu et al. 2023), the extended tanh-function approach (Zaman et al. 2023a, b), and many others (Arefin et al. 2022; Zaman et al. 2023). They have enhanced the dynamic approach by employing various methods, such as the generalized Kudryashov method (Akbar et al. 2022), the sinh-Gordon equation expansion method (Akbar et al. 2021), the \((G^{'}/G)\)-expansion (Islam et al. 2022), the tanh technique (Almusawa et al. 2022), the rational \((1/\Phi ^{'})\)-expansion approach (Islam et al. 2022).

Considerable investigation has previously been carried out to explore the dynamics of solitons, utilizing various nonlinear models, including Schrödinger model (Bo et al. 2023; Wen et al. 2023), Fractional foam drainage model (Yokuş et al. 2022), Bogoyavlenskii equation (Islam et al. 2023), shallow water equation (Akbar et al. 2023), and Modified equal-width equation (Khatun et al. 2022). One or more stochastic processes are used as terms in a stochastic differential equation (SDE), and another stochastic process is employed as the solution. SDEs are utilized to replicate a wide variety of phenomena, including stock prices and physically based models susceptible to thermal changes. Consequently, SDEs have become crucial for simulating phenomena in various fields such as biology, chemistry, physics, marine biology, and fluid dynamics (Prévôt and Röckner 2007).

Over the past decade, physicians have been passionately investigating various types of nonlinear solitonic systems in plasmas, including single waves, shock waves, and surface waves. Due to the presence of different volumes of dust grains in plasma, different types of wavelengths have been observed, such as acoustic mode (Akinyemi et al. 2021), dust Bernstein-Green-Kruskal mode (El-Taibany and Sabry 2005), dust acoustic mode (Anderson and Ulness 2015), and dust-up mode (low-wave mode) (Yang et al. 2012). In recent years, according to a research study, numerous literature works have focused on exploring the behavior of new waves (Bains et al. 2010), the imbalance of quantum beams (Ahmed et al. 2018), quantum modifications to the Zakharov equations, and quantum ion-acoustic waves (Gupta et al. 2015). Recently, the separation of ion-acoustic dust waves into magnetic dust plasma using the q-nonextensive velocity circulation, based on the bifurcation concept of balanced dynamical structures, has been investigated in several articles (Jansen et al. 2009). These articles have examined the differentiation of nonlinear waves in plasma physics (Jahan et al. 2019). Therefore, the main objective of our current research is to discover new systematic solutions for acoustic dust waves and nonlinear LWE (Long-Wave Equation), which are clearly defined by the size and dimensions of the 2D and 3D structures (Ghosh et al. 2012; Baluku and Hellberg 2008).

A fascinating area of study in recent times has been the application of bifurcation analysis to the study of differential equations (Liu et al. 2022; Talafha et al. 2023). Several authors have conducted research on the concepts of dynamic system bifurcation within both disturbed and unperturbed frameworks (Saha 2017). Samina et al. (2022) derived the bifurcation behavior, chaotic dynamics, and multistability analysis of the (2+1)-dimensional elliptic nonlinear Schr\(\ddot{o}\)dinger equation with external perturbation, utilizing bifurcation and chaos theories. Sprott (2011) investigated the prevalence of chaotic systems and identified them. The focus of the present study is to explore the temporal, quasi-periodic, sensitivity, and solitonic behavior of dust acoustic waves in three distinct plasma volumes with inertial ion-negative components. By considering the external influences of disturbances, we aim to understand the quasi-periodic behavior and the sensitivity of the disturbance scheme in non-magnetic plasma based on our expertise.

The mathematical modeling of exact processes that require accurate damping modeling is accomplished using fractional derivative approaches. Fractional derivatives offer advantages such as adaptability and non-locality. Unlike ordinary derivatives, these derivatives possess fractional order, which grants them greater flexibility in approximating actual information. Additionally, they incorporate non-locality, a feature lacking in ordinary derivatives. Fractional derivatives find application in various significant phenomena, including anomalous diffusion, electro-chemistry, acoustics, computational imaging, and magnetic fields. Fractional models tend to provide higher accuracy compared to integer models. However, solving fractional derivative stochastic differential equations (SDEs) is generally more challenging than solving conventional ones. In light of this, we have focused on examining the SFDSW equations as presented in Al-Askar et al. (2022).

$$\begin{aligned}{} & {} dw+[\beta {y}D_{\eta }^{\phi }y]d{\zeta }=\alpha {w}d{\mu }, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} dy+[m_{1}D_{\eta \eta \eta }^{\phi }y+ m_{2}{w}D_{\eta }^{\phi }y+m_{3}{y}D_{\eta }^{\phi }w] d{\zeta }=\alpha {y}d{\mu }. \end{aligned}$$
(2)

Here \(w=w(\eta ,\zeta )\), \(y=y(\eta ,\zeta )\). \(\beta \), \(m_j\), \(j=1,2,3\) are non-zero parameters. The conformable derivative (CD) is denoted as \(D^{\phi }\), \(0<\phi \le 1\). The function \(\mu =\mu (\zeta )\) corresponds to a standard Brownian motion (SBM), and \(\alpha \) represents the noise strength.

Equation (1) and (2) are an expanded version of the standard DSW. When \(\phi =1\), and \(\alpha =0\), then the above system transforms into the standard DSW equation, initially proposed by Drinfeld and Sokolov (1981); Sokolov (1984), and later refined by Wilson (1982). Furthermore, this model finds applications in plasma physics, various applied sciences, fluid and population dynamics, and electromagnetism. Given the significance of DSW model, numerous scholars have developed diverse methodologies to investigate exact solutions of the system, including Hirota’s bilinear (Alsallami et al. 2023), Jacobi elliptical function (Sahoo and Ray 2017), \((G'/G)\)-Expansion method (Al-Askar et al. 2022), complete discrimination for polynomial (Zhang and Han 2023), He’s variational approach (Wang and Wang 2023), truncated Painlevé (Ren et al. 2016), and mapping approach (Al-Askar et al. 2022).

This investigation will primarily focus on achieving its objectives from three distinct perspectives. Firstly, it aims to establish various soliton profiles through the application of a tanh method. Secondly, a pivotal aspect involves conducting a parameter-based analysis of the system under scrutiny, incorporating bifurcation and chaos theories. The detailed explanation of the bifurcation of the unperturbed system is illustrated through phase portraits. Additionally, the chaotic analysis of the perturbed system is determined and demonstrated using various tools, including time series and phase portraits. Furthermore, the study delves into the sensitivity and multistability of the examined system. The authors emphasize the novelty of this study, asserting that it presents an interesting perspective not previously explored for the considered system.

The outline of the paper is as follows: Sections (2) and  (3) provide preliminary information and present the mathematical model. The solution analysis for the proposed approach is discussed in Section (4). Section (5) focuses on the physical interpretation of the evaluated model. The bifurcation theory of the model under study is examined in Section (6). Section (7) explores the periodic and quasiperiodic properties of the model. The sensitivity analysis of the model is conducted in Section (8). Section (9) investigates the multistability of the model. The conclusion is presented in the final section of the paper.

2 Preliminaries

The suitable derivative and conventional Brown’s law are now being examined in terms of their characteristics and descriptions. The following is the definition of a suitable derivative:

Definition 2.1

The function’s conformable derivative (Al-Askar et al. 2022)

\(r=r(\eta ):[0,\infty )\rightarrow {\mathbb {R}}\)

for the independent variable \(\eta \) of the order \(\phi \), it is given as:

\(D_{\eta }^{\phi }r(\eta )=\lim _{\beta \rightarrow \infty }\frac{r(\eta +\beta \eta ^{1-\beta })-r(\eta )}{\beta }\),   \(\eta >0\),    \(\phi \in (0;1]\).

2.1 Properties

If \(g=g(\eta )\) and \(r=r(\eta )\) are \(\phi \)-differentiable for all positive \(\eta \),

  • \(D_{\eta }^{\phi }(T_{1}g+T_{2}r)=T_{1}D_{\eta }^{\phi }(g)+T_{2}D_{\eta }^{\phi }(r)\),   \(\forall ~~~T_{1},~T_{2}\in {\mathbb {R}}\),

  • \(D_{\eta }^{\phi }(t^{z})=zt^{(z-\phi )}\),   \(z\in {\mathbb {R}}\),

  • \(D_{\eta }^{\phi }(\lambda )=0\),  \(\forall ~~r(\eta )=\lambda \in {\mathbb {R}}\),

  • \(D_{\eta }^{\phi }(gr)=gD_{\eta }^{\phi }r+rD_{\eta }^{\phi }g\),

  • \(D_{\eta }^{\phi }(\frac{r}{g})=(\frac{gD_{\eta }^{\phi }(r)-rD_{\eta }^{\phi }(g)}{g^{2}})\),

  • \(D_{\eta }^{\phi }(r)(\eta )=\eta ^{(1-\phi )}\frac{dr}{d\eta }\),

  • \(D_{\eta }^{\phi }(r\circ g)(\eta )=\eta ^{(1-\phi )}g^{\prime }(\eta )r^{\prime }(g(\eta ))\).

Lemma

(Calin 2015) \(E(e^{\omega \mu (\zeta )})=e^{\frac{1}{2}\omega ^{2}\zeta },~~~~~~\omega \ge 0.\)

3 Mathematical model

3.1 Description of method

Assume that NLPDE with unknown variables \((\eta , \zeta )\) are given by,

$$\begin{aligned} H(Y, Y_{\eta }, Y_{\zeta }, Y_{\eta \eta }, Y_{\zeta \zeta },...)=0, \end{aligned}$$
(3)

where H is the polynomial including the unknown function \(Y(\eta ,\zeta )\). For obtaining the traveling wave patterns, the following transformation is used:

$$\begin{aligned} w(\eta ,\zeta )=W(\xi )e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )}, ~~~y(\eta , \zeta )=Y(\xi )e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )}~~~~\textrm{where}~~~\xi =\frac{1}{\lambda }\eta +\kappa \zeta , \end{aligned}$$
(4)

here W and Y are real deterministic functions. By plugging Eq. (4) in (3) to attain the nonlinear ODE as following,

$$\begin{aligned} G(Y, Y^{'}, Y^{''}...)=0, \end{aligned}$$
(5)

consider the result of Eq. (5) has a model,

$$\begin{aligned} Y(\xi )=\sum _{i=0}^{n} l_{i}U^{i}(\xi ), \end{aligned}$$
(6)

where

$$\begin{aligned} U(\xi )=tanh(\xi ), \end{aligned}$$
(7)

then \(Y^{'}(\xi )\) and \(Y^{''}(\xi )\) can be written as:

$$\begin{aligned}{} & {} \frac{dY}{d\xi }7(1-U^2)\frac{dY}{dU}, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \frac{d^{2}Y}{d\xi ^{2}}=(1-U^2)(-2U\frac{dY}{dU}+(1-U^2)\frac{d^2Y}{dU^2}). \end{aligned}$$
(9)

4 Solution analysis for the SFDSW model

Plugging Eq. (4) in Eqs. (1) and (2), we attain the ordinary differential equation which perhaps reported as:

$$\begin{aligned} dw= & {} [\kappa {W^{'}}d\zeta +\alpha {W}d\mu ]e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )},\nonumber \\ dy= & {} [\kappa {Y^{'}}d\zeta +\alpha {Y}d\mu ]e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )},\nonumber \\ D_{\eta }^{\lambda }w= & {} W^{'}e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )},\nonumber \\ D_{\eta }^{\lambda }y= & {} Y^{'}e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )},\nonumber \\ D_{\eta \eta \eta }^{\lambda }w= & {} Y^{'''}e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )}. \end{aligned}$$
(10)

Plugging Eq. (10) in Eqs. (1) and (2), we get:

$$\begin{aligned}{} & {} \kappa {W^{'}}+\beta {YY^{'}}e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )}=0, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \kappa {Y^{'}}+m_{1}Y^{'''}+[m_{2}WY^{'}+m_{3}W^{'}Y]e^{(\alpha \mu (\zeta )-\frac{1}{2}\alpha ^{2}\zeta )}=0, \end{aligned}$$
(12)

we have

$$\begin{aligned}{} & {} \kappa {W^{'}}+\beta {YY^{'}}e^{\frac{-1}{2}\alpha ^{2}\zeta } E(e^{\alpha }\mu (\zeta ))=0, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \kappa {Y^{'}}+m_{1}Y^{'''}+[m_{2}WY^{'}+m_{3}W^{'}Y]e^{\frac{-1}{2}\alpha ^{2}\zeta } E(e^{\alpha }\mu (\zeta ))=0. \end{aligned}$$
(14)

After using the Lemma in Eqs.(13-14), we have:

$$\begin{aligned}{} & {} \kappa {W^{'}}+\beta {YY^{'}}=0, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \kappa {Y^{'}}+m_{1}Y^{'''}+m_{2}WY^{'}+m_{3}W^{'}Y=0. \end{aligned}$$
(16)

On integrating the Eq. (15), we get:

$$\begin{aligned} W=\frac{-\beta }{2\kappa }Y^{2}+C. \end{aligned}$$
(17)

Plugging Eq. (17) in Eq. (16), we get:

$$\begin{aligned} m_{1}Y^{'''}-\left[ \frac{\beta {m_{2}}}{2\kappa }+\frac{\beta {m_{3}}}{\kappa }\right] Y^{2}Y^{'}+[\kappa +Cm_{2}]Y^{'}=0. \end{aligned}$$
(18)

On integrating the Eq. (18), we get:

$$\begin{aligned} m_{1}Y^{''}-\left[ \frac{\beta {m_{2}}}{6\kappa }+\frac{\beta {m_{3}}}{3\kappa }\right] Y^{3}+[\kappa +Cm_{2}]Y=0. \end{aligned}$$
(19)

We suppose that the Eq. (5) has a form of solution as mention below:

$$\begin{aligned} Y(\xi )=\sum _{i=0}^{n} a_{i}U^{i}(\xi ). \end{aligned}$$
(20)

Where \(l_i\) and \(i=0,1,2,...,n\) are constant. By balancing principle as \(n+2=3n\), we get \(n=1\). Therefore, the initial solution becomes:

$$\begin{aligned} Y(\xi )=a_{0}+a_{1}U(\xi ). \end{aligned}$$
(21)

By substituting Eq. (21) into Eq. (17) and equating the coefficients of the distinct terms of \(U^{i}\), a system of algebraic equations can be obtained as follows:

$$\begin{aligned} (U)^{0}~&: Ca_{0}m_{2}+\kappa a_{0}+2m_{1}-\frac{\beta m_{2}a_{0}^{3}}{2\kappa }-\frac{\beta m_{3}a_{0}^{3}}{\kappa }=0,\\ (U)^{1}~&: \kappa a_{1}+Cm_{2}a_{1}-2m_{1}a_{1}- \frac{3\beta m_{2}a_{0}^{2}a_{1}}{2\kappa }-\frac{3\beta m_{3}a_{0}^{2}a_{1}}{\kappa }=0,\\ (U)^{2}~&: \kappa +Cm_{2}-8m_{1}- \frac{3\beta m_{2}a_{0}^{2}}{2\kappa }-\frac{3\beta m_{2}a_{0}a_{1}^{2}}{2\kappa }-\frac{3\beta m_{3}a_{0}^{2}}{\kappa }-\frac{3\beta m_{3}a_{0}a_{1}^{2}}{\kappa }=0,\\ (U)^{3}~&: 2m_{1}a_{1}-\frac{\beta m_{2}a_{1}^{3}}{\kappa } -\frac{\beta m_{3}a_{1}^{3}}{\kappa }- \frac{3\beta m_{2}a_{0}a_{1}}{\kappa }- \frac{6\beta m_{3}a_{0}a_{1}}{\kappa }=0,\\ (U)^{4}&: 6m_{1}-\frac{3\beta m_{2}a_{0}^{2}}{2\kappa }-\frac{3\beta m_{2}a_{1}^{2}}{2\kappa }-\frac{3\beta m_{3}a_{0}}{\kappa }-\frac{3\beta m_{3}a_{1}^{2}}{\kappa }=0,\\ (U)^{5}&: -\frac{3\beta m_{2}a_{1}}{2\kappa }-\frac{3\beta m_{3}}{\kappa }=0,\\ (U)^{6}&: -\frac{\beta m_{2}}{2\kappa }- \frac{\beta m_{3}}{\kappa }=0. \end{aligned}$$

To solve the above equations with the support of Maple to get the successive solutions:

Set 1:

$$\begin{aligned} a_{0}=0, ~~~~ a_{1}=2\sqrt{\frac{m_{1}\kappa }{\beta m_{1}+2\beta m_{3}}},~~~ and ~~~C=-\frac{\kappa -2m_{1}}{\beta _{2}}. \end{aligned}$$
(22)

Set 2:

$$\begin{aligned} a_{0}=0, ~~~~ a_{1}=-2\sqrt{\frac{m_{1}\kappa }{\beta m_{1}+2\beta m_{3}}},~~~ and ~~~C=-\frac{\kappa -2m_{1}}{\beta _{2}}. \end{aligned}$$
(23)

Inserting Eq. (23) and (22) into Eq. (21), we can determine the following solutions:

$$\begin{aligned} Y_{1}(\xi )= & {} 2\sqrt{\frac{m_{1}\kappa }{\beta m_{1}+2\beta m_{3}}}tanh(\xi ). \end{aligned}$$
(24)
$$\begin{aligned} Y_{2}(\xi )= & {} -2\sqrt{\frac{m_{1}\kappa }{\beta m_{1}+2\beta m_{3}}}tanh(\xi ). \end{aligned}$$
(25)

5 Physical Interpretation

In this section, the results presented in this work will be compared with those obtained by other scholars who utilized diverse methodologies. The governing equation has been the subject of exploration by various researchers, as outlined in the introduction section. The results presented in this study have been contrasted with the findings reported by Alsallami et al. (2023) and Al-Askar et al. (2022). In Al-Askar et al. (2022), authors employed the \((G'/G)\) expansion method, yielding solutions in the form of exponential and trigonometric functions. Authors in Alsallami et al. (2023), on the other hand, employed Hirota’s method to obtain solutions such as the cross-Kink rational and Homoclinic breather wave solutions. In comparison to these two papers, the present article introduces innovative outcomes in dynamic behavior. The results, involving hyperbolic functions tanh, extend beyond the scope of the aforementioned papers. This distinction underscores the innovativeness of the findings presented in this article.

Furthermore, through the application of suitable parameter values, an array of varied formations such as dark solitons, V-shaped solitons, singular dark solitons, and bell-shaped solitons have been documented. To achieve this, we will utilize various parameter values that showcase distinct 2D and 3D graphs illustrating exclusive wave behaviors. By visualizing the arrangement and comprehending the related physical phenomena, we can observe a range of solutions represented by dark and bright shapes of solitons, along with bell-shaped solitons, periodic waves, kink solitons, and other types of solitons. The implementation of precise values for each parameter has allowed us to enhance numerous soliton features.

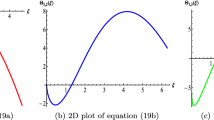
By selecting appropriate parameter values of Eq. (24), specifically \(\beta =0.2,~m_{1}=0.02,~m_{2}=-0.5,~m_{3}=0.03,~\kappa =0.7\), we obtain a predicted dark soliton as shown in Fig. 1. Dark solitons have garnered considerable attention in the field of nonlinear optics due to their stable transmission properties. In optical fibers, a stable optical soliton typically emerges when there is a balance between Kerr nonlinearity and group velocity dispersion (GVD). Bright solitons propagate in regions characterized by anomalous dispersion, while dark solitons are transmitted in regions with normal dispersion. The distinguishing feature of solitons, whether dark or bright, is their particle-like nature during interactions. The 3D graph represents the interval \(-7<\eta <7\) and \(0<\zeta <7\). The 2D graph is plotted at different values of \(\eta \) as \(\eta =1,~5,~9\) within the range of \(-4<\zeta <4\).

Fig. 1
figure 1

3D and 2D graphs of Eq. (24)

Full size image

The solution of Eq. (24) exhibits a soliton with a V-shaped structure, characterized by different values of \(m_{1}=0.002\) and \(m_{2}=0.03\), as shown in Fig. 2. The 3D plot illustrates the range \(0<\eta <4\) and \(-4<\zeta <4\). The 2D plot demonstrates the variation of \(\eta \) at values of 1, 5, and 9 within the range \(-4<\zeta <4\).

Fig. 2
figure 2

3D and 2D graphs of Eq. (24)

Full size image

The solution of Eq. (24) yields a bell-shaped soliton with a minor change in the values of \(m_{1}=1\) and the same value of \(m_{2}=1\), as depicted in Fig. 3. The 3D plot illustrates the range \(0<\eta <4\) and \(-4<\zeta <4\). The 2D plot represents the variation of \(\eta \) at values of 0.1, 0.5, and 0.9 within the range \(-4<\zeta <4\).

Fig. 3
figure 3

3D and 2D graphs of Eq. (24)

Full size image

In Fig. 4, we illustrate the variation of time \(\eta \) with respect to \(\zeta \). We observe the impact of \(m_{1}\) on fixed values of \(m_{2}=1\). As the value of \(m_{1}\) increases to 1.5, it exhibits discontinuity. The 3D plot represents the range \(0<\eta <4\) and \(-4<\zeta <4\). The 2D plot demonstrates the variation for \(\eta \) values of 0.1, 0.5, and 0.9 within the range \(-4<\zeta <4\). In contrast to recent literature, this paper presents novel solutions that have not been previously documented, as evidenced by a comparative analysis. These unique findings contribute innovatively to advancing our comprehension of soliton theory and the chaotic dynamics exhibited by fractional-order nonlinear systems, thereby enhancing the overall understanding in this field. The significance of obtaining solutions for SFDSW equations lies in their importance and utility in understanding various essential physical phenomena across applied sciences, plasma physics, fluid mechanics and population dynamics.

Fig. 4
figure 4

3D and 2D graphs of Eq. (24)

Full size image

6 Bifurcation theory

The concept of bifurcation refers to mathematical changes in the system and the quality of solutions provided by a group of differential equations. It is commonly used in the study of the mathematical structure of dynamic systems. Bifurcation occurs when a small change in the parameter values of a system leads to a sudden change in its behavior. It encompasses both local and global aspects of one-dimensional separation of operators operating in Banach’s permanent spaces, demonstrating how the theory can be applied to problems involving split equality. Additionally, this concept delves into standard structures such as stability and the composition of the dividing solutions in detail.

Equation(1) is where the methodology of bifurcation analysis is applied. The Galilean translation Eq. (17) in a dynamic system, such as, is subjected to analysis study.

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dY}{d\xi }=P,\\ \frac{dP}{d\xi }=AY^{3}-BY, \end{array}\right. } \end{aligned}$$
(26)

where \(A=\frac{\beta {m_{2}}}{2m_{1}\kappa }+ \frac{\beta {m_{3}}}{m_{1}\kappa }\) and \(B=\frac{\kappa +Cm_{2}}{m_{1}}\). The above-mentioned system (26) contains two equilibrium points, which are given below:

\(Y_{0}=(E_{0},0)\), \(Y_{1}=(E_{1},0)\) and \(Y_{2}=(E_{2},0)\).

Here, the values of \(E_{0}\), \(E_{1}\), and \(E_{2}\) are defined as follows:

\(E_{0}=0\), \(E_{1}=\sqrt{\frac{B}{A}}\), and \(E_{2}=-\sqrt{\frac{B}{A}}\).

In particular, we will introduce a specific type of bifurcation known as "Hopf bifurcation." This phenomenon occurs when a stable equilibrium point gives rise to periodic cycles as the bifurcation parameter reaches a critical value. This system will help us clarify the direction of classification for mathematical models. Homoclinic bifurcation, on the other hand, occurs when large invariant sets, such as periodic trajectories, intersect with the equilibrium point. This leads to a change in the topology of trajectories in phase space, which cannot be explained within a small region, unlike localized spatial bifurcation. In fact, the change in topology extends beyond what homoclinic bifurcation alone can account for.

Using the perspective of a dynamical system, the equilibrium points (\(P_{i}, Y_{i}\)) can be classified as follows: they are assigned as saddle points if \(M^{*}(P_{i}, Y_{i}) < 0\), center points if \(M^{*}(P_{i}, Y_{i}) > 0\) and the trace \(\tau _{1}(P_{i}, Y_{i}) = 0\), nodes if \(M^{*}(P_{i}, Y_{i}) > 0\) and \((\tau _{1}(P_{i}, Y_{i}))^{2} - 4\,M^{*}(P_{i}, \phi _{i}) > 0\), and zero points if \(M^{*}(P_{i}, Y_{i}) = 0\) with a Hopf index of zero for (\(P_{i}, Y_{i}\)). Here, \(M^{*}\) represents the Jacobian and \(\tau _{1}\) represents the trace of system (26).

  • \(A>0\), \(B<0\)

    We have plotted the phase portrait for Fig. 5 using the given parameter values \(A=0.5\) and \(B=-0.1\) for the equilibrium points \(E_{0}=(0,0)\), \(E_{1}=(1,0)\), and \(E_{2}=(-1,0)\). At these points, there are two nonlinear periodic trajectories: NPT(1, 0) at the equilibrium points \(E_{1}=(1,0)\) and \(E_{2}=(-1,0)\), and one super nonlinear periodic trajectory denoted as SNPT(3, 1). Additionally, there is one nonlinear homoclinic trajectory represented by NHT(1, 0). Consequently, the equilibrium point (0, 0) becomes a saddle point, while \(E_{1}=(1,0)\) and \(E_{2}=(-1,0)\) become center points, as shown in Fig. 5. Furthermore, the system (26) exhibits an infinite number of periodic trajectories both inside and outside the homoclinic trajectories, indicating the presence of an infinite number of periodic waves.

  • \(A>0,~B>0\)

    In Fig. 6, we set \(A=0.6\) and \(B=0.3\). The system (26) has three equilibrium points, namely \(E_{0}=(0,0)\), \(E_{1}=(1,0)\), and \(E_{2}=(-1,0)\) as shown in Fig. 6. There is only one nonlinear periodic trajectory NPT(1, 0) and the center point is named as \(E_{0}\), while P is a saddle point for NPT(1, 0). There are basically two saddle points, \(E_{1}=(1,0)\) and \(E_{2}=(-1,0)\). Therefore, the system has infinite periodic trajectories over (0, 0) and open bounded trajectories on the right and left sides of \(E_{1}\) and \(E_{2}\). Also, there are heteroclinic trajectories joining all the saddle points.

  • \(A<0\), \(B>0\)

    In Fig. 7, we plotted the phase portrait for \(A=-0.8\), \(B=0.5\). There is one nonlinear periodic trajectory denoted as NPT(1, 0) located at the center \(E_{0}=(0,0)\). Thus, the system (26) has an infinite family of periodic trajectories over (0, 0), which corresponds to an infinite periodic wave.

  • \(A<0\), \(B<0\)

    In Fig. 8, we plotted the phase portrait for the given parameters \(A=-0.5\), \(B=-0.3\) as shown. There is one saddle point located at the center \(E_{0}=(0,0)\) for open trajectories. Hence, the point (0, 0) is the only equilibrium point. The saddle point implies that the system has an infinite number of open bounded trajectories.

Fig. 5
figure 5

Bifurcation phenomena of dynamical system (26)

Full size image
Fig. 6
figure 6

Bifurcation phenomena of dynamical system(26)

Full size image
Fig. 7
figure 7

Bifurcation phenomena of dynamical system(26)

Full size image
Fig. 8
figure 8

Bifurcation phenomena of dynamical system (26)

Full size image

7 Quasi-periodic and chaotic pattern

In mathematics, a quasiperiodic wave is a type of motion created by a dynamical system that contains a finite number of frequencies. To add more interest, the perturbed term \(l_{0}\cos (\omega {t})\) is included in Eq. (1). Consequently, Eq. (10) with the perturbed term can be expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dY}{d\xi }=P, &{}\\ \displaystyle \frac{dP}{d\xi }=AY^{3}-BY+f_{0}\cos {(\omega {t})}, \end{array}\right. } \end{aligned}$$
(27)

where \(\omega \) is the frequency and \(f_0\) represents the power of the perturbation. System (27) does not include the trivial force, i.e., it is not involved in Eq. (26). To investigate the periodic and quasiperiodic behavior of Eq. (1) with the existence of perturbation by unknown variables, we will examine the consequences of the frequency on the target model. Here, we will maintain visible limits of the considered system modifications and discuss the consequences of the power and frequency of the perturbation. Figure 9 shows a 3D phase portrait and a time series graph for \(A=0.6\), \(B=0.1\), and \(a=0.5\), with the initial conditions (1.06, 1.1), \(f_0=1.05\), and \(\omega =1.9\). It is evident that a perturbed dynamical system (27) indicates periodic performance. While a specific pattern is found in three dimensions, outside of all these periodic waves, it can be seen in the time series graph, which continues to ensure periodic performance at particular values of the variables.

7.1 Case 1: \(f_{0}=0\)

By fixing \(\omega =1.1\), the quasi-periodic behavior of the perturbed dynamical system (27) is shown in Fig. 9a–c. Figure 9a–c depict the time series, 2D phase portrait, and 3D phase portrait, respectively. The time series shows a steady curve, and the phase portrait exhibits a regular trajectory overlaid on the other. This observation demonstrates that the system is essentially quasi-periodic.

Fig. 9
figure 9

Quasi-periodic phenomena with perturbed dynamical system (27) for the initial values (0.29, 0.13) with \(A=-13,~~B=5.307,~~a=0.1,~~f_0=4.5 ~~ and ~~ \omega =2.1\)

Full size image

7.2 Case 2: \(f_{0} \ne 0\)

We adjusted \(f_0=1.05\) and used the same settings as in Fig. 9 to obtain Fig. 10a–c, which display the time series and phase portrait accordingly. The time series generates packets of identical amplitude across a defined time period, while the phase portrait exhibits a predictable trajectory overlaid on the other, albeit with a different shape than in Fig. 9. These graphs depict the quasi-periodicity of the system.

Fig. 10
figure 10

Quasi-periodic phenomena without perturbed dynamical system (27) for the initial values (0.29, 0.13) with \(A=-13,~~B=5.307,~~a=0.1,~~f_0=0 ~~ and ~~ \omega =2.1\)

Full size image

8 Sensitive analysis

We will now continue investigating periodic and quasi-periodic chaotic phenomena using the sensitivity behavior of a strong structural solution (27), with the following initial conditions: Navy blue color is used to indicate \((V, W) = (0.029, 0)\), while pink color is used to represent \((V, W) = (0.013, 0)\). In Fig. 11, two results are computed while maintaining similar parameters to Fig. 8. It is clear to observe that even small changes in initial values can disrupt the results, demonstrating the quasi-periodic chaotic behavior of the curve with these boundary values. In Fig. 12, using the initial condition \((V, W) = (0.75, 0)\) represented by Navy blue color and \((V, W) = (0.8, 0)\) with pink color, two solutions are reported with the same parameter measurements as shown in Fig. 7. It is noteworthy that even slight variations in the initial values have no effect on the results, further strengthening the claim for chaotic behavior. In Fig. 13, using the initial condition \((V, W) = (0.03, 0)\) represented by Navy blue color and \((V, W) = (0.01, 0)\) with pink color, the two results are shown by considering the same variable values as those taken in Fig. 5. It is known that minor changes in the initial conditions have an effect on the results of specific values, indicating the quasi-periodic chaotic nature of those values.

Fig. 11
figure 11

Sensitivity behaviour of the dynamical system (26) with same parametric values taken in Fig. 8 with initial condition (V, W) = (0.029, 0) in Navy blue color and (V, W) = (0.013, 0) in pink color

Full size image
Fig. 12
figure 12

Sensitivity behaviour of the dynamical system (26) with same parametric values taken in Fig. 7 with initial condition (V, W) = (0.75, 0) in Navy blue color and (V, W) = (0.8, 0) in pink color

Full size image
Fig. 13
figure 13

Sensitivity behaviour of the dynamical system (26) with same parametric values taken in Fig. 5 with initial condition (V, W) = (0.03, 0) in Navy blue color and (V, W) = (0.01, 0) in pink color

Full size image

9 Multi-stability

This section will evaluate the multi-stability of the system (26). Multi-stability characterizes a flexible program with a limited parameter option, where diverse initial conditions result in the presence of two or more simultaneous outcomes. We employ a phase portrait and time series graphing approach to analyze the system (27) and explore its unique multi-stability characteristics. As shown in Fig. 14a, two separate snapshots are presented with parameter values \(a=4.3\), \(\omega =2.9\), \(A=-0.186\), \(B=0.07\), and \(f_0=-3.4067\). The initial condition \((V, W) =(1.19,1.099)\) is represented in blue, while the initial condition \((V, W) =(0.14,0.099)\) is represented in green. When considering the initial condition \((V, W) =(1.19,1.099)\), quasi-periodic behavior is observed, whereas the same set of primary variables \((V, W) =(0.14,0.099)\) exhibits periodic behavior in the hypothetical system.

Fig. 14
figure 14

Multi-stability of dynamical system (27) with fixed parametric values such as \(a=4.3,~\omega =2.9,~A=0.186,~B=0.07~and~f_{0}=3.4067\) and different initial conditions \((V,W)=(1.19,1.099)\) in blue colour and \((V,W)=(0.14,0.099)\) in green colour

Full size image

10 Conclusion

In this research, we effectively examined the stochastic-fractional Drinfel’d-Sokolov-Wilson model, a mathematical model applicable in the fields of electromagnetism and fluid mechanics. In our examination, we thoroughly scrutinized the equation through various lenses, encompassing soliton dynamics, bifurcation analysis, chaotic behaviors, and sensitivity analysis. Initially, we employed the tanh technique to identify the traveling wave solutions of the model, enabling the establishment of soliton solutions depicted in Figs. 1, 2, 3 and 4. Various categories of soliton solutions, including dark solitons, bell-shape solitons, and more, were observed in the models. The updated discussion revealed that the reported soliton solutions are novel and have not been previously documented in the literature. Additionally, we observed bifurcation, the qualitative behavior of quasi-periodic nonlinear waves and chaotic behaviors within the dynamical system, illustrating corresponding phase portraits as shown in Figs. 5, 6, 7, 8, 9 and10. It was evident that the observed model exhibits waves of nonlinear and super nonlinear periodicity. Lastly, an investigation has been conducted into the system’s sensitivity and multistability to initial conditions as presented in Figs. 11, 12, 13 and 14. It is anticipated that the results presented in this study, such as bifurcation, periodic and quasi-periodic behavior, chaos, sensitivity, and multi-stability, have implications for a wide range of nonlinear phenomena in the world. In contrast to recent literature, this paper presents novel solutions, as evidenced by a comparative analysis. The results, previously unreported, contribute innovatively to the comprehension of soliton theory and the chaotic tendencies within fractional order nonlinear systems. These groundbreaking findings not only advance our understanding but also lay the groundwork for refining research methodologies. Moving forward, this work serves as a catalyst for continued exploration into the dynamics of nonlinear systems. Therefore, this study may inspire further research into various nonlinear challenges.