1 Introduction

Many problems exist in different fields of study such as wave propagation, fluid mechanics, mechanical engineering, dynamical systems, chemistry, image processing, plasma physics, hydrodynamics, finance, biology, optics and other fields of engineering and science. Some scientists have proposed and researched nonlinear fractional partial differential equations (NFPDEs) (Zubair et al. 2018; Raza et al. 2019; Hosseini et al. 2020). Suggested numerous different definitions have been presented in the study (Yang et al. 2019; Park et al. 2020). Lately, investigators have begun to view a deficit at most of the fractional derivative definitions (Samko et al. 1993; Kilbas et al. 2006). Since fractional differential equations are an important field in plasma physics, mathematical physics, mathematical biology, nonlinear optics, applied mathematics, and quantum field theory, the solutions of these equations, along with their soliton-type solutions, have become very important. Fractional derivatives have an important place in the study of real-world problems so there is a different types of fractional derivatives for example Caputo fractional derivative, conformable derivative, modified Riemann-Liouville derivative, Riemann-Liouville derivative, beta derivative and many others. The universe is filled with events nonlinear and inner behaviors of this nonlinear are modeled for samples next to nonlinear alongside differential equations of fractional order as well as whole number order (Miller and Ross 1993; Hassani et al. 2020). It is thought that fractional-order equations analyze the intricate properties of complicated physical phenomena that occur in many fields of study on a small scale (Gomez-Aguilar et al. 2018; Bonyah et al. 2018). Later, scientists searched deeply to find approximate and suitable solutions nonlinear evolution equations, and as a result of their research, many methods have been developed recently to solve nonlinear evolution equations due to the differing opinions of scientists. On the instant, Seadawy handled the extended auxiliary equation procedure (Seadawy 2017), Duran et al. were interested in the modified \(\left( 1/G^{\prime }\right)\)-expansion practice (Duran et al. 2021a), Jianming et al. investigated the Backlund transformation procedure (Jianming et al. 2011), Yokus analyzed the extended finite difference procedure (Yokus 2018), Ablowitz and Clarkson handled the inverse scattering transformation practice (Ablowitz and Clarkson 1991), Duran et al. investigated the Bernoulli sub-equation function method (Duran et al. 2021b), Helal and Mehana investigated the Adomian decomposition practice (Helal and Mehana 2006), Al-Mdallal and Syam were interested in the sine–cosine procedure (Al-Mdallal and Syam 2007), Das and Ghosh paid attention to the \(\left( G^{\prime }/G\right)\) -expansion procedure (Das and Ghosh 2019), Islam and Akter handled the rational fractional \(\left( D_{\xi }^{\alpha }G/G\right)\)-expansion practice (Islam and Akter 2020), Mohyud-Din et al. handled the variational iteration practice (Mohyud-Din et al. 2009), Hashemi and Mirzazadeh were interested in the Lie symmetry practice (Hashemi and Mirzazadeh 2023), Wazwaz analyzed the sine-cosine procedure (Wazwaz 2004), Bekir investigated the \((G^{\prime }/G)\)-expansion procedure (Bekir 2008), Arshed et al. were interested in the first integral practice (Arshed et al. 2020), Biswas et al. handled the modified simple equation method (Biswas et al. 2018), Celik analyzed the F expansion practice (Çelik 2021), Kudryashov acquired the exact solutions of the Fisher model by the Kudryashov method (Kudryashov 2012), Kudryashov handled the first integral method (Kudryashov 2020), Kudryashov explored the general projective Riccati equations and the enhanced Kudryashov’s methods (Kudryashov 2023), Wang et al. applied the semi-inverse method to fractal (2 + 1)-Dimensional Zakharov–Kuznetsov model (Wang 2023a; Wang and Xu 2023; Wang et al. 2023a), Alquran applied the Maclaurin series to nonlinear equations (Alquran 2023a), Alquran applied the rational sine-cosine approach to second fourth-order Wazwaz equation (Alquran 2023b), Jaradat and Alquran applied the Kudryashov expansion method to (2 + 1)-dimensional two-mode Zakharov–Kuznetsov equation (Jaradat and Alquran 2020), Ghanbari applied the algorithm of the new method to the Oskolkov and the Oskolkov–Benjamin–Bona–Mahony–Burgers equations (Ghanbari 2021a), Ghanbari and Gómez–Aguilar applied the generalized exponential rational function procedure to the nonlinear Radhakrishnan–Kundu–Lakshmanan model (Ghanbari and Gómez-Aguilar 2019a), Sadaf et al. applied the \(\left( \frac{G^{\prime }}{G}, \frac{1}{G}\right)\)-expansion method to CI equation (Sadaf et al. 2023a), Mahmood et al. applied the modified Khater method to the (2 + 1)-dimensional Chaffee–Infante equation (Mahmood et al. 2023), Akram et al. applied the extended \(\left( \frac{G^{\prime }}{G^{2}}\right)\)-expansion method to the higher order nonlinear Schrödinger equation (Akram et al. 2023a, 2023b, c) and so on (Wang 2023b, c, d, e, f; Wang and Shi 2022; Wang et al. 2023b, c; Ali et al. 2019; Jaradat et al. 2018; Jaradat and Alquran 2022; Ghanbari 2022; Ghanbari and Gómez-Aguilar 2019b; Ghanbari and Baleanu 2019, 2020, 2023a, 2023b; Khater and Ghanbari 2021; Ghanbari 2019, 2021b; Ghanbari et al. 2018; Ghanbari and Akgül 2020; Ghanbari and Kuo 2019; Tian et al. 2022; Sadaf et al. 2023b.

The Chaffee–Infante (CI) model, which is useful for studying the diffusion formation of a gas in a uniform medium, is very important. Therefore, it has an important role in the field of mathematics and physics (Raza et al. 2021). The CI equation was first studied by Nathaniel Chafee and Ettore Infante. The most interesting aspect is a bifurcation in the system parameter that indicates the steepness of the potential. The CI model is very important in many areas, for example; such as ion-acoustic waves in plasma, fluid dynamics, plasma physics, sound waves, and electromagnetic waves Sriskandarajah and Smiley (1996). This model is the standard representation of endless-dimensional gradient systems in which the structure of the spherical attractor can be exactly characterized (Caraballo et al. 2007). The appropriate derivative time-fractional CI equation is as follows:

$$\begin{aligned} \left( \frac{\partial ^{\beta }u}{\partial t^{\beta }}\right) _{x}-\left( \frac{\partial ^{2}u}{\partial x^{2}}-\alpha u^{3}+\alpha u\right) _{x}+\theta \frac{\partial ^{2}u}{\partial y^{2}}=0 \end{aligned}$$
(1)

where \(\alpha\) represents the coefficient of diffusion and \(\theta\) represent degradation coefficient. The diffusion of a gas in a homogeneous medium is an important phenomenon in a physical context and the CI model provides a useful model to study such phenomena.

Scientists analyzed the (2 + 1) CI equation using many different solution methods, for example, Sakthivel and Chun applied the exp-function approach (Sakthivel and Chun 2010), Riaz et al. applied Lie symmetry analysis (Riaz et al. 2021), Mao applied the trial equation practice (Mao 2018), Qiang et al. applied the undetermined coefficient procedure (Qiang et al. 2013), Akbar et al. applied the first integral practice (Akbar et al. 2019), and Arshed et al. utilized the sinh-Gordon expansion practice (Arshed et al. 2023).

The beta derivative

Fractional derivatives are very important in scientific study fields. For this reason, fractional derivatives have been studied in depth and many definitions have been found, for example; Grunwald–Letnikov, Riemann–Liouville, the Caputo, modified Riemann–Liouville, and Atangana–Baleanu derivatives (Samko et al. 1993; Kilbas et al. 2006). In this paper, the beta derivative will be hadled. The most important property of this derivative is that the chain rule is applicable. Thus, we can reduce nonlinear differential equations to ordinary differential equations with the help of wave transformations. The beta derivative satisfies several properties that were as limitation for the fractional derivatives and has been used to model some physical problems. Basic definitions of the beta derivative are given as follows:

Definition

Let \(\ \psi \left( t\right)\) be a function defined for all non-negative t. The \(\beta\) derivative of \(T^{\beta }\left( \psi \left( t\right) \right)\) of order \(\beta\) is given by

$$\begin{aligned} T^{\beta }\left( \psi \left( t\right) \right) =\underset{\varepsilon \rightarrow 0}{\lim }\frac{\psi \left( t+\varepsilon \left( t+\frac{1}{ \Gamma \left( \beta \right) }\right) ^{1-\beta }\right) -\psi \left( t\right) }{\varepsilon }, \end{aligned}$$

where \(T^{\beta }\left( \psi \left( t\right) \right) =\frac{d^{\beta }\psi \left( t\right) }{dt^{\beta }}\) and \(0<\beta \le 1\)

Some rules are given for \(\beta\) derivative by the following theorem.

Theorem

Let \(\psi \left( t\right)\) and \(\varphi \left( t\right)\) be \(\beta\) -differentiable functions for all \(t>0\) and \(\beta \epsilon (0,1] .\) Some basic properties are discussed as follows:

  1. 1.

    \(T^{\beta }(a_{1}\psi (t)+a_{2}\varphi (t))=a_{1}T^{\beta }(\psi (t))+a_{2}T^{\beta }(\varphi (t)),\forall a_{1},a_{2}\in R\)

  2. 2.

    \(T^{\beta }(\psi (t)\varphi (t))=\varphi (t)T^{\beta }(\psi (t))+\psi (t)T^{\beta }(\varphi (t)),\)

  3. 3.

    \(T^{\beta }(\frac{\psi (t)}{\varphi (t)})=\frac{\varphi (t)T^{\beta }(\psi (t))-\psi (t)T^{\beta }(\varphi (t))}{\varphi (t)^{2}},\)

  4. 4.

    \(T^{\beta }(\psi (t))=\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{1-\beta }\frac{d\psi \left( t\right) }{dt}\) (Atangana et al. 2016).

The main procedure of this article is to find exact solutions to the CI model. The methods are explained in the second section. In chapter 3, the methods are applied to the CI equation. The stability test was applied to the exact solutions found in Sect. 4. In chapter 5, the exact solution graphs of the equation are given.

2 Methods

Think that nonlinear time fractional conformable differential equation as follows:

$$\begin{aligned} \Phi \left( u_{t}^{\beta },u_{x},u_{xx},\left( u_{x}\right) _{t}^{\beta },u_{yy},\ldots \right) =0, \end{aligned}$$
(2)

where u is a variable depending on x and t, \(\beta\) represents beta fractional order derivative. The wave transformation will be used as follows:

$$\begin{aligned} u\left( x,y,t\right) =U\left( \xi \right) , \end{aligned}$$
(3)

where

$$\begin{aligned} \xi =x+y-\frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) } \right) ^{\beta }. \end{aligned}$$
(4)

If we utilize the wave transformation to Eq. (2), the nonlinear ordinary differential equation is obtained as follows:

$$\begin{aligned} \Psi \left( U,U^{\prime },U^{\prime \prime },U^{\prime \prime \prime },\ldots \right) =0. \end{aligned}$$
(5)

2.1 The generalized Kudryashov procedure

We choose the solution for \(U(\xi )\) as follows:

$$\begin{aligned} U(\xi )=\ \frac{{{\sum \nolimits _{i=0}^{n} }}a_{i}\Omega ^{i}\left( \xi \right) }{\sum \nolimits _{j=0}^{m}b_{j}\Omega ^{j}\left( \xi \right) }, \end{aligned}$$
(6)

here \(a_{i},b_{j}\left( i=0,1,\ldots ,n,j=0,1,\ldots ,m\right)\) are constants and \(a_{n},b_{m}\) should be different from zero. \(\Omega \left( \xi \right)\) provides the following differential equation:

$$\begin{aligned} \frac{d\Omega }{d\xi }=\Omega ^{2}\left( \xi \right) -\Omega \left( \xi \right) . \end{aligned}$$
(7)

the solution of the Eq. (7) is given by:

$$\begin{aligned} \Omega \left( \xi \right) =\frac{1}{1+\chi e^{\xi }}. \end{aligned}$$
(8)

where \(\chi\) is the integral constant. Positive integers n and m are calculated by the homogeneous balancing principle, using the order of the highest-order derivative term and the degree of the highest-order nonlinear term. Expression (6) is written into equation (5) using (7) and the polynomial \(\Omega \left( \xi \right) ^{i-j}(i,j=1,2,3,\ldots )\) is obtained. An algebraic equation system is found by setting all coefficients of this polynomial dependent on \(\Omega \left( \xi \right)\) equal to zero. The obtained algebraic equation system is solved according to the coefficients \(a_{i},b_{j},v,\alpha\) and the solutions of equation (5) are obtained. The exact solutions of equation (2) are obtained by writing \(\xi =x+y-\frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\) to the solutions of equation (5) (Akbulut 2023; Akbar et al. 2021; Akbulut and Kaplan 2021).

2.2 The modifed Kudryashov procedure

We choose the solution for \(U(\xi )\) as follows:

$$\begin{aligned} U(\xi )=\ \underset{i=0}{\overset{n}{\sum }}a_{i}\left( \Omega \left( \xi \right) \right) ^{i}, \end{aligned}$$
(9)

where \(a_{i}\left( i=0,1,\ldots ,n\right)\) are constants and there should be \(a_{n}\ne 0\). \(\Omega \left( \xi \right)\) provides the following ordinary differential equation:

$$\begin{aligned} \frac{d\Omega }{d\xi }=\left( \Omega ^{2}\left( \xi \right) -\Omega \left( \xi \right) \right) \ln \omega \end{aligned}$$
(10)

the solution of the Eq. (10) is given by:

$$\begin{aligned} \Omega \left( \xi \right) =\frac{1}{1+\chi \omega ^{\xi }}. \end{aligned}$$
(11)

where \(\chi\) is the integral constant. n is calculated by the homogeneous balancing principle, using the order of the highest-order derivative term and the degree of the highest-order nonlinear term. Expression (9) is written into equation (5) using (10) and the polynomial \(\Omega \left( \xi \right) ^{i}(i=1,2,3,\ldots )\) is obtained. An algebraic equation system is found by setting all coefficients of this polynomial dependent on \(\Omega \left( \xi \right)\) equal to zero. This algebraic equation system is solved according to the coefficients \(a_{n},v,\alpha\) and the solutions of equation (5) are obtained. The exact solutions of equation (2) are obtained by putting \(\xi =x+y- \frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\) to the solutions of equation (5) (Akbulut 2023; Akbulut et al. 2022).

Remark

The solutions we found here are special cases of the solutions we found with the generalized Kudryashov method.

Remark

Our methods are different from the other methods in the literature because of the selected auxiliary equations are different.

3 Application of the methods

In this part, the given methods will be applied to Eq. (1). If we apply (4) to Eq. (1), the following ODE is obtained:

$$\begin{aligned} U^{\prime \prime }+\left( v-\theta \right) U^{\prime }+\alpha U\left( 1-U^{2}\right) =0 \end{aligned}$$
(12)

3.1 Generalized Kudryashov method

Balancing the highest power nonlineer term \(U^{3}\) and the highest order derivative \(U^{\prime }\), \(m=1\) and \(n=2\) are obtained. Thus, using (6) the solution of (12) can be given as follows:

$$\begin{aligned} U(\xi )=\frac{a_{0}+a_{1}\Omega +a_{2}\Omega ^{2}}{b_{0}+b_{1}\Omega } \end{aligned}$$
(13)

We substitute Eq. (13) in Eq. (12) and find a polynomial equation by substituting solution (7) for the result and set the coefficients \(a_{0},a_{1},a_{2},b_{0},b_{1},v,\alpha\) equal to zero and the following system of equations is obtained:

$$\begin{aligned} \begin{array}{l} -\alpha a_{0}^{3}+\alpha a_{0}b_{0}^{2}=0, \\ -b_{1}b_{0}a_{0}-b_{1}\theta a_{0}b_{0}+2b_{1}\alpha a_{0}b_{0}+b_{1}va_{0}b_{0} \\ -va_{1}b_{0}^{2}+\theta a_{1}b_{0}^{2}+b_{0}^{2}a_{1}+\alpha a_{1}b_{0}^{2}-3\alpha a_{0}^{2}a_{1}=0, \\ -b_{1}^{2}\theta a_{0}+b_{1}^{2}va_{0}+b_{1}^{2}a_{0}+b_{1}^{2}\alpha a_{0}+3b_{1}b_{0}a_{0}+b_{1}\theta a_{1}b_{0}-b_{1}va_{1}b_{0} \\ +2b_{1}\alpha a_{1}b_{0}-b_{1}va_{0}b_{0}+b_{1}\theta a_{0}b_{0}-b_{1}b_{0}a_{1}-3\alpha a_{0}a_{1}^{2}+\alpha a_{2}b_{0}^{2} \\ -3\alpha a_{0}^{2}a_{2}+4b_{0}^{2}a_{2}-2va_{2}b_{0}^{2}-\theta a_{1}b_{0}^{2}-3b_{0}^{2}a_{1}+va_{1}b_{0}^{2}+2\theta a_{2}b_{0}^{2}=0, \\ -b_{1}^{2}a_{0}+b_{1}^{2}\theta a_{0}+b_{1}^{2}\alpha a_{1}-b_{1}^{2}va_{0}+3b_{0}a_{2}b_{1}-2b_{1}b_{0}a_{0}+2b_{1}\alpha a_{2}b_{0}-b_{1}\theta a_{1}b_{0}+b_{1}va_{1}b_{0} \\ +3b_{1}\theta a_{2}b_{0}+b_{1}b_{0}a_{1}-3b_{1}va_{2}b_{0}-6\alpha a_{0}a_{1}a_{2}+2va_{2}b_{0}^{2}-10b_{0}^{2}a_{2}-\alpha a_{1}^{3}+2b_{0}^{2}a_{1}-2\theta a_{2}b_{0}^{2}=0, \\ 2a_{2}b_{1}^{2}-\alpha a_{2}^{3}=0, \\ -3a_{2}b_{1}^{2}-b_{1}^{2}\theta a_{2}+b_{1}^{2}va_{2}+6b_{0}a_{2}b_{1}-3\alpha a_{1}a_{2}^{2}=0, \\ b_{1}^{2}\theta a_{2}-b_{1}^{2}va_{2}+b_{1}^{2}\alpha a_{2}+a_{2}b_{1}^{2}-3b_{1}\theta a_{2}b_{0}+3b_{1}va_{2}b_{0} \\ -9b_{0}a_{2}b_{1}+6b_{0}^{2}a_{2}-3\alpha a_{0}a_{2}^{2}-3\alpha a_{1}^{2}a_{2}=0. \end{array} \end{aligned}$$

By solving these algebric equations system for \(a_{0},a_{1},a_{2},b_{0},b_{1},v\) and \(\alpha ,\) we obtain the following cases:

Set1

$$\begin{aligned} \left\{ a_{0}=0,a_{1}=0,a_{2}=\frac{b_{1}}{2},b_{0}=-\frac{b_{1}}{2} ,b_{1}=b_{1},v=6+\theta ,\alpha =8\right\} \end{aligned}$$
(14)

Substituting (14) into (3) without ignoring (13), we have the exact solution as follows:

$$\begin{aligned} u_{1}\left( x,y,t\right) =-\frac{1}{-1+A^{2}e^{2\left( x+y-\frac{v}{\beta } \left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(15)

Set2

$$\begin{aligned} \left\{ a_{0}=0,a_{1}=-\frac{a_{2}}{2},a_{2}=a_{2},b_{0}=0,b_{1}=-\frac{a_{2} }{2},v=\theta ,\alpha =\frac{1}{2}\right\} \end{aligned}$$
(16)

Substituting (16) into (3) without ignoring (13), we have the exact solution as follows:

$$\begin{aligned} u_{2}\left( x,y,t\right) =\frac{-1+Ae^{\left( x+y-\frac{v}{\beta }\left( t+ \frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}{ 1+Ae^{\left( x+y-\frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(17)

Set3

$$\begin{aligned} \left\{ a_{0}=0,a_{1}=\sqrt{2}b_{1}i,a_{2}=-\sqrt{2}b_{1}i,b_{0}=-\frac{b_{1} }{2},b_{1}=b_{1},v=\theta ,\alpha =-1\right\} \end{aligned}$$
(18)

Substituting (18) into (3) without ignoring (13), we have the exact solution as follows:

$$\begin{aligned} u_{3}\left( x,y,t\right) =\frac{-2i\sqrt{2}Ae^{\left( x+y-\frac{v}{\beta } \left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}{ -1+A^{2}e^{2\left( x+y-\frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(19)

Set4

$$\begin{aligned} \left\{ a_{0}=-\frac{b_{1}}{2},a_{1}=b_{1},a_{2}=-\frac{b_{1}}{2},b_{0}=- \frac{b_{1}}{2},b_{1}=b_{1},v=-6+\theta ,\alpha =8\right\} \end{aligned}$$
(20)

Substituting (20) into (3) without ignoring (13), we have the exact solution as follows:

$$\begin{aligned} u_{4}\left( x,y,t\right) =\frac{A^{2}e^{2\left( x+y-\frac{v}{\beta }\left( t+ \frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}{ -1+A^{2}e^{2\left( x+y-\frac{v}{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }} \end{aligned}$$
(21)

3.2 The modified Kudryashov method

Balancing the highest power nonlineer term \(U^{3}\) and the highest order derivative \(U^{\prime \prime }\), we obtain \(n=1.\) Using the method, the exact solution can be given as follows:

$$\begin{aligned} U(\xi )=a_{0}+a_{1}\Omega \end{aligned}$$
(22)

We substitute Eq. (22) in (12), and find a polynomial equation by substituting solution (10) for the result and set the coefficients \(a_{0},a_{1},v,\alpha\) equal to zero and we get the following system of equations:

$$\begin{aligned} & - \alpha a_{0}^{3} + \alpha a_{0} = 0, \\ & - 3\alpha a_{0}^{2} a_{1} + a_{1} \ln \left( \omega \right)^{2} - a_{1} \ln \left( \omega \right)v + a_{1} \ln \left( \omega \right)\theta + \alpha a_{1} = 0, \\ & - 3a_{1} \ln \left( \omega \right)^{2} - a_{1} \ln \left( \omega \right)\theta - 3\alpha a_{0} a_{1}^{2} + a_{1} \ln \left( \omega \right)v = 0, \\ & 2a_{1} \ln \left( \omega \right)^{2} - \alpha a_{1}^{3} = 0. \\ \end{aligned}$$
(23)

By solving these algebric equations system for \(a_{0},a_{1},v\) and \(\alpha ,\) the following cases are obtained.

Set1

$$\begin{aligned} \left\{ a_{0}=0,a_{1}=\pm 1,v=3\ln \left( \omega \right) +\theta ,\alpha =2\ln \left( \omega \right) ^{2}\right\} \end{aligned}$$
(24)

If we substitute (24) into (22), the exact solutions are obtained as follows:

$$\begin{aligned} u_{1,2}\left( x,y,t\right) =\pm \frac{1}{1+A\omega ^{\left( x+y-\frac{v}{ \beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(25)

Set2

$$\begin{aligned} \left\{ a_{0}=\pm 1,a_{1}=\mp 2,v=\theta ,\alpha =\frac{1}{2}\ln \left( \omega \right) ^{2}\right\} \end{aligned}$$
(26)

If we substitute (26) into (22), the exact solutions are obtained as follows:

$$\begin{aligned} u_{3,4}\left( x,y,t\right) =\pm 1\mp \frac{2}{1+A\omega ^{\left( x+y-\frac{v }{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(27)

Set3

$$\begin{aligned} \left\{ a_{0}=\pm 1,a_{1}=\mp 1,v=-3\ln \left( \omega \right) +\theta ,\alpha =2\ln \left( \omega \right) ^{2}\right\} \end{aligned}$$
(28)

If we substitute (28) into (22), the exact solutions are obtained as follows:

$$\begin{aligned} u_{5,6}\left( x,y,t\right) =\pm 1\mp \frac{1}{1+A\omega ^{\left( x+y-\frac{v }{\beta }\left( t+\frac{1}{\Gamma \left( \beta \right) }\right) ^{\beta }\right) }}. \end{aligned}$$
(29)

4 Figures of the results

In this part, plots of some results are given for arbitrary constants. Plots are given as three-dimensional, two-dimensional, and contour plots.

Fig. 1
figure 1

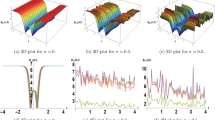
The dark wave of the Eq. (17) when \(A=0.8,\beta =0.5,\theta =1,v=1,y=0,a_{2}=1,b_{1}=1\)

Full size image

Figure 1 represents dark wave. Also, Fig. 1d is given to see how the solution changes for different values of \(\beta\).

Fig. 2
figure 2

The soliton wave of the Eq. (19) when \(A=0.8,\beta =0.5,\theta =1,v=1,y=0,b_{1}=1\)

Full size image

Figure 2 represents soliton wave. Also, Fig. 2d is given to see how the solution changes for different values of \(\beta\).

Fig. 3
figure 3

The kink wave of the Eq. (25) when \(A=0.1,\beta =0.7,\omega =0.2,\theta =1,v=3ln(2)+1,y=0\)

Full size image

Figure 3 represents kink wave. Also, Fig. 3d is given to see how the solution changes for different values of \(\beta\).

Fig. 4
figure 4

The dark wave of the Eq. (27) when \(A=0.2,\beta =0.8,\omega =0.8,\theta =1,v=1,y=0\)

Full size image

Figure 4 represents dark wave. Also, Fig. 4d is given to see how the solution changes for different values of \(\beta\).

5 Stability properties

Stability analysis is an important research area for nonlinear evolution equations. It helps to study how a system responds to external influences and how it behaves over time. The stability property obtained using the properties of the Hamilton system is tested on some solutions to show the usability of the model in applications. In this part of the study, the stability features of the solutions obtained for Set 5 and Set 6 are examined with the help of the properties of the Hamilton system.

The momentum in the Hamiltonian system

$$\begin{aligned} M_{H}=\frac{1}{2}\int _{-\epsilon }^{\epsilon }F^{2}\left( \xi \right) d\xi , \end{aligned}$$

where \(F\left( \xi \right)\) is the solution of the model and the essential circumstance for stability is formulated in the next form

$$\begin{aligned} \frac{\partial M}{\partial v}\mid _{v=v_{0}}>0, \end{aligned}$$

where \(v_{0}\) are optional constants (Yue et al. 2020a, b).

(17) in solution

$$\begin{aligned} \left\{ \theta =1,A=1,\beta =1,y=0\right\} \end{aligned}$$

by using custom parameters their values

$$\begin{aligned} M=2+\frac{4e^{-3}}{1+e^{-3}}-\frac{4e^{-1}}{e^{-1}+1}+\ln \left( e^{-2}\right) -4\ln \left( e^{-1}+1\right) +2\ln \left( 1+e^{-3}\right) +2\ln \left( 1+e\right) \end{aligned}$$

thus, the obtain

$$\begin{aligned} \frac{\partial M}{\partial v}\mid _{v=1}=0.584589133>0. \end{aligned}$$

(27) in solution

$$\begin{aligned} \left\{ \theta =1,\omega =2,A=1,\beta =1,y=0\right\} \end{aligned}$$

by using custom parameters their values

$$\begin{aligned}{} & {} \left( \frac{2}{v}+\frac{2^{2+2v}}{v\ln \left( 2\right) \left( 2^{2v}+2\right) }-\frac{2^{3+2v}}{v\ln \left( 2\right) \left( 2^{1+2v}+1\right) }+\frac{\ln \left( 2^{-v}\right) }{\ln \left( 2\right) v^{2}}-\frac{\ln \left( 2^{v}\right) }{\ln \left( 2\right) v^{2}}\right. \\{} & {} \quad \left. -\frac{2\ln \left( 2^{2v}+2\right) }{\ln \left( 2\right) ^{2}v^{2}} +\frac{2\ln \left( 2^{1+2v}+1\right) }{\ln \left( 2\right) ^{2}v^{2}}\right) _{v=1} \\{} & {} M=1-\frac{2\ln \left( 6\right) }{\ln \left( 2\right) ^{2}}-\frac{8}{9\ln \left( 2\right) }+\frac{\ln \left( \frac{1}{2}\right) }{ \ln \left( 2\right) }+\frac{2\ln \left( 9\right) }{\ln \left( 2\right) ^{2}} \end{aligned}$$

thus, the obtain

$$\begin{aligned} \frac{\partial M}{\partial v}\mid _{v=1}=0.405449408>0. \end{aligned}$$

As a result, this solution is stable. The same steps are applied to the next solutions obtained, and the stability feature of each is determined.

6 Conclusion

In this study, solutions of the local temporal fractional (2 + 1) dimensional Chaffee–Infante equation were obtained by generalized Kudryashov and modified Kudryashov methods. These two methods can be easily applied and offer different solutions compared to other methods in the literature. Since the methods are powerful and effective, the procedures used can be applied to different nonlinear differential equations. The generalized Kudryashov method produced four solutions, and the modified Kudryashov method produced 6 solutions. The resulting solutions are hyperbolic and rational functions. The obtained solutions were examined by stability test. As a result, the solutions are stable. 3D and 2D contour drawings were drawn for some families, and in these drawings, the graphs of soliton, kink, and dark solution were obtained. Maple software program was used to check the accuracy of the results. The CI equation provides a useful model for studying the diffusion of a gas in a uniform medium. In addition, ion-acoustic waves in plasma also play an important role in various scientific and technological fields, including fluid dynamics, plasma physics, signal processing through optical cables, sound waves, and electromagnetic waves. The results obtained have the potential to be useful in the fields of physics, mathematics and engineering.