On soliton solutions of Fokas dynamical model via analytical approaches

Abstract

The nonlinear (4+1)-dimensional Fokas equation (FE) has been demonstrated to be the integrable extension of the Kadomtsev–Petviashvili (KP) and Davey–Stewartson (DS) equations. In nonlinear wave theory, the governing model is one of the fundamental structures that explains the surface waves and interior waves in straits or channels with different depths and widths. In this study, the generalized unified approach, the generalized projective ricatti equation technique, and the new F/G-expansion technique are applied to investigate the higher dimensional nonlinear model analytically. As a result, several solutions are successfully achieved, including dark soliton, periodic type solitons, w-shaped soliton, and single-bell shaped solitons. Along with an explanation of their behavior, we also display a few of the equation’s exact solutions graphically. The results demonstrate the effectiveness and simplicity of the approaches mentioned in this article, demonstrating their applicability to a wide range of additional nonlinear evolution issues in numerous scientific and technical disciplines.

1 Introduction

Nonlinear partial differential equations (PDEs) are used to study a variety of physics and geometry problems. Numerous researchers, including engineers, chemists, mathematicians, physicists, and others, are interested in these nonlinear structures because they can be used to model a variety of real-world nonlinear problems. A wide range of natural and applied sciences use PDEs, including mathematical finance (An et al. 2021), biology (Friedman 2012), shallow water waves (Seadawy et al. 2017), fluid dynamics (Samuel et al. 2021), solid state physics, plasma physics, acoustics, and optical fibers (Rehman et al. 2022). The study of nonlinear physical structures is becoming extensively crucial and fascinating topic in the field of contemporary science. Currently, a number of prominent mathematicians and scientists are interested in the dynamical structures of many higher dimensional nonlinear models arising in diverse disciplines of science and engineering, which is expanding exponentially, such as Nasreen et al. (2023a, b, c, d, e), Ismael and Younas (2023), Seadawy et al. (2020).

The development of solitary wave solutions for nonlinear structures is of key importance to study the dynamics many crucial models arising in contemporary science and engineering, a number of analytical and numerical techniques have been developed. The bilinear transformation (Xu and Chow 2016), the Hirota bilinear, the extended trail function (Gepreel 2016), the tanh-coth expansion (Rani et al. 2021), the sub ODE (Yang et al. 2015), the extended Sinh-Gordon equation (Kumar et al. 2018), the first integral (Javeed et al. 2019), the extended simplest equation (Bilige et al. 2013), the modified Khater technique (Khater et al. 2021), new Kudryashov approach (Akinyemi et al. 2021), the modified direct algebraic method (Seadawy et al. 2020), the generalized auxiliary equation approach (Akinyemi et al. 2022), the generalized Riccati equation method (Lu et al. 2019), the modified simple equation method (Rasheed et al. 2021), the Lie symmetry approach (Sahoo et al. 2017), the extended Tanh method (Zahran and Khater 2016), the homogeneous balance methods Song and Liu (2022), the modified expansion method (Islam et al. 2023), the generalized Kudryashov scheme (Akbar et al. 2022), the rational $\left( 1/\phi '(\xi )\right)$-expansion method (Islam et al. 2022), the rational $\left( G'/G\right)$-expansion scheme (Islam et al. 2022), the modified $\left( 1/G'\right)$ -expansion method (Yokus et al. 2022), among others, have all been found in current decades using illustrative computation and many more (Akbar et al. 2023; Islam et al. 2023, 2022, 2023; Ozdemir et al. 2022).

This study aims to obtain travelling and solitary waves solutions to the nonlinear $(4+1)$-dimensional Fokas dynamical equation using three effective methods: the generalised unified technique (Rafiq et al. 2022), the generalised projective Riccati equation technique (Akram et al. 2021), and the new F/G-expansion technique (Mortazavi and Gachpazan 2016). Consider the nonlinear (4+1)-dimensional FE (Ullah et al. 2022) which reads

$$\begin{aligned} \begin{aligned}&4\frac{\partial }{\partial t}\left( \frac{\partial u}{\partial x}\right) -\frac{\partial ^3}{\partial x^3}\left( \frac{\partial u}{\partial y}\right) +\frac{\partial }{\partial x}\left( \frac{\partial ^3u}{\partial y^3}\right) +12u\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}\\&\quad +12u\frac{\partial }{\partial x}\left( \frac{\partial u}{\partial y}\right) -6\frac{\partial }{\partial z}\left( \frac{\partial u}{\partial w}\right) =0, \end{aligned} \end{aligned}$$

(1)

where $u=u(x,y,z,w,t)$ is a wave profile and velocity. Assume that this general Eq. (1) is used to represent the wave gesture in multidimensional broadcasting. It depicts the external wave’s distortion or dispersion. As a result, numerous sorts of Fokas equation solutions will provide us with suggestions for instructing the complex system of DS and KD models.

The FE model characterizes the internal and surface waves in rivers with varying physical conditions is being investigated by a number of researchers with the aid of various analytical techniques. For instance, Shahzad Sarwar used the generalised $\exp (-\phi )$-expansion technique and improved F-expansion technique to obtain the exact wave solutions of this model (Sarwar 2021). Investigations on travelling wave solutions and sensitivity analysis Three different approaches, including the modified Kudryashove approach, the modified extended tanh-function approach, and the exponential rational function approach, are used in this model by Kaplan et al. (2022). Finding the exact solutions to these models is therefore essential, and the literature has provided a number of effective methods for resolving these kinds of equations. As far as we know, the generalised unified method, the generalised projective ricatti equation technique, and the new F/G-expansion technique have not been used to solve the considered model in the literature.

This paper is organized as follows: In Sect. 2, a detail description of the proposed techniques is shown, while Sect. 3 is devoted to the applications of the two proposed techniques to the governing model Eq. (1). However Sect. 4 contains discussion and results also Sect. 5 contains conclusions.

2 Description of techniques

Suppose the NPDE in the following form,

$$\begin{aligned} F\left( \phi , \phi _t, \phi _x, \phi _{tt}, \phi _{xx}, \phi _{xt}, \phi _{yy}, \phi _{zz}, \phi _{yt},\cdots \right) =0, \end{aligned}$$

(2)

where F is a polynomial function in its argument. Also $\phi$ is a wave function of the variables x, y, z and t. Suppose the wave transformation of form,

$$\begin{aligned} u(x,y,z,w,t)=U(\eta ),~~~\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+ \nu \text {t}+\rho w+\epsilon . \end{aligned}$$

(3)

Putting Eq. (3) into Eq. (2), gives an ODE of the form,

$$\begin{aligned} Q\left( \phi ,\phi ',\phi '',\phi ''',\cdots \right) =0. \end{aligned}$$

(4)

2.1 Description of the generalized unified technique

This section contains the key ideas of the generalized unified method. The major process of approach are outlined below,

Step 1. Using the unified method, the obtained solutions of Eq. (4) are classed as polynomial or rational function solutions.

2.1.1 The polynomial function solution

The unified method indicates that in order to acquire the polynomial function solutions of Eq. (4),

$$\begin{aligned} U= & {} U(z)=\sum _{i=0}^n p_i \phi ^i(z),\nonumber \\ (\phi '(z))^p= & {} \sum _{i=0}^{p k} b_i \phi ^i(z),z=\sum _{s=1}^q \alpha _s x_s+\alpha _0 t, \end{aligned}$$

(5)

where $j=1,2,\cdots ,m,~p=1,2, p_i,b_i,\alpha _0,\alpha _s$ are to be determined later constants. It’s worth noting that in ODE Eq. (4), n and k are found by using the balancing principle between the higher derivative and higher power. A second criterion (the consistency requirement) is also employed, which states that the arbitrary function in Eq. (5) may be found consistently. When $p=1$, Eq. (5) yields elementary solutions (explicit or implicit), however when $p=2$, it yields elliptic solutions.

2.1.2 The rational function solution

To get the polynomial function solutions of Eq. (4), unified method suggests that

$$\begin{aligned} U= & {} U(z)=\frac{\sum _{i=0}^n p_i \phi ^i(z)}{\sum _{i=0}^r q_i \phi ^i(z)},\nonumber \\ (\phi '(z))^p= & {} \sum _{i=0}^{p k} b_i \phi ^i(z),z=\sum _{s=1}^q \alpha _s x_s+\alpha _0 t, \end{aligned}$$

(6)

where $j=1,2,\cdots ,m, ~~p=1,2, p_i,b_i,\alpha _0,\alpha _s$ are constants to be determined later. It is worth to be noticing that, n, r and k are determined by using the balancing principle between the higher derivative and higher power in ODE Eq. (4). Also, a second condition(the consistency condition), which asserts that the arbitrary function in Eq. (6) could be consistently determined, is used. When $p=1$, Eq. (6) solves to elementary solutions(explicit or the implicit solutions) while when $p=2$, it solves to elliptic solutions.

2.2 Description of the generalized projective Riccati equation technique

Step 1:Suppose that Eq. (4) has solution of the form,

$$\begin{aligned} U(\eta )=A_0+\sum _{i=1}^N \Omega (\eta )^{i-1}\left[ A_i \Omega (\eta )+B_i \gamma (\eta )\right] \end{aligned}$$

(7)

where $A_0$, $A_i$, $B_i$ are constants to be determined. The function $\Omega (\eta )$ and $\gamma (\eta )$ satisfies the ODE:

$$\begin{aligned} \Omega '(\eta )= & {} k{\Omega }(\eta )\gamma (\eta ) \end{aligned}$$

(8)

$$\begin{aligned} \gamma '(\eta )= & {} R_1+\text {k }\gamma (\eta )^2-M \Omega (\eta ),~~k=\pm 1, \end{aligned}$$

(9)

also

$$\begin{aligned} \gamma ^2(\eta )=-k(R_1-2 M \Omega (\eta ) +\frac{M^2+r_1}{R_1}\Omega ^2 (\eta )), \end{aligned}$$

(10)

where $r_1=\pm 1$, $R_1$ and M are non zero constants.

If $R_1=M=0$ Eq. (4) has the formal solution:

$$\begin{aligned} U(\eta )=\sum _{i=1}^N A_i \gamma ^i, \end{aligned}$$

(11)

where $\gamma (\eta )$ satisfies the ODE:

$$\begin{aligned} \gamma '(\eta )=\gamma ^2 \end{aligned}$$

(12)

Step 2: The positive integer N in Eq. (4) can be determined by using the balancing principle.

Step 3. Putting Eq. (7) combined with Eq. (8–10) into Eq. (4) or Eq. (11) along with Eq. (12) into Eq. (4), we have a polynomial in $\Omega ^j(\eta )\gamma ^i(\eta )$. Collecting all coefficients of the same $\Omega ^j(\eta )\gamma ^i(\eta )$ $(j=0,1,2,\cdots ;i=0,1,2,\cdots )$ together and setting all of the terms equals to zero, we get group of the algebraic equations, whose solutions yields the values of $A_0, A_i, B_i, \mu , \rho , R_1$.

Step 4. Equation (8–9) admits the following solutions:

Family I. If $k=-1,r_1=-1$, $R_1>0$, we have

$$\begin{aligned} \begin{aligned} \Omega (\eta )= & {} \frac{R_1 \text {sech}\left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1},\\ ~~~\gamma (\eta )= & {} \frac{R_1 \tanh \left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}. \end{aligned} \end{aligned}$$

(13)

Family II. If $k=-1,r_1=1$, $R_1>0$, we have

$$\begin{aligned} \begin{aligned} \Omega (\eta )= & {} \frac{R_1 \text {csch}\left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1},\\ ~~~\gamma (\eta )= & {} \frac{\sqrt{R_1} \coth \left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}. \end{aligned} \end{aligned}$$

(14)

Family III. If $k=1,r_1=-1$, $R_1>0$, we have

$$\begin{aligned} \begin{aligned} \Omega (\eta )= & {} \frac{R_1 \text {sech}\left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}, ~~~\gamma (\eta )=\frac{R_1 \tanh \left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1},\\ \Omega (\eta )= & {} \frac{R_1 \text {csch}\left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}, ~~~\gamma (\eta )=-\frac{\sqrt{R_1} \coth \left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}. \end{aligned} \end{aligned}$$

(15)

Family IV. If $R_1=M=0$, we have

$$\begin{aligned} \begin{aligned} \Omega (\eta )=\frac{C}{\eta }, ~~~\gamma (\eta )=\frac{1}{\text {k} \eta } \end{aligned} \end{aligned}$$

(16)

Putting the values of $A_0, A_i, B_i, \mu , \rho , R_1$ and using the Eqs. (13–16), the solutions of Eq. (2) can be obtained.

2.3 Description of the new F/G-expansion technique

The major process of F/G-expansion technique are outlined below,

Step 1. The solution of Eq. (4) is then assumed and may be written a polynomial in (F/G) as follows,

$$\begin{aligned} U(\eta ) =\sum _{i=0}^n A_i \left( \frac{F}{G}\right) ^i, \end{aligned}$$

(17)

where $G=G (\eta )$ and $F=F (\eta )$ satisfy

$$\begin{aligned} F'(\eta )=\lambda G(\eta ), ~~~ G'(\eta )=\mu F(\eta ). \end{aligned}$$

(18)

$A_0,A_1,...,A_m$, $\lambda$ and $\mu$ are constant to be calculated later, $a_m\ne 0$.

Step 2. Furthermore, N is positive integer that can be calculated by using the homogeneous balance principle between the higher derivatives and nonlinear terms in ODE Eq. (4). We may get the following solutions of $F(\eta )$ and $G(\eta )$, with the help of Eq. (18), which are listed as below,

Case I. If $\lambda>0, \mu >0$, we get hyperbolic function solution.

$$\begin{aligned} \begin{aligned} F(\eta )= & {} \frac{C_2 \sqrt{\lambda } \sinh \left( \sqrt{\lambda } \sqrt{\mu } \eta \right) }{\sqrt{\mu }}+C_1 \cosh \left( \sqrt{\lambda } \sqrt{\mu } \eta \right) ,\\ G(\eta )= & {} \frac{C_1 \sqrt{\mu } \sinh \left( \sqrt{\lambda } \sqrt{\mu } \eta \right) }{\sqrt{\lambda }}+C_2 \cosh \left( \sqrt{\lambda } \sqrt{\mu } \eta \right) . \end{aligned} \end{aligned}$$

(19)

Case II. If $\lambda<0, \mu <0$, we get hyperbolic function solution.

$$\begin{aligned} \begin{aligned} F(\eta )= & {} C_1 \cosh \left( \sqrt{-\lambda } \sqrt{-\mu } \eta \right) -\frac{C_2 \sqrt{-\lambda } \sinh \left( \sqrt{-\lambda } \sqrt{-\mu } \eta \right) }{\sqrt{-\mu }},\\ G(\eta )= & {} C_2 \cosh \left( \sqrt{-\lambda } \sqrt{-\mu } \eta \right) -\frac{C_1 \sqrt{-\mu } \sinh \left( \sqrt{-\lambda } \sqrt{-\mu } \eta \right) }{\sqrt{-\lambda }}. \end{aligned} \end{aligned}$$

(20)

Case III. If $\lambda >0, \mu <0$, we get trignomatric function solution.

$$\begin{aligned} \begin{aligned} F(\eta )= & {} \frac{C_2 \sqrt{\lambda } \sin \left( \sqrt{\lambda } \sqrt{-\mu } \eta \right) }{\sqrt{-\mu }}+C_1 \cos \left( \sqrt{\lambda } \sqrt{-\mu } \eta \right) ,\\ G(\eta )= & {} C_2 \cos \left( \sqrt{\lambda } \sqrt{-\mu } \eta \right) -\frac{C_1 \sqrt{-\mu } \sin \left( \sqrt{\lambda } \sqrt{-\mu } \eta \right) }{\sqrt{\lambda }}. \end{aligned} \end{aligned}$$

(21)

Case IV. If $\lambda <0, \mu >0$, we get trignomatric function solution.

$$\begin{aligned} \begin{aligned} F(\eta )= & {} C_1 \cos \left( \sqrt{-\lambda } \sqrt{\mu } \eta \right) -\frac{C_2 \sqrt{-\lambda } \sin \left( \sqrt{-\lambda } \sqrt{\mu } \eta \right) }{\sqrt{\mu }},\\ G(\eta )= & {} \frac{C_1 \sqrt{\mu } \sin \left( \sqrt{-\lambda } \sqrt{\mu } \eta \right) }{\sqrt{-\lambda }}+C_2 \cos \left( \sqrt{-\lambda } \sqrt{\mu } \eta \right) . \end{aligned} \end{aligned}$$

(22)

Step 3. Puting Eqs. (17, 18) in Eq. (4) a group of algebraic equations for$\left( \frac{F}{G}\right) ^i$ $(i = 1, 2,..., m)$ is obtained. Setting all $\left( \frac{F}{G}\right) ^i$ to zero and solving these nonlinear algebraic equations by using Mathematica, we get different accurate solutions of Eq. (2) according to Eqs. (18–22).

3 Mathematical analysis

The main purpose of this part is to obtain the exact solutions of the (4+1)-dimensional Fokas Eq. (1). We apply the transformation as follows

$$\begin{aligned} u(x,y,z,w,t)=U(\eta );~~~\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+ \nu \text {t}+\rho w+\epsilon , \end{aligned}$$

(23)

substituting values from Eq. (23) to Eq. (1) and we get the following form of ODE,

$$\begin{aligned} \alpha _1 \left( \alpha _2^2-\alpha _1^2\right) \alpha _2 U^4+U'' \left( 4 \alpha _1 \nu -6 \alpha _3 \rho \right) +12 \alpha _1 \alpha _2 \left( \text {UU}'\right) '=0. \end{aligned}$$

(24)

Integrating twice Eq. (24) w.r.t $(\eta )$, then

$$\begin{aligned} \alpha _1 \left( \alpha _2^2-\alpha _1^2\right) \alpha _2 U''+6 \alpha _1 \alpha _2 U^2+U \left( 4 \alpha _1 \nu -6 \alpha _3 \rho \right) =0. \end{aligned}$$

(25)

3.1 Application to the generalized unified method

3.1.1 The polynomial function solutions

To find the polynomial function solutions of the NFE, we assume that

$$\begin{aligned} U(\eta )= & {} \sum _{i=0}^N p_i \phi ^i(\eta ),\nonumber \\ (\phi '(\eta ))^p= & {} \sum _{i=0}^{k p} b_i \phi ^i(\eta ),~~~ p=1,2. \end{aligned}$$

(26)

By considering the homogenous balance principle in Eq. (25), we get

$N=2(k-1)$, $k=2,3,\cdots$ Here we confine ourselves to find these solutions when $k=2$ and $p=1$ or $p=2$. So, we suppose that the polynomial function solution of the ODE Eq. (25) is of the form

$$\begin{aligned} \begin{aligned} U(\eta )= & {} p_0(t)+ p_1(t)\phi (\eta )+p_2(t)\phi (\eta )^2,\\ (\phi '(\eta ))^p= & {} \sum _{i=0}^{2 p} b_i \phi ^i(\eta ),~~~ p=1,2. \end{aligned} \end{aligned}$$

(27)

3.1.2 The solitary wave solutions

To obtain such type of solutions, we put $p=1$ in auxiliary equation given in Eq. (27), then

$$\begin{aligned} U(\eta )= & {} p_0(t)+ p_1(t)\phi (\eta )+p_2(t)\phi (\eta )^2, \end{aligned}$$

(28)

$$\begin{aligned} \phi '(\eta )= & {} b_2(t) \phi (\eta )^2+b_1(t) \phi (\eta )+b_0(t). \end{aligned}$$

(29)

Substituting Eq. (28) and its necessary derivatives into Eq. (25) and gathering all same powers terms of $\phi (\eta )$. Setting each $\phi (\eta )$ polynomial equal to zero yields the following group of algebraic group of equations,

$$\begin{aligned}{} & {} -\alpha _2 \alpha _1^3 b_0(t) b_1(t) p_1(t)-2 \alpha _2 \alpha _1^3 b_0(t){}^2 p_2(t)+\alpha _2^3 \alpha _1 b_0(t) b_1(t) p_1(t)+2 \alpha _2^3 \alpha _1 b_0(t){}^2 p_2(t)\\{} & {} \quad + 4 \alpha _1 \nu p_0(t)-6 \alpha _3 \rho p_0(t)+6 \alpha _2 \alpha _1 p_0(t){}^2=0,\\{} & {} \quad -\alpha _2 \alpha _1^3 b_1(t){}^2 p_1(t)-2 \alpha _2 \alpha _1^3 b_0(t) b_2(t) p_1(t)-6 \alpha _2 \alpha _1^3 b_0(t) b_1(t) p_2(t)\\{} & {} \quad +\alpha _2^3 \alpha _1 b_1(t){}^2 p_1(t)+2 \alpha _2^3 \alpha _1 b_0(t) b_2(t) p_1(t)+6 \alpha _2^3 \alpha _1 b_0(t) b_1(t) p_2(t)\\{} & {} \quad +4 \alpha _1 \nu p_1(t)-6 \alpha _3 \rho p_1(t)+12 \alpha _2 \alpha _1 p_0(t) p_1(t)=0,\\{} & {} \quad -3 \alpha _2 \alpha _1^3 b_1(t) b_2(t) p_1(t)-4 \alpha _2 \alpha _1^3 b_1(t){}^2 p_2(t)-8 \alpha _2 \alpha _1^3 b_0(t) b_2(t) p_2(t)\\{} & {} \quad + 3 \alpha _2^3 \alpha _1 b_1(t) b_2(t) p_1(t)+4 \alpha _2^3 \alpha _1 b_1(t){}^2 p_2(t)\\{} & {} \quad + 8 \alpha _2^3 \alpha _1 b_0(t) b_2(t) p_2(t)+4 \alpha _1 \nu p_2(t)-6 \alpha _3 \rho p_2(t)\\{} & {} \quad + 6 \alpha _2 \alpha _1 p_1(t){}^2+12 \alpha _2 \alpha _1 p_0(t) p_2(t)=0,\\{} & {} \quad -2 \alpha _2 \alpha _1^3 b_2(t){}^2 p_1(t)-10 \alpha _2 \alpha _1^3 b_1(t) b_2(t) p_2(t)+2 \alpha _2^3 \alpha _1 b_2(t){}^2 p_1(t)\\{} & {} \quad + 10 \alpha _2^3 \alpha _1 b_1(t) b_2(t) p_2(t)+12 \alpha _2 \alpha _1 p_1(t) p_2(t)=0,\\{} & {} \quad -6 \alpha _2 \alpha _1^3 b_2(t){}^2 p_2(t)+6 \alpha _2^3 \alpha _1 b_2(t){}^2 p_2(t)+6 \alpha _2 \alpha _1 p_2(t){}^2=0. \end{aligned}$$

Using computer software Mathematica to solve the above algebraic group of equations. The following are the outcomes,

Family 1: Set 1.

$$\begin{aligned} p_0(t)= & {} -\left( \alpha _2^2-\alpha _1^2\right) b_0(t) b_2(t),\\ ~ p_1(t)= & {} -\left( \alpha _2^2-\alpha _1^2\right) b_1(t) b_2(t),\\ ~p_2(t)= & {} -\left( \alpha _2^2-\alpha _1^2\right) b_2(t){}^2,\\ ~\rho= & {} -\frac{\alpha _1 \left( -4 \nu +\alpha _2^3 \left( -R_1(t){}^2\right) +\alpha _1^2 \alpha _2 R_1(t){}^2\right) }{6 \alpha _3},\\ R_1(t)= & {} \sqrt{b_1^2-4 b_0 b_2(t)},~~~ R_1(t){}^2=b_1^2-4 b_0 b_2(t). \end{aligned}$$

Solving the auxiliary equation Eq. (29) and substituting together with the above results into Eq. (28), produces following categories of traveling wave solutions.

$$\begin{aligned} \begin{aligned} u_1(x,y,z,w,t)&=\frac{1}{4} (\alpha _1^2-\alpha _2^2) (b_1(t)+R_1(t) \tan (\frac{1}{2} \eta R_1(t))){}^2-\frac{1}{2} (\alpha _1^2-\alpha _2^2) b_1(t) (b_1(t)\\&+R_1(t) \tan (\frac{1}{2} \eta R_1(t)))+(\alpha _1^2-\alpha _2^2) b_0(t) b_2(t), \end{aligned} \end{aligned}$$

(30)

where $\eta =-\frac{\alpha _1 w \left( -4 \nu +\alpha _2^3 \left( -R_1(t){}^2\right) +\alpha _1^2 \alpha _2 R_1(t){}^2\right) }{6 \alpha _3}+\nu t+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon$.

Set 2.

$$\begin{aligned} p_1(t)=\alpha _1^2 b_1(t) b_2(t), ~p_2(t)=\alpha _1^2 b_2(t){}^2, ~\alpha _2=0, ~\rho =\frac{2 \alpha _1 \nu }{3 \alpha _3}, \end{aligned}$$

$$\begin{aligned} \begin{aligned} u_2(x,y,z,w,t)&=p_0(t)+\frac{1}{4} \alpha _1^2 (b_1(t)+R_1(t) \tan (\frac{1}{2} \eta R_1(t))){}^2\\&-\frac{1}{2} \alpha _1^2 b_1(t) (b_1(t)+R_1(t) \tan (\frac{1}{2} \eta R_1(t))), \end{aligned} \end{aligned}$$

(31)

where $\eta =\nu t+\frac{2 \alpha _1 \nu w}{3 \alpha _3}+\alpha _1 x+\alpha _3 z+\epsilon$.

3.1.3 The soliton wave solutions

To obtain such type of solutions, we put $p=2$ in auxiliary equation given in Eq. (27), then

$$\begin{aligned} U(\eta )= & {} p_0(t)+p_1(t)\phi (\eta ) +p_2(t)\phi (\eta )^2 \end{aligned}$$

(32)

$$\begin{aligned} \phi '(\eta )= & {} \phi (\eta ) \sqrt{b_2(t) \phi (\eta )^2+b_1(t) \phi (\eta )+b_0(t)}. \end{aligned}$$

(33)

Substituting Eq. (32) and its necessary derivatives into Eq. (25) and gathering all same powers terms of $\phi (\eta )$. Setting each $\phi (\eta )$ polynomial equal to zero yields the following group of algebraic group of equations,

$$\begin{aligned}{} & {} 4 \alpha _1 \nu p_0(t)-6 \alpha _3 \rho p_0(t)+6 \alpha _1 \alpha _2 p_0(t){}^2=0,\\{} & {} \quad -\alpha _2 \alpha _1^3 b_0(t) p_1(t)+\alpha _2^3 \alpha _1 b_0(t) p_1(t)+4 \alpha _1 \nu p_1(t)\\{} & {} \quad -6 \alpha _3 \rho p_1(t)+12 \alpha _2 \alpha _1 p_0(t) p_1(t)=0,\\{} & {} \quad \frac{1}{2} (-3) \alpha _2 \alpha _1^3 b_1(t) p_1(t)-4 \alpha _2 \alpha _1^3 b_0(t) p_2(t)+\frac{3}{2} \alpha _2^3 \alpha _1 b_1(t) p_1(t)+4 \alpha _2^3 \alpha _1 b_0(t) p_2(t)\\{} & {} \quad + 4 \alpha _1 \nu p_2(t)-6 \alpha _3 \rho p_2(t)+6 \alpha _2 \alpha _1 p_1(t){}^2+12 \alpha _2 \alpha _1 p_0(t) p_2(t)=0,\\{} & {} \quad -2 \alpha _2 \alpha _1^3 b_2(t) p_1(t)-5 \alpha _2 \alpha _1^3 b_1(t) p_2(t)+2 \alpha _2^3 \alpha _1 b_2(t) p_1(t)\\{} & {} \quad + 5 \alpha _2^3 \alpha _1 b_1(t) p_2(t)+12 \alpha _2 \alpha _1 p_1(t) p_2(t)=0,\\{} & {} \quad -6 \alpha _2 \alpha _1^3 b_2(t) p_2(t)+6 \alpha _2^3 \alpha _1 b_2(t) p_2(t)+6 \alpha _2 \alpha _1 p_2(t){}^2=0. \end{aligned}$$

On solving the above algebraic group of equations, the outcomes are,

Set 1.

$$\begin{aligned} b_0(t)= & {} \frac{b_1(t){}^2}{4 b_2(t)},\\ p_0(t)= & {} 0,\\ p_1(t)= & {} -\frac{1}{2}(\alpha _2^2-\alpha _1^2 b_1(t),\\ p_2(t)= & {} \alpha _1^2 b_2(t)-\alpha _2^2 b_2(t),\\ \rho= & {} \frac{\alpha _1(\alpha _2^3 b_1(t){}^2-\alpha _1^2 \alpha _2 b_1(t){}^2+16 \nu b_2(t))}{24 \alpha _3 b_2(t)}. \end{aligned}$$

Solving the auxiliary equation Eq. (33) and substituting together with the above results into Eq. (32), produces following categories of traveling wave solutions.

$$\begin{aligned} u_3(x,y,z,w,t)=\frac{b_1(t){}^4 \left( \alpha _1^2 b_2(t)-\alpha _2^2 b_2(t)\right) e^{\eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}}{b_2(t){}^2 \left( 2 b_1(t) e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}-1\right) {}^2}+\frac{\left( \alpha _2^2-\alpha _1^2\right) b_1(t){}^3 e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}}{2 b_2(t) \left( 2 b_1(t) e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}-1\right) }, \end{aligned}$$

(34)

Set 2.

$$\begin{aligned} b_0(t)= & {} \frac{b_1(t){}^2}{4 b_2(t)},\\ p_0(t)= & {} -\frac{(\alpha _2^2-\alpha _1^2) b_1(t){}^2}{24 b_2(t)},\\ p_1(t)= & {} -\frac{1}{2} (\alpha _2^2-\alpha _1^2) b_1(t),\\ p_2(t)= & {} \alpha _1^2 b_2(t)-\alpha _2^2 b_2(t),\\ \rho= & {} \frac{16 \alpha _1 \nu b_2(t)+\alpha _2 \alpha _1^3 b_1(t){}^2-\alpha _2^3 \alpha _1 b_1(t){}^2}{24 \alpha _3 b_2(t)}. \end{aligned}$$

$$\begin{aligned} \begin{aligned} u_4(x,y,z,w,t)&=-\frac{\left( \alpha _2^2-\alpha _1^2\right) b_1(t){}^2}{24 b_2(t)}+\frac{\left( \alpha _2^2-\alpha _1^2\right) b_1(t){}^3 e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}}{2 b_2(t) \left( 2 b_1(t) e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}-1\right) }\\ \quad &+\frac{b_1(t){}^4 \left( \alpha _1^2 b_2(t)-\alpha _2^2 b_2(t)\right) e^{\eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}}{b_2(t){}^2 \left( 2 b_1(t) e^{\frac{1}{2} \eta \sqrt{\frac{b_1(t){}^2}{b_2(t)}}}-1\right) {}^2}, \end{aligned} \end{aligned}$$

(35)

where $\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{\alpha _1 w \left( \alpha _2^3 b_1(t){}^2-\alpha _1^2 \alpha _2 b_1(t){}^2+16 \nu b_2(t)\right) }{24 \alpha _3 b_2(t)}+\epsilon$.

3.1.4 The eliptic wave solutions

To obtain such type of solutions, we put $p=2$ in auxiliary equation given in Eq. (27), then

$$\begin{aligned} U(\eta )= & {} p_0(t)+p_1(t)\phi (\eta )+\phi (\eta )^2 p_2(t) \end{aligned}$$

(36)

$$\begin{aligned} \phi '(\eta )= & {} \sqrt{b_4(t) \phi (\eta )^4+b_2(t) \phi (\eta )^2+b_0(t)}. \end{aligned}$$

(37)

Substituting Eq. (36) and its necessary derivatives into Eq. (25) and gathering all same powers terms of $\phi (\eta )$. Setting each $\phi (\eta )$ polynomial equal to zero yields the following group of algebraic group of equations. On solving the obtained algebraic group of equations, the outcomes are,

$$\begin{aligned} p_0(t)= & {} \frac{1}{3} (\sqrt{(\alpha _1^2-\alpha _2^2){}^2 (b_2(t){}^2-3 b_0(t) b_4(t))}+(\alpha _1^2-\alpha _2^2) b_2(t)),\\ p_1(t)= & {} 0,\\ p_2(t)= & {} \alpha _1^2 b_4(t)-\alpha _2^2 b_4(t),\\ \rho= & {} \frac{2 (\alpha _1 \nu +\alpha _2 \alpha _1 \sqrt{(\alpha _1^2-\alpha _2^2){}^2 (b_2(t){}^2-3 b_0(t) b_4(t))})}{3 \alpha _3}. \end{aligned}$$

Eq. (37) possesses different Jacobi elliptic function solutions for different choices of $b_i(t)$, $i=0,2,4$. According to the classification (), we choose,

$$\begin{aligned} b_0(t)=k^4-2 k^3+k^2, ~b_2(t)=-k^2+6 k-1, ~b_4(t)=-\frac{4}{k}, ~~~0<k<1, \end{aligned}$$

that yields a special case solution of Eq. (37) takes the form, $\phi (\eta )=\frac{k \text {cn}(\eta ,k) \text {dn}(\eta ,k)}{\text {ksn}^2(\eta ,k)+1}$ and the general solution of Eq. (1) is,

$$\begin{aligned} u_5(x,y,z,w,t)= & {} \frac{1}{3} \left( \sqrt{\left( \alpha _1^2-\alpha _2^2\right) {}^2 \left( b_2(t){}^2-3 b_0(t) b_4(t)\right) }+\left( \alpha _1^2-\alpha _2^2\right) b_2(t)\right) \nonumber \\{} & {} +\frac{k^2 \left( \alpha _1^2 b_4(t)-\alpha _2^2 b_4(t)\right) \text {cn}(\eta ,k)^2 \text {dn}(\eta ,k)^2}{\left( \text {ksn}^2(\eta ,k)+1\right) ^2}, \end{aligned}$$

(38)

where

$$\begin{aligned} \eta= & {} \alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\epsilon \nonumber \\{} & {} +\frac{2 w \left( \alpha _1 \nu +\alpha _2 \alpha _1 \sqrt{\left( \alpha _1^2-\alpha _2^2\right) {}^2 \left( \left( -k^2+6 k-1\right) ^2+\frac{12 \left( k^4-2 k^3+k^2\right) }{k}\right) }\right) }{3 \alpha _3} \end{aligned}$$

We mention that $0<k<1$ is called the modulus of the Jacobi elliptic functions. When $k\rightarrow 0$, $sn(\eta )$, $cn(\eta )$ and $dn(\eta )$ degenerate to $\text {sin}(\eta )$, $\text {cos}(\eta )$ and 1. While when $k\rightarrow 1$, $sn(\eta )$, $cn(\eta )$ and $dn(\eta )$ degenerate to $\text {tanh}(\eta )$, $\text {sech}(\eta )$ and $\text {sech}(\eta )$ respectively.

3.2 The rational solutions

To find the rational function solutions of the (4+1)-dimensional Fokas equation, we assume that

$$\begin{aligned} U(\eta )= & {} \frac{\sum _{i=0}^n p_i \phi ^i(\eta )}{\sum _{i=0}^r q_i \phi ^i(\eta )},~~~n\ge r, \nonumber \\ (\phi '(z))^p= & {} \sum _{i=0}^{p k} b_i \phi ^i(z),~~~p=1,2. \end{aligned}$$

(39)

By considering the homogenous balance principle in Eq. (25), we get

$N-r=2(k-1)$, $k=1,2,3,\cdots$ Here we fined these solutions when $k=1$ so $N=r$ and $p=2$. So from Eq. (39), we have two cases as follow

3.2.1 Case 1: the periodic type solutions

In this case, we assume that

$$\begin{aligned} U(\eta )= & {} \frac{\phi (\eta ) p_1(t)+p_0(t)}{\phi (\eta ) q_1(t)+q_0(t)},\nonumber \\ \phi '(\eta )= & {} \sqrt{b_0(t){}^2-b_2(t){}^2 \phi (\eta )^2}. \end{aligned}$$

(40)

Substituting Eq. (40) and its necessary derivatives into Eq. (25) and gathering all same powers terms of $\phi (\eta )$. Setting each $\phi (\eta )$ polynomial equal to zero yields the following group of algebraic group of equations. On solving the obtained algebraic group of equations, the outcomes are,

$$\begin{aligned} q_0(t)= & {} \frac{b_0(t) q_1(t)}{b_2(t)},\\ p_0(t)= & {} -\frac{1}{3} (\alpha _2^2-\alpha _1^2) b_0(t) b_2(t) q_1(t),\\ p_1(t)= & {} \frac{1}{6}(\alpha _2^2-\alpha _1^2) b_2(t){}^2 q_1(t),\\ \rho= & {} -\frac{\alpha _1 (\alpha _2^3 (-b_2(t){}^2)+\alpha _1^2 \alpha _2 b_2(t){}^2-4 \nu )}{6 \alpha _3}. \end{aligned}$$

By solving the auxiliary equation $\phi '(\eta )=\sqrt{b_0(t){}^2-b_2(t){}^2 \phi (\eta )^2}$ and substituting together with the obtained outcomes in Eq. (40), we get the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} u_6(x,y,z,w,t)=\frac{-\frac{\left( \alpha _2^2-\alpha _1^2\right) b_0(t) b_2(t) q_1(t) \tan \left( \eta b_2(t)\right) }{6 \sqrt{\tan ^2\left( \eta b_2(t)\right) +1}}-\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) b_0(t) b_2(t) q_1(t)}{\frac{b_0(t) q_1(t)}{b_2(t)}-\frac{b_0(t) q_1(t) \tan \left( \eta b_2(t)\right) }{b_2(t) \sqrt{\tan ^2\left( \eta b_2(t)\right) +1}}}, \end{aligned} \end{aligned}$$

(41)

where

$$\begin{aligned} \eta= & {} \nu t+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon \\{} & {} -\frac{\alpha _1 w \left( \alpha _2^3 \left( -b_2(t){}^2\right) +\alpha _1^2 \alpha _2 b_2(t){}^2-4 \nu \right) }{6 \alpha _3}. \end{aligned}$$

set 2.

$$\begin{aligned} q_0(t)= & {} \frac{b_0(t) q_1(t)}{b_2(t)},\\ p_0(t)= & {} -\frac{1}{3}(\alpha _2^2-\alpha _1^2) b_0(t) b_2(t) q_1(t),\\ p_1(t)= & {} -\frac{1}{3} (\alpha _2^2-\alpha _1^2) b_2(t){}^2 q_1(t),\\ \rho= & {} \frac{\alpha _1 (\alpha _2^3 (-b_2(t){}^2)+\alpha _1^2 \alpha _2 b_2(t){}^2+2 \nu )}{3 \alpha _3}, \end{aligned}$$

$$\begin{aligned} \begin{aligned} u_7(x,y,z,w,t)=\frac{\frac{\left( \alpha _2^2-\alpha _1^2\right) b_0(t) b_2(t) q_1(t) \tan \left( \eta b_2(t)\right) }{3 \sqrt{\tan ^2\left( \eta b_2(t)\right) +1}}-\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) b_0(t) b_2(t) q_1(t)}{\frac{b_0(t) q_1(t)}{b_2(t)}-\frac{b_0(t) q_1(t) \tan \left( \eta b_2(t)\right) }{b_2(t) \sqrt{\tan ^2\left( \eta b_2(t)\right) +1}}}, \end{aligned} \end{aligned}$$

(42)

where

$$\begin{aligned} \eta= & {} \nu t+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon \nonumber \\{} & {} +\frac{\alpha _1 w \left( \alpha _2^3 \left( -b_2(t){}^2\right) +\alpha _1^2 \alpha _2 b_2(t){}^2+2 \nu \right) }{3 \alpha _3}. \end{aligned}$$

3.2.2 The soliton type solutions

In this case, we assume that

$$\begin{aligned} U(\eta )= & {} \frac{\phi (\eta ) p_1(t)+p_0(t)}{\phi (\eta ) q_1(t)+q_0(t)},\nonumber \\{} & {} \phi '(\eta )=\sqrt{b_2(t) \phi (\eta )^2+b_1(t) \phi (\eta )+b_0(t)}. \end{aligned}$$

(43)

Substituting Eq. (43) and its necessary derivatives into Eq. (25) and gathering all same powers terms of $\phi (\eta )$. Setting each $\phi (\eta )$ polynomial equal to zero yields the following group of algebraic group of equations. On solving the obtained algebraic group of equations, the outcomes are.

Set 1.

$$\begin{aligned} q_0(t)= & {} 0,\\ b_0(t)= & {} -\frac{q_0(t) (b_2(t) q_0(t)-b_1(t) q_1(t))}{q_1(t){}^2},\\ p_0(t)= & {} -\frac{1}{12}(\alpha _2^2-\alpha _1^2) (3 b_1(t) q_1(t)-4 b_2(t) q_0(t)),\\ p_1(t)= & {} -\frac{1}{6}(\alpha _2^2-\alpha _1^2) b_2(t) q_1(t),\\ \rho= & {} \frac{4 \alpha _1 \nu +\alpha _2 \alpha _1^3 b_2(t)-\alpha _2^3 \alpha _1 b_2(t)}{6 \alpha _3}. \end{aligned}$$

By solving the auxiliary equation $\phi '(\eta )=\sqrt{b_2(t) \phi (\eta )^2+b_1(t) \phi (\eta )+b_0(t)}$ and substituting together with the obtained outcomes in Eq. (40), we get the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} u_9(x,y,z,w,t)=\frac{\frac{p_1(t) e^{-\eta \sqrt{b_2(t)}} \left( -2 b_1(t) e^{\eta \sqrt{b_2(t)}}+e^{2 \eta \sqrt{b_2(t)}}+b_1(t){}^2-4 b_0(t) b_2(t)\right) }{4 b_2(t)}+p_0(t)}{\frac{q_1(t) e^{-\eta \sqrt{b_2(t)}} \left( -2 b_1(t) e^{\eta \sqrt{b_2(t)}}+e^{2 \eta \sqrt{b_2(t)}}+b_1(t){}^2-4 b_0(t) b_2(t)\right) }{4 b_2(t)}+q_0(t)}, \end{aligned} \end{aligned}$$

(44)

where

$$\begin{aligned} \eta= & {} \nu t+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon \nonumber \\{} & {} +\frac{w \left( 4 \alpha _1 \nu +\alpha _2 \alpha _1^3 b_2(t)-\alpha _2^3 \alpha _1 b_2(t)\right) }{6 \alpha _3} \end{aligned}$$

3.3 Application to the generalized projective riccati equation method

By using the homogeneous balance rule we obtain the balancing term $N = 2$.

Thus solution of Eq. (25), of the form

$$\begin{aligned} U(\eta )=A_0+A_1 \Omega (\eta )+A_2 \Omega ^2 (\eta )+B_1 \gamma (\eta )+B_2 \Omega (\eta )\gamma (\eta ), \end{aligned}$$

(45)

where $A_0$, $A_1$, $A_2$, $B_1$ and $B_2$ are constants to be found by substituting Eq. (45) with Eqs. (8–10) into Eq. (25) and gathering all same powers terms of $\Omega ^j(\eta )\gamma ^i(\eta )$ $(j=0,1,2,\cdots ;i=0,1,2,\cdots )$together and setting all the obtained coefficients equals to be zero, we get the group of algebraic equations.

Family 1:

Putting $k= -1$ and $r_1=-1$ in obtained system of equations. Then by using Mathematica software to solve the obtained group of equations. The following are the outcomes,

Set 1.

$$\begin{aligned} A_1= & {} \frac{1}{2} (\alpha _2^2 M-\alpha _1^2 M),\\ A_0= & {} \frac{(\alpha _2^3 \alpha _1+i \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}-\alpha _1^3 \alpha _2) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{6 \alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2)},\\ B_1= & {} 0,\\ R_1= & {} -\frac{2 i (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}},\\ A_2= & {} \frac{i (\alpha _1^2-\alpha _2^2) \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}(M^2-1)}{8 \alpha _1 \nu -12 \alpha _3 \rho },\\ B_2= & {} -\frac{\sqrt{\frac{i (-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2){}^{3/2} (M^2-1) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\alpha _1^2 \alpha _2^2}}}{2 \sqrt{2} \sqrt{-(2 \alpha _1 \nu -3 \alpha _3 \rho ){}^2}}. \end{aligned}$$

Set 2.

$$\begin{aligned} B_1= & {} 0,\\ A_1= & {} \frac{1}{2} (\alpha _2^2 M-\alpha _1^2 M),\\ A_0= & {} -\frac{(\alpha _2 \alpha _1^3-\alpha _2^3 \alpha _1+i \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{6 \alpha _1^2 \alpha _2^2(\alpha _1^2-\alpha _2^2)},\\ R_1= & {} -\frac{2 i(2 \alpha _1 \nu -3 \alpha _3 \rho )}{\sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}},\\ A_2= & {} -\frac{i (\alpha _1^2-\alpha _2^2) \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2} (M^2-1)}{8 \alpha _1 \nu -12 \alpha _3 \rho },\\ B_2= & {} \frac{\sqrt{-\frac{i (-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2){}^{3/2} (M^2-1) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\alpha _1^2 \alpha _2^2}}}{2 \sqrt{2} \sqrt{-(2 \alpha _1 \nu -3 \alpha _3 \rho ){}^2}}. \end{aligned}$$

Putting above results into Eq. (45), produces following categories of traveling wave solutions.

$$\begin{aligned} u_{10}(x,y,z,w,t)= & {} A_0+\frac{A_2 R_1^2 \text {sech}^2\left( \eta \sqrt{R_1}\right) }{\left( M \text {sech}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{A_1 R_1 \text {sech}\left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}+\nonumber \\{} & {} \frac{B_2 R_1^2 \tanh \left( \eta \sqrt{R_1}\right) \text {sech}\left( \eta \sqrt{R_1}\right) }{\left( M \text {sech}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{B_1 R_1 \tanh \left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}, \end{aligned}$$

(46)

$$\begin{aligned} u_{11}(x,y,z,w,t)= & {} A_0+\frac{A_1 R_1 \text {sech}\left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}+\frac{A_2 R_1^2 \text {sech}^2\left( \eta \sqrt{R_1}\right) }{\left( M \text {sech}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\nonumber \\{} & {} \frac{B_2 R_1^2 \tanh \left( \eta \sqrt{R_1}\right) \text {sech}\left( \eta \sqrt{R_1}\right) }{\left( M \text {sech}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{B_1 R_1 \tanh \left( \eta \sqrt{R_1}\right) }{M \text {sech}\left( \eta \sqrt{R_1}\right) +1}, \end{aligned}$$

(47)

where

$$\begin{aligned} \eta =\nu \text {t}+\rho w+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon . \end{aligned}$$

Family 2.

Putting $k= -1$ and $r_1=1$ in obtained system of equations. Then by using Mathematica software to solve the obtained group of equations. The following are the outcomes,

Set 1.

$$\begin{aligned} B_1= & {} 0,\\ A_1= & {} \frac{1}{2}(\alpha _2^2 M-\alpha _1^2 M),\\ A_0= & {} -\frac{(\alpha _2 \alpha _1^3-\alpha _2^3 \alpha _1+i \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{6 \alpha _1^2 \alpha _2^2(\alpha _1^2-\alpha _2^2)},\\ R_1= & {} \frac{2 i (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}}\\ A_2= & {} -\frac{i(\alpha _1^2-\alpha _2^2) \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2} (M^2+1)}{8 \alpha _1 \nu -12 \alpha _3 \rho },\\ B_2= & {} \frac{\sqrt{-\frac{i(-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2){}^{3/2} (M^2+1) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\alpha _1^2 \alpha _2^2}}}{2 \sqrt{2} \sqrt{-(2 \alpha _1 \nu -3 \alpha _3 \rho ){}^2}}. \end{aligned}$$

Putting above results into Eq. (45), produces following categories of traveling wave solutions.

$$\begin{aligned} u_{12}(x,y,z,w,t)= & {} A_0+\frac{B_1 \sqrt{R_1} \coth \left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}+\frac{A_2 R_1^2 \text {csch}^2\left( \eta \sqrt{R_1}\right) }{\left( M \text {csch}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\nonumber \\{} & {} \frac{A_1 R_1 \text {csch}\left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}+\frac{B_2 R_1^{3/2} \coth \left( \eta \sqrt{R_1}\right) \text {csch}\left( \eta \sqrt{R_1}\right) }{\left( M \text {csch}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}. \end{aligned}$$

(48)

Set 2.

$$\begin{aligned} A_1= & {} \frac{1}{2} (\alpha _2^2 M-\alpha _1^2 M),\\ A_0= & {} \frac{(\alpha _2^3 \alpha _1+i \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}-\alpha _1^3 \alpha _2) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{6 \alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2)},\\ B_1= & {} 0,\\ R_1= & {} -\frac{2 i (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}},\\ A_2= & {} \frac{i (\alpha _1^2-\alpha _2^2) \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2}(M^2+1)}{8 \alpha _1 \nu -12 \alpha _3 \rho },\\ B_2= & {} -\frac{\sqrt{\frac{i (-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2){}^{3/2}(M^2+1) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\alpha _1^2 \alpha _2^2}}}{2 \sqrt{2} \sqrt{-(2 \alpha _1 \nu -3 \alpha _3 \rho ){}^2}}. \end{aligned}$$

Putting above results into Eq. (45), produces following categories of traveling wave solutions.

$$\begin{aligned} u_{13}(x,y,z,w,t)= & {} A_0+\frac{B_1 \sqrt{R_1} \coth \left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}+\frac{A_1 R_1 \text {csch}\left( \eta \sqrt{R_1}\right) }{M \text {csch}\left( \eta \sqrt{R_1}\right) +1}+\nonumber \\{} & {} \frac{A_2 R_1^2 \text {csch}^2\left( \eta \sqrt{R_1}\right) }{\left( M \text {csch}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{B_2 R_1^{3/2} \coth \left( \eta \sqrt{R_1}\right) \text {csch}\left( \eta \sqrt{R_1}\right) }{\left( M \text {csch}\left( \eta \sqrt{R_1}\right) +1\right) {}^2}, \end{aligned}$$

(49)

where

$$\begin{aligned} \eta = \nu \text {t}+\rho w+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon . \end{aligned}$$

Family 3:

Putting $k= 1$ and $r_1=-1$ in obtained system of equations. Then by using Mathematica software to solve the obtained group of equations. The following are the outcomes,

Set 1.

$$\begin{aligned} B_1= & {} 0,\\ A_1= & {} \frac{1}{2}(\alpha _1^2-\alpha _2^2) M,\\ A_0= & {} -\frac{(\alpha _2 \alpha _1^3-\alpha _2^3 \alpha _1+i \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2})(2 \alpha _1 \nu -3 \alpha _3 \rho )}{6 \alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2)},\\ R_1= & {} -\frac{2 i(2 \alpha _1 \nu -3 \alpha _3 \rho )}{\sqrt{-\alpha _1^2 \alpha _2^2(\alpha _1^2-\alpha _2^2){}^2}},\\ A_2= & {} -\frac{i (\alpha _1^2-\alpha _2^2) \sqrt{-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2} (M^2+1)}{8 \alpha _1 \nu -12 \alpha _3 \rho },\\ B_2= & {} -\frac{\sqrt{\frac{i (-\alpha _1^2 \alpha _2^2 (\alpha _1^2-\alpha _2^2){}^2){}^{3/2} (M^2+1) (2 \alpha _1 \nu -3 \alpha _3 \rho )}{\alpha _1^2 \alpha _2^2}}}{2 \sqrt{2} \sqrt{(2 \alpha _1 \nu -3 \alpha _3 \rho ){}^2}}. \end{aligned}$$

Putting above results into Eq. (45), produces following categories of traveling wave solutions.

$$\begin{aligned} u_{14}(x,y,z,w,t)= & {} A_0+\frac{A_2 R_1^2 \sec ^2\left( \eta \sqrt{R_1}\right) }{\left( M \sec \left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{A_1 R_1 \sec \left( \eta \sqrt{R_1}\right) }{M \sec \left( \eta \sqrt{R_1}\right) +1}+\nonumber \\{} & {} \frac{B_2 R_1^{3/2} \tan \left( \eta \sqrt{R_1}\right) \sec \left( \eta \sqrt{R_1}\right) }{\left( M \sec \left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{B_1 \sqrt{R_1} \tan \left( \eta \sqrt{R_1}\right) }{M \sec \left( \eta \sqrt{R_1}\right) +1}, \end{aligned}$$

(50)

$$\begin{aligned} u_{15}(x,y,z,w,t)= & {} A_0-\frac{B_1 \sqrt{R_1} \cot \left( \eta \sqrt{R_1}\right) }{M \csc \left( \eta \sqrt{R_1}\right) +1}+\frac{A_1 R_1 \csc \left( \eta \sqrt{R_1}\right) }{M \csc \left( \eta \sqrt{R_1}\right) +1}-\nonumber \\{} & {} \frac{B_2 R_1^{3/2} \cot \left( \eta \sqrt{R_1}\right) \csc \left( \eta \sqrt{R_1}\right) }{\left( M \csc \left( \eta \sqrt{R_1}\right) +1\right) {}^2}+\frac{A_2 R_1^2 \csc ^2\left( \eta \sqrt{R_1}\right) }{\left( M \csc \left( \eta \sqrt{R_1}\right) +1\right) {}^2}, \end{aligned}$$

(51)

where

$$\begin{aligned} \eta = \nu \text {t}+\rho w+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon . \end{aligned}$$

3.4 Application to the new F/G-expansion method

By using the homogeneous balance rule we obtain the balancing term $N = 2$.

Thus solution of Eq. (25), of the form

$$\begin{aligned} U(\eta )=A_0+A_1\frac{F(\eta )}{G(\eta )}+A_2 \left( \frac{F(\eta )}{G(\eta )}\right) ^2, \end{aligned}$$

(52)

where $A_0$, $A_1$, $A_2$ are constants to be found by substituting Eq. (52) with Eq. (18) into Eq. (25) and gathering all same powers terms of $\frac{F(\eta )}{G(\eta )}$ together and setting all the obtained coefficients equals to be zero, we get the group of algebraic equations.

$$\begin{aligned}{} & {} -2 \alpha _2 \alpha _1^3 A_2 \lambda ^2+2 \alpha _2^3 \alpha _1 A_2 \lambda ^2+4 \alpha _1 A_0 \nu -6 \alpha _3 A_0 \rho +6 \alpha _2 \alpha _1 A_0^2=0,\\{} & {} \quad 2 \alpha _2 \alpha _1^3 A_1 \lambda \mu -2 \alpha _2^3 \alpha _1 A_1 \lambda \mu +4 \alpha _1 A_1 \nu -6 \alpha _3 A_1 \rho +12 \alpha _2 \alpha _1 A_0 A_1=0,\\{} & {} \quad 8 \alpha _2 \alpha _1^3 A_2 \lambda \mu -8 \alpha _2^3 \alpha _1 A_2 \lambda \mu +4 \alpha _1 A_2 \nu -6 \alpha _3 A_2 \rho +6 \alpha _2 \alpha _1 A_1^2+12 \alpha _2 \alpha _1 A_0 A_2=0,\\{} & {} \quad 2 \alpha _2 \alpha _1^3 A_1 \mu ^2+2 \alpha _2^3 \alpha _1 A_1 \mu ^2+12 \alpha _2 \alpha _1 A_1 A_2=0,\\{} & {} \quad -6 \alpha _2 \alpha _1^3 A_2 \mu ^2+6 \alpha _2^3 \alpha _1 A_2 \mu ^2+6 \alpha _2 \alpha _1 A_2^2=0. \end{aligned}$$

Using computer software Mathematica to solve the above algebraic group of equations. The following are the outcomes,

Family 1: Set 1.

$$\begin{aligned} A_1=0, ~A_2=\alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2, ~A_0=\frac{1}{3} (\alpha _2^2-\alpha _1^2) \lambda \mu , ~\rho =\frac{2 \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}. \end{aligned}$$

Putting above results into Eq. (52), produces following categories of traveling wave solutions.

Case 1. When $\lambda>0, \mu >0$, we get hyperbolic function solution.

$$\begin{aligned} u_{16}(x,y,z,w,t)= & {} \frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( \frac{C_2 \sqrt{\lambda } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}+C_1 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\lambda }}+C_2 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2}, \end{aligned}$$

(53)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{16}(x,y,z,w,t)=\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tanh ^2\left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\mu }. \end{aligned}$$

(54)

Case II. When $\lambda<0, \mu <0$, we get hyperbolic function solution.

$$\begin{aligned} u_{17}(x,y,z,w,t)= & {} \frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( C_1 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}\right) {}^2}{\left( C_2 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\lambda }}\right) {}^2}, \end{aligned}$$

(55)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{17}(x,y,z,w,t)=\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tanh ^2\left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\mu }. \end{aligned}$$

(56)

Case III. When $\lambda >0, \mu <0$, we get trigonometric function solution.

$$\begin{aligned} u_{18}(x,y,z,w,t)= & {} \frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( \frac{C_2 \sqrt{\lambda } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}+C_1 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) \right) {}^2}{\left( C_2 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{\lambda }}\right) {}^2}, \end{aligned}$$

(57)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{18}(x,y,z,w,t)=\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu -\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tan ^2\left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\mu }. \end{aligned}$$

(58)

Case IV. When $\lambda <0, \mu >0$, we get trigonometric function solution.

$$\begin{aligned} u_{19}(x,y,z,w,t)= & {} \frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( C_1 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}\right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{-\lambda }}+C_2 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) \right) {}^2}, \end{aligned}$$

(59)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{19}(x,y,z,w,t)=\frac{1}{3} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu -\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tan ^2\left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\mu }. \end{aligned}$$

(60)

Family II: We have following results in family II:

$$\begin{aligned} A_1=0, ~A_2=\alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2, ~A_0=(\alpha _2^2-\alpha _1^2) \lambda \mu , ~\rho =\frac{2 (\alpha _2 \alpha _1^3 (-\lambda ) \mu +\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu )}{3 \alpha _3}. \end{aligned}$$

Putting above results into Eq. (52), produces following categories of traveling wave solutions.

Case 1. When $\lambda>0, \mu >0$, we get hyperbolic function solution.

$$\begin{aligned} u_{20}(x,y,z,w,t)= & {} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( \frac{C_2 \sqrt{\lambda } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}+C_1 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\lambda }}+C_2 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2} \end{aligned}$$

(61)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{20}(x,y,z,w,t)=\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tanh ^2\left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\mu }+\left( \alpha _2^2-\alpha _1^2\right) \lambda \mu . \end{aligned}$$

(62)

Case II. When $\lambda<0, \mu <0$, we get hyperbolic function solution.

$$\begin{aligned} u_{21}(x,y,z,w,t)= & {} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( C_1 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}\right) {}^2}{\left( C_2 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\lambda }}\right) {}^2}, \end{aligned}$$

(63)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{21}(x,y,z,w,t)=\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tanh ^2\left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\mu }+\left( \alpha _2^2-\alpha _1^2\right) \lambda \mu . \end{aligned}$$

(64)

Case III. When $\lambda >0, \mu <0$, we get trigonometric function solution.

$$\begin{aligned} u_{22}(x,y,z,w,t)= & {} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( \frac{C_2 \sqrt{\lambda } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}+C_1 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) \right) {}^2}{\left( C_2 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{\lambda }}\right) {}^2}, \end{aligned}$$

(65)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{22}(x,y,z,w,t)=\left( \alpha _2^2-\alpha _1^2\right) \lambda \mu -\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tan ^2\left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\mu }. \end{aligned}$$

(66)

Case IV. When $\lambda <0, \mu >0$, we get trigonometric function solution.

$$\begin{aligned} u_{23}(x,y,z,w,t)= & {} \left( \alpha _2^2-\alpha _1^2\right) \lambda \mu +\nonumber \\{} & {} \frac{\left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \left( C_1 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}\right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{-\lambda }}+C_2 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) \right) {}^2}, \end{aligned}$$

(67)

where $\eta =\alpha _1 x+\alpha _2 y+\alpha _3 z+\nu t+\frac{2 w \left( \alpha _2 \alpha _1^3 \lambda \mu -\alpha _2^3 \alpha _1 \lambda \mu +\alpha _1 \nu \right) }{3 \alpha _3}+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{23}(x,y,z,w,t)=\left( \alpha _2^2-\alpha _1^2\right) \lambda \mu -\frac{\lambda \left( \alpha _1^2 \mu ^2-\alpha _2^2 \mu ^2\right) \tan ^2\left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\mu }. \end{aligned}$$

(68)

Family III: We have following results in family III:

$$\begin{aligned} A_0=0,~A_1=0,~A_2=\alpha _1^2 \mu ^2,~\rho =\frac{2 \alpha _1 \nu }{3 \alpha _3}. \end{aligned}$$

Putting above results into Eq. (52), produces following categories of traveling wave solutions.

Case 1. When $\lambda>0, \mu >0$, we get hyperbolic function solution.

$$\begin{aligned} u_{24}(x,y,z,w,t)=\frac{\alpha _1^2 \mu ^2 \left( \frac{C_2 \sqrt{\lambda } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}+C_1 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sinh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) }{\sqrt{\lambda }}+C_2 \cosh \left( \eta \sqrt{\lambda } \sqrt{\mu }\right) \right) {}^2}, \end{aligned}$$

where $\eta =\nu t+\frac{2 \alpha _1 \nu w}{3 \alpha _3}+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{24}(x,y,z,w,t)=\alpha _1^2 \lambda \mu \tanh ^2\left( \eta \sqrt{\lambda } \sqrt{\mu }\right) . \end{aligned}$$

(69)

Case II. When $\lambda<0, \mu <0$, we get hyperbolic function solution.

$$\begin{aligned} u_{25}(x,y,z,w,t)=\frac{\alpha _1^2 \mu ^2 \left( C_1 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}\right) {}^2}{\left( C_2 \cosh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sinh \left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) }{\sqrt{-\lambda }}\right) {}^2}, \end{aligned}$$

where $\eta =\nu t+\frac{2 \alpha _1 \nu w}{3 \alpha _3}+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{25}(x,y,z,w,t)=\alpha _1^2 \lambda \mu \tanh ^2\left( \eta \sqrt{-\lambda } \sqrt{-\mu }\right) . \end{aligned}$$

(70)

Case III. When $\lambda >0, \mu <0$, we get trigonometric function solution.

$$\begin{aligned} u_{26}(x,y,z,w,t)=\frac{\alpha _1^2 \mu ^2 \left( \frac{C_2 \sqrt{\lambda } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{-\mu }}+C_1 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) \right) {}^2}{\left( C_2 \cos \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) -\frac{C_1 \sqrt{-\mu } \sin \left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) }{\sqrt{\lambda }}\right) {}^2}, \end{aligned}$$

where $\eta =\nu t+\frac{2 \alpha _1 \nu w}{3 \alpha _3}+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{26}(x,y,z,w,t)=\alpha _1^2 (-\lambda ) \mu \tan ^2\left( \eta \sqrt{\lambda } \sqrt{-\mu }\right) . \end{aligned}$$

(71)

Case IV. When $\lambda <0, \mu >0$, we get trigonometric function solution.

$$\begin{aligned} u_{27}(x,y,z,w,t)=\frac{\alpha _1^2 \mu ^2 \left( C_1 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) -\frac{C_2 \sqrt{-\lambda } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{\mu }}\right) {}^2}{\left( \frac{C_1 \sqrt{\mu } \sin \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) }{\sqrt{-\lambda }}+C_2 \cos \left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) \right) {}^2}, \end{aligned}$$

where $\eta =\nu t+\frac{2 \alpha _1 \nu w}{3 \alpha _3}+\alpha _1 x+\alpha _2 y+\alpha _3 z+\epsilon$, $C_1$ and $C_2$ are arbitrary constants.

If $C_1=0$, then we obtain the solitary wave solution,

$$\begin{aligned} u_{27}(x,y,z,w,t)=\alpha _1^2 (-\lambda ) \mu \tan ^2\left( \eta \sqrt{-\lambda } \sqrt{\mu }\right) . \end{aligned}$$

(72)

4 Discussion and results

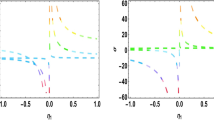
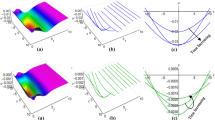
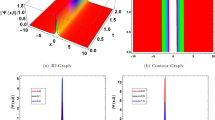
This section contain the graphical representation of some new exact solitary and traveling wave solutions of the NFE have been illustrated. The software Mathematica 11.0 is used to describe the behaviour of waves as a function of numerous factors. The 3D, contour and 2D graphs visualizes the nature of nonlinear wave solutions constructed from Eq. (1). To demonstrate the solutions by the considered approaches is observed for the Family-I, Family-II, Family-III. The Figs. 1, 2, 3, 5, 6) represents periodic type soliton for the set of appropriate values $b_0(t)=-2.23,b_2(t)=2.016, b_1(t)=-1.11, p_0(t)=1.24, y=1, \alpha _1=-1.43, \alpha _2=-2, \alpha _3=-1.1, R_1(t)=-1.13,\nu =-0.31,\epsilon =1, z=-1.12,w=-0.13, t=1$ and $b_0(t)=1.3,b_2(t)=-1.6, b_1(t)=-2.1, y=1, \alpha _1=1.12, \alpha _2=2, \alpha _3=0.1, R_1(t) =-0.3,\nu =0.1,\epsilon =1, z=-1.1,w=-3, t=1$ and  $b_0(t)=1.3,~b_2(t)=-1.6, ~b_1(t)=-3.1, ~y=1, ~\alpha _1=1.12, ~\alpha _2=2, ~\alpha _3=0.1, ~R_1(t) =-3.1,~\nu =2.1,~\epsilon =1, ~z=-1.1,~w=-3, ~t=1$ and $M=-1.3,~\alpha _1=-2.1, ~\alpha _2=-1.002, ~y=2, ~\alpha _3=-1.1, ~\nu =-1.1,~\epsilon =1, ~z=0.1,~w=-1.3, ~\rho =-2.3, ~t=1$ and $M=-1.3,~\alpha _1=-2.1, ~\alpha _2=-1.002, ~y=2, ~\alpha _3=-1.1, ~\nu =-1.1,~\epsilon =1, ~z=0.1,~w=-1.3, ~\rho =-2.3, ~t=1$. The Figs. 4, 8 represents singular bell and periodic shaped soliton for $M=-0.3,~\alpha _1=-1.1, ~\alpha _2=-2.2, ~y=2, ~\alpha _3=-0.1, ~\nu =0.1,~\epsilon =1, ~z=1.1,~w=-3, ~\rho =1.3, ~t=1$  and  $\lambda =-1.1,~\mu =-2.2, ~\nu =-3.2, ~y=1, ~\alpha _1=0.3, ~\alpha _2=1.03, ~\alpha _3=0.1, ~\rho =-1.1, ~\epsilon =1, ~z=-1.3,~w=-0.1, ~t=1$. The Fig. 7 represents W-shaped soliton structure for the set of appropriate values $\lambda =1.5,~\mu =1.1, ~\nu =-1.2, ~y=1, ~\alpha _1=0.3, ~\alpha _2=1.03, ~\alpha _3=1.001, ~\rho =-1.1, ~\epsilon =1, ~z=-1.003,~w=-0.1, ~t=1$. The Figs. 9, 10 represents dark shaped soliton for the set of appropriate values $\lambda =4.11,~\mu =0.04, ~\nu =0.2, ~y=1, ~\alpha _1=-1.3, ~\alpha _2=-0.03, ~\alpha _3=0.11, ~\rho =0.11, ~\epsilon =0.11, ~z=1.003,~w=-1.1, ~t=1$ and $\lambda =-2.003,~\mu =-1.07, ~\nu =0.002, ~y=1, ~\alpha _1=-1.3, ~\alpha _2=-0.03, ~\alpha _3=1.1, ~\rho =0.11, ~\epsilon =0.11, ~z=-0.003,~w=-1.1, ~t=1$.

Fig. 1

The graphs of $u_{2}(x,y,z,w,t)$ of Eq. (31). Values chosen are $b_0(t)=-2.23,~b_2(t)=2.016, ~b_1(t)=-1.11, ~p_0(t)=1.24, ~y=1, ~\alpha _1=-1.43, ~\alpha _2=-2, ~\alpha _3=-1.1, ~R_1(t) =-1.13,~\nu =-0.31,~\epsilon =1, ~z=-1.12,~w=-0.13, ~t=1$

Fig. 2

The graphs of $u_{3}(x,y,z,w,t)$ of Eq. (34). Values chosen are $b_0(t)=1.3,~b_2(t)=-1.6, ~b_1(t)=-2.1, ~y=1, ~\alpha _1=1.12, ~\alpha _2=2, ~\alpha _3=0.1, ~R_1(t) =-0.3,~\nu =0.1,~\epsilon =1, ~z=-1.1,~w=-3, ~t=1$

Fig. 3

The graphs of $u_{4}(x,y,z,w,t)$ of Eq. (35). Values chosen are $b_0(t)=1.3,~b_2(t)=-1.6, ~b_1(t)=-3.1, ~y=1, ~\alpha _1=1.12, ~\alpha _2=2, ~\alpha _3=0.1, ~R_1(t) =-3.1,~\nu =2.1,~\epsilon =1, ~z=-1.1,~w=-3, ~t=1$

Fig. 4

The graphs of $u_{10}(x,y,z,w,t)$ of Eq. (46). Values chosen are $M=-0.3,~\alpha _1=-1.1, ~\alpha _2=-2.2, ~y=2, ~\alpha _3=-0.1, ~\nu =0.1,~\epsilon =1, ~z=1.1,~w=-3, ~\rho =1.3, ~t=1$

Fig. 5

The graphs of $u_{12}(x,y,z,w,t)$ of Eq. (48). Values chosen are $M=-1.3,~\alpha _1=-2.1, ~\alpha _2=-1.002, ~y=2, ~\alpha _3=-1.1, ~\nu =-1.1,~\epsilon =1, ~z=0.1,~w=-1.3, ~\rho =-2.3, ~t=1$

Fig. 6

The graphs of $u_{15}(x,y,z,w,t)$ of Eq. (51). Values chosen are $M=-1.3,~\alpha _1=-2.1, ~\alpha _2=-1.002, ~y=2, ~\alpha _3=-1.1, ~\nu =-1.1,~\epsilon =1, ~z=0.1,~w=-1.3, ~\rho =-2.3, ~t=1$

Fig. 7

The graphs of $u_{16}(x,y,z,w,t)$ of Eq. (54). Values chosen are $\lambda =1.5,~\mu =1.1, ~\nu =-1.2, ~y=1, ~\alpha _1=0.3, ~\alpha _2=1.03, ~\alpha _3=1.001, ~\rho =-1.1, ~\epsilon =1, ~z=-1.003,~w=-0.1, ~t=1$

Fig. 8

The graphs of $u_{21}(x,y,z,w,t)$ of Eq. (64). Values chosen are $\lambda =-1.1,~\mu =-2.2, ~\nu =-3.2, ~y=1, ~\alpha _1=0.3, ~\alpha _2=1.03, ~\alpha _3=0.1, ~\rho =-1.1, ~\epsilon =1, ~z=-1.3,~w=-0.1, ~t=1$

Fig. 9

The graphs of $u_{24}(x,y,z,w,t)$ of Eq. (69). Values chosen are $\lambda =4.11,~\mu =0.04, ~\nu =0.2, ~y=1, ~\alpha _1=-1.3, ~\alpha _2=-0.03, ~\alpha _3=0.11, ~\rho =0.11, ~\epsilon =0.11, ~z=1.003,~w=-1.1, ~t=1$

Fig. 10

The graphs of $u_{25}(x,y,z,w,t)$ of Eq. (70). Values chosen are $\lambda =-2.003,~\mu =-1.07, ~\nu =0.002, ~y=1, ~\alpha _1=-1.3, ~\alpha _2=-0.03, ~\alpha _3=1.1, ~\rho =0.11, ~\epsilon =0.11, ~z=-0.003,~w=-1.1, ~t=1$

5 Conclusion

In this study, we have examined the (4+1)-dimensional nonlinear integrable Fokas equation and have analytically constructed several kinds of exact travelling wave and localised solutions. In addition to the singular and non-singular periodic solutions, breather solutions, Jacobi elliptic kind solutions, elliptic type solutions, exponential function solutions, and rational solutions are among the obtained solutions. The proposed techniques are efficient, clear, and could soon be used to investigate other higher dimensional NLEEs. Compared to the findings of earlier research, many of the new findings are more comprehensive. Several of the results are written as hyperbolic, trigonometric functions with arbitrary constant parameters. These findings are also helpful in understanding nonlinear wave dynamics in optics, hydrodynamics, solid state physics, and plasma. The higher dimensional Fokas equation is a useful multidimensional extension of the KP and DS equations, according to these results. This paper also provides an overview for reducing higher dimensional to the lower dimensional structures which is helpful to understand the nonlinear nature and dynamical behaviour of the governing model. We believe that by applying the approaches described in this work in the future, we will be able to resolve comparable higher-dimensional issues.