1 Introduction

Magnetic flux modeling is an important phase investigation approach that is designing the diversion of electromagnetic manufacturers and numerous applied researchers. Magnetic geometric systems are studied enveloping materials, polymers, liquids, foams, optical suspensions, and electromagnetic flux with microfluidic systems (Whitesides 2006; Leber et al. 2018; Eastman et al. 2001; Choi et al. 1999; Rogers et al. 2010; Ryu 2018; Ghadimi et al. 2011; Sun et al. 2017; Sarkar 2011; Ricca 2005; Fukami et al. 2019; Liu et al. 2020; Körpınar et al. 2021e, f; Ling et al. 2016; Körpınar and Körpınar 2021b, 2022c; Dai et al. 2015; Danesh et al. 2012).

The great advancements and constructions in the electromotive of the optical microscales are suitable for flux data analysis with development of advanced phase processing approaches. Some recent optical supplements related to evolution and geometric application of optical flux methods for investigation of spinning electromagnetic machines (Körpınar and Körpınar 2021c, 2022a, b; Körpınar et al. 2020a, 2022a; Daneshmehr and Rajabpoor 2014; Farajpour et al. 2014; Ghayesh and Farokhi 2017; Farokhi and Ghayesh 2015; Ghayesh and Farokhi 2017).

Optical geometric microscales are collected optical waves that effect at fixed velocity externally developing geometric shapes. Also, electromagnetic microscales are constructed by an optical phase of nonlinear heat and dynamical influences in complex medium. They are inspected in many optical models for nonlinear heat dynamics with diverse geometric phases of optical wave designs, such as dark, envelope, periodic, bright, compact on, singular, Jacobi elliptic function, optical, and many dynamical forms. Optical technological advancements engage numerical modeling to attend to the optical applications of electromagnetic fields and complex random systems with thermal energy minimizations (Körpınar and Körpınar 2021d, e; Sordo 2019; Körpınar et al. 2020b, 2021a, b, c, 2022b; Yan et al. 2019; Chou and Qu 2001; Marí Beffa et al. 2002; Marí Beffa 2009; Calini and Ivey 2005; Marí Beffa and Olver 2010; Körpınar 2020; Bhatnagar et al. (2019)).

Beneficial to optical soliton solutions to nonlinear heat evolution systems, there are indefinite dynamic modified methods have been established. Dynamical electromagnetic microscale systems are powerful designs for the optical geometric phase of hybrid fibers and spherical electromagnetic flux applications (Korpinar and Körpınar 2021a; Ashkin et al. 1986; Dholakia and Zemánek 2010; Burns et al. 1989; Chaumet and Nieto-Vesperinas 2001; Almaas and Brevik 2013; Körpınar et al. 2019a, b, 2021b; Dholakia and Zemánek 2010; Bliokh 2009; Bliokh et al. 2008; Fukumoto and Miyazaki 1991).

This work is prepared as: In Sect. 2, principle classifications and concepts of mKdV model are given. In Sects. 3–5, we obtain optical wave propagation \(alfa-\)microfluidic geometrical mKdV electrical flux. Then, we get antiferromagnetic electrical \(alfa-\)microfluidic geometrical mKdV spherical electromotive phase. Finally, we have axially electrical \(alfa-\) microfluidic mKdV electric flux path circuit and antiferromagnetic optical \(alfa-\)microfluidic mKdV electric flux. The conclusion is presented in Sect. 4.

2 Optical \(alfa-\)mKdV model

Optical mKdV modeling on \({\mathbb {S}}^{2}\) is given

$$\begin{aligned} {\textbf{r}}_{\pi }={\textbf{r}}_{sss}+\frac{3}{2}({\textbf{r}}_{ss}\times \left( {\textbf{r}}_{s}\times {\textbf{r}}_{ss}\right) )=\frac{1}{2}\left( 1+\Upsilon ^{2}\right) {\textbf{t}}+\Upsilon _{s}\textbf{n,} \end{aligned}$$

where

$$\begin{aligned} {\textbf{r}}_{\pi }= & {} \frac{1}{2}(\mathcal {F})\mathbf {t+}\Upsilon _{s} \textbf{n,} \\ {\textbf{t}}_{\pi }= & {} -\frac{1}{2}(\mathcal {F})\mathbf {r+(}\frac{1}{2} \Upsilon (\mathcal {F})+\Upsilon _{ss})\textbf{n,} \\ {\textbf{n}}_{\pi }= & {} -\Upsilon _{s}{\textbf{r}}-(\Upsilon _{ss}+\frac{1}{2} (\mathcal {F})\Upsilon )\textbf{t,} \end{aligned}$$

and frame equations are

$$\begin{aligned} {\textbf{r}}_{s}= & {} \textbf{t,} \\ {\textbf{t}}_{s}= & {} -{\textbf{r}}+\Upsilon \textbf{n,} \\ {\textbf{n}}_{s}= & {} -\Upsilon \mathbf {t.} \end{aligned}$$

Geometric product is defined

$$\begin{aligned} {\textbf{t}}={\textbf{n}}\times \mathbf {r,\ n}={\textbf{r}}\times \mathbf {t,\ r}= {\textbf{t}}\times \mathbf {n.} \end{aligned}$$

Compatibility conditons of \({\textbf{t}}_{s\pi }={\textbf{t}}_{\pi s},~{\textbf{n}} _{s\pi }={\textbf{n}}_{\pi s}\) is constructred

$$\begin{aligned} \Upsilon _{\pi }=\frac{3}{2}\mathcal {F}\Upsilon _{s}+\Upsilon _{sss}, \end{aligned}$$

where \(\Upsilon ^{2}+1=\mathcal {F}.\)

By Lorentz forces we get

$$\begin{aligned} \phi \left( {\textbf{r}}\right)= & {} \textbf{t,} \\ \phi \left( {\textbf{t}}\right)= & {} -{\textbf{r}}+\omega \textbf{n,} \\ \phi \left( {\textbf{n}}\right)= & {} -\omega \textbf{t,} \\ {\mathcal {B}}&\mathcal {=}&\omega {\textbf{r}}+\textbf{n,} \\ {\mathcal {E}}= & {} \mathbf {-(}\frac{\varpi }{\vartheta }+1){\textbf{r}}+(\frac{ \varpi }{\vartheta }\varkappa +\omega )\mathbf {n.} \end{aligned}$$

where \(\omega =g(\phi \left( {\textbf{t}}\right) ,{\textbf{n}}).\) Then

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{r}}\right)= & {} -{\textbf{r}}+\Upsilon \textbf{n,} \\ \nabla _{s}\phi \left( {\textbf{t}}\right)= & {} -(1+\omega \Upsilon ){\textbf{t}} +\omega _{s}\textbf{n,} \\ \nabla _{s}\phi \left( {\textbf{n}}\right)= & {} \omega {\textbf{r}}-\omega _{s} {\textbf{t}}-\omega \Upsilon \textbf{n,} \\ \nabla _{s}{\mathcal {B}}&\mathcal {=}&\omega _{s}\mathbf {r+(}\omega -\Upsilon ) \textbf{t,} \\ \nabla _{s}{\mathcal {E}}= & {} \mathbf {-(}\frac{\varpi }{\vartheta }+1){\textbf{t}} +(\omega _{s}+\frac{\varpi }{\vartheta }\varkappa _{s}){\textbf{n}}-\Upsilon (\omega +\frac{\varpi }{\vartheta }\varkappa )\textbf{t,} \end{aligned}$$

and

$$\begin{aligned} \nabla _{\pi }{\textbf{r}}= & {} \frac{1}{2}(\mathcal {F})\mathbf {t+}\Upsilon _{s} \textbf{n,} \\ \nabla _{\pi }{\textbf{t}}= & {} -\frac{1}{2}(\mathcal {F})\mathbf {r+(}\frac{ \Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})\textbf{n,} \\ \nabla _{\pi }{\textbf{n}}= & {} -\Upsilon _{s}{\textbf{r}}-(\Upsilon _{ss}+\frac{ \Upsilon }{2}(\mathcal {F}))\mathbf {t.} \end{aligned}$$

Also, mKdV motion conditions of fields are

$$\begin{aligned} \phi \left( {\textbf{r}}\right) \times \nabla _{s}\phi \left( {\textbf{r}} \right)= & {} \Upsilon {\textbf{r}}+\textbf{n,} \\ \phi \left( {\textbf{t}}\right) \times \nabla _{s}\phi \left( {\textbf{t}} \right)= & {} \omega (1+\omega \Upsilon ){\textbf{r}}+\omega _{s}{\textbf{t}} +(1+\omega \Upsilon )\textbf{n,} \\ \phi \left( {\textbf{n}}\right) \times \nabla _{s}\phi \left( {\textbf{n}} \right)= & {} \omega ^{2}\Upsilon \mathbf {r+}\omega ^{2}\textbf{n,} \end{aligned}$$

and

$$\begin{aligned} \nabla _{\pi }\phi \left( {\textbf{r}}\right)= & {} -\frac{1}{2}(\mathcal {F}) \mathbf {r+(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss})\textbf{n,} \\ \nabla _{\pi }\phi \left( {\textbf{t}}\right)= & {} -\Upsilon _{s}\omega \textbf{ r}-(\omega (\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))+\frac{1}{2} (\mathcal {F})){\textbf{t}}+(\omega _{\pi }-\Upsilon _{s})\textbf{n,} \\ \nabla _{\pi }\phi \left( {\textbf{n}}\right)= & {} \frac{\omega }{2} (\mathcal {F}){\textbf{r}}-\omega _{\pi }{\textbf{t}}-\omega (\frac{\Upsilon }{2} (\mathcal {F})+\Upsilon _{ss})\textbf{n,} \\ \nabla _{\pi }{\mathcal {B}}&\mathcal {=}&\mathcal {(}\omega _{\pi }-\Upsilon _{s}){\textbf{r}}+(\frac{\omega }{2}(\mathcal {F})-(\Upsilon _{ss}+\frac{ \Upsilon }{2}(\mathcal {F})))\mathbf {t+}\Upsilon _{s}\omega \textbf{n,} \\ \nabla _{\pi }{\mathcal {E}}= & {} -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {r-(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa )){\textbf{t}} \\{} & {} +((\omega _{\pi }+\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1))\mathbf {n.} \end{aligned}$$

3 Wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux

Surface flow \(alfa-\) microfluidical geometric mKdV spherical electromotive \(\phi ( {\textbf{r}})\) phase is

$$\begin{aligned} {\varvec{E}}^{{\mathcal {E}}}\phi \left( \mathbf {\alpha }\right)= & {} -\frac{d}{ d\pi }\int _{{\mathcal {F}}}(\mathbf {-(}\frac{1}{2}\mathbf {(}\frac{\varpi }{ \vartheta }+1)(\mathcal {F})+(\Upsilon _{ss} \\{} & {} +\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta } \varkappa ))\mathbf {(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss}- \frac{1}{2}(\mathcal {F})\Upsilon ))d{\mathcal {F}}. \end{aligned}$$

In a similar product, we get

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{r}}\right) \times \nabla _{\pi }\phi \left( {\textbf{r}}\right) =\mathbf {(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss}-\frac{1}{2}(\mathcal {F})\Upsilon )\mathbf {t.} \end{aligned}$$

Electrical \(alfa-\)microfluidical optical geometric mKdV free \(\phi ({\textbf{r}})\) surface flow density is

$$\begin{aligned} {\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{r}}\right) \mathcal {=}\mathbf { -(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega \\ +\frac{\varpi }{\vartheta }\varkappa ))\mathbf {(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss}-\frac{1}{2}(\mathcal {F})\Upsilon ). \end{aligned}$$

Wave propagation for \(alfa-\) microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux is

$$\begin{aligned} {\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{r}})=\int _{{\mathcal {F}}}(\mathbf {-(} \frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega \\ +\frac{\varpi }{\vartheta }\varkappa ))\mathbf {(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss}-\frac{1}{2}(\mathcal {F})\Upsilon ))d\mathcal {F }. \end{aligned}$$

Also, we get

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{r}}\right) \times \phi \left( {\textbf{r}} \right) \times \nabla _{s}\phi \left( {\textbf{r}}\right) =-(\mathcal {F}) \mathbf {t.} \end{aligned}$$

Antiferromagnetic electrical \(alfa-\) microfluidical axially mKdV free \(\phi ({\textbf{r}})\) surface flow density is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{r}}\right) =(\mathcal {F})\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa )). \end{aligned}$$

Antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{r}})=\int _{\mathcal {F }}((\mathcal {F})\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa )))d{\mathcal {F}}. \end{aligned}$$

Axially electrical \(alfa-\) microfluidical mKdV electric \(\phi \left( {\textbf{r}}\right)\) flux path circuit is

$$\begin{aligned} \mathbf {-(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))\mathbf {(}\frac{1}{2}\Upsilon (\mathcal {F})+\Upsilon _{ss}-\frac{1}{2}(\mathcal {F})\Upsilon )=0. \end{aligned}$$

Antiferromagnetic axially electrical \(alfa-\)microfluidical mKdV electric \(\phi \left( {\textbf{r}}\right)\) flux path circuit is

$$\begin{aligned} (\mathcal {F})\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa ))=0. \end{aligned}$$

Antiferromagnetic surface flow \(alfa-\) microfluidical mKdV spherical electromotive \(\phi ( {\textbf{r}})\) phase is

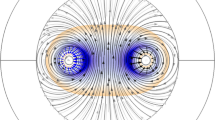
$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{E}}^{{\mathcal {E}}}\phi \left( {\textbf{r}}\right) =- \frac{d}{d\pi }\int _{{\mathcal {F}}}((\mathcal {F})\mathbf {(}\frac{1}{2}\mathbf { (}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta }\varkappa )))d\mathcal { F}. \end{aligned}$$

Figure 1 illustrates optical effect of diverse values of the thermal diffusion amplitude on axially antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux path circuit of geometric system.

Fig. 1
figure 1

Wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux

Full size image

4 Wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{t}})\) flux

Surface flow \(alfa-\) microfluidical geometric mKdV spherical electromotive \(\phi ( {\textbf{t}})\) phase is

$$\begin{aligned} {\varvec{E}}^{{\mathcal {E}}}\phi \left( {\textbf{t}}\right)= & {} -\frac{d}{d\pi } \int _{{\mathcal {F}}}(-\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta } \varkappa )(\omega _{s}(\omega (\Upsilon _{ss}+\frac{\Upsilon }{2} (\mathcal {F})) \\{} & {} +\frac{1}{2}(\mathcal {F}))-(1+\omega \Upsilon )(\omega _{\pi }-\Upsilon _{s}))+\Upsilon _{s}^{2}(\frac{\varpi }{\vartheta }+1))(1+\omega \Upsilon )\omega \\{} & {} +\Upsilon _{s}\omega \omega _{s}\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2} (\mathcal {F}))(\omega +\frac{\varpi }{\vartheta }\varkappa )))d{\mathcal {F}}. \end{aligned}$$

By utilizing product

$$\begin{aligned}{} & {} \nabla _{s}\phi \left( {\textbf{t}}\right) \times \nabla _{\pi }\phi \left( {\textbf{t}}\right) =(\omega _{s}(\omega (\Upsilon _{ss}+\frac{\Upsilon }{2} (\mathcal {F}))+\frac{1}{2}(\mathcal {F})) \\{} & {} \quad -(1+\omega \Upsilon )(\omega _{\pi }-\Upsilon _{s})){\textbf{r}}-\Upsilon _{s}\omega \omega _{s}{\textbf{t}}-(1+\omega \Upsilon )\Upsilon _{s}\omega \mathbf {n.} \end{aligned}$$

Electrical \(alfa-\)microfluidical optical geometric mKdV free \(\phi ({\textbf{t}})\) surface flow density is

$$\begin{aligned} {\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{t}}\right)= & {} -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )(\omega _{s}(\omega (\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))+\frac{1}{2}(\mathcal {F})) \\{} & {} -(1+\omega \Upsilon )(\omega _{\pi }-\Upsilon _{s}))+\Upsilon _{s}\omega \omega _{s}\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F})+(\Upsilon _{ss} \\{} & {} +\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta } \varkappa ))+\Upsilon _{s}^{2}(\frac{\varpi }{\vartheta }+1))(1+\omega \Upsilon )\omega . \end{aligned}$$

Wave propagation for \(alfa-\) microfluidical geometric mKdV electric \(\phi ({\textbf{t}})\) flux is

$$\begin{aligned} {\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{t}})= & {} \int _{{\mathcal {F}}}(\Upsilon _{s}\omega \omega _{s}\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{ \vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega \\{} & {} +\frac{\varpi }{\vartheta }\varkappa ))+\Upsilon _{s}^{2}(\frac{\varpi }{ \vartheta }+1))(1+\omega \Upsilon )\omega -\Upsilon _{s}(\omega +\frac{ \varpi }{\vartheta }\varkappa )(\omega _{s}(\omega (\Upsilon _{ss} \\{} & {} +\frac{\Upsilon }{2}(\mathcal {F}))+\frac{1}{2}(\mathcal {F}))-(1+\omega \Upsilon )(\omega _{\pi }-\Upsilon _{s})))d{\mathcal {F}}. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{t}}\right)= & {} -(1+\omega \Upsilon ){\textbf{t}} +\omega _{s}\textbf{n,} \\ \phi \left( {\textbf{t}}\right) \times \nabla _{s}\phi \left( {\textbf{t}} \right)= & {} \omega (1+\omega \Upsilon ){\textbf{r}}+\omega _{s}{\textbf{t}} +(1+\omega \Upsilon )\textbf{n,} \\ \nabla _{s}\phi \left( {\textbf{t}}\right) \times \phi \left( {\textbf{t}} \right) \times \nabla _{s}\phi \left( {\textbf{t}}\right)= & {} \mathbf {-(}\omega _{s}^{2}+(1+\omega \Upsilon )^{2}){\textbf{r}}+\omega _{s}\omega (1+\omega \Upsilon ){\textbf{t}}+\omega (1+\omega \Upsilon )^{2}\mathbf {n.} \end{aligned}$$

Antiferromagnetic electrical \(alfa-\) microfluidical axially mKdV free \(\phi ({\textbf{t}})\) surface flow density is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{t}}\right)= & {} \Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}^{2}+(1+\omega \Upsilon )^{2})\mathbf {-}\omega _{s}\mathbf {(}\frac{1}{2} \mathbf {(}\frac{\varpi }{\vartheta } \\{} & {} +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa ))\omega (1+\omega \Upsilon ) \\{} & {} +\omega (1+\omega \Upsilon )^{2}((\omega _{\pi }+\frac{\varpi }{\vartheta } \varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1)). \end{aligned}$$

Antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{t}})\) flux is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{t}})= & {} \int _{\mathcal {F }}(\omega (1+\omega \Upsilon )^{2}((\omega _{\pi }+\frac{\varpi }{\vartheta } \varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1)) \\{} & {} +\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}^{2}+(1+\omega \Upsilon )^{2})\mathbf {-}\omega _{s}\mathbf {(}\frac{1}{2} \mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F}) \\{} & {} +(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))\omega (1+\omega \Upsilon ))d{\mathcal {F}}. \end{aligned}$$

Axially electrical \(alfa-\) microfluidical geometric mKdV electric \(\phi \left( {\textbf{t}}\right)\) flux path circuit is

$$\begin{aligned}{} & {} \Upsilon _{s}^{2}(\frac{\varpi }{\vartheta }+1))(1+\omega \Upsilon )\omega -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )(\omega _{s}(\omega (\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F})) \\{} & {} \quad +\frac{1}{2}(\mathcal {F}))-(1+\omega \Upsilon )(\omega _{\pi }-\Upsilon _{s}))+\Upsilon _{s}\omega \omega _{s}\mathbf {(}\frac{1}{2}\mathbf {(}\frac{ \varpi }{\vartheta } \\{} & {} \quad +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa ))=0. \end{aligned}$$

Antiferromagnetic axially electrical \(alfa-\)microfluidical mKdV electric \(\phi \left( {\textbf{t}}\right)\) flux path circuit is

$$\begin{aligned}{} & {} \omega (1+\omega \Upsilon )^{2}((\omega _{\pi }+\frac{\varpi }{\vartheta } \varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1))\mathbf {-} \omega _{s}\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } \\{} & {} \quad +1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega + \frac{\varpi }{\vartheta }\varkappa ))\omega (1+\omega \Upsilon ) \\{} & {} \quad +\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}^{2}+(1+\omega \Upsilon )^{2})=0. \end{aligned}$$

Antiferromagnetic surface flow \(alfa-\) microfluidical mKdV spherical electromotive \(\phi ( {\textbf{t}})\) phase is

$$\begin{aligned} {}^{\mathcal{A}\mathcal{F}}{\varvec{E}}^{{\mathcal {E}}}\phi \left( {\textbf{t}}\right)= & {} - \frac{d}{d\pi }\int _{{\mathcal {F}}}(\mathbf {-}\omega _{s}\mathbf {(}\frac{1}{2} \mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss} \\{} & {} +\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta } \varkappa ))\omega (1+\omega \Upsilon )+\Upsilon _{s}(\omega +\frac{\varpi }{ \vartheta }\varkappa )\mathbf {(}\omega _{s}^{2} \\{} & {} +(1+\omega \Upsilon )^{2})+\omega (1+\omega \Upsilon )^{2}((\omega _{\pi }+ \frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{ \vartheta }+1)))d{\mathcal {F}}. \end{aligned}$$

Figure 2 illustrates optical effect of diverse values of the thermal diffusion amplitude on axially antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{t}})\) flux path circuit of geometric system.

Fig. 2
figure 2

Wave propagation for \(alfa-\) microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux

Full size image

5 Wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{n}})\) flux

Surface flow \(alfa-\) microfluidical geometric mKdV spherical electromotive \(\phi ( {\textbf{n}})\) phase is

$$\begin{aligned} {\varvec{E}}^{{\mathcal {E}}}\phi \left( {\textbf{n}}\right)= & {} -\frac{d}{d\pi } \int _{{\mathcal {F}}}(\mathbf {-}(\omega ^{2}(\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})-\frac{\Upsilon \omega ^{2}}{2}(\Upsilon ^{2} \\{} & {} +1))\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa )) \\{} & {} \mathbf {+(}\frac{\omega \omega _{s}}{2}(\mathcal {F})-\omega _{\pi }\omega )((\omega _{\pi }+\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}( \frac{\varpi }{\vartheta }+1)) \\{} & {} -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}\omega (\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})-\omega \Upsilon \omega _{\pi }))d{\mathcal {F}}. \end{aligned}$$

So, cross product is computed as follows

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{n}}\right)= & {} \omega {\textbf{r}}-\omega _{s} {\textbf{t}}-\omega \Upsilon \textbf{n,} \\ \nabla _{\pi }\phi \left( {\textbf{n}}\right)= & {} \frac{\omega }{2}(\mathcal {F}) {\textbf{r}}-\omega _{\pi }{\textbf{t}}-\omega (\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})\textbf{n,} \\ \nabla _{s}\phi \left( {\textbf{n}}\right) \times \nabla _{\pi }\phi \left( {\textbf{n}}\right)= & {} \mathbf {(}\omega _{s}\omega (\frac{\Upsilon }{2} (\mathcal {F})+\Upsilon _{ss})-\omega \Upsilon \omega _{\pi }){\textbf{r}} \\{} & {} +\mathbf {(}\omega ^{2}(\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})- \frac{\Upsilon \omega ^{2}}{2}(\mathcal {F}))\mathbf {t+(}\frac{\omega \omega _{s}}{2}(\mathcal {F})-\omega _{\pi }\omega )\mathbf {n.} \end{aligned}$$

Electrical \(alfa-\)microfluidical optical geometric mKdV free \(\phi ({\textbf{n}})\) surface flow density is

$$\begin{aligned} {\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{n}}\right)= & {} -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}\omega (\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})-\omega \Upsilon \omega _{\pi })\mathbf {-}(\omega ^{2}(\frac{\Upsilon }{2} (\mathcal {F}) \\{} & {} +\Upsilon _{ss})-\frac{\Upsilon \omega ^{2}}{2}(\mathcal {F}))\mathbf {(} \frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega \\{} & {} +\frac{\varpi }{\vartheta }\varkappa ))\mathbf {+(}\frac{\omega \omega _{s}}{2 }(\mathcal {F})-\omega _{\pi }\omega )((\omega _{\pi }+\frac{\varpi }{ \vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1)) \end{aligned}$$

Wave propagation for \(alfa-\) microfluidical geometric mKdV electric \(\phi ({\textbf{n}})\) flux is

$$\begin{aligned} {\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{n}})= & {} \int _{{\mathcal {F}}}(\mathbf {(} \frac{\omega \omega _{s}}{2}(\mathcal {F})-\omega _{\pi }\omega )((\omega _{\pi }+\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{ \varpi }{\vartheta }+1)) \\{} & {} -\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\mathbf {(}\omega _{s}\omega (\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})-\omega \Upsilon \omega _{\pi })\mathbf {-}(\omega ^{2}(\frac{\Upsilon }{2} (\mathcal {F})+\Upsilon _{ss}) \\{} & {} -\frac{\Upsilon \omega ^{2}}{2}(\mathcal {F}))\mathbf {(}\frac{1}{2}\mathbf {(} \frac{\varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss}+\frac{\Upsilon }{ 2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta }\varkappa )))d{\mathcal {F}}. \end{aligned}$$

Since

$$\begin{aligned} \nabla _{s}\phi \left( {\textbf{n}}\right)= & {} \omega {\textbf{r}}-\omega _{s} {\textbf{t}}-\omega \Upsilon {\textbf{n}} \\ \phi \left( {\textbf{n}}\right) \times \nabla _{s}\phi \left( {\textbf{n}} \right)= & {} \omega ^{2}\Upsilon \mathbf {r+}\omega ^{2}{\textbf{n}} \\ \nabla _{s}\phi \left( {\textbf{n}}\right) \times \phi \left( {\textbf{n}} \right) \times \nabla _{s}\phi \left( {\textbf{n}}\right)= & {} -\omega _{s}\omega ^{2}{\textbf{r}}-(\omega ^{3}+\omega ^{3}\Upsilon ^{2})\mathbf {t+} \omega ^{2}\Upsilon \omega _{s}{\textbf{n}} \end{aligned}$$

Antiferromagnetic electrical \(alfa-\) microfluidical axially mKdV free \(\phi ({\textbf{n}})\) surface flow density is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{L}}^{{\mathcal {E}}}\phi \left( {\textbf{n}}\right)= & {} \omega _{s}\omega ^{2}\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta } \varkappa )+\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F}) \\{} & {} +(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))(\omega ^{3}+\omega ^{3}\Upsilon ^{2}) \\{} & {} \mathbf {+}\omega ^{2}\Upsilon \omega _{s}((\omega _{\pi }+\frac{\varpi }{ \vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1)) \end{aligned}$$

Antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{n}})\) flux is

$$\begin{aligned} ^{\mathcal{A}\mathcal{F}}{\varvec{W}}^{{\mathcal {E}}}\phi ({\textbf{n}})= & {} \int _{\mathcal {F }}(((\omega _{\pi }+\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1))\omega ^{2}\Upsilon \omega _{s} \\{} & {} +\omega _{s}\omega ^{2}\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta } \varkappa )+\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F}) \\{} & {} +(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))(\omega ^{3}+\omega ^{3}\Upsilon ^{2}))d{\mathcal {F}}. \end{aligned}$$

Axially electrical \(alfa-\) microfluidical geometric mKdV electric \(\phi \left( {\textbf{n}}\right)\) flux path circuit is

$$\begin{aligned}{} & {} \mathbf {-}(\omega ^{2}(\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss})- \frac{\Upsilon \omega ^{2}}{2}(\mathcal {F}))\mathbf {(}\frac{1}{2}\mathbf {(} \frac{\varpi }{\vartheta }+1)(\mathcal {F}) \\{} & {} \quad +(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))-\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta } \varkappa )\mathbf {(}\omega _{s}\omega (\frac{\Upsilon }{2}(\mathcal {F})+\Upsilon _{ss}) \\{} & {} \quad -\omega \Upsilon \omega _{\pi })\mathbf {+(}\frac{\omega \omega _{s}}{2} (\mathcal {F})-\omega _{\pi }\omega )((\omega _{\pi }+\frac{\varpi }{ \vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1))=0. \end{aligned}$$

Antiferromagnetic axially electrical \(alfa-\)microfluidical mKdV electric \(\phi \left( {\textbf{n}}\right)\) flux path circuit is

$$\begin{aligned}{} & {} \omega _{s}((\omega _{\pi }+\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{\vartheta }+1))\omega ^{2}\Upsilon \\{} & {} \quad +\omega _{s}\omega ^{2}\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta } \varkappa )+\mathbf {(}\frac{1}{2}\mathbf {(}\frac{\varpi }{\vartheta } +1)(\mathcal {F}) \\{} & {} \quad +(\Upsilon _{ss}+\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{ \vartheta }\varkappa ))(\omega ^{3}+\omega ^{3}\Upsilon ^{2})=0. \end{aligned}$$

Antiferromagnetic surface flow \(alfa-\) microfluidical mKdV spherical electromotive \(\phi ( {\textbf{n}})\) phase is

$$\begin{aligned} {}^{\mathcal{A}\mathcal{F}}{\varvec{E}}^{{\mathcal {E}}}\phi \left( {\textbf{n}}\right)= & {} - \frac{d}{d\pi }\int _{{\mathcal {F}}}(\mathbf {(}\frac{1}{2}\mathbf {(}\frac{ \varpi }{\vartheta }+1)(\mathcal {F})+(\Upsilon _{ss} \\{} & {} +\frac{\Upsilon }{2}(\mathcal {F}))(\omega +\frac{\varpi }{\vartheta } \varkappa ))(\omega ^{3}+\omega ^{3}\Upsilon ^{2})\mathbf {+}\omega ^{2}\Upsilon \omega _{s}((\omega _{\pi } \\{} & {} +\frac{\varpi }{\vartheta }\varkappa _{\pi })-\Upsilon _{s}(\frac{\varpi }{ \vartheta }+1))+\Upsilon _{s}(\omega +\frac{\varpi }{\vartheta }\varkappa )\omega _{s}\omega ^{2})d{\mathcal {F}}. \end{aligned}$$

Figure 3 illustrates optical effect of diverse values of the thermal diffusion amplitude on axially antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV electric \(\phi ({\textbf{n}})\) flux path circuit of geometric system.

Fig. 3
figure 3

Wave propagation for \(alfa-\) microfluidical geometric mKdV electric \(\phi ({\textbf{r}})\) flux

Full size image

6 Conclusion

The optical geometric model for antiferromagnetic wave propagation \(alfa-\) microfluidical mKdV spherical electromotive phase is constructed for the first time in this study. Also, we obtain antiferromagnetic axially electrical \(alfa-\)microfluidical mKdV electric flux path circuit. We have electrical \(alfa-\)microfluidical geometrical mKdV free surface flow density in sphere space. Finally, we design antiferromagnetic wave propagation for \(alfa-\)microfluidical geometric mKdV surface flux density.