Skip to main content
SpringerLink
Log in

Parametric vibrations of imperfect Timoshenko microbeams

  • Technical Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

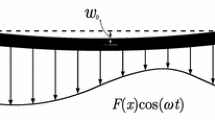
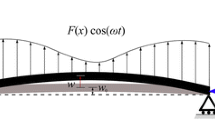
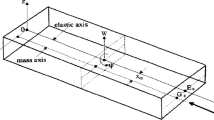
This paper examines the size-dependent nonlinear parametric vibrations of imperfect Timoshenko microbeams subject to a time-dependent axial load. Taking into account rotary inertia and shear deformation, the modified couple stress theory is employed so as to derive a continuous expression for the elastic potential energy of the system; the geometric imperfection is modelled via a small initial deflection in the transverse direction. The continuous model of the system is obtained via an energy balance method. A reduced-order model is obtained by means of a weighted residual method together with an assumed-mode technique. The double-dimensionalised form of the reduced-order model is solved by means of different numerical techniques and stability is analysed. It is shown that even small geometric imperfections may change the parametric response of the system not only quantitatively, but also qualitatively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Abdel-Rahman EM, Younis MI, Nayfeh AH (2002) Characterization of the mechanical behavior of an electrically actuated microbeam. J Micromech Microeng 12:759–766

    Article  Google Scholar 

  • Aboelkassem Y, Nayfeh AH, Ghommem M (2010) Bio-mass sensor using an electrostatically actuated microcantilever in a vacuum microchannel. Microsyst Technol 16:1749–1755

    Article  Google Scholar 

  • Abouelregal AE, Zenkour AM (2015) Generalized thermoelastic vibration of a microbeam with an axial force. Microsyst Technol 21:1427–1435

    Article  Google Scholar 

  • Akgöz B, Civalek Ö (2012) Analysis of micro-sized beams for various boundary conditions based on the strain gradient elasticity theory. Arch Appl Mech 82:423–443

    Article  MATH  Google Scholar 

  • Ansari R, Gholami R, Sahmani S (2011) Free vibration analysis of size-dependent functionally graded microbeams based on the strain gradient Timoshenko beam theory. Compos Struct 94:221–228

    Article  MATH  Google Scholar 

  • Antonello R, Oboe R, Prandi L et al (2009) Automatic mode matching in MEMS vibrating gyroscopes using extremum-seeking control. IEEE Trans Ind Electron 56:3880–3891

    Article  Google Scholar 

  • Asghari M, Kahrobaiyan M, Rahaeifard M et al (2011) Investigation of the size effects in Timoshenko beams based on the couple stress theory. Arch Appl Mech 81:863–874

    Article  MATH  Google Scholar 

  • Emam SA, Nayfeh AH (2009) Postbuckling and free vibrations of composite beams. Compos Struct 88:636–642

    Article  Google Scholar 

  • Farokhi H, Ghayesh M (2016) Size-dependent behaviour of electrically actuated microcantilever-based MEMS. Int J Mech Mater Des 12(3):301–315

    Article  Google Scholar 

  • Ghayesh MH (2012) Coupled longitudinal–transverse dynamics of an axially accelerating beam. J Sound Vib 331:5107–5124

    Article  Google Scholar 

  • Ghayesh MH, Farokhi H (2015) Nonlinear dynamics of microplates. Int J Eng Sci 86:60–73

    Article  MathSciNet  Google Scholar 

  • Gholipour A, Farokhi H, Ghayesh MH (2015) In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn 79:1771–1785

    Article  Google Scholar 

  • Kahrobaiyan MH, Rahaeifard M, Tajalli SA et al (2012) A strain gradient functionally graded Euler–Bernoulli beam formulation. Int J Eng Sci 52:65–76

    Article  MathSciNet  Google Scholar 

  • Karparvarfard SMH, Asghari M, Vatankhah R (2015) A geometrically nonlinear beam model based on the second strain gradient theory. Int J Eng Sci 91:63–75

    Article  MathSciNet  Google Scholar 

  • Ke L-L, Wang Y-S (2011) Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos Struct 93:342–350

    Article  Google Scholar 

  • Kong S, Zhou S, Nie Z et al (2008) The size-dependent natural frequency of Bernoulli–Euler micro-beams. Int J Eng Sci 46:427–437

    Article  MATH  Google Scholar 

  • Li Y, Packirisamy M, Bhat RB (2008) Shape optimizations and static/dynamic characterizations of deformable microplate structures with multiple electrostatic actuators. Microsyst Technol 14:255–266

    Article  Google Scholar 

  • Ma HM, Gao XL, Reddy JN (2008) A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J Mech Phys Solids 56:3379–3391

    Article  MathSciNet  MATH  Google Scholar 

  • Reddy JN (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45:288–307

    Article  MATH  Google Scholar 

  • Rembe C, Muller RS (2002) Measurement system for full three-dimensional motion characterization of MEMS. J Microelectromech Syst 11:479–488

    Article  Google Scholar 

  • Rezazadeh G, Fathalilou M, Shabani R (2009) Static and dynamic stabilities of a microbeam actuated by a piezoelectric voltage. Microsyst Technol 15:1785–1791

    Article  Google Scholar 

  • Tavakolian F, Farrokhabadi A, Mirzaei M (2015) Pull-in instability of double clamped microbeams under dispersion forces in the presence of thermal and residual stress effects using nonlocal elasticity theory. Microsyst Technol 23(4):839–848

    Article  Google Scholar 

  • Wang B, Zhao J, Zhou S (2010) A micro scale Timoshenko beam model based on strain gradient elasticity theory. Eur J Mech A Solids 29:591–599

    Article  Google Scholar 

  • Zhang WM, Meng G (2007) Nonlinear dynamic analysis of electrostatically actuated resonant MEMS sensors under parametric excitation. IEEE Sens J 7:370–380

    Article  Google Scholar 

  • Zheng Q, Dong L, Lee DH et al (2009) Active disturbance rejection control for MEMS gyroscopes. IEEE Trans Control Syst Technol 17:1432–1438

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Adelaide, Adelaide, SA, 5005, Australia

    Mergen H. Ghayesh

  2. Department of Mechanical Engineering, McGill University, Montreal, QC, H3A 0C3, Canada

    Hamed Farokhi

Authors
  1. Mergen H. Ghayesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hamed Farokhi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mergen H. Ghayesh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghayesh, M.H., Farokhi, H. Parametric vibrations of imperfect Timoshenko microbeams. Microsyst Technol 23, 4917–4929 (2017). https://doi.org/10.1007/s00542-017-3358-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-017-3358-0

Keywords

Search

Navigation