1 Introduction

The nonlinear partial differential equations (NPDEs) are widely used for the representation of physical problems arising in various branches of science and engineering, and often they describe real phenomena of complex nature in physics, fluid dynamics, and many other fields. For example, the Korteweg and de Vries equation (1895), Fisher’s equation (1951), the equation governing wave propagation in low-pass electrical transmission line (Houwe et al. 2020), the Biswas–Arshed equation (Sabi’u et al. 2019b), the Boussinesq-like equations (Shi et al. 2015; Mirhosseini-Alizamini et al. 2021), the incompressible Navier–Stokes equations in streamfunction‐vorticity formulation (Raza et al. 2021), the Sine–Gordon equation (Ben-Yu et al. 1986), and the nonlinear Schrodinger equation (Kato 1987). The Shynaray-IIA Equation (S-IIAE) are coupled system of nonlinear PDEs, whereas, it involves significant challenges of a serious nature, which are associated with intricate and nontrivial behaviors of the system (Myrzakulova et al. 2022). The well-known mathematical form of S-IIAE (Fahim et al. 2022) is expressed below:

$$ \begin{aligned} & iq_{t} + q_{xt} - i\left( {vq} \right)_{x} = 0, \\ & ir_{t} - r_{xt} - i\left( {vr} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} }}{m}\left( {rq} \right)_{t} = 0, \\ \end{aligned} $$
(1)

where \(q(x,t)\), \(r(x,t)\) and \(v(x,t)\) represent the unknown variables and they naturally depend on independent variables \(x\) and \(t\). Note that \(m\) and \(n\) are constants. The integrable property of this equation via the inverse scattering transform, other properties such as geometrical and gauge equivalence, and space curves integrable motion are extensively studied, see Sagidullayeva et al. (2022) and the reference therein.

The solution of NPDEs became a challenging problem in mathematics and engineering, especially to get the stability and consistency of such systems while finding numerical solutions (Shah et al. 2010; Hussain et al. 2019). The most commonly used numerical methods for solving the NPDE are the finite difference methods, spectral methods, finite element and finite volume methods (Ma and Yan 2006; Sod 1978; Fallah et al. 2000; Meuris et al. 2023). The non-numerical solutions of such equations are not an easy task all the time, therefore, the most serious concerns of researchers regarding the exact solutions to such equations have been addressed positively which is strictly based on the motivation of physical insights of the problem. The solitary wave methods are among the convincing methods for finding the exact solution to NPDEs. Previously, many methods have been used to find the exact solutions of NPDEs, such as the tanh method (Almatrafi 2023), the homogeneous balance method (Jafari et al. 2014), the sub-equation method (Akinyemi et al. 2021; Senol et al. 2021), the Kudryashov method and its modifications (Kudryashov 2012, 2020), the sine-Gordon methods (Baskonus et al. 2019; Kumar et al. 2017a; Fahim et al. 2022), the generalized algebraic and Q-expansion methods (Almatrafi and Alharbi 2023; Alharbi and Almatrafi 2022), the Jacobi elliptic function expansion method (Khan et al. 2022), and so on, see Iqbal (2018), Bilal et al. (2021), Seadawy et al. (2021, 2019), Iqbal et al. (2023), Khatri et al. (2019), Kumar et al. (2017b, 2021), Dahiya et al. (2021), Sabi’u et al. (2019a, 2022, 2023) for more details and the references therein. In addition, some of the most accurate and efficient techniques were designed with extreme efforts of researchers for the solutions of NLPDEs. However, some of these methods do not provide reasonable solutions to the system of NLPDEs adequately. Therefore, this prompted us to apply IMSSEM (Akinyemi 2021) for the solutions of S-IIAE. More precisely, the IMSSEM is a novel approach that combines and utilizes the strengths of existing methodologies to offer robust and versatile solutions for nonlinear NPDEs.

The primary objective of this research paper is to present the exact solution to the challenging S-IIAE for the first time in the literature using the IMSSEM (Akinyemi 2021), by employing this innovative method, we aim to overcome the limitations of traditional approaches and provide concise and elegant solutions to this complex equation.

The structure of this work is as follows: we give a brief introduction to the importance of NPDEs in science and engineering and some available methods for solving them in Sect. 1. Section 2 contains the methodology of the suggested technique for the solution of S-IIAE. In Sect. 3, we used the IMSSEM to solve the S-IIAE precisely. Section 4 addresses the graphical depiction of the solutions. Section 5 of the study contains its conclusion.

2 Methodology of the proposed improved modified Sardar sub-equation method

This section will elucidate the procedures of the IMSSEM (Akinyemi 2021) for solving NPDEs. Now, Let us consider the NLPDE

$$\mathrm{ F}\left({\text{u}},{{\text{u}}}_{{\text{t}}},{{\text{u}}}_{{\text{x}}},{{\text{u}}}_{{\text{xx}}},\cdots \right)=0, $$
(2)

where the function \(u=u(x,t)\) represents an unknown function in the given context. In order to proceed, we have introduced a wave transformation as follows:

$$\mathrm{ u}={\text{u}}\left(\eta \right)\mathrm{ where \eta }={\text{x}}-{\text{ct}}, $$
(3)

by using the transformation in Eq. (3) into the nonlinear PDE in Eq. (2), where \(c\ne 0\), we can reduce the PDE into an ODE of integer order

$${\text{N}}\left({{\text{u}}}^{\prime},{{\text{u}}}^{\prime\prime},{{\text{u}}}^{\prime\prime\prime},\cdots \right)=0. $$
(4)

We have solved the ODE (4) by using the IMSSEM, the technique has the standard form:

$$\mathrm{ u}\left(\upeta \right)={{\text{a}}}_{0}+\sum_{{\text{j}}=1}^{N}{{\text{a}}}_{{\text{j}}}{\upphi }^{{\text{j}}}\left(\upeta \right),\mathrm{ where }{{\text{a}}}_{N}\ne 0,$$
(5)

where \({a}_{j}\) \((j=\mathrm{0,1},\mathrm{2,3},\cdots N)\).

The value of \(N\) can be determined by homogeneous balancing procedure (HBP), by balancing the highest order nonlinear and highest order derivative term in Eq. (4). Therefore, the highest degree of \(\frac{{{\text{d}}}^{{\text{r}}}{\text{u}}}{{\text{d}}{\upxi }^{{\text{r}}}}\) is classified as:

$${\text{O}}\left(\frac{{{\text{d}}}^{{\text{r}}}{\text{u}}}{{\text{d}}{\upeta }^{{\text{r}}}}\right)={\text{n}}+\mathrm{r },$$
(6)
$$\mathrm{ O}{\left({{\text{u}}}^{{\text{q}}}\frac{{{\text{d}}}^{{\text{r}}}{\text{u}}}{{\text{d}}{\upeta }^{{\text{r}}}}\right)}^{s}={\text{qn}}+{\text{s}}({\text{n}}+{\text{r}}).$$
(7)

2.1 The enhanced improved modified Sardar sub-equation approach

The \(\upphi (\upeta )\) in Eq. (5) is considered the solution to the following equation:

$${\left({\upphi }^{\prime}\right)}^{2}\left(\upeta \right)={\updelta }_{2}{\upphi }^{4}\left(\upeta \right)+{\updelta }_{1}{\upphi }^{2}\left(\upeta \right)+{\updelta }_{0},$$
(8)

where \({\delta }_{i},i=\mathrm{0,1},2\) are constants to be determined, for more detail on Eq. (8) see Akinyemi (2021) and the references therein. The following set of solutions that satisfied Eq. (8) with \(C\) as the constant of integration are:

For \({\delta }_{0}={\delta }_{1}=0\) and \({\delta }_{2}>0,\) we obtained the rational solutions:

$${\upphi }_{1}^{\pm }\left(\upeta \right)=\pm \frac{1}{\sqrt{{\updelta }_{2}}\left(\upeta +{\text{C}}\right)}.$$
(9)

For \({\updelta }_{0}=0\) and \({\updelta }_{1}>0,\) the exponential solutions will be of the form:

$$ {\upphi }_{2}^{\pm }(\upeta )=\frac{4{\updelta }_{1}{{\text{e}}}^{\pm \sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)}}{{{\text{e}}}^{\pm 2\sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)}-4{\updelta }_{1}{\updelta }_{2}},$$
(10)
$${\upphi }_{3}^{\pm }\left(\upeta \right)=\frac{\pm 4{\updelta }_{1}{{\text{e}}}^{\pm \sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)}}{{1-{4\updelta }_{1}{\updelta }_{2}{\text{e}}}^{\pm 2\sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)}}.$$
(11)

The trigonometric hyperbolic solutions are as follows:

(i) For \({\updelta }_{0}=0\), \({\updelta }_{1}>0\) and \({\updelta }_{2}\ne 0\), we have

$${\upphi }_{4}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{{\updelta }_{1}}{{\updelta }_{2}}}{\text{sech}}\left(\sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(12)
$${\upphi }_{5}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{{\updelta }_{1}}{{\updelta }_{2}}}{\text{csch}}\left(\sqrt{{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right).$$
(13)

(ii) For \({\updelta }_{0}=\frac{{{\updelta }_{1}}^{2}}{4{\updelta }_{2}}\), \({\updelta }_{1}<0\) and \({\updelta }_{2}>0\), we have

$${\upphi }_{6}^{\pm }(\upeta )=\pm \sqrt{-\frac{{\updelta }_{1}}{{2\updelta }_{2}}}{\text{tanh}}\left(\sqrt{-\frac{{\updelta }_{1}}{2}}\left(\upeta +{\text{C}}\right)\right),$$
(14)
$${\upphi }_{7}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{{\updelta }_{1}}{{2\updelta }_{2}}}{\text{coth}}\left(\sqrt{-\frac{{\updelta }_{1}}{2}}\left(\upeta +{\text{C}}\right)\right),$$
(15)
$${\upphi }_{8}^{\pm }(\upeta )=\pm \sqrt{-\frac{{\updelta }_{1}}{{2\updelta }_{2}}}({\text{tanh}}\left(\sqrt{-2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{isech}}\left(\sqrt{-2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(16)
$${\upphi }_{9}^{\pm }(\upeta )=\pm \sqrt{-\frac{{\updelta }_{1}}{{2\updelta }_{2}}}({\text{coth}}\left(\sqrt{-2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{csch}}\left(\sqrt{-2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(17)
$${\upphi }_{10}(\upeta )=\pm \sqrt{-\frac{{\updelta }_{1}}{{8\updelta }_{2}}}({\text{tanh}}\left(\sqrt{-\frac{{\updelta }_{1}}{8}}\left(\upeta +{\text{C}}\right)\right)+{\text{coth}}\left(\sqrt{-\frac{{\updelta }_{1}}{8}}\left(\upeta +{\text{C}}\right)\right).$$
(18)

The solutions which have the form of trigonometric functions are presented below:

(i) For \({\updelta }_{0}=0\), \({\updelta }_{1}<0\) and \({\updelta }_{2}\ne 0\), we have

$${\upphi }_{11}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{{\updelta }_{1}}{{\updelta }_{2}}}{\text{sec}}\left(\sqrt{-{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(19)
$${\upphi }_{12}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{{\updelta }_{1}}{{\updelta }_{2}}}{\text{csc}}\left(\sqrt{-{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right).$$
(20)

(ii) For \({\updelta }_{0}=\frac{{{\updelta }_{1}}^{2}}{4{\updelta }_{2}}\), \({\updelta }_{1}>0\) and \({\updelta }_{2}>0\), we have

$${\upphi }_{13}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{{\updelta }_{1}}{{2\updelta }_{2}}}{\text{tan}}\left(\sqrt{\frac{{\updelta }_{1}}{2}}\left(\upeta +{\text{C}}\right)\right),$$
(21)
$${\upphi }_{14}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{{\updelta }_{1}}{{2\updelta }_{2}}}{\text{cot}}\left(\sqrt{\frac{{\updelta }_{1}}{2}}\left(\upeta +{\text{C}}\right)\right),$$
(22)
$${\upphi }_{15}^{\pm }(\upeta )=\pm \sqrt{\frac{{\updelta }_{1}}{{2\updelta }_{2}}}({\text{tan}}\left(\sqrt{2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{sec}}\left(\sqrt{2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(23)
$${\upphi }_{16}^{\pm }(\upeta )=\pm \sqrt{\frac{{\updelta }_{1}}{{2\updelta }_{2}}}({\text{cot}}\left(\sqrt{2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{csc}}\left(\sqrt{2{\updelta }_{1}}\left(\upeta +{\text{C}}\right)\right),$$
(24)
$${\upphi }_{17}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{{\updelta }_{1}}{{8\updelta }_{2}}}\left({\text{tan}}\left(\sqrt{\frac{{\updelta }_{1}}{8}}\left(\upeta +{\text{C}}\right)\right)-{\text{cot}}\left(\sqrt{\frac{{\updelta }_{1}}{8}}\left(\upeta +{\text{C}}\right)\right)\right).$$
(25)

Remember that we have substituted Eqs. (5 and 8) into Eq. (4), and equate all the coefficients of each power of \(\phi (\upeta )\) to zero and solve the resultant system of algebraic equations with the help of Maple. Eventually, we incorporated these constants (coefficients) into Eq. (5) and obtained the solution of distinct types as shown in Eqs. (9–25). As a result, we obtained different exact solutions for NPDEs.

3 Shynaray-IIA equation (S-IIAE) and its solutions by Sardar sub-equation method

In this section, we present the exact solutions of S-IIAE (1) by IMSSEM (Akinyemi 2021)

$$ \begin{aligned} & iq_{t} + q_{xt} - i\left( {vq} \right)_{x} = 0, \\ & ir_{t} - r_{xt} - i\left( {vr} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} }}{m}\left( {rq} \right)_{t} = 0. \\ \end{aligned} $$

In case when \(r=\epsilon \overline{q }\) \((\epsilon =\pm 1)\), the S-IIAE takes the following form

$$ \begin{aligned} & iq_{t} + q_{xt} - i\left( {vq} \right)_{x} = 0, \\ & v_{x} - \frac{{n^{2} }}{m}\left( {\left| q \right|^{2} } \right)_{t} = 0. \\ \end{aligned} $$
(26)

In the above equation \(m\), \(n\) and \(\epsilon \) are constants. By using the traveling wave transformation, Eq. (26) is reduced into the following ODE

$$ \begin{aligned} & q\left( {x,t} \right) = U\left( \eta \right)e^{{i\xi \left( {x,t} \right)}} , v\left( {x,t} \right) = G\left( \eta \right), \\ & \xi \left( {x,t} \right) = - \delta x + \omega t + \theta , \eta = x - ct, \\ \end{aligned} $$
(27)

where \(v, \theta , \omega , \delta \) characterize the frequency, phase constant, wave number and velocity of soliton, respectively. Substituting Eq. (27) into the first part of the system (26) and separating the real and imaginary parts, we have the real part of the form

$$ \begin{aligned} & cU^{\prime\prime}\left( \eta \right) + \omega \left( {1 - \delta } \right)U\left( \eta \right) + \delta G\left( \eta \right)U\left( \eta \right) + i\left( {\omega - c\left( {1 - \delta } \right)} \right)U^{\prime}\left( \eta \right) - G\left( \eta \right)U^{\prime}\left( \eta \right) - G^{\prime}\left( \eta \right)U\left( \eta \right) = 0, \\ & G^{\prime}\left( \eta \right) + \frac{{2cn^{2} }}{m}U\left( \eta \right)U^{\prime}\left( \eta \right) = 0. \\ \end{aligned} $$
(28)

Equation (28) is integrated, and we get

$$G\left(\eta \right)=-\frac{c\epsilon {n}^{2}}{m}{U}^{2}\left(\eta \right).$$
(29)

Substitute Eq. (29) into the first part of (28) and separate the real and imaginary parts as

$$c{U}^{{\prime}{\prime}}\left(\eta \right)+\omega \left(1-\delta \right)U\left(\eta \right)-\frac{\delta c\epsilon {n}^{2}}{m}{U}^{3}\left(\eta \right)=0,$$
(30)

where the imaginary part is given by

$$\left(\omega -c\left(1-\delta \right)\right){U}{\prime}\left(\eta \right)+\frac{3c\epsilon {n}^{2}}{m}{U}^{{\prime}{\prime}}\left(\eta \right){U}{\prime}\left(\eta \right)=0.$$
(31)

By using the HBP, by balancing the highest order derivative and highest order nonlinear term, we obtained \(N=1\). The determined value of \(N\) is substituted in Eq. (5), we obtain the simple form of the solution as:

$$U\left(\eta \right)={a}_{0}+{a}_{1}\phi \left(\eta \right). $$
(32)

3.1 Exact solutions of S-IIAE by IMSSEM

In this section, Eqs. (8 and 32) are substituted into Eq. (30) and we get the following equation with the aid of Maple.

$$ \begin{aligned} & \frac{1}{m}(\omega ma_{0} + \omega ma_{1} U\left( \eta \right) - \omega n\delta a_{0} - \omega m\delta a_{1} U\left( \eta \right) - \delta cn^{2} a_{0}^{3} \\ & \quad - 3\delta cn^{2} a_{0}^{2} a_{1}^{2} U\left( \eta \right) - 3\delta cn^{2} a_{0} a_{1}^{2} U^{2} \left( \eta \right) - \delta cn^{2} a_{1}^{3} U^{3} \left( \eta \right) \\ & \quad + 2ca_{1} U^{3} \left( \eta \right)m\delta_{2} + ca_{1} U\left( \eta \right)m\delta_{1} = 0. \\ \end{aligned} $$
(33)

By comparing the coefficients of various powers of \({U}^{i}(\eta )\), we get the system of algebraic equations of the following form, we have

$${U}^{0}: \frac{-{a}_{0}(-\omega m+\omega m\delta +\delta \epsilon c{n}^{2}{b}_{0}^{2})}{m}=0,$$
(34)
$${ U}^{1}: \frac{\omega m{a}_{1}-\omega m\delta {a}_{1}-3\delta \epsilon c{n}^{2}{a}_{0}^{2}{a}_{1}+c{a}_{1}m{\delta }_{1}}{m}=0,$$
(35)
$${U}^{2}: \frac{-3\delta \epsilon c{n}^{2}{a}_{0}{a}_{1}^{2}}{m}=0, $$
(36)
$${U}^{3}: \frac{-\delta \epsilon c{n}^{2}{a}_{1}^{3}+2c{a}_{1}m{\delta }_{2}}{m}=0.$$
(37)

Solving the above system of equations with the aid of Maple and get the coefficients:

$${a}_{0}=0,$$
(38)
$${ a}_{1}={a}_{1},$$
(39)
$${\delta }_{1}=\frac{\omega (-1+\delta )}{c},$$
(40)
$${\delta }_{2}=\frac{\delta \epsilon {n}^{2}{a}_{1}^{2}}{2m}.$$
(41)

Using Eqs. (39–41) in combination with Eqs. (9–25) and Eq. (32), we obtained the following solutions.

The rational solution of Eq. (1) for \({\delta }_{0}={\delta }_{1}=0\) and \({\delta }_{2}>0\) can be found as:

$${{\text{U}}}_{1}^{\pm }\left(\upeta \right)=\pm \frac{1}{\sqrt{{\updelta }_{2}}\left(\upeta +{\text{C}}\right)}.$$
(42)

The exponential solutions of Eq. (1) have the following form:

For \({\delta }_{0}=0\) and \({\delta }_{1}>0\), we have

$$ {{\text{U}}}_{2}^{\pm }(\upeta )=\frac{4\frac{\omega (-1+\delta )}{c}{{\text{e}}}^{\pm \sqrt{\frac{\omega (-1+\delta )}{c}}\left(\upeta +{\text{C}}\right)}}{{{\text{e}}}^{\pm 2\sqrt{\frac{\omega (-1+\delta )}{c}}\left(\upeta +{\text{C}}\right)}-2\frac{\omega (-1+\delta )\delta \epsilon {n}^{2}{a}_{1}^{2}}{cm}},$$
(43)
$${{\text{U}}}_{3}^{\pm }\left(\upeta \right)=\frac{\pm 4\frac{\omega \left(-1+\delta \right)}{c}{{\text{e}}}^{\pm \sqrt{\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)}}{{1-2\frac{\omega \left(-1+\delta \right)\delta \epsilon {n}^{2}{a}_{1}^{2}}{cm}{\text{e}}}^{\pm 2\sqrt{\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)}}.$$
(44)

The trigonometric and hyperbolic solutions of Eq. (1) are given as:

For \({\delta }_{0} = 0\), \({\delta }_{1} > 0\) and \({\delta }_{2} \ne 0\), we have

$${{\text{U}}}_{4}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{2m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{sech}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
(45)
$${{\text{U}}}_{5}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{2m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{csch}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +C\right)\right).$$
(46)

  • While for \({\delta }_{0}=\frac{{\delta }_{1}^{2}}{4{\delta }^{2}}, {\delta }_{1}<0\) and \({\delta }_{2}>0\), we get the solutions as:

    $${{\text{U}}}_{6}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{tanh}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{2c}}\left(\upeta +C\right)\right),$$
    (47)
    $${{\text{U}}}_{7}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{coth}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{2c}}\left(\upeta +C\right)\right),$$
    (48)
    $${{\text{U}}}_{8}^{\pm }(\upeta )=\pm \sqrt{-\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}({\text{tanh}}\left(\sqrt{-2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right) \pm {\text{isech}}\left(\sqrt{-2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right), $$
    (49)
    $${{\text{U}}}_{9}^{\pm }(\upeta )=\pm \sqrt{-\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}({\text{coth}}\left(\sqrt{-2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{csch}}\left(\sqrt{-2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
    (50)
    $${{\text{U}}}_{10}(\upeta )=\pm \sqrt{-\frac{m\omega \left(-1+\delta \right)}{4c\delta \epsilon {n}^{2}{a}_{1}^{2}}}({\text{tanh}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{8c}}\left(\upeta +{\text{C}}\right)\right)+{\text{coth}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{8c}}\left(\upeta +{\text{C}}\right)\right).$$
    (51)

  • The trigonometric solutions of Eq. (1) are stated as:

(i) For \({\updelta }_{0}=0\), \({\updelta }_{1}<0, {\updelta }_{2}\ne 0\) and \(\updelta <1\), we have

$${{\text{U}}}_{11}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{2m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{sec}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
(52)
$${{\text{U}}}_{12}^{\pm }\left(\upeta \right)=\pm \sqrt{-\frac{2m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{csc}}\left(\sqrt{-\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
(53)

(ii) For \({\updelta }_{0}=\frac{{{\updelta }_{1}}^{2}}{4{\updelta }_{2}}\), \({\updelta }_{1}>0, {\updelta }_{2}>0\) and \(\delta >1\), we have

$${{\text{U}}}_{13}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{tan}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{2c}}\left(\upeta +{\text{C}}\right)\right),$$
(54)
$${{\text{U}}}_{14}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}{\text{cot}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{2c}}\left(\upeta +{\text{C}}\right)\right),$$
(55)
$${{\text{U}}}_{15}^{\pm }(\upeta )=\pm \sqrt{\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}({\text{tan}}\left(\sqrt{2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{sec}}\left(\sqrt{2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
(56)
$${{\text{U}}}_{16}^{\pm }(\upeta )=\pm \sqrt{\frac{m\omega \left(-1+\delta \right)}{c\delta \epsilon {n}^{2}{a}_{1}^{2}}}({\text{cot}}\left(\sqrt{2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right)\pm {\text{csc}}\left(\sqrt{2\frac{\omega \left(-1+\delta \right)}{c}}\left(\upeta +{\text{C}}\right)\right),$$
(57)
$${{\text{U}}}_{17}^{\pm }\left(\upeta \right)=\pm \sqrt{\frac{m\omega \left(-1+\delta \right)}{4c\delta \epsilon {n}^{2}{a}_{1}^{2}}}\left({\text{tan}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{8c}}\left(\upeta +{\text{C}}\right)\right)-{\text{cot}}\left(\sqrt{\frac{\omega \left(-1+\delta \right)}{8c}}\left(\upeta +{\text{C}}\right)\right)\right).$$
(58)

Therefore, the corresponding solution to Eq. (26) can be obtained by using the transformations \(q\left(x,t\right)=U\left(\eta \right){e}^{i\xi \left(x,t\right)}, v\left(x,t\right)=G\left(\eta \right), r=\epsilon \overline{q }\) \((\epsilon =\pm 1)\), with \(G\left(\eta \right)=-\frac{c\epsilon {n}^{2}}{m}{U}^{2}\left(\eta \right).\)

4 The results and discussions

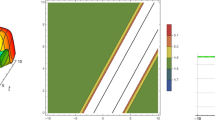
This section provides the result discussions on the derived solutions for the system of S-IIAE using IMSSEM. The derived solutions are rational, exponential, trigonometric and hyperbolic function solutions. for example, the solution Eq. (42) is a rational function solution, Eqs. (43) and (44) correspond to the exponential function solutions, Eqs. (45) to (51) represent the hyperbolic function solutions, and Eqs. (52) to (58) are trigonometric functions solutions. Moreover, Fig. 1 gives the graphical representations for some of the derived solitary wave solutions to Fig. 6. All the shapes in Figs. 1, 2, 3, 4, 5 and 6 are recovered using \(\upepsilon =1,\updelta =-0.5,\upomega =1,\mathrm{ a}=0,\upeta =1, {{\text{a}}}_{1}=2, c=1, k=1, C=1, y=0,\) and \(m=1\). Moreover, all the 2D plots are recovered at \(t=0.2\). It is important to note that for the sake of demonstration of some of the solitary wave structures in Figs. 1, 2, 3, 4, 5 and 6, we plotted the solutions \({\text{U}}(\upeta )\) and \({\text{G}}(\upeta )\) from the derived solutions Eqs. (42) to (58). Among the important recovered structure are the dark, bright, kink and multiple wave solitons. For example, Figs. 1, 2, 5b and 6b give the multiple wave solitons, Figs. 3a and 5a represent the kink soliton waves. Figures 3b and 5b represent the bright soliton whereas Figs. 4a and 6a represent the dark solitons.

Fig. 1
figure 1

The multiple soliton waves in 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{U}}}_{2}^{\pm }(\upeta ).\)

Full size image
Fig. 2
figure 2

The multiple soliton waves in 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{G}}}_{2}^{\pm }(\upeta ).\)

Full size image
Fig. 3
figure 3

a The kink soliton and b bright soliton in 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{U}}}_{10}^{\pm }(\upeta ).\)

Full size image
Fig. 4
figure 4

a The dark soliton, and b multiple wave soliton in 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{G}}}_{10}^{\pm }(\upeta ).\)

Full size image
Fig. 5
figure 5

a The anti-kink soliton and b bright soliton 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{U}}}_{15}^{\pm }(\upeta ).\)

Full size image
Fig. 6
figure 6

a The dark soliton, and b multiple wave soliton in 3D and 2D plots for the absolute, real and imaginary parts of \({{\text{G}}}_{15}^{\pm }(\upeta ).\)

Full size image

5 Conclusion

In this research paper, we presented a novel approach especially for obtaining the exact solutions to the S-IIAE, by employing the IMSSEM. The study successfully derived a family of exact solutions for these equations. These solutions provide valuable insights into the dynamics and behavior of S-IIAE and can be utilized in various fields of physics, and applied mathematics. The behavior of the solutions for the direct study is presented in two and three-dimensional graphs. The proposed technique offers a promising avenue for tackling other complex nonlinear equations and warrants further exploration in future research. Future studies of S-IIAE can be considered on the analytical, semi-analytical and numerical solutions to investigate a variety of interesting results related to the indicated model, including the modulation instability and consistency of the solutions, their physical feasibility, and lie symmetry analysis.