Let \(\alpha\) be quasi optical curve in the ordinary space. Then, quasi field equations are
$$\begin{aligned} \nabla _{s}\textbf{t}_{\textbf{q}}= & {} \kappa _{1}\textbf{n}_{\textbf{q} }+\kappa _{2}\textbf{b}_{\textbf{q}}, \\ \nabla _{s}\textbf{n}_{\textbf{q}}= & {} -\kappa _{1}\textbf{t}_{\textbf{q} }+\kappa _{3}\textbf{b}_{\textbf{q}}, \\ \nabla _{s}\textbf{b}_{\textbf{q}}= & {} -\kappa _{2}\textbf{t}_{\textbf{q} }-\kappa _{3}\textbf{n}_{\textbf{q}}, \end{aligned}$$
where \(\kappa _{1},\kappa _{1},\kappa _{1}\) are quasi curvatures.
Lorentz fields are given by
$$\begin{aligned} \phi (\textbf{t}_{\textbf{q}})= & {} \kappa _{1}\textbf{n}_{\textbf{q}}+\chi \textbf{b}_{\textbf{q}}, \\ \phi (\textbf{n}_{\textbf{q}})= & {} -\kappa _{1}\textbf{t}_{\textbf{q}}+\kappa _{3}\textbf{b}_{\textbf{q}}, \\ \phi (\textbf{b}_{\textbf{q}})= & {} -\chi \textbf{t}_{\textbf{q}}-\kappa _{3} \textbf{n}_{\textbf{q}}, \end{aligned}$$
where \(\chi =\phi (\textbf{t}_{\textbf{q}})\cdot \textbf{b}_{ \textbf{q}}.\) Electromagnetic fields are
$$\begin{aligned} \mathcal {B}= & {} \kappa _{3}\textbf{t}_{\textbf{q}}-\chi \textbf{n}_{\textbf{q} }+\kappa _{1}\textbf{b}_{\textbf{q}}, \\ \mathcal {E}= & {} -\frac{m}{e}\textbf{t}_{\textbf{q}}+\kappa _{1}(1-\frac{m}{e}) \textbf{n}_{\textbf{q}}\mathcal {+(}\chi -\frac{m}{e}\kappa _{2})\textbf{b}_{ \textbf{q}}, \end{aligned}$$
where mass m and electric charge e of charged particle \(\alpha\).
Putting
$$\begin{aligned} \frac{\partial \alpha }{\partial t}=\varepsilon _{1}\textbf{t}_{\textbf{q} }+\varepsilon _{2}\textbf{n}_{\textbf{q}}+\varepsilon _{3}\textbf{b}_{ \textbf{q}}, \end{aligned}$$
where \(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}\) are smooth potential.
\(\mathbf {\spadesuit }\) Flows quasi frame are
$$\begin{aligned} \nabla _{t}\textbf{t}_{\textbf{q}}= & {} \left( \varepsilon _{1}\kappa _{1} \mathbf {+}\dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\right) \textbf{n}_{\textbf{q}}+\left( \kappa _{2}\varepsilon _{1}+ \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}\right) \textbf{b}_{\textbf{q}}, \\ \nabla _{t}\textbf{n}_{\textbf{q}}= & {} -\left( \kappa _{1}\varepsilon _{1} \mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+}\dfrac{\partial \varepsilon _{2}}{\partial s}\right) \textbf{t}_{\textbf{q}}+\vartheta \textbf{b}_{\textbf{q}}, \\ \nabla _{t}\textbf{b}_{\textbf{q}}= & {} -\left( \kappa _{2}\varepsilon _{1}+\dfrac{ \partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}\right) \textbf{t} _{\textbf{q}}-\vartheta \textbf{n}_{\textbf{q}}, \end{aligned}$$
where \(\vartheta\) is evolution potential.
\(\divideontimes\) Optical normalization quasi operators are
$$\begin{aligned} \mathcal {N}\phi (\textbf{t}_{\textbf{q}})= & {} \left( \int _{\alpha }(\kappa _{1}^{2}+\kappa _{2}\chi )d\sigma \right) \textbf{t}_{q}+\kappa _{1}\textbf{n}_{ \textbf{q}}+\chi \textbf{b}_{\textbf{q}}, \\ \mathcal {N}\phi (\textbf{n}_{\textbf{q}})= & {} \left( \int _{\alpha }\kappa _{2}\kappa _{3}d\sigma \right) \textbf{t}_{q}+\kappa _{3}\textbf{b}_{\textbf{q}}, \\ \mathcal {N}\phi (\textbf{b}_{\textbf{q}})= & {} -\left( \int _{\alpha }\kappa _{1}\kappa _{3}d\sigma \right) \textbf{t}_{q}-\kappa _{3}\textbf{n}_{\textbf{q}}, \end{aligned}$$
and
$$\begin{aligned} \mathcal{N}\mathcal{B}= & {} \left( \int _{\alpha }(-\chi \kappa _{1}+\kappa _{2}\kappa _{1})d\sigma \right) \textbf{t}_{q}-\chi \textbf{n}_{\textbf{q}}+\kappa _{1}\textbf{ b}_{\textbf{q}}, \\ \mathcal{N}\mathcal{E}= & {} \left( \int _{\alpha }\left( \kappa _{1}^{2}\left( 1-\frac{m}{e}\right) +\left( \chi -\frac{m}{e}\kappa _{2}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\kappa _{1}\left( 1-\frac{m}{e}\right) \textbf{n}_{\textbf{q}}+\left( \chi -\frac{m }{e}\kappa _{2}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
Also, we get
$$\begin{aligned} \nabla _{s}\phi (\textbf{t}_{\textbf{q}})= & {} -(\kappa _{1}^{2}+\kappa _{2}\chi )\textbf{t}_{\textbf{q}}+(\dfrac{\partial }{\partial s}\kappa _{1}-\kappa _{3}\chi )\textbf{n}_{\textbf{q}}+\left( \dfrac{\partial }{\partial s} \chi +\kappa _{1}\kappa _{3}\right) \textbf{b}_{\textbf{q}}, \\ \nabla _{s}\phi (\textbf{n}_{\textbf{q}})= & {} -(\dfrac{\partial }{\partial s} \kappa _{1}+\kappa _{3}\kappa _{2})\textbf{t}_{\textbf{q}}-(\kappa _{1}^{2}+\kappa _{3}^{2})\textbf{n}_{\textbf{q}}+\left( \dfrac{\partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \textbf{b}_{\textbf{q}}, \\ \nabla _{s}\phi (\textbf{b}_{\textbf{q}})= & {} (\kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi )\textbf{t}_{\textbf{q}}-(\chi \kappa _{1}+\dfrac{ \partial }{\partial s}\kappa _{3})\textbf{n}_{\textbf{q}}-\left( \chi \kappa _{2}+\kappa _{3}^{2}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
and
$$\begin{aligned} \textbf{t}_{q}\times \nabla _{s}\phi (\textbf{t}_{\textbf{q}})= & {} \left( \dfrac{ \partial }{\partial s}\kappa _{1}-\kappa _{3}\chi \right) \textbf{b}_{\textbf{q}}-\left( \dfrac{\partial }{\partial s}\chi +\kappa _{1}\kappa _{3}\right) \textbf{n}_{ \textbf{q}}, \\ \textbf{t}_{q}\times \nabla _{s}\phi (\textbf{n}_{\textbf{q}})= & {} -\left( \kappa _{1}^{2}+\kappa _{3}^{2}\right) \textbf{b}_{\textbf{q}}-\left( \dfrac{\partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \textbf{n}_{\textbf{q}}, \\ \textbf{t}_{q}\times \nabla _{s}\phi (\textbf{b}_{\textbf{q}})= & {} -\left( \chi \kappa _{1}+\dfrac{\partial }{\partial s}\kappa _{3}\right) \textbf{b}_{\textbf{q} }+(\chi \kappa _{2}+\kappa _{3}^{2})\textbf{n}_{\textbf{q}}. \end{aligned}$$
\(\divideontimes\) Optical normalization quasi operators of above product fields are
$$\begin{aligned} \mathcal {N(}\textbf{t}_{q}\times \nabla _{s}\phi (\textbf{t}_{\textbf{q}}))= & {} \left( \int _{\alpha }\left( -\left( \dfrac{\partial }{\partial s}\chi +\kappa _{1}\kappa _{3}\right) \kappa _{1}+\left( \dfrac{\partial }{\partial s}\kappa _{1}-\kappa _{3}\chi \right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} -\left( \dfrac{\partial }{\partial s}\chi +\kappa _{1}\kappa _{3}\right) \textbf{n}_{ \textbf{q}}+\left( \dfrac{\partial }{\partial s}\kappa _{1}-\kappa _{3}\chi \right) \textbf{b}_{\textbf{q}}, \\ \mathcal {N(}\textbf{t}_{q}\times \nabla _{s}\phi (\textbf{n}_{\textbf{q}}))= & {} \left( \int _{\alpha }\left( -\left( \dfrac{\partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \kappa _{1}-\left( \kappa _{1}^{2}+\kappa _{3}^{2}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} -\left( \dfrac{\partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \textbf{n }_{\textbf{q}}-(\kappa _{1}^{2}+\kappa _{3}^{2})\textbf{b}_{\textbf{q}}, \\ \mathcal {N(}\textbf{t}_{q}\times \nabla _{s}\phi (\textbf{b}_{\textbf{q}}))= & {} \left( \int _{\alpha }\left( \left( \chi \kappa _{2}+\kappa _{3}^{2}\right) \kappa _{1}-\left( \chi \kappa _{1}+\dfrac{\partial }{\partial s}\kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\left( \chi \kappa _{2}+\kappa _{3}^{2}\right) \textbf{n}_{\textbf{q}}-\left( \chi \kappa _{1}+\dfrac{\partial }{\partial s}\kappa _{3}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
Then
$$\begin{aligned} \mathcal {R(}\phi (\textbf{t}_{\textbf{q}}))= & {} -\left( \int _{\alpha }\left( -\left( \dfrac{ \partial }{\partial s}\chi +\kappa _{1}\kappa _{3}\right) \kappa _{1}+\left( \dfrac{ \partial }{\partial s}\kappa _{1}-\kappa _{3}\chi \right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\left( \dfrac{\partial }{\partial s}\chi +\kappa _{1}\kappa _{3}\right) \textbf{n}_{ \textbf{q}}-\left( \dfrac{\partial }{\partial s}\kappa _{1}-\kappa _{3}\chi \right) \textbf{b}_{\textbf{q}}, \\ \mathcal {R(}\phi (\textbf{n}_{\textbf{q}}))= & {} -\left( \int _{\alpha }\left( -\left( \dfrac{ \partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \kappa _{1}-\left( \kappa _{1}^{2}+\kappa _{3}^{2}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\left( \dfrac{\partial }{\partial s}\kappa _{3}-\kappa _{1}\kappa _{2}\right) \textbf{n }_{\textbf{q}}+\left( \kappa _{1}^{2}+\kappa _{3}^{2}\right) \textbf{b}_{\textbf{q}}, \\ \mathcal {R(}\phi (\textbf{b}_{\textbf{q}}))= & {} -\left( \int _{\alpha }\left( \left( \chi \kappa _{2}+\kappa _{3}^{2}\right) \kappa _{1}-\left( \chi \kappa _{1}+\dfrac{\partial }{ \partial s}\kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} -\left( \chi \kappa _{2}+\kappa _{3}^{2}\right) \textbf{n}_{\textbf{q}}\\{} & {} +\left( \chi \kappa _{1}+\dfrac{\partial }{\partial s}\kappa _{3}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
For electromagnetic fields, we get
$$\begin{aligned} \nabla _{s}\mathcal {B}= & {} \left( \dfrac{\partial }{\partial s}\kappa _{3}+\chi \kappa _{1}-\kappa _{2}\kappa _{1}\right) \textbf{t}_{\textbf{q}}+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \textbf{n}_{\textbf{q}} \\{} & {} +\left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \textbf{b}_{\textbf{q}} \\ \nabla _{s}\mathcal {E}= & {} -\left( \kappa _{1}^{2}\left( 1-\frac{m}{e}\right) +\kappa _{2} \left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \textbf{t}_{\textbf{q}}+\left( \dfrac{ \partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e} \right. \\{} & {} -\left. \kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \textbf{n}_{\textbf{q} }+\left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \textbf{b} _{\textbf{q}} \end{aligned}$$
and
$$\begin{aligned} \textbf{t}_{q}\times \nabla _{s}\mathcal {B}= & {} -\left( \dfrac{\partial }{\partial s }\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \textbf{n}_{\textbf{q} }+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \textbf{b}_{\textbf{q}}, \\ \textbf{t}_{q}\times \nabla _{s}\mathcal {E}= & {} -\left( \dfrac{\partial }{ \partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e} \right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \textbf{n}_{\textbf{q}} \\{} & {} +\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{ m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \textbf{b}_{ \textbf{q}}. \end{aligned}$$
\(\divideontimes\) Optical normalization quasi operators of above product fields are
$$\begin{aligned} \mathcal {N(}\textbf{t}_{q}\times \nabla _{s}\mathcal {B)}= & {} \left( \int _{\alpha }\left( -\left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}-\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{ \partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} -\left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \textbf{n}_{\textbf{q}}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \textbf{b}_{\textbf{q}} \\ \mathcal {N}(\textbf{t}_{q}\times \nabla _{s}\mathcal {E})= & {} \left( \int _{\alpha }\left( - \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1}+\left( \dfrac{\partial }{\partial s}\kappa _{1}(1 \right. \right. \right. \\{} & {} \left. \left. \left. -\frac{m}{e})-\kappa _{1}\frac{m}{e}-\kappa _{3}(\chi -\frac{m}{e }\kappa _{2})\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}\mathcal {-}\left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1 -\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \textbf{n}_{\textbf{q}}+\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e }-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \textbf{b}_{\textbf{q} }. \end{aligned}$$
\(\divideontimes\) Recursional quasi operators of above product electromagnetic fields are
$$\begin{aligned} \mathcal {R(B})= & {} \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \textbf{n}_{\textbf{q}}-\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \textbf{b}_{\textbf{q}} \\ \mathcal {R(E)}= & {} \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s} \left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}\mathcal {+}\left( \dfrac{\partial }{ \partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e} \right) \kappa _{3} \right. \\{} & {} \left. -\frac{m}{e}\kappa _{2}\right) \textbf{n}_{\textbf{q}}-\left( \dfrac{\partial }{ \partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3} \left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
2.1 Recursional electromagnetical \(\phi (\textbf{t}_{\textbf{q}})\) microscale beam
\(\divideontimes\) Quasi \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\) recursional magnetical \(\phi (\textbf{t}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)microscale beam for quasi normal fiber is
$$\begin{aligned} _{qn}^{\mathcal {B}}\mathcal{R}\mathcal{M}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }={\mathcal {V}}_{b}^{qn}\int \int _{\mathcal {F}} {{\mathcal R}({\mathcal B}}) {\cdot {\mathcal N}} \nabla _{t}\phi \left( \textbf{t}_{\textbf{q}}\right) d{\mathcal {F}}, \end{aligned}$$
where \(\mathcal {V}_{b}^{qn}\) is recursional quasi magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)flexibility potential.
Firstly, normalized operator of flexible \(\phi (\textbf{t}_{\textbf{q}})\) is
$$\begin{aligned} \mathcal {N}\nabla _{t}\phi \left( \textbf{t}_{\textbf{q}}\right)= & {} \left( \int _{\alpha }\left( \left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \kappa _{1}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \\{} & {} +\left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \textbf{n}_{ \textbf{q}}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
where \(\vartheta =\nabla _{t}\textbf{n}_{\textbf{q}}\cdot \textbf{b}_{ \textbf{q}}.\)
\(\divideontimes\) Quasi optical \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\) flexible electroosmotic magnetical \(\phi (\textbf{t}_{\textbf{q}})\) normalized quasi optimistical density is
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \kappa _{1}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}\right) \kappa _{2}\right) d\sigma \right) +\left( -\vartheta \chi \right. \\{} & {} \left. +\dfrac{\partial \kappa _{1}}{\partial t}\right) \left( \dfrac{\partial }{\partial s} \kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) -\left( \kappa _{3}\kappa _{1}- \dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}\right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional normal magnetical \(\phi ( \textbf{t}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q} \textbf{n}_{\textbf{q}}-\)microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{R}\mathcal{M}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }= \mathcal {V}_{b}^{qn}\int \int _{\mathcal {F}}\left( -\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \left( \vartheta \kappa _{1}+ \dfrac{\partial \chi }{\partial t}\right) \right. \\{} & {} \left. +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \kappa _{1}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}\right) \kappa _{2}\right) d\sigma \right) \right. \\{} & {} \left. +\left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \right) d\mathcal {F}, \end{aligned}$$
where \(\mathcal {V}_{b}^{qn}\) is recursional quasi normal magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)flexibility potential.
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{t}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{\mathcal {F}} {{\mathcal R}({\mathcal B})}{ \cdot {\mathcal N}(}\phi \left( \textbf{t}_{\textbf{q}}\right) \times \nabla _{\textbf{t}_{\textbf{q} }}^{2}\phi (\textbf{t}_{\textbf{q}}))d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic flexibility potential.
By quasi model, we get
$$\begin{aligned}{} & {} \mathcal {N}\left( \phi \left( \textbf{t}_{\textbf{q}}\right) \times \nabla _{\textbf{t}_{ \textbf{q}}}\phi \left( \textbf{t}_{\textbf{q}}\right) \right) =\left( \int _{\alpha }\left( -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{1}+\kappa _{1}\left( \kappa _{1}^{2}\right. \right. \right. \\{} & {} \left. \left. \left. \mathbf {+}\kappa _{2}\chi \right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}-\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \textbf{n}_{\textbf{q}}\mathbf {+}\kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
Optical ferromagnetic \(\phi (\textbf{t}_{\textbf{q}})\) magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)optimistic density, we obtain
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}- \dfrac{\partial }{\partial s}\chi \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{1}+\kappa _{1}\left( \kappa _{1}^{2} \mathbf {+}\kappa _{2}\chi \right) \kappa _{2}\right) d\sigma \right) -\chi \left( \kappa _{1}^{2} \right. \\{} & {} \left. \mathbf {+}\kappa _{2}\chi \right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) -\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{1}\left( \kappa _{1}^{2}\mathbf { +}\kappa _{2}\chi \right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi \left( \textbf{t}_{\textbf{q}}\right)\) viscoelastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\left( -\chi \left( \kappa _{1}^{2} \mathbf {+}\kappa _{2}\chi \right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \right. \\{} & {} \left. +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{ \partial s}\kappa _{1} \right. \right. \right. \right. \\{} & {} \left. \left. \left. -\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}- \dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{1} \right. \right. \\{} & {} \left. \left. \left. +\kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{2}\right) d\sigma \right) -\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \right) d {\mathcal {F}}. \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{t}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q} \textbf{n}_{\textbf{q}}-\)microscale beam is
$$\begin{aligned} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) } {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}{{\mathcal R}({\mathcal E}}){ \cdot {\mathcal N}}\nabla _{t}\phi \left( \textbf{t}_{\textbf{q}}\right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
\(\divideontimes\) Optical quasi flexible \(\mathbb {Q}\textbf{n}_{ \textbf{q}}-\)electroosmotic electrical \(\phi (\textbf{t}_{\textbf{q }})\) normalized \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\) optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( \left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t} \right) \kappa _{1}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t} \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s }\left( \chi \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e} \kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{ e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) +\left( -\vartheta \chi +\dfrac{ \partial \kappa _{1}}{\partial t}\right) \left( \dfrac{\partial }{\partial s} \left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3} \right. \\{} & {} \left. -\frac{m}{e}\kappa _{2}\right) -(\dfrac{\partial }{\partial s}\kappa _{1}(1-\frac{m }{e})-\kappa _{1}\frac{m}{e}-\kappa _{3}(\chi -\frac{m}{e}\kappa _{2}))(\vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t}). \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{t}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }= {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \dfrac{\partial }{ \partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3} \left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \left( \vartheta \kappa _{1}+\dfrac{ \partial \chi }{\partial t}\right) \right. \\{} & {} \left. +\left( \int _{\alpha }\left( \left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t} \right) \kappa _{1}+\left( \vartheta \kappa _{1}+\dfrac{\partial \chi }{\partial t} \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s }\left( \chi -\frac{m}{e}\kappa _{2}\right) \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. +\kappa _{1}(1-\frac{m}{e})\kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e }-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \right. \\{} & {} \left. +\left( -\vartheta \chi +\dfrac{\partial \kappa _{1}}{\partial t}\right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
Normalized quasi ferromagnetic \(\phi (\textbf{t}_{\textbf{q}})\) electric quasi optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}=-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \\{} & {} +\left( \int _{\alpha }\left( -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{1}+\kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s} \left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1 \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3} \left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \\{} & {} -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{ e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal electrical \(\phi (\textbf{t}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( -\chi \left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) \left( \dfrac{\partial }{ \partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e} \right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \right. \\{} & {} \left. -\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m }{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{1}\left( \kappa _{1}^{2}\mathbf {+}\kappa _{2}\chi \right) +\left( \int _{\alpha }\left( -\chi \left( \kappa _{1}^{2}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. \mathbf {+}\kappa _{2}\chi \right) \kappa _{1}+\kappa _{1}\left( \kappa _{1}^{2}\mathbf {+} \kappa _{2}\chi \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{ \partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1- \frac{m}{e}\right) \kappa _{3} \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{ m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \right) d{\mathcal {F}}. \end{aligned}$$
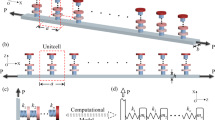
Optical quasi model for ferromagnetical normal recursional electric \(\phi (\textbf{t}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q}\textbf{ n}_{\textbf{q}}-\)microscale beam with optical ring quasi resonator is illustrated in Fig. 1.
2.2 Recursional electromagnetical \(\phi (\textbf{n}_{\textbf{q}})\) microscale beam
\(\divideontimes\) Quasi recursional normal magnetic \(\phi (\textbf{ n}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q}\textbf{n}_{ \textbf{q}}-\)microscale beam is presented
$$\begin{aligned} {^{\mathcal{B}}} {\mathcal{RM}}_{\phi( \textbf{n}_{\textbf{q}})} = {\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\mathcal{R(B}) \cdot \mathcal {N} \nabla_{t}\phi \left( \textbf{n}_{\textbf{q}}\right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)flexibility potential.
Quasi normalize operator for flexible \(\phi (\textbf{n}_{\textbf{q}})\) is
$$\begin{aligned}{} & {} \mathcal {N}\nabla _{t}\phi \left( \textbf{n}_{\textbf{q}}\right) =\left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \kappa _{1}+\left( \dfrac{\partial \kappa _{3}}{\partial t}\right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \textbf{t} _{q}-\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\varepsilon _{3}\kappa _{3} \right. \right. \\{} & {} \left. \left. \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \textbf{n}_{\textbf{q}}+\left( \dfrac{\partial \kappa _{3}}{\partial t} -\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
Magnetic normalize quasi \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{ \partial \varepsilon _{2}}{\partial s}\mathbf {-}\varepsilon _{3}\kappa _{3} \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \kappa _{1}+\left( \dfrac{\partial \kappa _{3}}{\partial t}\right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \kappa _{2}\right) d\sigma \right) -\left( \dfrac{ \partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\varepsilon _{3}\kappa _{3}\right. \right. \\{} & {} \left. \left. \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) -\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{ \partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \end{aligned}$$
\(\divideontimes\) Quasi recursional normal magnetical \(\phi ( \textbf{n}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }= {\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s} \right. \right. \right. \\{} & {} \left. \left. \left. +\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s }\mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. +\vartheta \kappa _{3}\right) \kappa _{1}+\left( \dfrac{\partial \kappa _{3}}{\partial t} -\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \right. \\{} & {} \left. -\left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s} \mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)flexibility potential.
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{n}_{\textbf{q}})\) flexible elastic quasi microscale beam is presented
$$\begin{aligned} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\mathcal {R(B}){ \cdot {\mathcal N}(}\phi (\textbf{n}_{\textbf{q}})\times \nabla _{\textbf{t}_{\textbf{q} }}^{2}\phi (\textbf{n}_{\textbf{q}}))d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic flexibility potential.
Normalized calculations, we get
$$\begin{aligned}{} & {} \mathcal {N}\left( \phi \left( \textbf{n}_{\textbf{q}}\right) \times \nabla _{\textbf{t}_{ \textbf{q}}}^{2}\phi \left( \textbf{n}_{\textbf{q}}\right) \right) =\left( \int _{\alpha }\left( \left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \kappa _{1}\right. \right. \\{} & {} \left. \left. +\left( \kappa _{1}^{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\kappa _{2}\right) d\sigma \right) \textbf{t}_{q}+\left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \textbf{n}_{\textbf{q}}+\left( \kappa _{1}^{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\textbf{b}_{\textbf{q}}. \end{aligned}$$
Ferromagnetic quasi normalized \(\phi (\textbf{n}_{\textbf{q}})\) optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }^{*}=\left( \int _{\alpha }\left( \left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \kappa _{1}+\left( \kappa _{1}^{2} \right. \right. \right. \\{} & {} \left. \left. \left. \mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) +\left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \left( \dfrac{\partial }{\partial s}\kappa _{1}\right. \\{} & {} \left. -\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) -\left( \kappa _{1}^{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s} \chi -\kappa _{3}\kappa _{1}\right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{n}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{t}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\left( \left( \kappa _{1}\left( \dfrac{ \partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{ \partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \left( \dfrac{\partial }{ \partial s}\kappa _{1} \right. \right. \\{} & {} \left. \left. -\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) +\left( \int _{\alpha }\left( \left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \kappa _{1}+\left( \kappa _{1}^{2} \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. \mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) -\left( \kappa _{1}^{2}\mathbf {+} \kappa _{3}^{2}\right) \kappa _{1}\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{ \partial s}\chi -\kappa _{3}\kappa _{1}\right) \right) d{\mathcal {F}}. \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{n}_{\textbf{q}})\) quasi microscale beam is presented
$$\begin{aligned} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }= {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}{{\mathcal R}({\mathcal E}}){ \cdot {\mathcal N}}\nabla _{t}\phi \left( \textbf{n}_{\textbf{q}}\right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
Quasi normalize electric \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)optimistic \(\phi (\textbf{n}_{\textbf{q}})\) density is
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s} \mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \kappa _{1}+\left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. +\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s} \left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1} \right. \right. \\{} & {} \left. \left. -\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m }{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-} \varepsilon _{3}\kappa _{3}\right. \right. \\{} & {} \left. \left. \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) -\left( \dfrac{ \partial }{\partial s}\kappa _{1}\left( 1\right. \right. \\{} & {} \left. \left. -\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e} \kappa _{2}\right) \right) \left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{ \partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{n}_{\textbf{q}})\) flexible elastic quasi microscale beam is presented
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }= {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\ \mathbf {-}\varepsilon _{3}\kappa _{3}\mathbf {+ }\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right. \right. \\{} & {} \left. \left. +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) +\left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-} \varepsilon _{3}\kappa _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \kappa _{1}+\vartheta \kappa _{3}\right) \kappa _{1}\right. \right. \right. \\{} & {} \left. \left. \left. +\left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{ \partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1- \frac{m}{e}\right) \kappa _{3}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{ m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \right. \\{} & {} \left. -\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m }{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \left( \dfrac{\partial \kappa _{3}}{\partial t}-\kappa _{1}\left( \dfrac{\partial \varepsilon _{3}}{ \partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right) \right) d {\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
Electric quasi optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }^{*}=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{ e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m }{e}\right) \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \kappa _{1}\right. \right. \\{} & {} \left. \left. +\left( \kappa _{1}^{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\kappa _{2}\right) d\sigma \right) +\left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e} \kappa _{2}\right) \right. \\{} & {} \left. +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) -\left( \dfrac{ \partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e} -\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \left( \kappa _{1}^{2}\mathbf { +}\kappa _{3}^{2}\right) \kappa _{1}. \end{aligned}$$
\(\divideontimes\) Optical ferromagnetical recursional electrical \(\phi (\textbf{n}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q} \textbf{n}_{\textbf{q}}-\)microscale beam is constructed
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{n}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( \left( \kappa _{1}\left( \dfrac{\partial \kappa _{3}}{\partial s}-\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s}+\kappa _{2}\kappa _{3}\right) \right) \left( \dfrac{\partial }{\partial s}\left( \chi \right. \right. \right. \\{} & {} \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e} \kappa _{2}\right) +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s} \left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3} \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{ m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \kappa _{1}\left( \dfrac{ \partial \kappa _{3}}{\partial s} \right. \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. \left. -\kappa _{2}\kappa _{1}\right) +\kappa _{3}\left( \dfrac{\partial \kappa _{1}}{\partial s} +\kappa _{2}\kappa _{3}\right) \right) \kappa _{1}+\left( \kappa _{1}^{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\kappa _{2}\right) d\sigma \right) \right. \\{} & {} \left. -\left( \dfrac{\partial }{\partial s}\kappa _{1}(1-\frac{m}{e})-\kappa _{1}\frac{m }{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \left( \kappa _{1}^{2} \mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}\right) d{\mathcal {F}}. \end{aligned}$$
Optical quasi model for ferromagnetic normal recursional electric \(\phi (\textbf{n}_{\textbf{q}})\) flexible elastic quasi normal \(\mathbb {Q} \textbf{n}_{\textbf{q}}-\)microscale beam with optical ring quasi resonator is illustrated in Fig. 2.
2.3 Recursional electromagnetical \(\phi (\textbf{b}_{\textbf{q}})\) microscale beam
Quasi normalize operator for flexible \(\phi (\textbf{b}_{\textbf{q}})\) is
$$\begin{aligned}{} & {} \mathcal {N}\nabla _{t}\phi \left( \textbf{b}_{\textbf{q}}\right) =\left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{ \partial \kappa _{3}}{\partial t}\right) \kappa _{1}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) \right. \right. \right. \\{} & {} \left. \left. \left. +\vartheta \kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}-\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3} \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{\partial \kappa _{3}}{ \partial t}\right) \textbf{n}_{\textbf{q}}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{ \partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \textbf{b}_{\textbf{q}}. \end{aligned}$$
Normalized electrical optimistic \(\phi (\textbf{b}_{\textbf{q}})\) density is
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi \right. \right. \right. \\{} & {} \left. \left. \left. -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{ \partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{ \partial \kappa _{3}}{\partial t}\right) \kappa _{1}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s} \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. +\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}-\left( \left( \dfrac{\partial \varepsilon _{2}}{ \partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{\partial \kappa _{3}}{\partial t}\right) \left( \dfrac{ \partial \kappa _{1}}{\partial s} \right. \\{} & {} \left. -\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) +\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{ \partial s}\chi -\kappa _{3}\kappa _{1}\right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{b}_{\textbf{q}})\) flexible elastic quasi microscale beam is constructed
$$\begin{aligned}{} & {} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }= {\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\left( \left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \right. \\{} & {} \left. +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{ \partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s} \right. \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. \left. \mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{\partial \kappa _{3}}{\partial t}\right) \kappa _{1}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q}\right. \\{} & {} \left. -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{ \partial \kappa _{3}}{\partial t}\right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic \(\mathbb {Q}\textbf{n}_{\textbf{q}}-\)flexibility potential.
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{b}_{\textbf{q}})\) flexible elastic quasi \(\mathbb {Q }\textbf{n}_{\textbf{q}}-\)microscale beam is defined
$$\begin{aligned} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\mathcal {R(B}){ \cdot {\mathcal N}(}\phi (\textbf{b}_{\textbf{q}})\times \nabla _{\textbf{t}_{\textbf{q} }}^{2}\phi (\textbf{b}_{\textbf{q}}))d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{b}^{qn}\) is recursional quasi normal magnetic flexibility potential.
Quasi normalized operator is
$$\begin{aligned}{} & {} \mathcal {N}\left. \left( \phi \left( \textbf{b}_{\textbf{q}}\right) \times \nabla _{\textbf{t}_{ \textbf{q}}}\phi \left( \textbf{b}_{\textbf{q}}\right) \right) =-\left( \int _{\alpha }\left( \chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}+\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \textbf{t} _{q} \\{} & {} -\chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \textbf{n}_{\textbf{q} }+\left( \chi \left( \dfrac{\partial \kappa _{3}}{\partial s}+\chi \kappa _{1}\right) -\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \textbf{b}_{ \textbf{q}}. \end{aligned}$$
Since
$$\begin{aligned}{} & {} ^{\mathcal {B}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }^{*}=-\left( \int _{\alpha }\left( \chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}+\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \kappa _{2}\right) d\sigma )\left( \int _{\alpha }\left( \left( \dfrac{\partial }{ \partial s}\kappa _{1}-\chi \kappa _{3} \right. \right. \right. \\{} & {} \left. \left. \left. +\kappa _{3}\kappa _{2}\right) \kappa _{1}+\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) -\chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3} \right. \\{} & {} \left. +\kappa _{3}\kappa _{2}\right) -\left( \chi \left( \dfrac{\partial \kappa _{3}}{\partial s} +\chi \kappa _{1}\right) -\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \left( \kappa _{3}\kappa _{1}-\dfrac{\partial \chi }{\partial s} -\kappa _{3}\kappa _{1}\right) \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal magnetical \(\phi (\textbf{b}_{\textbf{q}})\) flexible elastic quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {B}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{b}^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \chi \left( \dfrac{ \partial \kappa _{3}}{\partial s}+\chi \kappa _{1}\right) -\kappa _{3}\left( \dfrac{ \partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \left( \kappa _{3}\kappa _{1}- \dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \right. \\{} & {} \left. -\left( \int _{\alpha }\left( \chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}+\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s} \kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \kappa _{1}\right. \right. \\{} & {} \left. \left. \left. +\left( \kappa _{3}\kappa _{1}-\dfrac{\partial }{\partial s}\chi -\kappa _{3}\kappa _{1}\right) \kappa _{2}\right) d\sigma \right) -\chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \left( \dfrac{\partial }{\partial s}\kappa _{1}-\chi \kappa _{3}+\kappa _{3}\kappa _{2}\right) \right) d{\mathcal {F}}, \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{b}_{\textbf{q}})\) quasi microscale beam is defined
$$\begin{aligned} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }= {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\mathcal {R(E)}{ \cdot {\mathcal N}}\nabla _{t}\phi \left( \textbf{b}_{\textbf{q}}\right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
Quasi electric optimistic density is
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }=\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\left( \chi - \frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e} \kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1 \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e} \kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3} \mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi \right. \right. \right. \\{} & {} \left. \left. \left. +\dfrac{\partial \kappa _{3}}{\partial t}\right) \kappa _{1}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \kappa _{2}\right) d\sigma \right) -\left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right. \\{} & {} \left. +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \left( \left( \dfrac{ \partial \varepsilon _{2}}{\partial s}\mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{ \partial \kappa _{3}}{\partial t}\right) +\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1 \right. \right. \\{} & {} \left. \left. -\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e} \kappa _{2}\right) \right) \left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s} +\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \end{aligned}$$
\(\divideontimes\) Quasi recursional normal electrical \(\phi ( \textbf{b}_{\textbf{q}})\) viscoelastic microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }= {\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \dfrac{ \partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1- \frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s} \right. \right. \right. \\{} & {} \left. \left. \left. \mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{\partial \kappa _{3}}{\partial t}\right) +\left( \int _{\alpha }\left( \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}\right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{ m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( -\left( \left( \dfrac{\partial \varepsilon _{2}}{\partial s}\right. \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. \left. \mathbf {-}\kappa _{3}\varepsilon _{3}\mathbf {+}\kappa _{1}\varepsilon _{1}\right) \chi +\dfrac{\partial \kappa _{3}}{\partial t}\right) \kappa _{1}-\left( \chi \left( \dfrac{\partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \kappa _{2}\right) d\sigma \right) \textbf{t}_{q} \right. \\{} & {} \left. +\left( \dfrac{\partial }{\partial s}\kappa _{1}(1-\frac{m}{e})-\kappa _{1}\frac{m }{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \left( \chi \left( \dfrac{ \partial \varepsilon _{3}}{\partial s}+\varepsilon _{2}\kappa _{3}+\kappa _{2}\varepsilon _{1}\right) +\vartheta \kappa _{3}\right) \right) d{\mathcal {F}}, \end{aligned}$$
where \({\mathcal {V}}_{\varepsilon }^{qn}\) is recursional quasi normal magnetic electric potential.
Since
$$\begin{aligned}{} & {} ^{\mathcal {E}}\mathcal{N}\mathcal{D}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }^{*}=-\left( \int _{\alpha }\left( \chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}+\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \kappa _{2}\right) d\sigma )\left( \int _{\alpha }\left( \left( \dfrac{ \partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right. \right. \right. \\{} & {} \left. \left. \left. +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e }-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \\{} & {} -\chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{ e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \\{} & {} -\left( \chi \left( \dfrac{\partial \kappa _{3}}{\partial s}+\chi \kappa _{1}\right) -\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \left( \dfrac{ \partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) -\kappa _{1}\frac{m}{e} -\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) . \end{aligned}$$
\(\divideontimes\) Quasi recursional ferromagnetic normal electrical \(\phi (\textbf{b}_{\textbf{q}})\) quasi microscale beam is
$$\begin{aligned}{} & {} ^{\mathcal {E}}{\mathcal{R}}{\mathcal{M}}_{\phi \left( \textbf{b}_{\textbf{q}}\right) }^{*}={\mathcal {V}}_{\varepsilon }^{qn}\int \int _{{\mathcal {F}}}\left( -\left( \chi \left( \dfrac{\partial \kappa _{3}}{\partial s}+\chi \kappa _{1}\right) -\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{e}\right) \right. \right. \\{} & {} \left. \left. \left. -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) -\left( \int _{\alpha }\left( \chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \kappa _{1}+\kappa _{3}\left( \dfrac{\partial \chi }{\partial s}-\kappa _{3}\kappa _{1}\right) \right) \kappa _{2}\right) d\sigma \right) \left( \int _{\alpha }\left( \left( \dfrac{ \partial }{\partial s}\left( \chi \right. \right. \right. \right. \right. \\{} & {} \left. \left. \left. \left. -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{e}\right) \kappa _{3}-\frac{m}{e} \kappa _{2}\right) \kappa _{1}-\left( \dfrac{\partial }{\partial s}\kappa _{1}\left( 1-\frac{m}{ e}\right) -\kappa _{1}\frac{m}{e}-\kappa _{3}\left( \chi -\frac{m}{e}\kappa _{2}\right) \right) \kappa _{2}\right) d\sigma \right) \\{} & {} \left. -\chi \left( \chi \kappa _{2}\mathbf {+}\kappa _{3}^{2}\right) \left( \dfrac{\partial }{\partial s}\left( \chi -\frac{m}{e}\kappa _{2}\right) +\kappa _{1}\left( 1-\frac{m}{ e}\right) \kappa _{3}-\frac{m}{e}\kappa _{2}\right) \right) d{\mathcal {F}}. \end{aligned}$$
Optical quasi model for ferromagnetic normal recursional electric \(\phi (\textbf{b}_{\textbf{q}})\) flexible elastic quasi normal \(\mathbb {Q} \textbf{n}_{\textbf{q}}-\)microscale beam with optical ring quasi resonator is illustrated in Fig. 3.