1 Introduction

Silicon photonics is well known for becoming a leading technology in photonics enabling many devices in sub-wavelength dimensions. Plasmonics, as another promising branch of photonics, is playing a vital role in the realization of many devices and systems beyond the diffraction limit penetrating a wide range of applications such as integrated optics (Maier 2006), communications (Carvalho et al. 2020), high-sensitive sensing (Lee et al. 2021; Azzam et al. 2016), biomedical applications (Gamal et al. 2022), and others (Said et al. 2020). Also, plasmonics shows promise to merge photonics in its big sub-wavelength dimensions to electronics at the nanoscale for optoelectronic chips (Ozbay 2006; Atia et al. 2019). Optical waveguides are the key component of such photonic devices and optoelectronic chips. Both silicon photonics and plasmonics produce high-index contrast structures showing rapid variation in the fields at the interfaces between the silicon or the metal and the surrounding dielectric material. Thus, solving such high field values requires huge computational resources. Therefore, the efficient modeling techniques of such basic components, waveguides, are still a challenge and need much more considerable effort to correctly represent the light-matter interaction at such high-index contrast interfaces (Said et al. 2020).

The accuracy of the finite elements method (FEM) (Koshiba et al. 1982; Obayya et al. 2003; Said et al. 2020) and the finite difference method (FDM) (Lusse et al. 1994; Said et al. 2020) depends on the mesh. Moreover, nonphysical domain truncation techniques to represent infinite or semi-infinite computational domains are required. Perfectly matched layers (PMLs), or variants of transparent boundary conditions, are commonly conventional approaches that cause some numerical problems (Said et al. 2020). However, FEM based on “Master” and “Slave” nodes requires a considerable amount of logic for coupling the related degrees of freedom and does not easily lend itself to developing programs as extensions to existing general-purpose finite-element packages. Moreover, FEM based on “edge elements” of leaving the normal component of the expanded function free to jump across common faces of adjacent elements was shown to be a possible source of spurious surface charges on those faces and led to nonsymmetric systems of linear, algebraic equations and may lead to singularity (Lager and Mur 1998). In addition, these edge elements-based technique is computationally more expensive in terms of both storage requirements and efficiency of iterative solvers. Otherwise, the superposition of an auxiliary continuous function on linear nodal elements results in lower accuracy (Koshiba and Tsuji 2000). All these problems suggest the need for a new type of vectorial expansion function that combines the regularity properties of the nodal elements with the capability of modeling the behavior of the field strength across interfaces.

Alternatively, spectral methods and conformal maps are introduced as semi-analytical methods based on global basis functions to represent semi-infinite or infinite domains, eliminating the need for PMLs, by Laguerre or Hermite basis functions and others (Abdrabou et al. 2016). These techniques achieve faster convergence than conventional mesh-based methods (Said et al. 2020). The pseudo-spectral methods have the ability to properly apply the physical boundary conditions at the interfaces of the discontinuity between metal and dielectric materials, However, only 1D solver based on the pseudo-spectral method (Abdrabou et al. 2016) has been introduced for the accurate modal analysis of dielectric and plasmonic waveguides. Although pseudo-spectral methods have been successfully adopted for the accurate and fast modal analysis of dielectric waveguides (Huang 2010; Huang et al. 2005), they have never been used for 2D full-vectorial modal analysis of plasmonic waveguides or other high-index contrast devices like in silicon photonics.

In this paper, we introduce a 2D full-Vectorial modal analysis based on the rational Chebyshev Pseudo-spectral Method (V-RCPSM) to achieve high accuracy for high-index contrast waveguides with a reduction in computational resources. The efficiency and accuracy of V-RCPSM have been proven through the analysis of a rib waveguide and a plasmonic waveguide, the results have been compared with another full-vectorial modal solver, full vector finite-element method (Obayya et al. 2002). This is the first time, to the best of our knowledge, to develop such a technique, V-RCPSM, for the 2D full-vectorial modal analysis of the challenging high-index contrast waveguides like in silicon photonics and plasmonics. The paper is organized as follows: Sect. 2 presents V-RCPSM, the pseudospectral approach for the full-vectorial modal analysis based on the rational Chebyshev functions with Algebraic maps; Sect. 3 presents two examples to demonstrate the computational performances in convergence and accuracy of the proposed method; Sect. 4 draws the conclusions.

2 Full-vectorial modal analysis based on the rational Chebyshev pseudo-spectral method (V-RCPSM)

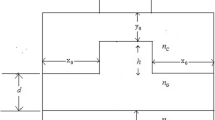
In the pseudo-spectral approach (Huang et al. 2005; Huang 2010) for the modal analysis of the transverse cross-section of the 3D waveguide shown in Fig. 1a, the computational domain, in the x-y plane, is divided into several finite and semi-infinite subdomains with uniform or continuous refractive index profiles as shown in Fig. 1b. To calculate the modes of the waveguide in Fig. 1b, we start from Maxwell’s equations in the frequency domain to obtain the vector wave equation for the magnetic field vector, H, as follows,

$$\begin{aligned} \nabla ^{2} H + k_0^{2} n^2 H + \frac{\nabla n^2}{n^2} (\nabla \times H) = 0, \end{aligned}$$
(1)

where n is the refractive index profile of the waveguide, and k is the wavenumber. For the full-vectorial 2D modal analysis, all electromagnetic fields are assumed to have a z dependence of \(e^{-j \beta z}\), then the continuity of the longitudinal components \(H_z\) and \(E_z\) can incorporate the coupled relations of \(H_x\) and \(H_y\) (Huang et al. 2005; Huang 2010). The two coupled components of the magnetic fields, \(H_x, H_y\), are derived as,

$$\begin{aligned}{} & {} \nabla ^{2} H_x + k_0^{2} (n^2 - n_{eff}^2) H_x - \frac{1}{n^2} \frac{\partial n^2}{\partial y} \frac{\partial H_x}{\partial y} + \frac{1}{n^2} \frac{\partial n^2}{\partial y} \frac{\partial H_y}{\partial x} = 0,\end{aligned}$$
(2)
$$\begin{aligned}{} & {} \nabla ^{2} H_y + k_0^{2} (n^2 - n_{eff}^2) H_y - \frac{1}{n^2} \frac{\partial n^2}{\partial x} \frac{\partial H_y}{\partial x} + \frac{1}{n^2} \frac{\partial n^2}{\partial x} \frac{\partial H_x}{\partial y} = 0, \end{aligned}$$
(3)

where \(n_{eff} = \beta / k_0\) is the effective index of the waveguide mode, and \(\beta \) is the propagation constant.

Fig. 1
figure 1

(a) Schematic for a 3D structure targeted to be analyzed by the 2D modal solver based on the Chebyshev pseudo-spectral method. (b) The 2D cross-section of the waveguide using the spectral method to divide the structure into subdomains: finite and semi-infinite subdomains

Full size image

2.1 Rational Chebyshev functions with algebraic maps

We now determine the appropriate basis functions by expanding the \(H_x\) and \(H_y\) components using the Chebyshev polynomials which are regarded as a better technique for expanding the optical fields in interior subdomains because of their mathematical robustness to non-periodic structures. The proposed method is based on the cardinal Chebyshev function first introduced for 1D modal analysis in Abdrabou et al. (2016), and here we extend the method for the 2D full-vectorial modal analysis (V-RCPSM) to solve the system of Eqs. 2 and 3. The magnetic field components, \(H_x\) and \(H_y\), are obtained by expanding the field in terms of mapped basis functions obtained by composing Chebyshev functions \(S_{i,j}(l)\) by the suitable conformal map for each subdomain (Abdrabou et al. 2016), the field expansion and its grid values in a subdomain at the collocation points take the form

$$\begin{aligned} H_l = \sum _{i=-M}^{N} \sum _{j=-M}^{N} u_{ij}^{(l)} S_{i}(x) S_{j}(y), l=x,y. \end{aligned}$$
(4)

The system of differential Eqs. 2 and 3 is thus converted to an algebraic eigenvalue problem.

$$\begin{aligned} \begin{bmatrix} A_{xx} &{} A_{xy}\\ A_{yx} &{} A_{yy} \end{bmatrix} \begin{Bmatrix} vec(u_{ij}^x)\\ vec(u_{ij}^y) \end{Bmatrix} = \beta ^2 \begin{Bmatrix} vec(u_{ij}^x)\\ vec(u_{ij}^y) \end{Bmatrix} \end{aligned}$$
(5)

where vec(.) is a vectorization operator and the matrices \(A_{xx}, A_{xy}, A_{yx}\) and \(A_{yy}\) are the differentiation matrices of the operators in Eqs. 2 and 3.

We adopt the linear maps (Abdrabou et al. 2016) for the 2D bounded subdomains. We apply the Dirichlet zero boundary condition (BC) at the infinity, x or \(y = \pm \infty \), and extend the algebraic maps (Abdrabou et al. 2016) for the 2D semi-infinite subdomains.

We expand the basis functions for each dimension individually. So, the conformal mappings are still 1D not 2D. For instance, if we suppose that the x direction extends to infinity, we map it with 1D conformal mapping like what is exactly used in Abdrabou et al. (2016). Other finite dimensions can be mapped by linear maps. So, mapping the 2D structures here is not 2D, it is by independent 1D maps, just like the cross product or set product of two 1D maps: conformal and/or linear maps, exactly as the same 1D maps in the previous paper (Abdrabou et al. 2016), but applied in each dimension separately.

Moreover, since we use an H formula, the magnetic field is zero outside. We are applying an infinite domain at the boundary of our physical domain, and then we truncate with Dirichlet BC at infinity. This means no matter what material we are using the field will smoothly decay in the infinite domain mimicking the field leaving our physical domain. The Dirichlet BC here will not cause any reflections since it is placed at infinity. Moreover, for other physical cases at the boundaries, other BC can be easily integrated with our V-RCPSM approach.

Extra details about the mathematical derivation for the full-vectorial H formulation, the conformal mapping, the treatment of boundary conditions, and the meshing strategy could be found in Huang et al. (2005); Huang (2010), and Abdrabou et al. (2016).

3 Numerical and simulation results

3.1 RIB waveguide

In order to show the numerical precision of the proposed method, V-RCPSM, we studied a standard rib waveguide of silicon surrounded by air. The cross-section of the structure is shown in Fig. 2. The rib width, w is \(3.0\,\upmu \hbox {m}\), the rib height, H, and the outer slab depth, D, is such that \(H + D = 1 \mu m\), and the operating wavelength is \(1.15 \mu m\). The refractive indices of the guiding, \(n_g\), and substrate, \(n_s\), regions are 3.44 and 3.4, respectively. Table 1 shows the values of the effective index of the fundamental mode \({H_{11}}^{y}\) as the outer slab depth, D, varies from 0.1 to 0.9 \(\mu m\), these being obtained by using our proposed full vectorial spectral method, V-RCPSM, and other vectorial formulations such as the full vector finite-element method (VFEM) with the results from Obayya et al. (2002). The results using this type of VFEM were calculated with a mesh of 5609 nodes, and the PML boundary condition is employed around the computational window. However, the results produced by our new spectral method, V-RCPSM, were calculated with a few basis functions in each region, 15 in the core and 10 in the cladding layers representing the degree of basis functions n Abdrabou et al. (2016) in each dimension and each domain, which produced a mesh of 3744 nodes (total number of unknowns) without any PML. As seen from Table 1, there is a very close agreement between the results from our new method V-RCPSM and other formulations.

Fig. 2
figure 2

RIB waveguide 2D cross-section

Full size image
Table 1 Effective index (\(n_{eff}\)) for the rib waveguide, shown in the previous figure, for different values of D computed by our new full vectorial spectral method, V-RCPSM, (Present) and full vectorial finite element method (VFEM) reported in Obayya et al. (2002)
Full size table

Figure 3a shows the dominant field component \(H_x\) of the fundamental mode using our method. As clearly shown in Fig. 3b, the peaks of the non-dominant field component, \(H_y\), around the dielectric corners reflect the accurate incorporation of the boundary condition at the interface between the different dielectric media.

Fig. 3
figure 3

(a) The dominant \(H_y\) field distribution and (b) the nondominant \(H_x\) field distribution for \(D = 0.8 \mu m\)

Full size image

Based on these promising results, we studied a 2D plasmonic waveguide and compared the results using FEM in the next example.

3.2 Plasmonic waveguide

To show the accuracy and the efficiency of our developed approach, V-RCPSM, we studied the conventional rectangular structure of the plasmonic waveguide introduced in Heikal et al. (2013) and shown in Fig. 4 with \(w=120nm\) and \(d=1200nm\). In this study, the refractive index of Gold is calculated using Johnson and Christy.

Fig. 4
figure 4

The 2D cross-section of a plasmonic waveguide

Full size image

The following Table 2 shows the convergence study of the effective refractive index (\(n_{eff}\)) of the first TM Mode of the plasmonic waveguide shown in Fig.  2 at \(1.5\mu m\) wavelength.

Table 2 V-RCPSM Convergence of the Effective Refractive Index (\(n_{eff}\)) of the First TM Mode at at \(1.5\mu m\) wavelength
Full size table

We found V-RCPSM converges at [38,38] basis functions for both the finite and semi-finite subdomains in the structure which produced 13689 unknowns leading to a characteristic matrix of size 27378. However, to get the same accuracy by the finite elements method (FEM) using the COMSOL software (Multiphysics 1998), we had to use two thin layers of extra meshing around the interfaces between the metal and the dielectric material to be able to capture the correct rapid field variation there, the width of each layer was 1nm with a maximum element size of 0.2nm and a minimum element size of 0.1nm. This extra meshing produces huge matrices with 740,528 elements and requires computational resources of 34.81 GB RAM during running FEM, COMSOL, for the 2D modal analysis at a single wavelength. Table 3 shows a comparison of the number of elements produced by our code of V-RCPSM vs. FEM, the COMSOL software.

Table 3 The number of elements produced by our code of V-RCPSM vs. FEM, the COMSOL software
Full size table

In general, pseudo-spectral methods have a fast exponential convergence rate as noticed clearly from Table 2. And with a reasonable and small number of basis functions n, we can get very accurate results as shown in Sect. 3. As n increases very much, the convergence curve starts to diverge. That could happen because Chebyshev nodes are concentrated around the boundaries. So, when we use a small number of basis functions, the nodes concentrated at the boundaries will catch and represent the concentrated field there very well which is perfect for plasmonics. However, when we increase the number of basis functions too much, the Chebyshev nodes will be very very close to each other, and hence the linear system will become very ill-conditioned with very large condition number because of the singularity which may lead matrices with dependent/ or zeros rows or columns. Fortunately, the beauty of the pseudo-spectral Chebyshev method can produce very accurate results with just a few basis functions n thanks to its fast convergence rate, no need to increase n leading to ill-conditioned matrices.

In Figs. 5 and 6, we compare \(n_{eff}\) and the propagation length, \(1/{im(\beta )}\), obtained by the spectral method, V-RCPSM, with those obtained by the finite elements method (FEM) using the COMSOL software, respectively. Figure 7a and b show the dominant and minor components of the magnetic field, \(H_{x}\) and \(H_{y}\), respectively, calculated by the spectral method, V-RCPSM, at \(1.5\mu m\) wavelength. The insets of Fig. 7a show the great ability of the Rational Chebyshev functions to correctly capture the rapid variation and the sharp fields of the plasmonic mode at the interface between the metal and the dielectric material.

Fig. 5
figure 5

Real part of \(n_{eff}\) using the spectral method (V-RCPSM) and FEM while changing the wavelength (\(\lambda \))

Full size image
Fig. 6
figure 6

Propagation length shown in log scale and calculated by \(1/{im(\beta )}\) using the spectral method (V-RCPSM) and FEM while changing the wavelength

Full size image
Fig. 7
figure 7

The absolute value of (a) the dominant component of the magnetic field, \(H_{x}\), and (b) the minor component of the magnetic field, \(H_{y}\), calculated by the presented method, V-RCPSM, at \(1.5\mu m\) wavelength. The insets in (a) represent the norm magnetic field plotted at the cut-line of \(x=0.2\mu m\)

Full size image

These results show great agreement between the FEM and the newly developed V-RCPSM. However, our V-RCPSM has achieved a great advantage over the FEM which is reducing the number of elements by 96% while getting the same accuracy as shown in Table 3.

4 Conclusion

The presented approach, V-RCPSM, was applied to the full-vectorial modal analysis of optical waveguides. The efficiency of our approach was demonstrated through the accurate calculation of the plasmonic and guided modes of two waveguides: the rib waveguide and the plasmonic waveguide. The adopted rational Chebyshev pseudo-spectral method captured the correct behavior of the sharp field at the high-index contrast interfaces of such waveguides and moreover yielded very good results with a number of basis functions less than that used by the conventional FEMs.