1 Introduction

The relation between the quasi-probability distributions and quantum correlations remains a significant issue in quantum information theory (Ferrie 2011; McConnell et al. 2015; Arkhipov et al. 2018). Numerous studies have shown that probabilistic quasi-distributions represent a composite measure, in which their positive values represent the classical correlations, whereas the negative values indicate the quantum correlations (Abd-Rabbou et al. 2019; Franco and Penna 2006). These distribution functions are widely used in the computation of quantum correlations within the classical dynamics of a nano-mechanical resonators (Mohamed and Metwally 2018). It also may be used to illuminate the quantum density state within the visualization of phase space (Miquel et al. 2002). In fact, there are three discrete quasi-probabilistic functions that are reconstructed in s-parametrized form: Husimi Q-function (Husimi 1940), Wigner function (Wigner et al. 1997; Chumakov and Klimov 2002) and Glauber-Sudarshan P-function (Sudarshan 1963), with \(\text {s}=-1,0,1\) respectively. What is more, there are different constructions of quasi-probability in accordance with the phase space, such as the radiation field (Moya-Cessa and Knight 1993), the SU(2) angular momentum basis via atomic coherent states (Agarwal 1981; Klimov et al. 2017), the SU(3) Lie algebra (Rowe et al. 1999), and SU(1,1) (Seyfarth et al. 2020). Of particular significance are the negative values of the Wigner function, which not only depict the entanglement and decoherence of the quantum system, but also play an integral role in quantum state tomography (López and Paz 2003; Dahl et al. 2006; Paz et al. 2004).

The Wigner function has been used to investigate the \(2N \times 2N\) discrete phase space of N orthogonal quantum systems, as demonstrated in Gibbons et al. (2004). For different quantum systems, the Wigner function has been widely discussed, including superconducting flux qubits (Reboiro et al. 2015), the accelerated two-qubit state in the presence of noise channels (Abd-Rabbou et al. 2019), tripartite W-state (Abd-Rabbou et al. 2020), GHZ state (Metwally et al. 2019), two non-equivalent resonators (Abgaryan et al. 2021), and a cavity coupled to atomic system (Mavrogordatos 2021). In addition, using Wigner distribution as a measure of quantum correlation for tripartite GHZ and W states have been studied experimentally (Ciampini et al. 2022).

From the perspective of physicists, quantum regimes are highly susceptible to interaction and environmental influence. Therefore, the impact of different environments on quantum correlations has garnered the attention of scientists. Studies have been conducted on the effect of acceleration processes on the entanglement of two-qubit and qubit-qutrit systems (Tian et al. 2012; Metwally 2017, 2019). Additionally, the influence of dephasing noisy environments on the information of two-qubit states has been examined (Yu and Eberly 2003; Karlsson et al. 2016). Recently, various classical noise channels have become an important factor in influencing quantum systems as they approach real-world scenarios (Lo and Chau 1999; Smith et al. 2011). The dynamics of quantum coherence, quantum correlation, and the degree of estimation in the presence of a classical coloured noise channel have been investigated (Khan and Shamirzaie 2020; Metwally and Ebrahim 2020). The quantum skew information and quantum coherence of an accelerated two-qubit system with random telegraph noise have been studied (Abd-Rabbou et al. 2022). The dynamics of entanglement, coherence, and mixedness of a tripartite quantum state have been analysed under power-law and random telegraph noises (Rahman et al. 2022).

In this paper, our aim is to investigate how the Wigner function can indicate entanglement in both Markovian and non-Markovian environments for an accelerated two-qubit system. To achieve this, we will not rely on the single mode approximation and instead transform the Minkowski quantum field modes into the Rindler ones. We will model the effect of the environment using classical random telegraph noise, which can be applied to qubits independently or commonly. As is well known, a density operator’s non-separability is characterized by negative elements in its Wigner function. This negativity can serve as an indicator of entanglement in a two-qubit system. The paper is structured as follows: Sect. 2 presents the physical model of the quantum system and reviews essential tools for accelerating systems. In Sect. 3, we introduce analytical forms of the quasi-probability distributions, namely the Wigner function and quantum concurrence. Section 4 is dedicated to constructing density operators in various scenarios. In Sect. 5, we provide explicit forms of the Wigner function and concurrence as measures of quantum entanglement for the mentioned density operators. We investigate their behaviours for accelerated systems and highlight the effects of noise, acceleration, and discarding the single-mode approximation. Finally, in Sect. 6, we summarize our results.

2 Quantum correlation measures

In this section, we will provide a mathematical review of the concurrence and negative values of the Wigner function, which may serve as a suitable measure of quantum correlations. Let us consider a density operator \({\hat{\varrho }}_{AB}\) with an X-structure. In the computational basis \(\{|00\rangle ,|01\rangle , |10\rangle , |11\rangle \}\), \({\hat{\varrho }}_{AB}\) can be expressed as follows,

$$\begin{aligned} {\hat{\varrho }}_{A B}&= {} \rho _{11}|00\rangle \langle 00| +\rho _{22}|01\rangle \langle 01| +\rho _{33} |10\rangle \langle 10| \\{} & {} \quad +\rho _{44} |11\rangle \langle 11| +(\rho _{14} |00\rangle \langle 11|+ \rho _{23} |01\rangle \langle 10|+ H.C.), \end{aligned}$$
(1)

where \(\rho _{ij}\) are corresponding components in the computational basis.

2.1 Concurrence

As it is widely recognized, the entanglement produced between two particles, denoted as A and B, can be conveniently quantified by means of concurrence. Specifically, the concurrence for the X-structure of a density operator \({\hat{\varrho }}_{AB}\) is defined as follows (Hill and Wootters 1997),

$$\begin{aligned} {\mathcal {C}}=\max [0,|\rho _{14}|-\sqrt{\rho _{22}\rho _{33}},|\rho _{23}|-\sqrt{ \rho _{11}\rho _{44}}]. \end{aligned}$$
(2)

The function \({\mathcal {C}}\) is constrained to the interval [0, 0.5]. When \({\mathcal {C}}=0\), the density operator \({\hat{\varrho }}_{AB}\) is completely separable, whereas it attains maximum entanglement at \({\mathcal {C}}=0.5\).

2.2 Wigner function

To capture non-classical correlations that go beyond entanglement, we will utilize the negative values of the Wigner function. Also, constructing the atomic Wigner probability distribution in Su(2) algebra for a two-qubit system can be provided valuable insights into the nature of non-classical correlations beyond entanglement. For a two-qubit system, the atomic Wigner distribution can be defined as (Agarwal 1981),

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{{\hat{\rho }}}(\theta ,\phi )=2\pi \ \textrm{Tr}&\bigg [{\hat{\varrho }} _{AB}\bigg (\bigotimes _{i\in \{a,b\}}\big ( {\hat{L}}^{(i)}_{0,0} {\textbf{Y}} ^{(i)}_{0,0}(\theta ,\phi )+ \sum _{n=-1}^{1} {\hat{L}}^{(i)}_{1,n} {\textbf{Y}} ^{(i)}_{1,n}(\theta ,\phi )\big )\bigg )\bigg ], \end{aligned} \end{aligned}$$
(3)

here \({\textbf{Y}}^i_{l,m}(\theta ,\phi )\) are the spherical harmonics functions, and \({\hat{L}}^{(i)}_{L,m}\) are the orthogonal irreducible tensor operators in \(\tfrac{1}{2}\)-spin representation are given by:

$$\begin{aligned} \begin{aligned}&{\hat{L}}^{\dagger (i)}_{L,m}=(-1)^m\sqrt{\tfrac{2L+1}{2}}\sum _{i,i^{\prime } =-\tfrac{1}{2}}^{\tfrac{1}{2}} C_{\tfrac{1}{2},i;L,-m}^{\tfrac{1}{2},i^{\prime }}|\tfrac{1}{2},i^{\prime }\rangle \langle \tfrac{1}{2},i| \end{aligned} \end{aligned}$$

where \(C_{\tfrac{1}{2},i;L,-m}^{\tfrac{1}{2},i^{\prime }}\) are the Clebsch-Gordon coefficients. Here \({\hat{L}}^{(i)}_{L,m}\) for our case can be calculated as:

$$\begin{aligned} \begin{aligned}&{\hat{L}}^{i}_{0,0}=\frac{1}{\sqrt{2}}(|0\rangle _i \langle 0|+ |1\rangle _i \langle 1|), \quad {\hat{L}}^{i}_{1,0}=\frac{-1}{\sqrt{2}}(|0\rangle _i \langle 0|- |1\rangle _i \langle 1|),\\&\quad {\hat{L}}^{i}_{1,-1}=|1\rangle _i \langle 0|=-{\hat{L}}^{i^{\dagger }}_{1,1} \end{aligned} \end{aligned}$$

After some straightforward calculation, one can get the Wigner function for the X-state (6) in \(\tfrac{1}{2}\)-spin representation as,

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_{{\hat{\rho }}}(\theta ,\phi )&=2\pi \bigg [ \rho _{11} \varLambda ^2_{11}+ \big (\rho _{22} + \rho _{33} \big ) \varLambda _{11}\varLambda _{00} + \rho _{44} \varLambda ^2_{00}\\&\quad +\big (\rho _{23} \varLambda _{01}\varLambda _{10}+\rho _{14} \varLambda ^2_{01}+H.C. \big ) \bigg ]. \end{aligned} \end{aligned}$$
(4)

where the functions \(\varLambda _{ij}\) are defined by the following spherical harmonics,

$$\begin{aligned} \begin{aligned}&\varLambda _{11}=\frac{1}{\sqrt{2}}({\textbf{Y}}_{0,0}(\theta ,\phi )-{\textbf{Y}} _{1,0}(\theta ,\phi )),\quad \varLambda _{01}=-{\textbf{Y}}_{1,1}(\theta ,\phi ), \\&\varLambda _{10}={\textbf{Y}}_{1,-1}(\theta ,\phi ),\quad \varLambda _{00}=\frac{ 1}{\sqrt{2}}({\textbf{Y}}_{0,0}(\theta ,\phi )+{\textbf{Y}}_{1,0}(\theta ,\phi )). \end{aligned} \end{aligned}$$

Via substituting the spherical harmonics with their values in eq. (4), and take the negative values of the Wigner function, one can obtain the atomic Wigner function of X-structure as,

$$\begin{aligned}{\mathcal {W}}_{{\hat{\rho }}}(\theta ,\phi ,t) & =\min \bigg \{0 , \frac{1}{4} \big [&1+ 2\sqrt{3} \cos \theta (\rho _{11}-\rho _{44})+3 \cos ^2 \theta (\rho _{11}-\rho _{22}-\rho _{33}+\rho _{44}) \\&\quad + 6 \sin ^2 \theta (\rho _{23} +\rho _{14} \cos 2\phi ) \big ] \bigg \}. \end{aligned}$$
(5)

For a two-qubit system, the function \({\mathcal {W}}_{{\hat{\rho }}}(\theta ,\phi ,t) \in [-0.5,0)\), where \({\mathcal {W}}_{{\hat{\rho }}}(\theta ,\phi ,t)=-0.5\) represents a maximally quantum correlation.

3 The basis formalism and the physical models

In this section, we present the fundamental formalism for studying the dynamics of quantum correlations between two observers, Alice and Bob, whose qubits are being subjected to interactions with their respective environments while one or both of them undergo uniform acceleration relative to an inertial coordinate system. We assume that each observer possesses a qubit and that their collective quantum state is initially prepared in a mixed state (\(t=0\) and prior to any quantum information task) with a density matrix of the following form,

$$\begin{aligned} \rho _{AB}(0)=x|\psi \rangle _{AB}\langle \psi |+\frac{(1-x)}{4}\mathbbm {1}, \end{aligned}$$
(6)

where \(A,\ B\) refer to Alice and Bob, respectively, \(|\psi \rangle _{AB}=\frac{ 1}{\sqrt{2}} (|00\rangle +|11\rangle )\), \(\mathbbm {1}\) is identity matrix on a four dimensional Hilbert space and \(x\in [0,1]\) is a measure for the purity of the state. Moreover, we ascribe 0’s and 1’s as the occupation of a fermionic quantum field, with specific energy E and momentum P. As outlined in the Introduction, our objective is to examine classical and quantum correlations among accelerating observers. Therefore, we assume that Bob and/or Alice uniformly accelerate with respect to an inertial observer after sharing the qubits. To investigate scenarios where some observers accelerate, quantization in non-inertial frames becomes necessary. Essentially, this involves quantizing the quantum field in non-inertial frames. It is widely recognized that an observer in a non-inertial frame with constant proper acceleration a perceives the vacuum state of the field as a thermal distribution of field quanta, which is known as the Unruh effect (Unruh 1976). This phenomenon has been extensively studied in the literature. The word line of an observer moving with constant proper acceleration is a two-fold hyperbolic curve, as illustrated in Figure 1 of reference (Bruschi et al. 2010). These hyperbolas are distinct and causally disconnected, located in two separate regions known as the right and left Rindler wedges. The right hyperbolic curve corresponds to the wordline of a real observer, while the left one corresponds to that of a fictitious observer. For accelerating observers, the appropriate basis for quantizing field modes is the Rindler basis (Takagi 1986), rather than the Minkowski or Unruh basis used by inertial observers. If the (anti)particle operators for Minkowski, Rindler and Unruh basis are \((a^{M}_{i},\, b^{M}_{i})\), \((a^{\Sigma }_{i},b^{\Sigma }_{i})\) and \((A^{{\mathcal {R}}}_{i},B^{{\mathcal {R}}}_{i}),\) respectively, where \(\Sigma =I,\, II\) are two wedges of Rindler coordinates and \({\mathcal {R}}=R,\, L\) are two independent basis for Unruh modes, then these modes are related by Bogoliubov transformations as (Bruschi et al. 2010; Takagi 1986):

$$\begin{aligned} a^{M}_{i}= & {} \int _{0}^{\infty }({\alpha ^{I}}^{*}_{ik}a^{I}_{k}+{\beta ^{I}}_{ik}b^{I\dagger }_{k}+ \alpha ^{II*}_{ik} a^{II}_{k}+\beta ^{II}_{ik}a^{II\dagger }_{k})\,\textrm{d}k\end{aligned}$$
(7)
$$\begin{aligned} A_{i}^{R}= & {} \cos {r} a_{i}^{I}+\sin {r} b_{i}^{II\dagger }\end{aligned}$$
(8)
$$\begin{aligned} A_{i}^{L}= & {} \cos {r} a_{i}^{II}-\sin {r} b_{i}^{I\dagger }. \end{aligned}$$
(9)

Here \(\alpha ^{\Sigma }_{ik}\) and \(\beta ^{\Sigma }_{ik}\) are the Bogoliubov coefficients, and the parameter r is related to the acceleration, a through \(\tan r=e^{-\pi \omega c/a}\) where \(\omega\) is the mode frequency which accelerating observer measures and c is the speed of light. The Unruh one particle creation operator is a combination of two contribution of Left and Right Unruh operators:

$$\begin{aligned} A^{U\dagger }_{i}={\textsf {R}}A^{R\dagger }_{i}+{\textsf {L}}A^{L\dagger }_{i} \end{aligned}$$
(10)

In Eq. (10), \({\textsf {R}}\) and \({\textsf {L}}\) are complex numbers satisfying the condition \(|{\textsf {R}}|^2+|{\textsf {L}}|^2=1\). By suitably localized Minkowski modes one can get the desired narrow peak of Unruh modes which are themselves related to single modes of Rindler basis. This setting just corresponds to \({\textsf {R}}=1\) (and hence \({\textsf {L}}=0\)), and is known as single mode approximation (SMA).

The Bogoliubov transformations between filed operators enable us to express the vacuum \(|0_k\rangle ^+_{\mathcal {M}}\) and the first excited state \(|1_k\rangle ^+_{\mathcal {M}}\) of the Dirac filed in Minkowski basis for a specific k-mode in terms of Rindler basis. Theses transformations are:

$$\begin{aligned} |0_k\rangle _{\mathcal {M}}^+&=\cos ^{2}{r} |0_k\rangle _{\text {I}}^+|0_{-k}\rangle _{ \text {II}}^-|0_{-k}\rangle _{\text {I}}^-|0_{k} \rangle _{\text {II}}^+ -\sin {r}\cos {r}|0_k\rangle _{\text {I}}^+|0_{-k}\rangle _{ \text {II}}^-|1_{-k}\rangle _{\text {I}}^-|1_{k} \rangle _{\text {II}}^+ \\&\quad +\sin {r}\cos {r}|1_k\rangle _{\text {I}}^+|1_{-k}\rangle _{ \text {II}}^-|0_{-k}\rangle _{\text {I}}^-|0_{k} \rangle _{\text {II}}^+ -\sin ^{2}{r}|1_k\rangle _{\text {I}}^+|1_{-k}\rangle _{ \text {II}}^-|1_{-k}\rangle _{\text {I}}^-|1_{k} \rangle _{\text {II}}^+ \\ |1_k\rangle _{\mathcal {M}}^+&={\textsf {R}}\left( \cos {r} |1_k\rangle _{\text {I}}^+|0_{-k}\rangle _{ \text {II}}^-|0_{-k}\rangle _{\text {I}}^-|0_{k} \rangle _{\text {II}}^+ -\sin {r} |1_k\rangle _{\text {I}}^+|0_{-k}\rangle _{ \text {II}}^-|1_{-k}\rangle _{\text {I}}^-|1_{k} \rangle _{\text {II}}^+ \right) \\&\quad +{\textsf {L}}\left( \cos {r} |0_k\rangle _{\text {I}}^+|0_{-k}\rangle _{ \text {II}}^-|1_{-k}\rangle _{\text {I}}^-|0_{k} \rangle _{\text {II}}^+ +\sin {r}|1_k\rangle _{\text {I}}^+|1_{-k}\rangle _{ \text {II}}^-|0_{-k}\rangle _{\text {I}}^-|1_{k} \rangle _{\text {II}}^+\right) \end{aligned}$$
(11)

It has been observed that Minkowski states can be represented using two separate Hilbert spaces for two causally disconnected regions, namely I and II, with positive and negative wave modes. The region that is inaccessible to the observer must be traced over. In our analysis, we consider the scenario where either one (Bob’s qubit) or both observers are simultaneously undergoing acceleration. The restriction of the state to the region I of Rindler coordinates results in the loss of prepared coherence, leading to a mixed state.

When only Bob accelerates, the density matrix (6) of bipartite system in the computational basis is expressed as:

$$\begin{aligned} \rho _{A{\bar{B}}}&=\rho _{11}^{\circ } |00\rangle \langle 00| +\rho _{22}^{\circ } |01\rangle \langle 01| +\rho _{33}^{\circ } |10\rangle \langle 10| +\rho _{44}^{\circ } |11\rangle \langle 11| +(\rho _{14}^{\circ } |00\rangle \langle 11|+H.C.), \end{aligned}$$
(12)

where \(\rho _{ij}^{\circ }\) are calculated as:

$$\begin{aligned} \rho _{11}^{\circ }&=\frac{1}{4} \cos (r_b){}^2 ((x-1) \left| {\textsf {R}}\right| ^2+2), \quad \rho _{22}^{\circ }=\frac{1}{4} (2 \sin (r_b){}^2-\cos (r_b){}^2 (x-1) \left| {\textsf {R}}\right| ^2), \\ \rho _{33}^{\circ }&= -\frac{1}{4} \cos (r_b){}^2 ((x+1) \left| {\textsf {R}} \right| ^2-2) , \quad \rho _{44}^{\circ }=\frac{1}{4} (\cos (r_b){}^2 (x+1) \left| {\textsf {R}}\right| ^2 +2 \sin (r_b){}^2) \\ \rho _{14}^{\circ }&=\frac{1}{2} x {\textsf {R}}^* \cos (r_b). \end{aligned}$$
(13)

Here, \(r_b\) denotes the acceleration parameter of Bob, and a asterisk over any parameters denotes the complex conjugation. A bar over each observer slat in this and subsequent subsections, implies that this partner accelerates.

If we assume that Alice’s and Bob’s qubits are accelerated collectively by the parameters of \(r_a\) and \(r_b\), respectively. The resulting density matrix of the bipartite system for the accessible region of each observer in Rindler coordinates can be expressed as follows:

$$\begin{aligned} \rho _{{\bar{A}}{\bar{B}}}= \rho _{11}^{\bullet } |00\rangle \langle 00| +\rho _{22}^{\bullet } |01\rangle \langle 01| +\rho _{33}^{\bullet } |10\rangle \langle 10| +\rho _{44}^{\bullet } |11\rangle \langle 11| +(\rho _{14}^{\bullet } |00\rangle \langle 11|+H.C.), \end{aligned}$$
(14)

where \(\rho _{ij}^{\bullet }\) are calculated as:

$$\begin{aligned} \rho _{11}^{\bullet }&= \frac{1}{4} \cos ^2(r_a) \cos ^2(r_b) \left( (x+1) \left| {\textsf {R}}\right| ^4-4 \left| {\textsf {R}}\right| ^2+4\right) , \\ \rho _{22}^{\bullet }&= -\frac{1}{4} \cos ^2(r_b) \left( (x+1) \left| {\textsf {R}}\right| ^4 \cos ^2(r_a)-2 \left| {\textsf {R}}\right| ^2 \cos (2 r_a)-4 \sin ^2(r_a)\right) , \\ \rho _{33}^{\bullet }&= -\frac{1}{4} \cos ^2(r_a) \left( (x+1) \left| {\textsf {R}}\right| ^4 \cos ^2(r_b)-2 \left| {\textsf {R}}\right| ^2 \cos (2 r_b)-4 \sin ^2(r_b)\right) , \\ \rho _{44}^{\bullet }&= \frac{1}{8} \left( 2 (x+1) \left| {\textsf {R}}\right| ^4 \cos ^2(r_a) \cos ^2(r_b)+2 \left| {\textsf {R}}\right| ^2 (\cos (2 r_a) \cos (2 r_b)+1) \right. \\&\quad \left. +8 \sin ^2(r_a) \sin ^2(r_b)\right) , \\ \rho _{14}^{\bullet }&=\frac{1}{2}\ x \ {\textsf {R}}^{*2} \cos (r_a) \cos (r_b). \end{aligned}$$
(15)

4 Effect of a classical stochastic noise

Now, we assume that both qubits (specifically, the accessible sector of them) are subjected to interaction with their respective environments. As previously mentioned, we define the environment as a classical stochastic field that manifests as random telegraph noise. The Hamiltonian \({\mathcal {H}}(t)\) that characterizes the evolution of a bipartite system interacting with a classical environment over a duration of time t can generally be expressed as,

$$\begin{aligned} {\mathcal {H}}(t) = {\mathcal {H}}_A \otimes \mathbbm {1} + \mathbbm {1} \otimes {\mathcal {H}}_B, \end{aligned}$$
(16)

where \(\mathbbm {1}\) represents the identity matrix on a two dimensional Hilbert space and \({\mathcal {H}}_{A(B)}\) is a single-qubit Hamiltonian describing its dynamics in the presence of noise which can be explicitly written as,

$$\begin{aligned} {\mathcal {H}}_{A(B)} = \epsilon \mathbbm {1}_{A(B)} + g_{A(B)}\chi _{A(B)}(t) \sigma _{x, A(B)}. \end{aligned}$$
(17)

Here, \(\epsilon\) represents the energy of a qubit in the absence of noise. The qubit-environment coupling strength is denoted by \(g_i\) (\(i=A,B\)) and is measured in units of inverse time. Additionally, \(\chi _{A(B)}\) is a characteristic parameter of classical noise that varies randomly. The Pauli spin flip matrix, represented by \(\sigma _x\), reflects the impact of classical noise on the qubit. As such, this Hamiltonian can effectively describe the stochastic time evolution of a quantum system, as a result the qubit’s evolved state to acquire a random phase represented by \(\Phi _i(t)=-\gamma \int _{0}^{t} \chi _i(t') dt'\). In this paper, the parameter \(\chi _i(t)\) represents random telegraph noise (RTN), which randomly fluctuates between ±1 at a rate of \(\gamma\). The second-order statistic of RTN is determined by its auto-correlation function \(K(t,t^{\prime })\), which is given by,

$$\begin{aligned} K(t,t^{\prime })=\left\langle \chi (t)\cdot \chi (t^{\prime })\right\rangle = \text {e}^{-2\gamma t}, \end{aligned}$$
(18)

where \(\langle \cdots \rangle\) denotes the average over all possible realizations of the process \(\chi (t)\). The collective impact of the noise on the evolved state can be determined by averaging the resulting density matrix over \(\Phi _i(t)\) using,

$$\begin{aligned} \rho _{AB}^{channel} (t)=\left\langle U(\chi _A,\chi _B,t) \rho _{AB} U^\dagger (\chi _A,\chi _B,t)\right\rangle , \end{aligned}$$
(19)

here, \(U(\chi _A,\chi _B,t)\) is the unitary operator for time evolution of the Hamiltonian (16) can be expressed as \(U(\chi _A,\chi _B,t)=\exp {[-i\int {\mathcal {H}}(t) \textrm{d}t]}\), where \(\hbar =1\). Depending on the switching rate and coupling strength with the environment, the noise behavior can exhibit either Markovian or non-Markovian characteristics. For \(\Gamma \equiv \gamma /g\gg 1\), which is referred to as the weak coupling regime, a Markovian regime is observed. Conversely, for \(\Gamma \equiv \gamma /g\ll 1\), known as the strong coupling regime, non-Markovian behavior is observed (Bordone et al. 2013). In this study, we consider two cases: (i) both qubits interact with a common environment, where \(\chi _{A}=\chi _{B}=\chi\) and \(g_{A}=g_B=g\); and (ii) each observer interacts independently with their own environment. In the subsequent sections, we present the density matrix of systems that correspond to different scenarios of accelerated states in the presence of classical stochastic noise.

4.1 The accelerated systems are interacted with a stochastic common environment

By utilizing the computational outlined of accelerated systems in Sect. 3, we can derive the density matrix of a system subject to varying acceleration within a shared environment. Furthermore, we will investigate the impact of this noise channel on both entanglement and the negative values of atomic Wigner function.

4.1.1 If Bob’s qubit is only accelerated

Firstly, it is assumed that Bob’s qubit is subjected to acceleration and the system as a whole is compelled to interact with a stochastic common environment. The resulting density matrix of the system at any given time t can be obtained as follows,

$$\begin{aligned} \rho ^{com}_{A{\bar{B}}}(t)&= \rho ^{c1}_{11} |00\rangle \langle 00| +\rho ^{c1}_{22} |01\rangle \langle 01| +\rho ^{c1}_{33} |10\rangle \langle 10| +\rho ^{c1}_{44} |11\rangle \langle 11| \\&\quad + (\rho ^{c1}_{23} |01\rangle \langle 10|+ \rho ^{c1}_{14} |00\rangle \langle 11|+ H.C.), \end{aligned}$$
(20)

with array components as:

$$\begin{aligned} \rho ^{c1}_{11}&=A_1+A_2 \ {\mathcal {D}}_2(\tau ,\gamma )+A_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c1}_{22}=A_4-A_2 \ {\mathcal {D}}_2(\tau ,\gamma )- A_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \\ \rho ^{c1}_{33}&=A_4+A_2 \ {\mathcal {D}}_2(\tau ,\gamma )- A_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c1}_{44}=A_1-A_2 \ {\mathcal {D}}_2(\tau ,\gamma )+ A_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \\ \rho ^{c1}_{14}&=A_5+A_6 \ {\mathcal {D}}_2(\tau ,\gamma )+ A_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c1}_{23}=A_3 \big (1- {\mathcal {D}}_4(\tau ,\gamma )\big ), \end{aligned}$$

where \(A_i\) are given by:

$$\begin{aligned} A_1&= \frac{1}{8} \big ( x \left| {\textsf {R}}\right| ^2 \cos ^2 (r_b)- x\ Re[{\textsf {R}}] \cos (r_b) +2 \big ), \quad A_2=\frac{1}{4} \big (\cos (2 r_b)- \cos ^2(r_b) \left| {\textsf {R}}\right| ^2 \big ) \\ A_3&=\frac{1}{8} \big ( x \left| {\textsf {R}}\right| ^2 \cos ^2 (r_b)+ x\ Re[{\textsf {R}}] \cos (r_b), \quad A_4=\frac{1}{8} \big (- x \left| {\textsf {R}}\right| ^2 \cos ^2 (r_b)+ x\ Re[{\textsf {R}}] \cos (r_b) +2 \big ) \\ A_5&= \frac{1}{8} x \cos (r_b) \big (3 Re[{\textsf {R}}]- \cos (r_b) \left| {\textsf {R}}\right| ^2 \big ), \quad A_6=\frac{1}{2} - i x\ Im [{\textsf {R}}] \cos (r_b) \end{aligned}$$

\({\mathcal {D}}_n(t,\gamma )\) corresponds to the average phase factor \(\textrm{e}^{i n\phi }\), which appears through time evolution and it is calculated as (Abel and Marquardt 2008):

$$\begin{aligned} {\mathcal {D}}_n(t,\gamma )= {\left\{ \begin{array}{ll} \textrm{e}^{-\gamma t}\left( \cosh {\delta _{ng} t}+\frac{\gamma }{\delta _{ng}} \sinh {\delta _{ng} t}\right) &{} \gamma >ng \\ \textrm{e}^{-\gamma t}\left( \cos {\delta _{ng} t}+\frac{\gamma }{\delta _{ng}} \sin {\delta _{ng} t}\right) &{} \gamma <ng \end{array}\right. } \end{aligned}$$
(21)

where \(\delta _{ng}=\sqrt{|\gamma ^2-(ng)^2|}\). The Wigner function Eq. (5) in this case is given by,

$$\begin{aligned} {\mathcal {W}}_{\rho ^{com}_{A{\bar{B}}}(t)}&=\min \bigg \{0, \frac{1}{16} \left| {\textsf {R}}\right| ^2 \cos ^2(r_b) \Bigl (4 \sqrt{3} \cos (\theta ) {\mathcal {D}}_2(\tau ,\gamma )-3 x \cos ^2(\theta ) \bigl (\cos (2 \phi ) \left( {\mathcal {D}}_4(\tau ,\gamma )-1\right) \\&\quad -3 {\mathcal {D}}_4(\tau ,\gamma )-1\bigr )-6 x \sin ^2(\phi ) \left( {\mathcal {D}}_4(\tau ,\gamma )-1\right) \Bigr ) \\&\quad -\frac{3}{4} x \sin ^2(\theta ) Im[{\textsf {R}}] \cos (r_b) \sin (2 \phi ) {\mathcal {D}}_2(\tau ,\gamma ) \\&\quad +\frac{1}{16} \left( 4-4 \sqrt{3} \cos (\theta ) \cos (2 r_b) {\mathcal {D}}_2(\tau ,\gamma )\right) \\&\quad -\frac{3}{16} x \cos (r_b) Re[{\textsf {R}}] \Bigl (-\left( 1-\cos ^2(\theta )\right) \cos (2 \phi ) \left( {\mathcal {D}}_4(\tau ,\gamma )+3\right) \\&\quad +\cos ^2(\theta ) \left( 3-3 {\mathcal {D}}_4(\tau ,\gamma )\right) +{\mathcal {D}}_4(\tau ,\gamma )-1\Bigr ) \bigg \} \end{aligned}$$
(22)
Fig. 1
figure 1

The contour plot of the Wigner function in \((\theta ,\phi )\) surface for the output state (20) with \(x=1, \tau =\pi , \ \Gamma =0.1,\), \(r_b=0.1\), and \({\textsf {R}}=1\)

Full size image

In Fig. 1, we present the contour plot of the negative values of Wigner function of the output state (20) on the \((\theta ,\phi )\) plane. It is assumed that the initial state (6) is maximally entangled state with \(x=1\), the acceleration parameter \(r_b=0.1\), the scaled time \(\tau =\pi\), \(\Gamma =0.1\), and \(|{\textsf {R}}|=1\). The negative values of the Wigner function are observed to form circular patterns around \((\phi ,\theta )=(\pi /2,\pi /2)\) and \((\pi /2,3\pi /2)\), indicating that quantum correlation can be captured in these regions. Hence, we can choose suitable values of \(\theta\) and \(\phi\) at these points in the presence of the stochastic common environment to explore quantum correlation. Computational analysis reveals that the acceleration of the qubit results in a decrease in the lower limits of the Wigner function (Abd-Rabbou et al. 2019). We will provide a comprehensive explanation of this phenomenon in the following section.

4.1.2 If two qubits are accelerated simultaneously

Let us consider the accelerated two-qubit system with density matrix given by Eq. (14) is forced to interact with a classical stochastic common environment. The evolved density operator \(\rho ^{com}_{{\bar{A}}{\bar{B}}}(t)\) at any time t can be calculated using Eq. (19) as follows,

$$\begin{aligned} \rho ^{com}_{{\bar{A}}{\bar{B}}}(t)&= \rho ^{c2}_{11} |00\rangle \langle 00| +\rho ^{c2}_{22} |01\rangle \langle 01| +\rho ^{c2}_{33} |10\rangle \langle 10| +\rho ^{c2}_{44} |11\rangle \langle 11| \\&\rho ^{c2}_{23}+ |01\rangle \langle 10| (\rho ^{c2}_{14} |00\rangle \langle 11|+ H.C.), \end{aligned}$$
(23)

where the elements are calculated as:

$$\begin{aligned} \rho ^{c2}_{11}&=B_1+B_2 \ {\mathcal {D}}_2(\tau ,\gamma )+B_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c2}_{22}=B_4+B_5 \ {\mathcal {D}}_2(\tau ,\gamma )+ B_6 \ {\mathcal {D}}_4(\tau ,\gamma ), \\ \rho ^{c2}_{33}&=B_4-B_5 \ {\mathcal {D}}_2(\tau ,\gamma )+ B_6 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c2}_{44}=B_1-B_2 \ {\mathcal {D}}_2(\tau ,\gamma )+ B_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \\ \rho ^{c2}_{14}&=B_7+B_8 \ {\mathcal {D}}_2(\tau ,\gamma )+B_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \quad \rho ^{c2}_{23}=B_3- B_3 \ {\mathcal {D}}_4(\tau ,\gamma ), \end{aligned}$$

with

$$\begin{aligned} B_1&=b_1-b_3-b_2+b_4, \quad B_2=\frac{-1}{8} \left| {\textsf {R}}\right| ^2 (\cos (2 r_a)+\cos (2 r_b)+2)+\frac{1}{4} (\cos (2 r_a)+\cos (2 r_b)) \\ B_3&=b_1-b_3+b_2+b_5, \quad B_4=-B_1, \quad B_5= \frac{1}{8} \left( \left| {\textsf {R}}\right| ^2-2\right) (\cos (2 r_a)-\cos (2 r_b)) \\ B_6&=-B_3, \quad B_7=-b_1+b_3 +3 b_2-b_5, \quad B_8=\frac{1}{4} x \left( \left( {\textsf {R}}^*\right) ^2-{\textsf {R}}^2\right) \cos (r_a) \cos (r_b) \end{aligned}$$

and

$$\begin{aligned} b_1&=\frac{1}{8} (x+1) \left| {\textsf {R}}\right| ^4 \cos (r_a)^2 \cos (r_b)^2, \quad b_2= \frac{1}{16} x \left( \left( {\textsf {R}}^*\right) ^2+{\textsf {R}}^2\right) \cos (r_a) \cos (r_b), \\ b_3&=\frac{1}{16} \left| {\textsf {R}}\right| ^2 (\cos (2 r_a) (2 \cos (2 r_b)+1)+\cos (2 r_b)),\\ \quad b_4&= \frac{1}{16} (\cos (2 r_a-2 r_b)+\cos (2 (r_a+r_b))+4) \\, b_5&=\frac{1}{8} \cos (2 r_a) \cos (2 r_b), \end{aligned}$$
Fig. 2
figure 2

The contour plot of the Wigner function in \((\theta ,\phi )\) surface for the output state (23) with \(x=1, \tau =\pi , \ \Gamma =0.1,\), \(r_a=r_b=0.1\), and \({\textsf {R}}=1\)

Full size image

The negative Wigner function behaviour of the output density state (23) is illustrated in Fig. 2. A comparison between Figs. 1 and 2 highlight the impact of the Unruh effect on quantum correlations among observers. Specifically, the region with negative Wigner function values is more confined in Fig. 2 than in Fig. 1. Since the general form of Wigner function in this cases is complicated, so, we present Wigner function with substitution the values \(\theta =\phi =\pi /2\). This choice for \(\theta ,\ \phi\) can be justified numerically as depicted in Fig. 2.

For these values of \(\theta\) and \(\phi\), the Wigner functions can gain the minimum values over the whole allowed range. With this remark, we can write,

$$\begin{aligned} {\mathcal {W}}_{\rho ^{com}_{{\bar{A}}{\bar{B}}}(t)}&=\min \bigg \{0, \frac{3}{16} \left| {\textsf {R}}\right| ^2 (\cos (2 r_a) (2 \cos (2 r_b)+1)+\cos (2 r_b)) \left( {\mathcal {D}}_4(\tau ,\gamma )-1\right) \\&\quad +\frac{3}{8} (x+1) \left| {\textsf {R}}\right| ^4 \cos (r_a)^2 \cos (r_b)^2 \left( 1-{\mathcal {D}}_4(\tau ,\gamma )\right) \\&\quad +\frac{3}{8} x \cos (r_a) \cos (r_b) \left( \ Im[{\textsf {R}}]^2-Re[{\textsf {R}}]^2\right) \left( {\mathcal {D}}_4(\tau ,\gamma )+1\right) \\&\quad -\frac{3}{4} (\cos (r_a)-\cos (r_b))^2 \left( {\mathcal {D}}_4(\tau ,\gamma )+1\right) +\frac{5}{8}-\frac{3}{8} {\mathcal {D}}_4(\tau ,\gamma ) \bigg \} \end{aligned}$$
(24)

4.2 The accelerated systems are interacted independently with their own stochastic environment

In this subsection, we assume that the subsystems are interacted independently with their own stochastic environments. In addition, either Bob’s qubit is individually accelerated or two qubits are accelerated simultaneously. So, we will treat these two cases in the following, separately.

4.2.1 If Bob’s qubit is only accelerated

When subsystems are brought to interact independently with their own stochastic environments, the initial density matrix (12) will evolve to:

$$\begin{aligned} \rho ^{in}_{A{\bar{B}}}(t)&= \rho ^{d1}_{11} |00\rangle \langle 00| +\rho ^{d1}_{22} |01\rangle \langle 01| +\rho ^{d1}_{33} |10\rangle \langle 10| \\&\quad +\rho ^{d1}_{44} |11\rangle \langle 11|+( \rho ^{d1}_{23}|01\rangle \langle 10| \rho ^{d1}_{14} |00\rangle \langle 11|+ H.C.), \end{aligned}$$

with array components as:

$$\begin{aligned} \rho ^{d1}_{11}&=\frac{1}{4}(1+C_1 \ {\mathcal {D}}_2(\tau ,\gamma _2 )+ C_2 \ {\mathcal {D}}_2(\tau ,\gamma _1 )\ {\mathcal {D}}_2(\tau ,\gamma _2 )), \\ \rho ^{d1}_{22}&=\frac{1}{4}(1-C_1 \ {\mathcal {D}}_2(\tau ,\gamma _2 )- C_2 \ {\mathcal {D}}_2(\tau ,\gamma _1 )\ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d1}_{33}&=\frac{1}{4}(1+C_1 \ {\mathcal {D}}_2(\tau ,\gamma _2 )- C_2 \ {\mathcal {D}}_2(\tau ,\gamma _1 )\ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d1}_{44}&=\frac{1}{4}(1-C_1 \ {\mathcal {D}}_2(\tau ,\gamma _2 )+ C_2 \ {\mathcal {D}}_2(\tau ,\gamma _1 )\ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d1}_{14}&=C_3 \big (1+ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 ) \big )+C_4 \big ( {\mathcal {D}}_2(\tau ,\gamma _1 )+{\mathcal {D}}_2(\tau ,\gamma _2 ) \big ) \\ \rho ^{d1}_{23}&=C_3 \big (1-{\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 ) \big )+C_4 \big ( {\mathcal {D}}_2(\tau ,\gamma _1 )- {\mathcal {D}}_2(\tau ,\gamma _2 ) \big ) \end{aligned}$$

where \(C_i\) are:

$$\begin{aligned} C_1&= \cos (2 r_b)-\left| {\textsf {R}}\right| ^2 \cos (r_b)^2, \quad C_2=\frac{1}{4} x \left| {\textsf {R}}\right| ^2 \cos (r_b)^2, \\ C_3&=\frac{1}{4} x Re[{\textsf {R}}] \cos (r_b), \quad C_4= -\frac{i}{4} x\ Im[{\textsf {R}}] \cos (r_b) \end{aligned}$$
(25)

where \({\mathcal {D}}_{2}(t,\gamma _i)\) is obtained from Eq. (21), and \(\gamma _{1(2)}\) refers to Alice (Bob)’s environment noise rate. The Wigner function in this case take the following form:

$$\begin{aligned} {\mathcal {W}}_{\rho ^{in}_{A{\bar{B}}}(t)}&= \min \bigg \{0, \frac{1}{4} \left| {\textsf {R}}\right| ^2 \cos (\theta ) \cos (r_b)^2 {\mathcal {D}}_2\left( \tau ,\gamma _2\right) \left( 3 x \cos (\theta ) {\mathcal {D}}_2\left( \tau ,\gamma _1\right) +\sqrt{3}\right) \\&\quad - \frac{3}{8} x \sin ^2(\theta ) \ Im[{\textsf {R}}] \cos (r_b) \sin (2 \phi ) \left( {\mathcal {D}}_2\left( \tau ,\gamma _1\right) +{\mathcal {D}}_2\left( \tau ,\gamma _2\right) \right) \\&\quad +\frac{1}{8} \left( 2-2 \sqrt{3} \cos (\theta ) \cos (2 r_b) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) \right) \\&\quad +\frac{3}{8} x \sin ^2(\theta ) \cos (r_b) Re[{\textsf {R}}] \left( \cos (2 \phi ) \left( {\mathcal {D}}_2\left( \tau ,\gamma _1\right) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) +1\right) \right. \\&\left. \quad -{\mathcal {D}}_2\left( \tau ,\gamma _1\right) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) +1\right) \bigg \} \end{aligned}$$
(26)
Fig. 3
figure 3

The contour plot of the Wigner function in \((\theta ,\phi )\) surface for the output state (25) with the same parameters as displayed in Fig. 1

Full size image

Similarly to Fig. 1, the contour plot of the Wigner function for the accelerated state (Eq. 25) is presented in Fig. 3. In this case, Bob’s qubit is only accelerated with \(r_b=0.1\), and the decoherence parameters of both baths are equal, with \(\Gamma _a=\Gamma _b=0.1\). The minimum bounds of the Wigner function are lower than those displayed in Fig. 1, indicating that the independent stochastic environment dissipates quantum correlation faster than the common environment. Furthermore, maximum bounds of quantum correlation accumulate at \((\phi , \theta )=(\pi /2,\pi /2)\) and \((\pi /2,3\pi /2)\), making these points suitable for capturing the quantum correlation of the state in the Wigner function.

4.2.2 If two qubits are accelerated simultaneously

Beginning from the initial density matrix Eq. (14), the evolved density matrix is calculated as:

$$\begin{aligned} \rho ^{in}_{{\bar{A}}{\bar{B}}}(t)&= \rho ^{d2}_{11} |00\rangle \langle 00| +\rho ^{d2}_{22} |01\rangle \langle 01| +\rho ^{d2}_{33} |10\rangle \langle 10| +\rho ^{d2}_{44} |11\rangle \langle 11| \\&\quad +(\rho ^{d2}_{23} |01\rangle \langle 10|+H.C.)+ (\rho ^{d2}_{14} |00\rangle \langle 11|+ H.C.), \end{aligned}$$
(27)

with

$$\begin{aligned} \rho ^{d2}_{11}&=\frac{1}{4}(1+{\mathcal {G}}_1 \ {\mathcal {D}}_2(\tau ,\gamma _1 )+ {\mathcal {G}}_2 \ {\mathcal {D}}_2(\tau ,\gamma _2 )+ {\mathcal {G}}_3\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d2}_{22}&=\frac{1}{4}(1+{\mathcal {G}}_1 \ {\mathcal {D}}_2(\tau ,\gamma _1 )- {\mathcal {G}}_2 \ {\mathcal {D}}_2(\tau ,\gamma _2 )- {\mathcal {G}}_3\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d2}_{33}&=\frac{1}{4}(1-{\mathcal {G}}_1 \ {\mathcal {D}}_2(\tau ,\gamma _1 )+ {\mathcal {G}}_2 \ {\mathcal {D}}_2(\tau ,\gamma _2 )- {\mathcal {G}}_3\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d2}_{44}&=\frac{1}{4}(1-{\mathcal {G}}_1 \ {\mathcal {D}}_2(\tau ,\gamma _1 )- {\mathcal {G}}_2 \ {\mathcal {D}}_2(\tau ,\gamma _2 )+ {\mathcal {G}}_3\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d2}_{14}&=({\mathcal {G}}_4+{\mathcal {G}}_5 \ {\mathcal {D}}_2(\tau ,\gamma _1 )+ {\mathcal {G}}_5 \ {\mathcal {D}}_2(\tau ,\gamma _2 )+{\mathcal {G}}_4\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \\ \rho ^{d2}_{23}&=({\mathcal {G}}_4+{\mathcal {G}}_5 \ {\mathcal {D}}_2(\tau ,\gamma _1 )- {\mathcal {G}}_5 \ {\mathcal {D}}_2(\tau ,\gamma _2 )-{\mathcal {G}}_4\ {\mathcal {D}}_2(\tau ,\gamma _1 ) \ {\mathcal {D}}_2(\tau ,\gamma _2 )) \end{aligned}$$

where \({\mathcal {G}}_i\) are:

$$\begin{aligned} {\mathcal {G}}_1&= \frac{1}{4} \cos (2 r_b)-\frac{1}{4} \left| {\textsf {R}}\right| ^2 \cos (r_b)^2 ,\quad {\mathcal {G}}_2=\frac{1}{4} \cos (2 r_a)-\frac{1}{4} \left| {\textsf {R}}\right| ^2 \cos (r_a)^2 \\ {\mathcal {G}}_3&=\frac{1}{4} (x+1) \left| {\textsf {R}}\right| ^4 \cos (r_a)^2 \cos (r_b)^2-\frac{1}{8} \left| {\textsf {R}}\right| ^2 (\cos (2 r_a) (2 \cos (2 r_b)+1)+\cos (2 r_b)) \\&\quad +\frac{1}{4} \cos (2 r_a) \cos (2 r_b) \\ {\mathcal {G}}_4&=\frac{1}{8} x \left( \left( {\textsf {R}}^*\right) ^2+{\textsf {R}}^2\right) \cos (r_a) \cos (r_b), \quad {\mathcal {G}}_5=\frac{1}{8} x \left( \left( {\textsf {R}}^*\right) ^2-{\textsf {R}}^2\right) \cos (r_a) \cos (r_b) \end{aligned}$$
(28)
Fig. 4
figure 4

The contour plot of the Wigner function in \((\theta ,\phi )\) surface for the output state (27) with the same parameters as displayed in Fig. 2

Full size image

Likewise, Fig. 4 illustrates that the Wigner function is centered at identical points for the preceding three scenarios. Here, we accelerated the initial two-qubit system and allowed them to interact independently with their respective stochastic noise. The center orange region is smaller than in the previous three cases, indicating independent environment decoherence of non-classical correlation. Furthermore, acceleration parameters exacerbate this decoherence.

For the output state (27), we obtained the Wigner function by substituting \(\theta =\phi =\pi /2\). This parameter selection is justified by Fig. 4, which indicates that these specific values of \(\theta\) and \(\phi\) correspond to the minimum values of the Wigner function. Consequently, the Wigner function reads,

$$\begin{aligned} {\mathcal {W}}_{\rho ^{in}_{{\bar{A}}{\bar{B}}}(t)}=\min \bigg \{0, \frac{1}{4} \left( 3 x \cos (r_a) \cos (r_b) \left( Im[{\textsf {R}}]^2-Re[{\textsf {R}}]^2\right) {\mathcal {D}}_2\left( \tau ,\gamma _1\right) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) +1\right) \bigg \} \end{aligned}$$
(29)

5 The quantum correlations and the entanglements: the results

Since the existence of quantum correlation in a system can be designated by the negative corresponding Wigner function, it is helpful to determine the sign of these functions. By solving the Eqs. (22, 24, 26, 29) in term of x, we get the following roots for the Wigner functions:

$$\begin{aligned} x_0^{{\mathcal {W}}_1}&= \frac{4}{3 \left( 2 \left| {\textsf {R}}\right| ^2 \cos ^2(r_b) \left( {\mathcal {D}}_4(\tau ,\gamma )-1\right) +2 \cos (r_b) Re[{\textsf {R}}] \left( {\mathcal {D}}_4(\tau ,\gamma )+1\right) \right) }, \\ x_0^{{\mathcal {W}}_2}&=\Bigl ( \sec (r_a) \sec (r_b) \biggl (6 \left( 1-{\mathcal {D}}_4(\tau ,\gamma )\right) \Bigl (\left| {\textsf {R}}\right| ^2 \cos ^2(r_b) \left( \left| {\textsf {R}}\right| ^2 \cos ^2(r_a)-\cos (2 r_a)\right) \\&\quad +\cos (2 r_b) \left( \cos (2 r_a)-\left| {\textsf {R}}\right| ^2 \cos ^2(r_a)\right) \Bigr )+4\biggr )\Bigr ) / \\&\Bigr ( 6\left| {\textsf {R}}\right| ^4 \cos (r_a) \cos (r_b) \left( {\mathcal {D}}_4(\tau ,\gamma )-1\right) +3 \left( \ Im[{\textsf {R}}]^2+Re[{\textsf {R}}]^2\right) \left( {\mathcal {D}}_4(\tau ,\gamma )+1\right) \Bigr ), \\ x_0^{{\mathcal {W}}_3}&= \frac{\sec (r_b)}{3 Re[{\textsf {R}}] {\mathcal {D}}_2\left( \tau ,\gamma _1\right) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) } \\ x_0^{{\mathcal {W}}_4}&=\frac{\sec (r_a) \sec (r_b)}{3 \left( Re[{\textsf {R}}]^2-\ Im[{\textsf {R}}]^2\right) {\mathcal {D}}_2\left( \tau ,\gamma _1\right) {\mathcal {D}}_2\left( \tau ,\gamma _2\right) }, \end{aligned}$$
(30)

where we have abbreviated \({\mathcal {W}}_{\rho ^{com}_{{A}{\bar{B}}}(t)}\), \({\mathcal {W}}_{\rho ^{com}_{{\bar{A}}{\bar{B}}}(t)}\), \({\mathcal {W}}_{\rho ^{in}_{{A}{\bar{B}}}(t)}\) and \({\mathcal {W}}_{\rho ^{in}_{{\bar{A}}{\bar{B}}}(t)}\), by \({\mathcal {W}}_1\),  \({\mathcal {W}}_2\),  \({\mathcal {W}}_3\)   and \({\mathcal {W}}_4\), respectively. We will also use this for easiness hereafter. For the later convenient, we will denote \({\mathcal{C}}_{1},{\mathcal{C}}_{2},{\mathcal{C}}_{3},{\mathcal{C}}_{4},\) as the corresponding concurrences for four cases in Sec. (4).

Fig. 5
figure 5

a Comparison of four situations of the Wigner functions and concurrences against x with the specified parameters \(\tau =\pi /2,\) \(\Gamma =\Gamma _1=\Gamma _2=0.05\), and \(r_b=0.3, \ r_a=0.4\) and \({\textsf {R}}=1\). The inset attached shows the detail of the plots around \(x\approx 0.4\), b the roots of the Wigner functions for four cases with \(\Gamma =\Gamma _1=\Gamma _2=0.01, ra=rb, x= 0.95, \tau =\pi /2, {\textsf {R}}=1\)

Full size image

In order to demonstrate the efficacy of the Wigner function in elucidating quantitative correlations, appropriate figures will be presented for comparison with concurrence. Figure 5a exhibits the Wigner function (\({\mathcal {W}}\)) and concurrence (\({\mathcal {C}}\)) as a function of the initial state’s purity parameter x, for specific values of \(\tau\), \(\Gamma\), and r as indicated in the caption. Throughout our discussion, we presume that the distribution angles are fixed at \(\theta =\phi =\dfrac{\pi }{2}\), where this point is related to the minimum value of the Wigner function in phase space. We consider the single mode approximation, \({\textsf {R}}=1\) for now. Later we will discard this approximation, and discuss on its effect on the correlations between observers.

It is inferred that to maintain the initial quantum correlation among observers, the value of x must exceed a certain threshold. Figure 5a illustrates that the system’s interaction with the environment is crucial in characterizing the correlation for specific parameters. Although for small values of accelerations the common environment condition provides a greater amount of correlations between observers, but by increasing the acceleration, the Unruh effect plays a prominent role to suppress quantum correlations. Indeed, for arbitrary values of acceleration, the status of observers concerning the inertial reference frame is determinative. For systems with equal initial conditions and noise strength, those with only accelerating observers exhibit more significant correlations than those with both accelerating and non-accelerating observers, regardless of any imposed noise configuration. Under this conditions, the lower bounds of the functions \({\mathcal {W}}_1\) and \({\mathcal {W}}_3\) exceed those of \({\mathcal {W}}_2\) and \({\mathcal {W}}_4\), respectively. This trend is also observed in the corresponding concurrences. The impact of acceleration on correlations becomes evident when comparing either \({\mathcal {W}}_1\) and \({\mathcal {W}}_3\), or \({\mathcal {W}}_2\) and \({\mathcal {W}}_4\). Notably, when two observers accelerate simultaneously, the correlation decreases more significantly than when only one observer accelerates. Therefore, for a non-inertial frame, it is advisable to provide them with a collective environment. Pure states are necessary to achieve high-quality quantum communication between both accelerating observers. To clarify the aforementioned statement, we have plotted the roots of the Wigner function for variable x, as given by Eq. (30), against the parameter \(r_b\) in Fig. 5b. It is noteworthy that we have set \(r_a=r_b\) for both cases discussed in Sects. 4.2.2 and 4.1.2. Our analysis reveals that as the acceleration increases, a purer state should be shared among the observers to maintain correlation. Furthermore, in cases where there is an independent environment, decoherence effects are more pronounced, necessitating a pure initial density matrix.

Fig. 6
figure 6

The effect of common or independent noise configurations on the quantum correlations against the acceleration parameter \(r_b\), with the parameters \(\tau =\pi ,\) \(x =0.9\) \(\Gamma =\Gamma _1=\Gamma _2=0.05\), a only Bob’s qubit is accelerated (\(r_a =0\)); the thick line correspond to \({\textsf {R}}=1\) and the thin line to \({\textsf {R}}=0.85\), b two qubits are accelerated with \(r_a =0.3\) or \(r_a =r_b\) which have specified in the corresponding legend; \({\textsf {R}}=1\) has been considered

Full size image

A comparative study was conducted between the common and independent stochastic environments of accelerated states with respect to the acceleration parameter \(r_b\), as depicted in Fig. 6. Here, \(\tau =\pi\) and \(\Gamma =\Gamma _1=\Gamma _2=0.05\). As Bob’s qubit is only accelerated, Fig. 6a illustrates that the functions \({\mathcal {W}}_1\), \({\mathcal {W}}_3\), \({\mathcal {C}}_1\), and \({\mathcal {C}}_3\) degrade to a non-zero value at the infinite acceleration limit (\(r_b\rightarrow \tfrac{\pi }{4}\)). The common noise configuration is more challenging to overcome than the independent noise configuration, where \({\mathcal {C}}_1\) is greater than \({\mathcal {C}}_3\). Wigner’s function provides an excellent indication of quantum correlation. Furthermore, the impact of disregarding the single mode approximation on the correlations of the states can be inferred from the blue curves in the same sub-figure. These curves correspond to a value of \({\textsf {R}}=0.85\). We incorporate the contribution of spacetime modes that are inaccessible to construct the Unruh mode. Consequently, by tracing over these inaccessible region modes, we forfeit this contribution and consequently more prepared correlations are lost due to the Unruh effect. To investigate the Unruh effect on systems with accelerating observers, Fig. 6b has been generated. The relevant quantities in this context are \({\mathcal {W}}_2\), \({\mathcal {W}}_4\), \({\mathcal {C}}_2\), and \({\mathcal {C}}_4\). As depicted in the figure, the quantum correlations and entanglements, namely \({\mathcal {W}}_2\), \({\mathcal {W}}_4\), \({\mathcal {C}}_2\), and \({\mathcal {C}}_4\), exhibit the deepest decay when both qubits are accelerated with identical values (\(r_a=r_b\)), as compared to when only the Alice qubit is accelerated with a constant value (\(r_a=0.3\)). Moreover, it is observed that the decoherence effect of the common noise environment is less pronounced than that of the independent environment.

Fig. 7
figure 7

The behaviour of correlation functions \({\mathcal {W}}_i\) and \({\mathcal {C}}_i\) against the rate \(\Gamma\) with the parameters \(\tau =\pi ,\) \(x =1\), and \(\Gamma =\Gamma _1=\Gamma _2\), \(r_a=r_b=0.1\), a \({\textsf {R}}=1\), b \({\textsf {R}}=0.85\). The inset in each subfigure display the corresponding plot for \(0<\Gamma <1\)

Full size image

To demonstrate the impact of different types of noise on the behavior of correlation functions with respect to the decoherence dimensionless rate \(\Gamma\), we have presented Fig. 7, where we have set \(\Gamma _a=\Gamma _b=\Gamma\). For small acceleration parameters (i.e., \(r_a=r_b=0.1\)) and \({\textsf {R}}=1\), Fig. 7a, b show that the correlation functions, namely \({\mathcal {W}}_1\), \({\mathcal {W}}_2\), (\({\mathcal {C}}_1\), and \({\mathcal {C}}_2\)), as well as the pair of \({\mathcal {W}}_3\) and \({\mathcal {W}}_4\), (\({\mathcal {C}}_3\), and \({\mathcal {C}}_4\)), are nearly the same for large values of \(\Gamma\).

In the Markovian regime, characterized by large values of \(\Gamma\), the Wigner function and concurrence of a common environment configuration are smaller than those of an independent environment configuration. Specifically, \({\mathcal {W}}_{1,2} < {\mathcal {W}}_{3,4}\) and \({\mathcal {C}}_{1,2} < {\mathcal {C}}_{3,4}\). Conversely, for small values of \(\Gamma\), the opposite is true. This observation is supported by the inset of Fig. 7a. In addition, in the non-Markovian regime (\(0< \Gamma < 1\), inset of Fig. 7a), quantum entanglement (\({\mathcal {C}}\)) extends over a wider range of \(\Gamma\) than quantum correlation as evidenced by the Wigner function (\({\mathcal {W}}\)). Therefore, we can conclude that the Wigner function is more susceptible to noise than concurrence. Another interesting phenomenon is the occurrence of quiescence in quantum entanglement due to variations in \(\Gamma\), which can be attributed to a transition from a Markovian to a non-Markovian regime of noise. Figure 7b displays the same quantities as Fig. 7a, except when the single mode approximation (\({\textsf {R}}=0.85\)) is not applied. The inset of this figure reveals that correlations degrade more rapidly than in the case where the single-mode approximation is used. Under these conditions, the Unruh effect can be amplified by the acceleration of observers. Specifically, Fig. 7b demonstrates that the curves in Fig. 7a, which were nearly identical, deviate significantly from each other.

Fig. 8
figure 8

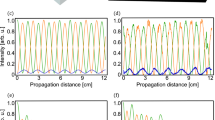
The behaviour of correlation functions \({\mathcal {W}}_i\) and \({\mathcal {C}}_i\) against the scaled time \(\tau\) with the parameters \(x =1\), and \(r_a=r_b=0.1\), a \(\Gamma =\Gamma _1=\Gamma _2=0.05\), and \({\textsf {R}}=1\), b the same as (a) but \({\textsf {R}}=0.85\), c \(\Gamma =\Gamma _1=\Gamma _2=50\) and \({\textsf {R}}=1\), and d the same as (c) but \({\textsf {R}}=0.85\) has been chosen

Full size image

The behaviour of the correlation function with respect to the dimensionless time \(\tau \equiv t\ g\) is presented in Fig. 8. Figure 8a, b depict the non-Markovian regime (\(\Gamma \ \ll 1\)) of noise. In Fig. 8a, the single mode approximation is assumed, while this assumption is discarded in Fig. 8b with \({\textsf {R}}=0.85\). A characteristic of the non-Markovian regime is a successive death and rebirth of correlation with damping amplitude. However, Wigner functions undergo deeper degradation in amplitude than entanglement. It is evident from Fig. 8a that correlations contained in systems with common environment configurations are more sensitive to noise than those displayed for the independent environments. Additionally, quantum correlation in the system, as witnessed by the Wigner function, may disappear for a period and reappear after a specific time. This collapse in quantum correlation is not observed for quantum entanglement, where oscillatory behaviour is found. The entanglement for common noise configuration varies more severely than independent noise configuration. The same relation between variation of the Wigner function with common environment against independent environments holds. So, when we imposed the subsystems to interact with an independent environment, a delay in the evolution of correlation is exhibited. When the single mode approximation is discarded, the impact of interaction time and acceleration becomes significant, and the Unruh effect distinguishes between systems with a single accelerating observer and those with both observers accelerating. The specifics of this behaviour are illustrated in the inset of the corresponding figures. Significantly, it has been observed that the application of independent noise channels can effectively reduce the frequency of entanglement death and rebirth, thereby increasing the duration of quantum correlations. This can be demonstrated by comparing \({\mathcal {C}}_{1,2}\) with \({\mathcal {C}}_{3,4}\). Unlike the concurrence, the Wigner function for independent environments experiences more periods of inactivity, while the common environment exhibits more rapid variations. This can be illustrated by comparing \({\mathcal {W}}_{1,2}\) with \({\mathcal {W}}_{3,4}\). A note on the difference between the Wigner function and quantum concurrence would be helpful. Although we have considered the Wigner function as an indicator of non-classical correlations, the quantum concurrence can specifically capture the quantum entanglement of the desired system. Therefore, it is not reasonable to expect that non-classical correlations will accurately reflect quantum entanglement. Interestingly, we have observed instances where the system and environment become separated in time and no correlation exists between them, yet the prepared quantum entanglement remains preserved between them. In Fig. 8c, d, we consider the non-Markovian regime at the other extreme (\(\Gamma \gg 1\)) for \({\textsf {R}}=1\) and \({\textsf {R}}=0.85\), respectively. During this time, the correlation decays monotonically with time, but in cases with independent environments, the correlation lasts much longer than in cases with common environment configurations. Figure 8d demonstrates that systems with both accelerating observers have a more fragile correlation than systems with only one accelerating observer.

6 Conclusion

In this study, we have investigated the behaviour of the Wigner function and quantum concurrence in a bipartite mixed entangled state under the influence of RTN and the Unruh effect. Our analysis involved an assessment of the Wigner function and quantum concurrence, and we focused on their behaviour about various parameters such as the purity parameter x, observers’ acceleration parameters \(r_a\) and \(r_b\), dimensionless evolution time, and dimensionless switching parameter \(\Gamma\). It is important to note that we did not rely on the single-mode approximation throughout our analysis. Furthermore, we explored how these quantities are affected by different environmental setups, specifically in terms of the independent/ common environment. By comparing our results, we have been able to conclude the behaviour of the Wigner function and quantum concurrence in this context. It has been demonstrated that the concurrence and the negative values of the Wigner function, two non-classical correlation indicators, are compatible with each other. Although the effect of acceleration as a decoherence agent has been established, it has been observed that the configuration of the environment has a more significant and dominant impact on the loss of entanglement and correlations. More intriguingly, it has been noted that quantum correlations and entanglement behave differently for independent and common environments in two regimes of Markovian and non-Markovian noises. Furthermore, by discarding the single-mode approximation, the degradation impact of the Unruh effect on correlations is further strengthened.