1 Introduction

A wavelength division multiplexing (WDM) technology is considered one the main networking forms of the next generation interconnection backbone network of the appropriate technologies such as next-generation applications based on 5 G, Internet of Things (IoT), and Fiber to the X (FTTX) (Pagare et al. 2021; Zhang et al. 2021; Garg et al. 2020). One of the factors that limit the increase in data rate in the WDM system is dispersion. To solve dispersion, many dispersion compensation techniques have been used, especially in the WDM system using a fiber Bragg grating (FBG) (Bassem A. Naguib et al. 2021). The FBG is an optical has some reflective planes in its core, where the distance between planes is uniform and its refractive index is different from the core. Chirped fiber Bragg grating (CFBG) is an especial type of FBG used in dispersion compensation techniques (Moustafa H. Aly et al. 2020, Taymour A. Hamdallah et al. 2009, Osama Mahran et al. 2006). CFBG has also an optical reflector in its core like FBG but the distance between reflectors is non-uniform (Bedir Yousif et al. 2020, Ahmed F. Sayed et al. 2017, Venghaus et al. 2017, Ashraf A.M. Khalaf et al. 2021). To enhance the dispersion compensation process in the CFBG core, an apodization function technique is applied to the core refractive index. Apodization functions are efficient functions used to apodize the refractive index along the CFBG core to suppress side lobes to narrow the bandwidth (A.Sharma et al. 2020; Ashry et al. 2014). Many dispersion compensation processes in CFBG are previously studied using apodization functions. In (Gupta et al. 2020), a CFBG is implemented with a tanh apodized function in the WDM system to compensate dispersion and to enhance performance. In (Ahmed F. Sayed et al. 2021), the spectral width of the light source is reduced to enhance the performance of a WDM system using cascaded apodized FBG unit with different apodization functions at transmitter and a CFBG with Gaussian function at receiver.

In (Moustafa H. Aly et al. 2020) many apodization functions have been investigated with a CFBG at the receiver to perform dispersion compensation and enhance the WDM performance, where both Q-factor and BER are noticed at different apodization functions. In (Nazmi A.Mohammed et al. 2018), a CFBG is used with different apodization techniques to produce a remarkable dispersion compensation profile that is suitable for wideband dispersion compensation specifications which can effectively cover the C- and/or a part of the L-bands. In (Meena et al. 2020), a novel CFBG model with a Gaussian apodization function has been designed as a dispersion compensator to enhance the WDM system performance.

In this paper, a new apodization profile is proposed from Cauchy –Sinc apodization profiles. The new function is applied with other apodization profiles to the CFBG as a post compensator in a WDM communication system. The new function not only aims to enhance the performance of the WDM communication system but also to enhance the power budget of the tested wavelength, 1550 µm, in the WDM communication system at a BER of 10−9, where the obtained results are compared with our previous work (Moustafa H. Aly et al. 2020).

The remainder of this paper is organized as follows. Section 2 introduces the basic model and analysis. The proposed system is presented and explained in Sec. 3. The simulation results are displayed and discussed in Sec. 4 followed by the evaluation in Sec. 5. Section 6 is devoted to the main conclusions.

2 Basic model and analysis

Here, some CFBG parameters and various types of common apodization profiles used in the dispersion compensation process are illustrated.

2.1 Chirped fiber bragg grating

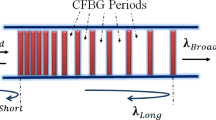
Figure 1 shows the main construction of the CFBG, with different spacings between the vertical plans. The reflection of various wavelengths is done from various positions along the core, where the short wavelengths are reflected from near end and the long ones from the far end.

Fig. 1
figure 1

Main structure of CFBG (Ahmed F. Sayed et al. 2021)

Full size image

The Bragg wavelength (the reflected wavelength), \(\lambda_{B}\)(z), reflected from any distance z along the grating core, whose refractive index, n(z), is given as (Kashyap et al. 1999; Venghaus et al. 2006; Agrawal et al. 2012)

$$ \lambda_{B} \left( z \right) = 2n\left( z \right)\Lambda \left( z \right) $$
(1)
$$ n\left( z \right) = n_{eff} + \Delta n g\left( z \right) cos \left\{ {\frac{2\pi z}{{\Lambda_{0} }}\left( {1 + xz} \right)} \right\} $$
(2)

\( x\) is defined as the linear chirp of the grating, g (z) is the apodization function, \(n_{eff}\) is the effective refractive index and \(\Delta n\) is the modulated refractive index of the grating (Nazmi et al. 2015; Nazmi et al. 2016). The periods between planes along grating core can be calculated as in (Ahmed et al. 2017)

$$ \Lambda \left( z \right) = \Lambda_{0} + x z $$
(3)

where \({\Lambda }_{0}\) is the start period in the CFBG core.

The chirp, ∆λ, between the longest and the shortest wavelengths, Fig. 1, can be calculated as (El-Gammal et al. 2015)

$$ \Delta {\uplambda } = 2n_{eff} \left( {{\Lambda }_{ long} - {\Lambda }_{short} } \right) $$
(4)

where \(\Lambda_{ long}\)is the longest period and \({\Lambda }_{short}\) the shortest period. The time delay, τ, for each wavelength along the CFBG with length \(l\) can be obtained as in (El-Gammal et al. 2015):

$$ \tau \left( \lambda \right) = \left( {\lambda_{B} - \lambda } \right)\frac{{2n_{eff} }}{\Delta \lambda c} l $$
(5)

with c the free space speed of light.

The dispersion, \(D_{g}\), of the CFBG can be obtained as (Venghaus et al. 2006):

$$ D_{g} = \frac{{2n_{eff} }}{\Delta \lambda c}l $$
(6)

2.2 The apodization functions

For the sake of comparison with our proposal, the most common apodization that will be studied and perform CFBG to compensate dispersion are illustrated as (Ashry et al. 2014; Moustafa H. Aly et al. 2020; Osama Mahran et al 2009):

2.2.1 Blackman

$$ g\left( z \right) = \left[ {\frac{{1 + 1.19\cos \left( x \right) + 0.19\cos \left( {2x} \right)}}{2.38}} \right] $$
(7)

where

$$ x = \left[ {\frac{{2\pi \left( {z - \frac{L}{2}} \right)}}{L}} \right] , 0 < z < L $$
(8)

2.2.2 Cauchy

$$ {\text{g}}\left( {\text{z}} \right){ = }\left[ {\frac{{{1 - }\left( {\frac{{{2}\left( {{\text{Z - }}\frac{{\text{L}}}{{2}}} \right)}}{{\text{L}}}} \right)^{{2}} }}{{{1 - }\left( {\frac{{{\text{2C}}\left( {{\text{Z - }}\frac{{\text{L}}}{{2}}} \right)}}{{\text{L}}}} \right)^{{2}} }}} \right] $$
(9)

where \({\text{C}} = 0.5,{ }0{ } < {\text{ z }} < {\text{ L }} \)

2.2.3 Hamming

$$ {\text{g}}\left( {\text{z}} \right) = \left[ {\frac{{1 + {\text{Hcos}}\left( {\frac{{2{\uppi }\left( {{\text{z}} - { }\frac{{\text{L}}}{2}} \right)}}{{\text{L}}}} \right)}}{{1 + {\text{H}}}}} \right] $$
(10)

where \({\text{H}} = 0.9,{ }0{ } < {\text{ z }} < {\text{ L }} \)

2.2.4 Gaussian

$$ {\text{g}}\left( {\text{z}} \right) = {\text{exp}}( - {\text{a}}\left( {{ }\frac{{\text{z}}}{{\text{l}}} - 0.5)^{2} } \right) $$
(11)

where \(\user2{ }{\text{a}} = 1,{ }0{ } < {\text{ z }} < {\text{ L}} \user2{ }\).

2.2.5 Sinc

$$ g\left( z \right) = \left[ {\frac{{{\text{A sin}}\left( x \right)}}{x}} \right] $$
(12)

where

$$ {\text{x}} = \left[ {\frac{{2\pi \left( {z - \frac{L}{2}} \right)}}{L}} \right] $$
(13)
$$ {\text{and }}0 < {\text{z }} < {\text{L and A}} = 3 $$

2.2.6 Hyper-tan (tanh)

$$ g\left( z \right) = \tanh \left( {s\frac{z}{l}} \right)\tanh \left( {\left( {s(1 - \frac{z}{l}} \right)} \right) + 1 - tanh^{2} \left( \frac{s}{2} \right) $$
(14)

where \( s = 6\).

3 The proposed model

The proposed model aims to enhance the WDM performance and power budget for the WDM system. It is a new proposed apodization function extracted from Cauchy and Sinc functions (Moustafa H. Aly et al. 2020).

3.1 The proposed apodization function

To simplify the Cauchy profile, in Eq. (9), one can define the parameter x, relating the distance (at any point in the fiber core) z and the grating length, L, as

$$ \frac{{2\left( {{\mathbf{Z}} - \frac{{\mathbf{L}}}{2}} \right)}}{{\mathbf{L}}} = {\text{x}} $$
(15)

Then, Cauchy function can be simplified as:

$$ {\text{g}}\left( {\text{z}} \right) = \left[ {\frac{{1 - {\text{x}}^{2} }}{{1 - \left( {{\text{cx}}} \right)^{2} }}} \right] $$
(16)

The Sinc profile (Ashry et al. 2014) also can be simplified as

$$ {\text{s}}\left( {\text{z}} \right) = \left[ {\frac{{{\text{A sin}}\left( {\text{y}} \right)}}{{\text{y}}}} \right] $$
(17)

with

$$ {\text{y}} = \left[ {\frac{{2{\uppi }\left( {{\text{z}} - \frac{{\text{L}}}{2}} \right)}}{{\text{L}}}} \right] $$
(18)

\({\text{where }}0 < {\text{z }} < {\text{L and A}} = 3\)

From Eqs. (15) and (18), the relation between y and x can be written as:

$$ {\text{y}} = {\pi x} $$
(19)

Substituting with y, Eq. (19), in Eq. (17), then the Sinc profile can be written as

$$ {\text{s}}\left( {\text{z}} \right) = \left[ {\frac{{{\text{A sin}}\left( {{\pi x}} \right)}}{{{\pi x}}}} \right] $$
(20)

Then, one can get the new profile m(z) by multiplying g(z) and s(z), Eqs. (16) and (20), as

$$ {\text{m}}\left( {\text{z}} \right) = \frac{{\text{A}}}{{{\pi x}}}\left[ {\frac{{1 - {\text{x}}^{2} }}{{1 - \left( {{\text{cx}}} \right)^{2} }}} \right]\sin \left( {{\pi x}} \right) $$
(21)

where A = 1 and C = 0.3 (Ashry et al. 2014).

Figure 2 displays the apodization function with the grating length for different apodization functions mentioned before with solid lines and the proposed one with the dashed line.

Fig. 2
figure 2

The apodization functions and grating length (mm)

Full size image

3.2 Implementation of the proposed apodization function

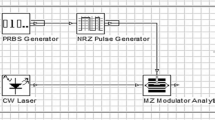
The system illustrated in Fig. 3 (Moustafa H. Aly et al. 2020) includes the CFBG with the proposed apodization function.

Fig. 3
figure 3

Simulated link with a post CFGB dispersion compensation unit (Moustafa H. Aly et al. 2020)

Full size image

The WDM system consists of three parts: the transmitter, the optical fiber, and the receiver.

3.2.1 The transmitter

A pseudo-random bit sequence generates data at a rate of 10 Gbps to NRZ pulse generator. It produces NRZ format pulses with a duty cycle of 1 to a Mach–Zender modulator with an extinction ratio of 30 dB. A light source with 0 dBm continuous power and 1550 nm wavelength is connected to the other side of the Mach–Zender modulator. The Mach–Zender modulates the optical signal from the light source with data from the NRZ driver which transmits it to the optical fiber.

3.2.2 The optical fiber

The optical fiber has the parameters 0.25 dB/km attenuation coefficient, 17 ps/nm.km dispersion coefficient and 110 km length and is connected to the Mach–Zender modulator.

3.2.3 The receiver

The optical signal suffers dispersion and losses. The losses are compensated by an erbium-doped fiber amplifier (EDFA) of 40 dB gain and 6 dB noise figure and the dispersion is compensated by the CFBG as a post dispersion compensator. A PIN photodetector of 1 A/W responsivity and 10 nA dark current converts the optical signal to an electrical one. A Bessel filter of 0.75 × bit rate cutoff frequency filters the output electrical signal. The transmission impairments stemming from optical fiber are restored from re-amplifying, re-shaping, and re-timing (3R). The eye diagram and the BER analyzer determine the WDM link performance. Tables 1 and 2 summarize the WDM link and the CFBG parameters, respectively, used in simulation.

Table 1 WDM link parameters (Moustafa H. Aly et al. 2020)
Full size table
Table 2 CFBG parameters ( Moustafa H. Aly et al. 2020)
Full size table

4 Simulation results and discussion

First, the simulation results for the proposed model is compared with the other mentioned apodization profile as reflectivity, delay, bandwidth, and filter line. Then, the performance evaluation parameters including Q-factor and BER are also investigated. Finally, the power budget that can be given by the model is discussed at \({10}^{-9}\) BER.

4.1 Reflectivity, delay, and filter line

Figure 4 shows the relation between reflectivity, delay, filter line, and the wavelength (nm) under full width half maximum (FWHM) bandwidth at-3 dB for CFBG parameters as in Table 2. For all apodization profiles, they show different bandwidth within the reflectivity curve.

Fig. 4
figure 4

Reflectivity, delay and filter line for each profile from a to g

Full size image

Each apodization profile exhibits a delay, where some ripples appear, especially in Gaussian and hyper-tan. In the other functions, the delay ripples are very small achieving a more efficient compensation process than the Gaussian and hyper-tan profiles. The filter line for each profile is illustrated, where it determines the time delay for each reflected wavelength for the compensation process along with the CFBG core.

Figure 5 summarizes the 3 dB bandwidth (FWHM) for each apodization profile including our proposed profile. The Gaussian one is the highest range with 1.82 nm and Blackman is the lowest with 1.548 nm.

Fig. 5
figure 5

Bandwidth range, FWHM, nm, for each apodization profile

Full size image

4.2 Grating index change and grating Length

Figure 6 illustrates the relationship between the grating index change as a function of an apodization profile and grating length for the proposed profile and the other apodization profiles.

Fig. 6
figure 6

Grating index change and grating length for different apodization profiles

Full size image

The figure shows each period and the color of its reflected wavelengths in the WDM range along with the grating core. Each profile also shows the reflected position of each wavelength and the value of the grating index change at this wavelength.

4.3 Q-factor

The optical signal suffers distortion in time because of the time delay occurs between the propagated wavelengths. The role of compensator at receiver is to compensate this time delay. So, it is important to show the relation between the bit period and the Q-factor of the received signal to evaluate the efficiency of the compensation process.

Figure 7 displays the Q-factor against the bit period for each apodization profile and the proposed model. It is noted, before time 0.2 ns, the Q-factor starts to increase gradually for all profiles until time 0.4 ns. After that, each profile gives different maximum peaks around time 0.5 ns. The proposed model is the highest peak followed by Hamming, Cauchy, Blackman, Hyper-tan, and the lowest one Gaussian. Then Q-factor starts to decrease gradually for all profiles till time 0.9 ns. Table 3 summarizes the maximum Q-factor for each profile and the propose one. Clearly, it is noted the proposed model gives the highest Q-factor (8.36).

Fig. 7
figure 7

Q-factor for each profile

Full size image
Table 3 Q-factor comparison for each profile
Full size table

4.4 BER

Figure 8 shows the BER for each profile. Before 0.2 ns, the BER for all profiles starts to decrease gradually till time 0.4 ns. After that, each profile gives a different peak down for BER around time 0.5 ns. The minimum peak down is achieved by the proposed model followed by Hamming, Cauchy, Blackman, Hyper-tan, Sinc, and Gaussian. Then, the BER for each profile starts to increase till time 0.9 ns.

Fig. 8
figure 8

BER for each profile

Full size image

Table 4 summarizes the minimum BER for each profile. The proposed model achieved the minimum BER 3.13 × 10−17.

Table 4 BER comparison for each profile
Full size table

4.5 Power budget

The proposed apodization function also reduced the transmitted power for one channel in the WDM system at 10−9 BER. Figure 9 shows the relationship between the BER and the transmitted power for each apodization profile. Below 15 dBm transmitted power, the BER for most of the apodization profiles starts to increase. At \(10^{ - 9}\) BER, the lowest transmitted power is achieved by the proposed model, followed by Hamming, Cauchy, Blackman, Hyper-tan, and Sinc, where the highest transmitted power is Gaussian. From Fig. 9, it is clear that the practical values of BER are achieved at below 0 dBm transmitted power.

Fig. 9
figure 9

Transmitted power for each profile

Full size image

Figure 10 shows the transmitted power comparisons for each profile as a power budget, where our proposed profile has the advantage of achieving the minimum required transmitted power.

Fig. 10
figure 10

Transmitted power comparisons for each profile

Full size image

5 Evaluation of Q-factor, BER and power budget

Table 5 shows the evaluation of our proposed profile in comparison with Ref. (Moustafa H. Aly et al. 2020). For the Q-factor, the proposed profile gives 8.36 (1.08% enhancement). Also, the BER is minimized to 3.13 × 10−17. The transmitted power is reduced to -5.55 dBm, which is 4% less than that found in the related work.

Table 5 Comparison with related work
Full size table

6 Conclusion

A new apodization profile is proposed and investigated to enhance the WDM system performance and reduce the power budget. The proposed profile is implemented in a CFBG as a post dispersion compensator in a WDM system for a distance 110 km. Reflectivity, delay, filter line, and bandwidth are compared for the proposed profile and other famous profiles. The proposed profile enhances the performance, where it gives 8.36 Q-factor and 3.13 × 10−17 BER. Also, the transmitted power is reduced to -5.55 dBm at 10−9 BER. The evaluation of the proposed profile is compared with the related work showing an enhancement in the Q-factor by 1.08%, a decrease in BER by 52.8%, and a reduction in the power budget by 4%.