Skip to main content
SpringerLink
Log in

Photo-thermal-elastic waves of excitation microstretch semiconductor medium under the impact of rotation and initial stress

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

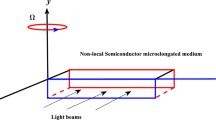
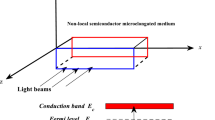
A novel mathematical-theoretical model is intreduced to study the microstretch properties of elastic semiconductor medium. The theoretical model is obtained during the photo-excitation transport processes in the generalized thermoelasticty theory. The new model can be called Microstretch-photo-thermoelasticity (MPT) theory, the MPT model is studied under the impact of hydrostatic initial stress. The carriers charge field (carrier density or plasma wave) appears due to optical excitation. During this model the interaction between thermal–mechanical-plasma waves is obtained when the medium is in a rotating case. When the medium is linear, isotropic and homogenous, the two dimension (2D) elastic and electronics deformation governing equations are investigated when the microinertia of the medium particles is taken into consideration. The basic physical variables are obtained with the mathematical plane harmonic wave technique to get the general solutions. The complete analytical solutions have been solved completely when some conditions from mechanical-thermal and plasma type are acted at the free surface of the medium. The silicon (Si) and Germanium (Ge) materials are used to make the numerical simulations. The numerical results are displayed graphically and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Abbreviations

\(\lambda ,\,\,\mu \quad \quad \;\) :

Lame’s elastic parameters

\(\delta_{n}\) :

The deformation potential difference

\(T\) :

The thermodynamic temperature

\(T_{0} \;\) :

The reference rest temperature

\(\hat{\gamma } = (3\lambda + 2\mu + k)\alpha_{{t_{1} }}\) :

The volume thermal expansion

\(\sigma_{ij}\) :

The stress coefficient tensor

\(\rho \quad \quad\) :

The density of the sample

\(\alpha_{{t_{1} }} ,\alpha_{{t_{2} }}\) :

Coefficients of linear thermal expansion

\({\text{e}}\) :

Cubical dilatation

\(C_{e}\) :

Specific heat of the material at constant strain

\(k\) :

The thermal conductivity

\(D_{E}\) :

The carrier diffusion coefficient

\(\tau\) :

The carrier lifetime

\(E_{g}\) :

The energy gap

\(e_{ij}\) :

Components of strain tensor

\(\Pi ,\Psi\) :

Two scalar functions

\(j_{0}\) :

The microinertia of microelement

\(m_{ij}\) :

Couple stress tensor

\(\alpha_{0} ,\lambda_{0} ,\lambda_{1}\) :

Microstretch elastic constants

\(\tau_{0} ,\nu_{0}\) :

Thermal relaxation times

\(\phi\) :

Rotation inertia vector

\(\phi^{*}\) :

The scalar microstretch

\(\lambda_{i}^{{}}\) :

The first moment (microstress) tensor

References

  • Abbas, I., Alzahrani, F., Elaiw, A.: A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 29, 328–343 (2019)

    Google Scholar 

  • Biot, M.: Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27, 240–253 (1956)

    ADS  MathSciNet  MATH  Google Scholar 

  • Carrera, E., Valvano, S.: A variable ESL/LW kinematic plate formulation for free-vibration thermoelastic analysis of laminated structures. J. Therm. Stresses 42(4), 452–474 (2019)

    Google Scholar 

  • Carrera, E., Valvano, S.: A variable kinematic shell formulation applied to thermal stress of laminated structures. J. Therm. Stresses 40(7), 803–827 (2017)

    Google Scholar 

  • Chadwick, P., Sneddon, I.N.: Plane waves in an elastic solid conducting heat. J. Mech. Phys. Solids 6, 223–230 (1958)

    ADS  MathSciNet  MATH  Google Scholar 

  • Chadwick, P.: Thermoelasticity: the dynamic theory. In: Hill, R., Sneddon, I.N. (eds.) Progress in Solid Mechanics, vol. I, pp. 263–328. North-Holland, Amsterdam (1960)

    Google Scholar 

  • Cicco, D., Nappa, L.: On the theory of thermomicrostretch elastic solids. J. Therm. Stress. 22(6), 565–580 (1999)

    MathSciNet  Google Scholar 

  • Cinefra, M., Valvano, S., Carrera, E.: Thermal stress analysis of laminated structures by a variable kinematic MITC9 shell element. J. Therm. Stresses 39(2), 121–141 (2016)

    Google Scholar 

  • Cinefra, M., Valvano, S., Carrera, E.: Heat conduction and thermal stress analysis of laminated composites by a variable kinematic MITC9 shell element. Curved Layer. Struct. 2, 301–320 (2015)

    Google Scholar 

  • Deresiewicz, H.: Plane waves in a thermoelastic solid. J. Acoust. Soc. Am. 29, 204–209 (1957)

    ADS  MathSciNet  Google Scholar 

  • Eringen, A.: Theory of thermo-microstretch elastic solids. Int. J. Eng. Sci. 28(12), 1291–1301 (1990)

    MathSciNet  MATH  Google Scholar 

  • Eringen, A.: Linear theory of micropolar elasticity. J. Math. Mech. 15, 909–923 (1966)

    MathSciNet  MATH  Google Scholar 

  • Ezzat, M., Abd-Elaal, M.: Free convection effects on a viscoelastic boundary layer flow with one relaxation time through a porous medium. J. Franklin Inst. 334(4), 685–706 (1997a)

    MathSciNet  MATH  Google Scholar 

  • Ezzat, M., Abd-Elaal, M.: State space approach to viscoelastic fluid flow of hydromagnetic fluctuating boundary-layer through a porous medium. Z. Angew. Math. Mech. 77, 197–207 (1997b)

    MathSciNet  MATH  Google Scholar 

  • Ezzat, M.: Free convection effects on perfectly conducting fluid. Int. J. Eng. Sci. 39(7), 799–819 (2001)

    MATH  Google Scholar 

  • Ezzat, M.: Hyperbolic thermal-plasma wave propagation in semiconductor of organic material. Waves Random Complex Media (2020). https://doi.org/10.1080/17455030.2020.1772524

    Article  Google Scholar 

  • Ezzat, M.: A novel model of fractional thermal and plasma transfer within a non-metallic plate. Smart Struct. Syst. 27(1), 73–87 (2021)

    Google Scholar 

  • Gordon, J., Leite, R., Moore, R., Porto, S., Whinnery, J.: Long-transient effects in lasers with inserted liquid samples. Bull. Am. Phys. Soc. 119, 501–510 (1964)

    Google Scholar 

  • Green, A., Lindsay, K.: Thermoelasticity. J. Elast. 2, 1–7 (1972)

    MATH  Google Scholar 

  • Khamis, A., El-Bary, A., Lotfy, Kh., Bakali, A.: Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alex. Eng. J. 59(1), 1–9 (2020)

    Google Scholar 

  • Kreuzer, L.: Ultralow gas concentration infrared absorption spectroscopy. J. Appl. Phys. 42, 2934 (1971)

    ADS  Google Scholar 

  • Lord, H., Shulman, Y.: A generalized dynamical theory of thermoelasticity. J Mech Phys Solid. 15, 299–309 (1967)

    ADS  MATH  Google Scholar 

  • Lotfy, Kh., Abo-Dahab, S.: Two-dimensional problem of two temperature generalized thermoelasticity with normal mode analysis under thermal shock problem. J. Comput. Theor. Nanosci. 12(8), 1709–1719 (2015)

    Google Scholar 

  • Lotfy, Kh.: The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field. Can. J. Phys. 94, 400–409 (2016)

    ADS  Google Scholar 

  • Lotfy, Kh.: A novel model of photothermal diffusion (PTD) fo polymer nano- composite semiconducting of thin circular plate. Phys. B- Condenced Matter 537, 320–328 (2018)

    ADS  Google Scholar 

  • Lotfy, Kh., Kumar, R., Hassan, W., Gabr, M.: Thermomagnetic effect with microtemperature in a semiconducting Photothermal excitation medium. Appl. Math. Mech. Engl. Ed. 39(6), 783–796 (2018)

    MathSciNet  MATH  Google Scholar 

  • Lotfy, Kh., Gabr, M.: Response of a semiconducting infinite medium under two temperature theory with photothermal excitation due to laser pulses. Opt. Laser Technol. 97, 198–208 (2017)

    ADS  Google Scholar 

  • Lotfy, Kh.: Photothermal waves for two temperature with a semiconducting medium under using a dual-phase-lag model and hydrostatic initial stress. Waves Random Complex Media 27(3), 482–501 (2017)

    ADS  MathSciNet  Google Scholar 

  • Lotfy, Kh.: A novel model for Photothermal excitation of variable thermal conductivity semiconductor elastic medium subjected to mechanical ramp type with two-temperature theory and magnetic field. Sci. Rep. (2019). https://doi.org/10.1038/s41598-019-39955-z

    Article  Google Scholar 

  • Lotfy, Kh.: Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. SILICON 11, 1863–1873 (2019b)

    Google Scholar 

  • Lotfy, Kh., El-Bary, A., El-Sharif, A.: Ramp-type heating micro-temperature for a rotator semiconducting material during photo-excited processes with magnetic field. Result. Phys. 19, 103338 (2020)

    Google Scholar 

  • Lotfy, Kh., Tantawi, R., Anwer, N.: Response of semiconductor medium of variable thermal conductivity due to laser pulses with two-temperature through photothermal process. SILICON 11, 2719–2730 (2019)

    Google Scholar 

  • Lotfy, Kh., Abo-Dahab, S., Tantawi, R., Anwer, N.: Thermomechanical response model of a reflection photo thermal diffusion waves (RPTD) for semiconductor medium. SILICON 12(1), 199–209 (2020b)

    Google Scholar 

  • Lotfy, Kh., Hassan, W., El-Bary, A., Kadry, M.: Response of electromagnetic and Thomson effect of semiconductor mediu due to laser pulses and thermal memories during photothermal excitation. Result. Phys. 16, 102877 (2020)

    Google Scholar 

  • Mahdy, A.: Numerical solutions for solving model time-fractional Fokker–planck equation. Numer. Method. Partial Diff. Equ. 37(2), 1120–1135 (2021)

    MathSciNet  Google Scholar 

  • Mahdy, A., Lotfy, Kh., Hassan, W., El-Bary, A.A.: Analytical solution of magneto photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source. Waves Random Complex Media (2020). https://doi.org/10.1080/17455030.2020.1717673

    Article  Google Scholar 

  • Mahdy, A., Gepreel, K., Lotfy, Kh., El-Bary, A.: A numerical method for solving the Rubella ailment disease model. Int. J. Mod. Phys. C 32, 71–15 (2021)

    MathSciNet  Google Scholar 

  • Mandelis, A., Nestoros, M., Christofides, C.: Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 36(2), 459–468 (1997)

    ADS  Google Scholar 

  • Misra, J., Chattopadhyay, N., Samanta, S.: Study of the thermoelastic interactions in an elastic half space subjected to a ramp-type heating-A state-space approach. Int. J. Eng. Sci. 34(5), 579–596 (1996)

    MATH  Google Scholar 

  • Mondal, S., Sur, A.: Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Random Complex Media (2020). https://doi.org/10.1080/17455030.2019.1705426

    Article  Google Scholar 

  • Othman, M., Lotfy, Kh.: The influence of gravity on 2-D problem of two temperature generalized thermoelastic medium with thermal relaxation. J. Comput. Theor. Nanosci. 12, 2587–2600 (2015)

    Google Scholar 

  • Othman, M., Lotfy, Kh.: Effect of rotating on plane waves in generalized thermo-microstretch elastic solid with one relaxation time. Multidiscip. Modeling Mat. Str. 7(1), 43–62 (2011)

    Google Scholar 

  • Othman, M., Lotfy, Kh.: On the plane waves of generalized thermo-microstretch elastic half-space under three theories. Int. Comm. Heat Mass Trans. 37(2), 192–200 (2010)

    Google Scholar 

  • Ramesh, G., Kumara, B., Gireesha, B., Rashidi, M.: Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. J. Appl. Fluid Mech. 9(3), 1115–1122 (2016)

    Google Scholar 

  • Singh, B.: Reflection and refraction of plane waves at a liquid/thermo-microstretch elastic solid interface. Int. J. Eng. Sci. 39(5), 583–598 (2001)

    MathSciNet  Google Scholar 

  • Song, Y., Todorovic, D.M., Cretin, B., Vairac, P.: Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 47, 1871 (2010)

    MATH  Google Scholar 

  • Tam, A.C. Ultrasensitive Laser Spectroscopy, pp. 1–108. Academic Press, New York (1983)

  • Tam, A.C.: Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 58, 381 (1986)

    ADS  Google Scholar 

  • Tam A.C., Photothermal Investigations in Solids and Fluids, pp. 1–33. Academic Press, Boston (1989)

  • Todorovic, D.M., Nikolic, P.M., Bojicic, A.I.: Photoacoustic frequency transmission technique: electronic deformation mechanism in semiconductors. J. Appl. Phys. 85, 7716–7726 (1999)

    ADS  Google Scholar 

  • Yasein M., Mabrouk N., Lotfy Kh. and EL-Bary A., The influence of variable thermal conductivity of semiconductor elastic medium during photothermal excitation subjected to thermal ramp type. Result. Phys., 15, 102766, (2019)

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Mathematics, College of Science and Humanities, Prince Sattam Bin Abdulaziz University, Aflaj, Riyadh, Saudi Arabia

    M. S. Mohamed & A. M. S. Mahdy

  2. Mathematics Department, Faculty of Science, Zagazig University, P.O. Box 44519, Zagazig, Egypt

    Kh. Lotfy

  3. Arab Academy for Science, Technology and Maritime Transport, P.O. Box 1029, Alexandria, Egypt

    A. El-Bary

  4. Department of Mathematics, Faculty of Science, Taibah University, Medina, Saudi Arabia

    Kh. Lotfy

Authors
  1. M. S. Mohamed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kh. Lotfy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. El-Bary
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. M. S. Mahdy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kh. Lotfy.

Ethics declarations

Conflict of interest

The authors confirmed no potential conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The basic coefficients of Eq. (38) are:

$$\Theta_{1} = A_{2} \,A_{7} - a_{3} a_{7} - A_{1} - A_{3} - A_{4} - A_{6} - \alpha_{1} + \frac{{a_{1} \,a_{11} - A_{5} }}{{a_{8} }}$$
(53)
$$\begin{gathered} \Theta_{2} = \left( {\frac{{a_{1} \,a_{11} - A_{5} }}{{a_{8} }} - A_{6} - A_{1} - b^{2} - \alpha_{1} - \frac{{A_{5} }}{{a_{8} }}} \right)a_{3} a_{7} - \varepsilon_{4} A_{7} \,a_{4} + \left( {\frac{{(b^{2} + A_{3} + A_{4} + A_{6} + \alpha_{1} )a_{11} }}{{a_{8} }} + \frac{{cA_{7} }}{{a_{8} }}} \right)a_{1} - \hfill \\ \frac{{\omega a_{11} \varepsilon_{1} A_{2} }}{{a_{8} }} - a_{14} A_{9} + (A_{2} A_{4} + A_{2} A_{3} + (b^{2} + \alpha_{1} )A_{2} )A_{7} + ( - A_{1} - A_{3} - A_{4} - \alpha_{1} )A_{6} + ( - A_{3} - A_{1} - \alpha_{1} )A_{4} \hfill \\ ( - A_{1} - \alpha_{1} )A_{3} - \alpha_{1} A_{3} + \varepsilon_{4} \varepsilon_{5} + \frac{{A_{2} A_{5} A_{7} - A_{5} A_{6} + ( - A_{1} - A_{3} - A_{4} - \alpha_{1} )A_{5} - c\omega \varepsilon_{1} }}{{a_{8} }} \hfill \\ \end{gathered}$$
(54)
$$\left. \begin{gathered} \Theta_{3} = - \varepsilon_{4} A_{7} a_{3} a_{4} + ( - (2b^{2} - \alpha_{1} )A_{2} A_{7} + ( - b^{2} - A_{1} - \alpha_{1} )A_{6} - (b^{2} + \alpha_{1} )A_{1} - b^{2} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )a_{3} )a_{7} \hfill \\ + ( - b^{2} \varepsilon_{4} - A_{3} \varepsilon_{4} - A_{4} \varepsilon_{4} )A_{7} \,a_{4} + ( - A_{6} - A_{4} - \alpha_{1} )A_{9} \,a_{14} + \hfill \\ ((A_{2} A_{3} - ( - b^{2} - \alpha_{1} )A_{2} A_{3} + b^{2} \alpha_{1} A_{2} )A_{7} + (( - A_{3} - A_{1} - \alpha_{1} )A_{4} \hfill \\ + ( - A_{1} - \alpha_{1} )A_{3} - \alpha_{1} A_{1} )A_{6} + (( - A_{1} - \alpha_{1} )A_{3} - \alpha_{1} A_{1} + \varepsilon_{4} \varepsilon_{5} )A_{4} + ( - \alpha_{1} A_{1} + \varepsilon_{4} \varepsilon_{5} )A_{3} + \varepsilon_{4} \varepsilon_{5} A_{1} \hfill \\ + \frac{1}{{a_{8} }}\left( \begin{gathered} \left( {\left( {\left( {2b^{2} + A_{6} + \alpha_{1} } \right)a_{11} + cA_{7} } \right)a_{1} - \omega \varepsilon_{1} A_{2} a_{11} + A_{2} A_{5} A_{7} - A_{5} A_{6} + \left( { - b^{2} - A_{1} - \alpha_{1} } \right)A_{5} - \omega c\varepsilon_{1} } \right) + \left( {\omega a_{11} \varepsilon_{1} \varepsilon_{4} - A_{5} A_{7} \varepsilon_{4} } \right)a_{4} \hfill \\ + (((b^{2} + A_{3} + A_{4} + \alpha_{1} )A_{6} + (b^{2} + A_{3} + \alpha_{1} )A_{4} - ( - b^{2} - \alpha_{1} )A_{3} + b^{2} \alpha_{1} - \varepsilon_{4} \varepsilon_{5} )a_{11} + (b^{2} c + cA_{3} + cA_{4} + c\alpha_{1} )A_{7} )a_{1} \hfill \\ \end{gathered} \right) \hfill \\ - A_{5} A_{9} a_{14} + ( - \omega \varepsilon_{1} A_{2} A_{4} - \omega \varepsilon_{1} A_{2} A_{3} - (b^{2} \omega \varepsilon_{1} + \omega \alpha_{1} \varepsilon_{1} )A_{2} )a_{11} + (A_{2} A_{4} + A_{2} A_{3} - ( - b^{2} - \alpha_{1} )A_{2} )A_{5} A_{7} + ( - A_{4} - A_{3} - A_{1} - \alpha_{1} ) \hfill \\ A_{5} A_{6} + (( - A_{3} - A_{1} - \alpha_{1} )A_{4} + ( - A_{1} - \alpha_{1} )A_{3} - \alpha_{1} A_{1} + \varepsilon_{4} \varepsilon_{5} )A_{5} - c\,\varepsilon_{1} A_{4} \hfill \\ - c\varepsilon_{1} \omega A_{3} - c\varepsilon_{1} \omega A_{1} - c\omega \varepsilon_{1} \alpha_{1} ) \hfill \\ \end{gathered} \right\}$$
(55)
$$\left. \begin{gathered} \Theta_{6} = \frac{1}{{a_{8} }}(((b^{4} \varepsilon_{4} (\omega a_{11} \varepsilon_{1} - A_{5} A_{7} \varepsilon_{4} ) + (((b^{4} a_{11} (A_{6} \alpha_{1} - \varepsilon_{4} \varepsilon_{5} ) + b^{2} c\alpha_{1} A_{7} )a_{1} \hfill \\ - b^{4} \omega \alpha_{1} \varepsilon_{1} A_{2} a_{11} + b^{4} \alpha_{1} A_{2} A_{5} A_{7} - b^{2} \alpha_{1} A_{1} A_{5} A_{6} + b^{2} \varepsilon_{4} \varepsilon_{5} A_{1} A_{5} - b^{2} c\omega \alpha_{1} \varepsilon_{1} A_{1} )a_{3} )a_{7} \hfill \\ + (b^{2} \omega A_{3} A_{4} \varepsilon_{1} \varepsilon_{4} - b^{2} A_{3} A_{4} A_{5} A_{7} \varepsilon_{4} ) + ((b^{2} A_{3} A_{4} A_{6} \alpha_{1} - b^{2} A_{3} A_{4} \varepsilon_{4} \varepsilon_{5} )a_{11} + b^{2} \alpha_{1} cA_{3} A_{4} A_{7} )a_{1} \hfill \\ + ( - c\omega A_{4} \alpha_{1} \varepsilon_{1} - A_{4} A_{5} A_{6} \alpha_{1} + A_{4} A_{5} \varepsilon_{4} \varepsilon_{5} )A_{9} a_{14} - b^{2} \alpha_{1} A_{2} \varepsilon_{1} A_{3} A_{4} a_{11} + b^{2} \alpha_{1} A_{2} A_{3} A_{4} A_{5} A_{7} \hfill \\ - \alpha_{1} A_{1} A_{3} A_{4} A_{5} A_{6} + \varepsilon_{4} \varepsilon_{5} A_{1} A_{3} A_{4} A_{5} - c\omega \varepsilon_{1} \alpha_{1} A_{1} A_{3} A_{4} ) \hfill \\ \end{gathered} \right\}$$
(56)
$$\left. \begin{gathered} \Theta_{4} = (((b^{4} + 2b^{2} \alpha_{1} )A_{2} - 2b^{2} a_{4} \varepsilon_{4} )A_{7} + (( - b^{2} - \alpha_{1} )A_{1} - b^{2} \alpha_{1} )A_{6} \hfill \\ + ( - b^{2} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{1} + b^{2} \varepsilon_{4} \varepsilon_{5} )a_{3} a_{7} + (( - A_{4} - \alpha_{1} )A_{6} - A_{4} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{9} a_{14} + \hfill \\ ((((b^{2} + \alpha_{1} )A_{2} - a_{4} \varepsilon_{2} )A_{3} + b^{2} \alpha_{1} A_{2} - b^{2} a_{4} \varepsilon_{4} )A_{4} + (\alpha_{1} b^{2} A_{2} - b^{2} a_{4} \varepsilon_{4} )A_{3} )A_{7} \hfill \\ + ((( - A_{1} - \alpha_{1} )A_{3} - A_{1} \alpha_{1} )A_{4} - A_{1} \alpha_{1} A_{3} )A_{6} + (( - A_{1} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{3} + \varepsilon_{4} \varepsilon_{5} A_{1} )A_{4} + \varepsilon_{4} \varepsilon_{5} A_{1} A_{3} + \hfill \\ \frac{1}{{a_{8} }}(((((2b^{2} + \alpha_{1} )A_{6} + b^{4} + 2b^{2} \alpha_{1} - \varepsilon_{4} \varepsilon_{5} )a_{11} + (2b^{2} c + c\alpha_{1} )A_{7} )a_{1} + (( - 2b^{2} \omega \varepsilon_{1} - \omega \alpha_{1} \varepsilon_{1} )A_{2} + \hfill \\ \omega a_{4} \varepsilon_{1} \varepsilon_{4} ) + ((2b^{2} + \alpha_{1} )A_{2} - a_{4} \varepsilon_{4} )A_{5} A_{7} + ( - b^{2} - A_{1} - \alpha_{1} )A_{5} A_{6} + (( - b^{2} - \alpha_{1} )A_{1} - b^{2} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{5} \hfill \\ - c\omega \varepsilon_{1} A_{1} - cb^{2} \omega \varepsilon_{1} - c\omega \alpha_{1} \varepsilon_{1} )a_{3} a_{7} + ((((b^{2} + A_{3} + \alpha_{1} )A_{4} + (b^{2} + \alpha_{1} )A_{3} + b^{2} \alpha_{1} )A_{6} \hfill \\ + ((b^{2} + \alpha_{1} )A_{3} + b^{2} \alpha_{1} - \varepsilon_{4} \varepsilon_{5} )A_{4} + (b^{2} \alpha_{1} - \varepsilon_{4} \varepsilon_{5} )A_{3} ) - b^{2} \varepsilon_{4} \varepsilon_{5} )a_{11} + ((b^{2} c + cA_{3} + \alpha_{1} c)A_{4} \hfill \\ + (b^{2} c + c\alpha_{1} )A_{3} + b^{2} c\alpha_{1} )A_{7} )a_{1} + ( - A_{5} A_{6} + ( - A_{4} - \alpha_{1} )A_{5} - c\omega \varepsilon_{1} )A_{9} a_{14} \hfill \\ + (( - \omega \varepsilon_{1} A_{2} A_{3} + ( - b^{2} \omega \varepsilon_{1} - \alpha_{1} \omega \varepsilon_{1} )A_{2} + \omega \varepsilon_{1} \varepsilon_{4} )A_{4} + (( - \omega b^{2} \varepsilon_{1} - \omega \alpha_{1} \varepsilon_{1} )A_{2} + \omega a_{4} \varepsilon_{1} \varepsilon_{4} )A_{3} \hfill \\ - b^{2} \alpha_{1} \omega \varepsilon_{1} A_{2} + b^{2} a_{4} \omega \varepsilon_{1} \varepsilon_{4} )a_{11} + ((A_{2} A_{3} + (b + \alpha_{1} )A_{2} - a_{4} \varepsilon_{1} )A_{4} + \varepsilon_{1} \varepsilon_{4} + ((b^{2} + \alpha_{1} )A_{2} - a_{4} \varepsilon_{4} )A_{3} \hfill \\ + b^{2} \alpha_{1} A_{2} - b^{2} a_{4} \varepsilon_{4} )A_{5} A_{7} + (( - A_{3} - A_{1} - \alpha_{1} )A_{4} + ( - A_{1} - \alpha_{1} )A_{3} - A_{1} \alpha_{1} )A_{5} A_{6} + \hfill \\ ((( - A_{1} - \alpha_{1} )A_{3} - A_{1} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{4} + ( - A_{1} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{3} + \varepsilon_{4} \varepsilon_{5} A_{1} \hfill \\ )A_{5} + ( - c\omega A_{1} \varepsilon_{1} - c\omega A_{3} \varepsilon_{1} - c\omega \alpha_{1} \varepsilon_{1} )A_{4} + ( - c\omega A_{1} \varepsilon_{1} - c\omega \alpha_{1} \varepsilon_{1} )A_{3} - c\omega \alpha_{1} \varepsilon_{1} A_{1} ) \hfill \\ \end{gathered} \right\}$$
(57)
$$\left. \begin{gathered} \Theta_{5} = ( - b^{4} \varepsilon_{4} A_{7} a_{3} a_{4} + (b^{4} A_{2} A_{7} \alpha_{1} - b^{2} A_{1} A_{6} + b^{2} A_{1} \varepsilon_{4} \varepsilon_{5} )a_{3} )a_{7} - b^{2} A_{3} A_{4} A_{7} \varepsilon_{4} a_{4} \hfill \\ + ( - A_{4} A_{6} \alpha_{1} + A_{4} \varepsilon_{4} \varepsilon_{5} )A_{9} a_{14} + b^{2} \alpha_{1} A_{2} A_{3} A_{4} A_{7} - \alpha_{1} A_{1} A_{3} A_{4} A_{6} + \varepsilon_{4} \varepsilon_{5} A_{1} A_{3} A_{4} \hfill \\ + \frac{1}{{a_{8} }}(((2b^{2} \omega a_{11} \varepsilon_{1} \varepsilon_{4} - 2b^{2} A_{5} A_{7} \varepsilon_{4} )a_{3} a_{4} + ((( - ( - b^{4} - 2b^{2} \alpha_{1} )A_{6} + b^{4} \alpha_{1} - 2b^{2} \varepsilon_{4} \varepsilon_{5} )a_{11} \hfill \\ - ( - b^{4} c - 2b^{2} c\alpha_{1} )A_{7} )a_{1} - (b^{4} \omega \varepsilon_{1} + 2b^{2} \alpha_{1} \omega \varepsilon_{1} )A_{2} a_{11} - ( - b^{4} - 2b^{2} \alpha_{1} )A_{2} A_{5} A_{7} \hfill \\ + ( - (b^{2} + \alpha_{1} )A_{1} - b^{2} )A_{5} A_{6} + ( - (b^{2} - \varepsilon_{4} \varepsilon_{5} )A_{1} + b^{2} \varepsilon_{4} \varepsilon_{5} )A_{5} - (b^{2} c\,\omega \,\varepsilon_{1} + c\alpha_{1} \omega \varepsilon_{1} )A_{1} \hfill \\ - b^{2} c\alpha_{1} \omega \varepsilon_{1} )a_{3} )a_{7} + (((b^{2} \omega \varepsilon_{1} \varepsilon_{4} + A_{3} \omega \varepsilon_{1} \varepsilon_{4} )A_{4} + b^{2} \varepsilon_{1} \varepsilon_{4} A_{3} )a_{11} + (( - b^{2} \varepsilon_{4} - A_{3} \varepsilon_{4} )A_{4} \hfill \\ - b^{2} \varepsilon_{4} A_{3} )A_{5} A_{7} )a_{4} + (((( - ( - b^{2} - \alpha_{1} )A_{3} + b^{2} \alpha_{1} )A_{4} + b^{2} \alpha_{1} A_{3} )A_{6} + ( - (b^{2} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{3} \hfill \\ - b^{2} \varepsilon_{4} \varepsilon_{5} )A_{4} - b^{2} \varepsilon_{4} \varepsilon_{5} A_{3} )a_{11} + (( - (b^{2} c - c\alpha_{1} )A_{3} + b^{2} \alpha_{1} c)A_{4} + b^{2} c\alpha_{1} A_{3} )A_{7} )a_{1} + (( - A_{4} - \alpha_{1} )A_{5} A_{6} \hfill \\ + ( - A_{4} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{5} - c\omega \varepsilon_{1} A_{4} - c\alpha_{1} \omega \varepsilon_{1} )A_{9} a_{14} + (( - (b^{2} \omega \varepsilon_{1} + \alpha_{1} \omega \varepsilon_{1} )A_{2} A_{3} - b^{2} \alpha_{1} \omega \varepsilon_{1} A_{2} )A_{4} \hfill \\ - b^{2} \varepsilon_{1} \alpha_{1} \omega A_{2} A_{3} )a_{11} + ( - ( - b^{2} - \alpha_{1} )A_{2} A_{3} + b^{2} \alpha_{1} A_{2} )A_{4} + b^{2} \alpha_{1} A_{2} A_{3} )A_{5} A_{7} + ((( - A_{1} - \alpha_{1} )A_{3} \hfill \\ - \alpha_{1} A_{1} )A_{4} - \alpha_{1} A_{1} A_{3} )A_{5} A_{6} + ((( - A_{1} \alpha_{1} + \varepsilon_{4} \varepsilon_{5} )A_{3} + \varepsilon_{4} \varepsilon_{5} A_{1} )A_{4} + \varepsilon_{4} \varepsilon_{5} A_{1} A_{3} )A_{5} + \hfill \\ (( - c\omega \varepsilon_{1} A_{1} - c\omega \alpha_{1} \varepsilon_{1} )A_{3} - c\omega \alpha_{1} \varepsilon_{1} A_{1} )A_{4} - c\omega \alpha_{1} \varepsilon_{1} A_{1} A_{3} ) \hfill \\ \end{gathered} \right\}$$
(58)

On the other hand, the basic coefficients of Eq. (47) are:

$$E_{1} = \frac{{\left( \begin{gathered} (\varepsilon_{1} \omega + A_{7} (a_{8} k_{n}^{2} - A_{5} ))(k_{n}^{2} - b^{2} )\left( {(k_{n}^{2} - A_{6} )(k_{n}^{2} - \alpha_{1} ) - \varepsilon_{4} \varepsilon_{5} } \right) - \hfill \\ \,\,\,\,\,A_{7} (k_{n}^{2} - b^{2} )(k_{n}^{2} - \alpha_{1} )\left[ {\varepsilon_{1} \omega A_{8} - \varepsilon_{4} \varepsilon_{5} + (k_{n}^{2} - A_{6} )(a_{8} k_{n}^{2} - A_{5} )} \right] \hfill \\ \end{gathered} \right)}}{{(k_{n}^{2} - \alpha_{1} )\left( {\varepsilon_{1} \omega A_{9} + (k_{n}^{2} - A_{6} )(a_{8} k_{n}^{2} - A_{5} )} \right) - \varepsilon_{4} \varepsilon_{5} }}$$
(59)
$$E_{2} = \frac{{\left( {(\varepsilon_{1} \omega + A_{7} (a_{8} k_{n}^{2} - A_{5} ))(k_{n}^{2} - b^{2} )(k_{n}^{2} - \alpha_{1} )} \right)}}{{(k_{n}^{2} - \alpha_{1} )\left( {\varepsilon_{1} \omega A_{9} + (k_{n}^{2} - A_{6} )(a_{8} k_{n}^{2} - A_{5} )} \right) - \varepsilon_{4} \varepsilon_{5} }}$$
(60)
$$E_{3} = \frac{{\varepsilon_{4} \left( {(\varepsilon_{1} \omega + A_{7} (a_{8} k_{n}^{2} - A_{5} ))(k_{n}^{2} - b^{2} )} \right)}}{{\varepsilon_{4} \varepsilon_{5} - (k_{n}^{2} - \alpha_{1} )\left( {\varepsilon_{1} \omega A_{9} + (k_{n}^{2} - A_{6} )(a_{8} k_{n}^{2} - A_{5} )} \right)}}$$
(61)
$$E_{4} = \frac{{a_{14} \left( {k_{n}^{2} - A_{4} )} \right)}}{{k_{n}^{4} - (a_{3} a_{7} + A_{3} + A_{7} )k_{n}^{2} + \left( {A_{3} A_{4} + b^{2} a_{3} a_{7} } \right)}}$$
(62)
$$E_{5} = \frac{{a{}_{7}a_{14} \left( {k_{n}^{2} - b^{2} )} \right)}}{{k_{n}^{4} - (a_{3} a_{7} + A_{3} + A_{7} )k_{n}^{2} + \left( {A_{3} A_{4} + b^{2} a_{3} a_{7} } \right)}}$$
(63)

The main parameters of Eqs. (52) can be obtained as:

$$\left. \begin{gathered} s_{1} = \,f_{1} k_{1} ,\quad s_{2} = \,f_{1} k_{2} ,\quad s_{3} = f_{2} + \lambda \,k_{3}^{2} - f_{3} ,\quad s_{4} = f_{2} + \lambda \,k_{4}^{2} - f_{3} , \hfill \\ s_{5} = f_{2} + \lambda \,\,k_{5}^{2} - f_{3} ,\quad s_{6} = f_{2} + \lambda \,\,k_{6}^{2} - f_{3} ,\quad f_{5} = b^{2} \mu .\quad \hfill \\ r_{1} = f_{5} + f_{4} \,\,k_{1}^{2} + k,\quad r_{2} = f_{5} + f_{4} \,k_{2}^{2} + k,\quad r_{3} = \,f_{1} k_{3} ,\quad \hfill \\ r_{4} = \,f_{1} k_{4} ,\quad r_{5} = \,f_{1} k_{5} ,\quad r_{6} = \,f_{1} k_{6} ,f_{1} = - i\,b\,(2\mu + k),\quad \hfill \\ f_{2} = \lambda_{0} - b^{2} \,(\lambda + 2\mu + k),\,f_{3} = \hat{\gamma }(1 + d_{n} ),\,f_{4} = \mu + k.\quad \hfill \\ \end{gathered} \right\}$$
(64)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mohamed, M.S., Lotfy, K., El-Bary, A. et al. Photo-thermal-elastic waves of excitation microstretch semiconductor medium under the impact of rotation and initial stress. Opt Quant Electron 54, 241 (2022). https://doi.org/10.1007/s11082-022-03533-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-022-03533-x

Keywords

Search

Navigation