Skip to main content
SpringerLink
Log in

Application of \(\tan (\phi (\xi )/2)\)-expansion method for the time-fractional Kuramoto–Sivashinsky equation

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

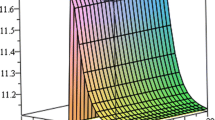
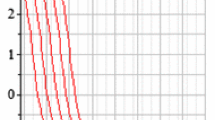
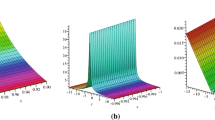
In this study, with the help of fractional complex transform and new analytical method namely, improved \(\tan (\phi (\xi )/2)\)-expansion method (ITEM), we obtained new solitary wave solution for time-fractional nonlinear Kuramoto–Sivashinsky equation. By using of the fractional complex transform we could convert a nonlinear fractional differential equation into its equivalent ordinary differential equation form. Description of the method is given and the obtained results reveal that the ITEM is a new significant method for exploring nonlinear partial differential models. It is worth mentioning that some of newly obtained solutions are identical to already published results as Tanh method Sahoo and Saha Ray (Phys A 434:240–245, 2015). Therefore, this method can be applied to study many other nonlinear fractional partial differential equations which frequently arise in engineering, mathematical physics and nonlinear optic. Moreover, by using Matlab, some graphical simulations were done to see the behavior of these solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  • Aghdaei, M.F., Manafian, J.: Optical soliton wave solutions to the resonant Davey–Stewartson system. Opt. Quant. Electron 48, 1–33 (2016)

    Article  Google Scholar 

  • Aghdaei, M.F., Manafianheris, J.: Exact solutions of the couple Boiti–Leon–Pempinelli system by the generalized \(\rm (\frac{G^{\prime }}{G})\)-expansion method. J. Math. Ext. 5, 91–104 (2011)

    MathSciNet  MATH  Google Scholar 

  • Alfaro, C.M., Depassier, M.C.: A five-mode bifurcation analysis of a Kuramoto–Sivashinsky equation with dispersion. Phys. Lett. A 184, 184–189 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Alfaro, C.M., Benguria, R.D., Depassier, M.C.: Finite mode analysis of the generalized Kuramoto–Sivashinsky equation. Physica D 61, 1–5 (1992)

    Article  ADS  MATH  Google Scholar 

  • Aslan, I., Marinakis, V.: Some remarks on Exp-function method and its applications. Commun. Theor. Phys. 56, 397–403 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Barker, B., Johnson, M.A., Noble, P., Rodrigues, L.M., Zumbruna, K.: Nonlinear modulational stability of periodic traveling-wave solutions of the generalized Kuramoto–Sivashinsky equation. Physica D 258, 11–46 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Bekir, A.: Application of the Exp-function method for nonlinear differential-difference equations. Appl. Math. Comput. 215(11), 352–362 (2010)

    ADS  MathSciNet  MATH  Google Scholar 

  • Bulut, H., Baskonus, H.M., Pandir, Y.: The modified trial equation method for fractional wave equation and time fractional generalized Burgers equation, Abstr. Appl. Anal. (2013). Article ID 636802

  • Chen, Y., Wang, Q.: Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic functions solutions to (1 + 1)-dimensional dispersive long wave equation. Chaos Solitons Fract. 24, 745–757 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Conte, R.: Exact solutions of nonlinear partial differential equations by singularity analysis. In: Lecture Notes in Physics, Springer, p. 183 (2003)

  • Debnath, L.: Nonlinear Partial Differential Equations for Scientists and Engineers, 2nd edn. Birkhäusher, Boston (2005)

    Book  MATH  Google Scholar 

  • Dehghan, M., Manafian, J.: The solution of the variable coefficients fourth-order parabolic partial differential equations by homotopy perturbation method. Z. Naturforsch 64a, 420–430 (2009)

    ADS  Google Scholar 

  • Dehghan, M., Manafian, J., Saadatmandi, A.: Solving nonlinear fractional partial differential equations using the homotopy analysis method. Num. Meth. Part. Differ. Eq. J. 26, 448–479 (2010)

    MathSciNet  MATH  Google Scholar 

  • Dehghan, M., Manafian, J., Saadatmandi, A.: Application of the Exp-function method for solving a partial differential equation arising in biology and population genetics, Int. J. Num. Methods Heat Fluid Flow 21, 736–753 (2011)

    Article  Google Scholar 

  • Ekici, M., Zhou, Q., Sonmezoglu, A., Manafian, J., Mirzazadeh, M.: The analytical study of solitons to the nonlinear Schödinger equation with resonant nonlinearity. Optik-Int. J. Light Electron Opt. 130, 378–382 (2017)

    Article  Google Scholar 

  • El-Ajou, A., Abu Arqub, O., Momani, S.: Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: a new iterative algorithm. J. Comput. Phys. 293, 81–95 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Eslami, M., Vajargah, Fathi, Mirzazadeh, M., Biswas, A.: Application of first integral method to fractional partial differential equations. Indian J. Phys. 88, 177–184 (2014)

    Article  ADS  Google Scholar 

  • Helal, M.A., Seadawy, A.R.: Variational method for the derivative nonlinear Schrödinger equation with computational applications. Phys. Scr. 80, 035004 (2009)

    Article  ADS  MATH  Google Scholar 

  • Jumarie, G.: Modified Riemann–Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 51, 1367–1376 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  • Khater, A.H., Temsah, R.S.: Numerical solutions of the generalized Kuramoto–Sivashinsky equation by Chebyshev spectral collocation methods. Comput. Math. Appl. 56, 1465–1472 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  • Kudryashov, N.: Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 14, 3507–3529 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Kudryashov, N., Loguinova, N.: Be careful with the Exp-function method. Commun. Nonlinear Sci. Numer. Simul. 14, 1881–1990 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Kurulay, M., Secer, A., Akinlar, M.A.: A new approximate analytical solution of Kuramoto–Sivashinsky equation using homotopy analysis method. Appl. Math. Inf. Sci. 7, 267–271 (2013)

    Article  MathSciNet  Google Scholar 

  • Manafian, J.: On the complex structures of the Biswas-Milovic equation for power, parabolic and dual parabolic law nonlinearities. Eur. Phys. J. Plus 130, 1–20 (2015)

    Article  Google Scholar 

  • Manafian, J.: Optical soliton solutions for Schrödinger type nonlinear evolutionequations by the \(tan(\phi /2)\)-expansion method. Optik-Int. J. Electron Opt. 127, 4222–4245 (2016)

    Article  Google Scholar 

  • Manafian, J., Lakestani, M.: Optical solitons with Biswas–Milovic equation for Kerr law nonlinearity. Eur. Phys. J. Plus 130, 1–12 (2015)

    Article  Google Scholar 

  • Manafian, J., Lakestani, M.: Application of \(tan(\phi /2)\)-expansion method for solving the Biswas–Milovic equation for Kerr law nonlinearity. Optik-Int. J. Electron Opt. 127, 2040–2054 (2016a)

    Article  Google Scholar 

  • Manafian, J., Lakestani, M.: Dispersive dark optical soliton with Tzitzéica type nonlinear evolution equations arising in nonlinear optics. Opt. Quant. Electron 48, 1–32 (2016b)

    Article  Google Scholar 

  • Manafian, J., Lakestani, M.: Abundant soliton solutions for the KunduEckhaus equation via \(tan(\phi /2)\)-expansion method. Optik-Int. J. Electron Opt. 127, 5543–5551 (2016c)

    Article  Google Scholar 

  • Manafian, J., Lakestani, M.: A new analytical approach to solve some of the fractional-order partial differential equations. Indian J. Phys. 91(3), 243–258 (2017)

    Article  ADS  Google Scholar 

  • Manafian, J., Lakestani, M., Bekir, A.: Study of the analytical treatment of the (2 + 1)-dimensional Zoomeron, the Duffing and the SRLW equations via a new analytical approach. Int. J. Appl. Comput. Math. 2, 243–268 (2016a)

    Article  MathSciNet  Google Scholar 

  • Manafian, J., Aghdaei, M.F., Zadahmad, M.: Analytic study of sixth-order thin-film equation by \(tan(\phi /2)\)-expansion method. Opt. Quant. Electron 48, 1–16 (2016b)

    Article  Google Scholar 

  • Marcinkevicius, R., Navickas, Z., Ragulskis, M., Telksnys, T.: Solitary solutions to a relativistic two-body problem. Astrophys. Space Sci. 361, 201–207 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Mirzazadeh, M.: Analytical study of solitons to nonlinear time fractional parabolic equations. Nonlinear Dyn. 85, 2569–2576 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  • Mirzazadeh, M., Eslami, M.: Exact multisoliton solutions of nonlinear Klein–Gordon equation in \(1+2\) dimensions. Eur. Phys. J. Plus 128, 1–9 (2015)

    Google Scholar 

  • Mirzazadeh, M., Eslami, M., Milovic, D., Biswas, A.: Topological solitons of resonant nonlinear Schödinger’s equation with dual-power law nonlinearity by G′/G-expansion technique. Optik-Int. J. Light Electron Opt. 125, 5480–5489 (2014)

    Article  Google Scholar 

  • Mirzazadeh, M., Eslami, M., Arnous, A.H.: Dark optical solitons of Biswas–Milovic equation with dual-power law nonlinearity. Eur. Phys. J. Plus 130, 1–7 (2015)

    Article  Google Scholar 

  • Mirzazadeh, M., Ekici, M., Zhou, Q., Biswas, A.: Exact solitons to generalized resonant dispersive nonlinear Schrödinger’s equation with power law nonlinearity. Optik-Int. J. Light Electron Opt. 130, 178–183 (2017)

    Article  Google Scholar 

  • Navickas, Z., Ragulskis, M.: How far one can go with the Exp-function method? Appl. Math. Comput. 211, 522–530 (2009)

    MATH  Google Scholar 

  • Navickas, Z., Bikulciene, L., Rahula, M., Ragulskis, M.: Algebraic operator method for the construction of solitary solutions to nonlinear differential equations. Commun. Nonlinear Sci. Num. Simul. 18, 1374–1389 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  • Navickas, Z., Marcinkevicius, R., Telksnys, T., Ragulskis, M.: Existence of second order solitary solutions to Riccati differential equations coupled with a multiplicative term. IMA J. Appl. Math. 81, 1163–1190 (2016)

    Article  MathSciNet  Google Scholar 

  • Navickas, Z., Ragulskis, M., Marcinkevicius, R., Telksnys, T.: Kink solitary solutions to generalized Riccati equations with polynomial coefficients. J. Math. Anal. Appl. 448, 156–170 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  • Rademacher, J.D.M., Wattenberg, R.W.: Viscous shocks in the destabilized Kuramoto–Sivashinsky equation. J. Comput. Nonlinear Dyn. 1, 336–347 (2006)

    Article  Google Scholar 

  • Sahoo, S., Saha Ray, S.: New approach to find exact solutions of time-fractional Kuramoto–Sivashinsky equation. Phys. A 434, 240–245 (2015)

    Article  MathSciNet  Google Scholar 

  • Seadawy, A.R.: Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus 130, 182 (2015)

    Article  Google Scholar 

  • Taghizadeh, N., Mirzazadeh, M., Rahimian, M., Akbari, M.: Application of the simplest equation method to some time-fractional partial differential equations. Ain Shams Eng. J. 4(4), 897–902 (2013)

    Article  Google Scholar 

  • Tariq, H., Akram, G.: New approach for exact solutions of time fractional Cahn–Allen equation and time fractional Phi-4 equation. Phys. A 473, 352–362 (2017)

    Article  MathSciNet  Google Scholar 

  • Tonti, E.: Variational formulation for every nonlinear problem. Int. J. Eng. Sci. 22, 1343–1371 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  • Wazwaz, A.M.: New solitary wave solutions to the Kuramoto–Sivashinsky and the Kawahara equations. Appl. Math. Comput. 182, 1642–1650 (2006)

    MathSciNet  MATH  Google Scholar 

  • Xu, F., Gao, Y., Yang, X., Zhang, H.: Construction of fractional power series solutions to fractional Boussinesq equations using residual power series method. Math. Probl. Eng. 15 (2016). Article ID 5492535

  • Yin, W., Xu, F., Zhang, W., Gao, Y.: Asymptotic expansion of the solutions to time-space fractional Kuramoto–Sivashinsky equations. Adv. Math. Phys., 9 (2016). Article ID 4632163

  • Zhao, X., Wang, L., Sun, W.: The repeated homogeneous balance method and its applications to nonlinear partial differential equations. Chaos Solitons Fract. 28, 448–453 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Zhou, Q., Mirzazadeh, M.: Analytical solitons for Langmuir waves in plasma physics with cubic nonlinearity and perturbations. Z. Naturforsch. (2016). doi:10.1515/zna-2016-0201

  • Zhou, Q., Yao, D., Chen, F.: Analytical study of optical solitons in media with Kerr and parabolic-law nonlinearities. J. Mod. Opt. 60, 1652–1657 (2013)

    Article  ADS  Google Scholar 

  • Zhou, Q., Zhu, Q., Bhrawy, A.H., Moraru, L., Biswas, A.: Optical solitons with spatially-dependent coefficients by Lie symmetry. Optoelectron. Adv. Mater.-Rapid Commun. 8, 800–803 (2014)

    Google Scholar 

  • Zhou, Q., Zhu, Q., Liu, Y., Yu, H., Yao, P., Biswas, A.: Thirring optical solitons in birefringent fibers with spatio-temporal dispersion and Kerr law nonlinearity. Laser Phys. 25, 015402 (2015)

    Article  ADS  Google Scholar 

  • Zhou, Q., Ekici, M., Sonmezoglu, A., Manafian, J., Khaleghizadeh, S., Mirzazadeh, M.: Exact solitary wave solutions to the generalized Fisher equation. Optik 127, 12085–12092 (2016)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Young Researchers and Elite Club, Ilkhchi Branch, Islamic Azad University, Ilkhchi, Iran

    Jalil Manafian

  2. Department of Mathematics, Payame Noor University, P.O. Box 19395-3697, Tehran, Iran

    Mohammadreza Foroutan

Authors
  1. Jalil Manafian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammadreza Foroutan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jalil Manafian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Manafian, J., Foroutan, M. Application of \(\tan (\phi (\xi )/2)\)-expansion method for the time-fractional Kuramoto–Sivashinsky equation. Opt Quant Electron 49, 272 (2017). https://doi.org/10.1007/s11082-017-1107-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-017-1107-3

Keywords

Mathematics Subject Classification

Search

Navigation