1 Introduction

It is commonly known that for strongly n-type doped MCT structures there are large differences between the experimental data of electron concentration and the numerical results obtained by using the Kane’s model of band structure (Kane 1957). Usually the numerical results are over one order of magnitude smaller than those obtained experimentally. This is the reason for the discrepancies between the values of the detector’s performances measured experimentally and those calculated numerically. To omit this issue some simple procedures are used to increase the values of the electron concentration. Sometimes the values of the electron effective mass are assumed to be much higher than the real values to increase the density of states in the conduction band (Wenus et al. 2001), or instead of Kane’s model, a hyperbolic model is applied (Chang et al. 2006). In this model the wave vector dependence of the conduction band energy differs significantly from Kane’s results (Kane 1957). Those “tricks” have no physical interpretation, and the corrections of the discrepancies should be found in another way. If we use these values of effective electron mass in calculations of electron mobility or tunneling current, we would get results of at least one order of magnitude lower than the experimental data. In this work we aim to find a correct and possibly simple way for the numerical calculation of the charge carrier concentration in doped structures (primarily those doped with donors). If we apply classical methods [see for example Schmit (1970) and Ariel-Altschul et al. (1992)] based on the assumption that isolated donor levels exist, this leads to results which are very much underrated in relation to the experimental results and it is impossible to explain why. On the other hand, the assumption in this case that the total ionization of donors takes place gives the incorrect values of the Fermi energy. In p-type materials, these difficulties can occur in practice only at the very high concentrations of acceptors. However, for MCT structures applied in long wavelength infrared radiation (LWIR) and mid wavelength infrared radiation (MWIR) detectors full activity of Indium being the donor can be achieved over a range from 3 × 1014 cm−3 to 1018 cm−3 (Mynbayev and Ivanov-Omskii 2006). In this work we try to solve the above problem by making the following assumptions:

  • It is possible to create a dopant bands in the MCT if the dopant concentration is high enough so that the interaction between the dopant atoms could be seen. Due to the considerably lower effective mass of conduction electrons than that of heavy holes, donor bands are still created at considerably lower dopant concentrations than acceptor bands are. One can find important and plentiful information about this issue in the monograph of (Shklovskii and Efros 1984).

  • The number of energy levels in the dopant bands depends on the kind of outer orbitals determining the energy states in the doping atoms.

  • We have assumed that the density of states in the dopant bands has a Gaussian distribution with standard deviation being the function of the dopant’s concentration.

  • It is possible to create the donor bands connected both with the hydrogen-like donor ground states as well as with donor excess states.

2 Numerical results and experimental verification

Schmit (1970) has calculated the intrinsic carrier concentration by determining the value of the reduced Fermi energy for which the electron concentration from the Kane model is equal to the hole concentration. In the calculations it has been assumed that the Kane model was applicable at elevated temperatures. The density of free holes in the valence band, under the assumption on the parabolic shape of the heavy-holes band, was taken from

$$p = 4\pi \left( {\frac{{2k_{B} T}}{{h^{2} }}} \right)^{3/2} m_{hh}^{*} \;^{3/2} F_{1/2} \left[ { - \left( {\eta + Y} \right)} \right]$$
(1)

where m *hh denotes the effective mass of a heavy hole, F1/2 is the Fermi–Dirac integral, \(\eta = \frac{{E_{C} - F}}{{k_{B} T}}\), \(Y = \frac{{E_{g} }}{{k_{B} T}}\), Eg is the band gap energy, k B is the Boltzmann’s constant, T is the temperature, and F is the Fermi energy, EC is energy of the bottom of conduction band and h is the Planck’s constant.

Ariel-Altschul et al. (1992) obtained the relation for electron concentration by considering the carrier degeneracy and non-parabolic conduction band. The electron concentration, with the Bebb’s non-parabolic approximation (Bebb and Ratiff 1961), being valid for both narrow and wide band semiconductors, is given by:

$$n = 8\pi 2^{1/2} \left( {\frac{{m_{e}^{*} k_{B} T}}{{h^{2} }}} \right)^{3/2} \mathop \int \limits_{0}^{\infty } \frac{{X^{1/2} \left( {1 + \beta X} \right)^{1/2} \left( {1 + 2\beta X} \right)}}{{1 + exp\left( {X - \eta } \right)}}dX\quad {\text{in}}\;{\text{m}}^{ - 3}$$
(2)

where \(\beta = \frac{1}{Y}\left( {1 - \frac{{m_{e}^{*} }}{{m_{0} }}} \right)^{2}\).

Poklonski et al. (2009) developed a model of hopping dc conductivity via the nearest boron atoms in moderately compensated diamond crystals. They have assumed that the energy of acceptor levels exhibits the Gaussian distribution due to the fluctuations of the electrostatic interaction of ionized acceptors with other ionized atoms, both acceptors and donors. We made a similar assumption that the energy of ionized acceptors and donors is influenced by fluctuations caused by interaction with other electrical charges distributed inside the semiconductor. Now the concentration of ionized acceptors may be expressed by:

$${\text{N}}_{\text{A}}^{ - } = \mathop \int \limits_{ - \infty }^{ + \infty } \frac{{{\text{N}}_{\text{A}} }}{{\sqrt {2\uppi} {\text{W}}}}{\text{e}}^{{\frac{{ - \left( {{\text{E}} - {\text{E}}_{\text{A}} } \right)^{2} }}{{2{\text{W}}^{2} }}}} \frac{1}{{1 +\upalpha\;{ \exp }\left( {\frac{{ {\text{E}} - {\text{F}}}}{{{\text{k}}_{\text{B}} {\text{T}}}}} \right)}}{\text{dE}}$$
(3)

Similarly the concentration of ionized donors reads:

$${\text{N}}_{\text{D}}^{ + } = \mathop \int \limits_{ - \infty }^{ + \infty } \frac{{{\text{N}}_{\text{D}} }}{{\sqrt {2\uppi} {\text{W}}}}{\text{e}}^{{\frac{{ - \left( {{\text{E}} - {\text{E}}_{\text{D}} } \right)^{2} }}{{2{\text{W}}^{2} }}}} \frac{1}{{1 +\upbeta_{1} { \exp }\left( {\frac{{ {\text{F}} - {\text{E}}}}{{{\text{k}}_{\text{B}} {\text{T}}}}} \right)}}{\text{dE}}$$
(4)

where NA and ND denotes the concentration of acceptors and donors, respectively, EA and ED denote the energy of the dopant levels, and α and β 1 are the degeneracy factors. In the past most researchers used α = 4 and β 1 = 2. In fact, determination of the proper degeneracy factor is very important and far from being obvious. Some simple rules which allow the determination of these factors are shown, for example in Look (1989).

Here E denotes energy. The means for these distributions are equal to \({\text{E}}_{\text{A}}\) and \({\text{E}}_{\text{D}} ,\) respectively, where \(E_{A} - E_{V}\) is the mean ionization energy of acceptors, and \({\text{E}}_{\text{C}} - {\text{E}}_{\text{D}}\) is the mean ionization energy of donors. The standard deviation W caused by interaction of the electron with all the other electric carriers inside the unit of semiconductor volume is approximated by the relation (Kane 1985):

$$W = \frac{1}{{2\pi^{{\frac{1}{2}}} }}\frac{{e^{{\frac{3}{2}}} }}{{\left( {\varepsilon \varepsilon_{0} } \right)^{{\frac{3}{4}}} }}\left( {k_{B} T} \right)^{{\frac{1}{4}}} \left( {N_{D} + N_{A} } \right)^{{\frac{1}{4}}}$$
(5)

The integration range in relations (3) and (4) may be limited to E A  − 3 W ≤ E ≤ E A  + 3 W for the acceptors and E D  − 3 W ≤ E ≤ E D  + 3 W for the donors. Errors of calculations are smaller than 0.2%. The ionization energy of a hydrogen-like donor impurity is:

$$E_{C} - E_{D} = 13.6\frac{{\left( {m_{e}^{*} /m_{0} } \right)}}{{\varepsilon^{2} }}\quad {\text{in}}\;{\text{eV}}$$
(6)

m * e and m 0 are the electron effective mass and the rest mass, respectively, e the electron charge, and ɛ the static dielectric constant. In the case of a hydrogen-like acceptor impurity must be taken into account the light holes and heavy holes (Capper and Garland 2011; Chen and Tregilgas 1987). This results in:

$$E_{A} - E_{V} = 13.6 \left( {0.44 + 0.56\frac{{m_{lh}^{*} }}{{m_{hh}^{*} }}} \right)\left( {\frac{{m_{hh}^{*} }}{{m_{0} }}} \right)/\varepsilon^{2} \quad {\text{in}}\;{\text{eV}}$$
(7)

Here \(m_{lh}^{*}\) is the light hole effective mass and m * hh is the heavy hole effective mass, respectively. The values of physical parameters of HgCdTe used in our calculations are taken from Capper (1994). In our calculations we have assumed (after Capper and Garland 2011) that E C  − E D  = 0.3 and 0.85 meV for x = 0.2 and x = 0.3 respectively, and E A  − E V  = 11 and 14 meV for x = 0.2 and x = 0.3, respectively. These values roughly agree with the values obtained by using Eqs. (6) and (7), however, our earlier simulations with different values of the center of gravity of donor band around the bottom of conduction band shown the weak influence on electron concentration. In all cases we have assumed the acceptor concentration to be 1013 cm−3. The bandgap narrowing is not considered in our calculations. Using relations (1)–(7) we can express the equation for electrical neutrality as:

$${\text{N}}_{\text{D}}^{ + } + {\text{p}} - {\text{N}}_{\text{A}}^{ - } - {\text{n}} = 0$$
(8)

In the solution of Eq. (8) we have determined the reduction of Fermi energy \(\eta\) and next \({\text{p}},{\text{n}},{\text{N}}_{\text{A}}^{ - }\) and \({\text{N}}_{\text{D}}^{ + }\). Unfortunately, in spite of the fact that in the case of the application of the above method to p-type materials the results obtained are usually consistent with the experimental ones, for n-type materials of the dopant concentration above 1015 cm−3 the results of the computations are much underrated in relation to the experimental data. The results of our computations are presented in Fig. 1a, b by dashed lines. The reason behind this behaviour is low density of states within the conduction band. Thus, additional energy states, which could be populated by electrons from the heavy-holes band should be found. It is well known that at sufficient impurity concentration there is the occurrence of a significant overlapping of electron wave functions for the neighbouring impurities enabling electrons to jump from one impurity to another and, in this way, to contribute significantly to the current. This type of metal–insulator transition depends on the effect of the electron–electron interactions and is often referred to as the Mott transition (Mott 1956; Conwell 1956). Despite the fact that there exists extensive literature in this field (Landsberg 1991) the nature of these transitions is not yet fully understood. The ionization energy of donor levels in narrow-gap MCT is below 1 meV (Capper and Garland 2011). Due to the fact that the ground donor level is degenerated β 1-fold, the donor band being created should contain β 1 N D energy levels. β 1 = 2 if the ground donor level is an s-like donor state. There should also exist the bands corresponding to the excited states of the donor level. The energy distance between the individual states of the donor level can be easily estimated on the basis of a hydrogen-like model. We have assumed that the density of ground states exhibits the Gaussian distribution with standard deviation determined by relation (5), however \({\text{n}}_{{{\text{D}}_{1} }} ,\) the electron concentration in this band, is determined by the relation:

Fig. 1
figure 1

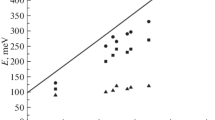
Lines denoted as n show electron concentration and these denoted as p the hole concentration, respectively as the function of donor concentration. a Structure with CdTe mole fraction x = 0.2 at 77 K. Experimental data are shown for epitaxial CdxHg1−xTe structures with near 0.2 mol fraction grown by MOCVD technology doped in iodine; (1) Murakami et al. (1993), (2) Mitra et al. (1994) structures deposited on CdZnTe (100)4° substrate, (3) Faraone and Antoszewski (2016). b Results for x = 0.3 at 77 K. Dashed lines show calculated results obtained by solving the relation (8) and without assumption of the existence of donor bands. Solid lines are obtained by solving relation (11) under the assumption that two donor bands exist, one connected with donor ground states and the second connected with donor excess states

Full size image
$${\text{n}}_{{{\text{D}}_{1} }} = \mathop \int \limits_{{{\text{E}}_{\text{C}} - 3{\text{W}}}}^{{{\text{E}}_{\text{C}} + 3{\text{W}}}} \frac{{\upbeta_{1} {\text{N}}_{\text{D}} }}{{\sqrt {2\uppi} {\text{W}}}}{\text{e}}^{{\frac{{ - \left( {{\text{E}} - {\text{E}}_{\text{C}} - {\text{E}}_{\text{D}} } \right)^{2} }}{{2{\text{W}}^{2} }}}} \frac{1}{{1 + { \exp }\left( {\frac{{{\text{E}} - {\text{F}}}}{{{\text{k}}_{\text{B}} {\text{T}}}}} \right)}}{\text{dE}}$$
(9)

The mean value of energy for this distribution may occur at an energy equal to ED.

In the hydrogen-like model the radius of the first excited state is four time higher than that for the unexcited state, thus the overlapping of the electron wave function may occur even for the low concentration of donor atoms. This is why we have assumed that it creates the additional donor band. We have also assumed that the density of states in this band also exhibits the Gaussian distribution with the standard deviation determined by relation (5), however \({\text{n}}_{{{\text{D}}_{2} }} ,\) the electron concentration in this band is determined by the relation:

$${\text{n}}_{{{\text{D}}_{2} }} = \mathop \int \limits_{{{\text{E}}_{\text{C}} - 3{\text{W}}}}^{{{\text{E}}_{\text{C}} + 3{\text{W}}}} \frac{{\upbeta_{2} {\text{N}}_{\text{D}} }}{{\sqrt {2\uppi} {\text{W}}}}{\text{e}}^{{\frac{{ - \left( {{\text{E}} - {\text{E}}_{\text{C}} } \right)^{2} }}{{2{\text{W}}^{2} }}}} \frac{1}{{1 + { \exp }\left( {\frac{{{\text{E}} - {\text{F}}}}{{{\text{k}}_{\text{B}} {\text{T}}}}} \right)}}{\text{dE}}$$
(10)

The overlap between impurity wave-functions is strong enough so that the impurity band must cover an appreciable range of energy. The mean for this distribution may occur at an energy above or equal to \({\text{E}}_{\text{C}}\).We have assumed equal to \({\text{E}}_{\text{C}}\). The overlapping between impurity electron wave-functions in excess states is greater than for electrons in ground state because of the larger orbits as a result of the hydrogen-like model. Therefore there should also exist the bands corresponding to the excited states of the donor level. We take into account two bands, first corresponding to the ground state and the second corresponding to the first excited state in the hydrogen-like model. The energy distance between the centers of gravity of this two bands assumed in our work roughly agrees with energy distance between ground state and excess states in hydrogen-like model for the fifth valence in donor atom in HgCdTe. The presence of these large impurity bands must have a considerable effect on the density of the electron states g(E) for the original conduction band. This idea is shown in Fig. 2a, b. \(\upbeta_{2}\) is the degeneracy of the first excess hydrogen-like donor state. Because it is orbital p, \(\upbeta_{2}\) should be equal to 6. Using relations (1), (2), (3), (9) and (10) we can express the equation for electrical neutrality as:

Fig. 2
figure 2

The density of states (in eV−1 cm−3) as the function of energy in material of mole fraction x = 0.2. The curve marked by NC presents the density of states in conduction band. Te value of energy denoted as Ec is the edge of the conduction band. Curves indicated by number 1 show the density of states in the donor band connected with ground donor states, and those indicated by number 2 show the density of states in the donor band connected with the excess states. a Structures with the donor concentration N D  = 1015 cm−3 at 77 K, b N D  = 1018 cm−3 at 77 K

Full size image
$${\text{N}}_{\text{D}}^{ + } + {\text{p}} - {\text{N}}_{\text{A}}^{ - } - {\text{n}} - {\text{n}}_{{{\text{D}}_{1} }} - {\text{n}}_{{{\text{D}}_{2} }} = 0$$
(11)

Here \({\text{N}}_{\text{D}}^{ + } = {\text{N}}_{\text{D}}\). In the solution of Eq. (11) we have determined the reduction of Fermi energy \(\eta\) and next \({\text{p}},{\text{N}}_{\text{A}}^{ - } ,{\text{n}}, {\text{n}}_{{{\text{D}}_{1} }}\) and \({\text{n}}_{{{\text{D}}_{2} }}\).The electron concentration is now the sum of \({\text{n }}, {\text{n}}_{{{\text{D}}_{1} }}\) and \({\text{n}}_{{{\text{D}}_{2} }}\). The calculated values of electron and hole concentrations are function of the donor concentration and are shown in Fig. 1a, b by solid lines for structures with mole fraction x = 0.2 and 0.3 working under temperature T = 77 K. As is seen in Fig. 1a, b the electron concentration calculated by using the classical relation (without the existence of donor bands taking into account) is in good agreement with the experimental data only for concentrations below 1015 cm−3. The discrepancies between the experimental and calculated results grow with the increase of the donor concentration. Thus for \({\text{N}}_{\text{D}} = 10^{18} \;{\text{cm}}^{ - 3}\) at 77 K the electron concentration is around 100 times lower than the donor concentration. Good agreement with experimental data gives relation (11) obtained under the assumption that two donor bands exist, one connected with donor ground states and the second connected with the donor excess state. In this case the electron concentration should be the sum of \({\text{n}} + {\text{n}}_{{{\text{D}}_{1} }} + {\text{n}}_{{{\text{D}}_{2} }}\) (solid lines). Figure 2a, b show the densities of state (in eV−1 cm−3) as the function of energy in the MCT with a mole fraction x = 0.2. The curve denotes as NC shows density of states in the conduction band. The value of energy E = 0 denoted on the figures as EC correspond to the edge of the conduction band. The curve noted by digit 1 shows the density of states in the donor band connected with the donor ground states having a mean value corresponds to the ionization energy ED. Digit 2 distinguishes the density of states in the donor band connected with donor excess states. We have assumed that the mean value of this band equals to energy of the edge of the conduction band. These two doping bands are very energy-narrow and increase with the increasing of dopants concentration as well as the rise of the temperature.

The computations of the electron concentration in which the existence of a donor band is taken into account demonstrate good consistency with the experiment. In Fig. 1a we have shown the experimental data obtained by Murakami et al. (1993) and Mitra et al. (1994) for CdxHg1−xTe layers with x mole fraction around x = 0.2, grown and doped with iodine in MOCVD processes. The concentration of electrons is practically equal to the donor concentration (solid lines in the graph). Similar conclusions can be formulated for the structures with mole fraction x = 0.3 produced in MBE processes by Microelectronics Research Group at the University of Western Australia in Perth (Faraone and Antoszewski 2016). These structures were doped with indium and iodine. The experimental results are shown in Fig. 1b.

3 Conclusions

A simple method for computing the concentration of charge carriers in CdxHg1−xTe structures doped with donors has been proposed. It is based on the assumption that donor bands are created overlapping the conduction band and have the effective density of states at least twice as high as the donor concentration. An approximate estimation based on the hydrogen-like model of donor states shows that the overlapping of electron wave function of the donor ground states takes places even for donor concentrations below 1015 cm−3. Our calculations have shown that in n-type doped CdxHg1−xTe narrow-gap structures, the electrons populated states located both in donor bands and in the conduction band. The electron concentration is practically equal to the concentration of donor atoms. These results are consistent with the experimental data.