Broadband dispersion measurement of photonic crystal fibers with nanostructured core

Abstract

Introduction of subwavelength inclusions in the core opens up an additional degree of freedom in shaping of dispersion characteristic in photonic crystal fibers (PCFs). We have developed a PCF with a nanostructured inclusion in the core to verify this concept. To suppress higher order modes, the photonic cladding structure of the developed fiber is composed of a first ring with linear filling factor of 0.95 and the remaining 5 rings with a lower linear filling factor of 0.4 with a lattice constant of $2.6\,\upmu \hbox {m}$. Diameter of the nano-inclusion in the core is 410 nm. For the fiber development, we used a pair of thermally matched soft glasses: Schott SF6 lead glass and an in-house synthesized NC21 borosilicate glass. In this paper, we report on dispersion measurements using a spectral interferomeric technique. A dispersion unbalanced Mach–Zehnder interferometer, combined with a supercontinuum source is used. Dispersion characteristics in wide range of wavelengths extending from 0.65 to $1.6\,\upmu \hbox {m}$, are measured and verified against calculated results.

Introduction

Chromatic dispersion is one of the most fundamental phenomena affecting propagation in optical fibers. Chromatic dispersion is of particular importance in telecommunication systems, where wavelength dependence of the refractive index results in detrimental broadening of propagating pulses.

Photonic crystal fibers (PCFs) enable control of dispersion characteristics in a broad spectral range by means of lattice constant and linear filling factor (Saitoh et al. 2003). In practice, the range of changes is limited by material dispersion of glass and effective mode area of the designed fiber. In supercontinuum generation, dispersion critically defines formation of new wavelength components in nonlinear optical fibers during broadening of spectrum (Dudley et al. 2006). Therefore, dispersion characteristic of optical fiber is a crucial criterion in designing of nonlinear optical fibers for supercontinuum applications.

All-solid photonic crystal fibers (ASPCFs) are an alternative approach to the more popular air-glass solid core PCFs. In this case, air holes are replaced with glass inclusions of a different refractive index to that of the background glass. The advantage of APCFs, as compared to the air hole-based PCFs, is the possibility of dispersion control with an additional parameter, which in this case is material dispersion of the second type of glass used for lattice design. Moreover, control of the fiber parameters during the drawing process is simpler and obtaining fiber parameters similar to the designed ones is straightforward (Buczynski et al. 2012a, b). The development of ASPCFs has been reported by several groups (Feng et al. 2003; Luan et al. 2004; Buczynski et al. 2012a, b) and successfully reported for supercontinuum generation (Kibler et al. 2009; Wang et al. 2012; Stepniewski et al. 2014). Introduction of subwavelength inclusions in the core enables an additional degree of freedom in shaping of dispersion profile, while maintaining a constant value of effective mode area (Buczynski et al. 2011).

Widely used techniques for dispersion charaterization, like the time-of-flight method or the modulation phase shift method (Cohen 1985), require use of long sections of optical fiber. Apart from high cost, mentioned techniques are inapplicable for optical fibers made of highly nonlinear glasses due to their high attenuation. Another approach is to use an interferometer combined with a broadband light source (Diddams and Diels 1995). A modified Mach–Zehnder interferometer technique enables measurement of dispersion characteristic in short lengths of optical fiber (Hlubina et al. 2007). We used this relatively cheap and easily applicable method for dispersion measurements of all-solid microstuctured fiber with nano-inclusion in the core.

Fiber design

We have developed an ASPCF with a nano-inclusion in the core based on modeling results recently reported in (Pniewski et al. 2013). The fiber preform is composed of structured all-solid rods consisting of NC21 glass rods integrated with SF6 glass capillaries into an all-solid structure at the fiber drawing tower. SF6 is a commercially available lead-silicate glass, characterized by high refractive index $n_{D}=1.805$ and NC21 is an in-house synthesized silicate glass, which refractive index is $n_{D}=1.518$. Spectral dependence of refractive index for the glasses used to fiber fabrication is shown in Fig. 1. Both glasses are thermally matched and enable crystallization-free optical fiber drawing in multiple thermal processing. Chemical compositions of glasses, along with experimentally measured thermo-physical properties, are presented in Tables 1 and 2.

Fig. 1

Wavelength dependence of refractive index for NC21 and SF6 glasses

Table 1 Chemical composition (in wt%) of lead-silicate SF6 glass and silicate NC21 glass

Table 2 Measured thermo-physical properties of the lead-silicate SF6 and silicate NC21 glasses

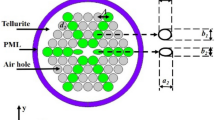
For preform fabrication, we used two types of circular SF6/NC21 glass capillaries with a diameter of 0.8 mm and linear filling factor of f = 0.4 and f = 0.95. All capillaries are ordered in a hexagonal lattice. 6 capillaries with high fill factor form first ring of photonic cladding while the capillaries with low filling factor creates remaining 5 rings of the cladding (Fig. 2a). A single SF6/NC21 glass capillary with filling factor of f = 0.18 was used as a core of the fiber. We used the standard stack and draw technique commonly applied for soft glass photonic crystal fiber fabrication, including soft glass photonic crystal fiber drawing. The final fibers had a regular, hexagonal lattice. The diameter of internal microstructure was $32.12\,\upmu \hbox {m}$, in which the linear filling factor for smaller holes was $d_{cl2}/\varLambda = 0.4$ and for the large holes was $d_{cl1}/\varLambda = 0.95$. The circular inclusion, which diameter $d_{incl}$ was only 410 nm, was located in the center of the core of $\varPhi _{core}=2.6\,\upmu \hbox {m}$ (Fig. 2b).

Fig. 2

All-solid photonic crystal fiber with nanostructure in the core: a cross-section of the subperform, b SEM image of final fiber cross-section

Experimental setup

In order to determine the loss of propagating mode in the fiber, the standard cut back method was applied. Measured loss for wavelength 780 nm reaches 20 dB/m. Relatively high attenuation is a result of material losses, which are typically several dB/m for heavy metal oxide silicate glasses, and of waveguide losses typical for small core fibers. Due to high attenuation the relatively short sample of the fiber with the length of 65.20 mm was measured in the Mach–Zehnder interferometer (MZI) setup (Fig. 3a). We used a supercontinuum (Koheras SuperK Compact) as light source, which was coupled to a variable fiber attenuator using a multimode optical fiber (MMF), to assure the appropriate signal level at the output of the input single mode optical fiber. Then the light was collimated using microscope objective (MO1) and the beam was divided after the first beamsplitter cube (BS1). Reference arm (left-bottom) of our unbalanced MZI contained variable neutral density filter (NDF) and tree mirrors of which two (M3 and M4) were placed on the linear manual stage, allowing compensation of the optical path of the measurement arm (top-right). In this second arm the beam was focused on the investigated fiber (FUT) thanks to MO2 and then output with MO3. The beam was directed on the second beamsplitter (BS2) with mirror M1, where the signal from the two arms was merged and collected with spectrometers (Ocean Optics Red Tide USB650 and Edmund Optics InGaAs NIR Spectrometer), after passing through a variable aperture (Ap), which enabled to filter the light propagating in the cladding of the fiber. The spectrometers covered spectral range from 350 to 1,000 nm and from 1,250 to 1,650 nm, respectively. As a result, the interference pattern in spectral domain was obtained, with characteristic wide fringe at wavelength for which the interferometer was compensated (Fig. 3b). Changing the length of the reference arm, we were able to measure optical path difference between measurement and reference arm in a wide spectral range, and then to determine the chromatic dispersion of the fiber.

Fig. 3

a Unbalanced Mach–Zehnder interferometer setup used for dispersion measurement, b interference image.

Results and discussion

Interferometer presented in Fig. 3a is unbalanced, which means that the calculation of the dispersion is not based on the absolute group index measurements, but on the relative measurement of $N$. It follows, that the $N$ value obtained in the measurements is reduced by an unknown constant $C$ and can be named as a relative, or a differential value of $N$. Therefore, using the Michelson interferometer, we estimated the optical path difference introduced by every optical component placed in the arms of the MZI: MO2, MO3 and NDF in the spectral range of 450–1,600 nm, and approximated the obtained data points with a polynomial fit.

This procedure simplifies the dispersion estimation using MZI in the following way:

$$\begin{aligned} 2\Delta L=\underbrace{d_{MO2} (N_{MO2} -1)}_{OPD\;\;of\;MO2}+\underbrace{d_{MO3} (N{ }_{MO3}-1)}_{OPD\;\;of\;MO3}-\underbrace{d_{NDF} (N_{NDF} -1)}_{OPD\;\;of\;NDF}+z(N_{FUT} -1), \end{aligned}$$

(1)

where $2\Delta L$ is the doubled reference arm compensation length, and the subsequent elements of this formula are optical path differences measured for the second and third microscope objectives (MO2 and MO3) and for the NDF. The last part is the unknown optical path difference of the fiber of length $z$. It is obvious, that all group refractive indices, as well as the $2\Delta L$ are wavelength functions, which was not included in formula (1) for clarity. Concluding, the relative group refractive index can be calculated using formula (2):

$$\begin{aligned} N_{FUT}^{relative} =\frac{2\Delta L-{ OPD}_{MO2} -{ OPD}_{MO3} +{ OPD}_{NDF} }{z}+1. \end{aligned}$$

(2)

Measured relative group index as a function of wavelength is shown in Fig. 4a and can be fitted with typical approximation curve, for instance the Laurent polynomial:

$$\begin{aligned} N_{FUT}^{relative} (\lambda )=\frac{A_1}{\lambda ^{4}}+\frac{A_2}{\lambda ^{2}}+A_3 +A_4 \lambda ^{2}+A_5 \lambda ^{4}. \end{aligned}$$

(3)

The dispersion of the fiber is defined as:

$$\begin{aligned} D=\frac{1}{c}\frac{dN_{abs}}{d\lambda }, \end{aligned}$$

(4)

where $c$ is the velocity of the light in the vacuum and $N_{abs}$ is absolute value of the group refractive index. We can apply formula (4) in following way:

$$\begin{aligned} D=\frac{1}{c}\frac{dN_{FUT}^{relative}}{d\lambda }, \end{aligned}$$

(5)

because the absolute and relative value of the group index are related by the unknown constant $C$:

$$\begin{aligned} N_{abs} =N_{FUT}^{relative} +C \end{aligned}$$

(6)

and the derivative of a constant is zero. The dispersion dependence upon wavelength calculated this way is presented in Fig. 4b, c, where circles are representing measurement data points.

Fig. 4

a Relative group refractive index of investigated fiber. Solid line represents Laurent polynomial fit, circles are measurement data. b Calculated and measured fiber dispersion—an overview. c Calculated and measured fiber dispersion in proximity of zero dispersion wavelength. Blue solid line on the dispersion characteristic shows numerically obtained dispersion of the fiber. Dash lines show material dispersion of the bulk glasses. (Color figure online)

The modal and dispersion properties of the PCFs were calculated using the finite element method (FEM) commonly used for modelling of PCFs. The material dispersion of the considered glasses is taken into account through the Sellmeier coefficients. We then compared the measurement results with simulated profiles obtained numerically, as described in details in our previous work (Pniewski et al. 2013) (blue curve).

We obtained a good agreement between modeling and experimental results. Both profiles match perfectly for short wavelengths. A small difference was observed for longer wavelengths above 1,100 nm. Slope of the dispersion profile is very small in this area. Small variation of dispersion value results in relatively large difference in wavelength. Based on performed simulation we predict the location of zero dispersion wavelength at 1,516 nm. Measurement results indicate that ZDW is located at 1,680 nm. Difference between modeled and measured results are related to some approximation assumed in the modeling. First of all we assumed sharp transition between SF6 and NC21 glasses. However diffusion occurs between glasses and transition between glasses is smoothed in a real fiber structure. Second source of error introduced into the simulation is uncertainty of geometric dimension reading from the SEM images. In addition, calculations introduce errors with limited mesh size and assumed material dispersion characteristics. As a result, developed fiber has ZDW shifted by 164 nm toward longer wavelengths with respect to design and cannot be used for efficient supercontinuum generation with 1,550 nm femtosecond fiber lasers as pump source as it was predicted in (Pniewski et al. 2013). For this purpose, further optimization of fiber design and fiber drawing is required for use with 1,550 fiber femtosecond sources. The dispersion curve can be lifted up and the zero wavelength can be pushed into the shorter wavelengths in a new fiber with larger pitch and with larger inclusion in the core. Currently the developed fiber can be considered for supercontinuum generation in anomalous dispersion range with thulium femtosecond lasers which operate around $2\,\upmu \hbox {m}$ (Wan et al. 2013).

Conclusions

New type of microstructured fiber with flat dispersion was designed and fabricated. A modified method of spectral interferometry for the chromatic dispersion measurements was used to verify its properties. The dispersion of an all-solid nano-inclusion microstructured fiber was measured in a wide spectral range between 600 and 1,800 nm. Taking into account the approximation curve of the measured dispersion, the zero dispersion wavelength was located in this fiber at 1,680 nm. The discrepancy between experimental and numerical results is assigned to the uncertainty of dimensions of the fabricated structure, taken from its SEM images for the calculations, which was related to the diffusion effect between the glasses.