Abstract
We report on characterization of a large solid core, photonic crystal fiber dedicated to broadband transmission range from visible to mid-infrared. We have fabricated a multi-mode photonic crystal fiber, made of a heavy metal-oxide glass based on the \(\hbox {PbO}{-}\hbox {Bi}_{2}\hbox {O}_{3}{-}\hbox {Ga}_{2}\hbox {O}_{3}\) system, modified with \(\hbox {SiO}_{2}\) and CdO, synthesized in-house, which shows good transmission up to \(4.5\,\upmu \hbox {m}\), as well as good rheological properties that permit multiple thermal processing steps without crystallization. The core of the fiber is created by replacement of central 60 tubes with solid rods. The photonic cladding is composed of 8 rings of air holes with a filling factor of 0.42. Simulation results shows that the fiber can be used for broadband transmission in the range of 430–3,000 nm. Calculated effective mode area of the fiber is \(295\,\upmu \hbox {m}^{2}\). We have measured attenuation of the fiber in the range 800–1,700 nm and its sensitivity to bending losses. Attenuation ranges from 1 to 4 dB/m in the considered range and bending losses are below 0.7 dB.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
In the last several years, large mode area (LMA) photonic crystal fibers (PCFs) have attracted a significant increase of attention from the research community. LMA PCFs are needed for high power beam delivery, where reduction of peak energy densities is necessary, and for collecting light over large areas and linking it to spectrometers or other optical systems, mainly in the near-infrared and mid-infrared spectral range. In conventional optical fibers, the mode area is limited by the accuracy in controlling low dopant concentrations in the fiber core. However, single mode performance with mode areas of 400 \(\upmu \hbox {m}^{2}\) at 1,550 nm has been reported (Baggett et al. 2001). An easier way for obtaining large mode area is to use PCF fibers, which do not suffer from constraints related to doping, in particular for short-wavelength applications, and can have no attenuation cut-off wavelength (Nielsen et al. 2004). In this case, the number of guided modes is determined by the geometrical properties of a photonic cladding, such as lattice constant and filling factor. Several successful approaches for the designing and fabrication of LMA PCFs have been reported (Ritari et al. 2003; Folkenberg et al. 2004; Chen 2007; Tan et al. 2008; Matsui et al. 2011). Recently, development of ultra large core PCFs have been presented with a mode area of 1,454 \(\upmu \hbox {m}^{2}\) (Napierała et al. 2011). Also LMA rod fibers are used in fiber amplifiers (Limpert et al. 2006). They can show extremely large effective mode areas up to 5,000 \(\upmu \hbox {m}^{2}\) (Jain et al. 2013), although their structures suffer from very large bending losses. Therefore only rigid fiber rods can be used in this case.
Most of the aforementioned research work focused on the designing and development of LMA PCFs for very limited wavelength ranges. Fibers investigated so far were commonly based on silica glass, which limits their application to the visible and near-infrared parts of spectrum. Furthermore, it is difficult to enlarge the effective mode area for broadband applications, because of the trade-off relationship between the cut-off wavelength and bending loss. To overcome this bottleneck Poli et al. considered a LMA PCF with a core with 19-lattice-cell defect (Poli et al. 2011). The PCF with core diameter up to \(100\,\upmu \hbox {m}\) are reported in this case.
Increasing number of MidIR sources and the demands of ulrabroadband spectroscopy and sensing, create a need for the development of new LMA PCFs, which can transmit also in the MidIR region (Waynant et al. 2001) and have low bending losses, with good mechanical properties and high resistance to laser damage.
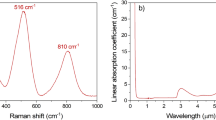
To meet those needs, various soft glasses, such as chalcogenide, tellurite or heavy metal oxide glasses, can be used. The chalcogenide glasses offer transparency in the range \(2{-}15\,\upmu \hbox {m}\), however they have a tendency towards crystallization during thermal processing (Bureau et al. 2009; Rave et al. 2004; France et al. 1987). On the other hand, heavy metal oxide and tellurite glasses offer limited transmission in MidIR up to \(5{-}6\,\upmu \hbox {m}\), but they offer transparency in the visible from 500 nm and in all near-infrared spectrum (Stępień et al. 2011; Lorenc et al. 2008). In this paper we present a LMA PCF made of heavy metal oxide glass, dedicated to broadband guidance in the visible, near- and, in part, mid-infrared region with limited number of guided modes.
2 Design of the large more area photonic crystal fiber
We studied influence of the fiber structure on the modal properties, attenuation and effective mode area in terms of the lattice constant \(\Lambda \), filling factor \(f\) as well as size of the fiber core and size of the photonic cladding. The glass selection is determined by transmission and rheological properties. For fiber drawing, we used the lead-bismuth-gallium CS-740 glass synthesized in-house, that is chemically similar to the PBG08 glass, previously used for PCF development (Stepien et al. 2012). The CS-740 glass offers high transmission over 60 % in the broadband range between 430 and 4,500 nm (Fig. 1). We have studied the fiber modal and dispersion properties, taking into account the material dispersion of bulk CS-740 glass through the Sellmeier coefficients (\(\hbox {B}_{1}=2.915,\,\hbox {B}_{2}=0.920,\,\hbox {B}_{3}= - 1.28,\,\hbox {C}_{1}=210.6,\hbox {C}_{2}=7.3 \, \,\times 10^{-3},\,\hbox {C}_{3}=220.2\)), where the refractive index \(n\) is defined as:
where \(\lambda \) denotes wavelength and \(B_{i}\) and \(C_{i}\) are Sellmeier coefficients.
The modal and dispersion properties of the PCF are calculated using the finite difference method. This approach allows to optimise effective mode area for the fundamental mode and the prediction of the modal, polarization and dispersion properties of the PCF. It si well know that there is a trade off between effective mode area of the fundamental mode, number of guided modes and bending losses (Martynkien et al. 2007; Poli et al. 2011).
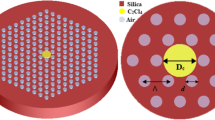
An optimal solution for the considered glass CS-740 is achieved for a structure with the core created by omitting 9 rings of air holes (60 elements) with a lattice constant of \(\Lambda =3.0 \, \upmu \hbox {m}\) and a filling factor of f = 0.47 (Fig. 2). A photonic cladding with 8 rings of air holes is assumed. This structure is a good compromise between the only few guided modes, relatively large effective mode area and bending loss of the fundamental mode. In this case we predict an effective guidance of 3 modes in a range of 0.5–2.4 \(\upmu \hbox {m}\). The higher modes are not guided beyond \(2.4\,\upmu \hbox {m}\) anymore and fibre becomes single mode. The effective mode area of the fundamental mode varies slightly with wavelength and practically remains the same for various filling factors of photonic cladding due to use of multiple defect core approach. The calculated effective mode area of the fundamental mode is 312 \(\upmu \hbox {m}^{2}\) at 1,550 nm (Fig. 3). In this case attenuation of the fibre structure is negligible—below 0.01 dB/km (material dispersion is not taken into account).
3 Manufacturing of the large mode area photonic crystal fiber
For the preform fabrication, we used circular glass capillaries with a diameter of 0.8 mm and a linear filling factor of f = 0.5, ordered in a hexagonal lattice. The core of the fiber was created by replacing 60 central capillaries with rods (9 elements in diameter). We have used the standard stack and draw technique, commonly employed for soft glass photonic crystal fiber development (Kujawa et al. 2012). The fabricated subpreform consisted of 8 rings of air-holes. It had a total diameter of 3.6 mm with a photonic structure diameter of 2.2 mm (Fig. 4a). The lattice constant was \(90\,\upmu \hbox {m}\) and air holes were \(40\,\upmu \hbox {m}\) in diameter. The core diameter was \(646\,\upmu \hbox {m}\). The subpreform was placed inside an additional tube and processed into the final fiber at the drawing tower.
A final PCF with the outer diameter of \(126\,\upmu \hbox {m}\) was obtained (Fig. 4b). Diameter of the photonic cladding is \(76\,\upmu \hbox {m}\), lattice constant is \(\Lambda =3.1\,\upmu \hbox {m}\) and air-hole diameter in the photonic cladding is \(\hbox {d}=1.3\,\upmu \hbox {m}\) (filling factor \(d/\Lambda = 0.42\)). The diameter of the core is \(21.5\,\upmu \hbox {m}\). Fabricated fiber has a very regular structure with air-hole diameter variation below 5 % (Fig. 4c).
Linear modal properties of the fabricated fiber were calculated based on the real structure obtained with SEM. The simulation took into account all the structural deformations that occurred during the drawing process. In the modeling we also took into account the dispersion of bulk CS-740 glass. According to the obtained results the fiber guides efficiently 3 modes for the wavelength of up to \(2.4\,\upmu \hbox {m}\), similarly to previous simulation results obtained for ideal structures. Beyond cut-off wavelength of \(2.4\,\upmu \hbox {m}\) only fundamental mode is guided. We calculated the effective refractive index for the fundamental mode of fiber up to \(5\,\upmu \hbox {m}\) (Fig. 5). However calculated losses of the structure show rapid growth of attenuation for wavelengths over \(3\,\upmu \hbox {m}\) (Fig. 6). This is a limit of the fiber performance in midIR. Effective mode area for the fundamental mode of the fiber is \(A_{eff} = 295\,\upmu \hbox {m}^{2}\).
4 Experimental results
Measurement setup for attenuation measurements in our LMA PCF is shown in Fig. 7. We used typical cut-back method commonly used for characterization of fiber losses. The setup comprised supercontinuum source and a near-infrared spectrometer allowing signal acquisition in the range of 800–1,700 nm. Two microscope objectives—10x/0.25 and 20x/0.40 mounted on high precision translation stages were user for coupling light into tested PCFs and decoupling light, respectively. For initial alignment of the setup a Ti:Sapphire 780 nm laser beam was used.
For the attenuation measurement the initial fiber length was 6 m. Measured attenuation are presented in Fig. 8. The attenuation in this spectral area ranges typically from 0.9 to 4 dB/m. We observe small oscillations of attenuation in all the spectrum and increase of attenuation at short wavelengths. Attenuation oscillations in LMA fiber originates from leakage losses and coupling between higher modes in the fiber. This phenomena was previously observed and described by Chen (2007).
Ritari et al. also noted that attenuation oscillations are attributed to low resistance of investigated LMA PCF structure for bending and twisting (Ritari et al. 2003). Therefore measurement of bending loses in are important to verify properties of the developed fiber. A mandrel with a set of standard diameters was used for fiber bending (Fig. 9). The setup was aligned and optimized using tunable laser at 1,556 nm.
Bending losses measured for the fabricated LMA PCF are shown in Fig. 10. The bending loss for the particular bend radius \(\hbox {R}_\mathrm{B}\) in relation to the infinity radius \(\hbox {R}_{\mathrm{B}{\infty }}\) was measured (Fig. 7a). As an infinity a value of \(\hbox {R}_{\mathrm{B}{\infty }}=200\,\hbox {mm}\) was used (Schulze et al. 2013). The relative loss for increasing radii is decreasing, all of the measurements can be linearly fit with a good accuracy and the loss level remains below 0.7 dB per loop, as shown for 1,556 nm in Fig. 10b. The wavelength of 1,556 was selected since optimization of setup alignment was performed for this particular wavelength. The present oscillations can come from, as mentioned before, low robustness of the fiber or energy coupling between the fundamental mode and the cladding modes of respective symmetry arising due to reflection from boundary between the solid and holey part of the cladding as in conventional double-clad fiber, as well as, the fiber’s angular twist (Martynkien et al. 2007; Olszewski et al. 2005). For twisted fiber the cladding modes have lower symmetry and propagate at larger distance from the core compared to untwisted fiber, so the coupling coefficient is much smaller and the oscillations are weaker.
5 Conclusions
A large mode area photonic crystal fiber was designed and fabricated using lead-bismuth-galate glass with enhanced transmission between 430 and 4,500 nm. The proposed fiber offers an advantage of broadband transmission range from visible till infrared range beyond transmission available in silica glass on one hand and chalcogenide glass on the other hand. The core of the fiber was created by replacement of the 60 central capillaries with rods giving a core diameter of \(21.5\,\upmu \hbox {m}\). The effective mode area for the fundamental mode of the fiber is \(\hbox {A}_{\mathrm{eff}}=295\,\upmu \hbox {m}^{2}\). The photonic cladding consists of 8 rings of air-holes with a diameter of \(1.3\,\upmu \hbox {m}\) and a lattice constant of \(3.1\,\upmu \hbox {m}\). The measurements of the attenuation and relative bending loss for different bending radiuses of the fiber were shown. The attenuation in the range of 800–1,700 nm ranges from 0.9 to 4 dB/m and the bending loss are smaller than 0.7 dB per loop.
References
Baggett, J.C., Monro, T.M., Furusawa, K., Richardson, D.J.: Comparative study of large-mode holey and conventional fibers. Opt. Lett. 26, 1045–1047 (2001)
Bureau, B., Maurugeon, S., Charpentier, F., Adam, J.-L., Boussard-Plédel, C., Xiang-Hua, Z.: Chalcogenide glass fibers for infrared sensing and space optics. Fiber. Integr. Opt. 28, 65–80 (2009)
Chen, M.Y.: Polarization and leakage properties of large-mode-area microstructured-core optical fibers. Opt. Express 15, 12498–12507 (2007)
Folkenberg, J., Nielsen, M., Mortensen, N., Jakobsen, C., Simonsen, H.: Polarization maintaining large mode area photonic crystal fiber. Opt. Express 12, 956–960 (2004)
France, P.W., Carter, S.F., Moore, M.W., Day, C.R.: Progress in fluoride fibres for optical communications. J. Br. Telecom Technol. 5, 28–44 (1987)
Jain, D., Baskiotis, C., Sahu, J.K.: Mode area scaling with multi-trench rod-type fibers. Opt. Express 21, 1448–1455 (2013)
Kujawa, I., Buczynski, R., Martynkien, T., Sadowski, M., Pysz, D., Stepien, R., Waddie, A.J., Taghizadeh, M.R.: Multiple defect core photonic crystal fiber with high birefringence induced by squeezed lattice with elliptical holes in soft glass. Opt. Fiber Technol. 18, 220–225 (2012)
Limpert, J., Schmidt, O., Rothhardt, J., Röser, F., Schreiber, T., Tünnermann, A., Ermeneux, S., Yvernault, P., Salin, F.: Extended single-mode photonic crystal fiber lasers. Opt. Express 14, 2715–2720 (2006)
Lorenc, D., Bugar, I., Aranyosiova, M., Buczynski, R., Pysz, D., Velic, D., Chorvat, D.: Linear and nonlinear properties of multicomponent glass photonic crystal fibers. Laser Phys. 18, 270–276 (2008)
Martynkien, T., Olszewski, J., Szpulak, M., Golojuch, G., Urbanczyk, W.: Experimental investigations of bending loss oscillations in large mode area photonic crystal fibers. Opt. Express 15, 13547–13556 (2007)
Matsui, T., Sakamoto, T., Tsujikawa, K., Tomita, S., Tsubokawa, M.: Single-mode photonic crystal fiber design with ultralarge effective area and low bending loss for ultrahigh speed WDM transmission. J. Lightwave Technol. 29, 511–515 (2011)
Napierała, M., Nasilowski, T., Bereś-Pawlik, E., Mergo, P., Berghmans, F., Thienpont, H.: Large-mode area photonic crystal fiber with double lattice constant structure and low bending loss. Opt. Express 19, 22628–22636 (2011)
Nielsen, M.D., Folkenberg, J.R., Mortensen, N.A., Bjarklev, A.: Bandwidth comparison of photonic crystal fibers and conventional single-mode fibers. Opt. Express 12, 430–435 (2004)
Olszewski, J., Szpulak, M., Urbańczyk, W.: Effect of coupling between fundamental and cladding modes on bending losses in photonic crystal fibers. Opt. Express 13, 6015–6022 (2005)
Poli, F., Coscelli, E., Alkeskjold, T.T., Passaro, D., Cucinotta, A., Leick, L., Broeng, J., Selleri, S.: Cut-off analysis of 19-cell Yb-doped double-cladding rod-type photonic crystal fibers. Opt. Express 19, 9896–9907 (2011)
Rave, E., Ephrat, P., Goldberg, M., Kedmi, E., Katzir, A.: Silver halide photonic crystal fibers for the middle infrared. Appl. Opt. 43, 2236–2241 (2004)
Ritari, T., Niemi, T., Ludvigsen, H., Wegmuller, M., Gisin, N., Folkenberg, J.R., Petterson, A.: Polarization mode dispersion of large mode-area photonic crystal fibers. Opt. Commun. 226, 233–239 (2003)
Schulze, C., Lorenz, A., Flamm, D., Hartung, A., Schroter, S., Bartelt, H., Duparre, M.: Mode resolved bend loss in few-mode optical fibers. Opt. Express 21, 3170–3181 (2013)
Stępień, R., Buczyński, R., Pysz, D., Kujawa, I., Mirkowska, M., Diduszko, R.: Development of thermally stable tellurite glasses designed for fabrication of microstructured optical fibers. J. Non. Cryst. Solids 357, 873–883 (2011)
Stepien, R., Pysz, D., Kujawa, I., Pniewski, J., Waddie, A.J., Taghizadeh, M.R., Buczynski, R.: Development of large-core photonic crystal fiber for hyperspectral transmission. Proceeding of SPIE 8426, 842614 (2012)
Tan, X., Geng, Y., Li, E., Wang, W., Wang, P., Yao, J.: Characterization of bent large-mode-area photonic crystal fiber. J. Opt. A Pure Appl. Opt. 10, 085303, 1–5 (2008)
Waynant, R., Ilev, I., Gannot, I.: Mid-infrared laser applications in medicine and biology. Philos. Trans. R. Soc. 359, 635–644 (2001)
Acknowledgments
This research is supported by the Polish MNiSW research grant N N515 506040 and the project operated within the Foundation for Polish Science Team Programme co-financed by the European Regional Development Fund, Operational Program Innovative Economy 2007–2013.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Stepien, R., Siwicki, B., Pysz, D. et al. Characterization of a large core photonic crystal fiber made of lead–bismuth–gallium oxide glass for broadband infrared transmission. Opt Quant Electron 46, 553–561 (2014). https://doi.org/10.1007/s11082-013-9835-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-013-9835-5