An ensemble of artificial neural network models to forecast hourly energy demand

Abstract

We propose an ensemble artificial neural network (EANN) methodology for predicting the day ahead energy demand of a district heating operator (DHO). Specifically, at the end of one day, we forecast the energy demand for each of the 24 h of the next day. Our methodology combines three artificial neural network (ANN) models, each capturing a different aspect of the predicted time series. In particular, the outcomes of the three ANN models are combined into a single forecast. This is done using a sequential ordered optimization procedure that establishes the weights of three models in the final output. We validate our EANN methodology using data obtained from a A2A, which is one of the major DHOs in Italy. The data pertains to a major metropolitan area in Northern Italy. We compared the performance of our EANN with the method currently used by the DHO, which is based on multiple linear regression requiring expert intervention. Furthermore, we compared our EANN with the state-of-the-art seasonal autoregressive integrated moving average and Echo State Network models. The results show that our EANN achieves better performance than the other three methods, both in terms of mean absolute percentage error (MAPE) and maximum absolute percentage error. Moreover, we demonstrate that the EANN produces good quality results for longer forecasting horizons. Finally, we note that the EANN is characterised by simplicity, as it requires little tuning of a handful of parameters. This simplicity facilitates its replicability in other cases.

1 Introduction

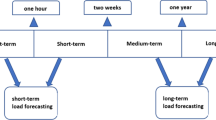
Energy production planning is a complex operation requiring accurate modelling of many system related interactions. The fact that energy typically cannot be stored, entails that forecasting its demand is of fundamental importance. In this context, establishing accurate demand forecasting is essential for integrated district heating operators (DHOs). These are namely regulated or municipal entities that vertically manage production, distribution and sales of heating through a district network. DHOs deploy medium-term and short-term load forecasting in their operational planning. Both these forecasts enable several optimization processes along the DHO value chain.

Medium-term load forecasts typically predict the demand up to one-week in advance (Hahn et al. 2009). Through medium-term forecasts, DHOs can analyse their expected financial performance with monthly or annual budgets. Based on these analyses, they may optimize their energy supply sources and short-term contracts, schedule preventive maintenance for generation units, and plan the development or revamping on network and customer facilities.

Short-term forecasts are typically done hours to days in advance with respect to delivery. For these forecasts, a DHO typically estimates with an hourly resolution the amount of heating they are going to produce and distribute to consumers. Such forecasts are essential to adequately dimension the unit commitment, i.e., the exact amount that each facility and generation unit has to provide (see e.g., Pineda and Morales 2016). The resulting commitments must adhere to the hydraulic and thermal constraints of the overall system (e.g., supply pressure, temperatures and flow rates). In turn, the operation of generation units should be properly planned accounting for their technical operative range, while maximizing efficiency and renewable heating exploitation. Both short-term and medium-term forecasts can be globally viewed as fundamental components of a DHO’s decision support system (DSS). An overview of such a system is shown in Fig. 1. In this paper we focus on developing an effective and replicable tool for short-term forecasts.

In general, leveraging data in decision making processes is becoming rather popular (Gambella et al. 2021). Indeed, in many industries (e.g., Shipping operations Beşikçi et al. 2016), machine learning (ML) is used to generate reliable predictions, which are then used in management science problems to derive optimised decisions. Capitalising on the success of ML techniques in producing reliable predictions, our methodology is based on artificial neural networks (ANNs).

Fig. 1

An overview of a DHO’s decision support system

In Europe, DHOs generally prioritise renewable sources in order to be aligned with the EU Emissions Trading System (ETS) goals. Therefore, fossil fuel or other integration sources are dispatched with a lower priority. Considering combined heat power facilities, often used by DHOs, production planning must comply with energy quantities exchanged in the day ahead market. In Italy, for example, the national energy market prices are published on a daily basis covering the subsequent 24 h. Therefore, in contrast with many production environments, where operational planning implies daily planning, an hourly-based plan is better suited to meet the dynamic pricing of energy commodities. Moreover, several DHOs plan their production at an urban level. In such cases, forecasting the energy demand is intricate due to the fact that it may be influenced by exogenous factors, e.g., weather conditions, as well as local features such as local holidays.

Several methodologies have been used to forecast energy demand. We highlight several of these in the subsequent section. The main contribution of this paper is the design of an effective easy-to-replicate methodology, that leverages ML techniques for the day-ahead forecast of hourly energy demand. Three different ANN forecasting models are combined. In particular, the same data is organized in different ways to create specific inputs for the three different ANN models. Each type of input yields an ANN model, that targets a different feature of demand variability, so as to meet as much as possible the diversified energy demand trend. To this aim, the final forecast is obtained by a weighted combination of the three ANN outputs, where the weights are tuned by iteratively solving a linear programming problem. Up to our knowledge, this is the first attempt to produce an ANN ensemble with ANNs involving inputs organized in such a way. As described in a subsequent section, our methodology may be particularly relevant for time-series forecasting as, together with the weights optimization procedure, it makes no assumptions on the stationarity of the time-series, but rather automatically adapts to it when detected.

Our proposed methodology is applied to a case study in a metropolitan area in the Northern Italy, which is a medium-sized city with about 200,000 inhabitants. The research in the paper is done in collaboration with A2A, which is one of the major DHOs in Italy. This DHO wanted an accurate point forecasting methodology for predicting the energy demand of the area in question. Most residential and commercial buildings in Italy are allowed to operate heating services from the 15th of October of the current solar year till the 15th of April of the next solar year, we refer to this period as a thermal season. We trained our procedure on data from about one and a half thermal seasons and tested it on another. The specific scientific contributions of the paper are as follows.

• Developing three ANN forecasting models based on three specific configurations of the same data for the day-ahead hourly demand. Specifically, at the end of one day, we forecast the energy demand for each of the 24 h of the next day.

• Establishing a weight optimization procedure combining the three ANN models into a single forecast.

• Extensively validating the procedure and its components, and showing that it significantly outperforms the forecasting mechanism used by the DHO. Despite the fact that the latter allows expert intervention.

• Showing that our procedure outperforms the state-of-the-art SARIMAX model, and an Echo State Network (ESN), which is a type of Deep Neural Network devised to overcome the typical complicated backpropagation-based training of such models.

• Demonstrating that our procedure produces good results also for longer forecasting horizons.

Aside from the previously mentioned scientific contributions, we would like to highlight a key practical contribution of our procedure. It is characterised by simplicity, as it requires little tuning of a handful of parameters. This simplicity facilitates its replicability in other cases.

The rest of the paper is organised as follows. In Sect. 2 we review the main literature. In Sect. 3 we present our procedure, including the description of the used data sets. In Sect. 4 we present our computational experiments. Finally, in Sect. 5 we present our conclusions.

2 Literature review

While long-term and medium term energy demand forecasts have been extensively studied in the literature (e.g., Angelopoulos et al. 2019; Kankal and Uzlu 2017; Kialashaki and Reisel 2013), this section is centred on short-term forecasts, which have also been extensively studied. In particular, we survey some of the main forecasting approaches related to the day ahead demand forecasts.

Hahn et al. (2009) broadly classify energy demand forecasting models into two main categories. 1) classical approaches, i.e., which apply concepts stemming from time series and regression analysis, and 2) approaches based on artificial and computational intelligence. In what follows we highlight some of the relatively recent contributions in both categories.

Fang and Lahdelma (2016) evaluated a number of multiple linear regression models and a seasonal autoregressive integrated moving average (SARIMA) model for forecasting heat demand of the city of Espoo. The models were evaluated by out-of-sample tests for the last 20 full weeks of the year. Among all tested models, the best performing one was mainly a linear regression with explanatory variables related to outdoor temperature and wind speed. Arora and Taylor (2018) propose a seasonal autoregressive moving average (SARMA) forecasting model to predict short-term load for France. In particular, the authors focus on special days, such as public holidays. They also incorporate subjective judgment using a rule-based methodology. Eight years of data were used as an estimation sample, and one year of data was used for the evaluation. Clements et al. (2016) develop a multiple equation time-series model for the day-ahead electricity load prediction. The model was validated on data from the Queensland region of Australia.

The other category of methodologies used for energy demand forecasting is based on artificial intelligence. Azadeh et al. (2014) develop a two-step ANNs method for short-term load forecasting. The first step models the daily demand, while the second step uses a model composed of 24 sub-networks forecasting hourly load of the next day. The models are trained and tested using data from the electricity market of Iran from 2003 till 2005. Johansson et al. (2017) develop an online ML algorithm for daily heat demand forecasting. Specifically, their model combines decision tree ML algorithms with an online functionality. The proposed method was applied to data from the city of Rottne. Ding et al. (2020) proposed a framework for the hour ahead and the day ahead electricity load forecasting. The framework is based on relevance vector machine, and uses wavelet transform and feature selection in a preprocessing step. A number of cases from the United Sates were considered. Torres et al. (2022) adopted a deep Long Short-Memory Network (LSTM) for the short-term forecast of the electricity consumption in Spain. The case study comprised data from January 2007 to June 2016, and used a forecasting horizon of four hours. Ensemble method approaches are also adopted. For example, Wu et al. (2023), proposed a method combining an adaptive network-based fuzzy inference system and an Elman Neural Network for the short-term electricity demand forecasting. The model was tested on a simulated case based on data collected in Serbia during 2021. Khwaja et al. (2020) combined bagging and boosting techniques to train an ensemble of ANNs. The method was used for the hourly energy demand forecast on a New England dataset. In particular, data from 2004 to 2007 was used for training, and from 2008 to 2009 for testing. The proposed approach revealed to be more accurate than a single ANN or single bagged and single boosted ensembles. A different ensemble approach, combining Bayesian ANNs, wavelet decomposition, and a genetic algorithm, was applied by Ghayekhloo et al. (2015) to different case studies obtained by the same New England dataset, improving the accuracy with respect to other standard forecasting methods.

Some authors examined both classical forecasting models and artificial intelligence methods. For example, Kurek et al. (2021) extensively analyzed the Warsaw district heating demand. Amongst others, ridge regression and autoregression with exogenous input were explored. Furthermore, two ANNs were trained. The models were trained using a three-year dataset and were used to predict the heat demand for the following 72 h. In Manno et al. (2022a), a shallow ANN enhanced with feedback data inputs was trained for the 24 h ahead forecast of the cooling and heating energy demand of three cases including the Politecnico di Milano university campus. The considered data was from June 2016 to February 2019 with hourly frequency.

Our methodology is benchmarked against the currently used forecasting method of A2A. While we cannot disclose the details of this methodology due to confidentiality agreements, we may say that it belongs to the category of classical forecasting methods. More precisely, the currently used forecasting method of A2A consists of multiple linear regression models. Similarly to Arora and Taylor (2018), this methodology accounts for special days and subjective judgment.

Building on the recent success of artificial intelligence methods to predict energy demand, we propose an ensemble of ANNs to forecast the hourly energy demand. We expand the idea of using an ensemble of models (e.g., Johansson et al. 2017) to ANNs. Furthermore, we develop a weight optimization procedure combining the ensemble of ANN models into a single forecast. Aside from comparing our methodology to the classical one used by the company, we also compare it with the state-of-the-art SARIMAX and ESNs. Our results show that our methodology outperforms the three other considered methodologies.

3 Methodology

We propose an ensemble artificial neural network (EANN) methodology for predicting the day ahead energy demand for each of the forthcoming 24 h time. These predictions are to be made at the end of the previous day. The algorithm is based on a weighted combination of three ANNs models according to an ensemble strategy (see e.g., Dietterich 2000; West et al. 2005). Each ANN model captures different aspects of the energy demand. In what follows we first present a brief overview of the ANN framework in Sect. 3.1, we then describe the available dataset in Sect. 3.2. We present our three developed ANN models in Sects. 3.3–3.5. We discuss our training strategy in Sect. 3.6. Finally, in Sect. 3.7 we present our weight optimization procedure, which unifies the output of the three ANN models into a single prediction by means of a simple and easy-to-use optimization mechanism.

3.1 The artificial neural network framework

Artificial Neural Networks are widely used supervised learning machines (see Haykin 1994; Bishop 1995 for comprehensive reviews). Consider a process producing an output $y \in \Re$ corresponding to an input $x \in \Re ^n$ according to an unknown functional relation $y=f(x)$, in supervised learning the goal is to train parameters of a certain model in order to approximate as best as possible the behavior of f. During the training phase, these parameters are calibrated on the basis of a set of $\ell$ available historical samples of the process, denoted as the training set (TR), for which both the input x and the output y are known. Formally, the training set is defined as

$$\begin{aligned} TR:=\{ (x^i,y^i), x^i \in \Re ^n, y^i \in \Re , i=1,\ldots ,\ell \}. \end{aligned}$$

(1)

The performance of the trained model is assessed through the testing set (TS), which is another set of historical samples (with known inputs and outputs) not included in TR.

In ANNs the training process is inspired by knowledge acquisition of nervous systems in complex biological organisms. In particular, ANNs work as input–output systems in which n input signals $x_1,x_2,\ldots ,x_n$ are propagated through a network of processing units (neurons) organized into hidden layers to produce a final output $\hat{y}$. In this work we focus on ANNs with a single scalar output $\hat{y} \in \Re$. Each neuron is associated to a nonlinear activation function which elaborates the sum of all incoming signals to generate a neuron output. During the training phase knowledge is acquired by calibrating the weights of the oriented connections between neurons.

In this paper we adopt ANNs with a single hidden layer, as the one reported in Fig. 2. Formally, in such an ANN, the weights of the incoming connections (input weights) of neuron $j=1, \dots , m$ are denoted by weights $\omega _{j1},\omega _{j2},\ldots ,\omega _{jn}$. Then, by denoting the activation function as g (generally continuous and sigmoidal), the output of neuron j is computed as $g(\sum _{i=1}^{n} \omega _{ji} x_{ji})$. Summing up the output of each neuron j by means of output weights $\lambda _j$, the final ANN output $\hat{y}$ is obtained. The training phase consists in minimizing a so called loss function, which is generally computed as the sum over all training points $i=1,\ldots ,\ell$ of a certain deviation between the output produced by the ANN (say $\hat{y}_i$) and its actual output $y_i$.

Fig. 2

An ANN with a single hidden layer made up of m neurons. Each neuron has an activation function g. The input signal i is connected to neuron j through a connection associated to weight $\omega _{ji}$, while the output signal of hidden neuron j is sent to the output layer through a connection with weight $\lambda _j$. Note that the $+$ symbol indicates a weighted sum

One of the most commonly used loss functions is the Mean Squared Error (MSE), computed as

$$\begin{aligned} \text{ MSE }=\frac{1}{2P}\sum _{i=1}^{\ell } (y_i-\hat{y}_i)^2 \end{aligned}$$

(2)

where $y_i$ and $\hat{y}_i$ denote the actual output and the one produced by the neural network for training sample i. The vast majority of training algorithms used to minimize the loss function are gradient-based methods, which exploit a procedure called backpropagation. This is an automated differentiation scheme based on the chain rule, to iteratively determine the gradient of the loss function with respect to the weights of the connections (see e.g., Bishop 2006).

Depending on their practical application, ANNs may be used for regression (continuous domain) or classification (discrete domain). In this paper we focus on regression, as we are interested in energy demand time series forecast. In this context, it is worth mentioning that ANNs can be categorized as feedforward neural networks (FNNs) (see e.g., Grippo et al. 2015), in which all the connections are oriented from the input layer to the output layer, and recurrent neural networks (RNNs) (see e.g., Rumelhart et al. 1986) including also feedback connections, i.e., connections may exist between units of the same layer, between units of different layers oriented in the output-input direction, or loop connections. Since it is well-known that FNNs with a single hidden layer can approximate any continuous function with any precision (see Leshno et al. 1993), they have been successfully applied in many practical real-world problems (see e.g., Cao et al. 2005; Beşikçi et al. 2016; Avenali et al. 2017; Manno et al. 2022b; Chelazzi et al. 2021; Clausen and Li 2022). However, the RNN structure is well suited for time series forecast (see e.g., Carbonneau et al. 2008; Chien and Ku 2015; Cao et al. 2012) as the feedback connections allow to retain past information capturing temporal correlations between occurrences. Nonetheless, determining the proper hyperparameters of RNNs and training them still remain complicated tasks (see e.g., Pascanu et al. 2013). Therefore, in order to provide an easily usable and editable tool for users who are not ML experts, we opted for FNNs with a single hidden layer. Nonetheless, we demonstrate in Sect. 4 that our FNN-based algorithm largely outperforms an ESN model, which is a widely used RNN architecture for time-series forecasting.

Inspired by Manno et al. (2022a), in our approach, the absence of feedback “memory" connections in FNNs has been counterbalanced by “enriching" the training samples with previous occurences of the target time series, in a nonlinear-autoregressive-exogenous (NARX) model fashion (see e.g., Chen et al. 1990), which is suited for linear and nonlinear time series forecasting (see e.g., Zhang 2001; Zhang et al. 2001). As will be demonstarted in the remainder of the paper, in the investigated application the ensemble of three FNNs simple models combined with a proper selection of the enriching inputs obtains better results, when compared to sophisticated RNNs. In what follows, we will refer to single hidden layer FNNs as ANNs.

3.2 Dataset description and preliminary analysis

As previously mentioned, our datasets relate to thermal seasons. We recall that a thermal season is from the 15th of October of a solar year till the 15th of April of the subsequent solar year. A2A is one of the major DHOs in Italy, and it was interested in forecasting the hourly energy demand throughout the thermal season for the considered metropolitan area.

A2A had an hourly forecasting system based on multiple linear regression models, which required for manual interventions by expert planners. The data provided by A2A for this work, including the observed and forecasted energy demand, refers to the following periods

• from the 1st of January 2017 till the 15th of April 2017,

• from the 28th of October 2017 till the 15th of April 2018,

• from the 15th of October 2018 till the 15th of April 2019.

Data are hourly, so that each sample of the dataset is associated to an hour $h=1,\dots 24$ of a day $d=1,\ldots ,D$. In particular, for hour h and day d the available data are:

• the energy demand for the entire metropolitan area, representing the target time series (i.e., the time series to be forecasted) and referred to as $E_{hd}$;

• the type of day $K_{hd}$ according to a categorization adopted by A2A, which, based on historical observations, has identified five categories days (see Table 1 for details);

• the hourly temperature forecast $T_{hd}$ obtained 24 h ahead.

Let E, T and K be the vectors containing elements $E_{hd}$, $T_{hd}$ and $K_{hd}$. We performed a correlation analysis between T and E. Considering all observations, the forecasted temperature T was significantly correlated with the target series E, with a $-0.63$ Pearson correlation coefficient (see e.g., Fisher 1992).

The correlation between K and E was rather weak, with a 0.09 Pearson correlation coefficient. This may be due to the imbalance among the number of obseravtions for each type of day in the dataset. In particular, by removing from K and E the occurrences associated to the most represented type of days, that is weekday and holiday (representing the $70\%$ of the sample), the correlation grows to $-0.19$. Moreover, by considering only vacation and pre-holiday the correlation grows to $-0.33$. This suggests that, despite the weak correlation of the whole time series, using K as a ML input may facilitate the discrimination between the less represented types of days.

Table 1 Number of observations for each day

Since samples are hourly, a further useful input for the ML is the hour h to which the sample is associated. By denoting with H the hours time series (cyclic, with elements from $\{1,\ldots ,24\}$), the correlation coefficient between H and E amounts to 0.13 revealing a moderate correlation, however by grouping the 24 h into three groups “morning" (from 09:00 to 16:00), “evening" (from 17:00 to 24:00), and “night" (from 01:00 to 08:00), the correlation grows to $-0.26$. Moreover, by considering exclusively the morning and evening subseries, the correlation grows to to 0.37. Therefore, including also h as ML input may be worthwhile for predictive purposes. We remark that all the previous correlations tests can be considered statistically significant as their associated p-values are quite below 0.05.

As a result of the previously discussed analyses, we conclude that for each sample observation the basic input for the ML consists of the following six elements:

• one for $T_{hd}$ measured in Celsius degrees and normalized in the interval $\left[ 0,1\right]$ as $(T_{hd}-T_{min})/T_{max}$, where $T_{min}=-20^{\circ }$ and $T_{max}=40^{\circ }$ are lower and upper bounds on the temperature during the thermal year,

• four to encode the five categorical type of days as a 4-dimensional binary vector according to a one-hot encoding,

• one for the hour $h=1,\ldots ,24$ (where value 1 stands for the time interval 00:00-01:00 a.m.) normalized in the interval $\left[ 0,1\right]$ as h/24.

As anticipated in Sect. 3.1, in addition to basic inputs, each sample is augmented with previous occurrences of the target time series in order to overcome the lack of feedback connections in the adopted neural structure. These further inputs are referred to as feedback inputs. Considering the autocorrelation plot of the target series E in Fig. 3, we observe that every 24 h there is a peak of positive correlation. This implies that the energy demand of a certain hour of a certain day is strongly related to the ones of the same hour of other days. Naturally, 24 h correlation peak tends to decrease for larger temporal distances between days, however at a distance of one week (168 time lags) it is still above the very high value of 0.8. For these reasons, we have chosen the feedback inputs to be at a time lag distance of $r\cdot 24$ with $r=1,2,\ldots ,7$. Note that considering inputs from the seven previous days entails that the autocorrelation is above 0.8. Moreover, including in the input the occurrences of the last seven days implies that, at the beginning of each thermal season, the first prediction can be made only after seven days. Thus, the EANN would be ready for use in its full potential one week after the beginning of each thermal season. Overall, our choice of inputs was geared by simplicity, hence our features are not too complex and the corresponding network is replicable.

Fig. 3

Autocorrelation plot of the target time series E with 168 time lags. Every point beyond the blue lines represent a significant correlation

In the next sections the three different predictive models are described in details. Motivated by the potential non-stationary behavior of the series, these models share the same basic inputs, they differ in terms of the type of target, the way feedback inputs are constructed and the way the final forecast is calculated on the basis of the neural network output.

3.3 The pure model

The pure model (pureM) is the most intuitive one, as it solely focuses on the target time series E. A general training sample associated to hour h of day d is composed by the following target $y_{hd}$ and input $x_{hd}$

$$\begin{aligned} y_{hd}=&E_{hd}, \end{aligned}$$

(3)

$$\begin{aligned} x_{hd}=&(T_{hd},K_{hd},h,E_{h,d-1},E_{h,d-2},\ldots ,E_{h,d-7}), \end{aligned}$$

(4)

where in addition to the three basic inputs ($T_{hd},K_{hd},h$), the energy demands of the same hour of the previous seven days are considered as feedback inputs (for notational simplicity, the normalizations and the one-hot encoding are not explicitly reported), and the target is simply the energy demand at hour h of day d. We recall that $T_{hd}$ is the 24 h ahead forecasted temperature.

Once the ANN is trained, in correspondence of an unseen input vector $x_{\bar{h}\bar{d}}$ associated to hour $\bar{h}$ of day $\bar{d}$ and structured as in (4), pureM provides an energy demand forecast $F_{\bar{h}\bar{d}}^{M1}$ (where superscipt M1 refers to the pureM) as

$$\begin{aligned} F^{M1}_{\bar{h}\bar{d}}=\hat{y}^{M1}_{\bar{h}\bar{d}}, \end{aligned}$$

(5)

where $\hat{y}^{M1}_{\bar{h}\bar{d}}$ is the output produced by the ANN for the $x_{\bar{h}\bar{d}}$ input. We note that pureM can be directly applied to the 24 h ahead forecast, as all the required inputs are available 24 h before the forecasted time instant.

3.4 The inter-day model

The inter-day model (interM) captures the inter-day energy deviation pattern. Thus, interM is focused on learning the difference between energy demands at the same hour of two consecutive days. The target $y_{hd}$ and input $x_{hd}$ are as follows

$$\begin{aligned} y_{hd}=&E_{hd}-E_{h,d-1}, \end{aligned}$$

(6)

$$\begin{aligned} x_{hd}=&(T_{hd},K_{hd},h,E_{h,d-1}-E_{h,d-2},E_{h,d-2}-E_{h,d-3},\dots \nonumber \\&\dots ,E_{h,d-6}-E_{h,d-7}). \end{aligned}$$

(7)

Since the target of interM is the difference of energy demand within a lag of 24 h, the feedback inputs are also 24 h deviations of the last seven days. Note that with respect to the pureM, there is one less feedback input, since $E_{h,d-7}-E_{h,d-8}$ is not considered.

A trained interM produces an output $\hat{y}^{M2}_{\bar{h}\bar{d}}$ (where superscript M2 refers to the interM) corresponding to an unseen input $x_{\bar{h}\bar{d}}$ which approximates the 24 h deviation $E_{\bar{h} \bar{d}}-E_{\bar{h},\bar{d}-1}$, therefore the actual energy demand forecast $F^{M2}_{\bar{h} \bar{d}}$ is obtained as

$$\begin{aligned} F^{M2}_{\bar{h}\bar{d}}=\hat{y}^{M2}_{\bar{h}\bar{d}}+E_{\bar{h},\bar{d}-1}. \end{aligned}$$

(8)

Note that $E_{\bar{h},\bar{d}-1}$ together with all the inputs considered in the interM, are available 24 ahead. Thus, this model can also be used to generate the 24 ahead forecast.

3.5 The intra-day model

The intra-day model (intraM) aims at learning the energy demand difference between two consecutive hours. It can be viewed as a way to capture the daily energy demand variation pattern. The target $y_{hd}$ and input $x_{hd}$ are as follows

$$\begin{aligned} y_{hd}=&E_{hd}-E_{h-1,d}, \end{aligned}$$

(9)

$$\begin{aligned} x_{hd}=&(T_{hd},K_{hd},h,E_{h,d-1}-E_{h-1,d-1},E_{h,d-2}-E_{h-1,d-2},\dots \nonumber \\&\dots ,E_{h,d-6}-E_{h-1,d-6}). \end{aligned}$$

(10)

Thus, the target is the energy demand difference between the current hour and the previous one, while the feedback inputs represent this difference in the previous six days. Similar to the interM, intraM has one less feedback input, compared to the pureM. Differently from the previous models, intraM is reconstructed recursively and cannot be directly applied to obtain the 24 h ahead energy demand forecast. Indeed, a trained intraM produces an output $\hat{y}^{M3}_{\bar{h}\bar{d}}$ (where superscript M3 refers to the intraM) corresponding to an unseen input $x_{\bar{h}\bar{d}}$ which approximates the hourly deviation $E_{\bar{h} \bar{d}}-E_{\bar{h}-1,\bar{d}}$. This quantity may be used to reconstruct the actual energy demand forecast as $F^{M3}_{\bar{h} \bar{d}}=\hat{y}^{M3}_{\bar{h}\bar{d}}+E_{\bar{h}-1,\bar{d}}$. We assume that predictions are performed at $t=1$ of everyday. Thus, with the exception of $\bar{h}=1$, $E_{\bar{h}-1,\bar{d}}$ is not available in the previous day. In particular, for $h=1$ the forecast is computed as

$$\begin{aligned} F^{M3}_{\bar{1}\bar{d}}=\hat{y}^{M3}_{1\bar{d}}+y_{24,\bar{d}-1}. \end{aligned}$$

(11)

For $\bar{h} \ne 1$ the term $E_{\bar{h}-1,\bar{d}}$ is approximated by its forecast (the one produced by the ensemble of the three models for the previous hour), i.e., $F_{\bar{h}-1,\bar{d}}$. Therefore, the intraM forecast is calculated as

$$\begin{aligned} F^{M3}_{\bar{h}\bar{d}}=\hat{y}^{M3}_{\bar{h}\bar{d}}+F_{\bar{h}-1,\bar{d}}. \end{aligned}$$

(12)

3.6 Training and forecasting: a rolling horizon approach

As previoulsy mentioned, due to the operational reasons related to the considered application, the 24 predictions associated to the next day should be generated at the end of the current day. Therefore, the implemented training and forecasting strategy consists of a 24 h rolling-horizon approach. In particular, let us consider the current day d, and suppose that input and output data are collected for the last T recent “thermal days" (including d). Let $\mathcal{T}^0$ be the set of days $\mathcal{T}^0=\{d,d-1,\ldots ,d-T+1\}$, where superscript 0 refers to the first rolling horizon step. Then, the forecast of the 24 hourly energy demands of $d+1$ is obtained by training the ANNs models with data associated to days in $\mathcal{T}^0$, according to the input extraction methodologies described in Sects. 3.3– 3.5. We note that from each day of $\mathcal{T}^0$, 24 hourly samples are extracted.

In the next rolling horizon step, day $d+1$ is inserted in the new set of days and the least recent day is discarded, formally $\mathcal{T}^1=\{\{\mathcal{T}^0 \cup {d+1} \}{\setminus }\{d-T+1\}\}$. Then the training is repeated to obtain the predictions of day $d+2$, and so on. It is worth mentioning that while our methodology is designed to forecast the day ahead, with mild alterations we are able to accurately forecast the demand with reasonable precision 48 or 72 h ahead. This will be be shown in Sect. 4.5.

3.7 Optimization of the weights

The previously described three models are used to capture different aspects of the investigated phenomenon. While pureM is the most general and simple out of the three, interM is expected to work well in case of sufficiently regular variations between consecutive days, while intraM learns the demand deviations between consecutive hours of the day. It is worth emphasizing that forecasting the 24 h seasonal difference series (interM) and the first order difference series (intraM) is much more sensible when both series are non-stationary. Here we make no assumptions about stationarity of both time series as our aim is to develop a very general methodology which is able to automatically adapt to different energy demand contexts. This does not constitute a limitation from a practical point of view, since ( as described in what follows), the weight optimization is able to (partially or totally) enable or disable all involved models when needed.In what follows, we develop a weight optimization strategy that produces a unified forecast from the three proposed models.

At each rolling horizon step, each model generates the 24 hly forecasts for next day $\bar{d}$, i.e., $F^{M1}_{h\bar{d}}$, $F^{M2}_{h\bar{d}}$ and $F^{M3}_{h\bar{d}}$, with $h=1,\ldots ,24$ depicting a general hour of day $\bar{d}$. Then the final forecast $F_{h\bar{d}}$ is obtained as a weighted sum of the latter. Formally,

$$\begin{aligned} F_{h\bar{d}}= w_{h}^{M1} F^{M1}_{h\bar{d}}+w_{h}^{M2} F^{M2}_{h\bar{d}}+w_{h}^{M3} F^{M3}_{h\bar{d}}, \end{aligned}$$

(13)

where $w_{h}^{Mi} \in \left[ 0,1\right]$ with $i=1,2,3$ being the weight associated to pureM, interM and intraM respectively, at hour h. Therefore, we represent all weights via weight matrix $W \in \Re ^{24 \times 3}$ as follows

$$\begin{aligned} W = \begin{pmatrix} w_{1}^{M1} &{} w_{1}^{M2} &{} w_{1}^{M3} \\ w_{2}^{M1} &{} w_{2}^{M2} &{} w_{2}^{M3} \\ \vdots &{} \vdots &{} \ddots \\ w_{24}^{M1} &{} w_{24}^{M2} &{} w_{24}^{M3} \end{pmatrix}. \end{aligned}$$

(14)

The choice of using hourly weights instead of a single weight per model allows more freedom, as each model may perform differently during the day.

The weights are determined by an optimization procedure. Specifically, we optimize the weights cyclically over P days, i.e., the optimization is carried out on the basis of data collected during the last P days. The weights are then kept constant for the next P days. After each cycle of P days the weights are reoptimized. This is done by minimizing a loss function representing a deviation between the observed values and the final forecasts. To this aim, the partial forecasts of each single model are needed. As previously mentioned, this is not an issue for pureM and interM, as the forecast of the former coincides with the model output (see (5)), and the latter is computed using the observed energy demand 24 h before (see (8)). This data is available for both these models in the last P days. However, when generating $F^{M3}_{h\bar{d}}$, which is associated with intraM, the the real observation or the final forecast $F_{h-1,\bar{d}}$ of the previous hour is required (see (11) and (12)). Note that the intraM forecast for $h=1$ can be computed from the real observation of hour 24 of day before according to (11)), to obtain $F_{h-1,\bar{d}}$. To obtain $F_{h-1,\bar{d}}$ for $h\ne 1$, the values of the weights are needed (see (13)) whose optimization is in turn based on the knowledge of the intraM partial forecasts.

Due to the above mentioned issues, we propose the sequential ordered optimization procedure (SOOP), which is performed considering one specific hour at a time. By doing so, when optimizing the weights associated to a certain hour $\bar{h} \ne 1$, the final forecasts associated to $\bar{h}-1$ are already available as their corresponding weights have been determined in the previous step of the SOOP. Formally, we define $D_{opt}$ by considering the partial forecasts of pureM and interM, as they can be directly computed from the available data, and maintaining the model output for the intraM, as

$$\begin{aligned} D_{opt}:=\Big \{ \Big (y_{hd}; F^{M3}_{hd}, F^{M2}_{hd},\hat{y}^{M3}_{hd}\Big ),h=1,\ldots ,24,d=\bar{d}-P+1,\ldots , \bar{d} \Big \}. \end{aligned}$$

(15)

The SOOP optimizes the weights according to two different criteria reflecting two different performance measures: the mean absolute percentage error (MAPE) and the maximum absolute percentage error (MaxAPE). Concerning the MAPE, the optimization problem solved by SOOP to determine the weights associated to hour $\bar{h}$ is as follows

$$\begin{aligned} \underset{w_{\bar{h}}^{M1},w_{\bar{h}}^{M2},w_{\bar{h}}^{M3} \in \left[ 0,1\right] }{{\text {argmin}}}\frac{1}{|P|} \sum \limits _{d \in P} \frac{|y_{\bar{h}d}- w_{\bar{h}}^{M1} F^{M1}_{\bar{h}d}-w_{\bar{h}}^{M2} F^{M2}_{\bar{h}d}-w_{\bar{h}}^{M3} F^{M3}_{\bar{h}d}|}{y_{\bar{h}d}}, \end{aligned}$$

(16)

whereas for the MaxAPE, the optimization problem solved by SOOP to determine the weights associated to hour $\bar{h}$ is as follows

$$\begin{aligned} \underset{w_{\bar{h}}^{M1},w_{\bar{h}}^{M2},w_{\bar{h}}^{M3} \in \left[ 0,1\right] }{{\text {argmin}}} \max \limits _{d \in P} \Big \{ \frac{|y_{\bar{h}d}- w_{\bar{h}}^{M1} F^{M1}_{\bar{h}d}-w_{\bar{h}}^{M2} F^{M2}_{\bar{h}d}-w_{\bar{h}}^{M3} F^{M3}_{\bar{h}d}|}{y_{\bar{h} d}} \Big \}. \end{aligned}$$

(17)

Notice that, without loss of generality, the weights are constrained in the interval $\left[ 0,1\right]$.

The scheme of the SOOP procedure is shown in Algorithm 1.

Algorithm 1

The SOOP procedure.

The SOOP procedure takes as input the $D_{opt}$ dataset of the last P days with respect to current day $\bar{d}$. During the initialization the intraM forecasts of the first hour of each day in $D_{opt}$ are obtained using the available $y_{24,d-1}$ values and applying equation (11).

In the main loop of Algorithm 1 each hour $\bar{h}$ of the day is considered incrementally. In particular, in the first step (point 1) the three weights associated to $\bar{h}$ are optimized by solving either problem (16) or (17). The specific choice between the two performance measures is a up to the user. The presence of the absolute value and the max operators results in optimizing non-smooth functions. However, as these functions contain only three variables and are defined over a bounded domain, the optimization problems are easily solved by an existing metaheuristic algorithm (see Sect. 4.3 for details).

In the second step of Algorithm 1, the final forecast of hour $\bar{h}$ for each day in $D_{opt}$ is computed by exploiting the weights determined at the previous step, and then these forecasts are exploited to generate the $F_{\bar{h}+1,d}^{M3}$ according to (12). Finally, the matrix of all optimized weights is returned.

4 Numerical experiments

The objective of this section is to assess, through extensive numerical experiments, the performance of the proposed EANN described in Sect. 3. To this end, the EANN is compared against three other forecasting methods, the one previously adopted by A2A, which we refer to as A2A-M, the SARIMAX (Box et al. 2015) and the Echo State Networks (ESNs) (Jaeger 2001). Due to privacy reasons, we cannot present the detailed steps of A2A-M. However, as already mentioned, this method is based on multiple linear regression and requires manual intervention by experts. The comparison with SARIMAX is motivated by the fact that it is a standard autoregressive model suited for seasonal time series and the presence of exogenous variables, frequently used to forecast energy consumption (see e.g., Vagropoulos et al. 2016 and reference therein). Concerning ESNs, they are powerful deep neural network structures (Goodfellow et al. 2016) with a “not deep" training phase, that are much easier with respect to other deep architectures. These features make them appealing for many application fields such as speech recognition or time series forecast (e.g., Skowronski and Harris 2007; Bianchi et al. 2015).

The rest of this section is organized as follows. In Sect. 4.1 the main elements of the SARIMAX model are presented, while in Sect. 4.2 we give an overview of ESNs, and specify its implementation details in the context of the considered setting. We describe our experimental setting in Sect. 4.3, and present the results for the day ahead forecasts in Sect. 4.4. In Sect. 4.5 we present the results obtained for other forecasting horizons.

4.1 SARIMAX

SARIMAX is an extension of the standard seasonal ARIMA model, which takes into account exogenous variables. Without entering into details (the interested reader is referred to Box et al. 2015), SARIMAX consists of the following components:

• seasonal (S);

• autoregressive (AR);

• moving average (MA);

• integrating (I);

• exogenous variables (X).

From a mathematical point of view, a SARIMAX model can be described by the following equation

$$\begin{aligned} {\phi _p(L)\Phi _P(L^s)\Delta ^d \Delta ^D_s y^t=\beta x^t + \theta _q(L) \Theta _Q(L^s) \epsilon ^t,} \end{aligned}$$

(18)

where $y^t$ is the target variable, $\phi _p(L)$ is the AR polynomial of order p, $\Phi _P(L^s)$ is the seasonal AR polynomial of order P, $\theta _q(L)$ is the MA polynomial of order q, $\Theta _Q(L^s)$ is the seasonal MA polynomial of order Q, L is the lag operator (for example $L^k(y^t)=y^{t-k}$), $\Delta ^d$ is the differencing operator of order d, $\Delta ^D_s$ is the seasonal differencing operator of order D, $x^t$ is the exogenous variables at time t with associated coefficient $\beta$, $\epsilon ^t$ is a white noise, and s is the seasonal component. The hyperparameters of the model are p, q, d, P, Q, D, and s. The adopted values for these hyperparameters are specified in Sect. 4.3.

4.2 Echo state networks

ESNs are made up of three layers: a standard input layer as in ANNs, a “deep" hidden layer called reservoir, and a linear output layer called the readout. A simplified scheme of an ESN is depicted in Fig. 4.

Fig. 4

A simplified scheme of an ESN. In the input layer there are the $x_1,\ldots ,x_n$ input signals which are forward propagated to the reservoir made up of $h_1,\ldots ,h_r$ hidden units connected to each other by means of a variety of different connection patterns. The signals outgoing from the reservoir are sent to the output layer y through feedforward connections

In principle, ESNs are dynamic systems that propagate the current signal from the input layer to the output layer by passing through the reservoir. The reservoir is a chaotic layer comprised by a large amount of connection patterns (including feedback connections) reproducing multiple temporal dynamics. Thus, the reservoir is able to represent temporal relations between the current signal and past signals, and generate the desired forecast at the output layer. For a more comprehensive overview of ESN we refer the reader to Jaeger (2001). In ESNs the input and reservoir weights are randomly determined, while the weights associated to the feedforward connections between the reservoir and the output layer are actually trained. Therefore, compared to other RNNs, an ESN’s training procedure is less time consuming and intricate. Specifically, such procedures typically entail solving a relatively simple convex unconstrained optimization problem. This feature makes ESNs very attractive for inexperienced users. Thus, we saw fit to test ESNs as a possible alternative to our ANN-based approach.

4.3 Experimental settings

Our experimental setup for the ANNs adopted in the EANN, SARIMAX and ESN includes training set TR, which is composed of the 24 hourly samples associated to the days from the 1st of January 2017 to 15th of April 2017 and from the 28th of October 2017 to 15th of April 2018 (see Sect. 3.2). This time period approximately covers one and a half thermal seasons. Specifically, the set TR consists of 275 training days corrsponding to 6600 hourly samples. The testing set TS is composed of the 24 hourly samples associated to the days from the 22th of October 2018 till the 4th of April 2019. This time period approximately covers a thermal season. The choice of these data sets was determined based on the availability of reliable hourly data in the case study. In principle, we validated our model using the forecasted temperature as this is the information available at the time of making the forecast. Our results could have been further verified using the actual observed temperature rather than the forecasted one. However, this information was not available at the company.

We recall that the feedback input of the EANN method require the heating demand observation of the seven previous days. In the considered case, the demand between the 8th to the 14th of October is null, as this period is not contained in the thermal season. Therefore, we excluded the first week of the thermal season in our analysis. Furthermore, we have excluded the 25th of February 2019, 23th and 25th of March 2019, and the period from the 5th to the 15th of April 2019, as the forecasts of A2A-M were not available for these days. Thus, the set TS was made up of 3888 hourly samples, corresponding to 162 days. All experiments have been carried out on a Linux system running on an Intel Core i7-6700HQ CPU 2.60GHz x 8 with 8 GB of RAM.

Our EANN method contains three neural network models. Theses have been implemented in Python 3.6 by adopting the MLPRegressor() function of the freely available scikit-learn package. To determine the hyperparameters values of the ANNs models, we performed a grid-search on a time series split cross-validation (where essentially the training and testing data are taken from temporarily consecutive periods, see Bishop 2006 for cross-validation and Korstanje 2021 for time series split) with five splits on the TR samples. In particular, the hyperparameters included in the grid-search, their grid of values and the determined best ones are reported in Table 2.

Table 2 The hyperparameters considered in the ANNs grid-search

For the other hyperparameters, the default values have been used. Concerning the rolling horizon strategy described in Sect. 3.6, from the above discussion the training horizon T amounts to 275 days, $\mathcal{T}^0$ include all days associated to samples in TR and the first prediction (testing) day d is the 22th of October 2018. Since the training of ANNs is formulated as nonconvex nonlinear optimization problem, the trained model and its predictions are affected by the random starting solution of the optimization phase. To mitigate this effect, at each testing day the final 24 hourly forecasts are obtained by averaging the predictions from 10 different random initializations for each of three models. The best value of the weights optimization horizon P has been determined by a simple enumeration precedure, and set equal to 28 accordingly. Concerning the resolution of problems (16) or (17) in step 1. of the SOOP algorithm, note that by introducing auxiliary variables to replace the absolute values and the max operator, they can be modeled as linear programming problems and solved by off-the-shelf solvers. In particular, the linprog() function of the scipy package has been used. In the first 28 days, the SOOP procedure could not be applied due to the lack of previous historical data required in $D_{opt}$. Therefore, in that period only the pureM has been considered.

Also for the SARIMAX model, a rolling horizon strategy like the one described in Sect. 3.6 has been adopted. However, differently from EANN, a one week long training horizon (168 hly samples hours) has been used, since preliminary experiments showed that longer or shorter training periods led to substantially worst performance. This may be due to the evident weekly demand pattern. The SARIMAX hyperparameters have been set to $p,P,D,Q=1$, $d,q=0$, and $s=24$. Except for s, whose value is straightforwardly derived by the strong daily seasonality, for all other parameters, we tested all possible 0 or 1 combinations, and selected the best performing combination. The SARIMAX model was implemented using the SARIMAX() function of the statsmodel package of Python.

The ESN was implemented using the keras Python package. Also ESN models depend on several hyperparameters. Among them we mention the number of reservoir neurons ($N_r$), the regularization parameter in the ridge regression ($\lambda$), and the spectral radius of the incidence matrix of reservoir connections ($\rho$). The latter is very important for the ESN perfromance, indeed its value should not overly exceed the value of one to prevent explosion of the signals, but it should also be sufficiently large to avoid a premature decay of the influence of past states (see e.g., Bianchi et al. 2016). Analogously to ANNs, the ESN hyperparameters values have been determined by means of a grid-search with 5-fold cross-validation. However, in this case a finer resolution of the grid was used, as ESNs’ performance is more sensitive to the hyperparameters than that of ANNs’. The grid values and the best ones are reported in Table 3.

Table 3 The hyperparameters considered in the ESN grid-search

It is worth mentioning that, while in the ANN strategy the models are re-trained at each rolling horizon step (each testing day), the ESN is trained once and then the trained model is used as a dynamic system which sequentially generates the predictions for the whole testing period.

4.4 Results

In this section we consider forecasting the day ahead. We report the results of different variants of the proposed EANN method over the TS described in Sect. 4.3, compared with those of A2A-M and ESN. We denote by $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$ the EANN versions in which problems (16) and (17) are, respectively, considered in the SOOP procedure.

We mainly consider the MAPE and the MaxAPE as performance measures, since these were identified as most relevant by the A2A company. However, for the sake of completeness, we report also performance in terms of MSE, which is the loss function used for the training of all ANN models and of the ESN, and in terms of Root Mean Squared Error (RMSE), which is analogous to MSE but is expressed in the same scale as the data.

The results are reported for both the whole testing period, and also disaggregated for each of the six periods of 28 consecutive days corresponding to the five steps of weights optimization. Recall that at each weight optimization step the weights of the three models remain unaltered at fixed values for the whole period and, at the end of the period, they are optimized again for the subsequent one. Furthermore, we report the results for each of the single ANN models (pureM, interM, and intraM) to highlight the added value of combining them in the EANN strategy.

Table 4 reports the results for the whole testing horizon (22th of October 2018–4the of April 2019). Since the weights of the model are not available in the first period of 28 days (22nd of October–18th of November), exclusively for this period only pureM (which taken singularly performs better than interM and intraM) has been considered for both $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$. Note that $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$ are better than SARIMAX and outperform A2A-M and ESN in terms of MAPE, and they outperform all the compared methods in terms of MaxAPE. In particular, $\text{ EANN}_{MAPE}$ obtains the best MAPE value (6.69%), which is more than $1\%$ better than SARIMAX ($7.96\%$), and almost halving the corresponding A2A-M value ($12.50\%$). $\text{ EANN}_{MaxAPE}$ obtains the best MaxAPE value($41.29\%$) by more than halving the A2A-M ($107.83\%$) which in this case is the second best alternative. The differences are more marked in the comparison with ESN, as the latter shows to be the least competitive method for both performance criteria. It is worth mentioning that $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$ are able to achieve the best MAPE and MaxAPE respectively. This implies that the considered equations (16) and (17) are effective in determining weights which are suited for the two criteria. Moreover, $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$ outperform all compared methods also in terms of MSE and RMSE.

Table 5 reports the results for the partial testing horizon in which the three weighted models are used, i.e., excluding the first 28 days. This table also reports the results obtained by the $\text{ combineM }$ model, which is a single ANN model inclunding all the inputs used for pureM, interM and IntraM (with overlapping inputs considered only once). In other words, combineM is obtained by extending pureM with the inputs of interM and intraM. The comparison with $\text{ combineM }$ is used to asses the benefit of the optimized weighted sum of three separate models with respect to the plain inclusion of all considered inputs in a single ANN. It is worth pointing out that this comparison can be applied only in the period where the three weighted models are used, for this reason it is inserted in this table. Models $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$ consistently achieve the best MAPE and MaxAPE, with approximately the same relative improvements observed in Table 4. The difference in MAPE between $\text{ EANN}_{MAPE}$ and pureM is around $1\%$. Furthermore, the difference in MaxAPE between $\text{ EANN}_{MAPE}$ and pureM is around $3\%$. Moreover, the results obtained by combineM, being substantially comparable with those of pureM, show the advantage of the proposed $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$.

Tables 6 and 7 report the MAPE and MaxAPE results disaggregated for each period of 28 consecutive days associated to the weights optimization steps. If we consider only the five blocks in which the ensemble method is actually applied (columns (II)–(VI) of Tables 6 and 7), four times over five the best MAPE is obtained by $\text{ EANN}_{MAPE}$ and one time by pureM, while three times over five the best MaxAPE is obtained by $\text{ EANN}_{MaxAPE}$ and two times by pureM.

The first and the last periods (columns (I) and (VI) of Tables 6 and 7) are the most difficult to forecast. Indeed, in these periods, corresponding approximately to mid autumn and the beginning of spring, are characterized by large temperature fluctuations implying a more erratic energy demand profile. In such cases, the EANN tends to be even more preferable than A2A-M and ESN, especially with respect to the MAPE, and only SARIMAX achieve comparable (though worse) performance.

It is worth pointing out that the MAPE and MaxAPE performances obtained by, respectively, $\text{ EANN}_{MAPE}$ and $\text{ EANN}_{MaxAPE}$, are better than those obtained by the single ANN models pureM, interM, and intraM.

The disaggregated MSE and RMSE results reported, respectively, in Table 8 and 9 essentially confirm the previous results. Indeed, $\text{ EANN}_{MAPE}$ achieves the best performance on the last four periods, while pureM on the first two.

Table 4 Results on the testing period from the 22th of October 2018 till the 4th of April 2019, excluding the 25th of February and the 23th and 25th of March 2019

Table 5 Results on the testing period from the 19th of November 2018 till the 4th of April 2019, excluding the 25th of February and the 23th and 25th of March 2019

Table 6 MAPE results for groups of 28 days

Table 7 MaxMAPE results for groups of 28 days

Table 8 MSE results for groups of 28 days

Table 9 RMSE results for groups of 28 days

While Fig. 5 depicts the actual energy demand profile and the forecast of all the compared methods, Fig. 6 shows the absolute error profiles of three five-day periods related to the different main type of demand patterns. The absolute error at time instant i is computed as $|y^i-\hat{y}^i|$ with $y^i, \hat{y}^i$ being the actual and the forecast demand. The top subfigure (6.a) is associated to mid-autumn, the central one (6.b) corresponds to mid-winter, and the bottom one (6.c) to the beginning of spring. The $\text{ EANN}_{MAPE}$ profile tends to be lower than the other profiles (so closer to the actual demand) and generally with less pronounced peaks, especially for the extreme periods which are more difficult to be predicted.

We conclude this section by mentioning the potential financial gains that could be achieved by the EANN. Based on back-testing analysis conducted by A2A, each percentage point reduction in the 24 ahead MAPE may contribute to a reduction of 2 to 4% in the DHO’s operational costs (e.g., including fuel, electricity, ETS). Thus, reducing the MAPE from 12.5 to 6.69% (as reported in Table 4) can yield significant cost savings in the considered application.

Fig. 5

The energy demand profiles for TS. The magenta vertical line separates the first period of 28 days from the others

Fig. 6

Three five-day profiles: absolute error profiles in the first (a), central (b) and last (c) periods of testing horizon

4.5 Results for different forecast horizons

Performing forecasts for longer planning horizons is useful to plan several operational activities. In practice, such forecasts are used to have a general idea of the demand, and are later refined by the more accurate day ahead forecasts. Although the EANN is designed to perform a day ahead forecast, it can also be used to generate predictions for longer forecasting horizons, without any structural changes. The main challenge in such cases is the relatively extended time lag between the available information and the forecasting horizon.

Since our method is designed for using observations of energy demand collected up to 24 h before the predictions, for longer forecasting horizons it automatically operates a recursive multi-step approach (see e.g., Galicia et al. 2019). Accordingly, the lacking energy demand observations are substituted by their EANN forecasts. For example, if at hour $h\ne 24$ of day d we should make a prediction of the energy demand 25 h later, that is $F_{h+1,d+1}$, then the EANN would determine the forecast of the energy demand of next hour $F_{h+1,d}$, and would then construct the feedback inputs of pureM, interM and intraM by replacing $E_{h+1,d}$ with $F_{h+1,d}$. Considering for example pureM, equation (4) would be replaced by

$$\begin{aligned} x_{h+1,d+1}= (T_{h+1,d+1},K_{h+1,d+1},h+1,{\varvec{ F_{h+1,d}}},E_{h+1,d-1},\ldots ,E_{h+1,d-6}), \end{aligned}$$

(19)

where $E_{h+1,d-1},\ldots ,E_{h+1,d-6}$ are available data. For the 26 h later forecast ($F_{h+2,d+1}$), the EANN would determine $F_{h+2,d}$ and then set the inputs as

$$\begin{aligned} x_{h+2,d+1}= (T_{h+2,d+1},K_{h+2,d+1},h+2,{\varvec{F_{h+2,d}}},E_{h+2,d-1},\ldots ,E_{h+2,d-6}). \end{aligned}$$

(20)

For forecasting horizons between 48 and 72 h two feedback inputs would be replaced by their forecast. If we consider a 49 h ahead forecast, the inputs would be

$$\begin{aligned} x_{h+1,d+2}= (T_{h+1,d+2},K_{h+1,d+2},h+1,{\varvec{ F_{h+1,d+1},F_{h+1,d}}},E_{h+1,d-1}\dots ,E_{h+1,d-4}), \end{aligned}$$

(21)

and so on. Equations (7) and (10) are modified accordingly.

It is worth pointing out that replacing $E_{h+1,d}$ with $F_{h+1,d}$ would propagate the prediction error made on $F_{h+1,d}$ to $F_{h+1,d+1}$. This effect is amplified with longer forecasting horizons, as more predictions would be used in the feedback inputs. However, the EANN does not suffer too much from this error propagation. Indeed, we tested the $\text{ EANN}_{MAPE}$ version on the same testing set adopted for the experiments of Sect. 4.4 for the 48 and 72 h ahead forecast. Due to the structure of the feedback inputs, for the 48 and 72 h ahead forecast we had to remove the first two days of the testing horizon. The results, reported in Table 10, show that the EANN is able to produce better predictions with a 48 and 72 h ahead forecast than $\text{ SARIMAX }$ and than the A2A-M with the “simpler" day ahead forecast (see Table 4).¹ This is due to the fact that the propagation of the error phenomenon is mitigated by the very accurate predictions of the $\text{ EANN}_{MAPE}$ model.

Table 10 Results on the whole testing horizon for the 48 and 72 h ahead forecast for $\text{ EANN}_{MAPE}$ and $\text{ SARIMAX }$

5 Conclusions

We proposed the EANN method to forecast the day ahead hourly heating demand of a city or an urban district. The EANN combines a weighted sum of three different single hidden layer feedforward ANN models with a rolling horizon strategy. Each ANN model captures a different aspect of the predicted time series. Furthermore, we devise a sequential ordered optimization procedure to determine the weights of three models in the final output. The procedure was tailored to two different performance criteria.

Our EANN was validated using A2A data related to a metropolitan area in Northern Italy, and it was trained on data of half 2016/2017 and entire 2017/2018 thermal seasons, and then tested on roughly the entire 2018/2019 thermal season. We compared our method with the one used by A2A, namely A2A-M, which is based on multiple linear regression requiring expert intervention. Furthermore, we also compared our method with the autoregressive SARIMAX model and with a deep neural network architecture, namely an ESN. The comparisons show that EANN is better than all other methods on all considered performance criteria, almost halving the prediction errors with respect to A2A-M. Thus, our methodology promises significant cost savings. The sequential ordered optimization procedure reveals to be effective in calibrating the models’ weights so as to meet the considered performance measure. We have also demonstrated that the EANN can be used for longer forecasting horizons. Indeed, fairly good performance is achieved considering 48 and 72 h ahead forecast.

Finally, it is worth mentioning that the EANN can be applied in an automated way. Thus, differently from A2A-M, the EANN does not require human intervention. Moreover, leveraging a simple neural network architecture, the EANN is suited for being used by non experts in machine learning. Furthermore, a potential future extension could be to consider quantiles as optimal point forecasts (see e.g., Gneiting 2011), in case of distinct overestimation and underestimation costs.