1 Introduction

We consider abstract source detection problems for time-dependent data on graphs. Given a graph consisting of nodes and weighted edges, random noise, and a mathematical model for a spreading process on the nodes of the graph we want to determine optimal strategies to query oracles (i.e., observing one or several nodes at a particular time) and to use the available measurement information to infer the most probable source of the spreading process. Depending on the setting, the subproblems may have to be solved while the underlying process is ongoing. The first one can be interpreted as an experimental design problem, focusing on the collection of information. The second one is the source detection (or localization, inversion, identification, resolving) problem, exploiting the gained information to identify the source. While both problems are well understood in various circumstances, especially in Euclidean spaces, we are not aware of a rigorous abstract treatment on graphs.

Most source detection problems on graphs have been tackled from a practical viewpoint. In Chartrand and Zhang (2003) fire localization in buildings and the coast guard LoRaN stations are investigated. Other applications are the classification of chemical compounds (Chartrand et al. 2000; Chartrand and Zhang 2003) or the spread of information or diseases (Tillquist et al. 2021). All this is related to the metric dimension of a graph, which is an important concept for source detection on graphs.

Detecting the source of a pollution in water networks is a practically relevant task. Much research in this area is focused on the sensorics, i.e., which chemical or biological markers have to be tested to distinguish different kinds of pollution sources (Baker et al. 2003; Sidhu et al. 2013; Bernhard and Field 2000; Noblet et al. 2004). Additionally, location dependent visualization and interpolation schemes are used (Costanzo et al. 2001). Some researchers also try to detect the source in space. In Laird et al. (2003) mainly linear simplified models are used in an optimization framework. Here, flow conditions are assumed to be known and then used to calculate time delays of pollution concentration over the network. These delays are used in a quadratic optimization problem to calculate pollution injection profiles over time for all nodes. A similar flow model based approach to the offline problem can be found in Marlim and Kang (2020). In Eliades and Polycarpou (2011) the online case is considered with the goal to place a minimal number of sensors to identify the source. The spread of computer viruses and fault propagation in information networks have been modeled as spreading phenomenon on a graph as well, Shah and Zaman (2010); Coffman et al. (2002). In Shah and Zaman (2010) a stochastic model is used to describe the infection between nodes in the network. In Coffman et al. (2002) ordinary differential equations (ODEs) are used. The spread of epidemics can be modeled as a phenomenon on a graph (Newman 2002; Colizza and Vespignani 2007; Ganesh et al. 2005; Ball and Lyne 2002). The spreading can be described by a stochastic process or by deterministic ODEs, allowing for analysis of, e.g., thresholds that decide if an epidemics dies out or continues spreading, sizes of infected subpopulations, vaccination schemes to suppress outbreaks, or speed of propagation. The source detection of epidemics was investigated using correlation (Brockmann and Helbing 2013), spectrality (Fioriti and Chinnici 2012), Bayesian (Altarelli et al. 2014) or centrality based estimators (Yu et al. 2022; Luo et al. 2014; Comin and da Fontoura Costa 2011).

Similarly, objects that produce sound can be detected with distributed microphones as a sensor network. Applications range from localizing the talker in a room for camera pointing (Benesty 2000; Wang and Chu 1997; Brandstein 1997) to surveillance of outside areas (like crossroads, valleys, or industrial facilities) and underwater areas (sonar) (Krim and Viberg 1996; Chen et al. 2002). Acoustic waves traveling through air usually have a constant velocity. Like in our setting later, the time distance relationship is linear. The least squares approach in Yao et al. (1998), which was also applied to sonar, radar, or radio applications, is similar to our approach. The main difference is the use of distances in the Euclidean space and the a priori knowledge of the velocity. Seismic waves were considered in Singh et al. (2000); Kanamori and Rivera (2008), focussing on partial differential equations describing the elastodynamics of the ground. The detection of objects in astronomical images is considered in Hopkins et al. (2002). Examplary medical applications are neural source detection in the brain for epilepsy research (Jatoi et al. 2014) and the mapping and prediction of focal cardiac arrhythmias (Weber et al. 2017).

Although all these applications address source detection, there are typically distinct features and requirements. What exactly can be observed on the nodes of the graph? Is there one unique source or are there multiple sources? Shall measurement errors be taken into account? What are the assumptions on the spreading process? In the following we make an effort to formalize one particular type of source detection problem, motivated mainly by investigations of electrocardiac conduction in the human heart. As detailed in (Weber et al. 2017), source detection based on measurements on the heart surface is routinely performed by clinicians. This application motivates the choices we shall make with respect to the particular problem class under consideration, e.g., by only considering a single source and the signal timing due to the shortest path between two nodes. However, we shall comment in several remarks where a further generalization is possible and what theoretical and algorithmic implications would be. Our motivation is to work in a general and abstract framework with clearly defined assumptions that allow a closer investigation on the one hand, and allow a transfer to source detection problems with slightly different assumptions on the other hand.

Methodological research for source detection problems with measurement errors focuses on ill-posed linear problems (Malioutov et al. 2005) and parameter estimation for source detection (Beck et al. 2008). The problem of choosing graph oracle queries is an experimental design problem. Designing an experiment to optimize an information criteria is called optimal experimental design (Fedorov 2010; Kiefer 1959). Different objective functions have been suggested and analyzed. A very early idea was to minimize the variance of the model prediction (Smith 1918). This is now referred to as G-optimal and is equivalent to the so called D-optimal criterion (Kiefer and Wolfowitz 1959). The D-optimal criterion (Wald 1943) maximizes the determinant of the Fisher information matrix. Another criterion is to minimize the variance of the parameter estimators of the model (Elfving 1952), referred to as A-optimality.

Our focus here is different, as we assume an underlying discrete structure, the special metric space of graphs. For the deterministic setting without measurement errors, the experimental design problem on graphs can be formulated as the problem of determining a metric basis of a graph, i.e., a minimal cardinality set of nodes that allows a unique identification of all possible sources. It is proven in Khuller et al. (1996a) by a reduction from 3-SAT that the associated decision version of the metric dimension problem is NP-complete. The metric dimension is the cardinality of a metric basis. In Chapter 3 of Tillquist et al. (2021) a simple brute force algorithm is presented, which calculates the metric dimension of a graph in exponential time. To find a metric basis one can enumerate all possible vertex sets from small to large cardinality until a basis is found. In Hauptmann et al. (2012) an \((1+(1+o(1))\log (n))\)-approximation algorithms is given which runs in \(\mathscr {O}(n^3)\), with \(n = \text {card}(V)\). The metric dimension can not be approximated within \(o(\log (n))\) (Hartung and Nichterlein 2013). For unweighted graphs fixed parameter tractability with special parameters has been proven in Belmonte et al. (2015) and Eppstein (2015). In both articles algorithms are developed, which compute the metric dimension. In Belmonte et al. (2015) the authors design an algorithm which decides if the metric dimension of a graph is lesser or equal to k for a given \(k \in {\mathbb {N}}\). They have proven that the problem is fixed parameter tractable with the parameter \(\Delta + tl\), where \(\Delta \) is the max-degree and tl is the tree-length of the graph. In Eppstein (2015) the metric dimension problem is proven to be fixed parameter tractable with the max leaf number of the graph as the parameter.

Related to the metric dimension is finding a minimal doubly resolving set. Doubly resolving sets, introduced by Cáceres et al. (2007a), calculate with an unknown start time of the signal. So, two vertices \(v\ne w\) are doubly resolved by x and y iff \(d(v,x)-d(v,y) \ne d(w,x)-d(w,y)\). This is equivalent to: \(\not \exists t\) such that \(d(v,x)= t+ d(w,x)\) and \(d(v,y)= t+ d(w,y)\) holds. In Kratica et al. (2009) it is proven that deciding if there exists a doubly resolving set of size k is NP-complete. Adding a constant velocity of the signal as another unknown to the signal spreading process results in the spread dimension problem we shall introduce in this paper, which to our knowledge was never considered before. We do not propose an algorithm to calculate a metric or a spread basis exactly in this paper, although this is an open and interesting field of research. Instead, we use the formalization of the problem class to get a general understanding of the source detection problem in a stochastic setting. For this case involving measurement errors, we shall propose a new algorithm.

The main contributions of this paper are a unifying problem definition for a wide range of applications, including problems with weighted and/or directed graphs, limited and deterministic/stochastic spreading information, online/offline settings, and linear dynamics. An algorithm is proposed for the stochastic setting. We discuss convergence and show practical performance and robustness over a wide range of test problems with different properties.

The paper is organized as follows. In Sect. 2 we provide basic definitions and formalize the source detection problem we are interested in. We also provide a simple example graph that will be used throughout the paper for an illustration of concepts. In Sect. 3 we consider the special deterministic case in which the oracle provides exact measurements. We generalize the metric dimension by introducing the spread dimension of a graph as a tool to solve the deterministic case. In Sect. 4 we discuss the stochastic problem. Based on linear regression and experimental design we present a solution algorithm and discuss its convergence properties in the limit. In Sect. 5 we present numerical results. In Sect. 6 we summarize our findings.

2 Source detection problem

We begin with a definition of the considered problem class. First, we define the underlying discrete structure.

Definition 1

(Graph) We consider a directed weighted graph \(G=(V,E)\) with positive edge lengths \(\ell (e) > 0\) for all \(e \in E\) and shortest-path-distances \(d_{i,j}\) with respect to the length function \(\ell \) between nodes i and j for all \(i,j \in V\). Let \(n:= \#V:= \text {card}(V)\) and \(\#E:= \text {card}(E)\).

Assumption 1

(Graph) We assume to have complete knowledge of the graph G and the length function \(\ell \), and hence also of the distance function d.

In practical applications, the nodes \(i \in V\) correspond to spatial locations where measurements are possible. Examples are communities, airports, cities, or countries for infectious diseases, points on a 3d surface grid of the human heart, or sensors in water distribution networks. The edges correspond to connections between the nodes, along which “something may be passed on”. This might, e.g., be a viral load via infections, electrical excitation of cells, or transported and diffused pollutant. In the interest of a simplification, and taking the risk that this term does not intuitively match every application, we will simply use the term signal to denote this in a general way in the following. We consider a dynamic process on a time horizon \(\mathscr {T}:= [t_s,t_f]\) that originates from an a priori unknown source \(s \in V\) and spreads the signal via edges to other nodes of the graph.

Definition 2

(Signal spreading process) A signal spreading process is a map \(t: V \times V \mapsto \mathscr {T}\) that assigns signal arrival times \(t_i(s)\) to all nodes \(i \in V\) for all possible source nodes \(s \in V\).

We are not interested here in the strength of the signal, which may be relevant for certain applications. Also the definition implies that only the timing of the first arrival of the signal is relevant, and not the arrival time via alternative paths. In electrophysiology, cardiac cells lose temporarily the ability to conduct electrical excitation after passing on the signal. Also in other contexts, such as the spreading of an epidemics, it becomes difficult to differentiate where new cases come from. It is an interesting question though, how for other applications the additional information via alternative paths can be used. Note that the times \(t_s\) and \(t_f\) are often unknown. The initial time \(t_s\), also called offset and indicating when the signal started at source node s, needs to be estimated. The end time \(t_f\) is not relevant for the mathematical model. The edge lengths \(\ell (e)\) quantify the distances the signal needs to travel to arrive at adjacent nodes. We make some assumptions for the following.

Assumption 2

(Signal spreading process) We assume that

  1. (1)

    The source \(s \in V\) is unique.

  2. (2)

    Signal spreading takes place in a diffusive way, i.e., a signal is passed on from a node i to all nodes j that are adjacent to i.

  3. (3)

    We assume a constant and homogeneous spreading velocity \(1/c > 0\). Hence, for a given source node s and known distance \(d_{s,i}\) we have

    $$\begin{aligned} t_i:= t_s + c \cdot d_{s,i} \end{aligned}$$

    as the arrival time at node \(i \in V\).

Adapting the concepts investigated in this paper to scenarios with multiple sources seems to be interesting and can be done in rather straightforward ways. Here, one may consider different variants, e.g., intended to model applications in which at each node one may request the arrival times of all signals or only the earliest arrival time of any signal. With applications in electrophysiological or epidemic source detection problems in mind, we focus on single source problems, though. While the second assumption is rather technical, the third assumption is an important restriction of the problem class to a linear model. We note that some applications might need less restrictive assumptions. For example, infections or electric conduction on the heart surface do not have a constant velocity in reality. However, we imagine that the velocity being an average velocity on the corresponding shortest paths helps to mitigate the negative effects of approximating the process with a linear one. We now look at the available measurement procedure, abstracted as a data oracle. An oracle allows to query nodes \(i \in V\) and obtain measurement data \(r_i\). The \(r_i\) indicate noise-corrupted times when the signal arrived at node i.

Definition 3

(Data oracle) A data oracle is a map \(r: V \mapsto \mathscr {T}\) providing values \(r_i \in \mathscr {T}\) for each \(i \in V\).

This assumption states that it is possible to obtain measurements from any node. Usually, there will be costs associated to querying the oracle. It is the explicit goal of our approach to minimize the number of queries to the oracle.

Assumption 3

(Data oracle output) We assume

$$\begin{aligned} r_i = t_i + \epsilon _i = t_s + c \cdot d_{s,i} + \epsilon _i \end{aligned}$$

with a random variable \(\epsilon _i \in {\mathbb {R}}\) as measurement error for each \(i \in V\) and for given \(s \in V\), \(c>0\) and \(t_s \in {\mathbb {R}}\). We call the special case of \(\epsilon _i = 0 \; \forall \; i \in V\) the deterministic and the general case the stochastic version, assuming to know the distributions of the \(\epsilon _i\) for all \(i \in V\).

Assumption 4

(Data oracle) We assume that we query the oracle after all relevant times \(t_i\), i.e., data \(r_i\) is available at the time of oracle query. In particular, we do not have the possibility to change the process.

Definition 4

(Source detection problem) We consider a graph, a signal spreading process, and an oracle as specified in Definitions 1, 2, 3 and the above assumptions. We denote the task to minimize the number of oracle queries to determine the source node \(s \in V\) (possibly up to a tolerance with respect to graph distance) as the source detection problem.

The queries of the oracle provide (noisy) arrival times \(r_i\), which can be used to infer the unknown offset \(t_s\), the velocity 1/c, and the source \(s \in V\). In this paper, we consider the following general approach to source detection.

Definition 5

(Source detection) The general source detection approach is: Repeat \(i=1 \ldots i_{\text {max}}\) rounds of

  1. (S1)

    Choosing \(k_i\) nodes \(S_i = \{ i_1,\dots ,i_{k_i} \} \subseteq V\),

  2. (S2)

    Querying the oracle to obtain \(r_{S_i} \in {\mathbb {R}}^{k_i}\), and

  3. (S3)

    Estimating a current best guess for the source \(j^* \in V\)

If \(j^*=s\) holds, then we call the approach successful. The source detection problem is to find a successful approach with a minimal number \(N=\sum _{i=1}^{i_{\text {max}}} k_i\) of oracle queries.

The special case of \(i_{\text {max}} = 1\) is called the offline version of the problem. It corresponds to a situation where it is not possible to do calculations between queries to the oracle. The online version for \(i_{\text {max}}\ge 2\) is not to be confused with more general concepts in online optimization, such as model predictive or dual control. Assumption 4 relates to the properties of the source detection problem and states that our approach starts after the end of the spreading process at time \(t_f\). Note that some processes such as cardiac excitations have a repetitive nature and a fast timescale, compare (Weber et al. 2017). Thus, the results of the considered problem class may find application not only in a posteriori analysis, but also in ongoing processes.

The oracle queries in (S2) Can be practically difficult and/or expensive, giving rise to our approach to minimize their overall number. Thus, all nodes chosen in (S1) Have to provide as much information as possible. The problem to identify the corresponding nodes can be seen as an optimal experimental design problem on a graph. The estimation or source inversion problem in (S3) Can be approached based on regression. Note that the main assumption for this model is a spreading of arrival times from the source s to all other vertices via shortest paths at a constant velocity \(1/c > 0\). We also assumed that the answer of the oracle does not depend on the round in which it is queried. According to the classification in Jiang et al. (2014), the above setting corresponds to sensor observations in contrast to the the snapshot or full information cases.

In the interest of simplicity and if not stated otherwise, we will use notation, definitions, and assumptions from this section, without explicit reference. We shall use the following example for illustration throughout this paper.

Example 1

(Graph) The graph \(G=(V,E)\) has nodes

$$\begin{aligned} V=\{0,1,2,3,4,5,6,7,8,9\} \end{aligned}$$

and weights \(\ell (e)=1\) for all undirected edges e in

$$\begin{aligned} \begin{aligned} E=\{&\{0,5\}, \hspace{-0.08cm} \{0,6\}, \hspace{-0.08cm} \{0,7\}, \hspace{-0.08cm} \{0,8\}, \hspace{-0.08cm} \{0,9\}, \hspace{-0.08cm} \{1,2\}, \hspace{-0.08cm} \{1,4\}, \hspace{-0.08cm} \{1,5\},\\&\{2,4\}, \hspace{-0.08cm} \{2,5\}, \hspace{-0.08cm} \{3,5\}, \hspace{-0.08cm} \{4,5\}, \hspace{-0.08cm} \{5,6\}, \hspace{-0.08cm} \{6,7\}, \hspace{-0.08cm} \{6,8\}, \hspace{-0.08cm} \{6,9\} \}.\end{aligned} \end{aligned}$$
Fig. 1
figure 1

Left: visualization of the example graph. Right: symmetric matrix with shortest path distances \(d_{i,j}\)

Full size image

The main contribution of this paper is the formulation of an Algorithm specifying the pseude code of Definition 5 and the analysis of its performance on a new benchmark library of stochastic source detection problems. Before we get there, we need a better understanding of such problems without measurement errors.

3 Deterministic case

In this section we discuss the deterministic offline version of the source detection problem, i.e., \(i_{\text {max}}=1\) and \(\epsilon _i = 0 \; \forall \; i \in V\). This problem class deserves special attention, because it is interesting in its own right, it is the idealized limit case of stochastic online versions, and because algorithmic ideas can be iteratively used in more complex settings. Note that it is purely combinatorial, asking for subsets of V for which the oracle answer allows to infer (or resolve) the source.

Of practical relevance is the possibility to verify a source via querying the oracle. Under the assumptions above one possibility is a local enumeration.

Definition 6

(Source certificate) A node \(s \in V\) is the source of the spreading process if and only if \(t_s\) is finite and \(t_s < t_j\) for all nodes j with \((v_j, v_s) \in E\).

We start by considering the special case with \(t_s=0\) and \(c=1\), where the oracle returns \(r_i = d_{s,i}\) for \(i \in V\). To solve the source detection problem we need to choose a minimal cardinality subset of V in S1) for which we question the oracle in S2). The answer shall enable us to calculate the source in S3) no matter which vertex in V actually is the source. This concept is known in graph theory as the metric dimension of a graph (Chartrand and Zhang 2003; Chartrand et al. 2000; Melter and Tomescu 1984; Tillquist et al. 2021) and depends on the basis of a graph. Classically, the metric dimension of a graph is defined for unweighted graphs, i.e., \(\ell (e)=1 \;\forall \; e \in E\). We generalize this to weighted graphs (V, E) with weights \(\ell (e) > 0\) for \(e \in E\).

Definition 7

(B-metric equivalence) Given a subset \(B \subseteq V\), two nodes \(i,j \in V\) are B-metric equivalent if \(d_{i,k} = d_{j,k} \; \forall \; k \in B\).

Definition 8

(Metric-resolving set) A set \(B \subseteq V\) is metric resolving, if \(i,j \in V\) are B-metric equivalent if and only if \(i=j\).

Thus, B is metric-resolving if it uniquely defines all \(v \in V\) by their shortest path distances to the elements of B.

Definition 9

(Metric basis) A (metric) basis B is a metric-resolving set with minimal cardinality.

Definition 10

(Metric dimension) Given a weighted graph \(G=(V,E)\), the metric dimension is the cardinality of one of its metric bases.

There are different ways to check if a set B is metric-resolving. Equivalently to Definition 8, one can check if either \(\sum _{k \in B} | d_{j,k}-d_{i,k} | = 0\) or (anticipating the stochastic regression case) if \(\sum _{k \in B}(d_{j,k}-d_{i,k})^2=0\) for all pairs of nodes \(i<j \in V\). If the value is strictly positive for (the minimum of) all pairs, then B is metric-resolving.

Example 2

The graph from Example 1 has metric dimension 5 and one metric basis is \(B:= \{1,2,6,7,9\}\). Figure 2 shows that B is a resolving set, as there are no zeros on the off-diagonal. One can show (e.g., by enumeration) that no basis with fewer nodes exists.

Fig. 2
figure 2

Left: the graph from Example 1 with the basis in gray. Right: symmetric matrix with entries \(\sum _{k \in B}(d_{j,k}-d_{i,k})^2\) for the metric basis from Example 2

Full size image

If a basis has been found in S1), e.g., by running one of the algorithms with exponential runtime complexity mentioned in the introduction, and the oracle queries returned \(r_k\) for all \(k \in B\) in S2), the source \(s \in V\) can be uniquely determined in S3) by calculating \(d_{i,k}\) for all \(i \in V\) and \(k\in B\) and comparing it to \(r_k = d_{s,k}\).

Example 3

Assume that for the basis B from Example 2 the oracle returns \(r_{\{1,2,6,7,9\}} = (3,3,1,2,2)\). Comparison with the full distance table on the right hand side of Fig. 1 reveals the source node \(s=8\).

We are interested in a generalization of this concept to arbitrary and a priori unknown velocity \(1/c>0\) and offset \(t_s \in {\mathbb {R}}\). Again, we want to be able to uniquely determine the source, now for arbitrary \(c>0\), \(t_s\), and \(s \in V\). While the concepts of a metric basis and of doubly resolving sets (Cáceres et al. 2007b; Kratica et al. 2009) can be found in the literature, the spread basis is a novel concept.

Definition 11

(B-spread equivalence) For \(B \subseteq V\), two nodes \(i,j \in V\) are B-spread equivalent if

$$\begin{aligned} \exists t_i, t_j \in {\mathbb {R}}, c_i, c_j >0: \;\; t_i + c_i d_{i,k} = t_j + c_j \; d_{j,k} \quad \;\; \; k \in B. \end{aligned}$$

Note that with the choice of \(t = (t_j - t_i) / c_i\) and \(c = c_j/c_i\) this is equivalent to

$$\begin{aligned} \exists t \in {\mathbb {R}}, c >0: \quad d_{i,k} = t + c \; d_{j,k} \quad \forall \; k \in B. \end{aligned}$$

Definition 12

(Spread-resolving set) A set \(B \subseteq V\) is spread-resolving, if \(i,j \in V\) are B-spread equivalent if and only if \(i=j\).

Definition 13

(Spread Basis) A spread basis B is a spread-resolving set with minimal cardinality.

Definition 14

(Spread dimension) Given a weighted graph \(G=(V,E)\), the spread dimension is the cardinality of one of its spread bases.

Although the interpretation of a velocity 1/c is not well posed for \(c=0\), we will require \(c \ge 0\) instead of \(c>0\) in the following minimization problems to avoid open sets. To find a spread basis we consider the objective function

$$\begin{aligned} J_{j}(t,c,r_S)=\sum _{k \in S}(t+c\,d_{j,k}-r_k)^2. \end{aligned}$$
(1)

Minimizing this objective with \(r_k=d_{i,k}\) and constraint \(c\ge 0\) results in an optimal objective value \(\phi _{i,j}(S)\) depending on i, j, and S. As above, an equivalent criterion to check if a set \(S \subset V\) is spread-resolving is to check if

$$\begin{aligned} \phi ^*(S) = \min _{i,j \not = i \in V} \phi _{i,j}(S) = \min _{i,j \not = i \in V} \min _{t, c \ge 0} J_{j}(t,c,d_{i,S}) \end{aligned}$$
(2)

is strictly positive, compare Example 4. Note that the inner minimization of (2) provides the values for t and c.

Proposition 1

(Sign symmetric objective) For any subset S of V the objective values \(\phi _{i,j}(S)\) are sign symmetric, i.e., for \(i,j \in V\) we have

$$\begin{aligned} \begin{aligned}&\phi _{i,j}(S) = 0 \quad \Longleftrightarrow \quad \phi _{j,i}(S) = 0 \\&\quad \phi _{i,j}(S)> 0 \quad \Longleftrightarrow \quad \phi _{j,i}(S) > 0. \end{aligned} \end{aligned}$$
(3)

Proof

For \(\phi _{i,j}(S) = 0\) with \(c>0\) and \(t_s\) we have by equations (1) and (2):

$$\begin{aligned} c\,d_{j,k}+t_s=d_{i,k}\, \forall \, k \in S. \end{aligned}$$

Reformulating this results in

$$\begin{aligned} 1/c\,d_{i,k}-t_s/c=d_{j,k}\, \forall \, k \in S \end{aligned}$$

with new slope \(1/c>0\) and offset \(-t_s/c\). Then by equations (1) and (2) again we have \(\phi _{j,i}(S) = 0\). The second part follows from the first due to \(\phi _{j,i}(S) \ge 0\). \(\square \)

Example 4

For the graph from Example 1 the metric basis \(B = \{1,2,6,7,9\}\) is not spread-resolving. E.g., for \(t_s = c = 1\) we have \(d_{8,k} = t_s + d_{6_k}\). The graph has spread dimension 7 and \(B^{\text {sp}}:= \{1,2,3,6,7,8,9\}\) ia a spread basis.

Fig. 3
figure 3

Top: matrix with objective values \(\phi _{i,j}(B^{\text {sp}})\) for the spread-basis from Example 4. Bottom: matrix with objective values \(\phi _{i,j}(B)\) for the metric basis from Example 2. Both are not symmetric, as \(\phi _{i,j}\) can differ from \(\phi _{j,i}\)

Full size image

Figure 3 shows that \(B^{\text {sp}}\) is spread-resolving, as only diagonal values are zero, and that B is not spread-resolving, as \(\phi _{6,8}(B)=\phi _{8,6}(B)=0\).

Our considerations suggest a (not necessarily efficient) approach to find a spread basis. In (2), one can detect infeasibility or solve the inner minimization problem analytically and enumerate the outer minimization problem over all (modulo symmetry because of Proposition 1) pairs of nodes and all subsets S of V. Checking if \(\phi ^*(S)>0\) allows to find a spread-resolving set S of minimal cardinality, similar to the metric case. Efficient algorithms to determine the spread basis are interesting, but beyond the scope of this paper.

To close the section, we collect some results on bounds for the spread dimension. We are interested in behavior for large \(n = \#V\), hence we assume \(n \ge 4\) to avoid the discussion of special cases for the following results. If all edges have equal length, a trivial upper bound on the spread dimension is \(n-1\). This bound is active for the special case of complete graphs.

Proposition 2

(Dimension of complete graphs) Let G be a complete graph with equal weight \(\ell > 0\) on all edges. Then the spread dimension of G is \(n-1\).

Proof

We have \(r_s=t_s\) and the same oracle answer \(r_i = t_s + c \ell > t_s\) for all \(i \in V \backslash \{s\}\) and for all choices \(t_s\) and \(c>0\). Hence, the source s can only be identified if either \(s \in B\), or if s is the only node in \(V \backslash B\). As the spread basis needs to identify all possible s, we have necessarily \(\text {card}(B)=n-1\). \(\square \)

If the edge weights are not identical, we may even need all n nodes in the spread basis. Thus, complete graphs are the worst case in terms of an upper bound for the spread dimension. However, also other topologies, such as star graphs, may have large spread dimensions.

By definition, the metric dimension is a lower bound for the spread dimension. Furthermore, we have the following lower bound for all graphs.

Proposition 3

(Lower bound for dimension) Let G be a graph as in Definition 1 with \(n \ge 4\). Then the spread dimension of G is at least 3.

Proof

Assume a spread basis \(B=\{i,j\}\) of cardinality two. Choose \(v,w \in V \backslash B\) with \(v \not = w\).

If \(d_{v,i} = d_{v,j}\) and \(d_{w,i} = d_{w,j}\) hold then with

$$\begin{aligned} c:= \frac{d_{v,i}}{d_{w,i}} = \frac{d_{v,j}}{d_{w,j}} \end{aligned}$$

we obtain \(d_{v,i} = c d_{w,i}\) and \(d_{v,j}=cd_{w,j}\), contradicting B being spread-resolving.

Let hence w.l.o.g. \(v \in V \backslash B\) be such that \(d_{v,i} > d_{v,j}\). Now we can choose \(t_s = -d_{v,j} c\) and \(c=\frac{d_{j,i}}{d_{v,i}-d_{v,j}}>0\) and obtain for \(v,j \in V\)

$$\begin{aligned} d_{j,k} = d_{v,k}c + t_s = (d_{v,k} - d_{v,j}) \frac{d_{j,i}}{d_{v,i}-d_{v,j}} \quad \forall \; k \in B, \end{aligned}$$

contradicting Definition 12 of a spread-resolving set. \(\square \)

Again, there are graphs for which this bound is sharp, independent of n.

Proposition 4

(Lower bound 3 is active) Let \(V=\{1,\dots ,n\}\) and \(E=\{\{1,2\},\{2,3\},\dots ,\{n-1,n\}\}\) for \(n \ge 4\). The chain graph has spread dimension 3 and \(B=\{1,2,n\}\) is a basis.

Proof

Let \(B=\{1,2,n\}\). First we note that the distance between two nodes \(i,j \in V\) is \(d_{i,j}=|i-j|\).

Let w.l.o.g. \(a<b \in V\) and \(\Delta =b-a>0\). We consider the three equations

$$\begin{aligned} d_{a,k} = t_s + c \; d_{b,k} \quad \forall \; k \in B \end{aligned}$$

from Definition 11 and show that no \(t_s, c>0\) exist which satisfy all of them.

If \(a>1\), we have the distances of a to the basis as \(d_{a,1}=a-1,\,d_{a,2}=a-2,\,d_{a,n}=n-a\) and distances of b accordingly \(d_{b,1}=a-1+\Delta ,\,d_{b,2}=a-2+\Delta ,\,d_{b,n}=n-a-\Delta \). While the first two equations result in \(t_s=-\Delta \) and \(c=1\), the equation for \(k=n\) is incorrect with these values.

If \(a=1\), we have distances \(0,1,n-1\) and \(b-1,b-2,n-b\), respectively. Here the first two equations result in \(t_s=b-1\) and \(c=-1\), but negative c values are not permitted.

Thus, B is a spread-resolving set. With Proposition 3, it is also a spread basis. \(\square \)

Propositions 3 and 4 are no deep results, but illustrate that there is not necessarily a connection between the number of nodes n and the spread dimension. This should be considered when the numerical results in Sect. 5 are analyzed.

Summarizing, the spread dimension can be anything between 3 and n for graphs with n nodes. The examples of chain and star graphs show that it is not the absolute number of edges, but rather the graph topology that impacts the spread dimension. Tailored results for specific graph topologies are interesting, but beyond the scope of this paper.

4 Stochastic case

In this section we consider the more general case with random measurement errors \(\epsilon _k\). The measurements \(r_k\) become random variables, and thus also the estimated parameters \(t_s\), c, and \(s \in V\). For large variances, it may be necessary to measure multiple times at a particular node. We start by updating some definitions.

Definition 15

(Stochastic source certificate) We call a node s the probable source of the spreading process, if \(t_s\) is finite and passes a given statistical test for the hypothesis \(t_s < t_j\) for all nodes \(j \in V\) with an edge \((v_j, s) \in E\).

This definition does not help directly to identify a probable source s, as we would have to query the whole graph (possibly multiple times if the measurement errors are large) to check it for all possible nodes \(j \in V\). Therefore we look at the quality to explain the queried data from spread resolving tests. In the following, we assume normally distributed, independent measurement errors \(\epsilon _k \sim \mathscr {N}(0,\sigma ^2)\), although we keep definitions general to facilitate a transfer to different error models. Here, we compare objective function values of linear regressions, similar to the deterministic case. We start by looking at the source inversion (resolving) problem S3) from Definition 5.

Definition 16

(Source estimator) Given a multiset (nodes can be queried multiple times) of nodes \(\widehat{S}\) and the corresponding oracle answers \(r_{\widehat{S}}\), we define the source estimator similar to (1) as

$$\begin{aligned} j^*&:= \arg \min _{j \in V} \; J^*_{j,\widehat{S}} := \arg \min _{j \in V} \; \min _{t_s, c\ge 0}J_{j,\widehat{S}}(t_s,c) \end{aligned}$$
(4)
$$\begin{aligned}&:= \arg \min _{j \in V} \; \min _{t_s, c\ge 0} \; \sum _{k \in \widehat{S}}(c\,d_{j,k}+t_s-r_k)^2 \end{aligned}$$
(5)

as the most likely source for \(\widehat{S}\) in a least squares sense (omitting \(\sigma \)).

For fixed source estimate \(j \in V\), the solution of the linear regression problem can be derived analytically [Bingham and Fry (2010), pages 4–5 for the unconstrained solution] as

$$\begin{aligned} c(j,\widehat{S})&= \max \left( 0,\frac{\sum _{i \in \widehat{S}}(r_i-\bar{r})(d_{j,i}-\bar{d}(j))}{\sum _{i \in \widehat{S}}(d_{j,i}-\bar{d}(j))^2} \right) , \end{aligned}$$
(6)
$$\begin{aligned} t_s(j,\widehat{S})&= \bar{r}-c(j,\widehat{S}) \; \bar{d}(j) \end{aligned}$$
(7)

with \(\bar{r} = \text {mean}(r_{\widehat{S}})\) and \(\bar{d}(j) = \text {mean}(d_{j,\widehat{S}})\). This allows to evalute \(J^*_{j,\widehat{S}}\) for all \(j \in V\) and derive an estimate \(j^*\) via enumeration, similar to the deterministic case. If the source can be resolved with a certain probability depends obviously on the choice of the multiset \(\widehat{S}\). The estimated parameters in (6–7) are dependent on which node j is currently assumed the best one, hence the dependency on j. But as a solution of (6), the velocity is related to the shortest path and hence to edges, not to a node.

We define a heuristic stopping criterium based on objective function values of linear regressions as follows.

Definition 17

(Stochastic spread-resolving set) Given a source estimate \(j^* \in V\), a multiset \(\widehat{S}\), a radius \(\gamma >0\), and values \(J^*_{j,\widehat{S}} \;\; \forall \, j \in V\), we define the neighborhood

$$\begin{aligned} B^{j^*}_{\gamma }=\{i \in V:\; d_{j^*,i} \le \gamma \;\} \end{aligned}$$
(8)

and the value

$$\begin{aligned} \Delta J( j^*, \widehat{S}):= \frac{\left( \min _{j \in V \setminus B^{j^*}_{\gamma }} J^*_{j,\widehat{S}}\right) -J^*_{j^*,\widehat{S}}}{J^*_{j^*,\widehat{S}}} \end{aligned}$$
(9)

and call the multiset \(\widehat{S}\) stochastically spread-resolving (SSR), if a statistical test for \(\Delta J( j^*, \widehat{S})\) is successful.

In our examples and benchmark results we use, for given \(a,b \in {\mathbb {R}}_+\) and \(\alpha \in (0,1)\), an F-Test, which is successful if

$$\begin{aligned} \Delta J( j^*, \widehat{S}) \; \frac{b}{a} \ge F^{-1}_{a,b}(\alpha ). \end{aligned}$$
(10)

Example 5

(Stochastic source inversion) We consider our example graph with oracle queries at \(\widehat{S}=\{1,4,6,7,9\}\) resulting in

$$\begin{aligned} r_{\widehat{S}} = (1.44327,0.31493,3.43784,5.48041,4.77700). \end{aligned}$$

We can calculate best fit regression lines for all ten nodes:

Node

c

\(t_s\)

Objective value

0, 6, 7, 8, 9

\(1e-10\)

3.09069

19.09375

1

1.49215

0.40482

3.95344

2

2.12480

\(- 1.15892\)

1.03461

3

3.39669

\(- 5.06137\)

5.24874

4

1.65808

0.10614

0.39891

5

3.39669

\(- 1.66468\)

5.24874

The smallest objective value is obtained for node 4. However, \(\widehat{S}\) does not spread-resolve nodes 3 and 5 (e.g., for \(t_s=c=1\) we have \(d_{3,k}=t_s+cd_{5,k}\)), resulting in not distinguishable optimal solutions (objective, c) with different \(t_s\). For \(a=b=1\), \(\alpha = 0.05\) and the ball \(B^2_{1.5}= \{1,2,4\}\) the F-test fails with 12.158 and a cutoff value of 161.45. Thus \(\widehat{S}\) is not SSR, and 4 is not a probable source, which is accurate as \(r_B\) was simulated for \(s=2, c=2, t_s=-1\), and a standard deviation of 1.

It remains the question how to obtain a SSR multiset \(\widehat{S}\). For this experimental design problem S1) in Definition 5 we use A-optimality, i.e., we choose oracle queries that minimize the following function.

Definition 18

(Set Variance) For a given multiset \(\widehat{S}\), variances \(\sigma _j\), and \(\lambda \in [0,1]\) we define the set variance

$$\begin{aligned} \Phi (\widehat{S}):= \sum _{j \in V} \lambda \frac{\text {Var}[c(j,\widehat{S})]}{\sigma _j^2} + (1-\lambda ) \frac{\text {Var}[t_s(j,\widehat{S})]}{\sigma _j^2}, \end{aligned}$$
(11)

using the variances of the parameter estimates (6–7) according to [Weisberg (2005),Sect. 2.4]

$$\begin{aligned} \text {Var}[c(j,\widehat{S})] = \frac{\sigma ^2}{\sum _{i \in \widehat{S}}(d_{j,i}-\bar{d}(j))^2}, \qquad \text {Var}[t_s(j,\widehat{S})] = \frac{\sigma ^2\sum _{i \in \widehat{S}}d_{j,i}^2}{|\widehat{S}|\sum _{i \in \widehat{V}}(d_{j,i}-\bar{d}(j))^2}, \end{aligned}$$

with an unknown, but fixed \(\sigma ^2\).

As we are using a multiset \(\hat{S}\), the cardinality of \(\hat{S}\) is not bounded and it makes sense to consider the limit behavior when nodes are queried more and more often. In the interest of convergence, we restrict the multiplicities of the multiset \(\widehat{S}\). The number of queries per node must not differ by more than 1. This avoids that specific nodes are queried significantly more often than others.

Definition 19

(Feasible Oracle Queries) Let V be given. A multiset \(\widehat{S}\) of V is called feasible, if the multiplicities of all \(i \in V\) within \(\widehat{S}\) do not differ by more than 1. We denote by \(V^{\widehat{S}}\) the subset of V containing all nodes that can be added to a feasible \(\widehat{S}\) and maintain feasibility.

We can now formulate a source detection algorithm realizing Definition 5.

Algorithm 1
figure a

Stochastic Source Detection

Full size image

The goal of Algorithm 1 is to find a probable source \(j^*\) with a small number of oracle queries, assuming considerable practical costs (e.g., increased risk of side effects for intracardiac measurements). Concerning the computational complexity per iteration of Algorithm 1, the main calculations happen in Lines 5, 6, and 10. The inner optimization problems can be solved analytically, compare (6–7), with an effort proportional to |V|. This is similar to calculating the set variance in (11). The overall effort to evaluate all objective functions \(J^*_{j,\widehat{S}}\) and minimizing over \(V \setminus B^{j^*}_{\gamma }\) in Line 8 and over \(V^{\widehat{S}}\) in Line 10 is then propotional to \(|V|^2\), where clever look-up tables can be applied to increase performance. Note that the distance resolution in Line 7 is calculated by dividing the estimated standard deviation by the estimated slope \(c(j^*,\widehat{S})\).

Given the general applicability of Algorithm 1 and the stochasticity of the task, we can not expect that the algorithm has a deterministic bound on the number of necessary iterations. Yet, we can expect that for \(\widehat{S}\) large enough, the correct source \(j^* = s\) will be identified in Line 6 of Algorithm 1. To see this, let \(c^*\) and \(t_s^*\) denote the unknown values for velocity and offset of the spreading process. Observe that for increasing cardinality of \(\widehat{S}\) and with Definition 19 we have the standard setting of a linear least squares problem with convergence of \((c(s,\widehat{S}), t_s(s,\widehat{S})) \mapsto (c^*, t_s^*)\). Thus, the objective function value

$$\begin{aligned} J^*_{s,\widehat{S}}&= \min _{t_s, c\ge 0} \; \sum _{k \in \widehat{S}} \left( c\,d_{s,k}+t_s-r_k\right) ^2 \\&= \sum _{k \in \widehat{S}} \left( c(s,\widehat{S}) \,d_{s,k} + t_s(s,\widehat{S}) - (d_{s,k} c^* + t_s^* + \epsilon _k)\right) ^2 \\&= \sum _{k \in \widehat{S}} \left( (c(s,\widehat{S})-c^*) \,d_{s,k} + (t_s(s,\widehat{S}) - t_s^*) - \epsilon _k\right) ^2 \end{aligned}$$

can be expected to depend in the limit of more and more queries according to Definition 19 only on the measurement errors \(\epsilon _k\) and will be chosen with probability 1 for some \(i_{\text {max}}\) large enough, if we remove the heuristic stopping criterion in Lines 8–9 in Algorithm 1. A more detailed study of the mean and variance of \(J^*_{j,\widehat{S}} - J^*_{s,\widehat{S}}\) for \(j \in V \backslash \{ s \}\) can be performed individually for different statistical assumptions on \(\epsilon _k\), which is beyond the scope of this paper.

This short analysis shows why the stochastic source inversion problem is challenging. For small cardinalities of \(\widehat{S}\), but also for non-balanced distributions of queries over the nodes of \(\widehat{S}\), the noise in \(\epsilon _k\) and possible cancellation effects in the terms

$$\begin{aligned} c(j,\widehat{S})\,d_{j,k} - c^* \,d_{s,k} + (t_s(j,\widehat{S}) - t_s^*) - \epsilon _k \end{aligned}$$

may lead to values \(J^*_{j,\widehat{S}} < J^*_{s,\widehat{S}}\) for \(j \in V \backslash \{ s \}\). The stopping criterium and Definition 19 provide hyperparameters that can and have to be specified for particular applications.

5 Numerical results

5.1 Implementation

We have implemented Algorithm 1 in octave 5.2.0Eaton et al. (2020). The code is available with a permissive license on the website https://github.com/TobiasWeber/IMLR.

The implementation is a set of octave functions and scripts meant to work in any octave installation with the statistics package. For Algorithm 1 only core octave was used. Data structures for graph representation were taken from the octave network toolbox (Bounova 2016), where also simple graph information and manipulation algorithms can be found. However, the algorihm works standalone as we implemented a different shortest path algorithm for efficiency reasons. It is closely related to the fast matrix multiplication shortest path algorithms and more suited to the octave programming language than the Dijkstra algorithm in the toolbox. For the numerical random scenarios and errors we used the statistics package of octave.

Remark 1

(Treating infinities) There are two different sources of infinite values. For directed graphs that are not strongly connected or graphs that are not connected, some pairs of nodes might have no shortest path between them, or just in one direction. The infinity pattern can be exploited to find the source by a clustering into connected subgraphs. These subgraphs can be used in step S3), and determined in an extra run of S1) by replacing infinity by 1 and finite values by 0. Also the variances \(\text {Var}[c(j,\widehat{S})]\) and \(\text {Var}[t_s(j,\widehat{S})]\) in Def. 18 may be infinite. As we are minimizing, this is not a problem though, if implemented carefully. If all variances in \(V^{\widehat{S}}\) are infinite, we “minimize” by counting the non finite values in the sum over the variances and choose the “solution” with the least infinities (or NaNs).

In the following and if not stated otherwise, we use hyperparameters \(\alpha = 0.05\), \(a=1\), and \(b=|\widehat{S}|-4\) (see Def. 17) and \(\lambda =0\) and \(\sigma _j=1+J^*_{j,\widehat{S}}\) (see Def. 18). Here, the \(\sigma _j\) were chosen to have larger weight on nodes with a smaller objective function value.

5.2 Illustration on example graph

We use our example graph with the same spreading process as in Example 5 (\(s=2, c=2, t_s=-1\)) to illustrate the behavior of Algorithm 1. The output for an instance with “average” behavior in terms of iteration count is as follows.

Iter

\(i^+\)

\(j^*\)

\(c(j^*,\widehat{S})\)

\(t_s(j^*,\widehat{S})\)

\(\frac{J^*_{j^*,\widehat{S}}}{|\widehat{S}|}\)

\(\displaystyle \min _{j \in V \setminus B^{j^*}_{\gamma }} \frac{J^*_{j,\widehat{S}}}{|\widehat{S}|}\)

\(\alpha ^*\)

1, 2

0, 5

5

3.34

\(- 0.38\)

0.00

0.00

1.0000

3

1

2

3.79

\(- 4.62\)

0.14

0.14

1.0000

4

7

1

2.09

\(- 1.67\)

0.25

0.32

1.0000

5

2

4

2.97

\(- 3.89\)

0.37

0.55

0.6137

6

4

2

2.25

\(- 2.19\)

0.52

0.72

0.4716

7

8

2

2.44

\(- 2.34\)

0.53

0.72

0.3800

8

3

2

2.48

\(- 2.30\)

0.53

0.70

0.3255

9

9

2

2.71

\(- 2.52\)

0.74

0.90

0.3434

10

6

2

2.72

\(- 2.48\)

0.70

0.85

0.3054

11

2

2

2.56

\(- 2.10\)

0.73

0.95

0.1905

12

1

2

2.60

\(- 2.24\)

0.72

1.21

0.0494

The initialization in Line 1 results in \(\{i_1,i_2\} = \{0,5\}\). Until iteration 10 all nodes are selected once. In iterations 11 and 12 a second query at nodes 2 and 1 results in objective function values that are far enough apart such that the heuristic termination criterion (10) is fulfilled. In this instance the feasibility requirement in Def. 19 leads to oracle queries that might not be necessary.

Fig. 4
figure 4

Convergence of confidence values \(\alpha ^*\)

Full size image

The last column depicts the converging \(\alpha ^*\) value, obtained by evaluating (10) (stopping criterion is that \(\alpha ^*\) is below 0.05), also shown in Fig. 4. The parameters \(c(j^*,\widehat{S})\) and \(t_s(j^*,\widehat{S})\) converge slowly towards the real values and are still inaccurate at termination. The resulting regression line is a good fit for the measurements, though, compare Fig. 5.

Fig. 5
figure 5

Regression after iteration 12 at the true (and estimated) source node s. Despite significant outliers, the estimated spreading approximates the true spreading quite well

Full size image

In summary, the strict termination criterion and feasibility requirement for oracle queries seem to be robust and avoid early termination, even when by chance a good fit is achieved as in the iterations 2 and 3.

5.3 Problem instances

We used graph instances that we collected in three sets.

5.3.1 Col

The first set is an operations research library (Beasley 1990) with 30 instances from Fleurent and Ferland (1996) and 79 DIMACS graph coloring instances (Johnson and Trick 1996) from different sources, e.g., (Johnson et al. 1991; Leighton 1979).

5.3.2 Misc

The second set comprises miscellaneous instances. It contains three simple water network instances from the epanet software for modeling of water networks (Rossman 2000), eight train networks from the lintim software (Albert et al. 2020), five instances from Mark Newman’s webpage [62] (original sources (Watts and Strogatz 1998; Lusseau et al. 2003; Zachary 1977; Knuth 1993)), seven instances from the Weizmann laboratory collection of complex networks 2, (Mangan and Alon 2003; Milo et al. 2002, 2004), and 41 instances from the Pajek dataset (Batagelj and Mrvar 2006).

5.3.3 Snap

The last set of instances is a subset of the Stanford large network dataset collection (Snap). It contains 16 graphs derived from an internet topology (Leskovec et al. 2005), 9.629 graphs describing user interaction on the music streaming service deezer (Rozemberczki et al. 2020), five graphs describing email interactions of members in a large European research institution (Leskovec et al. 2007), and ten graphs as friend networks of Facebook users (Leskovec and Mcauley 2012).

For all of the different sources and their different graph formats parsers in octave are available. From the set of all graphs in these three libraries we selected those that have a possible spreading process application. Some of the instances are directed graphs, some are weighted, others are not connected. If not provided, edge weights were set to one.

As discussed above, the runtime of Algorithm 1 is proportional to \(|V|^2\) in its inner optimization problems. For larger graphs we recommend a more sophisticated implementation, e.g., using hashed look-up tables. We do not expect qualitatively different behavior for larger instances, but rather for different parameter values. In the interest of using the available computational time for multiple realizations of the random parameters s, c, and \(t_s\), we thus restricted our investigation to graphs with 1000 or less nodes.

We conducted 100 randomized test runs on each instance (only the comparatively large number of 9629 deezer graphs were only run once, to avoid domination effects). For each run different random realizations of s (uniform distribution over all nodes), c (exponential distribution, mean 1), and \(t_s\) (Gaussian distribution, mean 0 and standard deviation 10) were considered. We used \(\sigma = \frac{1}{5} c\) as standard deviation for all random errors \(\epsilon _k\) of oracle queries. Note that these settings were arbitrarily chosen and fixed after an early trial and error phase, balancing realistic orders of error magnitude and resulting numbers of iterations. As expected, smaller variances led to a reduction in the number of iterations. As early experiments with other values (data not shown) did not result in qualitatively different results, we kept them constant throughout the numerical experiments to be able to focus on the study of iteration numbers in relation to graph properties. We emphasize that the least squares problems in (5) are linked to the assumption of independent and identically normal distributed errors \(\epsilon _k\) via maximum likelihood. For other distributions and/or statistical assumptions different minimization subproblems need to be solved.

5.4 Benchmark library: convergence

To evaluate the convergence behavior of Algorithm 1, we assess the quality of the detected source \(j^*\) in comparison to the true source \(s_k\) of instance k. We use the following normalization and evaluation measure.

Definition 20

(Normalization) Let Q be the set of all instances (test runs) and \(k \in Q\) a specific one.

Let \(i_k\) be the number of iterations until Algorithm 1 terminated for instance k. We then transform all iterations \(i \in \{i_{\text {min}}=3, \ldots , i_k\}\) to normalized iterations \(i_n \) via \(i_n = (i-i_{\text {min}}) / (i_k-i_{\text {min}}) \in [0,1]\), omitting the dependence on k for notational simplicity. Then we define

$$\begin{aligned} q(k,i_n):= \frac{\left| \left\{ j \in V: \; J^*_{j,\widehat{S}} \le J^*_{s,\widehat{S}} \right\} \right| }{\left| \; V \; \right| } \end{aligned}$$
(12)

as the uniqueness level of a given true source s for an oracle query set \(\widehat{S}\). It depends on the instance \(k \in Q\) and on the normalized iteration counter \(i_n\) of Algorithm 1. The level \(q(k,i_n) \in \left[ \frac{1}{|V|},1\right] \) is evaluated for the least squares function \(J^*_{j,\widehat{S}_{k,i_n}}\). If \(q(k,i_n)=\frac{1}{|V|}\) then \(j^* = s\).

In other words, the values \(q(k,i_n)\) indicate how many nodes j result, when assumed to be the source, in parameter fit objective functions (5) with a smaller value than that of the true source node s. In (5) the current best guess for a resolving set \(\widehat{S}\), which is modified in each iteration \(i_n\), plays a role. First, Table 1 shows the median and mean distances between \(j^*\) and s after termination (i.e., \(i_n = 1\)) of Algorithm 1, indicating its accuracy.

Table 1 Distance between \(j^*\) at \(i_n=1\) and s for different test sets Q
Full size table

There are no significant differences between the test sets, indicating the general applicability of Algorithm 1. In the interest of simplification, we present results from now on for Q as the union of the sets Col, Misc, and Snap.

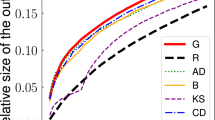
Second, to investigate the efficiency of Algorithm 1, we illustrate in Fig. 6 the uniqueness level q as a function of normalized iterations and instances \(k\in Q\).

Fig. 6
figure 6

Using Definition 20, \(q(k,i_n)\) is visualized for all instances \(k \in Q\). Left: a color gradient indicates for how many instances \(k \in Q\) the value \(q(k,i_n)\) is in a given box. While for small iteration numbers \(i_n\) the values \(J^*_{s_k,\widehat{S}_{k,i_n}}\) are almost randomly distributed among all \(j \in V\), for large iterations we have \(J^*_{s_k,\widehat{S}_{k,i_n}} \le J^*_{j,\widehat{S}_{k,i_n}}\) for almost all instances k and all \(j \in V\), indicating the probable proximity of \(j^*\) to the true source \(s_k\) of instance k. Right: for different values of \(\delta \) the lines plot the fraction \(|Q_1(i_n)| / |Q|\) with \(Q_1(i_n):= \{k \in Q: \; q(k,i_n) \le \delta + \frac{1}{|V|}\}\). E.g., for \(\delta = 0\) the lowest blue line depicts the fraction of instances for which at iteration \(i_n\) the source \(s_k\) was the unique minimizer of \(J^*\), increasing from approximately 5 to 95%

Full size image

Both plots indicate that for the chosen sets \(\widehat{S}_{k,i_n}\) the termination criterion is a good choice and that Algorithm 1 is well-posed in the sense that at termination, the true source \(s_k\) is detected with high probability (as \(q(k,i_n=1) \approx 0\) for almost all \(k\in Q\)). From Fig. 6 we deduce on the one hand that an earlier termination of Algorithm 1, as seemed plausible from the example in Sect. 5.2, would often result in \(j^*\) that are not minimal with respect to the least squares regression. On the other hand, more iterations are not necessary.

5.5 Benchmark library: number of iterations

In this section we have a closer look at how the iteration numbers \(i_k\) until Algorithm 1 terminated relate to properties of the graphs. Figure 7 (left) shows them for different graph sizes \(n=| V |\). For most \(k \in Q\) we have \(i_k \le \frac{1}{2} n\). As the spread dimension is the number of necessary oracle queries (iterations in the online case), this is plausible when looking at the upper bound from Proposition 2 for complete graphs. Note that the spread dimension is not a strict lower bound on \(i_k\) due to the advantage that in the online setting we can place oracle queries with knowledge gained in previous iterations.

Fig. 7
figure 7

Color gradients showing how many instances \(k \in Q\) needed (on the y-axis) how many iterations until termination of Algorithm 1. Left: Plotted over the graph size \(n=|V|\), suggesting a linear relation \(i_k \le c_1 n\) for a constant \(c_1\) and most \(k \in Q\). Right: Plotted over the spread dimension \(\beta \), suggesting a linear relation \(i_k \le c_2 \beta \) for a constant \(c_2\) and most \(k \in Q_\text {small}\) where \(Q_\text {small} \subseteq Q\) contains all graphs in Q with \(n\le 60\). Up to this size a brute force enumeration of the spread dimension was computationally feasible

Full size image

For small graphs (\(n\le 60\)), we could determine the spread dimension by brute force enumeration. The result in Fig. 7 (right) confirms the impression that the number of iterations of Algorithm 1 is in many cases below the spread dimension, and only in few cases above. Thus it seems valid to see \(i_k\), at least for the chosen variance of measurement errors, as an approximation of the spread dimension.

This result does not consider other graph properties. An investigation of the topological diameter and of the connectivity (number of edges divided by n) of the graph did not reveal obvious correlations (negative results are not shown here, the color gradients were rather erratic). Known results for the metric dimension \(\beta \), which is a lower bound for the spread dimension as discussed in Sect. 4, indicate that the graph topology could have a strong impact (on the lower and not necessarily active bound). E.g., for the diameter d it was shown that

$$\begin{aligned} n \le \left( { \left\lfloor {\frac{2d}{3}}\right\rfloor + 1}\right) ^\beta +\beta \sum _{i=1}^{\lceil {d/3} \rceil } (2i-1)^{\beta -1} \end{aligned}$$

by [Hernando et al. (2007), Theorem 3.1]. Also the simpler, but less strict inequality

$$\begin{aligned} n \le d^\beta + \beta \end{aligned}$$

from Khuller et al. (1996b) emphasizes the role of the diameter. Not finding a correlation between the diameter d and \(i_k\) might indicate that the diameter is not as relevant for the spread dimension as it is for the metric dimension or that \(i_k\) differs from the spread dimension for specific graphs. Note also that the spread dimension depends on the edge weights of the graph. Two graphs with the same edge sets can have different spread dimensions, if the edge weights are different.

6 Conclusions

6.1 Contribution 1

We formalized the source detection problem in graphs and discussed some of its theoretical properties. We showed that the well-known concept of the metric basis and metric dimension of a graph is related to the specific case of deterministic source detection. We generalized this concept towards spreading processes by the novel concept of the spread dimension, and towards stochastic measurement errors via stochastic spread-resolving sets.

In future work, these concepts should be further investigated from a graph theoretic point of view. In particular, identify complexity class, efficient algorithms to find a spread basis, and generalize towards more general scenarios, e.g., including multiple sources.

6.2 Contribution 2

We developed an algorithm for the stochastic source detection problem. Unprecedented, Algorithm 1 can solve problems belonging to a general problem class. It consists of a source estimation and of an experimental design part. For the source estimation we discussed convergence to the true source under a constraint on the query set \(\widehat{S}\). To choose oracle queries for this set we proposed a heuristic solution based on the concept of A-optimality in experimental design and a constraint on multiple measurements.

It is unclear how this heuristic can be further improved. A detailed study on relaxing Definition 19, e.g., by allowing the numbers of queries to differ by \(k>1\), seems promising. The connection between graph properties on the one hand and spread dimension and iteration numbers on the other hand should be investigated in future research.

6.3 Contribution 3

We performed a numerical study based on a novel benchmark library for source detection problems. The results indicate well-posedness of Algorithm 1 and a relation between the graph size n and the spread dimension on the one hand, and the number of iterations until termination on the other. Algorithm 1 proved to be robust over a wide variety of different graphs (weighted/unweighted, directed/undirected, connected/unconnected) and for stochastic disturbances.

So far, two of the three main parts (termination and choice of \(\widehat{S}\)) are only heuristic, whereas the link to quadratic regression is well-posed in the limit. Another future direction of research is hence the application to practical source detection problems with real world data. Also larger problem instances with \(n > 1000\) and special cases should be further investigated. For those it will be worthwhile to investigate graph decomposition approaches. Promising concepts from graph theory are the modular decomposition and to a lesser degree the split decomposition of a graph. A very simple and efficient meta algorithm for a graph with more than one (strongly) connected component is to query a node in each connected component once, until the oracle answer is finite. Then the source in this connected component and the rest of the search can continue there, e.g., with Algorithm 1.

In general, the class of source detection on graphs is important from a practical point of view, especially given the omnipresence of networks in modern life. At the same time, this new problem class may stimulate theoretical and algorithmic research.