Pathfollowing for parametric mathematical programs with complementarity constraints

Abstract

In this paper we study procedures for pathfollowing parametric mathematical programs with complementarity constraints. We present two algorithms, one based on the penalty approach for solving standalone MPCCs, and one based on tracing active set bifurcations arising from doubly-active complementarity constraints. We demonstrate the performance of these two approaches on a variety of examples with different types of stationary points and also a simple engineering problem with phase changes.

1 Introduction

We are interested in tracing an approximate path of solutions to a parametric mathematical program with complementarity constraints (PMPCC). Specifically, we study the problem,

where $f:{\mathbb {R}}^{n+2n_c}\times {\mathbb {R}} \rightarrow {\mathbb {R}}$, $g:{\mathbb {R}}^{n+2n_c}\times {\mathbb {R}} \rightarrow {\mathbb {R}}^{m_q}$, $h:{\mathbb {R}}^{n+2n_c}\times {\mathbb {R}} \rightarrow {\mathbb {R}}^{m_e}$ and $a\perp b$ for $a,b\in {\mathbb {R}}$ implies that either a or b or both of them are zero. The more general case of nonlinear complementarity constraints can be covered by this form using slack variables. We will denote the feasible set as X(t), i.e., $X(t):=\{x:\,g(x,t) \ge 0,\, h(x,t) = 0,\,0\le x_{j}\perp x_{j+n_c}\ge 0,\text { for all }j\in \{n+1,\ldots ,n+n_c\}\}$. We consider the situation wherein one has a reasonably accurate estimate of the solution for (PMPCC(t)) at $t=0$ and intends to find the solution at $t=1$ using parametric sensitivity, i.e., the directional derivative of solutions to (PMPCC(t)), or some related problem that approximates it, with respect to t.

A primary motivation for this problem arises in real-time nonlinear model predictive control (NMPC). Using the advanced step NMPC (Zavala and Biegler 2009) or the real-time iteration (Diehl et al. 2005) framework, one can pathfollow along the solution of an optimization problem defining the discretized optimal control problem using sensitivity updates from the predicted and measured state. Instead of solving the full NMPC optimization problem when new process measurements arrive, a fast approximation of the updated optimal solution is found using one or several pathfollowing steps. See Diehl et al. (2005), Zavala and Biegler (2009), Jäschke et al. (2014), Suwartadi et al. (2017) for illustrations of this approach. NMPC is performed in practice by forming of a sequence of discretized optimal control problems into nonlinear programs (NLPs) and performing these pathfollowing schemes. These algorithms are not applicable to (PMPCC(t)). The problem (PMPCC(t)) can be re-written as an NLP by writing the complementarity constraint as $x_i x_{i+n_c}\le 0$ along with $x_i\ge 0$ and $x_{i+n_c}\ge 0$, but under this reformulation, certain stringent regularity conditions required for guarantees in the pathfollowing procedures are not generally satisfied. This presents an important open problem as there are several applications arising in process control engineering wherein the dynamic process has a complementarity structure due to switching conditions and phase transitions, e.g., see Baumrucker et al. (2008), Raghunathan and Biegler (2003). For this class of problems there do not yet exist efficient pathfollowing algorithms, and it is the objective of this paper to investigate how pathfollowing can be realized for problems with this challenging complementarity structure.

The main contribution of this paper is the first study of pathfollowing for PMPCCs. Currently, there is no literature presenting an algorithm to trace the solution of a parametric MPCC from an approximate solution at one value of a parameter to another. In this paper we develop and study two methods based on NLP approximations of the underlying MPCC for tracking the solution with respect to a parameter change. In particular, we study the penalty method for solving MPCCs, and also, noting the importance of doubly-active complementarity constraints in indicating potential branching points of the PMPCC solution set, an “active-set” procedure that traces the parametric NLP solutions corresponding to each branch.

We found that the guarantees and experimental performance of pathfollowing resembles solving standalone MPCCs in an analogous manner. In particular, the penalty method is able to trace, just as the penalty method is able to solve, stationary points satisfying weak necessary conditions, with weak in the sense of a relatively larger class of problems for which descent directions exist. It is simple to implement, however, and for problems without attractive but unsatisfactory stationary points or many bi-active constraints it performs just as well and reliably as pathfollowing on a standard parametric NLP. However, for problems in which B-stationarity, the tightest form of computable stationarity is sought for, which is also difficult to solve as a standalone problem, a more complicated and combinatorial approach is necessary. Given the necessary tracking of different potential branches, the gain in reliability of quality solutions comes at the cost of a more difficult to implement and slower pathfollowing algorithm.

1.1 Previous literature

Parametric optimization for standard parametric NLPs (PNLPs) has enjoyed two periods of intensive activity. First, around the publication of the seminal book (Guddat et al. 1990), and more recently with the development of higher quality nonlinear models for process control and the rise of nonlinear model predictive control, e.g., Diehl et al. (2005), Zavala and Anitescu (2010), Dinh et al. (2012), Dontchev et al. (2013). In Kungurtsev and Jäschke (2017) an algorithm was presented for pathfollowing PNLPs satisfying weak constraint qualifications. The procedures are based on sensitivity, in particular, the directional derivative of the solution of an NLP subject to a differential parameter change, whose properties depend on the constraint qualifications holding at the solution.

In general, for MPCCs reformulated as NLPs, it is possible that Guignard’s constraint qualification holds, but otherwise the complementarity constraints define the feasible region to be such that, typically, the stronger constraint qualifications in the literature fail. Thus only the second algorithm in Kungurtsev and Diehl (2014) for generic branching could potentially be applicable for pathfollowing MPCCs. The algorithm requires an approximation to the complete characterization of the optimal Lagrange multiplier set, a computationally challenging task, and in general is not tailored for MPCCs specifically.

There are a number of algorithms for solving standalone MPCCs. For a classic text, see Luo et al. (1996). Most algorithms are based on regularization or penalization (Ralph and Wright 2004), and have been proven to find C-stationary points of the problem (a stationarity notion specific to MPCCs that will be discussed in the next section). Some regularization methods are able to converge to M-stationary points; a number of methods have been developed, for a detailed comparison of some of these methods, see Hoheisel et al. (2013). C-stationary and M-stationary points could have non-trivial directions of descent, however, so a filter sequential linear complementarity based approach was presented in Leyffer and Munson (2007) to only obtain solutions satisfying B-stationarity, a stationarity measure for which no feasible descent directions exist for the linearization of the problem.

Sensitivity of MPCCs is studied in Scheel and Scholtes (2000), Bouza et al. (2008), Jongen et al. (2012). In combination with algorithmic pathfollowing ideas for PNLP and algorithms for solving standalone MPCCs, these form the inspiration for the procedures and analysis presented in this paper.

2 Background

In this section we first review the optimality conditions of a standalone MPCC, and then proceed to describe the general properties of the solution paths of PMPCCs as the value of the parameter changes, and finally review pathfollowing procedures for parametric NLPs.

2.1 Optimality conditions and constraint qualifications

In this section we present some definitions of regularity properties and optimality conditions specific to MPCCs. We introduce the index sets

$$\begin{aligned}{} & {} {\mathcal {N}}_c:=\{n+1,\ldots ,n+2n_c\},\\{} & {} {\mathcal {N}}^-_c:=\{n+1,\ldots ,n+n_c\},\text { and } {\mathcal {N}}^+_c:= \{n+n_c+1,\ldots ,n+2n_c\} \end{aligned}$$

in order to make the notation in the sequel more compact.

Let us denote the index sets of active complementary components associated with a point $x^*\in X(t)$ as,

$$\begin{aligned} {\mathcal {A}}_1(x^*,t):= \{i| i\in {\mathcal {N}}_c^-,\, x^*_i=0\}\text { and } {\mathcal {A}}_2(x^*,t):= \{i| i\in {\mathcal {N}}_c^+,\, x^*_i=0\}. \end{aligned}$$

We also define the set of complementarity constraints that are bi-active as follows,

$$\begin{aligned} {\mathcal {A}}^0_1(x^*,t):= \{i| i\in {\mathcal {N}}_c^-,\, x^*_i=0,\,x^*_{i+n_c}=0\}\text { and } {\mathcal {A}}^0_2(x^*,t):= \{i| i\in {\mathcal {N}}_c^+,\, x^*_i=0,\,x^*_{i-n_c}=0\}. \end{aligned}$$

These play an important role in the regularity of MPCCs, as bi-active constraints pose some of the primary difficulties associated with solving them.

Denote

$$\begin{aligned} {\mathcal {J}}(x^*,t):=\{I \subseteq \{i| i\in {\mathcal {A}}_1(x^*,t)\cup {\mathcal {A}}_2(x^*,t)\}:\, \forall i\in {\mathcal {N}}_c^-, \{i,i+n_c\}\cap I\ne \emptyset \} \end{aligned}$$

to be the collection of all sets of optimization variable indices corresponding to complementarity variables which are active and such that at least one from every complementarity pair of indices is included in the set.

We now present three related NLPs to (PMPCC(t)) based around a point $x^*\in X(t)$ [see Scheel and Scholtes (2000) for more details]. The first, the tightened NLP, given t, is defined as,

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{n+2n_c}} &{} f(x,t) \\ \text {s.t.} &{} g(x,t) \ge 0, \\ &{} h(x,t) = 0, \\ &{} x_i = 0 \text { for }i\in {\mathcal {N}}_c\text { such that }x^*_i = 0, \\ &{} x_i \ge 0 \text { for }i\in {\mathcal {N}}_c\text { such that }x^*_i > 0, \end{array} \end{aligned}$$

(1)

Next, the relaxed NLP is defined as,

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{n+2n_c}} &{} f(x,t) \\ \text {s.t.} &{} g(x,t) \ge 0, \\ &{} h(x,t) = 0, \\ &{} x_i = 0, \, x_{i+n_c}\ge 0 \text { for }i\in {\mathcal {N}}_c^-\text { such that }x^*_i = 0\text { and }x^*_{i+n_c}>0, \\ &{} x_i = 0, \, x_{i-n_c}\ge 0 \text { for }i\in {\mathcal {N}}_c^+\text { such that }x^*_i = 0\text { and }x^*_{i-n_c}>0, \\ &{} x_i, x_{i+n_c} \ge 0 \text { for }i\in {\mathcal {N}}_c^-\text { such that }x^*_i=0\text { and }x^*_{i+n_c}=0. \end{array} \end{aligned}$$

(2)

It holds that if $x^*$ is a local minimizer of the relaxed NLP then it is a local minimizer of the MPCC, and if it is a local minimizer of the MPCC then it is a local minimizer of the tightened NLP. It holds that if either $x^*_i>0$ or $x^*_{i+n_c}>0$ for all $i\in {\mathcal {N}}_c^-$ then the two converse assertions hold.

The Index $I\in {\mathcal {J}}(x^*,t)$ NLP is defined as,

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{n+2n_c}} &{} f(x,t), \\ \text {s.t.} &{} g(x,t) \ge 0, \\ &{} h(x,t) = 0, \\ &{} x_i = 0, \, i\in I, \\ &{} x_i\ge 0, \, i\in {\mathcal {N}}_c\setminus I. \end{array} \end{aligned}$$

(3)

We will denote the MPCC Lagrangian with multipliers $(\lambda , \mu , \sigma )$ as,

$$\begin{aligned} {\mathcal {L}}(x,\lambda ,\mu ,\sigma ,t) = f(x,t)-\lambda ^T g(x,t)-\mu ^T h(x,t)- \sigma ^T x, \end{aligned}$$

(4)

where it is assumed that $\sigma _i=0$ for $i\le n$.

Now we present the definitions of the various stationarity concepts for MPCC that are used in this work. Note that there are multiple equivalent ways of formalizing these concepts, and we present just one in accordance to preference for the exposition of our results. Other (equivalent) definitions may be useful in different contexts can be found in, e.g. Scheel and Scholtes (2000). We say that $x^*$ satisfies weak, or W-stationarity, for the parametric MPCC at t if there exist multipliers $(\lambda ^*, \mu ^*, \sigma ^*)$ such that,

$$\begin{aligned} \begin{array}{l} \nabla _x f(x^*,t) - \nabla _x g(x^*,t)^T\lambda ^*- \nabla _x h(x^*,t)^T \mu ^*- \sigma ^* =0,\\ (\lambda ^*)^T g(x^*,t) =0, \, \lambda ^*\ge 0,\,g(x^*,t) \ge 0, \, h(x^*,t)=0,\\ 0\le x^*_{i}\perp x^*_{i+n_c}\ge 0,\text { for all }i\in {\mathcal {N}}_c^-, \\ \sigma ^*_i = 0\text { for }i<n+1, \\ \sigma ^*_i x^*_i = 0, \text { for }i\in {\mathcal {N}}_c. \end{array} \end{aligned}$$

(5)

The point $x^*$ is (Clarke) C-stationary if there exists a dual tuple $(\lambda ^*, \mu ^*, \sigma ^*)$ satisfying (5) and $\sigma ^*_{i}\sigma ^*_{i+n_c}\ge 0$ for all $i\in {\mathcal {N}}_c^-$.

It is (Mordukhovich) M-stationary if there exists $(\lambda ^*, \mu ^*, \sigma ^*)$ satisfying the W-stationarity multiplier conditions and, in addition, $\sigma ^*_{i}>0$, $\sigma ^*_{i+n_c}>0$, or $\sigma ^*_{i}\sigma ^*_{i+n_c}=0$ for all $i\in {\mathcal {N}}_c^-$.

The point is (strongly) S-stationary if there exists $(\lambda ^*, \mu ^*, \sigma ^*)$ satisfying the corresponding W-stationarity conditions and, in addition $\sigma ^*_{i}\ge 0$ for all $i\in {\mathcal {A}}^0_1(x^*,t)\cup {\mathcal {A}}^0_2(x^*,t)$. This is the strongest notion of stationarity. It is equivalent to the KKT property of the relaxed NLP (2).

The tightest notion of stationarity we review here is (Bouligand) B-stationarity, which implies that no linear feasible descent direction exists. B-stationarity holds for a feasible point $x^*$ if $d=0$ is the solution to the following linear mathematical program with complementarity constraints (LPCC),

$$\begin{aligned} \begin{array}{rl} \min _{d\in {\mathbb {R}}^{n+2n_c}} &{} \nabla _x f(x^*,t)^T d \\ \text {s.t.} &{} g(x^*,t) +\nabla _x g(x^*,t) d\ge 0, \\ &{} h(x^*,t)+\nabla _x h(x^*,t) d = 0, \\ &{} 0\le x_i^*+d_i\perp x_{i+n_c}^*+d_{i+n_c}\ge 0,\,i\in {\mathcal {N}}_c^-. \end{array} \end{aligned}$$

(6)

This is equivalent to $x^*\in X(t)$ and $x^*$ being stationary for all index I NLPs for $I\in {\mathcal {J}}(x^*,t)$. If ${\mathcal {A}}^0_1(x^*,t)={\mathcal {A}}^0_2(x^*,t)=\emptyset$ then B-stationarity is equivalent to S-stationarity. Thus, by the criterion of set inclusion of stationarity measures, S-stationarity is the strongest, by which we mean every other stationarity condition is satisfied when (but not only when) S-stationarity holds. On the other hand B-stationarity is the tightest stationarity measure, in that there is a strict set inclusion of MPCC problems and points $x^*$ which are local minimizers for an MPCC for which B-stationarity holds, but not necessarily S (or C, M, or W) stationarity. Otherwise, S-stationarity, as the strictly strongest set of conditions defined above, implies B-stationarity. Note that in the disjunctive programming literature (Gfrerer 2014), this condition is also referred to as linearized B-stationarity.¹

Constraint Qualifications for MPCC are defined as follows. A point ${\bar{x}}\in X(t)$ is said to satisfy the MPCC-Linear Independence Constraint Qualification (MPCC-LICQ) if $\bar{x}$ satisfies LICQ for the tightened NLP (1) defined with $x^*=\bar{x}$. Analogously, ${\bar{x}}$ can satisfy the MPCC-MFCQ and other corresponding qualifications.

There are a number of second order conditions, here we present the strongest and most relevant for this paper, whose definition appears in, e.g. Scheel and Scholtes (2000).

Theorem 2.1

(Scheel and Scholtes 2000, Theorem 7)

• If $x^*$ is a local minimizer of (PMPCC(t)) at t and the MPCC-LICQ condition holds at $x^*$, then it is an S-stationary point with unique corresponding multipliers $(\lambda ^*,\mu ^*,\sigma ^*)$ satisfying

  $$\begin{aligned} d^T \frac{\partial ^2}{\partial x^2}{\mathcal {L}}(x^*,\lambda ^*,\mu ^*,\sigma ^*,t)d\ge 0 \end{aligned}$$

  for any d feasible for (6) and $\nabla _x f(x^*,t)^T d=0$. This corresponds to the MPCC-SONC (second order necessary condition).

• If $x^*$ is a S-stationary point of (PMPCC(t)) at t, and for every direction $d\ne 0$ feasible for (6) and satisfying $d^T \nabla _x f(x^*,t)=0$, there exist $(\lambda ^*,\mu ^*,\sigma ^*)$ corresponding to S-stationarity for $x^*$ such that

  $$\begin{aligned} d^T \frac{\partial ^2}{\partial x^2} {\mathcal {L}}(x^*,\lambda ^*,\mu ^*,\sigma ^*,t)d> 0 \end{aligned}$$

  then $x^*$ is a strict local minimizer of (PMPCC(t)) at t. This corresponds to the MPCC-SOSC (second order sufficiency condition).

There are a number of other necessary second order optimality conditions corresponding to each of the types of critical points describd above, see, e.g. Guo et al. (2013). It is beyond the scope of the paper to describe each of the conditions, only to say that they correspond to standard notions of second order optimality with critical directions corresponding to cones natural to M- and C-stationarity. Note that given that descent directions can exist in the case of M- and C-stationary points, there is no corresponding notion of sufficient optimality conditions for these points.

2.2 Properties of the parametric solution path

Given the combinatorial structure of MPCCs, it is natural to consider that at a solution $x^*$ of an MPCC, the parametric sensitivity properties will be partially inherited from one or more index $I\in {\mathcal {J}}(x^*,t)$ NLPs. This is formalized in Scheel and Scholtes (2000, Theorem 9) which states that if the LICQ and the strong second order sufficiency condition hold at $x^*$ for every index I NLP, then there are unique local minimizers to t-perturbations of every NLP.

The primal solution path as a function of t for the parametric index I NLP around a base point will have a particular set of continuity properties (Lipschitz piecewise continuity, for instance, under the LICQ and the SOSC), and the same path, as long as it is feasible for the parametric MPCC, will define a path satisfying some level of stationarity for the parametric MPCC with the same continuity properties.

For a reference on the type of continuity properties solution paths to parametric NLPs may have, see Guddat et al. (1990). The paper (Bouza et al. 2008) gives some of the implications these may have for PMPCCs.

Consider the condition of upper level strict complementarity.

Definition 2.1

Upper level strict complementarity holds at $(x^*,\lambda ^*, \mu ^*, \sigma ^*)$ satisfying (5) for (PMPCC(t)) at t if $\sigma ^*_i\ne 0$ for all $i\in {\mathcal {A}}^0_1(x^*,t)\cup {\mathcal {A}}^0_2(x^*,t)$.

Theorem 11 in Scheel and Scholtes (2000) states that given this condition and a linear independence condition on the Jacobians of particular sets of constraints, there exists a unique path of solutions for local perturbations of t in (PMPCC(t)). These solutions maintain B-stationarity or C-stationarity, as the case may be, and if B-stationarity and the MPCC-SOSC hold, then they are local minimizers. Upper level strict complementarity will be used below in the application of a penalty method for tracing parametric MPCC solutions, in Sect. 3.1.

We shall also use the notion of partial strict complementarity.

Definition 2.2

Partial strict complementarity holds at $(x^*,\lambda ^*, \mu ^*, \sigma ^*)$ satisfying (5) for (PMPCC(t)) at t if $\sigma ^*_i+\sigma ^*_{i+n_c}>0$ for $i\in {\mathcal {N}}_c^-$.

For a comprehensive exposition on the strong stability properties of S-stationary, C-stationary, and M-stationary points please see Jongen et al. (2012). For a work studying the value function, or the evaluation of the objective function at the problem solution as a function of parameters, see Guo et al. (2014). Another paper that studies the stability of the more general class of mathematical programs with geometric constraints, wherein constraint values must live in some closed set, that includes the complementarity set and other nonconvex domains, is Guo et al. (2012).

2.3 Pathfollowing for parametric nonlinear programming

We recall here some basic notions about pathfollowing for standard (non-complementarity) parametric nonlinear programming. Thus in this section we consider (PMPCC(t)) with $n_c=0$. In pathfollowing algorithms we trace the (approximate) solution of a parametric optimization problem along a parameter t, starting from $t=0$ to $t=1$. For a standard reference on this topic, see Guddat et al. (1990).

Let $(x^*,\lambda ^*,\mu ^*)$ be a primal-dual tuple satisfying stationarity, i.e., the system (5) (note that these are the standard first order KKT conditions when $n_c=0$). Let $\Lambda (x^*,t)$ correspond to the set of all $(\lambda ^*,\mu ^*)$ satisfying the conditions for $x^*$. Define, ${\mathcal {I}}(x^*,t)$ to be the set of inequality constraint indices such that for $i\in {\mathcal {I}}(x^*,t)$, $g_i(x^*,t)=0$, ${\mathcal {I}}_0(x^*,\lambda ^*,t)\subseteq {\mathcal {I}}(x^*,t)$ to be the set such that $i\in {\mathcal {I}}_0(x^*,\lambda ^*,t)$ implies that $\lambda ^*_i=0$ and ${\mathcal {I}}_+(x^*,\lambda ^*,t)\subseteq {\mathcal {I}}(x^*,t)$ to be the set such that $i\in {\mathcal {I}}_+(x^*,\lambda ^*,t)$ implies that $\lambda ^*_i>0$. We define ${\mathcal {I}}_+ (x^*,t) = \cup _{(\lambda ^*,\mu ^*)\in \Lambda (x^*,t)} {\mathcal {I}}_+(x^*,\lambda ^*,t)$ and ${\mathcal {I}}_0(x^*,t) = \cap _{(\lambda ^*,\mu ^*)\in \Lambda (x^*,t)} {\mathcal {I}}_0(x^*,\lambda ^*,t)$, the index set of constraints corresponding to a positive multiplier component for at least one element of the set of optimal multipliers and those associated with only null multipliers, respectively.

The Lagrangian function for the NLP is ${\mathcal {L}}(x, \lambda ,\mu ,t) = f(x,t) - g(x,t)^T \lambda -h(x,t)^T \mu$. The Hessian of the Lagrangian with respect to x is denoted by

$$\begin{aligned} H(x,\lambda ,\mu ,t):= \nabla ^2_{xx} f(x,t) - \sum _{i=1}^{m_q} \lambda _i \nabla ^2_{xx} g_i(x,t)- \sum _{i=1}^{m_e} \mu _i \nabla ^2_{xx} h_i(x,t). \end{aligned}$$

The most important second order condition for pathfollowing is the strong form of the second order sufficiency condition, defined as follows.

Definition 2.3

(Strong second order sufficient conditions (SSOSC)) The vectors $(x^*,\lambda ^*,\mu ^*)$ satisfy the strong second order sufficient optimality conditions at t if they satisfy the first-order KKT conditions ((5) with $n_c=0$) and

$$\begin{aligned} d^T H(x^*,\lambda ^*,\mu ^*,t) d > 0 \text { for all } d\in \tilde{{\mathcal {C}}}(x^*,\lambda ^*,\mu ^*,t)\setminus \{ 0 \}, \end{aligned}$$

(7)

where $d\in \tilde{{\mathcal {C}}}(x^*,\lambda ^*,\mu ^*,t)$ if $\nabla _x g_i(x^*,t)^T d=0$ for all $i\in {\mathcal {I}}_+(x^*,\lambda ^*,t)$ and $\nabla _x h(x^*,t) d =0$.

It will also be useful to know the (general) second order sufficient conditions for optimality.

Definition 2.4

(Second order sufficient conditions (SOSC)) The vectors $(x^*,\lambda ^*,\mu ^*)$ satisfy the second order sufficient optimality conditions at t if they satisfy the first-order KKT conditions ((5) with $n_c=0$) and

$$\begin{aligned} d^T H(x^*,\lambda ^*,\mu ^*,t) d > 0 \text { for all } d\in \hat{{\mathcal {C}}}(x^*,\lambda ^*,\mu ^*,t)\setminus \{ 0 \}, \end{aligned}$$

(8)

where $d\in \hat{{\mathcal {C}}}(x^*,\lambda ^*,\mu ^*,t)$ if $\nabla _x g_i(x^*,t)^T d=0$ for $i\in {\mathcal {I}}_+(x^*,\lambda ^*,t)$, $\nabla _x g_i(x^*,t)^T d\ge 0$ for $i\in {\mathcal {I}}_0(x^*,\lambda ^*,t)$, and $\nabla _x h(x^*,t) d =0$.

Recalling (Jittorntrum 1984), we know that there is a quadratic program (QP) whose solution characterizes the directional derivative of the solution to the parametric NLP at a primal-dual solution $(x^*,\lambda ^*,\mu ^*)$ at t. In Kungurtsev and Diehl (2014) [see also Diehl (2001)] a predictor-corrector QP is introduced, which incorporates the directional derivative of the solution together with a step towards the solution at the next value of the homotopy parameter in one QP. It is noted that by lifting the nonlinear dependence (i.e., introducing a variable $x_{n+2n_c+1}$ in place of t in the problem functions and adding the constraint $x_{n+2n_c+1}=t$) any parametric NLP can be written such that $\nabla ^2_{xt} f(x,t)$, $\nabla _t g(x,t)$ and $\nabla _t h(x,t)$ are all constant.² We consider starting with an approximate solution $({\bar{x}},{\bar{\lambda }},{\bar{\mu }})$ which is sufficiently close to the primal-dual solution $(x^*(t),\lambda ^*(t),\mu ^*(t))$ at the initial value of the parameter t. Let $\Delta t$ be the stepsize for t and consider an iteration of pathfollowing. The predictor-corrector QP is given as,

$$\begin{aligned} \begin{array}{rl} \min _{\Delta x\in {\mathbb {R}}^n} &{} \nabla _x f({\bar{x}},t+\Delta t)^T \Delta x+\frac{1}{2}\Delta x^T H({\bar{x}},{\bar{\lambda }},{\bar{\mu }},t) \Delta x \\ \text {s.t.} &{} h({\bar{x}},t)+\nabla _t h({\bar{x}},t) \Delta t+\nabla _x h({\bar{x}},t) \Delta x = 0, \\ &{} g_i({\bar{x}},t)+\nabla _t g_i({\bar{x}},t)^T \Delta t+\nabla _x g_i({\bar{x}},t)^T \Delta x = 0, \text { for }i\in {\mathcal {I}}_+({\bar{x}},{\bar{\lambda }},t), \\ &{} g_i({\bar{x}},t)+\nabla _t g_i({\bar{x}},t)^T\Delta t+\nabla _x g_i({\bar{x}},t)^T \Delta x \ge 0, \text { for } i\in {\mathcal {I}}_0({\bar{x}},{\bar{\lambda }},t). \end{array} \end{aligned}$$

(9)

Starting at $t=0$ with a given initial approximate solution $(x,\lambda ,\mu )$, we iteratively solve (9), take a step in the direction of the primal-dual QP solution, and perform an estimate of the strongly and weakly active sets for $t=0<t_1<t_2<\cdots <t_N=1$. If the original problem satisfies the SSOSC throughout the path, this QP is has a unique solution, as it is strongly convex along the subspace defined by the linearization of the constraints, and this procedure is well defined.

The active sets ${\mathcal {I}}_+({\bar{x}},{\bar{\lambda }},t)$ and ${\mathcal {I}}_0({\bar{x}},{\bar{\lambda }},t)$ are estimated along the path using a technique based on Facchinei et al. (1998), also used in Kungurtsev and Diehl (2014). In particular, for a standard NLP (i.e., $n_c=0$), we define the optimality residual as

$$\begin{aligned} \eta (x,\lambda ,\mu ,t) = \left\| \begin{pmatrix} \nabla _x f(x,t)-\nabla _x h(x,t)^T\mu -\nabla _x g(x,t)^T\lambda \\ \min (g(x,t),\lambda ) \\ h(x,t) \end{pmatrix} \right\| _\infty , \end{aligned}$$

(10)

and estimate the active sets as follows,

$$\begin{aligned} \begin{array}{l} \bar{{\mathcal {I}}}(x,\lambda ,\mu ,t) = \{i:\, g_i(x,t)\le \eta (x,\lambda ,\mu ,t)^{\gamma }\}, \\ \bar{{\mathcal {I}}}_+(x,\lambda ,\mu ,t) = \{i\in {\mathcal {I}}(x,\lambda ,\mu ,t):\, \lambda _i>\eta (x,\lambda ,\mu ,t)^{\gamma }\},\\ \bar{{\mathcal {I}}}_0(x,\lambda ,\mu ,t) = \bar{{\mathcal {I}}}(x,\lambda ,\mu ,t)\setminus \bar{{\mathcal {I}}}_+(x,\lambda ,\mu ,t), \end{array} \end{aligned}$$

(11)

where $0<\gamma <1$.

For the MPCC pathfollowing algorithms discussed later in Sect. 3, we trace the MPCC solutions by tracing some auxiliary parametric NLPs by estimating, at each value of t, the active sets as above, and computing the steps using (9).

3 Algorithms

3.1 Penalty method

In order to obtain a solution of (PMPCC(t)) for a given t, the standard penalty method instead solves the NLP,

for some penalty parameter $\rho >0$.

There are several important results relating the stationarity properties of the original problem (PMPCC(t)) and its relaxed penalty surrogate problem ($P_\rho (t)$).

Theorem 3.1

(Ralph and Wright 2004, Theorem 5.1–5.2, Proposition 5.3)

• If $x^*$ is S-stationary for (PMPCC(t)) at t then for $\rho$ sufficiently large, $x^*$ is stationary for ($P_\rho (t)$). Furthermore, if the MPCC-LICQ, MPCC-MFCQ, or MPCC-SOSC hold for (PMPCC(t)) at t at $x^*$ then the LICQ, MFCQ or SOSC hold at ($P_\rho (t)$) at t at $x^*$, respectively.

• If $x^*$ is stationary for ($P_\rho (t)$) and $x^*\in X(t)$, then it is S-stationary for (PMPCC(t)). Furthermore if the LICQ and SOSC hold at $x^*$ for ($P_\rho (t)$) at t, then the MPCC-LICQ and MPCC-SOSC hold at $x^*$ for (PMPCC(t)) at t.

• If $x^*$ is S-stationary with associated $(\lambda ^*,\mu ^*,\sigma ^*)$ for (PMPCC(t)) at t, and the MPCC-LICQ and partial strict complementarity hold at $x^*$, then for $\rho$ sufficiently large, there is a neighborhood ${\mathcal {B}}$ of $x^*$ such that every stationary point of ($P_\rho (t)$) in ${\mathcal {B}}$ is an S-stationary point for (PMPCC(t)).

From the proofs in Ralph and Wright (2004), the minimum $\rho$ that is required for the first two results of this Theorem is equal to,

$$\begin{aligned} {\bar{\rho }}_1 = 1+\max \left( 0,\max _{i\in {\mathcal {A}}_1(x^*,t)\setminus {\mathcal {A}}_1^0(x^*,t)} \frac{\sigma ^*_i}{x^*_{i+n_c}}, \max _{i\in {\mathcal {A}}_2(x^*,t)\setminus {\mathcal {A}}_2^0(x^*,t)} \frac{\sigma ^*_i}{x^*_{i-n_c}}\right) , \end{aligned}$$

(12)

and for the third result, it must satisfy,

$$\begin{aligned} \rho \xi +\max _i \sigma ^*_i-\xi > 0, \end{aligned}$$

where $\xi$ is equal to,

$$\begin{aligned} \xi =\frac{1}{2} \min \left( \min _{i\in \left( {\mathcal {A}}_1(x^*,t)+n_c\right) \cup \left( {\mathcal {A}}_2(x^*,t)-n_c\right) } x^*_i,\min _{i:\sigma ^*_i>0} \sigma ^*_i\right) . \end{aligned}$$

Note, however, that the MPCC-SOSC does not imply the strong second order sufficiency conditions for the penalty NLP, which is required for the theoretical convergence properties of the predictor-corrector QP (9) for pathfollowing.

One can obtain the multipliers $\sigma ^*$ from the solution of the penalty function minimization by taking,

$$\begin{aligned} \sigma ^*_i = \left\{ \begin{array}{lr} z^*_i-\rho x^*_{i+n_c}, &{} i \in {\mathcal {N}}_c^-,\\ z^*_i-\rho x^*_{i-n_c}, &{} i \in {\mathcal {N}}_c^+, \end{array}\right. \end{aligned}$$

(13)

where $z^*$ are the multipliers for the bound constraints $x_i\ge 0,\,i\in {\mathcal {N}}_c$ in the penalty problem (see Coulibaly and Orban 2012).

3.1.1 Description of the penalty pathfollowing algorithm

Now we describe an algorithm that approximately traces the solution trajectory (PMPCC(t)) by following the solution path of the corresponding parametric penalty formulation.

We write the penalty objective as,

$$\begin{aligned} f_p(x,t;\rho ) = f(x,t)+\rho \sum _{i\in {\mathcal {N}}_c^-} x_i x_{i+n_c} \end{aligned}$$

and correspondingly the Lagrangian of the penalty problem as,

$$\begin{aligned} {\mathcal {L}}_p(x,\lambda ,\mu ,z,t;\rho ) = f_p(x,t;\rho )-\lambda ^T g(x,t)-\mu ^T h(x,t)-z^T x \end{aligned}$$

with Hessian matrix,

$$\begin{aligned} H_p(x,\lambda ,\mu ,t;\rho ) = \nabla ^2_{xx} {\mathcal {L}}_p(x,\lambda ,\mu ,z,t;\rho ). \end{aligned}$$

We present the Penalty Pathfollowing Algorithm as Algorithm 1. We start with a point close to $x^*(0)$ and estimate both the strongly and weakly active inequality constraints using (11). This set includes the complementarity variables treated as constraints, i.e. $x_i\ge 0$ for $i\in {\mathcal {N}}_c$ are included and identified as being (strongly) active or not. We shall denote the index set of the complementarity variables deemed strongly active to be $\bar{{\mathcal {N}}}_c^+(x,(\lambda ,z),\mu ,t).$ Note that when discussing the penalty method, $\eta$ given in (10) includes the dual complementarity measure $\min (x_{{\mathcal {N}}_c},z)$, i.e.,

$$\begin{aligned} \eta (x,\lambda ,\mu ,z,t) = \left\| \begin{pmatrix} \nabla _x f_{\rho }(x,t;\rho )-\nabla _x h(x,t)^T\mu -\nabla _x g(x,t)^T\lambda -z\\ \min (g(x,t),\lambda ) \\ h(x,t) \\ \min (x_{{\mathcal {N}}_c},z) \end{pmatrix} \right\| _\infty , \end{aligned}$$

(14)

Note that if the strongly active set is identified correctly and upper level strict complementarity holds, then the solution set of the tightened NLP is equivalent to the MPCC, and thus $\eta$ is an error bound for the latter.

At each iteration, the predictor-corrector QP (9) is constructed for ($P_\rho (t)$) and solved to obtain the primal-dual tuple $(\Delta x, ({\hat{\lambda }},{\hat{z}}), {\hat{\mu }})$.

3.1.2 Theoretical guarantees

The tracking convergence guarantees associated with the penalty algorithm is given below in Theorem 3.2. In particular we use the aforementioned correspondence between necessary and sufficient optimality conditions for the MPCC and the associated penalty problem to show that for a well behaved PMPCC, there is sufficient regularity for the penalty formulation that the solutions are isolated, and thus 1) the problem satisfying complementarity is the only solution to the penalty form and 2) the QP (15), which is its linearization, has a unique solution. Then from standard results in pathfollowing for NLPs the procedure is shown to generate a set of iterates with theoretical tracking guarantees to the parametric solution curve.

In general, for well-behaved problems the procedure successfully traces the solutions, but has several limitations. First, only S-stationary points are guaranteed to be traced. This does not necessarily imply that weaker notions of stationarity that could be spurious, like M or C-stationarity, will not be traced, and it also implies that not all B-stationary points will be traced. Furthermore, an “a posteriori” assumption must hold, that the SSOSC conditions hold for the penalty problem associated with the MPCC. The SOSC for the original MPCC is not enough to ensure the predictor-corrector QP is able to generate the solution path for the MPCC.

Theorem 3.2

Assume there exists $x^*:[0,1]\rightarrow {\mathbb {R}}^{n+2n_c}$ such that $x^*(t)$ is an isolated S-stationary point for (PMPCC(t)) satisfying MPCC-SOSC and MPCC-LICQ³ for all t, and partial strict complementarity holds for all dual vectors $(\lambda ^*,\mu ^*,\sigma ^*)$ corresponding to S-stationarity with $x^*(t)$ for all $t\in {\mathcal {D}}$ for a set ${\mathcal {D}}\subseteq [0,1]$ satisfying $\{0,1\}\in {\mathcal {D}}$, and $[0,1]\setminus {\mathcal {D}}$ is a finite set of points. Then there exists a $\rho$ sufficiently large such that, for all $t\in {\mathcal {D}}$, $x^*(t)$ is a solution for ($P_\rho (t)$) at t. Furthermore consider the iterations of Algorithm 1 performed with this $\rho$ appearing in the subproblem (15) with such sufficiently large $\rho$. Denote by ${\mathcal {T}}$ the set of pathfollowing parameters $\{t_0=0,t_1,t_2,\ldots \}$. If it holds that,

• 1. there is an initial estimate $x_0$ sufficiently close to $x^*(0)$,

• 2. the SSOSC holds for ($P_\rho (t)$) for $x^*(t)$ for all $t\in [0,1]$,

• 3. there exists only a finite $\{t^a_k\}\subseteq [0,1]$ for which

  $$\begin{aligned} \mathop {\lim \inf }\limits _{t\rightarrow (t^a_k)^-} {\mathcal {A}}_1(x^*(t),t)\cup {\mathcal {A}}_2(x^*(t),t) \ne \mathop {\lim \inf }\limits _{t\rightarrow (t^a_k)^+} {\mathcal {A}}_1(x^*(t),t)\cup {\mathcal {A}}_2(x^*(t),t) \end{aligned}$$

  i.e., the number of optimal complementarity active set changes across $x^*(t)$ is finite,

• 4. $t_k\in {\mathcal {D}}$ for all k,

Then it holds that Algorithm 1 successfully generates an approximate solution path $\{(t_k,x_k)\}$ with ${\mathcal {T}}=\{t_0=0,t_1,\ldots ,t_k,\ldots ,t_K=1\}$ finite, i.e., for any $\epsilon$, there exists a $\epsilon _0$ such that if $\Vert x_0-x^*(0)\Vert \le \epsilon _0$ then $\Vert x_k-x^*(t_k)\Vert \le \epsilon$ for all $k=0,1,\ldots ,K$.

Proof Outline: There are two primary steps of the proof. First is to show that there is a one to one locally unique correspondence between $x^*(t)$ as a solution of the original problem and as a solution to the penalty formulation. After establishing this, we can use the results on the properties of the penalty formulation above to infer that corresponding strong regularity conditions are satisfied for the penalty problem along the entire path ${\mathcal {T}}$. What remains is to show that the required minimal $\rho$ for the aforementioned equivalence to hold must be bounded across the homotopy, which corresponds to the quantity defined in (12) having a uniform bound across $t\in [0,1]$. Strong regularity for the penalty problem already implies local boundedness of the primal-dual solution for $t\in {\mathcal {D}}$, thus the onus is to show that the quantity in (12) cannot grow without bound as one approaches some $t\in [0,1]\setminus {\mathcal {D}}$, which correspond to points at which strict complementarity is lost, i.e., active set changes for the complementarity variables. We split the proof into two cases as depending on the form of the bifurcation occurring at these exceptional points.

Proof

First consider $x^*(0)$ as given by the conditions of the Theorem, i.e., satisfying S-stationarity for (PMPCC(t)) at $t=0$. From Theorem 3.1 we can conclude that $x^*(0)$ is a solution to ($P_\rho (t)$) at $t=0$ for all $\rho \ge {\hat{\rho }}_0$ for some ${\hat{\rho }}_0$. Furthermore, the LICQ and, by the second assumption in the Theorem, the SSOSC hold at $x^*(0)$ as a solution to $(P_\rho (0))$. We can extend this to say that these conditions hold for all $x^*(t)$ as solutions to ($P_\rho (t)$), due to the stability of the LICQ and SSOSC (Kojima 1980, Corollary 5.6) and the assumption of $x^*(t)$ being an isolated solution path. The final statement of Theorem 3.1, that there is a neighborhood ${\mathcal {B}}(t)$ of $x^*(t)$ such that every stationary point of ($P_\rho (t)$) in ${\mathcal {B}}(t)$ is an S-stationary point for (PMPCC(t)), implies there is a one-to-one correspondence between $x^*(t)$ as a solution to ($P_\rho (t)$) and for the MPCC in a region around $x^*(t)$ for all $t\in {\mathcal {D}}$.

Now we show that for all $t\in {\mathcal {D}}$, the right-hand side of (12) is uniformly bounded by some ${\hat{\rho }}$ for all primal-dual complementarity solutions $x^*(t),\sigma ^*(t)$, i.e., that the required $\rho$ to satisfy the correspondence between solutions to (PMPCC(t)) and ($P_\rho (t)$) has a uniform lower bound. Now for $t \notin \{t^a_k\}$ the solution $x^*(t)$ is also a solution to the tightened NLP, and since the LICQ and SSOSC hold, its primal-dual solution set is Lipschitz stable (Bonnans and Shapiro 2013, Theorem 4.51).

Together with no components of $x^*(t)$ changing from positive to zero (inactive to active) or vice versa for such t, we obtain for any small $\delta >0$, the uniform boundedness of the quantity in (12) for solutions associated with $t\in (t^a_{k-1}+\delta ,t^a_{k}-\delta )$. Thus we must only consider the change in $\bar{\rho }_1$ in (12) across and close to active set changes $t^a_k$. Without loss of generality, consider that there is only one complementarity constraint, i.e., $n_c=1$. Now, given a $t^c\in \{t^a_k\}$, again without loss of generality, we can consider two exhaustive cases.

Case 1: For t with $t^c-\delta<t<t^c$, the index $i\in {\mathcal {N}}_c$, and, without loss of generality, assume $i\in {\mathcal {N}}_c^-$, corresponds to an inactive primal solution component (i.e., $x_i^*(t)>0$), and for t satisfying $t^c\le t\le t^c+\delta$, $x_i^*(t)=0$ (is active). In addition, $x^*_{i+n_c}(t) = 0$ for all t with $t^c-\delta<t<t^c+\delta$. By complementarity of the solution set and Partial Strict Complementarity for $t\in [t^c-\delta ,t^c+\delta ]\setminus \{t^c\}$, we also have $\sigma ^*_i(t)=0$ and $\sigma ^*_{i+n_c}(t)>0$ for t with $t^c-\delta<t<t^c$.

Given the continuity of the primal-dual solution set to the tightened NLP for $t<t^c$ as established in the first part of the proof, it must be that $x^*_i(t^c)=0$ (by the case assumption) and $\sigma _i^*(t^c)=0$ (by continuity of the tightened NLP multipliers) for a primal-dual solution to the tightened NLP at $t^c$ based around $x^*(t^c)$. With $\sigma ^*_i(t),\sigma ^*_{i+n_c}(t)\ge 0$, one can see the one to one correspondence of the dual solution set to the tightened NLP and the set of multipliers satisfying S-stationarity for (PMPCC(t)) at $t^c$ with $x^*(t^c)$. Now, for $t\ge t^c$, $\{i,i+n_c\}\subseteq {\mathcal {A}}_1^0(x^*(t),t)\cup {\mathcal {A}}_2^0(x^*(t),t)$ and so by the definition of $\bar{\rho }$ in (12), indices i and $i+n_c$ are not included in the set under consideration, and $\bar{\rho }$ is simply 1 for $t^c\le t\le t^c+\delta$.

Thus, for $t^c-\delta<t<t^c+\delta$, we need only be concerned with $t<t^c$, and since $\sigma ^*_i(t)=0$ for such t, we are left with showing boundedness of the quantity $\frac{\sigma ^*_{i+n_c}}{x^*_{i}}$ for $t^c-\delta<t<t^c$. Now for $t\rightarrow _- t^c$ we have $x^*_i(t)\rightarrow 0$ but possibly $\sigma ^*_{i+n_c}(t)\ge \bar{\sigma }$ and thus the expression$\frac{\sigma ^*_{i+n_c}}{x^*_{i}}$ is now unbounded. However, notice that in this scenario, given that $x^*(t)$ with $\sigma ^*(t)$ as multipliers for the conditions $x_j\ge 0$, $j\in {\mathcal {N}}_c$, is a primal-dual solution to the tightened NLP, we notice that for ($P_\rho (t)$) for any $\rho \ge 0$,

$$\begin{aligned} \begin{array}{l} \nabla _{x_i} f_p(x^*(t),t;\rho ) = \nabla _{x_i} f(x^*(t))+\rho x^*_{i+n_c}(t)= \nabla _{x_i} f(x^*(t)) = \sigma ^*_i(t) = 0\\ \nabla _{x_{i+n_c}} f_p(x^*(t),t;\rho ) = \nabla _{x_{i+n_c}} f(x^*(t))+\rho x^*_{i}(t) = \sigma ^*_{i+n_c}+\rho x^*_i(t) \end{array} \end{aligned}$$

where the final equalities come from weak stationarity, assuming without loss of generality that there are no general inequality and equality constraints, or that the sum of their multiplier weighted gradients is equal to zero. From this, it can be seen that the necessary optimality conditions of the penalty problem hold for $x^*(t)$ with $\sigma ^\rho _{i}(t)=\sigma ^*_{i}(t)=0$ and $\sigma ^\rho _{i+n_c}(t)=\sigma ^*_{i+n_c}(t)+\rho x^*_{i}(t)$ for all $\rho \ge 0$. We have already established the local uniqueness of the solutions to ($P_\rho (t)$), thus, this primal-dual pair is the only solution and must be the one the algorithm tracks.

Case 2: it holds that $x^*_i(t)>0$ and $x^*_{i+n_c}(t)=0$ for $t<t^c$, and $x^*_i(t)=0$ and $x^*_{i+n_c}(t)>0$ for $t>t^c$. Note that a multiplier tuple satisfying S-stationarity with $x^*(t)$ must satisfy $\sigma ^*_{i}(t)=0$ for $t\le t^c$ and $\sigma ^*_{i+n_c}(t)=0$ for $t\ge t^c$. Thus Partial Strict Complementarity does not hold at $t^c$. Otherwise, for consistency with the assumption on ${\mathcal {D}}$ it must hold that $\sigma ^*_{i}(t)>0$ for $t> t^c$ and $\sigma ^*_{i+n_c}(t)>0$ for $t< t^c$. By the Theorem assumptions, the Algorithm never attempts to solve the pathfollowing problem for $t_k=t^c$. At $t=t^c$ the situation is now defined exactly as in (Bouza et al. 2008, Proposition 4.4). In particular, for the two tightened NLPs, with $x_i=0$ fixed for $t>t^c$ and $x_{i+n_c}=0$ fixed for $t<t^c$, $x^*(t)$ is optimal with the associated $\sigma ^*(t)$ as optimal multipliers for the complementarity constraints now as variable bound inequality constraints. As according to Bouza et al. (2008, Proposition 4.4) there is one homotopy path of solutions that is feasible and it is characterized by,

$$\begin{aligned} \begin{array}{ll} \lim \limits _{\alpha \rightarrow 0^+} \frac{x^*_i(t^c+\alpha )-x^*_i(t^c)}{\alpha } = 0, &{} \lim \limits _{\alpha \rightarrow 0^-} \frac{x^*_i(t^c+\alpha )-x^*_i(t^c)}{\alpha } \ne 0, \\ \lim \limits _{\alpha \rightarrow 0^+} \frac{x^*_{i+n_c}(t^c+\alpha )-x^*_{i+n_c}(t^c)}{\alpha } \ne 0, &{} \lim \limits _{\alpha \rightarrow 0^-} \frac{x^*_{i+n_c}(t^c+\alpha )-x^*_{i+n_c}(t^c)}{\alpha } = 0 \\ \lim \limits _{\alpha \rightarrow 0^+} \frac{\sigma ^*_i(t^c+\alpha )-\sigma ^*_i(t^c)}{\alpha } \ne 0, &{} \lim \limits _{\alpha \rightarrow 0^-} \frac{\sigma ^*_i(t^c+\alpha )-\sigma ^*_i(t^c)}{\alpha } = 0, \\ \lim \limits _{\alpha \rightarrow 0^+} \frac{\sigma ^*_{i+n_c}(t^c+\alpha )-\sigma ^*_{i+n_c}(t^c)}{\alpha } = 0, &{} \lim \limits _{\alpha \rightarrow 0^-} \frac{\sigma ^*_{i+n_c}(t^c+\alpha )-\sigma ^*_{i+n_c}(t^c)}{\alpha } \ne 0 \\ \end{array} \end{aligned}$$

which imply the uniform boundedness of the quantity defined by (12) as $t\rightarrow t^c$.

Now we can bring $x_0$ as close as necessary to $x^*(0)$ such that the conditions of Kungurtsev and Diehl (2014, Theorem 4.2) are satisfied as applied to ($P_\rho (t)$).⁴ Thus the predictor-corrector QP (15) associated with the appropriate active and strongly active set estimates, is able to successfully trace a primal-dual solution with $\Vert x_k-x^*(t_k)\Vert \le \epsilon$.

For illustration of the main ideas in the proof, we point to Fig. 1.

We now discuss the assumptions in the previous Theorem. The first is standard and natural. The second indicates the gap between the second order necessary and sufficient conditions can only be assumed away, and cannot be guaranteed by any preceding assumptions. The third assumption simply indicates that there are a finite number of active set changes along the solution path, which is expected to hold except for cases of increasingly oscillatory behavior (e.g., with a function of the form $\sin (1/x)$).

It could be of concern that the assumption in the Theorem that $t_k\in {\mathcal {D}}$ for all k is a posteriori, i.e., depending on the outcome of the Algorithm rather than an a priori condition on the problem itself. However, note that since $[0,1]\setminus {\mathcal {D}}$ is finite, also by assumption, and yet $t_k\in {\mathbb {R}}$, then this should reasonably be satisfied, and otherwise can be assured with probability one by adding a tiny perturbation to $t_k$.

Fig. 1

Illustration of the cases described in Theorem 1. The figures on top are potential primal-dual solution paths, as the parameter t changes, the solution undergoes an active set change at $t_c$. This is reflected in the blue lines showing the value of the primal solution of a complementarity pair. The green lines show two possible scenarios of the change in the dual solutions, for Case 1, on the left, and Case 2, on the right, respectively. The figures at the bottom represent the value of thereshold $\rho$ required in the main result, as the parameter t changes. Note that in the first case, this value approaches infinity asymptotically as $t\rightarrow t_c$, but the structure of the problem remains such that a smaller penalty parameter is adequate

3.2 Active set index method

The next pathfollowing algorithm is intended to trace B-stationary points, which as indicated describe the tightest computable notion of necessary first order optimality. Their importance and the combinatorial approach of the active set algorithm described here is inspired by the “SLPEC-EQP" algorithm presented in Leyffer and Munson (2007) and more recently (Kirches et al. 2022) [see also Lenders (2018, Chapter 7)].

In this line of work, it was observed that M, C and W-stationary points could have linearly feasible descent directions, and B-stationarity is the precise stationarity concept associated with the lack of such descent directions. S-stationarity is the strongest notion of stationarity, but an algorithm with guarantees in finding only S-stationarity could neglect finding points that are B- but not S-stationary.

Consider the LPCC,

$$\begin{aligned} \begin{array}{rl} \min _{d\in {\mathbb {R}}^{n+2n_c}} &{} \nabla _x f(x,t)^T d, \\ \text {s.t.} &{} g(x,t)+\nabla _x g(x,t) d \ge 0,\\ &{} h(x,t)+\nabla _x h(x,t) d = 0, \\ &{} 0\le x_i+d_i \perp x_{i+n_c}+d_{i+n_c}\ge 0, \, i\in {\mathcal {N}}_c^-,\\ &{} \Vert d\Vert _\infty \le \beta , \end{array} \end{aligned}$$

(16)

where $\beta >0$ is a trust-region parameter. It is clear from considering the LPCC associated with the definition of B-stationarity (6) that $d=0$ being the solution to (16) corresponds to B-stationarity. The algorithms in Leyffer and Munson (2007) and Kirches et al. (2022) solve this LPCC, using the solution to estimate the active set and subsequently perform acceleration steps on the active set. The authors prove the global convergence of this procedure to a B-stationary point. Recall that $d=0$ solving the LPCC ((6) and (16)) at some $(x^*,t)$ implies that every index I NLP for $I\in {\mathcal {J}}(x^*,t)$ is optimal. We focus on estimating the set ${\mathcal {J}}(x^*,t)$, noting that the double active set indicates possible branching in the directional derivative of the solution.

Thus, given t and an initial point x that we expect to be close to a solution for problem (PMPCC(t)) at t, we first seek to estimate the active set of complementarity variables at the optimal point closest to x. Denoting ${\mathcal {B}}(t)$ as the set of B-stationary points for (PMPCC(t)) at t, we write this as,

$$\begin{aligned} {\mathcal {A}}^0(x,t):=\{i\in {\mathcal {N}}_c:x^*_i=0 \text { for }x^*\in \text {argmin}_{y\in {\mathcal {B}}(t)}\Vert y-x\Vert \} \end{aligned}$$

Next we must identify the set of index I NLPs which requires a reliable active set identification procedure for MPCCs. However, there is no certifiably accurate method to do this and we make the following assumption.

Assumption 1

We have a reliable means of estimating ${\mathcal {A}}^0(x,t)$ from x, if x is sufficiently close to $x^*(t)$, a B-stationary point of (PMPCC(t)).

Heuristically, we consider i as active, and thus a potential member of the index I NLP when $x_i\le \epsilon _0$ for some (problem-tuned) tolerance $\epsilon _0$. Practically, we form the set of branches based on the estimate of the corresponding doubly-active set, i.e., $\{i:x_i\le \epsilon _0,\,x_{i+n_c}\le \epsilon _0\}$.

We then use this to form an estimate of the set ${\mathcal {J}}(x^*,t)$ and perform parametric pathfollowing on every NLP. Denote this estimate to be $C_0(x,t)$, i.e.,

$$\begin{aligned} C_{0}(x,t):= \{I\subseteq {\mathcal {A}}^0(x,t)|\forall i\in {\mathcal {N}}_c^-:\, |I\cap \{i,i+n_c\}|=1\}. \end{aligned}$$

(17)

3.2.1 Description of the algorithm

We present the Active Set MPCC pathfollowing algorithm as Algorithm 2. First, given an approximate B-stationary solution x to the MPCC at $t=0$, we estimate and prune the set of index I NLPs. For each $I\in C_0(x,0)$ defined in (17), we form the NLP and solve it using an appropriate solver for standalone NLPs in order to obtain the multiplier estimates for the initial (PMPCC(t)) at $t=0$. If no appropriate dual variable approximate solutions (i.e., with the right signs) exist, then this I is not in $C_0(x,t)$ and we discard it. Otherwise, for every I in $C_0(x,t)$, the corresponding predictor-corrector QP is then used to obtain the next solution. The QP we solve is the following (assuming, again, affine as welldependence of $g(x,\cdot )$ and $\nabla _x f(x,\cdot )$ with respect to the parameter t).

$$\begin{aligned} \begin{array}{rl} \min _{\Delta x} &{} \nabla _x f(x,t)^T \Delta x+\frac{1}{2}\Delta x^T H(x,\lambda ,\mu ,t) \Delta x\\ \text {s.t.} &{} h(x,t)+\nabla _t h(x,t) \Delta t+\nabla _x h(x,t) \Delta x = 0, \\ &{} g_i(x,t)+\nabla _t g_i(x,t)^T \Delta t+\nabla _x g_i(x,t)^T \Delta x = 0, \text { for }i\in \bar{{\mathcal {I}}}_+(x,\lambda ,\mu ,t), \\ &{} g_i(x,t)+\nabla _t g_i(x,t)^T\Delta t+\nabla _x g_i(x,t)^T \Delta x \ge 0, \text { for } i\in \bar{{\mathcal {I}}}_0(x,\lambda ,\mu ,t), \\ &{} x_i = 0, \, i\in {\mathcal {A}}^0(I),\\ &{} x_i \ge 0, \, i\in {\mathcal {N}}_c\setminus {\mathcal {A}}^0(I) \end{array} \end{aligned}$$

(18)

where ${\mathcal {A}}^0(I)$ is the active set designated by index I. We solve the QP for every feasible I to obtain a set of solutions $\{\Delta x_I\}$.

We then check, after the step, if the solution still satisfies the full set of complementarity constraints. Then, for each I, we recalculate $C_0(x+\Delta x_I,t+\Delta t)$ if necessary and investigate if the new primal solution estimate remains stationary for every single index I NLP in $C_0(x+\Delta x_I,t+\Delta t)$ by obtaining the appropriate dual solution minimizing the stationarity norm,

$$\begin{aligned}{} & {} \min _{\sigma _{I_+}\ge 0, \lambda \ge 0} \Vert \nabla _x f(x+\Delta x_I,t+\Delta t)-\nabla _x g(x+\Delta x_I,t+\Delta t)^T \lambda \nonumber \\ {}{} & {} \quad -\nabla _x h(x+\Delta x_I,t+\Delta t)^T\mu -\sigma \Vert ^2 \end{aligned}$$

(19)

where $I_+\subseteq {\mathcal {N}}_c$ is a set such that $i\in I_+$ implies $x_i= 0$. In particular, if the objective value of (19) is less than $\epsilon _0$ then we consider it approximately stationary in our Algorithm.

If the point $x+\Delta x_I$ is not feasible, or not approximately optimal for every $I\in C_0(x+\Delta x,t+\Delta t)$, then we cut this branch and proceed to starting the next branch, i.e., move on to the next I. Finally, if it tracks the solution until the final iterate at $t=1$, for the sake of completeness we pathfollow the other branches as well.

3.2.2 Theoretical guarantees

Given that the algorithm consists of pathfollowing the set of index I NLPs, the convergence properties can be inferred from the corresponding results for standard NLP pathfollowing using the predictor-corrector QP as presented in Kungurtsev and Diehl (2014).

Theorem 3.3

Assume there exists a set $\{x^*_k\}_{k=1,\ldots ,K}$ of functions $x^*_k(t):[t_{a_k},t_{b_k}]\rightarrow {\mathbb {R}}^{n+2n_c}$, $k=1,\ldots ,K$ such that $x_k(t)$ is B-stationary for $t\in [t_{a_k},t_{b_k}]$ for all $k\in \{1,\ldots ,K\}$ and $\cup _k [t_{a_k},t_{b_k}]=[0,1]$. Assume that for every $k_1\in \{1,\ldots ,K\}$ there exists some $k_2\in \{1,\ldots ,K\}$ such that for some $t^{k_1k_2}\in [0,1]$ it holds that $x^*_{k_1}(t^{k_1k_2})=x^*_{k_2}(t^{k_1k_2})$. Assume this set is maximal, i.e., there is no ${\hat{K}}> K$ that strictly includes $\{x^*_k\}_{k=1,\ldots ,K}$ such that these conditions are satisfied. Given an initial point $x_1(0)$ sufficiently close to $x^*_{{\hat{k}}}(0)$ for some ${\hat{k}}$, and desired threshold D, Algorithm 2 will generate a set of iterates $\{x_l(t_j)\}_{l=1,\ldots ,\bar{K},j=1,\ldots ,J_l}$ with ${\bar{K}}\le K$ such that $\Vert x_l(t_j)-x_k^*(t_j)\Vert \le D$ for some $k\in \{1,\ldots ,K\}$ for all $l\in \{1,\ldots ,\bar{K}\}$ and $j\in \{1,\ldots ,J_l\}$ and $t_j\in [t_{a_k},t_{b_k}]$ for this k and $\max \limits _{j}\{t_j\}=1$.

Proof

Under Assumption 1, since B-stationarity is equivalent to a set of NLPs satisfying the first order necessary optimality conditions, $x_1(0)$ is an approximate stationary point to each Index I NLP found in $C_{0}(x,0)$. If there exists a branch $x^*_{{\hat{k}}}(t_0+\Delta t)$ for any $\Delta t>0$, then by Kungurtsev and Diehl (2014, Theorem 4.2) the active set estimation and predictor-corrector QP will trace it to desired accuracy. By the fact that the distance to the solution of any NLP is $O(\cdot )$ of the value of the optimality residual $\eta (\cdot )$ (see, e.g. Hager and Gowda 1999), a true B-stationary point will satisfy a low objective value of (19) for every index I NLP.

If during the pathfollowing another constraint becomes doubly-active at ${\bar{t}}$, it is added to $C_{0}(x({\bar{t}}),{\bar{t}})$, and subsequently traced from ${\bar{t}}$ on. $\square$

4 Examples

In this section we present the results of Algorithms 1 and 2 on a set of toy problems and a phase transition engineering case study. We performed the experiments using MATLAB 2018a. The initial point was obtained using fmincon with the SQP option, constraint tolerance 1e-7 and step tolerance 1e-12 for the penalty algorithm, and the multistart based global optimization toolbox for the active set algorithm. Quadprog with the default settings was used to solve the subproblems. A constraint is considered active if it is so approximately under a tolerance of 1e-5. $\Delta t$ is initialized to 0.1 and is increased or decreased by a factor of $\alpha =1.5$ upon a successful or unsuccessful pathfollowing step.

4.1 Example 1

Consider the problem,

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{2}} &{} (x_1-t)^2+(x_2+t)^2 \\ \text {s.t.} &{} 0\le x_1 \perp x_2\ge 0. \end{array} \end{aligned}$$

For $t<0$, $(0,-t)$ is a local minimizer and the origin is W-stationary. For $t=0$, the origin is a strongly stationary local minimizer. For $t>0$, (t, 0) is a local minimizer and the origin is W-stationary.

Penalty Method

The penalty method is able to successfully trace the solution $(0,-t)$ for $t\in [-1,0]$ through (t, 0) for $t\in [0,1]$.

The primal solutions as well as the complementarity multiplier estimates given by (13) are shown in Fig. 2.

Fig. 2

Illustration of the traced solutions to Example 1 found using the penalty algorithm. The circles are the points visited by the method. As expected, since the solutions are all S-stationary, the complementarity multipliers are zero when the corresponding variable is inactive and become positive as they become active, and vice versa. 

Active Set Method

The active set method is able to successfully trace the solution $(0,-t)$ for $t\in [-1,0]$ through (t, 0) for $t\in [0,1]$. It recognizes the double-active set at $t=0$ and discards the branch of the Index I NLP associated with the path of solutions for $t\in [-1,0]$, switching to the other branch thereafter.

4.2 Example 2

This problem is inspired by Leyffer and Munson (2007).

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{2}} &{} (x_1-t)^2+x_2^3+x_2^2 \\ \text {s.t.} &{} 0\le x_1 \perp x_2\ge 0. \end{array} \end{aligned}$$

For $t<0$, the origin is the local minimizer and only stationary point. For $t>0$, the point (t, 0) is a local minimizer and the origin is M-stationary.

Penalty Method

In this case, the penalty method always traces the origin for $t\in [-1,0]$, and the local minimizer (t, 0) for $t\in [0,1]$. Thus it does not appear to follow the M-stationary point. The set of points traced along the homotopy is shown in Fig. 3.

Fig. 3

Illustration of the penalty algorithm solutions for Example 2 

Active Set Method

The active set method traces two solutions along the bi-active set for $t\in [-1,0]$. Subsequently, the solution branch for which $x_1=0$ stops pathfollowing at $t=0$ and the one with $x_2=0$ pathfollows successfully along (t, 0) for $t\in [0,1]$. The solutions are shown in Fig. 4.

Fig. 4

Illustration of the active set algorithm solutions for Example 2 

4.3 Example 3

This problem arises from Scheel and Scholtes (2000). Consider,

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{2}} &{} (x_1-t)^2+(x_2-t)^2 \\ \text {s.t.} &{} 0\le x_1 \perp x_2\ge 0. \end{array} \end{aligned}$$

For $t\le 0$, the origin is the unique minimizer, and is S-stationary. For $t>0$, the origin is C-stationary, and (t, 0) and (0, t) are both local minimizers. For any t, the Lagrangian Hessian is $\nabla ^2_{xx} {\mathcal {L}} = \begin{pmatrix} 2 &{} 0 \\ 0 &{} 2 \end{pmatrix}$, as this matrix is positive definite, it is also positive definite on any cone of directions. We illustrate the problem in Fig. 5.

Fig. 5

Illustration of Example 3. The level sets of the objective function at $t=-1$ and $t=1$ are drawn as circles. As t traces from $-1$ to 1, the level sets move continuously from the bottom left to the top right. The local minimizers are marked as red dots. Up until $t=0$, i.e., for $t\in [-1,0]$, the unique local minimizer is the origin. For $t\in (0,1]$ there are two local minimizers, (t, 0) and (0, t). In addition, there is a C-stationary point at the origin, for which clearly both axes are a descent direction, indicating the weakness of this stationarity condition 

Penalty Method

Note that for $t=0$, the Lagrangian Hessian for ($P_\rho (t)$) is $\nabla ^2_{xx} {\mathcal {L}}_p = \begin{pmatrix} 2 &{} \rho \\ \rho &{} 2 \end{pmatrix}$. At the origin, every multiplier is null, i.e., $\sigma _{1,2}^*=z_{1,2}^*-\rho x^*=0$, thus for ($P_\rho (t)$) at $t=0$, no constraint is strongly active and both variables are weakly active at the origin, i.e., $x^*_1=x^*_2=z^*_1=z_2^*=0$. Thus, although $\nabla ^2_{xx} {\mathcal {L}}_p$ is positive definite along the cone of feasible directions, which are $\begin{pmatrix} 1&0 \end{pmatrix}^T$ and $\begin{pmatrix} 0&1 \end{pmatrix}^T$, for proper pathfollowing of ($P_\rho (t)$) using (15), the strong SOSC conditions must hold for ($P_\rho (t)$) at $x^*$, and $\nabla ^2_{xx} {\mathcal {L}}_p$ must be positive definite on the subspace orthogonal to the null-space of the strongly active constraint gradients, which is trivially ${\mathbb {R}}^2$, and thus includes $\begin{pmatrix} 1&-1 \end{pmatrix}^T$. Thus, predictably the penalty algorithm is not able to pathfollow past $t=0$, in particular, as the reduced Hessian in the constraint gradient null-space of the pathfollowing QP (9) is indefinite, the corresponding QP is nonconvex. Thus, theoretical guarantees on NLP pathfollowing do not apply to the corresponding predictor-corrector QP for this problem.

The optimality conditions for the QP (9) based from the origin are,

$$\begin{aligned} \begin{array}{l} -2t + 2\Delta x_1 +\rho \Delta x_2 = 0, \\ -2t + 2 \Delta x_2 +\rho \Delta x_1 = 0, \\ \Delta x_1\ge 0, \, \Delta x_2\ge 0. \end{array} \end{aligned}$$

From these equations, it must hold that $\Delta x_1=\Delta x_2>0$. Note that this is not a feasible direction for the original problem, and thus the QP for the pathfollowing of ($P_\rho (t)$) for any $\rho >0$ does not correspond to pathfollowing for the original MPCC.

The penalty method is able to trace the origin solution for $t<0$, and for $t>0$ it appears to pick either local minimizer with equal probability, while never converging to the C-stationary point, and finds it impossible to pathfollow too close to $t=0$.

Active Set Method The active set method, started at $t=-1$, recognizes the presence of the doubly-active set and proceeds with two separate solution paths, one with fixed $x_1=0$ and the other with fixed $x_2=0$. The algorithm is able to follow the origin for $t\in [-1,0]$ and each path follows the separate local minimizers ((t, 0) and (0, t) for $t\in [0,1]$). The two branches of solutions are shown in Fig. 6.

Fig. 6

Illustration of the active set algorithm solutions for Example 3 

4.4 Example 4

This problem is original to this paper. It illustrates how the penalty method can fail to find local minimizers that are B-stationary but not S-stationary, whereas the active set method can do so. Note that this problem fails the MPCC-LICQ condition.

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{2}} &{} (x_1-1)^2+(x_2+t)^2 \\ \text {s.t.} &{} x_2-x_1\ge 0, \\ &{} 0\le x_1 \perp x_2\ge 0. \end{array} \end{aligned}$$

For all $t\in [0,1]$ the origin is the unique local minimizer. The stationarity conditions for the problem are,

$$\begin{aligned} \begin{array}{l} \sigma _1-\lambda =-2,\\ \sigma _2+\lambda =2t,\\ \lambda \ge 0. \end{array} \end{aligned}$$

Thus $x^*=(0,0)$ with both $(\lambda ^*,\sigma _1^*,\sigma _2^*)=(2,0,2t-2)$ and $(\lambda ^*,\sigma _1^*,\sigma _2^*)=(2t,2t-2,0)$ is M-stationary, and furthermore for the index $\{1\}$ NLP, the second set of multipliers is optimal as well as $(0,-2,2t)$, and for the index $\{2\}$ NLP the first set is optimal, and thus the origin is also B-stationary for all $t\in [0,1]$.

Penalty Method

The standalone penalty method is unable to find a satisfactory initial point. Initializing from one of the stationary points does not result in any successful pathfollowing step.

Active Set Method

The active set method is able to trace both index I NLPs for this set of problems, tracing the origin for $t=[0,1]$ along the multipliers $(0,-2,2t)$ for the index $\{2\}$ NLP and $(2,0,2t-2)$ for the index $\{1\}$ NLP. The primal and dual solutions traced are shown in Fig. 7.

Fig. 7

Illustration of the active set algorithm solutions for Example 5 

4.5 Example 5

This problem arises in the MacMPEC collection of MPCC problems (Leyffer 2000).

$$\begin{aligned} \begin{array}{rl} \min _{x\in {\mathbb {R}}^{3}} &{} x_1+x_2-(1-t) x_3 \\ \text {s.t.} &{} 4x_1-x_3\ge 0, \\ &{} 4x_2-x_3\ge 0,\\ &{} 0\le x_1 \perp x_2\ge 0. \end{array} \end{aligned}$$

The point $x^*=(0,0,0)$ is a B-stationary global minimizer for $t\in [0,\frac{3}{4}]$ and an S-stationary global minimizer for $t\in \left[ \frac{1}{2},1\right]$. The problem does not satisfy MPCC-LICQ, and two options of multipliers are $\lambda ^*=(0,1-t)$ with $\sigma ^*=(1,-3+4t)$ as well as $\lambda ^*=(1-t,0)$ and $\sigma ^*=(-3+4t,1)$, indicating that $x^*$ is optimal for both the index $\{1\}$ and index $\{2\}$ NLP, but is otherwise only W-stationary. There are other multipliers that are M-stationary, however, that are not found by either solver.

Penalty Method

The penalty method is unable to find a satisfactory initial point, i.e., a solution at $t=0$. Initializing from one of the stationary points does not result in any successful pathfollowing step, with the error that every predictor-corrector QP problem is non-convex (note that the problem itself is linear, but the penalty method adds a bilinear term to the objective). For $t\in [\frac{3}{4},1]$ the algorithm is able to pathfollow the solution $x^*=(0,0,0)$.

Active Set Method

The active set method pathfollows along the origin, doing so twice, once for each index in the double active set, for $t\in [0,1]$.

4.6 Example 6

We now consider a nonlinear example, to demonstrate the properties of the pathfollowing algorithms on a nonlinear problem.

$$\begin{aligned} \begin{array}{lrl} \min _{x\in {\mathbb {R}}^{2}} &{} e^{-x_1+x_2} &{} \\ \text {s.t.} &{} (x_1-2)^2+(x_2+1)^2 &{} \ge 6+2t, \\ &{} x_1 &{} \le 1,\\ &{} 0\le x_1 \perp x_2 &{} \ge 0. \end{array} \end{aligned}$$

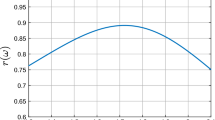
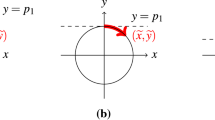
The constraints and solutions are shown in Fig. 8a. The point must lie outside of the circle and to the left of $x_1\le 1$, and the objective function seeks to increase $x_1$ and decrease $x_2$. As t changes from $-1$ to 1, the circle expands, modifying the feasible region to exclude any part of the $x_1$-axis. The solution is always S-stationary. We plot the result of the penalty algorithm applied to this problem in Fig. 8b and the active set based procedure performs similarly.

Fig. 8

Nonlinear Example

4.7 Flash calculation example

This section describes a classic chemical engineering problem appearing in, e.g., Skogestad (2008, Chapter 7). It models vapor/liquid equilibrium, wherein the Gibbs energy is minimized at some given temperature and pressure. In this case we consider pressure to be fixed and vary the temperature. Pathfollowing for a similar PMPCC was considered in Nakama et al. (2022), using a different approach that does not attempt to trace each branch.

During the operation of chemical processes, sometimes the thermodynamic phase in a system is not known a-priori. It may be liquid, gas, or a mixture of both, and each of these three cases must be described by a different set of equations. For example in natural gas liquification plants, some sections of the heat exchangers may be filled with liquid, which evaporates as the operating conditions change. A priori, it is not known what conditions will be present, and when optimizing the operation one can model the system using complementarity constraints. A large scale optimization model of a full process is out of the scope of this article, but we present a case as a proof of concept that the algorithms from this paper can be applied successfully to such a system.

We consider an exogenous feed stream F that is separated into vapor V and liquid L product, of three different compounds $\{y_i\}$ and $\{x_i\}$, respectively. The relative split of F to V and L as well as the quantity of each of the three compounds in each phase are considered variables we must solve for. They must satisfy $\sum _i x_i=1$ and $\sum _i y_i=1$, and $x_iL+y_iV=z_iF$ for the total given quantities $\{z_i\}$. Using Raoult’s law, we have that,

$$\begin{aligned} y_i/x_i = K_i = p_i^{sat}(T)/p \end{aligned}$$

where $p_i^{sat}$ is a nonlinear function of temperature,

$$\begin{aligned} p_i^{sat} = 10^{A_i-\frac{B_i}{T+C_i}}. \end{aligned}$$

where $A_i$, $B_i$ and $C_i$ are physical constants.

The fraction $a\in [0,1]=V/F$ of gas is determined by the Rachford-Rice equation, however, with a caveat. Specifically, attempt to solve the following equation for $a_t$:

$$\begin{aligned} \sum _i \frac{z_i (K_i-1)}{1+a_t(K_i-1)} = 0. \end{aligned}$$

Now, the bubble point temperature is $T_b=382.64$ and the dew point $T_d=393.30$, and thus for $T<T_b$, the solution for $a_t$ will be negative, but clearly the ratio a cannot be negative, instead it implies that every substance must be a liquid, i.e., $a=0$ and similarly for $T>T_b$, the solution for $a_t$ will be greater than one, but clearly every substance must be gas, i.e., $a=1$.

Thus, we need to, after solving the Rachford-Rice equation for $a_t$, obtain the value of a by $\max (0,\min (1,a_t))$, a nonsmooth operation problematic for gradient-based optimization solvers. To avoid this, the true ratio of gas a will be determined by the complementarity system,

$$\begin{aligned} \begin{array}{l} a-s_v+s_l-a_t=0,\\ 0\le s_l \perp L \ge 0,\\ 0 \le s_v \perp V \ge 0, \\ 0\le a\le 1, \end{array} \end{aligned}$$

where we introduce slack variables $s_l$ and $s_v$ complementary with L and V (i.e., $s_l$ is zero if L is positive, and L is zero if $s_l$ is positive) to compute a from $a_t$ by solving the first equation.

The resulting problem is a nonlinear complementarity system involving the 13 variables V, L, $\{x_i\}_{i=1,2,3}$, $\{y_i\}_{i=1,2,3}$, a, $a_t$, T, $s_v$ and $s_l$. In addition, the nonlinear equations relating temperature to the component distributions are ill-conditioned. Thus, to define the MPCC, we,

• lift Raoult’s law and the Rachford-Rice equation, making $K_i$, $\frac{1}{(K_i-1)}$ (which we write as $k_i$), $\log p_i^{sat}$ variables, alongside V, L, $x_i$, $y_i$, a, $a_t$, T, $s_v$ and $s_l$ for a total of $n=22$.

• We consider T as both a parameter and a variable, by defining an additional equality constraint $T=T_{\text {target}}$, and we trace the solution for $T_{\text {target}}=380$ to 400.

• If we were to add the constraint defining the proportial of gas as $a=\frac{V}{F}$, then all of these equations define a nonlinear complementarity problem (NCP). However, when taking into account active constraints at the solutions of the NCP, the entire system does not satisfy MPCC-LICQ, thus we do not make the vapor fraction $a=V/F$ a hard constraint, but define our objective to be,

  $$\begin{aligned} f(a,V) = \frac{1}{2}(aF-V)^2 \end{aligned}$$

and thus define an MPCC.

In summary, the MPCC we solve is defined as follows,

$$\begin{aligned} \begin{array}{rl} \min \limits _{V,L,\{x_i\},\{y_i\},a,a_t,T,s_v,s_l} &{} \frac{1}{2}(aF-V)^2 \\ \text {s.t. } &{} k_i = \frac{1}{(K_i-1)}, \, i=1,2,3\\ &{} q_i = \log p_i^{sat}, \, i=1,2,3 \\ &{} q_i = \log (10) (A_i-\frac{B_i}{T+C_i}), \, i=1,2,3\\ &{} K_i = p_i^{sat}/p, \, i=1,2,3\\ &{} \sum _i \frac{z_i }{k_i+a_t} = 0, \\ &{} a-s_v+s_l-a_t=0,\\ &{} 0\le s_l \perp L \ge 0,\\ &{} 0 \le s_v \perp V \ge 0, \\ &{} 0\le a\le 1. \end{array} \end{aligned}$$

(20)

The constants we use in the experiments are given in Table 1.

Table 1 Constants used in the flash calculation

4.7.1 Penalty method

The penalty method accurately tracks the solution, achieving the liquid–gas balance as expected.

Every solution is a S-stationary point, and the objective function is strictly convex, which means that for any point satisfying the first order necessary conditions for optimality, the second order sufficient conditions also hold. Thus all the necessary conditions for the convergence of the penalty method for solving the MPCC and tracing a parametric curve are satisfied.

The solutions for all of the variables are given in Fig. 9. As expected, the variables X and $s_x$, as well as Y and $s_y$ are complementary, with the slacks being positive when their corresponding complementary variables are zero, and zero when they are inactive. The proportion of gas a corresponds to V. The variables $k_i$ (representing $\frac{1}{(K_i-1)}$) appear to vary the most nonlinearly, resembling an exponential function with respect to the parameter, which is equivalent to the temperature.

Note that the required step-size for pathfollowing is generally fairly small, and gets smaller during active set changes.

Fig. 9

Primal solutions for the Liquid-Phase flow problem 

4.7.2 Active set method

The active set method also traces the set of solutions. At each active set change, a double-active set was recognized. The previous branch was eventually cut, and the other branch initiated. Although the method converged for this problem, it took considerable tuning with regards to tolerances for the double-active constraints, on the one hand, and the required tolerance for checking the other index I NLPs, while tracing a branch, on the other. In particular, numerically, a double-active constraint will stay active for a few homotopy steps before being seen as no longer bi-active, and meanwhile the steps must still be accepted as valid for all index I NLPs.

4.8 Discussion

The two phase flow example illustrates the general efficacy of the two Algorithms on a real problem. The simpler problems indicate some subtle distinctions of the two methods. In particular, the penalty method is easier to tune and implement, traces S-stationary but not B-stationary points, and also can trace C-stationary points, which may not be desired by the user. By contrast, the active set method is able to trace B-stationary points and does not trace spurious stationary points. However, since it must trace every combination of selections of doubly-active constraints, it is generally slower and more difficult to tune for problems with many complementarity constraints and suspected bi-activity.

5 Conclusion

In this paper we studied the parametric mathematical program with complementarity constraints, presenting the first investigation of algorithmically pathfollowing these programs. We formulated two algorithms, one based on the penalty method for standalone MPCCs, and one based on following the possible branches of NLPs suggested by double-active constraints and the B-stationarity condition. We studied their performance on a set of examples constructed to distinguish the types of parametric properties there could be, illustrating the performance on this set of problems, as well as a “real-world” problem associated with chemical process engineering.

Pathfollowing parametric optimization problems can be important in a number of applications, including nonlinear model predictive control, as well as assessing the practical sensitivity of a solution with respect to a parameter in industrial design. We intend that this work presents a solid first step in the development of literature and algorithms for the pathfollowing of parametric MPCCs. In general, the tradeoffs associated with seeking tighter versus looser notions of stationarity inherent to standalone methods for solving MPCCs carries over to pathfollowing parametric ones, and we expect this to enrich further understanding of MPCCs in general and algorithms for pathfollowing parametric MPCCs in particular.