1 Introduction

The equations describing the behaviour of materials with elastic properties are widely studied in mechanics. Especially, the simplified case of linear elasticity is of interest. The system of equations considered in this article describes the behaviour of an elastic material subject to surface loads. Our material is considered to be periodically heterogeneous. Specifically, on a microscopic scale, one substance envelops another substance in a periodically repeating pattern. These kind of materials can be produced amongst other techniques by additive manufacturing and find applications in many fields, for example as light weight structures in aeronautics or as synthetic bone material in medical applications, see e.g. Hopkinson et al. (2006), Wang et al. (2016) and the references therein.

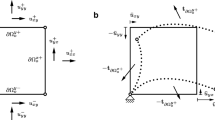
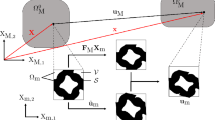
We aim in this article at optimizing the shapes in the periodically repeating pattern on the microscopic scale. Therefore, an objective function depending on the shapes in the pattern is defined. It describes a desired macroscopic property, which is achieved when the function’s minimal solution is found. In order to solve this minimization problem, methods of shape sensitivity analysis are employed. Thus, we are able to compute Hadamard’s shape gradient, which allows for the application of gradient based optimization methods to find the optimal shape, compare with Delfour and Zolesio (2001), Murat and Simon (1976), Pironneau (1984), and Sokolowski and Zolesio (1992) for example. In Fig. 1, a schematic of an optimal design problem is displayed. It aims at finding a microstructure of the material that minimizes the compliance of a pillar with a force acting on top of it.

Fig. 1
figure 1

The optimized microstructure of the material minimizes the compliance of the pillar. It deforms less under the force F which acts on its top

Full size image

Note that the optimal design of periodic structures has already been considered in many works, see Adachi et al. (2006), Ferrer et al. (2018), Hollister et al. (2002), Lin et al. (2004), Luo et al. (2017), Sigmund (1995), Wang and Kang (2019), and Wormser et al. (2017) for some of the respective results and applications. The methodology used therein is mainly based on the forward simulation of the material properties of a given microstructure. In contrast, in Allaire et al. (2019), Barbarosie (2003), Dambrine and Harbrecht (2020), Faure et al. (2017), Geoffroy-Donders et al. (2020), Haslinger and Dvořák (1995), Hübner et al. (2019), Wang et al. (2004), shape sensitivity analysis has been used. The shape derivative of the coefficients of the homogenized tensor, expressed as volume integrals, have been computed in Allaire et al. (2019), Barbarosie (2003) in case of piecewise constant material properties. Note that these shape derivatives have also been derived in the context of a level set representation of the inclusion in Nika and Constantinescu (2019). The novelty of this work is the use of Reynolds transport theorem to compute the shape derivative. Especially, we characterize the local shape derivative and allow for locally varying material coefficients, which was not done before. Note that the local shape derivative is an important tool in shape uncertainty quantification, compare Harbrecht and Li (2013) or Harbrecht et al. (2008) for example. Therefore, we follow the ideas and computations presented in Dambrine and Harbrecht (2020) and Harbrecht et al. (2022) for an elliptic diffusion problem. We emphasize that the numerical results presented in this article are in two spatial dimensions. They serve as a proof of concept and foundation for future works, where we will consider the optimization of three-dimensional problems.

This article is structured as follows. In Sect. 2, we introduce the system of equations and objects we treat in this article. Especially, we briefly discuss the notation of the computations with tensors. Moreover, homogenization through a multiscale ansatz is performed. The result of the homogenization procedure is a system of equations describing a homogeneous approximation to our material. This new system contains the homogenized elasticity tensor, also called the effective elasticity tensor. Next, the objective functions under consideration are introduced. From then on, we consider a composite material, which consists of two intertwined materials with different elastic properties.

In Sect. 3, the shape derivative of the coefficients of the effective tensor is computed. To this end, we first compute the local shape derivative of the cell functions, then the shape derivative of the material coefficients, and finally the shape derivative of the least squares and compliance functional under consideration. These steps are repeated for the special case of a partly hollow material. In the two-dimensional setting, this corresponds to the special case of a perforated plate, while in the three-dimensional setting, we arrive at a scaffold structure, a partly hollow three-dimensional structure.

The implementation in the two-dimensional setting is presented in Sect. 4. We use a parametrization by a finite Fourier series to represent the sought interface between the two materials in the microcell. Then, we apply parametric finite elements to discretize the state equation under consideration. Finite elements are also used in the macroscopic domain. By means of finite differences we verify our theoretical findings and the implementation.

The following two sections are dedicated to numerical experiments. In Sect. 5, we optimize for various material parameters the shape of the interface between the two given materials. Especially, we consider nonhomogeneous material parameters, different initial guesses, and also the situation where there is a void instead of an interior material. In Sect. 6, the compliance of a porous material is minimized by finding an optimal void within its microstructure. Finally, in Sect. 7, we state concluding remarks.

2 Notation, homogenization and objective

2.1 Linear elasticity system

Consider a fixed, bounded domain \(\Omega \subset {\mathbb {R}}^n\), which is the reference configuration of an elastic body, subject to a body force \(\varvec{f}\). The structure \(\Omega\) is clamped on \(\Gamma _D\subset \partial \Omega\) and subject to surface loads \(\varvec{g}\) on \(\Gamma _N\subset \partial \Omega\). Here, \(\Gamma _D\) and \(\Gamma _N\) are assumed to be fixed such that \(\Gamma _D\cap \Gamma _N=\emptyset\). The displacement \(\varvec{u}\) is then the solution of the system

$$\begin{aligned} \left\{ \begin{array}{ll} -{\text {div}}(\varvec{\sigma }\big (\varvec{u})\big ) = \varvec{f} &{}\quad \text {in } \Omega , \\ \varvec{u} = \varvec{0} &{}\quad \text {on } \Gamma _D, \\ \varvec{\sigma }(\varvec{u})\varvec{n} = \varvec{g}&{}\quad \text {on } \Gamma _N, \\ \varvec{\sigma }(\varvec{u})\varvec{n} = \varvec{0}&{}\quad \text {on } \Gamma = \partial \Omega {\setminus } \left( \Gamma _D\cup \Gamma _N\right) , \end{array}\right. \end{aligned}$$
(2.1)

where the Cauchy stress tensor for the displacement \(\varvec{u}\) is defined as

$$\begin{aligned} \varvec{\sigma }(\varvec{u}) {:}{=}\lambda {\text {tr}} \left( \nabla \varvec{u} \right) id + \mu \left( \nabla \varvec{u} + \nabla \varvec{u}^\intercal \right) \end{aligned}$$
(2.2)

with the two Lamé constants \(\lambda >0\) and \(\mu >0\) and the identity matrix id. This system of equations corresponds to the system introduced in Braess (2001).

Next, we shall introduce the fourth order elasticity tensor, which allows to express the Cauchy stress tensor in terms of a tensor and of the displacement. To this end, we first introduce some notation for tensors.

2.2 Tensor notation

The tensor notation applied in this article follows in wide parts Itskov (2007). Let \(n\in {\mathbb {N}}\), a, b, c, d be column vectors in \({\mathbb {R}}^n\), B, C, D matrices in \({\mathbb {R}}^{n\times n}\) and id the respective identity matrix. The Frobenius product of two matrices is defined as

$$\begin{aligned} B : C = \sum _{i,j=1}^{n} b_{ij} c_{ij}. \end{aligned}$$

The tensor product for vectors is defined by the relation

$$\begin{aligned} (a \otimes b) c = (b^\intercal c) a. \end{aligned}$$

Whereas, in case of matrices, we have the two tensor products

$$\begin{aligned} (B \otimes C) : D = B D C \quad \text {and} \quad (B \odot C) : D = B ( C : D ). \end{aligned}$$

There hold the following two relations for matrices which are given by tensor products of vectors:

$$\begin{aligned} (a\otimes b)\otimes (c\otimes d) = a\otimes b\otimes c\otimes d \quad \text {and}\quad (a\otimes b)\odot (c\otimes d) = a\otimes c\otimes d\otimes b. \end{aligned}$$

Moreover, we use the classical transposition operation for matrices, while for fourth order tensors there is the transposition operation

$$\begin{aligned} (a\otimes b\otimes c\otimes d)^\intercal = a\otimes c\otimes b\otimes d. \end{aligned}$$

The Frobenius product of a fourth-order tensor \(\varvec{A}\) and a matrix B is computed as

$$\begin{aligned} \varvec{A} : B&= \left( \sum _{i,j,k,l=1}^n a_{ijkl} (e_i \otimes e_j \otimes e_k \otimes e_l) \right) : \left( \sum _{j,k=1}^n b_{jk} (e_j \otimes e_k) \right) \\&= \sum _{i,j,k,l=1}^n a_{ijkl} b_{jk} (e_i \otimes e_l), \end{aligned}$$

where \(e_i\), \(i=1,\ldots ,n\), denotes the canonical basis of vectors.

With the Lamé constants \(\lambda\) and \(\mu\), the fourth-order elasticity tensor \(\varvec{A}\), satisfying the relation \(\varvec{A}: \nabla \varvec{u} = \varvec{\sigma }(\varvec{u})\), can be expressed as

$$\begin{aligned} \varvec{A} = \lambda (id\odot id) + \mu \big ((id\otimes id) + (id\otimes id)^\intercal \big ). \end{aligned}$$
(2.3)

Especially, with the tensor computation rules above, we find

$$\begin{aligned} \varvec{A} : B = \lambda {\text {tr}} \left( B \right) id + \mu \left( B + B^\intercal \right) , \end{aligned}$$

which for \(B{:}{=}\nabla u\) corresponds to the Cauchy stress tensor in (2.2).

Remark 1

In some works on linear elasticity, for instance Braess (2001) and Geoffroy-Donders (2018), the elasticity tensor is defined differently. The notation from Itskov (2007) was chosen in this article since it contains all the objects used in the following pages in a single work. Furthermore, the super-symmetric identity tensor which is introduced in Itskov (2007) allows to combine the elasticity and strain tensor, often denoted by \(\varvec{A}\) and \(\varvec{\epsilon }\), respectively, resulting in the elasticity tensor expression (2.3).

Instead of defining the elasticity tensor by means of the Lamé constants \(\lambda\) and \(\mu\), we can define it through the elasticity modulus \(E>0\) and the Poisson ratio \(0<\nu <1/2\). The elasticity modulus is proportional to the resistance a material opposes to its deformation. The Poisson ratio is a description of the influence of stresses on displacements perpendicular to the specific direction of loading. For soft materials such as rubber it is near 0.5 and for typical solids around 0.2–0.3. The Lamé constants are derived from these two numbers by the formulas

$$\begin{aligned} \lambda = \frac{E\nu }{(1+\nu )(1-2\nu )} \quad \text {and} \quad \mu = \frac{E}{2(1+\nu )}. \end{aligned}$$
(2.4)

A fourth-order tensor \(\varvec{A}\) is called to be uniformly elliptic if there exists a constant \(\alpha >0\) such that

$$\begin{aligned} (\varvec{A} : B):B \ge \alpha B : B\quad \text {for all }B\in {\mathbb {R}}^{n\times n}. \end{aligned}$$
(2.5)

This property is always satisfied for the elasticity tensor \(\varvec{A}\) defined by E and \(\nu\). Thus, we denote the admissible elasticity tensor by the image of the function

$$\begin{aligned} {\mathcal {M}}: (0,\infty )\times (0,1/2)\rightarrow {\mathbb {R}}^{n^4}, \ (E,\nu ) \mapsto \varvec{A}\text { such that }(2.3) \text { and } (2.5) \text { are satisfied}. \end{aligned}$$

2.3 The multiscale ansatz and composite materials

The homogenization procedure considered in this article follows closely Allaire (2002). Homogenization is concerned with the situation where the elasticity tensor \(\varvec{A}\) is oscillatory. To this end, we denote the unit cell by \(Y=[0,1]^n\) and write \(\varvec{y}{:}{=}\varvec{x}/\varepsilon\) for any \(\varvec{x}\in \Omega\) and \(\varepsilon >0\). We assume \(\varvec{A}(\varvec{y})\) to be Y-periodic, satisfying \(\varvec{A}(\varvec{y})={\mathcal {M}}\big (E(\varvec{y}), \nu (\varvec{y})\big )\) for all \(\varvec{y}\in Y\) with \(E(\varvec{y})>0\) and \(0<\nu (\varvec{y}) <1/2\). Then, in order to approximate the displacement in (2.1), one makes the multiscale ansatz

$$\begin{aligned} \varvec{u}_{\epsilon }(\varvec{x}) {:}{=}\varvec{u}_0\bigg (\varvec{x},\frac{\varvec{x}}{\epsilon }\bigg ) + \epsilon \varvec{u}_1\bigg (\varvec{x},\frac{\varvec{x}}{\epsilon }\bigg ) + \epsilon ^2\varvec{u}_2\bigg (\varvec{x},\frac{\varvec{x}}{\epsilon }\bigg ) +\cdots , \end{aligned}$$
(2.6)

where \(\varvec{u}_j(\varvec{x},\varvec{y})\) are Y-periodic functions in \(\varvec{y}\) for all \(j=0,1,\dots\). Note that this ansatz does not take into account the boundary conditions of (2.1) and extra terms would be needed to capture boundary layers, see e.g. Cioranescu and Saint Jean Paulin (1999).

Following Allaire (2002), this ansatz shows that the solution \(\varvec{u}_{\epsilon }\) of the equation

$$\begin{aligned} -{\text {div}}\left( \varvec{A}\left( \frac{\varvec{x}}{\epsilon }\right) : \nabla \varvec{u}_{\epsilon }(\varvec{x}) \right) = \varvec{f}(\varvec{x}) \end{aligned}$$

can be approximated for \(0<\epsilon \ll 1\) by the solution \(\varvec{u}\) of the homogenized equation

$$\begin{aligned} -{\text {div}}\left( \varvec{A}^{*} : \nabla \varvec{u}(\varvec{x}) \right) = \varvec{f}(\varvec{x}). \end{aligned}$$

To characterize the effective tensor \(\varvec{A}^{*}\), we introduce the cell problems

$$\begin{aligned} {\text {div}}\Big (\varvec{A}(\varvec{y}) : \big (e_{ij} + \nabla \varvec{w}_{ij}(\varvec{y}) \big )\Big )=\varvec{0}, \quad \varvec{w}_{ij}\in [H_{{\text {per}}}^1(Y)]^n, \quad ( \varvec{w}_{ij} , \mathbbm {1} )_{[L^2(Y)]^n} = 0, \end{aligned}$$
(2.7)

where \(e_{ij} {:}{=}e_i\otimes e_j\), \(i,j=1,\ldots ,n\), denotes the basis of matrices and

$$\begin{aligned}{}[H_{{\text {per}}}^1(Y)]^n&{:}{=}\big \lbrace \varvec{w}=(w_1,\ldots ,w_n):\ {w_i\in H_{loc}^1({\mathbb {R}}^n)} \text { such that}\\ w_i(\varvec{y})&= w_i(\varvec{y}+ke_j) \text { for all } \mathbf{y}\in Y \text { and } k\in {\mathbb {Z}}, i,j=1,\ldots ,n \big \rbrace \end{aligned}$$

is the space of Y-perioric \(H^1\)-functions, equipped with the norm \(\Vert \cdot \Vert _{H^1(Y)}\). Then, for all \(i,j,k,l=1,\ldots ,n\), the entries of the effective tensor are given by

$$\begin{aligned} a_{ijkl}^{*}( \omega ) = \int _Y \left( \varvec{A}(\varvec{y}) : \left( e_{il} + \nabla \varvec{w}_{il}(\varvec{y}) \right) \right) : \left( e_{jk} + \nabla \varvec{w}_{jk}(\varvec{y}) \right) \,\mathrm {d}\varvec{y}. \end{aligned}$$
(2.8)

A composite material consists of two materials with different elastic properties, see Fig. 1 for an illustration. We model such a material by defining the elastic tensor

$$\begin{aligned} \varvec{A}(\varvec{y}) = \varvec{A}_1(\varvec{y}) + \big (\varvec{A}_2(\varvec{y}) - \varvec{A}_1(\varvec{y})\big ) \mathbbm {1}_{\omega }(\varvec{y}), \end{aligned}$$
(2.9)

where \(\omega\) is an open and connected subset of Y. Under the assumption that \(\varvec{A}_1(\varvec{y}) ={\mathcal {M}}\big (E_1(\varvec{y}),\nu _1(\varvec{y})\big )\) and \(\varvec{A}_2(\varvec{y}) ={\mathcal {M}}\big (E_2(\varvec{y}),\nu _2(\varvec{y})\big )\) for all \(\varvec{y}\in Y\) and \(E_1,E_2,\nu _1,\nu _2\in C^1(Y)\), this is a piecewise smooth, fourth-order elasticity tensor for all choices of \(\omega\).

The normal vector \(\varvec{n}\) on \(\partial \omega\) indicates the direction from the interior of \(\omega\) to the exterior \(Y{\setminus }{\overline{\omega }}\). The jump of a function \(\varvec{f}\) through the interface \(\partial \omega\) at a point \(\varvec{y}\in \partial \omega\) is thus given by

$$\begin{aligned} \left[ \varvec{f}(\varvec{y}) \right] = \varvec{f}^+(\varvec{y})-\varvec{f}^-(\varvec{y}) {:}{=}\lim _{t\rightarrow 0^{+}} \varvec{f}\big (\varvec{y}+t\varvec{n}(\varvec{y})\big ) -\lim _{t\rightarrow 0^{-}} \varvec{f}\big (\varvec{y}+t\varvec{n}(\varvec{y})\big ). \end{aligned}$$

For composite materials, the cell problem (2.7) is augmented with the two transmission conditions on the interface \(\partial \omega\)

$$\begin{aligned} \left[ \varvec{w}_{ij}(\varvec{y}) \right] = \varvec{0} \quad \text { and } \quad \left[ \varvec{A}(\varvec{y}) : \big ( e_{ij}+\nabla \varvec{w}_{ij}(\varvec{y}) \big ) \right] \varvec{n}(\varvec{y}) = \varvec{0} \quad \text { for } \varvec{y} \in \partial \omega . \end{aligned}$$
(2.10)

With these conditions, the variational formulation of the cell problem (2.7) for \(\varvec{v}\in [H_{{\text {per}}}^1(Y)]^n\) becomes

$$\begin{aligned} \int _Y \left( \varvec{A}(\varvec{y}) :(e_{ij} + \nabla \varvec{w}_{ij} ) \right) :\nabla \varvec{v} \,\mathrm {d}\varvec{y} = \varvec{0}. \end{aligned}$$
(2.11)

Formula (2.11) together with (2.8) shows the dependency of the homogenized elasticity tensor \(\varvec{A}^{*}(\omega )\) on the choice of the interface \(\omega\). Also, \(\varvec{A}^{*}(\omega )\) inherits the symmetry properties and the uniform ellipticity from the elasticity tensor \(\varvec{A}(\varvec{y})\). Therefore, the homogenized system on \(\Omega\), written in the form

$$\begin{aligned} \left\{ \begin{array}{ll} -{\text {div}}\big ( \varvec{\sigma }^{*}( \omega , \varvec{u} ) \big ) = \varvec{f}&{}\quad \text {in } \Omega , \\ \varvec{u} = \varvec{0}&{}\quad \text {on } \Gamma _D, \\ \varvec{\sigma }^{*}\big ( \omega , \varvec{u} \big )\varvec{n} = \varvec{g}&{}\quad \text {on } \Gamma _N, \\ \varvec{\sigma }^{*}\big ( \omega , \varvec{u} \big )\varvec{n} = \varvec{0}&{}\quad \text {on } \Gamma = \partial \Omega {\setminus } \left( \Gamma _D\cup \Gamma _N\right) , \end{array}\right. \end{aligned}$$
(2.12)

with the (effective) Cauchy stress tensor is \(\varvec{\sigma }^{*} (\omega ,\varvec{u}){:}{=}\varvec{A}^{*}(\omega ):\nabla \varvec{u}\), has a unique solution for all sufficiently smooth subsets \(\omega\).

2.4 Goal of optimization

In this article, we consider two objective functions. For a given material, we aim to minimize one of the two objective functions, which depend on the inclusions present within the repeating pattern in the microstructure of those materials.

Firstly, we ask for the shape \(\omega \subset Y\), such that the least squares matching

$$\begin{aligned} J_{LS}(\omega ) {:}{=}\frac{1}{2} \Vert {\varvec{B}} - \varvec{A}^{*}(\omega ) \Vert _F^2 = \frac{1}{2} \sum _{i,j,k,l=1}^n \left( b_{ijkl} - a_{ijkl}^{*}(\omega ) \right) ^2 \end{aligned}$$
(2.13)

between the effective tensor \(\varvec{A}^{*}(\omega )\) and a desired elasticity tensor \(\varvec{B}\in {\mathbb {R}}^{n^4}\) with coefficients \(b_{ijkl}\) is minimized with respect to the Frobenius norm \(\Vert \cdot \Vert _F\). Note that not all desired elasticity tensors \(\varvec{B}\) can be attained, since they might not satisfy the Hashin–Shtrikman bounds, see Hashin and Shtrikman (1963).

Secondly, we consider an elastic body described by \(\Omega\). In the microstructure of \(\Omega\), we ask for the shape \(\omega \subset Y\), which minimizes the compliance functional

$$\begin{aligned} C(\omega )&= \int _\Omega \left( \varvec{A}^{*}( \omega ) : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} = \int _\Omega \langle \varvec{f} , \varvec{u} \rangle \,\mathrm {d}\varvec{x} + \int _{\Gamma _N} \langle \varvec{g} , \varvec{u} \rangle \,\mathrm {d}s, \end{aligned}$$
(2.14)

where \(\varvec{f}\) and \(\varvec{g}\) are forces given in (2.12).

In a porous material, the compliance is minimized by simply filling the holes. In order to exclude this trivial solution, we impose a volume constraint \(|\omega | = \omega _0\) on the void. To this end, the objective function considered in order to minimize the compliance of the elastic body \(\Omega\) under the given volume constraint is

$$\begin{aligned} J_C(\omega ,\lambda ){:}{=}\int _\Omega \left( \varvec{A}^{*}( \omega ) : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} + \lambda \left( |\omega | - \omega _0 \right) + \frac{\alpha }{2} \left( |\omega | - \omega _0 \right) ^2, \end{aligned}$$
(2.15)

where \(\lambda \in {\mathbb {R}}\) is the Langrange multiplier to be maximized and \(\alpha \in {\mathbb {R}}^+\) is an appropriately chosen constant. This augmented Lagrangian functional allows to enforce the volume constraint without taking \(\alpha \rightarrow \infty\) throughout the optimization process. Only the Lagrange multiplier \(\lambda\) is updated by

$$\begin{aligned} \lambda _{k+1} = \lambda _k + \alpha (|\omega | - \omega _0), \quad k=0,1,\ldots , \end{aligned}$$
(2.16)

whenever \(J_C(\omega ,\lambda )\) has been minimized with respect to \(\omega\), cf. Nocedal and Wright (2006).

In order to optimize the objective functions above by a gradient based optimization method, we shall compute the shape derivative of \(J_{LS}(\omega )\) and \(J_C(\omega,\lambda )\). We begin by finding an expression for the shape derivative of the coefficients of the effective tensor \(\varvec{A}^{*}( \omega )\).

3 Shape derivative of the effective tensor

3.1 Local shape derivative

We introduce a vector field \(\varvec{h}:Y \rightarrow Y\) that vanishes on the boundary \(\partial Y\) and consider the perturbation of identity operator \(T_t {:}{=}\varvec{I} + t\varvec{h}\). \(T_t\) is a diffeomorphism for t small enough, which preserves Y. We define the function

$$\begin{aligned} \varvec{\phi }_{ij}(\varvec{y}) {:}{=}\varvec{w}_{ij}(\varvec{y}) + \varvec{y}_{ij} \quad \text {for}\ i,j=1,\ldots ,n, \end{aligned}$$

where \(\varvec{w}_{ij}\) is the unique solution of the cell problem (2.7) and \(\varvec{y}_{ij}\) is a column vector with entries 0 except in the i-th row the entry \(y_j\). Then, \(\nabla \varvec{y}_{ij}=e_{ij}\) and the cell problem (2.7) becomes

$$\begin{aligned} {\text {div}}( \varvec{A} : \nabla \varvec{\phi }_{ij} )=\varvec{0} \quad \text {for}\ i,j=1,\ldots ,n. \end{aligned}$$
(3.1)

For a function \(\varvec{v} \in [H_{{\text {per}}}^1(Y)]^n\), we compute the gradient of \(\varvec{v}\) by \(\nabla \varvec{v} = (\partial _j v_i)_{1\le i,j \le n}\) and define the normal component of the gradient as

$$\begin{aligned} \nabla _{\varvec{n}}\varvec{v} {:}{=}\nabla \varvec{v}{\varvec{n}}{\varvec{n}}^\intercal = (\partial _{\varvec{n}}\varvec{v}){\varvec{n}}^\intercal . \end{aligned}$$

Moreover, it follows that the jump of the function \(\varvec{v}\) through \(\partial \omega\) satisfies

$$\begin{aligned} \left[ \nabla \varvec{v} \right] = \left[ \nabla _{\varvec{n}} \varvec{v} \right] , \end{aligned}$$
(3.2)

since functions in \([H_{{\text {per}}}^1(Y)]^n\) satisfy \([\varvec{v}]=\varvec{0}\) almost everywhere on \(\partial \omega\).

We present next the following theorem, which specifies the system of equations the local shape derivative \(\delta \varvec{\phi }_{ij}\) satisfies on Y. As the local shape derivative has a jump at \(\partial \omega\), we introduce the broken \(H^1\)-space in accordance with

$$\begin{aligned} {\mathcal {X}}{:}{=}\big \{f\in L^2(Y): f|_{Y{\setminus }{\overline{\omega }}} \in H_{\text {per}}^1(Y{\setminus }{\overline{\omega }})\ \text {and}\ f|_{\omega } \in H^1(\omega )\big \}. \end{aligned}$$

Theorem 1

(Shape derivative of the cell problem) The shape derivative \(\delta \varvec{\phi }_{ij}\) in \({\mathcal {X}}\) of the function \(\varvec{\phi }_{ij} = \varvec{w}_{ij} + \varvec{y}_{ij}\) is the solution in Y of the transmission problem

$$\begin{aligned} {\text {div}}\left( \varvec{A} : \nabla \delta \varvec{\phi }_{ij} \right)&= \varvec{0}&\text { in } \omega \cup Y {\setminus } {\overline{\omega }},\end{aligned}$$
(3.3a)
$$\begin{aligned}&[\Delta \Phi_{ij}]= - \langle \varvec{h} , \varvec{n} \rangle \left[ \partial _{\varvec{n}} \varvec{\phi }_{ij}\right]&\text { on } \partial \omega ,\end{aligned}$$
(3.3b)
$$\begin{aligned} \left[ \left( \varvec{A} : \nabla \delta \varvec{\phi }_{ij} \right) \varvec{n} \right]&= \left[ {\text {div}}_{\varvec{\tau }} \left( \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \right) \right]&\text { on } \partial \omega . \end{aligned}$$
(3.3c)

Here, \(\nabla _{\varvec{\tau }}\varvec{\phi }_{ij}{:}{=}\nabla \varvec{\phi }_{ij} - \nabla _{\varvec{n}}\varvec{\phi }_{ij} = \nabla \varvec{\phi }_{ij}(\varvec{I}-\varvec{n}\varvec{n}^\intercal )\) is the surface gradient of the function \(\varvec{\phi }_{ij}\) and, given a matrix function \(B=(b_1,\ldots ,b_n)^\intercal \in C^1(\partial \omega ,{\mathbb {R}}^{n\times n})\), the surface divergence is \({\text {div}}_{\varvec{\tau }} (B) {:}{=}\big (\mathrm {tr} (\nabla _{\varvec{\tau }} b_1),\ldots ,\mathrm {tr}(\nabla _{\varvec{\tau }} b_n)\big )^\intercal\).

Proof

The proof is carried out in the usual way, compare with Dambrine and Harbrecht (2020). We prove that the material derivative exists, characterize it, and finally express the shape derivative.

1. Computation of the material derivative. Let \(\varvec{\phi }_{ij}^t(\varvec{y})\) be the unique solution of the cell problem (2.7) on the perturbed domain \(Y_t{:}{=}\lbrace y + t \varvec{h}(\varvec{y}) \big | y\in Y \rbrace\) and set

$$\begin{aligned} \varvec{A}_t (\varvec{y}) {:}{=}\varvec{A}_1\big ( T_t(\varvec{y}) \big ) + \Big (\varvec{A}_2\left( T_t(\varvec{y}) \right) - \varvec{A}_1\big ( T_t(\varvec{y}) \big )\Big ) \mathbbm {1}_{\omega }(\varvec{y}). \end{aligned}$$

Then, the transported function \(\tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) {:}{=}\varvec{\phi }_{ij}^t\big (T_t(\varvec{y})\big )\), satisfies the variational equation

$$\begin{aligned} \begin{aligned} \int _Y \bigg ( \varvec{A}_t (\varvec{y}) :&\left( \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y})\left( \nabla T_t(\varvec{y}) \right) ^{-1}\right) \bigg ) \\&\qquad : \left( \nabla \varvec{v}(\varvec{y})\left( \nabla T_t(\varvec{y}) \right) ^{-1}\right) \det \! \left( \nabla T_t(\varvec{y}) \right) \mathrm {d}\varvec{y} = 0 \end{aligned} \end{aligned}$$
(3.4)

for all \(\varvec{v}\in [H_{{\text {per}}}^1(Y)]^n\). Using the property \(A:(BC)=(AC^\intercal ):B\) of the Frobenius product for square matrices A, B, C and subtracting the Eq. (2.11) from the Eq. (3.4) above, we find for any \(t>0\)

$$\begin{aligned} \int _Y \bigg \lbrace \det \! \left( \nabla T_t(\varvec{y}) \right) \bigg ( \varvec{A}_t (\varvec{y}) :&\left( \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y})\left( \nabla T_t(\varvec{y}) \right) ^{-1} \right) \bigg )\left( \nabla T_t(\varvec{y}) \right) ^{-\intercal } \\&\quad - \left( \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij}(\varvec{y}) \right) \bigg \rbrace : \nabla \varvec{v}(\varvec{y}) \,\mathrm {d}\varvec{y} = 0 \end{aligned}$$

for all \(\varvec{v}\in [H_{{\text {per}}}^1(Y)]^n\). Now, to this equation we add and subtract equal terms in order to obtain the equivalent equation

$$\begin{aligned} \begin{aligned} \int _Y \bigg \lbrace&\bigg ( \tilde{\varvec{A}}(t,\varvec{y}) : \left( \left( \nabla T_t(\varvec{y}) \right) ^{-1} \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) \right) \bigg ) \left( \left( \nabla T_t(\varvec{y}) \right) ^{-\intercal } - \varvec{I} \right) \\&+ \left( \! \tilde{\varvec{A}}(t,y) : \left( \! \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) \! \right) \! \left( \! \left( \nabla T_t(\varvec{y}) \right) ^{-1} - \varvec{I} \right) \right) \\&+ \left( \det \!\left( \nabla T_t(\varvec{y}) \right) - 1 \right) \left( \varvec{A}\left( T_t(\varvec{y}) \right) : \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) \right) \\&+ \left( \! \left( \! \varvec{A}_t (\varvec{y}) \! - \varvec{A}(\varvec{y}) \right) : \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) \right) \bigg \rbrace : \nabla \varvec{v} \,\mathrm {d}\varvec{y} \\&\quad = -\int _Y \left( \! \varvec{A}(\varvec{y}) : \left( \! \nabla \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) - \nabla \varvec{\phi }_{ij}(\varvec{y}) \right) \! \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y}, \end{aligned} \end{aligned}$$
(3.5)

where \(\tilde{\varvec{A}}(t,\varvec{y}) {:}{=}\det \big ( \nabla T_t(\varvec{y})\big ) \varvec{A}_t (\varvec{y})\). The four functions \(t\mapsto \left( \nabla T_t(\varvec{y}) \right) ^{-1}\), \(t\mapsto \det \big ( \nabla T_t(\varvec{y})\big )\), \(t\mapsto \varvec{A}_1\left( T_t(\varvec{y})\right)\), and \(t\mapsto \varvec{A}_2\left( T_t(\varvec{y})\right)\) are differentiable at each \(\varvec{y}\in Y\). Replacing \(\varvec{v}\) by \(\tilde{\varvec{\phi }}_{ij}(t,\cdot )-\varvec{\phi }_{ij}\) in (3.5), it follows that \(\big (\tilde{\varvec{\phi }}_{ij}(t,\cdot ) - \varvec{\phi }_{ij}\big ) / t\) converges weakly in \([H_{{\text {per}}}^1(Y)]^n\) to the material derivative \(\dot{\varvec{\phi }}_{ij}\in [H_{{\text {per}}}^1(Y)]^n\). Next, one uses \(\big (\tilde{\varvec{\phi }}_{ij}(t,\cdot ) - \varvec{\phi }_{ij}\big ) / t\) as test function in (3.5) and divides the equation by \(t>0\) to show that \(\nabla \big ( \tilde{\varvec{\phi }}_{ij}(t,\varvec{y}) - \varvec{\phi }_{ij}(\varvec{y}) \big ) / t\) converges strongly in \([L^2(Y)]^n\) to \(\nabla \dot{\varvec{\phi }}_{ij}\). Poincaré’s inequality finally implies that \(\big (\tilde{\varvec{\phi }}_{ij}(t,\cdot ) - \varvec{\phi }_{ij}(t)\big ) / t\) converges strongly in \([H_{{\text {per}}}^1(Y)]^n\) to the material derivative \(\dot{\varvec{\phi }}_{ij}\). The details of these arguments can be found by straightforward adaption of the proof for the case of conductivity, see Henrot and Privat (2010).

With the reasoning above, the material derivative exists and satisfies the variational problem: find \(\dot{\varvec{\phi }}_{ij}\in [H_{{\text {per}}}^1(Y)]^n\) such that

$$\begin{aligned} \begin{aligned} \int _Y&\left( \varvec{A} : \nabla \dot{\varvec{\phi }}_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} = \int _Y \bigg \lbrace \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \left( \nabla \varvec{h} \right) ^\intercal + \varvec{A} : \left( \nabla \varvec{\phi }_{ij} \nabla \varvec{h} \right) \\&- {\text {div}}( \varvec{h} ) \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \bigg \rbrace : \nabla \varvec{v} \,\mathrm {d}\varvec{y} - \int _{Y{\setminus }{\overline{\omega }}} \left( \left( \varvec{h} ( \nabla \otimes \varvec{A}_1 ) \right) : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} \\&- \int _{\omega } \left( \left( \varvec{h} ( \nabla \otimes \varvec{A}_2 ) \right) : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y}. \end{aligned} \end{aligned}$$
(3.6)

In this equation, for \(m=1,2\), \(\left( \varvec{h} ( \nabla \otimes \varvec{A}_m ) \right)\) denotes the fourth order tensor with entries \(\langle \varvec{h}(\varvec{y}), \nabla a_{ijkl}^m(\varvec{y}) \rangle\), where \(a_{ijkl}^m\) are the entries of \(\varvec{A}_m(\varvec{y})\).

2. Recovering the shape derivative. Employing integration by parts in (3.6), we can rewrite the weak problem solved by the material derivative as

$$\begin{aligned} \begin{aligned}&\int _Y \left( \varvec{A} : \nabla \dot{\varvec{\phi }}_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} = \int _{\partial \omega } \left[ \Big \langle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \varvec{n}, \nabla \varvec{v} \varvec{h}\Big \rangle \right] - \left[ \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \right] \mathrm {d}o\\&\qquad \qquad + \int _{Y{\setminus }{\overline{\omega }}} \left( \varvec{A}_1 : \nabla \left( \nabla \varvec{\phi }_{ij} \varvec{h} \right) \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} + \int _\omega \left( \varvec{A}_2 : \nabla \left( \nabla \varvec{\phi }_{ij} \varvec{h} \right) \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y}. \end{aligned} \end{aligned}$$

From Delfour and Zolesio (2001), we have the relation \(\dot{\varvec{\phi }}_{ij} = \delta \varvec{\phi }_{ij} + \nabla \varvec{\phi }_{ij} \varvec{h}\) between the shape derivative and the material derivative. Thus, we can replace the material derivative in (3.6) by the shape derivative to arrive at

$$\begin{aligned} \begin{aligned}&\int _{Y{\setminus }{\overline{\omega }}} \left( \varvec{A}_1 : \nabla \delta \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} + \int _\omega \left( \varvec{A}_2 : \nabla \delta \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} \\&\qquad \qquad = - \int _{\partial \omega } \left[ \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \right] - \left[ \Big \langle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \varvec{n}, \nabla \varvec{v} \varvec{h} \Big \rangle \right] \mathrm {d}o. \end{aligned} \end{aligned}$$
(3.7)

Since \(\dot{ \varvec{\phi } }_{ij}\) has no jump at \(\partial \omega\) as a function in \([H_{{\text {per}}}^1(Y)]^n\), we conclude the first transmission condition for \(\delta \varvec{\phi }_{ij}\) at the interface \(\partial \omega\):

$$\begin{aligned}{}[\delta \varvec{\phi }_{ij} ] = - [ \nabla \varvec{\phi }_{ij} \varvec{h} ] = -\left[ \langle \varvec{h} , \varvec{n} \rangle \partial _{\varvec{n}} \varvec{\phi }_{ij}\right] . \end{aligned}$$

Next, with (2.10), (3.2), and the symmetry of the matrix \(\varvec{A} : \nabla \varvec{\phi }_{ij}\), we rewrite (3.7) as

$$\begin{aligned} \begin{aligned}&\int _{Y{\setminus }{\overline{\omega }}} \left( \varvec{A}_1 : \nabla \delta \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} + \int _\omega \left( \varvec{A}_2 : \nabla \delta \varvec{\phi }_{ij} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{y} \\&\qquad {=} - \int _{\partial \omega } \left[ \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) : \nabla _{\varvec{\tau }} \varvec{v} \right] \mathrm {d}o. \end{aligned} \end{aligned}$$
(3.8)

We proceed with integration by parts over \(\omega\) and \(Y{\setminus } {\overline{\omega }}\) on the left-hand side and with integration by parts over the closed surface \(\partial \omega\) on the right-hand side of the equation. By using (2.10) again, this yields

$$\begin{aligned} \begin{aligned}&\int _{Y{\setminus }{\overline{\omega }}} \Big \langle {\text {div}}\left( \varvec{A}_1 : \nabla \delta \varvec{\phi }_{ij} ) \right) , \varvec{v} \Big \rangle \,\mathrm {d}\varvec{y} + \int _\omega \Big \langle {\text {div}}\left( \varvec{A}_2 : \nabla \delta \varvec{\phi }_{ij} ) \right) , \varvec{v} \Big \rangle \,\mathrm {d}\varvec{y} \\&\quad - \int _{\partial \omega } \left[ \Big \langle \left( \varvec{A} : \nabla \delta \varvec{\phi }_{ij} \right) \varvec{n} , \varvec{v}\Big \rangle \right] \mathrm {d}o = - \int _{\partial \omega } \left[ \Big \langle {\text {div}}_{\varvec{\tau }} \left( \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \right) , \varvec{v}\Big \rangle \right] \mathrm {d}o. \end{aligned} \end{aligned}$$

We deduce that \(\delta \varvec{\phi }_{ij}\) is harmonic in both subdomains \(\omega\) and \(Y{\setminus } {\overline{\omega }}\), while the second transmission condition is also deduced from this equation.\(\square\)

3.2 Sensitivity of the effective tensor

From Delfour and Zolesio (2001) or Sokolowski and Zolesio (1992), given a function \(f:{\mathbb {R}}\times {\mathbb {R}}^n \rightarrow {\mathbb {R}}\), we have

$$\begin{aligned} \left( \frac{ \mathrm {d} }{ \mathrm {d} t } \int _{T_t(Y)} f(t,\varvec{y}) \,\mathrm {d}{\varvec{y}} \right) _{|t=0} = \int _Y \frac{ \mathrm {d} }{ \mathrm {d} t } f(t,\varvec{y}) + {\text {div}}\big (f(0,\varvec{y}) \varvec{h}\big )\,\mathrm {d}\varvec{y}. \end{aligned}$$
(3.9)

This formula appears in the literature in Hadamard’s shape calculus and also as the Reynolds transport theorem in continuum mechanics.

Theorem 2

(Shape derivative of the coefficients of the effective tensor) The shape derivatives of the entries \(a_{ijkl}^{*}\) of the effective tensor given by (2.8) are

$$\begin{aligned} \begin{aligned}&\delta a_{iklj}^{*} (\omega )[\varvec{h}] = -\! \int _{\partial \omega }\! \langle \varvec{h} , \varvec{n} \rangle \bigg \lbrace \Big [ \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{kl}\Big ] : \nabla _{\varvec{\tau }} \varvec{\phi }_{ij} - \Big \langle \left( \varvec{A}_2(\varvec{y}) : \nabla \varvec{\phi }_{ij}^- \right) \varvec{n} , \left[ \nabla \varvec{\phi }_{kl} \right] \varvec{n}\Big \rangle \bigg \rbrace \,\mathrm {d}o, \end{aligned} \end{aligned}$$

where \(\varvec{\phi }_{ij}(\varvec{y}) = \varvec{w}_{ij}(\varvec{y}) + \varvec{y}_{ij}\) with \(\varvec{w}_{ij}\in [H_{{\text {per}}}^1(Y)]^n\) are the unique solutions of the cell problem (2.7) for all \(i,j=1,\ldots ,n\).

Proof

We set \(f(t,\varvec{y}) = \big (\varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij}^t(\varvec{y})\big ) : \nabla \varvec{\phi }_{kl}^t(\varvec{y})\). Since the value of the function \(\delta \varvec{\phi }_{ij}\) has a jump through \(\partial \omega\), we want to consider \(\nabla \delta \varvec{\phi }_{ij}\) inside and outside the interface separately. Therefore, we introduce the set \(\Theta\), which may designate either the set \(Y{\setminus }{\overline{\omega }}\) or \(\omega\). Then, for the first term in the Reynolds transport theorem (3.9), we find

$$\begin{aligned} \int _\Theta \frac{ \mathrm {d} }{ \mathrm {d} t } f(t,\varvec{y}) \,\mathrm {d}\varvec{y}&= \int _\Theta \left( \varvec{A}(\varvec{y}) : \nabla \delta \varvec{\phi }_{ij} \right) : \nabla \varvec{\phi }_{kl} + \left( \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij} \right) : \nabla \delta \varvec{\phi }_{kl} \,\mathrm {d}\varvec{y}. \end{aligned}$$

Hence, we arrive at

$$\begin{aligned} \int _Y \frac{ \mathrm {d} }{ \mathrm {d} t } f(t,\varvec{y}) \,\mathrm {d}\varvec{y}&= - \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \bigg \lbrace \Big [ \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij} \Big ] : \nabla _{\varvec{\tau }} \varvec{\phi }_{kl} + \Big [ \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{kl} \Big ] : \nabla _{\varvec{\tau }} \varvec{\phi }_{ij} \bigg \rbrace \,\mathrm {d}o, \end{aligned}$$

where we added the equation with \(\Theta = Y{\setminus }{\overline{\omega }}\) to the one with \(\Theta = \omega\) and used the results from Theorem 1.

We compute next the second term in the Reynolds transport theorem (3.9) by using the divergence theorem, the identity \(P:\big (Q(\varvec{n}\otimes \varvec{n})\big )=\mathrm {tr} \big (P\varvec{n}\varvec{n}^ \intercal Q^\intercal \big )=\langle P\varvec{n},Q\varvec{n} \rangle\) for matrices \(P,Q\in {\mathbb {R}}^{n\times n}\), and the second transmission condition in (2.10)

$$\begin{aligned} \begin{aligned} \int _Y&{\text {div}}\left( f(0,\varvec{y}) \varvec{h} \right) \mathrm {d}\varvec{y} = \int _{\partial \omega } \left[ f(0,\varvec{y}) \langle \varvec{h} , \varvec{n} \rangle \right] \mathrm {d}o = \int _{\partial \omega } \left[ \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{\phi }_{kl} \right] \mathrm {d}o \\&= \int _{\partial \omega } \Bigg \lbrace \left[ \varvec{A}(\varvec{y}) : \nabla \varvec{\phi }_{ij} \right] : \nabla _{\varvec{\tau }} \varvec{\phi }_{kl} + \Big \langle \left( \varvec{A}_2(\varvec{y}) : \nabla \varvec{\phi }_{ij}^- \right) \varvec{n} , \left[ \nabla \varvec{\phi }_{kl} \right] \varvec{n}\Big \rangle \Bigg \rbrace \langle \varvec{h} , \varvec{n} \rangle \,\mathrm {d}o. \end{aligned} \end{aligned}$$

Putting the two terms together yields the desired result of the theorem.\(\square\)

Remark 2

  1. 1.

    By substituting back \(\varvec{\phi }_{ij} = \varvec{w}_{ij} + \varvec{y}_{ij}\), we arrive at the computable expression

    $$\begin{aligned} \begin{aligned}&\delta a_{iklj}^{*} (\omega )[\varvec{h}] = -\int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \bigg \lbrace \Big [\varvec{A}(\varvec{y}) : \nabla ( \varvec{w}_{kl} + \varvec{y}_{kl} )\Big ] : \nabla _{\varvec{\tau }} ( \varvec{w}_{ij} + \varvec{y}_{ij} ) \\&\qquad \qquad \qquad \qquad - \Big \langle \left( \varvec{A}_2 (\varvec{y}) : ( \nabla \varvec{w}_{ij}^- + \varvec{y}_{ij} ) \right) \varvec{n}, \left( \nabla \varvec{w}_{kl}^+ - \nabla \varvec{w}_{kl}^- \right) \varvec{n}\Big \rangle \bigg \rbrace \,\mathrm {d}o, \end{aligned} \end{aligned}$$
    (3.10)

    where \(n_{ij} = e_{ij} \varvec{n}\) denotes the vector with the i-th component of \(\varvec{n}\) at the j-th position and the j-th component of \(\varvec{n}\) at the i-th position.

  2. 2.

    The homogenized elasticity tensor \(\varvec{A}^{*}\) satisfies \((\varvec{A}^{*}:\nabla \varvec{\phi }_{ij}):\nabla \varvec{\phi }_{kl} = (\varvec{A}^{*}:\nabla \varvec{\phi }_{kl}): \nabla \varvec{\phi }_{ij}\). However, in the implementation with the finite element method using linear basis functions, numerical inaccuracies are introduced when trying to resolve the second transmission condition in (2.10). This condition is used in the proofs of Theorems 1 and 2. Without using the second transmission condition, the shape derivative of the coefficients of the homogenized tensor can be written as

    $$\begin{aligned} \begin{aligned} \delta a_{iklj}^{*}(\omega )[\varvec{h}] = \int _{\partial \omega } \Big [ (\varvec{A}:\nabla \varvec{\phi }_{ij}) : \big ( \nabla \varvec{\phi }_{kl} (\varvec{h}\otimes \varvec{n}) \big ) +&(\varvec{A}:\nabla \varvec{\phi }_{kl}) : \big ( \nabla \varvec{\phi }_{ij} (\varvec{h}\otimes \varvec{n}) \big ) \\&- \langle \varvec{h}, \varvec{n} \rangle (\varvec{A}:\nabla \varvec{\phi }_{kl}) : \nabla \varvec{\phi }_{ij} \Big ] \,\mathrm {d}o. \end{aligned} \end{aligned}$$
    (3.11)

    Formula (3.11) has the advantage of explicitly preserving the symmetry of the homogenized tensor. In contrast, using formula (3.10) together the symmetrization \((\delta a_{iklj}^{*} + \delta a_{kijl}^{*} )/2\) reestablishes the symmetry in the implementation while omitting terms being equal to 0. In our numerical examples, this variant turned out to be more accurate.

3.3 Shape derivative of the objective functions

For the least squares matching, with the help of Theorem 2 and the chain rule

$$\begin{aligned} \delta J_{LS}(\omega ) [ \varvec{h} ] = \sum _{i,j,k,l=1}^n \left( a_{ijkl}^{*}(\omega ) - b_{ijkl} \right) \delta a_{ijkl}^{*} (\omega )[\varvec{h}], \end{aligned}$$

we can easily determine the shape derivative of the objective \(J_{LS}(\omega )\) given by (2.13).

Proposition 1

The shape derivative of the objective function \(J_{LS}(\omega )\) from (2.13) reads

$$\begin{aligned} \begin{aligned} \delta J_{LS}(\omega ) [ \varvec{h} ] = \sum _{i,j,k,l=1}^n&\left( b_{ijkl} - a_{ijkl}^{*}(\omega ) \right) \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \Big \lbrace \left[ \varvec{A} : \nabla \varvec{\phi }_{kl} \right] : \nabla _{\varvec{\tau }} \varvec{\phi }_{ij} \\&\qquad \qquad \qquad \qquad - \Big \langle \left( \varvec{A}_2 : \nabla \varvec{\phi }_{ij}^- \right) \varvec{n} , \left[ \nabla \varvec{\phi }_{kl} \right] \varvec{n}\Big \rangle \Big \rbrace \,\mathrm {d}o. \end{aligned} \end{aligned}$$
(3.12)

For the computation of the shape derivative of the objective function \(J_C(\omega )\), we use the notation

$$\begin{aligned} \omega _t{:}{=}T_t(\omega ) = \left\{ y+t\varvec{h}(y) \,\big |\, y\in \omega \right\} \end{aligned}$$

and

$$\begin{aligned} \varvec{A}_t^{*}{:}{=}\varvec{A}^{*}( \omega _t ), \quad \varvec{A}^{*}{:}{=}\varvec{A}^{*}( \omega ),\\ \varvec{u}_t{:}{=}\varvec{u}( \omega _t , \cdot ), \quad \varvec{u}{:}{=}\varvec{u}( \omega , \cdot ), \end{aligned}$$

where \(t\ge 0\) and \(\varvec{u}( \omega , \cdot )\) is the displacement function in case of the interface \(\omega\), being the solution of (2.12).

The following two lemmata are required to express the shape derivative of the compliance functional (2.14).

Lemma 1

For \(t>0\), a vector field \(\varvec{h}\) and \(\omega \subset Y\), it holds for all \(\varvec{v} \in [H^1(\Omega )]^n\)

$$\begin{aligned} \int _\Omega \left( \varvec{A}^{*} : \nabla \delta \varvec{u}[\varvec{h}] \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x} = - \int _\Omega \left( \delta \varvec{A}^{*}( \omega )[\varvec{h}] : \nabla \varvec{u} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x}. \end{aligned}$$

Proof

Expressing the variational formulation of (2.12) once for \(\omega\) and once for \(\omega _t\), then subtracting one expression from the other and dividing by t, we obtain for any \(\varvec{v}\in [H^1(\Omega )]^n\)

$$\begin{aligned} 0 = \frac{1}{t} \bigg \lbrace \int _\Omega \left( ( \varvec{A}_t^{*} - \varvec{A}^{*} ) : \nabla \varvec{u}_t \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x} + \int _\Omega \left( \varvec{A}^{*} : \nabla ( \varvec{u}_t - \varvec{u} ) \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x} \bigg \rbrace . \end{aligned}$$

Taking the limit \(t\rightarrow 0\) leads to

$$\begin{aligned} 0 = \int _\Omega \left( \delta \varvec{A}^{*}( \omega )[\varvec{h}] : \nabla \varvec{u} \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x} + \int _\Omega \left( \varvec{A}^{*} : \nabla \delta \varvec{u}[\varvec{h}] \right) : \nabla \varvec{v} \,\mathrm {d}\varvec{x} \end{aligned}$$

and the claim follows.\(\square\)

Lemma 2

For a vector field \(\varvec{h}\), the shape derivative of the compliance (2.14) reads

$$\begin{aligned} \delta C( \omega )[\varvec{h}] = - \int _\Omega \left( \delta \varvec{A}^{*}( \omega )[\varvec{h}] : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x}. \end{aligned}$$

Proof

We find

$$\begin{aligned} \frac{ C( \omega _t ) - C( \omega ) }{t}&= \frac{1}{t} \bigg \lbrace \int _\Omega \left( \varvec{A}_t^{*} : \nabla \varvec{u}_t \right) : \nabla \varvec{u}_t \,\mathrm {d}\varvec{x} - \int _\Omega \left( \varvec{A}^{*} : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} \bigg \rbrace \\&= \frac{1}{t} \bigg \lbrace \int _\Omega \left( \varvec{A}_t^{*} : \nabla \varvec{u}_t \right) : \nabla ( \varvec{u}_t - \varvec{u} ) + \left( \varvec{A}_t^{*} : \nabla ( \varvec{u}_t - \varvec{u} ) \right) : \nabla \varvec{u} \\&\quad + \left( ( \varvec{A}_t^{*} - \varvec{A}^{*} ) : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} \bigg \rbrace . \end{aligned}$$

This expression converges for \(t\rightarrow 0\) to

$$\begin{aligned} \delta C( \omega )[\varvec{h}] = \int _\Omega \left( \varvec{A}^{*} : \nabla \varvec{u} \right) : \nabla \delta \varvec{u}[\varvec{h}] + \left( \varvec{A}^{*} : \nabla \delta \varvec{u}[\varvec{h}] \right) : \nabla \varvec{u} + \left( \delta \varvec{A}^{*}[\varvec{h}] : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x}. \end{aligned}$$

The first two terms in this result are equal due to the symmetry properties of \(\varvec{A}^{*}\). By using Lemma 1, we thus conclude the desired result.

Combining the shape derivative of the volume of the inclusion

$$\begin{aligned} \delta |\omega | [\varvec{h}] = \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \,\mathrm {d}o \end{aligned}$$
(3.13)

with Lemma 2 and the chain rule, we obtain the following result.

Proposition 2

The shape derivative of the objective function \(J_{C}(\omega,\lambda )\) from (2.15) reads

$$\begin{aligned} \delta J_{C} (\omega,\lambda )[\varvec{h}] = - \int _\Omega \left( \delta \varvec{A}^{*}( \omega )[\varvec{h}] : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} + \left( \lambda + \alpha \left( |\omega | - \omega _0 \right) \right) \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \,\mathrm {d}o, \end{aligned}$$
(3.14)

where the entries of the fourth order tensor \(\delta \varvec{A}^{*}( \omega )[\varvec{h}]\) are given by the expressions from Theorem 2.

3.4 Perforated plates and scaffold structures

We consider now the n-dimensional unit cube \(Y=[0,1]^n\) with a hole \(\omega\) such that \(\omega \Subset Y\). This corresponds to the limiting case \(\varvec{A}_2 \rightarrow \varvec{0}\) in (2.9) for a composite material. In two spatial dimensions, we get perforated plates, while in three spatial dimensions, we get scaffold structures.

The previous results remain similar when considering \(Y{\setminus }{\overline{\omega }}\) instead of Y. This means that the cell problem becomes: seek \(\varvec{w}_{ij}\in [H_{{\text {per}}}^1(Y{\setminus }{\overline{\omega }})]^n\) with \((\varvec{w}_{ij},\mathbbm {1} )_{[L^2(Y{\setminus }{\overline{\omega }})]^n}\) such that

$$\begin{aligned} {\text {div}}\left( \varvec{A} : (e_{ij} + \nabla \varvec{w}_{ij} ) \right)&= \varvec{0}&\text {in}\ Y{\setminus }{\overline{\omega }},\\ \left( \varvec{A} : \nabla \varvec{w}_{ij} \right) \varvec{n}&= - \left( \varvec{A} : e_{ij} \right) \varvec{n}&\text {on}\ \partial \omega . \end{aligned}$$

The homogenized equation in the present situation is

$$\begin{aligned} -{\text {div}}\left( \varvec{A}^{*}( \omega ) : \nabla \varvec{u}(\varvec{x}) \right) = (1-|\omega |)\varvec{f}(\varvec{x}), \end{aligned}$$

while the coefficients of the effective tensor are

$$\begin{aligned} a_{ijkl}^{*}( \omega ) = \int _{Y{\setminus }{\overline{\omega }}} \left( \varvec{A}(\varvec{y}) : \left( e_{il} + \nabla \varvec{w}_{il}(\varvec{y}) \right) \right) : \left( e_{jk} + \nabla \varvec{w}_{jk}(\varvec{y}) \right) \mathrm {d}\varvec{y}. \end{aligned}$$

Moreover, the system for the shape derivative reads

$$\begin{aligned} {\text {div}}\left( \varvec{A} : \nabla \delta \varvec{\phi }_{ij} \right)&= \varvec{0}&\text {in } Y {\setminus } {\overline{\omega }},\\ \delta \varvec{\phi }_{ij}&= - \langle \varvec{h} , \varvec{n} \rangle \partial _{\varvec{n}} \varvec{\phi }_{ij}&\text {on } \partial \omega ,\\ \left( \varvec{A} : \nabla \delta \varvec{\phi }_{ij} \right) \varvec{n}&= {\text {div}}_{\varvec{\tau }} \left( \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) \right)&\text {on } \partial \omega . \end{aligned}$$

This implies that the shape derivative of the coefficients of the homogenized tensor is given by

$$\begin{aligned} \delta a_{iklj}^{*} (\omega )[\varvec{h}] = - \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{\phi }_{kl} \,\mathrm {d}o. \end{aligned}$$
(3.15)

Consequently, the shape derivative of the objective function from (2.13) reads

$$\begin{aligned} \delta J_{LS}(\omega ) [ \varvec{h} ] = \sum _{i,j,k,l=1}^n \left( b_{ijkl} - a_{ijkl}^{*}(\omega ) \right) \int _{\partial \omega } \langle \varvec{h} , \varvec{n} \rangle \left( \varvec{A} : \nabla \varvec{\phi }_{ij} \right) : \nabla \varvec{\phi }_{kl} \,\mathrm {d}o. \end{aligned}$$
(3.16)

Furthermore, the shape derivative \(\delta J_{C} (\omega,\lambda )[\varvec{h}]\) of the objective function \(J_C(\omega,\lambda )\) from (2.15) remains identical to (3.14), except for the entries of the fourth order tensor \(\delta \varvec{A}^{*}( \omega )[\varvec{h}]\) which are now given by the formula (3.15).

4 Implementation and verification

4.1 Implementation using finite elements

Our implementation is for the two-dimensional case, i.e. \(n=2\), and was implemented in Matlab.

In the microstructure of the material, we assume that the sought domain \(\omega\) is starlike with respect to the midpoint of the unit cell. The boundary \(\partial \omega\) of the interface is represented in polar coordinates by the function

$$\begin{aligned} \varvec{\gamma }( \phi ) {:}{=}r(\phi ) \left( \!\! \begin{array}{c} \cos (\phi ) \\ \sin (\phi ) \end{array} \!\!\right) , \qquad \text{ for } \phi \in [0,2\pi ) , \end{aligned}$$
(4.1)

where the radial function \(r(\phi )\) is given by the finite Fourier series

$$\begin{aligned} r(\phi ) {:}{=}\frac{a_0}{2} + \sum _{k=1}^N \left\{ a_k \cos ( k \phi ) + a_{-k} \sin ( k \phi ) \right\} , \end{aligned}$$
(4.2)

where \(N\in {\mathbb {N}}\) and \(\left( a_{-N},\ldots ,a_0,\ldots , a_N \right) \in {\mathbb {R}}^{2N+1}\).

The domain \(Y=[0,1]\times [0,1]\) is discretized by parametric finite elements with a macro triangulation which is composed of 8 triangles and 8 squares in order to resolve the interface \(\partial \omega\) exactly. Each of these elements is transformed from a reference geometry by the help of a diffeomorphism into Y. The squares are generated by Coons patches and the triangles with the Zenisek’s formula from Zenisek (1990). The mesh on the reference triangle is composed of \(4^\ell\) triangular elements while the mesh of the reference square is composed \(2\times 4^\ell\) triangular elements. Therefore, on Y, we place \(24\times 4^\ell\) triangular elements on the refinement level \(\ell\). The resulting macro parametrization and mesh of the domain Y is displayed in Fig. 2.

Fig. 2
figure 2

Left-hand side: Parametric representation of Y by quadrangular and triangular patches for resolving the interface exactly. Right-hand side: Mesh on Y on refinement level \(\ell =2\)

Full size image

Based on the variational formulation of the cell problem (2.11), we define the bilinear form and the linear form

$$\begin{aligned} \begin{aligned} B(\varvec{w},\varvec{v})&{:}{=}\int _Y\big ( \varvec{A}(\varvec{y}) : \nabla \varvec{w}(\varvec{y})\big ) :\nabla \varvec{v}(\varvec{y}) \,\mathrm {d}\varvec{y},\\ L(\varvec{v})&{:}{=}- \int _Y \left( \varvec{A}(\varvec{y}) : e_{ij} \right) :\nabla \varvec{v}(\varvec{y})\,\mathrm {d}\varvec{y}, \end{aligned} \end{aligned}$$
(4.3)

respectively, where \(\varvec{w},\varvec{v}\in [H_{{\text {per}}}^1(Y)]^2\). The kernel of the bilinear function B, namely the set of functions \(\varvec{r}\in [H_{{\text {per}}}^1(Y)]^2\) such that \(B(\varvec{r},\varvec{v}) = B(\varvec{v},\varvec{r}) = 0\) for all \(\varvec{v}\in [H_{{\text {per}}}^1(Y)]^2\), contains the functions which are constant in one dimension and vanish in the other dimension, i.e. \(\varvec{r}_1(\varvec{y}) {:}{=}(1,0)^\intercal\) and \(\varvec{r}_2(\varvec{y}){:}{=}(0,1)^\intercal\). The rotations are linear functions in both dimensions, thus not periodic and not contained in \([H_{{\text {per}}}^1(Y)]^2\). Therefore, the linear span of \(\varvec{r}_1\) and \(\varvec{r}_2\), which is the set of constant vector fields, are all rigid body motions which need to be considered in this periodic setting on the cell Y. In order to make our problem well-posed, we use Lagrange multipliers: We want to find \(\varvec{w}\in [H_{{\text {per}}}^1(Y)]^2\), such that

$$\begin{aligned} B(\varvec{w},\varvec{v}) + \sum _{i=1}^2 \lambda _i \langle \varvec{r}_i, \varvec{v} \rangle = L(\varvec{v})\ \text {for all}\ \varvec{v}\in [H_{{\text {per}}}^1(Y)]^2, \end{aligned}$$

subject to \(\langle \varvec{r}_i,\varvec{w} \rangle = 0\) for \(i=1,2\). As we have \(B(\varvec{r}_i,\varvec{r}_i) = 0\) and \(L(\varvec{r}_i)=0\) for \(i=1,2\), we can replace \(\lambda _i\) by the constraint and obtain: seek \(\varvec{w}\in [H_{{\text {per}}}^1(Y)]^2\), such that

$$\begin{aligned} B(\varvec{w},\varvec{v}) + \sum _{i=1}^2 \langle \varvec{r}_i, \varvec{w} \rangle \langle \varvec{r}_i, \varvec{v} \rangle = L(\varvec{v})\ \text {for all}\ \varvec{v}\in [H_{{\text {per}}}^1(Y)]^2. \end{aligned}$$

For this modified problem, we use piecewise linear finite elements to find an approximation to the solution of the cell problem (2.7). Since the interface is resolved by the triangulation, the convergence order of our implementation is of second order in the mesh size h with respect to the \([L^2(Y)]^2\)-norm.

At the macroscopic scale, we consider a rectangular elastic body \(\Omega\), i.e. a pillar of a certain height and width. At its bottom, homogeneous Dirichlet boundaries are imposed, which means that the pillar is fixed at its bottom edge. On its top edge, a constant force is applied, expressed through a nonhomogeneous Neumann boundary condition and the function \(\varvec{g}\). The remaining two boundaries can move freely in space which corresponds to homogeneous Neumann boundary conditions at these boundaries. Moreover, there is no volume force, i.e., \(\varvec{f}=\mathbf{0}\). This setting is implemented analogously to Alberty et al. (2002). Piecewise linear finite elements are used to solve the respective variational formulation.

4.2 Verification of the shape derivative through finite differences

Choose \(N\in {\mathbb {N}}\) and let the coefficients \(\left( a_{-N},\ldots , a_0,\ldots , a_N \right) \in {\mathbb {R}}^{2N+1}\) be describing the interface in our numerical experiments in accordance with (4.1) and (4.2). We use the computable and symmetric expression \((\delta a_{ijkl}^{*} (\omega )[\varvec{h}] + \delta a_{jilk}^{*} (\omega )[\varvec{h}] ) / 2\) from Remark 2 to evaluate the shape derivative of the coefficients of the homogenized tensor. We evaluate this expression in the midpoint of the edge lying on the interface of the triangular elements. As deformation functions, we use the functions

$$\begin{aligned} \varvec{q}_{k}(\phi ) {:}{=}\left( \!\! \begin{array}{c} \cos (\phi ) \\ \sin (\phi ) \end{array} \!\!\right) \times \left\{ \!\! \begin{array}{ll} \sin (k\phi ), &{} \text {if}\ -N\le k<0,\\ \cos (k\phi ), &{} \text {if}\ 0\le k\le N. \end{array} \right. \end{aligned}$$
(4.4)

Thus, we obtain the shape derivative of the coefficients of the homegenized elasticity tensor with respect to the \(2N+1\) directions \(\varvec{q}_{k}\). We compare these \(2N+1\) results with an approximation of the shape derivative obtained by first order finite differences. We compute these from the expression (2.8) of the coefficients of the homogenized tensor \(a_{ijkl}^{*}\), once evaluated on Y with the interface given by the function \(r(\phi )\) from (4.2) and once evaluated on Y with the interface given by the function \(r(\phi ) + \varepsilon \varvec{q}_k(\phi )\). For our test runs, we set \(\varepsilon = 10^{-8}\).

Fig. 3
figure 3

Sum of the \(\ell _2\)-norms of the absolute and the relative differences between the computable formula (3.10) and the finite difference approximation of the shape derivative in four different settings. The interface is either circular or a slightly perturbed circle, composite and hollow materials are considered, and the mesh refinement levels \(\ell\) of the finite element method range from 0 to 7. As a means of comparison, the plots of linear and quadratic decay are shown where needed

Full size image

The material properties are chosen as follows. To realize a composite material, we define the elasticity tensor outside of the interface by the values \(E = 1 \,\mathrm{Pa}\) and \(\nu = 0.3\) and inside of the interface by \(E = 2 \,\mathrm{Pa}\) and \(\nu = 0.2\). Whereas, to obtain a perforated plate, we use \(E = 1 \,\mathrm{Pa}\) and \(\nu = 0.3\) outside of the interface and no material inside of the interface, cf. (2.4). The boundary under consideration is a circle of radius 1/4 on one hand and a respective perturbed version of this circle on the other hand, the same perturbed circle as shown in the mesh plots in Fig. 2.

In Fig. 3, the convergence of the evaluation of the formula (2.8) towards the respective finite difference can be observed in all of the four cases. Therefore, we can conclude that our implementation is correct.

4.3 Computation of the volume of the inclusion

In our implementation, the definition of the inclusion by the functions \(\varvec{\gamma }\) and r from (4.1) and (4.2), respectively, allows for a simple computation of the volume of the inclusion \(\omega\) by the formula

$$\begin{aligned} |\omega | = \frac{\pi }{2}\left( \frac{a_0^2}{2} + \sum _{k=1}^N \Big (a_k^2 + a_{-k}^2\Big ) \right) . \end{aligned}$$

With this formula, the computation (3.13) and the functions \(\varvec{q}_k\) from (4.4), the shape derivative of the volume of the inclusion \(\omega\) is

$$\begin{aligned} \delta |\omega | [\varvec{q}_k] = \int _{\partial \omega } \!\langle \varvec{q}_k , \varvec{n} \rangle \,\mathrm {d}o = \pi a_k. \end{aligned}$$

Therefore, the shape derivative of the function (2.15) is expressed by

$$\begin{aligned} \delta J_{\omega _0} (\omega,\lambda )[\varvec{q}_k] = - \int _\Omega \left( \delta \varvec{A}^{*}( \omega )[\varvec{q}_k] : \nabla \varvec{u} \right) : \nabla \varvec{u} \,\mathrm {d}\varvec{x} + \pi a_k \left( \lambda + \alpha ( |\omega | - \omega _0 ) \right) . \end{aligned}$$
(4.5)

The entries of the fourth order tensor \(\delta \varvec{A}^{*}( \omega )[\varvec{q}_k]\) are given by (3.15) in case of a porous material.

5 Numerical results: least squares matching

We use the expressions (3.12) and (3.16) in order to compute the shape derivative of the objective function (2.13) inside an implementation of the gradient descent method with quadratic line search. The aim of the procedure is to find optimal interface shapes which minimize the objective function (2.13) for different settings. In the examples below, we choose \(N=32\) in (4.2). The algorithm was always stopped after 75 gradient steps. The results of five settings within a composite material and one within a perforated plate are presented. The computation of these examples is based on 98 304 and 65 536 finite elements for composite materials and for perforated plates, respectively, which corresponds to the mesh refinement level \(\ell =6\) in our implementation. In the following five settings, the materials under consideration are defined by \(E_1{:}{=}2 \,\mathrm{Pa}\) and \(\lambda _1{:}{=}0.3\) outside of the interface, and in the case of composite materials as \(E_2{:}{=}5 \,\mathrm{Pa}\) and \(\lambda _2{:}{=}0.2\) inside the interface. The other material parameters are then specified in the respective setting.

5.1 First example: anisotropic tensor for a composite material

In our first experiment, we compute the homogenized tensor \(\varvec{A}\) for a composite material, where the interface is described by the circle of radius 1/4. Then, for the desired homogenized elastictiy tensor \({\varvec{B}}\), we introduce an anisotropy into \(\varvec{A}\) by adapting the two values \(b_{1111} {:}{=}a_{1111} + \delta /2\) and \(b_{2222} {:}{=}a_{2222} - \delta /2\). With the starting profile chosen to be the circle of radius 1/4 , we apply the gradient descent method for different values of \(\delta\). The optimized shapes we found are shown in Fig. 4. The histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the optimization process are displayed in Fig. 5.

Fig. 4
figure 4

Example 5.1: Optimal shapes in a composite material found for an anisotropic desired elasticity tensor with the anisotropy measured by \(\delta = b_{1111}-b_{2222}\), where the initial guess is the circle of radius 1/4

Full size image
Fig. 5
figure 5

Example 5.1: Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the optimization runs. In the run with \(\delta =0\) the optimal shape is the initial shape

Full size image

5.2 Second example: anisotropic tensor for a perforated plate

In this example, we consider perforated plates. We proceed similarly as in the first example to construct the desired homogenized elasticity tensor \({\varvec{B}}\). We compute the homogenized elasticity tensor \(\varvec{A}\) for the circle with radius 1/4 and introduce an anisotropy by setting \(b_{1111} = a_{1111} + \delta /2\) and \(b_{2222} = a_{2222} - \delta /2\). Again, starting at the circle with radius 1/4, we then apply the gradient descent method to compute the optimal shapes for different values of \(\delta\). The optimized shapes we found are shown in Fig. 6. The histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the optimization process are displayed in Fig. 7.

Fig. 6
figure 6

Example 5.2: Optimized shapes in a perforated plate found for an anisotropic desired homogenized elasticity tensor with the anisotropy measured by \(\delta = b_{1111} -b_{2222}\), where the initial guess is the circle of radius 1/4

Full size image
Fig. 7
figure 7

Example 5.2: Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the optimization runs. The values related to the runs of \(\delta\) and \(-\delta\) evolve equally. In the run with \(\delta =0\) the optimal shape is the initial shape

Full size image

5.3 Third example: various starting profiles for one anisotropic tensor

In our third experiment, we are concerned with the uniqueness of optimal shapes for the shape optimization problem under consideration. We consider the desired homogenized elasticity tensor to be anisotropic, namely the desired homogenized tensor from Sect. 5.1 with \(\delta =-0.04\). We choose our initial guess to be the circle of radius 1/4 for the first run, an axes-aligned ellipse for the second run, its rotated version for the third run, and finally we randomly perturb the circle for the last run, compare with the first row in Fig. 8. We apply the gradient descent method to optimize the shape for these various initial guesses. The results are shown in the second row of Fig. 8. The histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the optimization process are displayed in Fig. 9. This example indicates strongly that the solution is not unique as all optimized shapes exhibit both, small values of the objective function and small norms of the discrete shape gradient. Indeed, the same has already been observed in Dambrine and Harbrecht (2020) in case of a second order diffusion equation.

Fig. 8
figure 8

Example 5.3: Starting and optimized shapes found in a composite material for a specific anisotropic desired homogenized elasticity tensor (second row), where the various initial guesses are the circle of radius 1/4 and perturbations of this circle (first row)

Full size image
Fig. 9
figure 9

Example 5.3: Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the optimization runs

Full size image

5.4 Fourth example: inhomogeneous material inside a composite material

In the fourth example, we consider the elasticity modulus \(E(\varvec{y})\) and the Poisson ratio \(\lambda (\varvec{y})\) to be nonconstant functions in the interior of the interface, namely

$$\begin{aligned} E(\varvec{y}){:}{=}\frac{E_2}{2} \big (1+\sin (\pi y_1)+\sin (\pi y_2)\big ) \quad \text {and}\quad \lambda (\varvec{y}){:}{=}\lambda _2 e^{-(2y_1-1)^2-(2y_2-1)^2}. \end{aligned}$$
(5.1)

In the exterior of the interface, we keep the same homogeneous material properties as in the previous examples, given by \(E_1\) and \(\lambda _1\). We moreover use the anisotropic desired homogenized tensor from Sect. 5.1 with \(\delta =-0.04\) as desired homogenized elasticity tensor \(\varvec{B}\). We take the four different initial guesses from Sect. 5.3 and apply the gradient descent method. We obtain for these initial guesses the optimized shapes shown in Fig. 10. The histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the optimization process are displayed in Fig. 11. Again, the optimal shape seems not to be unique.

Fig. 10
figure 10

Example 5.4: The composite material is defined by \(E_1\) and \(\lambda _1\) outside and a heterogeneous material on the inside of the interface, described by the functions \(E(\varvec{y})\) and \(\lambda (\varvec{y})\) from (5.1). Optimized shapes found for an anisotropic desired homogenized elasticity tensor are shown, where the initial guesses as in Fig. 8 have been used

Full size image
Fig. 11
figure 11

Example 5.4: Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the optimization runs

Full size image

5.5 Fifth example: convergence towards an inverted composite material

In this example, the desired homogenized tensor represents a composite material which has material properties \(E_1\) and \(\lambda _1\) inside and \(E_2\) and \(\lambda _2\) outside of the interface. This correponds to a setting where the two materials of the composite materials we considered yet have switched their position. In order to define the desired homogenized elasticity tensor \(\varvec{B}\), we consider a circle with radius of 0.48. This ensures that an attainable desired tensor is derived. We use the same initial guesses as in Sect. 5.3, which yields the optimized shapes found in Fig. 12. The histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the optimization process are displayed in Fig. 13.

Fig. 12
figure 12

Example 5.5: Optimal shapes found for a desired homogenized elasticity tensor in case of the inverted composite material. The initial guesses are the ones shown in the first row of Fig. 8

Full size image
Fig. 13
figure 13

Example 5.5: Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the optimization runs

Full size image

6 Numerical results: compliance minimization

We shall next study cases for which we want to minimize the compliance of an object. In our first example, we consider a pillar with holes in its microstructure, subject to a force on its top. In our second example, we consider a beam, attached to the wall on one side and with a force acting from atop on the opposite side. The beam is composed of inhomogeneous materials in its microstructure.

In our implementation, we use the energy functional (4.5) in order to compute the shape derivative of the objective function (2.15) of the gradient descent method. In each step of the optimization process, we need to approximate the macroscopic solution \(\varvec{u}\) of the system of equations (2.12), describing the displacement of the material within the pillar or the beam, respectively, subject to the force \(\varvec{g}\), as well as the solutions \(\varvec{w}_{ij}\) of the cell problems (2.7) at the microscopic scale. For both examples, we choose \(N=32\) in the Fourier series (4.2). The macrostructure, meaning the pillar in the first example and the beam in the second example, is meshed with \(8\,192\) triangular elements. The microstructure is computed on refinement level \(\ell =5\), which yields \(16\,384\) triangular elements in the case of the hollow material and \(24\,576\) in the composite material. In both cases, the Lagrange multiplier \(\lambda\) in the functional (2.15) is initially set to 0 and is updated in accordance with (2.16) whenever the \(\ell _2\)-norm of the shape gradient has been halved.

6.1 First example: compliance minimization in a partly hollow pillar

We consider a two-dimensional pillar of 10 m height and 5 m width. It is composed of a material with elasticity modulus \(E=50\,\mathrm{Pa}\) and Poisson ratio 0.2. In this pillar, we aim at finding an optimal design for the shape of the holes in its microstructure, such that the compliance of the pillar is minimized while \(10\%\) of the pillar remain hollow.

The parameter \(\alpha\) in the objective function (2.15) is set to \(\alpha =2\times 10^4\). We want \(10\%\) of the material to be hollow in its microstructure, thus we set \(\omega _0=0.1\). A downward pointing force of \(10\,\mathrm{N}\) is applied on each point on the top of the pillar, i.e. \(\varvec{g}(\varvec{x}) = (0,-10)^\intercal\) for \(\varvec{x}\in [0,5]\times 10\).

We start the optimization run with a circle of radius 0.25 as initial guess. The optimization run is halted after 20 steps since the interface elongates so far that it would leave the cell. Hereby, the value of \(\lambda\) is updated 6 times during the optimization run and the value of the \(\ell _2\)-norm of the shape gradient evolves from approximately 35 to 49. We have \(J_C(\omega _0,0)\approx 247\) at the beginning of the optimization run when evaluating the objective function (2.15) with \(\lambda =0\), and at the end in step 20 we have \(J_C(\omega _{20},0)\approx 107\).

The results of the optimization run are displayed in Fig. 14 while the histories of the objective function and of the \(\ell _2\)-norm of the shape gradient during the compliance minimization process are displayed in Fig. 15. The result corresponds to the intuitive solution of the inclusion getting thin and stretching vertically to reduce the compliance of the porous material whilst retaining a certain volume.

Fig. 14
figure 14

In the top plots, the initial and optimized inclusions in the microstructure of the porous material are shown. The bottom plots show the pillar of height 10 m and width 5 m, experiencing a downward force of \(10\,\mathrm{N}\) at its top. Three settings are seen, one with the initial microstructure (left), one with the optimized microstructure (middle), and finally one with the material without holes (right)

Full size image
Fig. 15
figure 15

Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the compliance minimization run in a pillar

Full size image

6.2 Second example: compliance minimization in an inhomogeneous beam

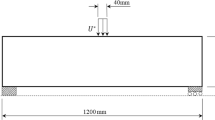
We consider a two-dimensional beam of 1 m height and 10 m width. The beam is made of a material with elasticity modulus \(E=100\,\mathrm{Pa}\) and Poisson ratio 0.3 within the inclusions of its microstructure. Outside of the inclusions, the material is inhomogeneous with an elasticity modulus \({\tilde{E}}(r)\le 20\,\mathrm{Pa}\) and a Poisson ratio \({\tilde{\nu }}(r)\ge 0.2\), where for \(r>0\)

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{E}}(r) = 20\big (1-\frac{f(r)}{2}\big )\,\mathrm{Pa}, \\ {\tilde{\nu }}(r) = 0.2\big (1+\frac{3}{4}f(r)\big ), \end{array} \right. \quad \text {with}\quad f(r) = -2r^3+3r^2. \end{aligned}$$

If we consider a point \(\varvec{y}_0\in \partial Y\) and a point \(\varvec{y}\) on the line from \(\varvec{y}_0\) to the microcell’s midpoint \(\varvec{y}_M\), then the elasticity modulus and Poisson ratio of the material in the point \(\varvec{y}\) are given by the evaluation of the functions \({\tilde{E}}(r)\) and \({\tilde{\nu }}(r)\) at \(r :=\Vert \varvec{y}-\varvec{y}_0\Vert _2/ \Vert \varvec{y}_M-\varvec{y}_0\Vert _2\). This setting accounts for a material that is increasingly compressed when getting closer to the inclusion. We thereby followed the description of the evolution of the elasticity modulus and the Poisson ratio of an increasingly compressed material in Alliche (2016). Note that the inhomogeneity in the material around the inclusion can be interpreted to be caused by the manufacturing process. The material around the inclusion is compressed, thus creating space for the material to be added inside the inclusion. In this way, the density of the material increases around the inclusion which results in this inhomogeneous material considered in this example.

The beam is fixed at its left edge and a downward force of \(0.01\,\mathrm{N}\) acts at the upper right corner of the beam, i.e. \(\varvec{g}(\varvec{x}) = (0,-0.01)^\intercal\) for \(\varvec{x}=(10,1)\) and \(\varvec{g}(\varvec{x}) = \varvec{0}\) elsewhere. We then aim at finding an optimal design for the shape of the inclusions in its microstructure, such that the beam’s compliance is minimized while the material contained in the inclusion is \(25\%\) of the material in the beam, i.e. \(\omega _0 = 0.25\). To this end, we set the parameter \(\alpha\) in the objective function (2.15) to \(\alpha =2\times 10^{-1}\). This value differs from the value of \(\alpha\) in Sect. 6.1 because in both examples \(\alpha\) has been chosen proportionally to the value of the compliance (2.14) evaluated at the initial shape \(\omega _0\). The initial compliance is \(\sim \!\!10^{2}\) in Sect. 6.1 while here it is \(\sim \!\!10^{-2}\).

Fig. 16
figure 16

On the right, the initial and optimized inclusions in the microstructure of the composite material are shown. The left-hand side shows three plots of a beam of height 1 m and width \(10\,\mathrm{m}\) experiencing a downward force of \(0.01\,\mathrm{N}\) on its right upper corner. Three settings are seen, one with the initial microstructure (top), one with the optimized microstructure (middle), and finally one with the material composed solely of the more elastic material (bottom)

Full size image
Fig. 17
figure 17

Convergence history curves of the objective function and the \(\ell _2\)-norm of the shape gradient during the compliance minimization run in a beam

Full size image

We start the optimization run with a circle of radius 0.1 as initial guess. The optimization was halted after 16 optimization steps, since the quadratic line search suggested to use a step size smaller than \(10^{-7}\) in five consecutive optimization steps. The outcome of the optimization run is found in Fig. 16. During the optimization run, the value of \(\lambda\) was updated once after the tenth optimization step, which is visible in Fig. 17. The value of the \(\ell _2\)-norm of the shape gradient evolves from approximately \(3.19 \times 10^{-2}\) to \(9.79\times 10^{-3}\). We have \(J_C(\omega _0,0)\approx 1.66\times 10^{-2}\) at the beginning of the optimization run when evaluating the objective function (2.15) with \(\lambda =0\), and at the end in step 16 we have \(J_C(\omega _{16},0)\approx 7.14\times 10^{-3}\).

7 Conclusion

In this article, shape sensitivity analysis of the effective tensor in case of periodic materials has been performed. In particular, we computed the Hadamard representation of the shape derivative of the least squares matching of a desired material tensor. Numerical experiments by means of a finite element implementation in the two-dimensional setting have been presented for composite materials and for perforated plates. Likewise to Dambrine and Harbrecht (2020), it has been observed that the computed optimal shapes depend on the initial guess, which means that the solution of the problem under consideration seems to be in general not unique. We emphasize, however, that a volume constraint as in the case of compliance optimization is not necessary when considering the least squares matching—the optimization algorithm stagnates in the (nonunique) minimum.