Abstract
Most parallel surrogate-based optimization algorithms focus only on the mechanisms for generating multiple updating points in each cycle, and rather less attention has been paid to producing them through the cooperation of several algorithms. For this purpose, a surrogate-based cooperative optimization framework is here proposed. Firstly, a class of parallel surrogate-based optimization algorithms is developed, based on the idea of viewing the infill sampling criterion as a bi-objective optimization problem. Each algorithm of this class is called a Sequential Multipoint Infill Sampling Algorithm (SMISA) and is the combination resulting from choosing a surrogate model, an exploitation measure, an exploration measure and a multi-objective optimization approach to its solution. SMISAs are the basic algorithms on which collaboration mechanisms are established. Many SMISAs can be defined, and the focus has been on scalar approaches for bi-objective problems such as the \(\varepsilon \)-constrained method, revisiting the Parallel Constrained Optimization using Response Surfaces (CORS-RBF) method and the Efficient Global Optimization with Pseudo Expected Improvement (EGO-PEI) algorithm as instances of SMISAs. In addition, a parallel version of the Lower Confidence Bound-based (LCB) algorithm is given as a member within the SMISA class. Secondly, we propose a cooperative optimization framework between the SMISAs. The cooperation between SMISAs occurs in two ways: (1) they share solutions and their objective function values to update their surrogate models and (2) they use the sampled points obtained from different SMISAs to guide their own search process. Some convergence results for this cooperative framework are given under weak conditions. A numerical comparison between EGO-PEI, Parallel CORS-RBF and a cooperative method using both, named CPEI, shows that CPEI improves the performance of the baseline algorithms. The numerical results were derived from 17 analytic tests and they show the reduction of wall-clock time with respect to the increase in the number of processors.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In many engineering applications, such as thermodynamic analysis, engine design, structural analysis or reservoir simulation, computer simulations are used as models of real systems. The search of the optimal simulation parameters often involves optimizing such models. These applications are notable examples of black-box optimization in which the analytical expression of the objective function and/or the constraints are unknown. The challenges of handling black-box functions are: (1) they are computationally expensive, i.e., these simulations are time consuming and (2) no gradient-based methods can be used, and thus analytically-based stopping criteria are not available. For example, in problems with black-box functions such as those in Jakobsson et al. (2010), each engine simulation takes around 48 h, or in Rezaveisi et al. (2014), the evaluation of a reservoir simulation may take several days.
Contemporary simulation-based optimization methods include heuristic methods, stochastic approximations and surrogate-based methods. Metaheuristics are global optimization methods, but require a large number of iterations to achieve convergence, and are impractical for these problems. In order to deal with the high computational cost, surrogate models [also known as meta-models or Response Surface Methods (RSMs)] are commonly applied in the literature, mainly because they use a limited number of function evaluations.
This paper focuses on parallel surrogate-based optimization methods. The inclusion of multiple points per major iteration to update the surrogate model allows us to take advantage of parallel computing capabilities, and offers great potential for reducing the wall-clock time required to solve a global optimization problem.
Previous algorithms (Viana et al. 2013; Liu et al. 2017) have taken into account multiple surrogate models, working independently or via multi-objective optimization, to derive multi-point infill sampling criteria. This study proposes a complementary approach based on the cooperation of parallel surrogate-based optimization methods. To achieve this goal, first, we introduce a formal definition of the class of algorithms that can cooperate with each other. Each algorithm in the class is named Sequential Multi-point Infill Sampling Algorithm (SMISA). The definition of a SMISA requires the introduction of the so-called exploitation and exploration measures. A combination of both measures describes a bi-objective problem that, together with the solution method, defines the SMISA. The key point is that the exploration measures are independent of the surrogate model and this means that: (1) the SMISAs may generate sequentially q points per cycle by updating the exploration measure and (2) there is coordination between these SMISAs through exploration measures. This framework not only allows existing parallel infill criteria to be described but is also a way to generate new methods. This framework has been applied to derive a parallel version of the Lower Confidence Bound-based algorithm given in Dennis and Torczon (1997).
The motivation of this cooperation is to create a more robust parallel infill criterion by combining several with complementary features. For example, different algorithms can be used, each of them suitable for certain problems depending on their dimensionality, the level of uncertainty, the grade of multimodality, etc. Through sharing their infill samples during the infill selection process, the performance of the ensemble infill criterion could be better than its components.
The remainder of the paper is organized as follows. Section 2 describes the state-of-the-art approaches. Section 3 introduces the proposed surrogate-based cooperative optimization framework, and its theoretical properties are described in Sect. 4. Section 5 illustrates the performance of these algorithms on a number of benchmark functions. Finally, our concluding remarks are given in Sect. 6.
2 Prior research
We consider the following optimization problem:
where the objective function is not known in a closed form, i.e. it is a black-box function. We will assume that the value of the objective function can be calculated, for example, by doing a simulation or experiment in a laboratory (for instance, chemically) to give the value of f or at least to obtain an approximate value for f. This approximation can be caused by a truncation of the execution or to the introduction of noise in the experiment, when it is not possible to control all the parameters involved.
We assume that the problem (1) has the following features:
-
1.
\({{\mathcal{D}}}\) is a compact set of \(\mathop {\mathbb {R}}\nolimits ^\nu \);
-
2.
\(x\in {\mathcal{D}}\) is a vector of continuous variables;
-
3.
f is continuous on \({\mathcal{D}}\);
-
4.
there is a single objective function;
-
5.
f is expensive to evaluate;
-
6.
f is a black-box function and no analytical derivatives of f are available.
Surrogate-based optimization techniques are a successful strategy for solving this kind of computationally expensive optimization problem. A prototype scheme is shown in Algorithm 1.

The procedure begins with an initialization phase in which a set of samples is chosen. In this phase, experimental design techniques such as Symmetric Latin Hypercube Designs (SLHD) (Ye et al. 2000), CORNER (Müller 2012) or Minimax and Maximin distance designs (Johnson et al. 1990) are usually used.
In Step 2, an approximation of the expensive objective function is built using the set of sampled points; this is the so-called surrogate model. Several surrogate models have been proposed for approximating the expensive objective function, such as polynomial response surface models, moving least squares, radial basis functions (RBFs), kriging methods, artificial neural networks, support vector regression or combinations of these. A review of these methods is given in Vu et al. (2017) and Forrester and Keane (2009). This approximation of the objective function may have a local character, such as polynomial response surfaces which are defined on a region of interest. In contrast, with global approximations such as artificial neural networks, radial basis functions or kriging methods, all the points for which the objective values are known are used to build the surrogate model for the expensive function.
In Step 3, an infill sampling criterion is designed using the surrogate model. The point selection criterion should balance the information from the unexplored feasible region with the search in promising areas of the design space (according to the surrogate model). From a global optimization view, these issues are respectively known as exploration and exploitation stages. Depending on the weights of these factors, the search is driven more towards optimization or to filling of the feasible region.
This is a sequential scheme in which a single point is introduced at each major iteration. To enable the incorporation of multiple new samples at each updating cycle, parallel infill strategies have been proposed in recent years to reduce the optimization wall-clock time. A taxonomy of these methods can be considered according to two fundamental features: (1) the use of single/multiple infill criteria and (2) how they approach the exploration/exploitation stages. In essence, it is a bi-objective optimization problem and this can be approached through Pareto dominance or by weighting to balance exploration and exploitation. A rough taxonomy classifies parallel algorithms into three large groups:
-
Single infill criterion These methods address the bi-objective nature of the exploration/exploitation dilemma through scalarization methods in multi-objective optimization such as the weighting methods. This group of methods uses one optimization on one parametrized infill criterion to select a new point and leads to a sequential point generation scheme. Within these methods, a distinction should be made between those that employ an uncertainty-based criterion and a distance-based criterion. The algorithms q-points Expected Improvement (q-EI) (Ginsbourger et al. 2010), Kriging Believer (KB), Constant Liar (CL), Efficient Global Optimization with Pseudo Expected Improvement (EGO-PEI) (Zhan et al. 2017), Local Metric Stochastic RBF with Restart (LMSRBF-R) (Regis and Shoemaker 2009), Parallel Constrained Optimization using Response Surfaces (Parallel CORS-RBF) (Regis and Shoemaker 2007c) and parallel Gutmann-RBF (Regis and Shoemaker 2007b, c) fall into this category.
-
Multiple infill criteria addressed with a multi-objective approach The use of multiple infill criteria allows a multi-objective optimization problem to be stated. These methods select q points from the Pareto frontier as the new set of points to be sampled. Some examples in this category are Multi-Objective Infill criterion for Model-Based Optimization (MOI-MBO) (Bischl et al. 2014) and Surrogate Optimization with Pareto Selection (SOP) (Krityakierne et al. 2016).
-
Multiple independent infill criteria. These techniques employ multiple infill criteria, derived from multiple surrogate models and/or multiple measures, and get q points from q different criteria. The algorithms Multiple Surrogate Efficient Global Optimization (MSEGO) (Viana et al. 2013) and that given in Beaucaire et al. (2019) belong to this category.
We will now review the above methods starting with the first group for uncertainty-based measures. The simplest infill criterion considers the addition of a single point at the current iteration. In Jones et al. (1998) Efficient Global Optimization (EGO) is proposed, which is one of the most widespread methods. This method is based on kriging basis functions (Krige 1951), which provide the error in the estimates of the surrogate model. EGO uses the Expected Improvement (EI) metric to define the infill criterion which balances the need for a surrogate objective value (exploitation) together with the uncertainty of the model (exploration).
The first parallelization strategy of EI was based on introducing all the maxima found in the EI by the search algorithm (Schonlau 1997; Sóbester et al. 2004). In Ginsbourger et al. (2010) the EI approach is generalized to a multi-point optimization criterion, the so-called q-EI. Ginsbourger et al. (2010) analyzes the analytic formula for the case \(q = 2 \), but solving for the case \(q>2\) requires expensive Monte Carlo simulations of Gaussian vectors. To reduce the corresponding computational burden, two heuristics, Kriging Believer (KB) and Constant Liar (CL), are introduced to obtain approximately q-EI optimal designs. Parr et al. (2012) uses the q-EI criterion to handle constraints using a probabilistic approach. Zhan et al. (2017) proposes a new infill criterion named Pseudo Expected Improvement (PEI) defined by the multiplication of the EI criterion by an influence function of the sampled points. This method selects sequentially the q candidate points by the optimization of the PEI criterion. The resulting algorithm is called EGO-PEI and numerically it is shown that EGO-PEI gains significant improvements when compared with CL.
The methods based on a single infill criterion that do not have an uncertainty structure use distance-based refinements. For general surrogate models, Regis and Shoemaker (2007a) introduces the Metric Stochastic Response Surface method (MSRS) to choose the candidate point as the best weighted score from two criteria: estimated function value obtained from the response surface model, and minimum distance from previously evaluated points. Regis and Shoemaker (2009) proposes a parallel extension of MSRS to reduce the total elapsed time required by response surface-based global optimization methods. The numerical experiments show that the so-called LMSRBF-R is competitive with the alternative parallel RBF methods.
The CORS-RBF algorithm was introduced in Regis and Shoemaker (2005, 2007b). This method chooses the next point by optimizing the surrogate model but restricts the feasible region, requiring the new point to be away from the current points by a certain threshold. This threshold is iterated between a set of values allowing exploration stages for large values and, in other iterations, exploitation stages for small values. This sampling strategy is dense and converges to the global optimum. A parallel version of CORS-RBF is introduced in Regis and Shoemaker (2007c).
Gutmann (2001) proposes a radial basis function method for global optimization (Gutmann-RBF). The infill criterion used is simply to add a new single point and it is based on the “least bumpy” of the interpolation surface. This criterion requires an estimate of the optimal value of the problem. This value changes from iteration to iteration in order to balance the exploration and exploitation stages. Regis and Shoemaker (2007b, c) parallelize the Gutmann-RBF based on the parametrization of the Bumpiness Minimization Subproblem (BMS).
Under a multi-objective perspective, the multiple infill criteria are addressed simultaneously instead of aggregating them into a single criterion. These methods give an approximate Pareto frontier of q points. Bischl et al. (2014) proposes the MOI-MBO method, which is based on kriging models and takes into account both the diversity and the expected improvement of the proposed points. The numerical experiments show that MOI-MBO outperforms single-step EGO. Horn and Bischl (2016) applies an extension of this algorithm to the hyperparameter tuning problems in machine-learning algorithms.
Krityakierne et al. (2016) proposes a parallel surrogate-based algorithm where simultaneous candidate searches are performed around the Pareto centers, called SOP, which considers the trade-off between exploration and exploitation stages as a bi-objective optimization problem where the two objectives are the expensive function value of the point and the minimum distance of the point to previously evaluated points. In SOP, unlike in LMSRBF-R, the new points are randomly obtained from the different centers.
An example of algorithms from the third group is the MSEGO algorithm, given in Viana et al. (2013). MSEGO uses q general surrogate models. MSEGO imports error estimates from different instances of kriging models and uses them with all other surrogates; as a result, a different EI is obtained for each surrogate, and maximizing EIs, provides up to q points per cycle. Liu et al. (2017) addresses the aerodynamic shape optimization of transonic wings by using a combination of multiple infill criteria, with each criterion choosing a different sample point. This method does not establish coordination mechanisms between criteria.
A class of parallel methods that can be seen as an adaptation of metaheuristic algorithms to expensive black-box optimization problems are parallel surrogate-assisted evolutionary algorithms (Díaz-Manríquez et al. 2016).
Potter and Jong (1994) proposes a cooperative co-evolutionary framework for optimization. Its initial objective was to improve the performance of Genetic Algorithms and other Evolutionary Algorithm-based optimizers. This seminal work has been extended and applied to large-scale black-box optimization by using surrogate models (Yi et al. 2016; Omidvar et al. 2017; Wang et al. 2018; Blanchard et al. 2019, among others). These approaches divide the problem into several smaller subproblems and then solve them individually by using an evolutionary algorithm. The cooperative strategy is established between individuals from the different subpopulations. Each individual is concatenated with the best candidates from the other subpopulations, to form a complete candidate solution, which is then fed into the objective function. The cooperation strategy between the evolutionary algorithms leads to a partition of the search space and allows the so-called curse of dimensionality to be addressed.
In a situation of surrogate-based multiobjective evolutionary algorithms, Martinez Zapotecas and Coello Coello (2013) used cooperative RBF networks, with the aim of improving the prediction of the objective function values. The cooperative strategy used in evolutionary algorithms is a mechanism to improve the performance of the algorithm, but in this paper it is used to coordinate several infill sampling criteria.
We have not reviewed other types of parallel algorithms as they deviate from the methods proposed in this article and the interested readers can consult a more comprehensive review of the literature in Haftka et al. (2016).
3 A surrogate-based cooperative optimization framework
The section is structured as follows. First, we define the class of algorithms that can be used to cooperate to find the optimal solution. Each algorithm of this class is named Sequential Multi-point Infill Sampling Algorithm (SMISA). The definition of a SMISA is based on bi-objective optimization to derive q-points infill sampling criteria using a single surrogate model. The algorithms of this class (the SMISAs) are those that may be chosen to work cooperatively.
We then describe a synchronous cooperative scheme for SMISAs in which parallel computing capabilities are used to evaluate the expensive objective function.
3.1 SMISA: a type of q-points infill sampling criterion based on a single surrogate model
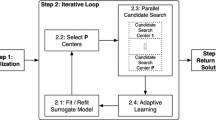
In order to solve the optimization problem described in Sect. 2, we are interested in algorithms that have a general structure like that shown in Fig. 1. The essential characteristic is that the sampling strategy does not generate a single point y per cycle but a set \(Y^t=\{y^*_1,\ldots ,y^*_q\}\) of q points in each major iteration t.
In these algorithms, the number of retained points may be up to k. This is because, in the infill criterion with q points, the number of generated points can become large, thus taking more time to update the surrogate model. We propose a criterion called the pruning strategy to restrict the number of retained points to update the surrogate model. This is secondary in this research and is analyzed in “Appendix 2”.
The SMISAs exhibit the structure shown in Fig. 1. A first step in the formalization of a SMISA is the stating of the infill sampling criterion, based on two essential criteria:
-
1.
reduction of the level of uncertainty in the region and
-
2.
the sampled area is close to the most promising regions.
Conditions (1) and (2) will define respectively the exploration and exploitation capacities of the resulting SMISA. Mathematically, it is bi-objective in nature and can be expressed as:
The formalization of the problem (2), in this paper called the sampling problem, requires the definition of indexes to measure criteria (1) and (2). In this paper, exploration measure means an index that allows us to evaluate the quality of a new solution with respect to the uncertainty of the whole search space, while exploitation measure is an index that allows us to estimate the improvement of the objective function at a new point. These concepts will be formalized as follows.
Definition 1
(Exploration measure) An exploration measure of a set \({\mathcal {D}}\) sampled on the set \(Z \subseteq {\mathcal {D}}\) is any function
where \(\mathcal P({\mathcal {D}})\) is the power set of \({\mathcal {D}}\) and for all \(x\in {\mathcal {D}}\) and for all \(Z,Z'\subseteq {\mathcal {D}}\), the following conditions are satisfied:
-
1.
\(d_{Z\cup Z'}(x)\le d_Z(x)\),
-
2
\(d_Z(x) \ge 0\),
-
3.
\(d_Z(x)=0 \Rightarrow x\in cl(Z)\), where cl(Z) is the closure set of Z.
Condition (1) indicates that the uncertainty decreases if new points are added to the sampled set, Condition (2) expresses that there is always uncertainty and, when the cardinality of Z is finite, Condition (3) implies that if there is no uncertainty at a point x, i.e. \(d_Z(x) =0\), then it must have been sampled, i.e. \(x\in Z\). Note that the cardinality of Z is finite in the practical application of the algorithms.
The exploitation measures estimate the objective function at a point x or alternatively, the improvement in the objective function with respect to a set of previously sampled points. Several measures of this type have been defined in the literature. We have provided a definition of the exploitation measure using the lowest common denominator of all of them, to be able to accommodate them in a unified definition; the essential element is that they use a decreasing transformation of the surrogate model to do so.
Definition 2
(Exploitation measure) Let \(Z\subseteq {\mathcal {D}}\) and let \(S_Z(x)\) be a surrogate model of f(x), defined on the set Z, then an exploitation measure is a transformation of \(S_Z(x)\), i.e. \(w_Z(x):=\psi (S_Z(x),x)\), in which the function \(\psi (s,x)\) is decreasing on the variable s for all \(x\in {\mathcal {D}}\).
The infill sampling criterion has a bi-objective nature: (1) a goal defined by means of the exploration measure \(d_X(y)\) to weigh the current uncertainty level of the different parts of the region \({\mathcal {D}}\) and (2) a second goal expressed by the exploitation measure \(w_X(y)\) to assess the quality of y to be a minimum of the objective function. The infill sampling criterion, i.e the sampling problem, is stated as:
-
Bi-objective infill sampling criterion
$$\begin{aligned} \hbox {Maximize }&\quad {\mathbf {F}}= \left( d_X(y), w_X(y) \right) ^\top \nonumber \\ \hbox {Subject to:}&\quad y\in {{\mathcal {D}}} \end{aligned}$$(3)
The parallel infill criterion consists of the selection of q points of the Pareto frontier of the bi-objective problem (3). A basic multi-objective optimization method is the \(\varepsilon \)-constrained method, which maximizes one objective subject to the additional constraint derived from the other objective. One issue with this approach is that it is necessary to preselect which objective to maximize. We consider:
where \(\varepsilon \) represents the worst value \(d_X\) that is allowed to be taken. It has been shown that if the solution to the problem (4) is unique, then it is a Pareto optimal solution.
Note that, unlike what happens with the exploitation measures, the exploration measures are independent of the function f(x). It allows the exploration measure to be updated each time a new point is obtained. In each major iteration, the surrogate model \(S_X(x)\) is updated on the set of sampled points X, and it is necessary to know the value of the objective function f(x) at every point \(x\in X\), but the exploration measure \(d_X(y)\) can be updated each time in problem (4), which is solved without the need to evaluate the objective function at these new points. We now formalize this. Let \(\{y^*_1,\ldots ,y^*_{j-1}\}\) be the previously generated points and let \(Z_j \subseteq X \cup \{y^*_1,\ldots ,y^*_{j-1}\}\), we define the jth point \(y^*_j\) to be added to the sampled points as an optimal solution of the problem:
-
Modified\({\varvec{\varepsilon }}\)-constrained method\(\rightarrow \)Hard multi-point infill criterion
$$\begin{aligned} \hbox {Maximize }&\quad w_X(y_j)\nonumber \\ \hbox {Subject to: }&\quad d_{Z_j}(y_j)\ge \varepsilon _j\nonumber \\&\quad y_j\in {{\mathcal {D}}} \end{aligned}$$(5)
The selection of values of \(\varepsilon _j\) is problematic as for many values of \(\varepsilon _j\) there will be no feasible solution. A way of choosing \(\varepsilon _j\) to avoid this is to set \(\varepsilon _j=\beta _j \varDelta _j\) with \(\varDelta _j={\mathop {{\hbox {Maximize }}}\nolimits_{x \in {{\mathcal {D}}}}}d_{Z_j}(x) \) and \(0\le \beta _j <1\).
The problem (5) may contain many local minima and optimizers such as metaheuristics may be good choices to address it. These methods have been developed intensively for unconstrained optimization (García-Ródenas et al. 2019) leading to the consideration of another way to scalarize a bi-objective optimization problem. Assuming that the exploitation measure satisfies \(w_X(y)>0\) for all \(y\in {\mathcal {D}}\), the following sampling problem is stated:
-
Alternative scalarization approach\(\rightarrow \)Soft multi-point infill criterion
$$\begin{aligned} \hbox {Maximize }&\quad d_{Z_j}(y_j) w_X(y_j)\nonumber \\ \hbox {Subject to: }&\quad y_j\in {{\mathcal {D}}} \end{aligned}$$(6)
If we compare the two problems (5) and (6), we observe that the problem (6) attempts to satisfy the constraints of the problem (5) in a soft way. For this reason, we refer to the approach (5) as hard and the criterion (6) as soft.
The sequential multi-point infill sampling criterion is summarized in Algorithm 2.

Once the above definitions have been introduced, we will formalize the following concept.
Definition 3
(SMISA) A Sequential Multi-point Infill Sampling Algorithm (SMISA) is any algorithm of the parallel surrogate-based optimization framework given in Fig. 1 in which the infill sampling criterion is defined by Algorithm 2.
The SMISA framework only includes sequential infill sampling processes. Other approaches, such as q-EI or multimodal optimization, do not belong to this algorithmic class. The objective in formulating this class of algorithms is to determine which can be included in the cooperative scheme. Furthermore, this unified overview also allows the development of new algorithms by combining elements of the existing ones.
3.2 Instances of sequential multi-point infill sampling algorithms
There are several algorithms described in the literature that fall within this framework. Two noteworthy examples are: EGO-PEI, developed in Zhan et al. (2017) and Parallel CORS-RBF, described in Regis and Shoemaker (2007c). This section outlines the realization of these algorithms as instances of SMISAs, and a new one is being proposed, which consists of a parallel version of the Lower Bound Confidence-based algorithm (Dennis and Torczon 1997).
3.2.1 The Parallel CORS-RBF
The Parallel CORS-RBF is a hard approach in which the exploitation measure \(w_X(s)\) is chosen as
being \(S_X(s)\) a radial basis function. In this example \(\psi (s,x)=-s\), and \(\frac{\partial \psi }{\partial s}=-1<0\) and it decreases for all x.
The Parallel CORS-RBF uses as exploration measure:
where \(\Vert \cdot \Vert _2\) is the Euclidean norm. The measure \(d_Z(x)\) calculates the shortest distance between x and the elements of the set Z. The infill problems for Parallel CORS-RBF become:
-
Parallel CORS-RBF
$$\begin{aligned} \hbox {Minimize }&\quad S_X(y_j)\nonumber \\ \hbox {Subject to: }&\quad d_{Z_j}(y_j)\ge \varepsilon _j\nonumber \\&\quad y_j\in {{\mathcal {D}}} \end{aligned}$$(9)
where the set \(Z_j\) is defined by \(Z_j=X\cup \{y^*_1,\ldots ,y^*_{j-1}\}\) and the parameters \(\varepsilon _j\) are derived from the above parameters \(\beta _j\).
3.2.2 The EGO-PEI
The EGO-PEI algorithm (Zhan et al. 2017) is based on kriging models. A simple kriging model can be built as follows:
where \(\mu \) is the mean of the Gaussian process, and \(\varepsilon (x)\) is the noise term which is normally distributed with mean zero and variance \(\sigma ^2\). The errors on two points \(x,z\in {{\mathcal {D}}}\), i.e. \(\varepsilon (x)\) and \(\varepsilon (z)\), are correlated and the correlation depends on the distance between these points:
EGO-PEI uses a soft multi-point infill sampling criterion in which the exploration measure is the product of correlations between the sampled points and the new point:
Note that, \(d^{\mathrm{EGO-PEI}}_Z(x)\) satisfies the properties (1)–(3) of a exploration measure.
To define the exploitation measure the EGO-PEI algorithm chooses the expected improvement (Jones et al. 1998):
where \(f_{min}\) is the current best function value, i.e. \( f_{min}={\mathop {\mathrm{min}}\nolimits_{x\in X}} f(x)\) ; \(\varPhi \) and \(\phi \) are the normal cumulative distribution and density functions, respectively.
To demonstrate that the expected improvement is an exploitation measure, we express \(\hbox {EI}_X(x)=\psi (S_X(x),x)\) where \(\psi (s,z)=\sigma _X (x) \bigg (z \varPhi (z) +\phi (z) \bigg ) \hbox { and }z(s,x)=\frac{f_{min}-s}{\sigma _X(x)}.\) Applying the chain rule, \(\dfrac{\partial \psi (s,x)}{\partial s}=\dfrac{\partial \psi }{\partial z}\cdot \dfrac{\partial z }{\partial s}= \sigma _X (x) \left( \varPhi (z) +z\phi (z)+\phi '(z) \right) \left( \dfrac{-1}{\sigma _X(x)} \right) .\) From the definition of \(\phi (z)=\frac{1}{\sqrt{2\pi }} e^{-\frac{1}{2}z^2}\), there holds that \(z\phi (z)+\phi '(z)=0\), and thus \( \dfrac{\partial \psi (s,x)}{\partial s}=- \varPhi (z)<0\) because \(0<\varPhi (z)<1\) for all z. The condition \(\frac{\partial \psi }{\partial s}<0\) is satisfied.
Finally, the sampling problem is stated:
-
EGO-PEI
$$\begin{aligned} \hbox {Maximize }&\quad d^{\text {EGO-PEI}}_{Z_j}(y_j) EI_{X}(y_j)\nonumber \\ \hbox {Subject to: }&\quad y_j\in {{\mathcal {D}}} \end{aligned}$$(13)
where \(Z_j=\{y^*_1,\ldots ,y^*_{j-1}\}\).
3.2.3 The parallel lower confidence bound-based algorithm
This section introduces a novel parallel surrogate-based optimization algorithm. This algorithm can be seen as a parallel version of the Lower Confidence Bound-based (LCB) algorithm proposed by Dennis and Torczon (1997). This method is based on kriging models, and it employs the infill sampling criterion:
where \(\alpha >0.\) A simple interpretation of this infill criterion within the SMISA considers \(-S_X(x)\) as the exploitation measure, the standard deviation \(\sigma _X(y)\ge 0\) as the exploration measure, and the weighted sum method as optimizer for multiobjective optimization of (2).
We now re-interpret it as a soft infill sampling criterion, highlighting the great degree of generality of the soft approach. We chose
where \(\mu < {\mathop {\mathrm{min}}\nolimits_{x\in \mathcal {D}}} S_X(x)\). The exploitation measure is decreasing in the surrogate model and positive. The soft infill sampling criterion becomes:
We now show that problem (17) is equivalent to problem (14). We will apply a refinement of the arguments given in Jagannathan (1966) for fractional optimization. Both problems are parameterized, respectively by \(\mu \) and \(\alpha \). We will demonstrate that given an arbitrary value \(\alpha >0\) there is a parameter \(\mu \) so that the fractional problem has the same solutions. Let \(\alpha >0\) and let \(y^*\) be an optimal solution to the problem (14) for this value of the parameter \(\alpha \), we define \(\mu =S_X(y^*)-\alpha \sigma _X(y^*)\). From the optimality of \(y^*\) for (14), the following holds:
From the definition of \(\mu \), we express Eq. (18) as
Because \(-\alpha \sigma _X(y)\le 0\) for all y, Eq. (19) leads to the inequality \(S_X(y)-\mu \ge 0\) for all \(y\in \mathcal {D}\). Using this inequality to express Eq. (19) as
which, on the other hand, holds as an equality for \(y=y^*\)
and this in turn, proves the optimality of \(y^*\) for the soft infill sampling criterion.
The identification of the exploration and exploitation measures in the infill sampling criterion allows the introduction of the parallelization procedure for the algorithm. The key point is that the standard deviation \(\sigma _X(y)\) does not depend on the values f(y) in kriging models. Both parametric infill sampling criteria are equivalent. The formulation (14) is computationally advantageous because some fractional optimization techniques, such as Dinkelbach’s method (Ródenas et al. 1999), lead to the resolution of a sequence of optimization problems with the same structure as (14) instead of solving a single problem of this kind. Finally, the parallel sampling problem is stated:
-
Parallel-LCB
$$\begin{aligned} \hbox {Minimize }&\quad S_{X}(y_j) -\alpha \sigma _{Z_j}(y_j)\nonumber \\ \hbox {Subject to: }&\quad y_j\in {{\mathcal {D}}} \end{aligned}$$
where \(Z_j=X\cup \{y^*_1,\ldots ,y^*_{j-1}\}\).
The upper confidence bound-based algorithm (Srinivas et al. 2010) is obtained by replacing \(-\,\alpha \) with \(+\,\alpha \) in the infill sampling criterion. The interpretation of this algorithm within SMISA supports the use of the lower bounds instead of upper bounds.
3.3 Coordination of the sequential multi-point infill sampling algorithms
We assume the case shown in Fig. 2 in which multiple surrogate models and multiple exploitation/exploration measures are being used in the optimization. Certain combinations of these options, in conjunction with a soft or hard approach, provide the available SMISAs. In this section we have developed a synchronous scheme for multiple SMISAs. This scheme is a generalization of a single SMISA to the case of considering multiple SMISAs.
The cooperation mechanisms are established in two ways: the first is to share the points generated in the updating of the surrogate models, and the second is that each SMISA takes into account, in the sampling process, the regions that are being explored by the rest of the SMISAs to avoid over-emphasis on these regions. The aim is to derive ensemble infill sampling criterion in which the performance will be better than their components SMISAs.
Algorithm 3 shows the cooperative scheme. In this approach, the infill sampling problems (5) and (6) are still solved in a sequential manner. When updating the exploration measures, both the points generated by a given SMISA and the rest of the SMISAs are taken into account.

4 Convergence analysis
In this section, we analyze the convergence of the cooperative algorithms using multiple SMISAs. We denote by \( x^* \in {{\mathcal{D}}}\) a solution of our optimization problem, i.e., \(f(x^*)={\mathop {{\hbox {minimize }}}\nolimits_{x\in {{\mathcal{D}}} }} f(x)\).
The starting point for our analysis is provided by the following theorem showing that it is sufficient for an algorithm to generate a dense set of points in the feasible region to demonstrate its convergence.
Theorem 1
(Torn and Zilinskas 1989) Let\({{\mathcal{D}}}\)be a compact set. Then an algorithm converges to the global minimum of every continuous function on\({{\mathcal{D}}}\)if and only if its sequence of iterations is everywhere dense in\({{\mathcal{D}}}\).
Since every dense set has an infinite number of points, we will assume that the SMISAs do not perform the pruning operation and so retain all generated points (i.e \( k = +\infty \)). We introduce the superscript (s) associated with the SMISA and the subscript n to refer to the nth internal iteration of the algorithm s. In this way, the following notation \( y^{(s)}_n \hbox { for all } n \hbox { and for } s=1,\ldots ,p \) refers to the nth generated point by the SMISA s. We will begin our discussion on the convergence of the cooperative approach assuming that a particular SMISA algorithm \(s'\) employs the hard approach (Case a).
Theorem 2
(Convergence of the cooperative algorithm: Case a) Letf(x) be continuous functions on a compact set\({{\mathcal{D}}}\). Suppose that there exists a SMISA\(s'\), that employs a hard approach (5) satisfying the following assumptions:
-
1.
the exploration measure\(d^{(s')}_{Z_n}(y)\)is given by (8),
-
2.
the rule to select the parameters\(\varepsilon ^{(s')}_n\)is:
$$\begin{aligned} \varepsilon ^{(s')}_n=\beta ^{(s')}_n \varDelta ^{(s')}_n\, {where} \,\varDelta ^{(s')}_n=\underset{x \in {{\mathcal {D}}}}{\hbox {Maximize }}d^{(s')}_{Z_n}(x)\, {and} \,0\le \beta _n^{(s')} <1\,{and}\,\underset{n\rightarrow \infty }{\limsup } \beta ^{(s')}_n >0, \end{aligned}$$ -
3.
the relationship\(\{y^{(s')}_1,\ldots ,y^{(s')}_{n-1}\}\subseteq Z^{(s')}_n\)is satisfied, and
-
4.
it generates an infinite sequence\(\{y^{(s')}_1,y^{(s')}_2,\ldots \}\);
then the cooperative algorithm converges to the global minimum.
Proof
See “Appendix 1”. \(\square \)
Next, we will analyze the convergence of another configuration of the cooperative algorithms, consisting in a particular SMISA using a soft approach (Case b).
Theorem 3
(Convergence of the cooperative algorithm: Case b) Letf(x) be a continuous function on a compact set\({{\mathcal{D}}}\). Suppose that there exists a SMISA\(s'\)that employs a soft approach (6), satisfying the following assumptions:
-
1.
the exploration measures\(d^{(s')}_{Z_n}(y)\)are given by (8),
-
2.
the exploitation measure satisfies
$$\begin{aligned} 0<m<w_X(x)< M \hbox { for all } x\in {{\mathcal {D}}} \hbox { and for all } X\subset {{\mathcal {D}}}, \end{aligned}$$(22) -
3.
the relationship\(\{y^{(s')}_1,\ldots ,y^{(s')}_{n-1}\}\subseteq Z^{(s')}_n\)holds, and
-
4.
it generates an infinite sequence\(\{y^{(s')}_1,y^{(s')}_2,\ldots \}\);
then this cooperative algorithm converges to a global minimum.
Proof
See “Appendix 1”. \(\square \)
Theorems 2 and 3 can be applied to a single SMISA, obtaining as corollaries two sufficient conditions of convergence for the algorithmic class SMISAs. In general, any sufficient condition of convergence of the cooperative algorithm should be applicable to a single SMISA and therefore would establish the convergence of the sole SMISA. The convergence of a certain SMISA \(s'\) is an implicit assumption for any sufficient condition of convergence of a cooperative algorithm.
5 Numerical experiments
5.1 Parallel surrogate-based optimization algorithms
The algorithm proposed in this paper describes a cooperative strategy among a family of parallel surrogate-based optimization algorithms (defined in Sect. 3.1). As previously mentioned, each element of this algorithmic class is called a SMISA. They share the points sampled to update the surrogate models and their exploration measures enable them to be coordinated. It is therefore essential to define SMISAs that may be complementary in the search tasks.
In this numerical experiment the selection of the parallel surrogate optimization algorithms has taken into account an important point found in the work of Díaz-Manríquez et al. (2011). Díaz-Manríquez et al. (2011) compared four meta-modeling techniques, polynomial approximation, kriging, radial basis functions (RBF) and support vector regression (SVR), in order to select the most suitable technique to be combined with evolutionary optimization algorithms. They found that the best approach to be used in low dimensionality problems can be kriging or even SVR. In contrast, when trying to optimize a high dimensional problem, then, the best technique is RBF. For this reason, two types of surrogate models have been used in the numerical experiments: RBF Thin Plate Spline (TPS) and kriging models.
We have chosen the following radial-basis-based algorithm: CORS-RBF, introduced in Regis and Shoemaker (2007c). Regis and Shoemaker reported good results for CORS-RBF compared to a parallel multistart derivative-based algorithm, a parallel multistart derivative-free trust-region algorithm, and a parallel evolutionary algorithm. The CORS-RBF method has a comparable performance to the parallel Gutmann-RBF method. The CORS-RBF algorithm can be a good state-of-the-art exponent in algorithms based on radial basis.
A state-of-the-art parallel EGO algorithm is the Constant Liar approach. Zhan et al. (2017) proposed the EGO-PEI algorithm and conducted a numerical experiment on 6 test problems, showing that the EGO-PEI algorithm performs significantly better than the Constant Liar approach. This result is the motivation for choosing EGO-PEI as a representative of the parallel algorithms based on kriging models.
As shown in Sect. 3.2 CORS-RBF and EGO-PEI algorithms are instances of this family of parallel surrogate optimization algorithms and they have been chosen as SMISAs; the resulting cooperative algorithm is named CPEI. A proper acronym for this algorithm could be CORS-RBF \(+\) EGO-PEI, but due to its excessive length we have preferred to shorten it to CPEI. We are interested in creating a strategy that combines the advantages of CORS-RBF and EGO-PEI regarding the dimensionality of the problem.
We also conduct a numerical experiment on the performance of Parallel Lower Confidence Bound-based algorithm in “Appendix 3”. Parallel LCB is proposed as a new instance of the SMISA framework and it is also based on kriging models. For this reason, Parallel LCB is compared with EGO-PEI. This experiment addresses the secondary objective of showing that SMISA contains novel algorithms that can be considered as part of the state of the art.
5.2 Test problems
We use seven benchmark functions taken from Dixon–Szegö test bed (Dixon and Szegö 1978) and ten benchmark noiseless functions taken from the Real-Parameter Black-Box Optimization Benchmarking (BBOB) test suite (Hansen et al. 2009), namely functions F15–F24. The first set of functions has been widely used in the literature and is composed of small-size problems (see Table 1 for descriptive statistics); these test functions have one global minimum. All test functions of the second suite (see Table 2) have 10 dimensions and are multimodal, their actual search region is given as \([-5,5]^{10}\). The test problems are analytic so we do not need to worry about the computational time.
5.3 Experimental setup
We use a thin plate spline RBF interpolation model for CORS-RBF and CPEI. The kriging models for EGO-PEI and CPEI are built using the DACE (Design and Analysis of Computer Experiments) toolbox (Lophaven et al. 2002) with the following setting: Zero-order polynomial regression function (regpoly0), Gaussian correlation function (corrgauss) and the initial guess on the hyperparameter \(\theta \) is set to 1. Note that the CPEI is convergent by applying Theorem 2. The parameters \(\beta _n\) of CORS-RBF have been taken by cycling their values in the list \(\{0.9, 0.75, 0.25, 0.05, 0.03, 0\}\) and therefore the CPEI meets the hypothesis (2) of Theorem 2. Hypotheses (1) and (3) are satisfied due to the CORS-RBF definition and therefore CPEI and CORS-RBF are convergent by Theorem 2.
We use a SLHD sampling (Ye et al. 2000) to generate the initial design for all three algorithms. The size of the initial experiment was set to \(2(\nu +1)\) points. All algorithms use the same initial experimental design in order to mitigate the effect of the initial experiment on the performance. We ran twenty trials for each algorithm, for each value of q and for each test problem.
The three algorithms are run with \(q=4\), \(q=8\) and \(q=12\) function evaluations per cycle. Each algorithm requires solving q infill sampling problems per main iteration. The pseudo-expected improvement function is optimized by Particle Swarm Optimization (PSO) (function particleswarm in MATLAB). The PSO algorithm is executed with the following setting:
-
1.
Swarm size: 50
-
2.
Maximum iterations: 100
-
3.
Self adjustment weight (\(c_1\)): 1.49
-
4.
Social adjustment weight (\(c_2\)): 1.49
The infill sampling criterion for CORS-RBF is a constrained optimization problem and we use the Interior Point (IP) algorithm (function fmincon in MATLAB). The interior point method is executed using the default values and setting:
-
1.
Maximum iterations: 1000
-
2.
Maximum function evaluations: 3000
The experiments were done on a computer with the AMD Ryzen 5 1600X processor of 3.6 GHz and 6 cores for parallelization. The RAM available was 16 GB and the version of MATLAB used was R2017b. Note that in carrying out the experiments, a total of 244,784 points were generated by solving the corresponding sampling problems (optimization problems) in Dixon–Szegö test and 1,432,800 points in BBOB test suite. The computational cost of carrying out these experiments was 20 computing days.
5.4 Experiment 1: Analysis of the performance on a limited computational budget
Experiment 1 corresponds to the practical scenario in which computational resources limit the number of function evaluations that it is possible to perform. In this experiment that number has been set to a maximum of 100 principal iterations. The goal was to test whether the proposed CPEI algorithm achieves an objective function value significantly better than EGO-PEI and CORS-RBF algorithms.
Tables 3 and 4 show respectively the mean and the standard deviation of the objective function values achieved in the 20 trials for the Dixon–Szegö and BBOB test suites. In addition, the Mann–Whitney–Wilcoxon signed rank test is used to identify whether or not two algorithms are significantly different. The algorithm in each row is compared to the CPEI method and the symbol “−” represents the fact that CPEI cannot be compared to itself. When the calculated p value is smaller than the significance level \(\alpha =0.05\), we reject the null hypothesis and both algorithms are significantly different with respect to the value of the objective function for a given number of cycles. In this case, we indicate with \(h=1\) that CPEI outperforms the other algorithm and with \(h=-1\), otherwise. We use the value \(h=0\) to indicate that the null hypothesis cannot be rejected.
When doing more function evaluations per iteration, it should be expected that the algorithm improves the objective function value in less wall-clock time. Zhan et al. (2017) has observed that when more points are included in one cycle, the best results are not necessarily obtained with the greatest q value. This phenomenon may come about because multi-point infill sampling problems [such as those defined in Eqs. (5) and (6)] are highly multi-modal and their optimization becomes increasingly difficult.Footnote 1 A highlight supported by the numerical results is that this phenomenon is not present in our implementation of the CPEI algorithm, and the best results are obtained when \(q=12\) for all test problems. On the other hand, the best configuration of the EGO-PEI and CORS-RBF algorithms is reached respectively when \(q=4\) and \(q=8\) for problem F15. This is a relevant feature of the cooperative algorithms that makes it possible to take advantage of a larger number of processors.
The results confirm the initial assumption and agree with what is emphasized in the literature, that kriging models work well for low-dimensional problems such as the Dixon–Szegö test bed (fewer than 6 dimensions) while the radial basis models are a good alternative for the larger ones such as the BBOB test suite (10 dimensions). It has been observed that EGO-PEI outperforms CORS-RBF in Dixon–Szegö test bed whereas the opposite occurs for BBOB test suite. CPEI has behaved as the best alternative between CORS-RBF and EGO-PEI. If we consider the total of the 17 test problems and for \(q=12\), it is observed that CPEI wins in 4 problems to CORS-RBF (\(h=1\)), behaves like it in 13 problems (\(h=0\)) and CPEI is never worse than CORS-RBF (\(h=-1\)). If we analyze the results for the EGO-PEI we find that CPEI wins over EGO-PEI in 6 problems (\(h=1\)), ties in 10 (\(h=0\)) and loses in 1 (\(h=-1\)).
If we consider all values of q and count which configurations achieve the best results, we find that CPEI is the best option for 9 problems, CORS-RBF for 7 problems and the EGO-PEI for 6 problems. When a tie occurs, all tied algorithms are considered the best option.
If we observe which algorithm is the worst for \(q=12\), we observe that CPEI is worst in only two of the total of 17 problems: F21 and Shekel7. The conclusion drawn from Experiment 1 is that the cooperation strategy improves the robustness of the resulting algorithm, showing that for the case analyzed and for the algorithms tested, CPEI is a good choice both for problems of small dimensions and for larger.
5.5 Experiment 2: Analysis of performance to establish a predefined relative error
Experiment 1 compares the algorithms in terms of the objective function value for a given number of cycles; in Experiment 2, on the other hand, the number of iterations is not fixed and what is set is the relative error to be reached. The comparison is carried out in terms of number of cycles. Due to the great diversity of dimension in the test problems, we have considered several stopping criteria. For Dixon–Szegö problems (with dimension less than 10) we have used the same criterion as that used in Jakobsson et al. (2010), that is, the procedure stops if this relative error is smaller than \(1\%\) or a maximum of 100 major iterations has been reached. The difficulty in solving the BBOB test suite is very diverse and has led us to apply several relative errors. We have used a relative error of \(150\%\) for problems F15 and F24, of \(20\%\) for F18, of \(5\%\) for F16, of \(2\%\) for F21 and F23 and for the rest of the problems we have considered a relative error of \(15\%\). The algorithm also stops if a maximum of 100 major iterations is reached. In order to evaluate the effect of the choice of the relative errors we have shown the progress of the algorithms on the BBOB test suite in Figs. 3 and 4. It can be observed that the algorithms maintain their ranking throughout the optimization process. Therefore, the choice of a given error affects the rate of convergence but not the ranking between them.
The metrics compared are the number of cycles needed to find the optimum of the benchmark problems and the success convergence rate to achieve a near optimal solution. Both tests are solved 20 times with each algorithm and each function and the mean and standard deviation of the number of cycles required to achieve the given relative error are reported. In addition, the convergence success rate is calculated, i.e. the quotient between the number of times that a solution within the given relative error is reached and the number of attempts (in our case twenty), expressed as a percentage.
Tables 5 and 6 show the results for the Dixon–Szegö and BBOB test suites, respectively. In addition, the Mann–Whitney–Wilcoxon rank sum test is used to identify whether or not two algorithms are significantly different with respect to the number of cycles. For any algorithm \({\mathcal {A}}\), we write \(h=0\) if \({\mathcal {A}}\) and CPEI are not significantly different, we write \(h=1\) if CPEI is significantly better than \({\mathcal {A}}\) at the \(5\%\) level of significance, and we write \(h=-1\), otherwise. The difference between this test and the one used in the Experiment 1 is that in this case we consider independent samples instead of paired samples.
The first notable fact is that when the number of processors q is increased the three algorithms improve their performance. This result is essential for the efficient parallelization of the optimization of computationally expensive black-box problems, allowing the use of a large number of processors. For this reason, we note the results obtained with \(q=12\) processors.
Now we will analyze the best configuration of the algorithms, obtained when \(q=12\). If we compare CPEI with CORS-RBF, we observe that CPEI is significantly better than CORS-RBF in 6 of the 17 problems, in the other 11 problems their differences are not significant. If we compare CPEI with EGO-PEI, we observe that in 4 problems CPEI is significantly better than EGO-PEI, in 3 problems CPEI is significantly worse than EGO-PEI and in the rest of the problems (a total of 10) there are no significant differences between them. The advantage of CPEI over EGO-PEI is seen in the convergence rate. Using a significance level of \(5\%\) and the McNemar test on paired proportions we find that CPEI has a significantly better convergence rate than EGO-PEI on problems F15, F17, F18, F19 and Hartman6. There are no significant differences for the rest of the problems.
To summarize, if we analyze which is the best algorithm to solve a given problem, whether or not this improvement is statistically significant, we observe that CPEI is the best at 9 problems, EGO-PEI at 6 and CORS-RBF at 2. This shows that cooperation between CORS-RBF and EGO-PEI improves the baseline algorithms.
6 Conclusions and future research
Parallel surrogate-based optimization allows the wall-clock time needed for optimizing expensive objective functions to be reduced. The performance of these techniques varies from one problem to another depending on their characteristics, such as their dimensionality, the existence of noise, and so on. As suggested by the “No Free Lunch Theorem” (Wolpert and Macready 1997) no algorithm is best for solving all types of optimization problem. An area that is presently the subject of intensive research is to combine the best features from different algorithms to come up with a more effective algorithm in a wider domain of applications.
This paper introduces a framework to develop surrogate-based cooperative optimization strategies to address computationally expensive black-box problems. The essential methodological contributions of this article are: (1) a formal definition of a class of parallel optimization algorithms based on a bi-objective approach; each algorithm of this class is called a Sequential Multi-point Infill Sampling Algorithm (SMISA); (2) a mechanism for the coordination of SMISAs and (3) a theoretical analysis on their convergence.
Within this framework, we have focused on the combination of a parallel RBF-based algorithm, CORS-RBF, and a parallel kriging-based method, EGO-PEI. The former algorithm is called CPEI, and has been designed with the goal of obtaining a more robust convergence algorithm in a wider class of optimization problems.
In the numerical experiments, we compared CPEI with CORS-RBF and EGO-PEI on the Dixon–Szegö test bed and the F15–F24 benchmark functions taken from the BBOB test suite. The results have two major highlight: (1) the reduction of wall-clock time with respect to the number of processors q and (2) the cooperative strategy improves the convergence properties of the baseline algorithms in terms of relative error achieved and successful convergence rate.
This is a generic algorithmic class and allows multiple instances not analyzed in this study. As evidence of this, we have proposed a parallel version of the Lower Confidence Bound-based algorithm (Dennis and Torczon 1997). Another notable example is that of homogeneous cooperative strategies (García-Ródenas et al. 2017) i.e. using the same surrogate-based optimization method with different targets. The simplest example is to run different instances of an algorithm, for example CORS-RBF, but using different Latin hypercube designs and/or different hyperparameters for the RBF functions.
Emmerich et al. (2006) shows that the time complexity for the training of the kriging models is \(O(Nk^3 \nu +k^2 \nu )\), where N is the number of iterations needed to adjust the metamodel parameters, \(\nu \) is the dimension of search space, and k is the number of training data points. The cooperative framework aims to implement massively parallelizable instances and this computational cost highlights the need to address the problem of restricting the number of points when updating the surrogate model. This issue constitutes a future line of research. A pilot experiment is discussed in “Appendix 2”: Pruning strategy but it will be necessary to make a comparison with other methods proposed in the literature, such as Liu et al. (2014) and Tian et al. (2019).
References
Beaucaire P, Beauthier Ch, Sainvitu C (2019) Multi-point infill sampling strategies exploiting multiple surrogate models. In: Proceedings of the genetic and evolutionary computation conference companion, GECCO ’19, New York, NY, USA. Association for Computing Machinery, pp 1559–1567
Bischl B, Wessing S, Bauer N, Friedrichs K, Weihs C (2014) MOI-MBO: multiobjective infill for parallel model-based optimization. Revised Selected Papers. In: Pardalos PM, Resende MGC, Vogiatzis C, Walteros JL (eds) Learning and intelligent optimization: 8th international conference, Lion 8, Gainesville, FL, USA, February 16–21, 2014. Springer, Cham, pp 173–186
Blanchard J, Beauthier C, Carletti T (2019) A surrogate-assisted cooperative co-evolutionary algorithm using recursive differential grouping as decomposition strategy. In: 2019 IEEE congress on evolutionary computation, CEC 2019—proceedings, pp 689–696
Dennis JE, Torczon V (1997) Managing approximation models in optimisation. In: Alexandrov NM, Hussaini N (eds) Multidisciplinary design optimisation: state-of-the-art. SIAM, Philadelphia, pp 330–347
Díaz-Manríquez A, Toscano-Pulido G, Gómez-Flores W (2011) On the selection of surrogate models in evolutionary optimization algorithms. In: 2011 IEEE congress of evolutionary computation (CEC), pp 2155–2162
Díaz-Manríquez A, Toscano G, Barron-Zambrano JH, Tello-Leal E (2016) A review of surrogate assisted multiobjective evolutionary algorithms. Computational intelligence and neuroscience 2016. Hindawi Publishing Corporation
Dixon LCW, Szegö G (1978) The global optimization problem: an introduction. Towards Glob Optim 2:1–15
Emmerich MTM, Giannakoglou KC, Naujoks B (2006) Single- and multiobjective evolutionary optimization assisted by Gaussian random field metamodels. IEEE Trans Evol Comput 10(4):421–439
Forrester AIJ, Keane AJ (2009) Recent advances in surrogate-based optimization. Prog Aerosp Sci 45(1–3):50–79
García-Ródenas R, Linares LJ, López-Gómez JA (2017) A cooperative brain storm optimization algorithm. In: 2017 IEEE congress on evolutionary computation (CEC), pp 838–845
García-Ródenas R, Linares LJ, López-Gómez JA (2019) A memetic chaotic gravitational search algorithm for unconstrained global optimization problems. Appl Soft Comput J 79:14–29
Ginsbourger D, Riche R, Carraro L (2010) Kriging is well-suited to parallelize optimization, chapter 6. In: Tenne Y, Goh C-K (eds) Computational intelligence in expensive optimization problems. Springer, Berlin, pp 131–162
Gutmann H-M (2001) A radial basis function method for global optimization. J Glob Optim 19(3):201–227
Haftka RT, Villanueva D, Chaudhuri A (2016) Parallel surrogate-assisted global optimization with expensive functions—a survey. Struct Multidiscip Optim 54(1):3–13
Hansen N, Finck S, Ros R, Auger A (2009) Real-parameter black-box optimization benchmarking 2009: noiseless functions definitions. Technical Report RR-6829, INRIA
Horn D, Bischl B (2016) Multi-objective parameter configuration of machine learning algorithms using model-based optimization. In: 2016 IEEE symposium series on computational intelligence (SSCI), pp 1–8
Jagannathan R (1966) On some properties of programming problems in parametric form pertaining to fractional programming. Manag Sci 12(7):609–615
Jakobsson S, Patriksson M, Rudholm J, Wojciechowski A (2010) A method for simulation based optimization using radial basis functions. Optim Eng 11(4):501–532
Johnson ME, Moore LM, Ylvisaker D (1990) Minimax and maximin distance designs. J Stat Plan Inference 26:131–148
Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13(4):455–492
Krige DG (1951) A statistical approach to some basic mine valuation problems on the Witwatersrand. J Chem Met Min Soc S Afr 52(6):119–139
Krityakierne T, Akhtar T, Shoemaker CA (2016) SOP: parallel surrogate global optimization with Pareto center selection for computationally expensive single objective problems. J Glob Optim 66(3):417–437
Liu B, Zhang Q, Gielen G (2014) A Gaussian process surrogate model assisted evolutionary algorithm for medium scale expensive optimization problems. IEEE Trans Evol Comput 18(2):180–192
Liu J, Song W-P, Han Z-H, Zhang Y (2017) Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models. Struct Multidiscip Optim 55(3):925–943
Lophaven SN, Nielsen H, Sndergaard J (2002) DACE—a MATLAB kriging toolbox
Martinez Zapotecas S, Coello Coello C (2013) MOEA/D assisted by rbf networks for expensive multi-objective optimization problems. In: Genetic and evolutionary computation conference, GECCO ’13, Amsterdam, The Netherlands, July 6–10, 2013, pp 1405–1412
Müller J (2012) User guide for Modularized Surrogate Model Toolbox
Omidvar MN, Yang M, Mei Y, Li X, Yao X (2017) DG2: a faster and more accurate differential grouping for large-scale black-box optimization. IEEE Trans Evol Comput 21(6):929–942
Parr JM, Keane AJ, Forrester AIJ, Holden CME (2012) Infill sampling criteria for surrogate-based optimization with constraint handling. Eng Optim 44(10):1147–1166
Potter MA, Jong KAD (1994) A cooperative coevolutionary approach to function optimization. In: Proceedings of the international conference on evolutionary computation. The Third conference on parallel problem solving from nature: parallel problem solving from nature, pp 249–257
Regis RG, Shoemaker CA (2005) Constrained global optimization of expensive black box functions using radial basis functions. J Glob Optim 31(1):153–171
Regis RG, Shoemaker CA (2007a) A stochastic radial basis function method for the global optimization of expensive functions. INFORMS J Comput 19(4):497–509
Regis RG, Shoemaker CA (2007b) Improved strategies for radial basis function methods for global optimization. J Glob Optim 37(1):113–135
Regis RG, Shoemaker CA (2007c) Parallel radial basis function methods for the global optimization of expensive functions. Eur J Oper Res 182(2):514–535
Regis RG, Shoemaker CA (2009) Parallel stochastic global optimization using radial basis functions. INFORMS J Comput 21(3):411–426
Rezaveisi M, Sepehrnoori K, Johns RT (2014) Tie-simplex-based phase-behavior modeling in an IMPEC reservoir simulator. SPE J 19(2):327–339
Ródenas RG, López ML, Verastegui D (1999) Extensions of Dinkelbach’s algorithm for solving non-linear fractional programming problems. Top 7(1):33–70
Schonlau M (1997) Computer experiments and global optimization. Ph.D. thesis, University of Waterloo, Waterloo, Ontario, Canada
Sóbester A, Leary SJ, Keane AJ (2004) A parallel updating scheme for approximating and optimizing high fidelity computer simulations. Struct Multidiscip Optim 27(5):371–383
Srinivas N, Krause A, Kakade S, Seeger M (2010) Gaussian process optimization in the bandit setting: no regret and experimental design. In: Proceedings of the 27th international conference on international conference on machine learning, ICML’10, Madison, WI, USA. Omnipress, pp 1015–1022
Tian J, Tan Y, Zeng J, Sun C, Jin Y (2019) Multi-objective infill criterion driven Gaussian process-assisted particle swarm optimization of high-dimensional expensive problems. IEEE Trans Evol Comput 23(3):459–472
Torn A, Zilinskas A (1989) Global optimization, vol 350. Lecture Notes in Computer Science, Springer, Berlin
Viana FA, Haftka RT, Watson LT (2013) Efficient global optimization algorithm assisted by multiple surrogate techniques. J Glob Optim 56(2):669–689
Vu KK, D’Ambrosio C, Hamadi Y, Liberti L (2017) Surrogate-based methods for black-box optimization. Int Trans Oper Res 24(3):393–424
Wang Y, Liu H, Wei F, Zong T, Li X (2018) Cooperative coevolution with formula-based variable grouping for large-scale global optimization. Evol Comput 26(4):569–596
Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1(1):67–82
Ye KQ, Li W, Sudjianto A (2000) Algorithmic construction of optimal symmetric Latin hypercube designs. J Stat Plan Inference 90:145–159
Yi M, Xiaodong L, Xin Y, Omidvar MN (2016) A competitive divide-and-conquer algorithm for unconstrained large-scale black-box optimization. ACM Trans Math Soft 42(2):1–24
Zhan D, Qian J, Cheng Y (2017) Pseudo expected improvement criterion for parallel EGO algorithm. J Glob Optim 68(3):641–662
Acknowledgements
This research was supported by Ministerio de Economía, Industria y Competitividad-FEDER EU grant with number TRA2016-76914-C3-2-P and the FPU fellowship from Ministerio de Educación, Cultura y Deportes with number FPU16/00792. We would like to express our thanks to the two reviewers for their extremely valuable comments which have allowed us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
This appendix sets out the proofs of the mathematical propositions contained in the article.
-
Theorem 2.
Proof
We will show that the set \(Y^{\infty }=\bigcup _{{s= 1}}^{p}\, \bigcup _{n\ge 1} y^{(s)}_n\) is dense in \({{\mathcal{D}}}\) and, by using Theorem 1, the cooperative algorithm is convergent.
By contradiction, we assume that the set \(Y^\infty \) is not dense on \({\mathcal {D}}\), thus the set \(Y^{(s')}\cup X^0\), where \(Y^{(s')}=\bigcup _{n\ge 1} y^{(s')}_n\), is not dense. We focus only on the SMISA \(s'\) in the proof and we will delete the superscript \((s')\) associated with this SMISA to simplify the notation.
As the set \(Y \cup X^0\) is not dense on \({\mathcal {D}}\), there exists a radius \(\delta _1>0\) and \(x_1\in {{\mathcal {D}}}\) such as the open ball \(B(x_1,\delta _1)\) satisfying:
and Eq. (23) leads to:
From hypothesis (2), \({\mathop {\limsup }\nolimits_{n\rightarrow \infty }}\quad \beta _n >0\) and thus there exists a parameter \(\delta _2>0\) and a subsequence \(\{n_v\}\) satisfying:
Using the Eqs. (24) and (25), we find:
From here, we call \(\delta =\delta _1\delta _2>0\) and we denote the subsequence \(n_v\) simply by v.
If \(v<v'\), from assumptions (1) and (3), then:
The Eq. (27) guarantees that the open balls with centers \(y_{v}\) and \(y_{v'}\), and radius \(\frac{\delta }{2}\) have an empty intersection, i.e
On the other hand, the following inclusion holds:
From the compactness of the set \({\mathcal {D}}\), this covering has a finite sub-covering, i.e. there exist a finite set of centers \(z_1,\ldots ,z_m\), such as:
The sequence \(\{y_v\}\) contains an infinite number of distinct terms because \(d(y_v,y_{v'})>\delta >0\) for all \(v<v'\). Thus, there exists a ball containing two or more terms of \(\{y_v\}\). Let \(v_1\) and \(v_2\) be two different terms belonging to the same ball, then:
The relationship (31) is contradicts the Eq. (27). This contradiction proves that the set \(Y^{\infty }\) is dense and the proof is completed. \(\square \)
-
Theorem 3.
Proof
Consider the case a by analogy. We will show that the set \(Y^{\infty }=\bigcup _{{s= 1}}^{p}\, Y^{(s)}\), where \(Y^{(s)}=\bigcup _{n\ge 1} y^{(s)}_n\), is dense in \({{\mathcal{D}}}\) and, by using Theorem 1, the algorithm is convergent.
By contradiction, we assume that the set \(Y^\infty \) is not dense on \({\mathcal {D}}\), thus \(Y^{(s')}\cup X^0\) is not a dense set and this implies that there exist a radius \(\delta >0\) and a point \(x_1\in {{\mathcal {D}}}\) satisfying, \(B(x',\delta )\subseteq {{\mathcal {D}}}\) and
The proof is exclusively based on the SMISA \(s'\) and for this reason we will omit the superscript \(s'\) to simplify the notation.
Since the sequence \(\{y_n\}\) is contained in the compact set \({{\mathcal {D}}}\), there is a subsequence \(y_{n_v}\) that converges to \(y^*\in {{\mathcal {D}}}\). To simplify the notation we simply denote the subsequence by \(\{y_{v}\}\). Since it is a convergent sequence, then it is a Cauchy sequence, and if \(\varepsilon =\frac{m}{M}\delta >0\) there is a positive integer \(v_0\) such that:
From which we obtain:
Let \(v_1>v_0\) be a positive integer and let t be the main iteration for the SMISA \(s'\) in which the point \(y_{v_1}\) has been obtained, then given Eq. (34) and assumption (2) :
From Eq. (32), it follows that \(d_{Z_{v_1}}(x') >\delta \), and using the assumption (2),
Finally, from the optimality of \(y_{v_1}\), we get:
which contradicts the Eq. (35) and the proof is completed. \(\square \)
Appendix 2: Pruning strategy
The multi-point infill sampling strategies, as they include points in groups of q, may have as result that even if the number of major iterations remains limited, the set of stored points will be of significant size.
Haftka et al. (2016) points out that the overhead cost of surrogate fitting and prediction may become large when the number of samples increases. It will be shown in a computational experiment. In this appendix we introduce the so-called pruning strategy that limits the number of points stored to a maximum of k points. When this value is exceeded, the strategy is activated and those points that provide less sampling information are deleted.
To define this strategy we introduce for each point \( x \in X \) the following index:
where \(\widehat{w}_X(x)=\psi (f(x),x)\ge 0\), i.e. it is obtained by replacing the definition of \(w_X(x)\) in the surrogate model with the function f(x) itself. This index estimates the information provided by the point x on the location of a solution to the optimization problem.
The problem to be solved is to find a subsample \( X' \subseteq X \) of cardinality k, denoted as \(|X'|=k\), which contains the maximum information. Mathematically, we write:
We propose a greedy algorithm to solve the previous combinatorial optimization problem. This algorithm removes the worst of the points \(\widetilde{x}\) and recalculates the index \( \varGamma \) over the resulting set of points \(X {\backslash } \{\widetilde{x}\}\). This procedure is repeated until a sample of cardinality k is obtained. Algorithm 4 shows a recursive coding of the greedy algorithm.

The overhead cost of surrogate fitting and prediction is cubic in the number of retained points and it may become considerable when the number of samples increase. This is the motivation to introduce the pruning strategy and due to this reason is recommendable to consider two set of samples, the first one obtained by the application of pruning rule, \(X'^t\), that is used to fit the surrogate models and the second one is the full samples \(X^t\) that act as a memory of the whole search process and it is only used in the definition of the exploration measures.
Figure 5 illustrates the pruning strategy used to minimize the function \( f(x, y) = x y \) on the region \( [0,1] \times [0,1] \). The set of optimal solutions is represented by the red segments (those solutions for which \( x = 0 \) or \( y = 0 \)). On all the graphs, the contour lines are superimposed. Initially, the region \( [0,1] \times [0,1] \) with 100 points is uniformly sampled. The circles are computed using as radius the value \(\frac{1}{2}d_{X {{\backslash }} \{x\}}(x)\) and they represent the areas of influence of each point x in the sample X. By chance, very close points exist in non-promising regions (small circles in the upper right corner). If we apply the pruning strategy to exclude 50 points (figure \( k = 50 \)) these points near to non-promising regions are eliminated. It is shown that the lower left corner contains more points in the sample than the upper right. If the pruning strategy is intensive (figure \( k = 10 \)) the points try to approximate the set of optimal solutions.
Figure 6 shows the mean efficiency and time required to update the surrogate kriging models within the EGO algorithm and when it is used in combination with the pruning strategy for \(k = 45\) points. We have run 10 trials for both EGO versions and 400 main iterations have been applied to optimize the Hartman 6 function. It can be seen how the computational cost of updating the kriging model increases and how the pruning strategy prevents this, whereas the efficiency is similar in both versions.
Appendix 3: Comparative between EGO-PEI and parallel lower confidence bound-based algorithm
Section 3.2.3 defines a parallel version of the Lower Confidence Bound-based (LCB) algorithm through the SMISA framework. The purpose of this experiment is to compare the performance of this novel algorithm and the EGO-PEI. This experiment is carried out on a BBOB test suite, setting \(q=12\). Both approaches use the same experimental setup as in Sect. 5.3. i.e. the same kriging models and the same optimizer for the infill sampling criterion. The parameter \(\alpha \) of the Eq. (14) is set to 2. Table 7 shows the mean and standard deviation for the best objective function value reached in 100 major iterations. The results show that Parallel LCB wins in 7 problems whereas EGO-PEI in 3. If we take into account the Wilcoxon signed rank test, we observe that the Parallel LCB outperforms EGO-PEI meaningfully in three test problems, and fails in one problem.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
García-García, J.C., García-Ródenas, R. & Codina, E. A surrogate-based cooperative optimization framework for computationally expensive black-box problems. Optim Eng 21, 1053–1093 (2020). https://doi.org/10.1007/s11081-020-09526-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-020-09526-7