Controlling the Kelvin force: basic strategies and applications to magnetic drug targeting

Abstract

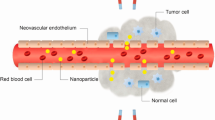
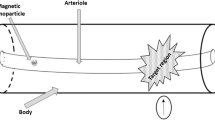
Motivated by problems arising in magnetic drug targeting, we propose to generate an almost constant Kelvin (magnetic) force in a target subdomain, moving along a prescribed trajectory. This is carried out by solving a minimization problem with a tracking type cost functional. The magnetic sources are assumed to be dipoles and the control variables are the magnetic field intensity, the source location and the magnetic field direction. The resulting magnetic field is shown to effectively steer the drug concentration, governed by a drift-diffusion PDE, from an initial to a desired location with limited spreading.

Appendix

The stopping criteria considered in Sect. 5 depends on the discrete $L^2$-norm of the projected gradient. However, it makes sense to consider the discrete $H^1$-norm instead, since the topology is $H^1$ for the variable ${\varvec{\alpha }}$. With this in mind, we notice that ${\mathcal {J}}'({\varvec{v}}) : V\times V \rightarrow {\mathbb {R}}$, in Theorem 3 with $V = \{{\varvec{v}} \in [{\mathrm {H}}^1(0,T)]^{n_p} \ : \ {\varvec{v}}(0) = {\varvec{0}} \}$, is linear and continuous. Thus, the Riesz representation theorem implies that, for all $(\bar{{\varvec{\alpha }}},\bar{{\varvec{\theta }}}) \in {\mathcal {H}}_{ad}\times {\mathcal {V}}_{ad}$ there exists an element $\nabla {\mathcal {J}}(\bar{{\varvec{\alpha }}},\bar{{\varvec{\theta }}}) \in V\times V$ (call it a gradient) such that

$$\begin{aligned} {\mathcal {J}}'(\bar{{\varvec{\alpha }}},\bar{{\varvec{\theta }}})\left\langle ({\varvec{\alpha }},{\varvec{\theta }}) \right\rangle = \left( \nabla {\mathcal {J}}(\bar{{\varvec{\alpha }}},\bar{{\varvec{\theta }}}),({\varvec{\alpha }},{\varvec{\theta }})\right) _V, \quad \forall ({\varvec{\alpha }},{\varvec{\theta }}) \in V. \end{aligned}$$

To get an expression for $\nabla {\mathcal {J}}$ in the discrete space, given $({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau ) \in {\mathcal {H}}^\tau _{ad}\times {\mathcal {V}}^\tau _{ad}$, we solve for $({\varvec{u}}_\tau ,{\varvec{w}}_\tau ) \in V_\tau \times V_\tau \subset [{\mathrm {H}}^1(0,T)]^{2n_p}$, $V_\tau :={\mathbb {P}}^1_\tau \cap V$, satisfying

$$\begin{aligned}&\int _0^T \partial _t {\varvec{u}}_\tau \, \partial _t {\varvec{v}}^\tau _1 \; dt+ \int _0^T \partial _t {\varvec{w}}_\tau \, \partial _t {\varvec{v}}^\tau _2 \; dt = {\mathcal {J}}'({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau )\langle ({\varvec{v}}^\tau _1,{\varvec{v}}^\tau _2)\rangle \quad \forall ({\varvec{v}}^\tau _1,{\varvec{v}}^\tau _2) \in V_\tau \times V_\tau , \end{aligned}$$

and set $\nabla {\mathcal {J}}({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau ) = ({\varvec{u}}_\tau ,{\varvec{w}}_\tau )$. By taking into account the previous representative of the gradient, we use projected BFGS to solve the optimization problem with a stopping criterion given by

$$\begin{aligned} \Vert ({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau )-{\mathbb {P}}^\tau _{[{\varvec{\alpha }}_*,{\varvec{\alpha }}^*,{\varvec{\theta }}_*,{\varvec{\theta }}^*]}(({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau )-\nabla {\mathcal {J}}({\varvec{\alpha }}_\tau ,{\varvec{\theta }}_\tau ))\Vert _{V\times V} < {\mathtt {Tol}}. \end{aligned}$$

(6.10)

Here, ${{{\mathbb {P}}}^{\tau }}_{[{\varvec{\alpha }}_*,{\varvec{\alpha }}^*,{\varvec{\theta }}_*,{\varvec{\theta }}^*]}$ denotes the $H^1$-projection onto the admissible set ${\mathcal {H}}^{\tau }_{ad}\times {\mathcal {V}}^{\tau }_{ad}$. Next we state how to compute this projection in the continuous setting. If ${\varvec{w}}\in (V\oplus {\varvec{\alpha }}_0)\times ( V\oplus {\varvec{\theta }}_0)$ is given then the $H^1$- projection onto ${\mathcal {H}}_{ad}\times {\mathcal {V}}_{ad}$, denoted by ${\varvec{p}}={\mathbb {P}}_{[{\varvec{\alpha }}_*,{\varvec{\alpha }}^*,{\varvec{\theta }}_*,{\varvec{\theta }}^*]}({\varvec{w}})$, is the solution to the following problem: find ${\varvec{p}}\in {\mathcal {H}}_{ad}\times {\mathcal {V}}_{ad}$ such that

$$\begin{aligned} \begin{aligned}&\langle {\varvec{p}}-{\varvec{w}} ,{\varvec{v}}-{\varvec{p}}\rangle \\&\quad =\int _0^T d_t \left( {\varvec{p}}-{\varvec{w}}\right) \cdot d_t\left( {\varvec{v}}-{\varvec{p}}\right) + \left( {\varvec{p}}-{\varvec{w}}\right) \cdot ({\varvec{v}}-{\varvec{p}}) \ge 0 \quad \forall \, {\varvec{v}}\in {\mathcal {H}}_{ad}\times {\mathcal {V}}_{ad}. \end{aligned} \end{aligned}$$

We refer to Antil et al. (2018, Appendix A) about how to compute this projection for the continuous case. The same ideas presented for ${\mathcal {J}}$ apply to Problem 2 defined in Sect. 3.2. Notice that, unlike the discrete $L^2$-norm considered in Sect. 5, dealing with the $H^1$-topology requires the computation of a variational inequality.

Table 3 Here $({\varvec{\alpha }}_0,{\varvec{\phi }}_0)$ denotes the initial values. Moreover, $({\varvec{\alpha }}_*,{\varvec{\phi }}_*)$ and $({\varvec{\alpha }}^*,{\varvec{\phi }}^*)$ denote the upper and lower bounds in the admissible sets

Table 4 Number of iterations for the $H^1$ and $\ell ^2$ norm topologies as we refine the mesh in the time domain. Here N denotes the number of time steps. We observe mesh independence in the case of $H^1$

We compare the grid-dependence of the optimization algorithm with respect to the $\ell ^2$-norm and $H^1$-norm. With this in mind, we consider Problem 3.1 with the same $\varOmega$, T, number of dipoles, $D_t$, and target vector field ${\mathbf {f}}_2$ as in the second problem of Sect. 5.1. Here the admissible set is characterized by Table 3. The initial guess $({\varvec{\alpha }}_{int},{\varvec{\phi }}_{int})$ is a constant function given by the initial condition, namely $({\varvec{\alpha }}_{int}(t),{\varvec{\phi }}_{int}(t))=({\varvec{\alpha }}_0,{\varvec{\phi }}_0)$ for all $t\in [0,0.75]$. The values of ${\varvec{\alpha }}_0$ and ${\varvec{\phi }}_0$ are motivated by the numerical solution presented in Sect. 5.1 (see Fig. 5). We have solved problem (4.10) with the termination criterion given by (5.1) and (6.10) for the $\ell ^2$ and $H^1$ norm topologies, respectively. The tolerance for both cases is set to ${\texttt {Tol}}=3\times 10^{-5}$. The iteration counts for both cases are presented in Table 4. We observe mesh-independence in the iteration for the $H^1$-norm topology, with fewer iterations compared to the $\ell ^2$-norm topology.