Abstract
This paper draws upon a critical analysis of the three RCA indexes in Vollrath (1991) to propose a new class of RCA indexes. The baseline RCA index in this new class rests on the overall structure of trade, is symmetric, avoids size bias and is compatible with the Kunimoto-Vollrath principle. Possible modifications of the baseline RCA index are subsequently suggested to take into account GDP per capita data and to use adjusted trade data with the aim of better measuring comparative advantages. These modified versions together with the baseline RCA index give rise to a whole new class of RCA indexes. An application to the Euro area indicates that this new class is able to rank countries according to their respective levels of comparative advantages in a more consistent way than alternative RCA indexes. Furthermore, the new class of RCA indexes provides second-best solutions for time stationarity and the desirable distributional characteristics of an RCA index.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The concept of comparative advantage is a cornerstone of economic theory. Since the seminal paper of Balassa (1965), comparative advantages have usually been measured by Revealed Comparative Advantage (RCA) indexesFootnote 1. RCA indexes are computed on the basis of trade data and provide synthetic measures of comparative advantages (Danna-Buitrago 2017). According to (French 2017) p.83 “the concept is simple but powerful: if, according to Ricardian trade theory, differences in relative productivity determine the pattern of trade, then the (observable) pattern of trade can be used to infer (unobservable) differences in relative productivity”. However, the appropriate way to use trade data to compute an RCA index is still under debate (Liu and Gao 2019).
In this regard, here a new class of RCA indexes is proposed with the aim of improving the measurement of comparative advantages. Our starting point is a critical analysis of the three RCA indexes proposed by Vollrath (1991), which is a reference point in the literature on RCA indexes (among the most recent citations of Vollrath (1991), see for example:Jambor and Babu (2016); Benesova et al. (2017); Brakman and Van Marrewijk (2017); Deb and Hauk (2017); French (2017); Sawyer et al. (2017); Seleka and Kebakile (2017); Algieri et al. (2018); Cai et al. (2018); Grundke and Moser (2019); Liu and Gao (2019); Saki et al. (2019); Yazdani and Pirpour (2020)). We then suggest an RCA index that overcomes drawbacks identified in Thomas Vollrath’s RCA indexes. Thereafter, we propose two modifications of the new RCA index that take into account GDP per capita data in addition to trade data or use adjusted trade data instead of “raw” trade data. Therefore, the new RCA index is a baseline index to which different modifications can be applied, giving rise to a new class of RCA indexes. Furthermore, the new class is applied to the nineteen countries that form the Euro area to evaluate whether it provides better measures of comparative advantages than alternative RCA indexes in a given empirical case.
The remainder of this paper is organized as follows. Section 1 presents Thomas Vollrath’s RCA indexes. Section 2 points out drawbacks of these RCA indexes and elaborates the aforementioned new RCA index to provide solutions to these drawbacks. Section 3 describes possible modifications of this RCA index in relation to GDP per capita data and adjusted trade data. Section 4 provides the empirical evaluation in the case of the Euro area. Concluding remarks are given in Sect. 5.
2 An Overview of Thomas Vollrath’s RCA Indexes
Vollrath (1991) conceptualizes three RCA indexes: the Relative Trade Advantage (RTA) index, the Relative Export Advantage (REA) index and the Revealed Competitiveness (RC) index (see also Vollrath (1987; 1989)). Let J be a set of countries (the “trade area”, i.e. the world or the members of some regional trade agreement), K a set of commodities, and T a set of time periods. \(X_{ikt}\) denotes the exports of commodity \(k\in K\) by country \(i\in J\) toward the other countries in J in time period t. Thereafter:
-
\(X_{i\mathcal {K}t}\) denotes the exports of all commodities except k by i in t; that is, \(X_{i\mathcal {K}t}=\sum _{l\in \mathcal {K}}X_{ilt}\), where \(\mathcal {K}=K\setminus \{k\}\).
-
\(X_{\mathcal {J}kt}\) represents the exports of k by all countries except i in t; that is, \(X_{\mathcal {J}kt}=\sum _{j\in \mathcal {J}}X_{jkt}\), where \(\mathcal {J}=J\setminus \{i\}\).
-
Lastly, we write as \(X_{\mathcal {J}\mathcal {K}t}\) the exports of all commodities except k by all countries except i in t; that is, \(X_{\mathcal {J}\mathcal {K}t}=\sum _{j\in \mathcal {J}}\sum _{l\in \mathcal {K}}X_{jlt}\).
In addition, let \(M_{ikt}\), \(M_{i\mathcal {K}t}\), \(M_{\mathcal {J}kt}\) and \(M_{\mathcal {J}\mathcal {K}t}\) be the same types of variables defined for imports. Lastly, \(\text {RTA}_{ikt}\), \(\text {REA}_{ikt}\) and \(\text {RC}_{ikt}\) denote the RTA, REA and RC indexes associated with (i, k, t), respectivelyFootnote 2. Thereafter:
The RTA index computes the value of \(X_{ikt}\) normalized by \(X_{i\mathcal {K}t}\), which is the exports of k by i normalized by the exports of products other than k by i. Similarly, the RTA index computes the value of \(X_{\mathcal {J}kt}\) normalized by \(X_{\mathcal {J}\mathcal {K}t}\), which is the exports of k by the countries other than i normalized by the exports of products other than k by the countries other than i. The normalized values of \(M_{ikt}\) and \(M_{\mathcal {J}kt}\) are calculated in the same way. If the normalized value of \(X_{ikt}\) is greater than the normalized value of \(X_{\mathcal {J}kt}\), then i has a higher propensity to export k than the other countries. This could be seen as the consequence of comparative advantages. Therefore, the ratio of \(X_{ikt}/X_{i\mathcal {K}t}\) to \(X_{\mathcal {J}kt}/X_{\mathcal {J}\mathcal {K}t}\), which is named the ratio of relative export advantage (RXA), is greater than 1. However, the normalized value of \(M_{ikt}\) may be greater than the normalized value of \(M_{\mathcal {J}kt}\). Furthermore, the difference between the normalized value of \(M_{ikt}\) and the normalized value of \(M_{\mathcal {J}kt}\) may be greater than the corresponding difference in exports. If so, the ratio of \(M_{ikt}/M_{i\mathcal {K}t}\) to \(M_{\mathcal {J}kt}/M_{\mathcal {J}\mathcal {K}t}\), which is named the ratio of relative import advantage (RMA), will be greater than the RXA ratio, and there should not exist comparative advantages for i even if \(\text {RXA}_{ikt}>1\).
Following the logic of the RTA index, i has comparative advantages for k in t if \(\text {RXA}_{ikt}>\text {RMA}_{ikt}\). Eventually, the RTA index is calculated as the difference between the RXA ratio and the RMA ratio, so the inequality \(\mathrm{RTA}_{ikt}>0\) reveals comparative advantages, whereas the inequality \(\mathrm{RTA}_{ikt}<0\) reveals comparative disadvantages.
Note that the inequality \(\text {RTA}_{ikt}>0\) may be implied not only by \(\text {RXA}_{ikt}>\text {RMA}_{ikt}>1\) (as mentioned before) but also by \(1>\text {RXA}_{ikt}>\text {RMA}_{ikt}\). The RTA index may reveal comparative advantages even if the normalized value of exports of k by i is smaller than the normalized value of exports of k by the countries different from i, provided that the corresponding RXA ratio is greater than the RMA ratio. Each ratio separately suggests the existence of comparative advantages or disadvantages through the comparison with their “neutral” value, which is equal to 1. An RXA ratio greater (less) than 1 suggests the existence of comparative advantages (disadvantages), whereas an RMA ratio greater (less) than 1 suggests the existence of comparative disadvantages (advantages). However, calculating the RXA and RMA ratios is only the first step. The second step is to compare the two ratios. If the RXA ratio is greater than 1, the RTA index implies the existence of comparative advantages only if the RMA ratio is smaller than the RXA ratio. Similarly, if the RXA ratio is less than 1, the RTA index implies the existence of comparative disadvantages only if the RXA ratio is smaller than the RMA ratio. The RTA index implies the existence of comparative advantage on the basis of the RXA ratio relative to the RMA ratio. The RXA and RMA ratios have their own neutral values, i.e. 1. Thus for the RTA index, which calculates the difference between the two ratios, this neutral value becomes zero.
The RC index calculates the difference between the respective logarithms of each ratio, and the REA index is the log of the first ratio. According to Vollrath (1989), the use of logarithms is intended to ease the interpretation of the RXA and RMA ratios. Before comparison with the RMA ratio, the RXA ratio suggests the existence of comparative advantages if its value is greater than 1 and comparative disadvantages if its value belongs to the interval [0, 1). Conversely, the RMA ratio suggests the existence of comparative advantages if its value belongs to the interval [0, 1) and comparative disadvantages if its value belongs to the interval \((1,+\infty )\) (before being compared with the RXA ratio). Therefore, the interval associated with comparative advantages does not have the same length as the interval associated with comparative disadvantages. Using logarithms is a solution to this “asymmetry” because the interval [0, 1) is converted into \((-\infty ,0)\) and the interval \((1,+\infty )\) is converted into \((0,+\infty )\). As a result, the RXA and RMA ratios are “symmetric” around zero. Eventually, as for the RTA index, a positive value of the RC/REA index reveals comparative advantages, and a negative value reveals comparative disadvantages.
3 Drawbacks of Thomas Vollrath’s RCA Indexes and Their Solutions
The three RCA indexes suffer from some drawbacks. First, the REA index ignores imports even though, like the RTA and RC indexes, using both export and import data makes it possible to “embody both the relative demand and relative supply dimensions \((\cdots )\)” of comparative advantages and therefore remain “consistent with the real world phenomenon of two-way trade” (Vollrath 1991, p. 276; see also Giraldo and Jaramillo 2018). According to Vollrath (1987), ignoring imports might be necessary because of the “noncomparability between import and export data which arises because the former contains certain handling, transportation, and spoilage costs not embedded into the latter” (p. 20). However, given that the exports of some countries are the imports of other countries, it is possible to deduce import data from export data or vice versa, so that exports and imports can be expressed in a homogeneous way. Furthermore, Vollrath (1987) suggests that “handling, transportation, and spoilage costs are small relative to the value of traded commodities” (p. 20), so the corresponding bias is unlikely to be significant.
Consequently, the RTA and RC indexes should be preferred to the REA index. Nevertheless, the RTA and RC indexes face numeric exceptions. The first numeric exception is division by zero, which occurs if \(X_{i\mathcal {K}t}=0\) or \(M_{i\mathcal {K}t}=0\), i.e. the countries other than i do not export or import k. As a result, it is impossible to calculate \(X_{ikt}/X_{i\mathcal {K}t}\) or \(M_{ikt}/M_{i\mathcal {K}t}\), and the RTA and RC indexes are left undefined even though there should be a measure of comparative advantages if i is the sole exporter/importer of k. With a lower commodity aggregation, commodities are more specific, so the likelihood of \(X_{i\mathcal {K}t}=0\) or \(M_{i\mathcal {K}t}=0\) is higher. Similarly, a smaller trade area implies a higher likelihood of \(X_{i\mathcal {K}t}=0\) or \(M_{i\mathcal {K}t}=0\). According to Vollrath (1991), the interest in removing exports and imports associated with i and/or k is to “make clear distinctions between a specific commodity and all other commodities and between a specific country and the rest of the world, eliminating country and commodity double counting in world trade” (p. 276). Nonetheless, this may prevent the calculation of the RTA and RC indexes.
In the case of the RC index, another numeric exception is the log of zero. Even if \(X_{i\mathcal {K}t}\ne 0\) and \(M_{i\mathcal {K}t}\ne 0\), \(X_{ikt}=0\) or \(M_{ikt}=0\) is possible, which means that i does not export or import k. Consequently, the log of the RXA ratio or the RMA ratio cannot be calculated, and once again, the RC index is left undefined. This also applies to the REA index, which is the log of the RXA ratio. In addition, Vollrath (1991) notes that the log implies that the RC and REA indexes are characterized by an “extreme sensitivity to small values of exports or imports of the specified commodity” (p. 277). Indeed, small values of \(X_{ikt}\) and \(M_{ikt}\) lead to small values of \(\text {RXA}_{ikt}\) and \(\text {RMA}_{ikt}\), respectively. In turn, these small values of \(\text {RXA}_{ikt}\) and \(\text {RMA}_{ikt}\) lead to large negative values of \(\ln \left( \text {RXA}_{ikt}\right)\) and \(\ln \left( \text {RMA}_{ikt}\right)\), which might distort the measurement of comparative advantages.
To overcome the aforementioned drawbacks, we first suggest preserving the exports/imports associated with k and/or i when exports/imports are aggregated across products and/or countriesFootnote 3. Put differently, exports/imports are added up across K instead of \(\mathcal {K}\) and/or J instead of \(\mathcal {J}\). Consequently:
-
\(X_{iKt}=\sum _{l \in K}X_{ilt}\) substitutes for \(X_{i\mathcal {K}t}\) (where \(\mathcal {K}=K\setminus \{k\}\));
-
\(X_{Jkt}=\sum _{j \in J}X_{jkt}\) substitutes for \(X_{\mathcal {J}kt}\) (where \(\mathcal {J}=J\setminus \{i\}\));
-
\(X_{JKt}=\sum _{j \in J}\sum _{l \in K}X_{jlt}\) substitutes for \(X_{\mathcal {J}\mathcal {K}t}\);
-
The same substitutions apply to import data.
Second, we suggest using \((x-1)/(x+1)\) as the approximation of \(\ln (x)\) around 1 (see Fig. 1) because this approximation is defined even if \(x=0\) and maintains the symmetry around zero (Dalum et al. 1998; Laursen 2015). In addition, this approximation is lower bounded by -1 and therefore avoids large negative values of the log. The approximation \((x-1)/(x+1)\) implies that the interval revealing comparative advantages is (0, 1] instead of \((0,+\infty )\) for the RXA ratio and that the interval revealing comparative disadvantages is \([-1,0)\) instead of \((-\infty ,0)\); the converse is true for the RMA ratio. Consequently, \(\text {RTA}'\), \(\text {REA}'\) and \(\text {RC}'\) are the modified versions of RTA, REA and RC, respectively:
Each index embodies the ratio of \(X_{ikt}/X_{ikt}\) to \(X_{Jkt}/X_{JKt}\), which is the standard RCA index à la Balassa (1965), hereafter referred to as the BX ratio. In addition, the \(\text {REA}'\) index corresponds to the “symmetric” version of the BX index elaborated by Dalum et al. (1998). The ratio of \(M_{ikt}/M_{ikt}\) to \(M_{Jkt}/M_{JKt}\) is the import-equivalent of the BX ratio and is referred to as the BM ratio. The \(\text {RC}'\) index applies the symmetric transformation suggested by Dalum et al. (1998) to both the BX and BM ratios. The \(\text {RTA}'\) index ranges from \(-\infty\) to \(+\infty\), the \(\text {REA}'\) index ranges from -1 to 1, and the \(\text {RC}'\) index ranges from -2 to 2. For the three indexes, zero is the neutral value that reveals the absence of comparative advantages and disadvantages.
By using J instead of \(\mathcal {J}\) and K instead of \(\mathcal {K}\), the measurement of comparative advantages is no longer based on a comparison of the exports/imports of k by i normalized by the exports/imports of products other than k by i with the exports/imports of k by the countries other than i normalized by the exports/imports of products other than k by the countries other than i. Rather, BX and BM measure comparative advantages by comparing the share of k in i’s exports/imports in t with the same share at the level of J.
It is possible that \(X_{Jkt}=0\), which is equivalent to \(M_{Jkt}=0\) and indicates that no country exports k and logically no country imports k. In this case, the BX and BM ratios cannot be calculated due to the division by zero. Nonetheless, this numeric exception can be solved. Indeed, if no country exports/imports k, then no country should have comparative advantages or disadvantages. Consequently, the BX and BM ratios should be set to 1, which is their neutral value, without any further calculation. Ultimately, \(\text {BX}_{ikt}=\text {BM}_{ikt}=1\) implies that the three indexes are equal to their neutral value, which is zero.
The literature has emphasized the size bias that affects the BX ratio: small values of \(X_{iKt}\) lead to great values of the BX index. Put differently, small exports of i (which can be seen as a proxy of i’s size) lead the BX ratio to reveal strong comparative advantages, which can be considered a contradictionFootnote 4 (De Benedictis and Tamberi 2004). Similarly, small values of \(M_{iKt}\) leads to large values of the BM ratio. Therefore, small imports of i paradoxically lead the BM ratio to reveal strong comparative disadvantages. This is the reason why the \(\text {RTA}'\) index may yield misleading measures of comparative advantages. This is not the case for the \(\text {REA}'\) and \(\text {RC}'\) indexes because their log-approximation implies an upper bound, i.e. 1, which prevents these indexes from having abnormal large values. However, the \(\text {REA}'\) index still suffers from the same drawback as the REA index; that is, imports are not taken into account.
Ultimately, to overcome the drawbacks of the RCA indexes suggested by Vollrath (1991) and the other drawbacks arising from the proposed transformations of these indexes, the \(\text {RC}'\) index warrants consideration as an alternative RCA index. The \(\text {RC}'\) index arises from a specific combination of the BX and BM ratios into a formula that measures comparative advantages:
-
The BX and BM ratios replace the RXA and RMA ratios to avoid the unsolvable numeric exceptions that affect the RXA and RMA ratios. These numeric exceptions arise when comparative advantages are measured for single exporter/importer countries in the trade area under consideration.
-
Instead of using the BX ratio alone to measure comparative advantages, as in the case of the standard RCA index à la Balassa (1965), the BX and BM ratios are combined together in a formula that captures both the supply and demand dimensions of comparative advantages.
-
The BX and BM ratios are transformed according to the log-approximation of Dalum et al. (1998) to make them symmetric and avoid size bias. In addition, contrary to the log itself (which is applied by Vollrath (1991) to the RXA and RMA ratios to calculate the REA and RC indexes), the approximation of the log is defined even if \(\text {BX}=0\) or \(\text {BM}=0\).
-
Finally, the \(\text {RC}'\) index is the difference between \((\text {BX}-1)/(\text {BX}+1)\) and \((\text {BM}-1)/(\text {BM}+1)\) and replaces the difference between RXA and RMA (namely the RTA index) and the difference between the log of RXA and the log of RMA (namely the RC index).
The \(\text {RC}'\) index can be conceptualized as an “additive” extension of the standard RCA index à la Balassa (1965) to imports with the symmetric transformation à la Dalum et al. (1998). The word “additive” emphasizes that the \(\text {RC}'\) index is computed as the difference between the symmetric transformation of the BX ratio and the symmetric transformation of the BM ratioFootnote 5.
4 Further Improvements
The \(\text {RC}'\) index can be modified to make the measurement of comparative advantages more robust from a theoretical standpoint. We propose three modifications. Each modification gives rise to a variant form of the \(\text {RC}'\) index. The first modification aims to take into account the GDP per capita of all countries in J for the measurement of comparative advantages. Indeed, if a country i has a higher GDP per capita than another country j, this can be interpreted as the existence of higher factor endowments for i than for j, which gives i greater potential to have higher comparative advantages than jFootnote 6 (Jambor 2014). Consequently, if despite higher factor endowments i reaches the same value of the \(\text {RC}'\) index as j for a given product-period pair, then i should logically have lower comparative advantages than j (if \(\text {RC}'_{ikt}=\text {RC}'_{jkt}>0\)) or higher comparative disadvantages (if \(\text {RC}'_{ikt}=\text {RC}'_{jkt}<0\)). In this regard, the first modification is to weight \(\text {RC}'_{ikt}\) by a number given by a continuous function \(f_i\) whose domain is the J-dimensional vector of GDP per capita in t for each country in J, that is, \(y_t:=\left\langle y_{jt}\right\rangle _{j\in J}\). This number captures the effect of GDP per capita structure on the comparative advantages of i. To the best of our knowledge, no other RCA index available in the literature does so. Consequently, we define the \(\text {RC}^{y}\) index calculated for a given (i, k, t) as the \(\text {RC}'\) index adjusted by \(f_i(y_t)\):
The function \(f_i\) should have the following five properties:
-
1.
The values of \(f_i(y_t)\) cannot be negative. A negative value would change the sign of the \(\text {RC}'\) index and therefore convert comparative advantages into comparative disadvantages and vice versa. To avoid this inconsistency, zero must be the minimum of \(f_i\).
-
2.
\(f_i\) has a (global) maximum. This captures the fact that the differences in GDP per capita should generate limited differences in comparative advantages.
-
3.
\(\partial f_i/\partial y_{it}<0\): If the GDP per capita of i is higher, then \(f_i(y_{t})\) is smaller, leading to a decrease in \(\text {RC}'_{ikt}>0\) or an increase in \(\text {RC}'_{ikt}<0\). Because \(f_i(y_t)\ge 0\), a higher value of \(y_{it}\) gives rise to a value of the \(\text {RC}'\) index closer to zero.
-
4.
\(\partial f_i/\partial y_{jt}>0\) \(\forall j \ne i\): If the GDP per capita of a country different from i is higher, then \(f_i(y_{t})\) is larger, leading to an increase in \(\text{RC}'_{ikt}>0\) or a decrease in \(\text {RC}'_{ikt}<0\). As there exists a maximum value of \(f_i(y_t)\), the increase in \(\text{RC}'_{ikt}\) cannot generate a value of \(\text {RC}^{y}\) greater than this maximum.
-
5.
\(f_{i}(y_{t})=1\) if \(y_{it}=\hat{y}_{t}\), where \(\hat{y}_{t}\) is a representative measure of \(y_{t}\). If the GDP per capita of i GDP is equal to the GDP per capita of a “typical” country among J, then weighting \(\text {RC}'_{ikt}\) by \(f_i(y_t)\) should not modify \(\text {RC}'_{ikt}\). Ultimately, the equality \(y_{it}=\hat{y}_{t}\) leads \(f_i(y_t)\) to be equal to 1.
Incorporating GDP per capita structure into the computation of an RCA index under the aforementioned five properties of \(f_i\) is an alternative to understanding comparative advantages through a regression in which the independent variable is GDP per capita and the dependent variable is an RCA index that rests solely upon trade flows. Weighting \(\text {RC}'\) by \(f_i(y_t)\) instead of using \(\text {RC}'\) per se is intended to provide a more relevant measure of comparative advantages without relying on a subsequent regression technique.
We suggest using the following form of \(f_i\):
This conceptualization of \(f_i\) is compatible with the aforementioned list of properties that \(f_i\) should have. In particular, the maximum of \(f_i\) is the value of e (second property). In addition, the representative value of \(y_t\) is \(\frac{1}{\# J}\sum _{j \in J}y_{jt}\), i.e. the mean of \(y_t\). If \(y_{it}\) is equal to the mean of \(y_t\), then \(f_i(y_t)=1\) because \(f_i\) calculates the value of e to the power of zero. This is consistent with the fifth property. Equation 4 is a starting point, and further research should study other conceptualizations of \(f_i\).
The second modification arises from the RCA indexes in terms of contribution to the trade balance (CTB); see below. Before calculating a CTB index, De Saint Vaulry (2008) suggests adjusting trade flows so that the share of k in total trade among J is the same for all periods in T and equal to the share associated with the period considered as a reference. This adjustment is assumed to eliminate short-term fluctuations in trade flows and therefore improve the ability of trade flows to reveal comparative advantages (Stellian and Danna-Buitrago 2019). Let \(r\in T\) be the reference period. The share of k in total trade among J in t is calculated as \((X_{Jkt}+M_{Jkt})/(X_{JKt}+M_{JKt})\). To make \((X_{Jkt}+M_{Jkt})/(X_{JKt}+M_{JKt})\) equal to \((X_{Jkr}+M_{Jkr})/(X_{JKr}+M_{JKr})\), every \(X_{ikt}\) and \(M_{ikt}\) must be scaled by the ratio of \((X_{Jkr}+M_{Jkr})/(X_{JKr}+M_{JKr})\) to \((X_{Jkt}+M_{Jkt})/(X_{JKt}+M_{JKt})\). Let \(v_{kt}^{r}\) be this kind of ratio associated with (k, t, r). The adjusted values of \(X_{ikt}\) and \(M_{ikt}\), denoted as \(X^{r}_{ikt}\) and \(M^{r}_{ikt}\), are therefore calculated as follows:
The second modification of the \(\text {RC}'\) index is to calculate the \(\text {RC}'\) index with the adjusted values of trade flows. Indeed, the adjustment of trade flows in Eq. 5 can be applied to RCA indexes beyond the CTB indexes. Consequently, to calculate the \(\text {RC}'\) index with adjusted trade flows:
-
\(X^{r}_{iKt}=\sum _{l\in K}X^{r}_{ilt}\) substitutes for \(X_{iKt}\) (defined as \(\sum _{l\in K}X_{ilt}\));
-
\(X^{r}_{Jkt}=\sum _{j\in J}X^{r}_{jkt}\) substitutes for \(X_{Jkt}\) (defined as \(\sum _{j\in J}X_{jkt}\));
-
\(X^{r}_{JKt}=\sum _{j\in J}\sum _{l\in K}X^{r}_{jlt}\) substitutes for \(X_{JKt}\) (defined as \(\sum _{j\in J}\sum _{l\in K}X^{r}_{jlt}\));
-
The same substitutions apply to import data.
Let \(\text {RC}^{r}_{ikt}\) be the \(\text {RC}'\) index calculated with adjusted trade flows. The \(\text {RC}^{r}\) index is calculated as follows:
The third modification combines the two previous modifications; that is, the \(\text {RC}'\) index is calculated with both adjusted trade flows and GDP per capita. We denote as \(\text {RC}^{yr}_{ikt}\) this third modification of the \(\text {RC}'\) index:
Table 1 recapitulates the four RCA indexes suggested in the present paper. These RCA indexes possess valuable features from a theoretical standpoint. First, they calculate comparative advantages on the basis of both exports and imports, which better captures the supply and demand dimensions of comparative advantagesFootnote 7 (Vollrath 1991). Second, they calculate comparative advantages for a given country-product pair on the basis of all trade flows across both countries (J) and products (K). This is consistent with the relative nature of comparative advantages; that is, comparative advantages associated with any country-product pair depend on the overall structure of trade flows across J and across K (Yu et al. 2009). If only the trade flows associated with (i, k) in t are used to calculate an RCA index for (i, k, t), namely \(X_{ikt}\) and \(M_{ikt}\), the measure of comparative advantages may be inconsistent. Similarly, calculating an RCA for (i, k, t) on the basis of trade flows associated with i only – \(\{X_{ilt},M_{ilt}\}_{k\in K}\) – or on the basis of trade flows associated with k only – \(\{X_{jkt},M_{jkt}\}_{j\in J}\) – would not entirely reflect the relative nature of comparative advantages.
Third, the \(\text {RC}'\), \(\text {RC}^y\), \(\text {RC}^r\) and \(\text {RC}^{yr}\) indexes are consistent with the interpretation by Vollrath (1991) of the principle enunciated by Kunimoto (1977). According to that interpretation, an RCA index should compare the actual value of exports associated with (i, k, t), given by \(X_{ikt}\), with a theoretical “expected” value that reveals the absence of comparative advantages and disadvantages. i has a comparative advantage for k in t if the value of \(X_{ikt}\) is greater than the corresponding theoretical value. Conversely, \(X_{ikt}\) smaller than the theoretical value of \(X_{ikt}\) reveals comparative disadvantages. The theoretical value is calculated as total exports of i weighted by the share of k in total exports of J in t. Hence the theoretical value of \(X_{ikt}\) is \((X_{Jkt}/X_{JKt})\times X_{iKt}\). Consequently, the BX ratio is equal to the ratio of \(X_{ikt}\) to its theoretical value because \((X_{ikt}/X_{iKt})/(X_{Jkt}/X_{JKt})=X_{ikt}/((X_{Jkt}/X_{JKt})\times X_{iKt})\). A BX ratio greater than 1 suggests the existence of comparative advantages and simultaneously indicates that the actual value of \(X_{ikt}\) is greater than its theoretical value. Ultimately, the BX ratio is consistent with the Kunimoto-Vollrath principle. Such consistency also applies to the BM ratio, as the theoretical value of \(M_{ikt}\) is calculated as \((M_{Jkt}/M_{JKt})\times M_{iKt}\). Ultimately, the \(\text {RC}'\) and \(\text {RC}^y\) indexes are consistent with the Kunimoto-Vollrath principle because they are based on the BX and BM ratios, as are the \(\text {RC}^r\) and \(\text {RC}^{yr}\) indexes, with the sole difference that these two last indexes are based on adjusted trade flowsFootnote 8.
Now the question is “to what extent do the \(\text {RC}'\), \(\text {RC}^y\), \(\text {RC}^r\) and \(\text {RC}^{yr}\) indexes give consistent measures of comparative advantages for a given empirical case?”. The following section addresses this point.
5 An Empirical Evaluation
Assume that an RCA index is applied to a given configuration of \(J\times K\times T\). This application gives a set of \(\#J\times \#K\times \#T\) values of the RCA index under consideration. It is possible to evaluate the quality of this set according to three criteria (Stellian and Danna-Buitrago 2019):
-
Time stationarity: The values of an RCA index computed for \(J\times K\times T\) should have low volatility over time due to the ex ante nature of comparative advantages.
-
Shape: The distribution of the values of an RCA index computed for \(J\times K\times T\) should be symmetric to capture the fact that, by construction, comparative disadvantages counterbalance comparative advantages. In addition, such a distribution should have thin tails because strong comparative (dis)advantages are relatively rare from an empirical standpoint.
-
Ordinal ranking bias: The values of an RCA index computed for \(J\times K\times T\) should rank countries in a consistent way.
In this section, we evaluate the \(\text {RC}'\), \(\text {RC}^y\), \(\text {RC}^r\) and \(\text {RC}^{yr}\) indexes according to these three criteria. The evaluation must compare the quality of the comparative advantage measurements of these four RCA indexes relative not only to one another but also to other RCA indexes. Sect. 4.1 presents the alternative RCA indexes considered in the present paper. Then, Sect. 4.2 describes the empirical case used for the evaluation and the corresponding methodology. Last, Sect. 4.3 presents and discusses the subsequent results.
5.1 Alternative RCA Indexes
There are many RCA indexes in the literatureFootnote 9. For instance, the RCA index à la Balassa (1965), identified as the BX ratio in the present paper, is still the reference in the literature (French 2017). However, only the aforementioned CTB indexes share the same valuable features as the \(\text {RC}'\), \(\text {RC}^y\), \(\text {RC}^r\) and \(\text {RC}^{yr}\) indexes:
-
1.
The CTB indexes are export/import RCA indexes.
-
2.
They measure comparative advantages of a given country-product pair on the basis on the overall structure of trade flows.
-
3.
They are consistent with the Kunimoto-Vollrath principle.
The basic CTB index (Lafay 1987; 1992) compares the trade balance associated with (i, k, t), i.e. \(X_{ikt}-M_{ikt}\), with a theoretical value of \(X_{ikt}-M_{ikt}\) that would reveal the absence of comparative advantages or disadvantages. The Kunimoto-Vollrath principle is thus extended to trade balance. For this purpose, the basic CTB index starts from the principle that i would have neither comparative advantages nor comparative disadvantages in t if the total trade balance of i in t, i.e. \(X_{iKt}-M_{iKt}\), is distributed according to the share of each product in the total trade between all countries in J. Consequently, the theoretical value of \(X_{ikt}-M_{ikt}\) is calculated as the product of \(X_{iKt}-M_{iKt}\) and the ratio of \(X_{Jkt}+M_{Jkt}\) to \(X_{JKt}+M_{JKt}\). This ratio corresponds to the share of k in total trade among J in t. Ultimately, the theoretical value of \(X_{iKt}-M_{iKt}\) is calculated as \(\left( (X_{Jkt}+M_{Jkt})/(X_{JKt}+M_{JKt})\right) \times (X_{iKt}-M_{iKt})\). The basic CTB index is computed as the difference between the actual trade balance and the corresponding theoretical value before normalization by total trade by all countries in J for all products in K (in t), i.e. \(X_{JKt}+M_{JKt}\):
A variant form of the basic CTB index uses the GDP of i as the normalization variable (De Saint Vaulry 2008; Stellian and Danna-Buitrago 2017):
where \(Y_{it}\) denotes the GDP of i in t and the superscript Y in \(\text {CTB}^{Y}_{ikt}\) refers to this alternative normalization. In addition, the \(\text {CTB}^{Y}\) index can be calculated with adjusted trade flows, giving rise to the CTB index referred to as the \(\text {CTB}^{Yr}\) index (De Saint Vaulry 2008; Stellian and Danna-Buitrago 2019):
Similar to the new class of RCA indexes, CTB indexes are by construction symmetric and avoid size bias.
Most of the other RCA indexes available in the literature are modifications of the standard BX ratio; specifically, the log-approximation of the BX ratio by Dalum et al. (1998) is defined as \((\text {BX}-1)/(\text {BX}+1)\). Another RCA index calculates the difference between \(X_{ikt}/X_{iKt}\) and \(X_{Jkt}/X_{JKt}\) instead of dividing the first term by the latter term (Hoen and Oosterhaven 2006). This additive version of the BX ratio can be written as \((X_{ikt}-(X_{Jkt}/X_{JKt})\times X_{iKt})/X_{iKt}\) and therefore reads as the difference between exports and its expected value –in accordance with the Kunimoto-Vollrath principle– before normalization by a country’s exports. Another additive version consists of substituting \(X_{JKt}\) for \(X_{iKt}\) as the normalization variable, namely total exports in the trade area under consideration (Yu et al. 2009). In addition, normalization of the BX ratio by the across-product mean for a given country (Proudman and Redding 1998; Proudman and Redding 2000) or the across-country mean for a given product (Amador et al. 2011) has been suggested.
These RCA indexes address some shortcomings of the BX ratio; specifically, the log-approximation of the BX ratio and the additive versions of that ratio restore symmetry (Yu et al. 2009). Furthermore, as explained previously, the log-approximation of the BX ratio eliminates the size bias thanks to its upper bound. The additive versions of the BX ratio similarly avoid size bias thanks to their upper bounds (1 and 1/4, respectively; see Yu et al. 2009). Normalization of the BX ratio by the across-product/country mean does not restore symmetry but at least attenuates the size bias, provided that the corresponding mean is greater than one to reduce the values taken by the BX ratio, including abnormal large values implied by the size bias.
However, \(\text {RC}'\), its variants and CTB indexes not only avoid the same type of shortcomings but also are export-import RCA indexes and therefore are able to capture both the supply-side and demand-side of comparative advantages. The modifications of the BX ratio remain based on export data only and are not able to represent comparative advantages beyond their traditional conceptualization according to Ricardian theoryFootnote 10.
Export-import RCA indexes other than the new class of RCA indexes and the CTB indexes also exist. The RCA index from Michaely (1962) consists of the difference between \(X_{ikt}/X_{iKt}\) and \(M_{ikt}/M_{iKt}\). Balassa (1986) proposes the calculation of \((X_{ikt}-M_{ikt})/(X_{ikt}+M_{ikt})\), and Donges and Riedel (1977) suggests normalizing \((X_{ikt}-M_{ikt})/(X_{ikt}+M_{ikt})\) by the same ratio calculated for all products throughout K before subtracting 1 and multiplying the subsequent difference by -1 or 1 depending on the sign of the trade balance of i (in t). The main weakness of these RCA indexes is that they are not based on the overall structure of trade flows. Only the trade flows associated with a given country are employed to measure comparative advantages. Consequently, it is not possible to make a consistent connection with the relative nature of comparative advantages.
Another RCA index that warrants consideration is the recent regression-based RCA index from Leromain and Orefice (2014), here referred to as the Z index. This index is of interest because it is based on the Ricardian model of Costinot et al. (2012), which combines heterogeneity in productivity across varieties of the same product with the features of the standard Ricardian model of international trade (constant returns to scale, perfect competition, labor as the unique factor of production, and equilibrium, among other features). In addition, it is the sole RCA index computed from disaggregated trade data. Denote \(x_{ijkt}\) as the trade flow of k from i to another country j in t (hence \(X_{ikt}=\sum _{j \in J}x_{ijkt}\) and \(M_{ikt}=\sum _{j \in J}x_{jikt}\)). The Z index starts from the OLS estimation of the following equation:
that is, the log of \(x_{ijkt}\) is decomposed additively into an exporter-importer fixed effect (\(\delta _{ijt}\)), an exporter-product fixed effect (\(\delta _{ikt}\)) and an importer-product fixed effect (\(\delta _{jkt}\)). \(\epsilon _{ijkt}\) is the residual term specific to (i, j, k, t). Comparative advantages are assumed to determine the exporter-product fixed effect. In this regard, \(z_{ikt}\) is defined as a proxy for the Ricardian fundamental productivity level of i with respect to k in t. After estimating \(\delta _{ikt}\), \(z_{ikt}\) is computed as \(\exp (\delta _{ikt}/\theta )\) where \(\theta\) captures heterogeneity in productivity across varieties of the same product k. The Z index is based on \(z_{ikt}\) and the following variables: \(\bar{z}_{it}=(^{1}/_{\#K})\sum _{l\in K}z_{ilt}\) is the average productivity of i across products in t; \(\bar{z}_{kt}=(^{1}/_{\#J})\sum _{j\in J}z_{jkt}\) is the average productivity for k across countries in t; and \(\bar{z}_{t}=(^{1}/_{\#J}{_{\times \#K}}){\sum _{j\in J}}\sum _{l\in K}z_{jlt}\) is the average productivity across countries and products in t. The Z index is the ratio of \(z_{ikt}/\bar{z}_{it}\) to \(\bar{z}_{kt}/\bar{z}_{t}\):
The numerator is the value of \(z_{ikt}\) normalized by the average productivity of i in t, and the denominator is the same value at the level of J. Therefore, if the Z index is greater than 1, i has higher productivity for k than the other countries on average, which echoes the traditional definition of comparative advantages à la Ricardo. Note that, however, the Z index cannot capture “qualitative” comparative advantages arising from product differentiation, specifically quality (Stellian and Danna-Buitrago 2019).
In summary, the most robust RCA indexes from a theoretical standpoint–that is, robustness before any consideration of a specific case of comparative advantages–are the \(\text {RC}'\) index and its modifications, as well as the CTB indexes and the Z index. For this reason, our empirical evaluation will focus on these RCA indexes.
5.2 Data and Methodolgy
Our empirical case corresponds to the nineteen countries in the Euro area. Therefore, J comprises Austria, Belgium, Cyprus, Estonia, Finland, France, Germany, Greece, Ireland, Italy, Latvia, Lithuania, Luxembourg, Malta, Netherlands, Portugal, Slovakia, Slovenia and Spain. Concerning K, we use the 3-digit Standard International Trade Classification, which mainly comprises 255 product categories distributed among food, live animals, beverages, tobacco, crude materials, oils/fats/waxes, chemicals and related products, manufactured goods, machinery and transport equipment, and miscellaneous manufactured articles. Concerning T, we calculate RCA indexes for each year from 1995 to 2018 using trade data from UNCTADstat. GDP and GDP per capita data are taken from World Bank national accounts data.
Concerning the Z index, the value of \(\theta\) in Eq. 12 is set to 6.534 (Costinot et al. 2012; Leromain and Orefice 2014). For the adjustment of trade flows in the \(\text {RC}^r\), \(\text {RC}^{yr}\) and \(\text {CTB}^{Yr}\) indexes, we use three alternative reference years (r). We use the first (1995) and last (2018) available years to make a “forward-looking” adjustment of trade flows and a “backward-looking” adjustment of trade flows, respectively (Stellian and Danna-Buitrago 2017). We also use 1999 as a reference year because 1999 was the year of introduction of the euro. Ultimately, comparative advantages are calculated for \(19\times 255 \times 24 =116280\) combinations of countries, products and periods, and these calculations are performed according to fourteen RCA indexes:
-
\(\text {RC}'\) and \(\text {RC}^{y}\);
-
\(\text {RC}^{r}\) and \(\text {RC}^{yr}\) with \(r\in \{1995,1999,2018\}\);
-
CTB and \(\text {CTB}^{Y}\);
-
\(\text {CTB}^{Yr}\) with \(r\in \{1995,1999,2018\}\); and
-
Z.
Table 2 presents descriptive statistics for each index. An online appendix contains bar charts representing the frequency distributions of each RCA index and Excel worksheets containing all calculations.
The quality of the empirical values of comparative advantages in the universe \(J\times K \times T\) described previously is evaluated following the path suggested by Leromain and Orefice (2014) and Stellian and Danna-Buitrago (2019). In what follows, we describe the tools employed for each criterion assessing the empirical accuracy of CTB indexes (time stationarity, shape and ordinal ranking bias).
Time stationarity The first way to check for time stationarity is the Harris-Tzavalis panel-data unit-root test. The null hypothesis is \(\rho =1\) in the following AR(1) process:
where \(\text {RCA}_{ikt}\) is the value of an RCA index associated with (i, k, t), \(\gamma _{ik}\) is an intercept specific to each country-product pair (the panels) and \(\varepsilon _{ikt}\) is the residual term associated with each country-product-period triplet. If the null hypothesis is rejected, namely \(|\rho |< 1\), the RCA index exhibits short-term deviations and finite variance around a time-constant mean for the universe \(J\times K \times T\) under consideration, leading to time stationarity of the RCA index.
The Harris-Tzavalis panel-data unit-root test is a preliminary step because this test verifies whether time stationarity of an RCA index exists. If the null hypothesis is rejected, then additional measures describe the magnitude of time stationarity. The first measure arises from standard deviation. It is possible to calculate the across-time standard deviation of an RCA index for a given country-product pair. Time stationarity is higher if this standard deviation is closer to zero for the country-product pair under consideration. From the set of \(\# J\times \# K\) measures of standard deviation associated with \(J\times K\), we compute the across-product average of that set for each country. Ultimately, we rank the RCA indexes according to the distances of their respective averages from zero. This gives rises to \(\#J\) rankings. Ultimately, we calculate the across-country mean rank for each RCA index. This mean rank measures the score of each RCA index from the vantage point of standard deviation. A smaller mean rank implies a better score.
Two other measures of time stationarity arise from the OLS estimation of the following equation:
This regression is based on \(\#K\) observations for a given country. Each observation corresponds to a product. The dependent variable is the value of the RCA index calculated for (i, k) in the final period in T, which is written as \(t_1\) (2018 in our case), and the independent variable is the value of the RCA index calculated for (i, k) in the initial period in T, which is written as \(t_0\) (1995). Time stationarity is higher if the distance of \(\alpha _{1i}\) from 1 is smaller and the distance of \(\alpha _{0i}\) from zero is smaller. Indeed, if \(\alpha _{1i}=1\) and \(\alpha _{0i}=0\), then \(\text {RCA}_{ikt_1}=\text {RCA}_{ikt_0}+\varepsilon _{ik}\), which means that for country i the values of the RCA index in \(t_1\) deviate from the values of the RCA index in \(t_0\) only by the residual term (\(\varepsilon _{ik}\)).
For each country, we rank the RCA indexes according to the distances of their respective values of \(\alpha _{1i}\) from 1, and we calculate the across-country mean rank for each RCA index. Similarly, we rank the RCA indexes according to the distance of their respective values of \(\alpha _{0i}\) from 0 and calculate the across-country mean rank for each RCA index.
Lastly, three additional measures of time stationarity arise from the OLS estimation of the following equation:
This regression is based on \(\#J\times \#K\) observations throughout countries and products. The regression differs from the former equation in two ways: \(\alpha\)-like coefficients are calculated for the whole trade area instead of a single country (hence there is no subscript i), and \(\gamma _i\) is a fixed effect that implies a specific intercept for each country, which is useful to control for country heterogeneity in the estimation. As for Eq. 14, time stationarity is higher if the distance of \(\alpha _{1}\) from 1 is smaller and the distance of \(\alpha _{0}\) from zero is smaller. In addition, time stationarity is higher if the distance of \(\gamma _{i}\) from 0 is smaller. We rank the RCA indexes according to the distances of their respective values of \(\alpha _{1}\) from 1 and the distances of their respective values of \(\alpha _0\) from 0. Ultimately, for each country we rank the RCA indexes according to the distances of their respective values of \(\gamma _{i}\) from 0 (excluding the country whose corresponding value of \(\gamma _i\) must be set to zero for the estimation), and we calculate the across-country mean rank for each RCA index.
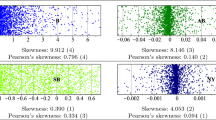
Shape Stellian and Danna-Buitrago (2019) use skewness and mean minus median to measure the symmetry of an RCA index, and kurtosis to measure tail thinness. Symmetry is higher if both statistics are closer to zero, and tail thinness is higher if kurtosis is higher. We suggest dividing mean minus median by standard deviation to obtain a dimensionless unit of symmetryFootnote 11, just as skewness is the third central moment normalized by standard deviation to the power of 3/2. A dimensionless unit enables more consistent comparisons between RCA indexes with different scales like those as in the present paper. In addition, we suggest using a measure of tail thinness other than kurtosis. This statistic is usually viewed as a measure of the concentration of a distribution about its mean such that higher kurtosis implies higher concentration and therefore increases the likelihood of thinner tails. However, the correspondence between kurtosis and concentration is not true in general (Westfall 2014). Consequently, to avoid misleading interpretations of kurtosis, we suggest replacing kurtosis with another measure, namely the number of values beyond one standard deviation of the mean. A smaller number of “outliers” implies thinner tails.
Ultimately, from the set of \(\# J\times \# T\) measures of skewness associated with \(J\times T\), we compute the across-time average of that set for each country, and we rank the RCA indexes according to the distance of their respective averages from zero. Ultimately, we calculate the across-country mean rank for each RCA index. The same process is applied to the normalized mean minus median and mean numbers of outliers.
Ordinal ranking bias For each country i and period t, it is possible to calculate a pair of \(\# K\) integers. The first integer is the across-product rank of k for i in t. The second integer is the across-country rank of i in t with respect to k. For each country, we compute the correlation coefficient throughout the \(\#K \times \# T\) pairs of integers, which gives the Spearman’s rank order coefficient. If this coefficient is close to 1, the products for which i has the highest values of the RCA index compared to the other products tend to be the products for which i has the highest values of the RCA index compared to the other countries. On the contrary, the products for which i has the lowest values of the RCA index compared to the other products tend to be the products for which i has the lowest values of the RCA index compared to the other countries. The same applies to intermediate ranks. Ultimately, a Spearman’s rank order coefficient close to 1 suggests a correspondence between the intra-country ranks and the inter-country ranks determined by an RCA index and hence a lower ordinal ranking bias. In this regard, for each country, we rank the RCA indexes according to the distances of their respective Spearman’s rank order coefficients from 1. This enables the calculation of the across-country mean rank for each RCA index.
The second measure of the ordinal ranking bias is suggested by Stellian and Danna-Buitrago (2019). For each country and period, it is possible to distribute the values of an RCA index – one value per product – between \(\# J\) subsets. The first subset comprises the values that rank i first compared with the other countries. The second subset comprises the values that rank i second (compared with the other countries), and so on, until the last subset, which comprises the values that rank i last. Then, we calculate the mean value of each subset. Thereafter:
-
1.
We count how many values that are not included in the subset associated with the first rank are greater than the mean value of the subset associated with the first rank. For example, if i ranks first with a mean value equal to 1.5 but second or lower with a value equal to 2 (which does not belong to the subset associated with rank 1), then this amounts to an inconsistency in the country ranking by the RCA index under consideration.
-
2.
We count how many values that are not included in the subset associated with the last rank (i.e. rank \(\# J\)) are lower than the mean value of the subset associated with the last rank. For example, if i ranks last with a mean value equal to 0.25 but penultimate or higher with a value equal to 0.10 (which does not belong to the subset associated with rank \(\# J\)), then this amounts to an inconsistency in the country ranking by the RCA index under consideration.
-
3.
For the intermediate ranks, the same logic applies. First, we count how many values associated with every rank lower than x (i.e. ranks \(x+1, x+2, \cdots \# J\)) are higher than the mean value of the subset associated with rank x. Then, we count how many values associated with every rank greater than x (i.e. ranks \(1,2,\cdots , x-1\)) are lower than the mean value of the subset associated with rank x.
We compute the number of such inconsistencies for each country and each period. Then, for each country, we calculate the across-time average number of inconsistencies, and we rank the RCA indexes
5.3 Results and Discussion
Table 3 presents the Harris-Tzavalis unit root tests checking for time stationarity. All RCA indexes lead to rejection of the null hypothesis, so all RCA indexes can be considered stationary over time. However, the magnitude of time stationarity differs from one RCA index to another. Figure 2 shows the corresponding ranking according to standard deviation, \(\alpha _{1i}\), \(\alpha _{0i}\), \(\alpha _{0}\), \(\alpha _{1}\) and \(\gamma _{i}\); the intermediate computations and estimations are available in the online appendix. For standard deviation, \(\alpha _{1i}\), \(\alpha _{0i}\) and \(\gamma _{i}\), each graph comprises 14 lines in polar coordinates. Each line represents an RCA index and contains 19 points along the radial axis. Each point represents a country placed in alphabetical order, and the color of a point gives the rank of the corresponding RCA index for the country under consideration. Colors range from green for rank 1 to red for rank 14, with evenly spaced colors for intermediate ranks. For example, in the case of standard deviation, the predominance of green for CTB (C1 in the graph) indicates that this RCA index tends to have the lowest standard deviation for almost all countries. Similarly, in the case of \(\gamma _i\), the predominance of red for Z indicates that this RCA index tends to have the greatest distances from zero regarding country-specific effects (Eq. 15).
Ranks concerning shape and ordinal ranking bias are shown according to the same logic of visualization in Fig. 3. Ultimately, the across-country mean ranks are presented in Table 4, which gathers all the scores obtained through the different measures of time stationarity, shape and ordinal ranking bias. For each criterion, the final score achieved by an RCA index is calculated as the mean of each score.
Table 4 suggests that no RCA index has the best score for all criteria. The best score regarding time stationarity is achieved by the CTB index, the \(\text {CTB}^{y,2018}\) index gives the best score concerning shape, and the ordinal ranking bias is minimized by the \(\text {RC}'\) index. Generally speaking, the scores show that the whole class of CTB indexes gives the best performances in terms of both time stationarity and shape. Nevertheless, the \(\text {RC}'\) index and the modified versions of this index show the best scores concerning the ordinal ranking bias (except \(RC^{y,2018}\), whose score is lower than Z), whereas the CTB indexes give the poorest performance. In addition, the \(\text {RC}'\) index and the modified versions of this index give good second-best performances in terms of both time stationarity and shape.
Consequently, our empirical example shows that the new class of RCA indexes suggested in the present paper is able to give good measures of comparative advantages in the Euro area and may usefully complement the measurements given by the CTB indexes, particularly concerning the ordinal ranking bias. On the one hand, the criteria of time stationarity and shape assess the consistency of the empirical measures of comparative advantages by an RCA index with theory and stylized facts. For example, the time stationarity of RCA indexes is evaluated because theory suggests that comparative advantages are sticky over time. Similarly, the mean number of outliers is calculated because stylized facts suggest that countries tend to exhibit a low frequency of strong comparative advantages or disadvantages. On the other hand, ordinal ranking bias concerns the informational content provided by an RCA index about intra- and inter-country rankings independently of the consistency of the empirical values of an RCA index with desirable features arising from theory or stylized facts. In this regard, the new class of RCA indexes achieves a well-balanced compromise between informational content and desirable features regarding time stationarity and shape. The CTB indexes show better performance concerning the aforesaid desirable features but their informational content is of lower quality; and the Z index matches neither the same quality of the new class of RCA indexes (except one) nor the consistency of the CTB indexes with time stationarity and shape.
Other results arise from Table 4. First, \(\text {RC}'\) has a better score than \(\text {RC}^y\) for ordinal ranking bias but not for shape. Consequently, the way GDP per capita is taken into account is able to enhance shape but not the ordinal ranking bias. Second, \(\text {RC}^{1995}\) provides better scores than \(\text {RC}^{1999}\) and \(\text {RC}^{2018}\) for all criteria. Consequently, when the \(\text {RC}'\) index is calculated with adjusted trade flows, better measures of comparative advantages are obtained with an adjustment on the basis of the first available year (1995). However, these scores are lower than the score obtained by \(\text {RC}'\) regarding ordinal ranking bias, namely without adjusting trade flows. The scores are roughly the same for shape. In addition, \(\text {RC}^{1995}\) is associated with a better score than \(\text {RC}'\) for time stationarity, and the score obtained by \(\text {RC}^{1999}\) is close to the score obtained by \(\text {RC}'\). Consequently, adjusting trade flows does not always provide better measures of comparative advantages. The same conclusion arises from a comparison of the scores obtained by \(\text {RC}^y\), \(\text {RC}^{y,1995}\), \(\text {RC}^{y,1999}\) and \(\text {RC}^{y,2018}\). This conclusion does not question the idea of adjusting trade flows. Rather, it calls for the development of other methods to calculate adjusted trade flows (see Eq. 5). Following the same logic, it is possible to inquire into other specifications of the function \(f_i\) that modify the computation of \(\text {RC}'\) (see Eq. 4). The aim is to obtain better empirical scores compared not only to \(\text {RC}'\) but also to the class of CTB indexes and the Z index.
6 Conclusion
This paper revises the widely cited Revealed Comparative Advantage (RCA) indexes from Vollrath (1991) to propose a new RCA index that combines an additive extension of the standard RCA index à la Balassa (1965) to imports with the symmetric transformation à la Dalum et al. (1998). This new RCA index can be modified to take into account GDP per capita, which is a proxy for factor endowments, with the aim of better measuring comparative advantages. In addition, we apply the adjustment process of trade flows initially used for RCA indexes in terms of Contribution to the Trade Balance (CTB). These modifications of the new RCA index give rise to a whole class of new RCA indexes. The quality of comparative advantage measurements of eight RCA indexes of this class is evaluated against five CTB indexes and the regression-based RCA index from Leromain and Orefice (2014) in the case of the Euro area. The eight new RCA indexes under consideration arise from taking into account GDP per capita or adjusting trade flows according to three different reference years (the first available year, 1995, the last available year, 2018, and the year the Euro area was created, 1999). These fourteen RCA indexes have consistent theoretical foundations, and their evaluation is based on three criteria: the ability of an RCA index to be stationary over time, a symmetric distribution with thin tails (“shape”), and the relative absence of ordinal ranking bias. The score obtained by each RCA index regarding each criterion is computed according to the tools elaborated in Stellian and Danna-Buitrago (2019). These tools comprise unit-root panel data tests, dispersion and shape statistics, regressions, Spearman’s rank order coefficient and another non-parametric analysis of ordinal ranking bias.
All but one of the new RCA indexes are better able to avoid ordinal ranking bias, and although they are not associated with the best scores regarding time stationarity and shape, they are second-best solutions for these two criteria. By “second-best”, we mean that the scores are lower than the scores obtained by the CTB indexes but higher than the scores of the index from Leromain and Orefice (2014). The new class of RCA indexes thus can usefully complement the CTB indexes, which have already proved accurate from an empirical standpoint in measuring comparative advantages (Danna-Buitrago 2017; Stellian and Danna-Buitrago 2019).
Similar empirical evaluations of the suggested new class of RCA indexes should be made for trade areas other than the Euro area to obtain a broader view of the quality of comparative advantage measurements. In addition, as already suggested at the end of Sect. 4, it is possible to inquire into different ways of taking into account GDP per capita and adjusting trade flows. This opens avenues for further investigation with the same objective as the present paper: to improve the measurement of comparative advantages by RCA indexes. Furthermore, although our method of empirical evaluation rests upon a comprehensive set of tools, there is room for enhancement. Two points are worth mentioning. First, Eqs. 14 and 15, which give various measures of time stationarity, do not take into account the values taken by an RCA index throughout the whole set of periods but only the initial and last periods. It would be useful to inquire into other equations whose estimates rest upon the whole set of periods, for example dynamic panel data models. Second, the final scores are calculated on the basis of simple arithmetic mean values across countries for a given variable (e.g. skewness), across variables for a given criterion (e.g. shape), and ultimately across criteria. Computing simple arithmetic mean values can be considered the standard technique to generate synthetic scores of empirical accuracy of RCA indexes. Nevertheless, other techniques may deserve attention, for example arithmetic mean values with specific weights for each country and/or each variable associated with a given criterion and/or each criterion.
Ultimately, this paper supports the application of the new class of RCA indexes in international economics. Specifically, empirical patterns of international specialization can be studied. For a given country-product pair, if \(\text {RC}'\) or other RCA index conceptualized in this paper is greater than a given positive value over several successive years, this can be seen as a signal of international specialization of that country for that productFootnote 12 (Stellian and Danna-Buitrago 2017). Instead of using an absolute value, the determination of which should be further discussed, international specialization can be associated with countries with the highest RCA metric each year in the time span under considerationFootnote 13 (Stellian and Danna-Buitrago 2019). In turn, these insights about international specialization can be helpful for economic policyFootnote 14.
Notes
Another way to measure comparative advantages is the Domestic Resource Cost (DRC) method (Cai et al. 2009), which is beyond the scope of this paper.
Time periods are not explicitly mentioned in the notation used by Vollrath (1987; 1989; 1991) as well as many other works on comparative advantages, for example Leromain and Orefice (2014) and French (2017). However, to remain consistent with other RCA indexes presented below whose calculation depends on trade flows from two different periods, we prefer to include periods in our notation.
This drawback is avoided by the original indexes, as they are based on \(\mathcal {J}\) instead of J. However, as explained before, substituting \(\mathcal {J}\) for J imposes another drawback (index possibly undefined due to division by zero).
Algieri et al. (2018) proposes an “extended Balassa index”, which consists of calculating the ratio of BX to BM instead of the difference between BX and BM. Nonetheless, unlike the \(\text {RTA}'\) index, the extended Balassa index is not symmetric and does not avoid the size bias.
In accordance with the Heckscher-Ohlin theory, factor endowments contribute to the determination of comparative advantages in relation to the relative abundance of different factors and their relative intensiveness in different techniques of production. Here, the link between factor endowments and comparative advantages places greater emphasis on the fact that higher factor endowments imply more available resources for improving productivity and differentiating products. For example, higher factor endowments may imply more knowledge and skills for elaborating high-quality varieties of some products and ultimately creating comparative advantages for these products.
This point has already been made in Section 3 and was the motive for rejecting the calculation of an RCA index solely on the basis of the RXA ratio (REA and \(\text {REA}'\)).
Note that the Kunimoto-Vollrath principle calculates theoretical values of exports and imports on the basis of the overall structure of trade flows. Consequently, being consistent with this principle logically implies being consistent with the relative nature of comparative advantages.
Yu et al. (2009) show that the additive version of the BX ratio possesses additivity across products: if k is divided into two sub-products \(k_1\) and \(k_2\), \(\text {RCA}_{ik_1t}+\text {RCA}_{ik_2t}=\text {RCA}_{ikt}\). Furthermore, the additive version of the BX ratio normalized by \(X_{JKt}\) possesses additivity across countries: if two countries \(i_1\) and \(i_2\) are taken together as a single country, \(\text {RCA}_{i_1kt}+\text {RCA}_{i_2kt}=\text {RCA}_{ikt}\). Additivity makes an RCA index insensitive to the classification of commodities and countries. Nonetheless, it is possible to show that the basic CTB index possesses additivity. In addition, the other CTB indexes and the new class of RCA indexes do not possess full additivity but compensate for this deficiency by using both export and import data, GDP-scaled measures and adjusted trade flows. Consequently, additivity is not sufficient to include some variants of BX in the empirical analysis.
This statistic is close to Pearson’s second coefficient of skewness. The difference lies in the multiplicative factor of 3 applied to (mean minus median)/\(\sigma\). Nevertheless, because the same multiplicative factor is uniformly applied to every normalized mean minus median, using this factor simply implies a monotonic transformation. Consequently, the multiplicative factor of 3 does not make a difference when the normalized mean minus median is used to rank RCA indexes, and we can ignore it.
In this regard, let \(Q\subseteq \mathbb {R}_{+}\) be the interval whose values are those that reveal comparative advantages according to a given RCA index (e.g. \(Q=(0,2]\) for \(\text {RC}'\)). Comparative advantages can be defined as q-sustainable for (i, k) over time span \(U\subseteq T\) with \(q\in Q\) if \(\text {RCA}_{ikt}>q\) \(\forall t\in U\) (Stellian and Danna-Buitrago 2017).
Comparative advantages can be defined as sustainable for (i, k) over time span \(U\subseteq T\) in trade area J if \(\text {RCA}_{ikt}>\text {RCA}_{jkt}\) \(\forall (j,t)\in (J\setminus \{i\})\times U\) (Stellian and Danna-Buitrago 2019). Comparative advantage sustainability and comparative advantage q-sustainability usefully complement the methodology in terms of the Markov transition matrix from De Benedictis and Tamberi (2004) to analyze the dynamics of specialization.
References
Algieri B, Aquino A, Succurro M (2018) International competitive advantages in tourism: An eclectic view. Tour Manag Perspect 25:41–52
Amador J, Cabral S, Maria JR (2011) A simple cross-country index of trade specialization. Open Econ Rev 22(3):447–461
Balassa BA (1965) Trade liberalization and revealed comparative advantage. The Manchester School of Economic and Social Studies 33(2):92–123
Balassa BA (1986) Comparative advantages in manufactured goods: a reappraisal. Rev Econ Stat 68(2):315–319
Benesova I, Maitah M, Smutka L, Tomsik K, Ishchukova N (2017) Perspectives of the Russian agricultural exports in terms of comparative advantage. Agric Econ 63(7):318–330
Brakman S, Van Marrewijk C (2017) A closer look at revealed comparative advantage: Gross-versus value-added trade flows. Pap Reg Sci 96(1):61–92
Cai J, Leung P, Hishamunda N (2009) Assessment of comparative advantage in aquaculture. FAO Fisheries and Aquaculture Technical Paper 528
Cai J, Zhao H, Coyte PC (2018) The effect of intellectual property rights protection on the international competitiveness of the pharmaceutical manufacturing industry in China. Eng Econ 29(1):62–71
Costinot A, Donaldson D, Komunjer I (2012) What goods do countries trade? A quantitative exploration of Ricardo’s ideas. Rev Econ Stud 79:581–068
Dalum B, Laursen K, Villumsen G (1998) Structural change in OECD export specialisation patterns: de-specialisation and ’stickiness’. Int Rev Appl Econ 12(3):423–443
Danna-Buitrago JP (2017) Alianza del Pacífico+4 y la especialización regional de Colombia: Una aproximación desde las ventajas comparativas. Cuadernos de Administración 55:39–52
De Benedictis L, Tamberi M (2004) Overall specialization empirics: Techniques and applications. Open Econ Rev 15(4):323–346
De Saint Vaulry A (2008) Base de données CHELEM – commerce international du CEPII Tech Rep 9, Paris, Centre d’études Prospectives et d’Informations Internationales
Deb K, Hauk WR (2017) RCA indices, multinational production and the Ricardian trade model. IEEP 14(1):1–25
Donges J, Riedel J (1977) The expansion of manufactured exports in developing countries: an empirical assessment of supply and demand issues. Weltwirtschaftliches Arch 113(1):58–87
French S (2017) Revealed comparative advantage: what is it good for? J Int Econ 106:83–103
Giraldo I, Jaramillo F (2018) Productivity, demand, and the home market effect. Open Econ Rev 29(3):517–545
Grundke R, Moser C (2019) Hidden protectionism? evidence from non-tariff barriers to trade in the United States. J Int Econ 117:143–157
Hoen AR, Oosterhaven J (2006) On the measurement of comparative advantage. Ann Reg Sci 40(3):677–691
Jambor A (2014) Country-specific determinants of horizontal and vertical intra-industry agri-food trade: The case of the EU new member states. J Agric Econ 65(3):663–682
Jambor A, Babu S (2016) The competitiveness of global agriculture. In Competitiveness of global agriculture. Springer pp. 99–129
Kunimoto K (1977) Typology of trade intensity indices. Hitotsubashi J Eco 17(2):15–32
Lafay G (1987) Avantage comparatif et compétitivité. Économie Prospective Internationale 29:39–52
Lafay G (1992) The measurement of revealed comparative advantages. In: Dagenais MG, Muet PA (eds) International Trade Modelling. Chapman & Hall, London, pp 209–234
Laursen K (2015) Revealed comparative advantage and the alternatives as measures of international specialization. Eurasian Bus Rev 5(1):99–115
Leromain E, Orefice G (2014) New revealed comparative advantage index: dataset and empirical distribution. Int Eco 139:48–70
Liu B, Gao J (2019) Understanding the non-gaussian distribution of revealed comparative advantage index and its alter. Int Eco 158:1–11
Michaely M (1962) Concentration in International Trade. North-Holland, Amsterdam
Proudman J, Redding S (1998) Openness and Growth. Bank of England, London
Proudman J, Redding S (2000) Evolving patterns of international trade. Rev Int Econ 8(3):373–396
Saki Z, Moore M, Kandilov I, Rothenberg L, Godfrey AB (2019) Revealed comparative advantage for US textiles and apparel. Competitiveness Review: An International Business Journal 29(4):462–478
Sawyer WC, Tochkov K, Yu W (2017) Regional and sectoral patterns and determinants of comparative advantage in China. Front Econ China 12(1):7
Seleka TB, Kebakile PG (2017) Export competitiveness of Botswana’s beef industry. Int Trade J 31(1):76–101
Stellian R, Danna-Buitrago JP (2017) Competitividad de los productos agropecuarios colombianos en el marco del tratado de libre comercio con Estados Unidos: análisis de las ventajas comparativas. Revista CEPAL 122:139–163
Stellian R, Danna-Buitrago JP (2019) Revealed comparative advantages and regional specialization: evidence from Colombia in the Pacific Alliance. Journal of Applied Economics 22(1):349–379
Vollrath TL (1987) Revealed competitive advantage for wheat. Economic Research Service Staff Report (US Department of Agriculture) AGES861030
Vollrath TL (1989) Competitiveness and protection in world agriculture. Agriculture Information Bulletin (US Department of Agriculture) 567
Vollrath TL (1991) A theoretical evaluation of alternative trade intensity measures of revealed comparative advantage. Weltwirtschaftliches Archiv 127(2):265–280
Westfall PH (2014) Kurtosis as peakedness, 1905-2014: R.I.P. Am Stat 68(3):191–195
Yazdani M, Pirpour H (2020) Evaluating the effect of intra-industry trade on the bilateral trade productivity for petroleum products of iran. Energy Econ 86:103933
Yu R, Cai J, Leung PS (2009) The normalized revealed comparative advantage index. Ann Reg Sci 43(1):267–282
Funding
Financial support was received from Pontificia Universidad Javeriana.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Danna-Buitrago, J.P., Stellian, R. A New Class of Revealed Comparative Advantage Indexes. Open Econ Rev 33, 477–503 (2022). https://doi.org/10.1007/s11079-021-09636-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11079-021-09636-4