How should Central Banks Respond to Non-neutral Inflation Expectations?

Abstract

This paper investigates the net real inflation effect on output in ten countries, comprising both advanced and developing countries. An indicator is introduced to compute the net inflation effect on output (NIEO) based on the difference between two concepts of core inflation, where both are computed using the decomposition of VAR residuals. We find that for all countries, when inflation is increasing the NIEO is significantly positive and is negative during periods of decreasing inflation. Typically, countries which follow anti-inflationary policies if the NIEO is of small magnitude suffer relatively minimal damage in output, whereas if the same policies are undertaken when the NIEO is large the damaging effects on output could be much greater. This suggests that the NIEO could be a useful indicator of the likely effects of policy, especially for countries which have frequent episodes of high inflation, and in those countries which employ inflation-targeting policy, as the timing of monetary policy actions could be optimized to take account of this real effect of inflation.

1 Introduction

This article was presented at the fourth ISCEF (Paris, April, 14–16, 2016, www.iscef.com)

The question of the existence and nature of the association between inflation and real output growth (hereafter ‘growth’) has been of great interest over recent decades. This question is significant, for example, for those monetary authorities which aim to achieve an inflation target without unnecessary disruption of real activity. Several theoretical and empirical studies have explored the link between inflation and economic growth (Bruno and Easterly 1996; Grier and Perry 1998; Mallik and Chowdhury 2001; Fountas et al. 2006; Grier and Grier 2006; Fountas and Karanasos 2007; Fountas 2010). As expected, there has been substantial argument over the reality and magnitude of the association between inflation and growth. The empirical and theoretical findings concerning the relationship between inflation and growth are inconclusive. Many studies support the view that the relationship between inflation and growth is non-linear, indicating a positive association at low levels of inflation and a negative association at high rates of inflation².

There is general consensus among economists that permanent and anticipated changes in the inflation rate have no effect on real economic activities in the long-run, although high inflation exerts a negative impact on output in the short-run.³ Bruno and Easterly (1996, 1998) found no evidence of any consistent relationship between inflation and growth at any level. However, the evidence suggests that growth declines rapidly during high inflation periods but then stabilises once inflation declines. Considerable evidence suggests that a continued high inflation rate might have a harmful effect on real growth, even in the long-run.⁴ It has been argued that the negative long-term association between inflation and growth is based on the assumption that high inflation influences the price signalling mechanism, leading to a misallocation of resources in market economies. Researchers have also often highlighted the costs of inflation uncertainty, related to high inflation and the lack of central bank credibility (Ball 1992). Grier and Grier (2006) and Hartmann and Roestel (2013) examined the effect of inflation uncertainty on output growth and found that inflation uncertainty considerably lessens growth. It is worth questioning what would be the inflection point (threshold level), at which the direction of the inflation-growth relationship would change. Fischer (1993) argued that moderate inflation facilitates growth while high inflation produces uncertainty and damages economic performance and there is some further evidence of this (Blanchard et al. 2010).

Inflation targeting is a monetary policy regime that has had significant implications for sustainable price stability. Recently many central banks have amplified the importance of inflation targeting as a major economic policy in which the focus is on high and continued growth as well as stable inflation. Anti-inflation policy is costly, causing reductions in output and employment due to sluggishly adjusting prices and wages, as well as reduced demand for goods and services, because higher interest rates encourage saving and discourage consumers and investors from spending and borrowing. Svensson (2010) supported flexible inflation targeting, whereby central banks not only aim at stabilizing inflation around the given target but also the stability of real economic activity. There has also been consideration of the related question of which measure of inflation is most relevant to the conduct of monetary policy. Many suggest that stabilizing inflation in the sticky-price sector is a better policy and that the flexible-price sector can be ignored, arguing that in sticky-price sectors, price setters are slow to update and do not react immediately to economic changes (Aoki 2001; Mankiw and Reis 2002; 2003; Benigno and Benigno 2004). Once the aim of stable inflation is established and credibility is enhanced, the monetary policy regime should be concerned with minimizing the variability of growth (Shah and Ahmad 2016).

The primary purpose of this paper is to demonstrate that the likely changes of output arising from policy actions depend in part upon the state of inflation and that therefore monetary policy timing can be chosen to reduce the resulting variations in output. Firstly, in this context we compute an indicator which is the difference between expected and output-neutral inflation, based on decomposition of VAR residuals. Secondly, we suggest that policy-makers could use this indicator to assess the likely consequences of monetary actions; in particular, it is an indicator of the output loss (gain) which might arise from an anti-inflationary action (expansionary action), depending upon the current state of inflation expectations. We define the indicator as the Net Inflation Effect on Output (NIEO). Finally, we run a three-variable VAR model to assess the impact of interest rate shocks on growth and inflation, in order to determine how the monetary policy shocks affect macro-variables in these countries. If it is found that the monetary transmission mechanism within these countries is very strong then this will give further emphasis to the importance of the NIEO when considering monetary policy actions.

The empirical analysis considers ten countries, including three countries which have experienced high inflation in the last three decades, each with different inflation dynamics over the last 25 years - Argentina, Iran and Venezuela. Argentina suffered from a period of hyperinflation in 1989–90 and suffered high inflation (about 33%) and depression (GDP declined at −16.3%) in 2002. Iran has experienced high inflation episodes of more than 50% in 1995 and about 40% in 2013. Venezuela has experienced two major episodes of high inflation during the period under study, when annual inflation exceeded 100% in 1989 and 1995. All three have typically had high average inflation throughout the last three decades.

The analysis relates this inflation experience to the monetary policies which have been followed in these countries. For each of the ten countries the VAR model has been estimated by multiple least squares and NIEO has been calculated according to these estimates. It is found that the NIEO is generally positively correlated with the headline inflation rate and is strongly significant during periods of high inflation. It is also found that interest rate changes do have a substantial effect on the macro-variables. For each of the countries, the NIEO is used to argue that if interest rate changes had been enacted at different times the effects of these changes on output might have been more beneficial. The specifics of these cases are discussed amongst the empirical results.

The remainder of the paper is structured as follows: Section 2 presents the theoretical definitions of expected inflation and output-neutral inflation and explains how these are used to compute the NIEO; Section 3 explains the empirical method used to compute the NIEO indicator; Section 4 presents the properties of the data and considers the statistical significance of the results; Section 5 discusses the analysis of the impact of interest rate shocks on inflation and growth; Section 6 details the empirical results in terms of the relationship between the computed NIEO indicators and the monetary policy followed in each of the three countries and the final section concludes.

2 The Theoretical Model

The primary objective of this paper is to measure the indicator NIEO for the purposes of monetary policy formulation. The indicator NIEO is the difference between two concepts of core inflation. One concept is that of Eckstein (1981), which defines core inflation as the increase in the expected costs of production (referred to hereafter as expected inflation). This Eckstein definition of core inflation is the long-run (trend) inflation rate and is consistent with the long-run vertical Phillips curve that is related to anticipated inflation. Furthermore, it explicitly excludes cyclical excess demand influences on inflation that might be consistent with the short-term non-vertical Phillips curve (Roger 1998). Eckstein’s definition of core inflation can be expressed as:

$$ {\uppi}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{e}}+{\mathrm{v}}_{\mathrm{t}} $$

(1)

Eckstein decomposes headline inflation π_t into two components: expected (core) inflation, ${\uppi}_{\mathrm{t}}^{\mathrm{e}}$, and v_t, which is a shock (unexpected at t − 1) that is a combination of the cyclical variations in inflation (arising from excess aggregate demand movements) and transient supply shocks. By contrast, in the Quah and Vahey (1995) definition, core inflation is the component of inflation that has no real effect on output in the medium and long-run, although it could have some effect over the short-run. This is referred to as output-neutral inflation.⁵This concept of core inflation does incorporate cyclical variations in inflation associated with demand shocks. According to this definition headline inflation can be broken into an output-neutral component and a non-output -neutral component. The Quah and Vahey decomposition of headline inflation is:

$$ {\uppi}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{n}}+{\upomega}_{\mathrm{t}} $$

(2)

where output-neutral inflation is ${\uppi}_{\mathrm{t}}^{\mathrm{n}}$ and ω_t is the non-output-neutral component of inflation that is related to persistent effects on output. The evaluation of ${\uppi}_{\mathrm{t}}^{\mathrm{n}}$ is also based on information available at time t − 1. In a flexible price economy, there is no difference between the Eckstein and Quah and Vahey concepts of core inflation because both should be fully output-neutral. However, in a sticky price economy, prices may not be fully flexible in the short-term because some individual relative prices cannot be fully adjusted after a shock, which could therefore have long-lasting effects on output, even if fully expected (Benigno and Benigno 2004). Fischer (1977) and Mankiw and Reis (2002) highlighted that some sectoral prices are set in advance by nominal contracts and price setters are slow in changing their sectoral prices because there are costs related with adjusting prices. In a sticky prices world, the Quah and Vahey concept of core inflation should be more strongly correlated with output than Eckstein’s concept of core inflation because the former includes cyclical influences on inflation. According to Roger (1998), the Quah and Vahey definition of core inflation could be more appropriate if policy makers are interested in the short to medium-term effects of policies. Substituting into Eq. (2) from Eq. (1), we get:

$$ {\upomega}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{e}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}}+{\mathrm{v}}_{\mathrm{t}} $$

(3)

Taking the conditional expectation gives the non-output-neutral component of inflation, because it is evaluated on the basis of information available at time t − 1 for time t.

$$ {\mathrm{E}}_{\mathrm{t}-1}{\upomega}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{e}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}} $$

(4)

where E_t − 1 denotes an expected value conditional on observations available at time t-1 and for all agents apart from the central bank, E_t − 1v _t  = 0. For the central bank the expectation is not zero, as part of the eventual shock is the unanticipated component of monetary policy, which the central bank can choose. For example, a contractionary policy (an increase in the interest rate) would be equivalent to a negative expected value on the part of the central bank.

The short-run aggregate supply function provides a useful simplified theoretical framework with which to explain the relationship between growth and inflation, e.g.

$$ {\mathrm{x}}_{\mathrm{t}}=\upphi \left({\uppi}_{\mathrm{t}}-{\uppi}_{\mathrm{t}}^{\mathrm{e}}\right)\kern4em \upphi >0, $$

(5)

According to this equation, the output-gap x_t depends on headline inflation π_t and the expected inflation ${\uppi}_{\mathrm{t}}^{\mathrm{e}}$, which is based on inflation at t − 1. The parameter ϕ, which is greater than zero, tells us how much the output-gap responds when inflation fluctuates around its expected value. According to the basic neoclassical model, the expected inflation is equal to output-neutral inflation ${\uppi}_{\mathrm{t}}^{\mathrm{e}}={\uppi}_{\mathrm{t}}^{\mathrm{n}}$. However, supposing some nominal rigidity of prices (for example, gradual adjustment of information sets a la Mankiw and Reis (2002), following Fischer (1977)), where some individual relative prices are not fully adjusted after a shock, would imply that these need not be equal, i.e. as prices are sticky, observed inflation is non-neutral in the short-run and likewise expected inflation will not be equal to the long-run neutral value. Although the VAR model below is not explicitly derived from a micro-founded theoretical model, this short-run non-neutrality of inflation is in keeping with the sticky price/New Keynesian DSGE literature.⁶ The previous equations lead to:

$$ {\mathrm{x}}_{\mathrm{t}}=\upphi \left({\uppi}_{\mathrm{t}}^{\mathrm{e}}+{\mathrm{v}}_{\mathrm{t}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}}\right) $$

(6)

Therefore, the conditional expected value of the output-gap is:

$$ {\mathrm{E}}_{\mathrm{t}-1}{\mathrm{x}}_{\mathrm{t}}=\upphi {\mathrm{E}}_{\mathrm{t}-1}{\upomega}_{\mathrm{t}}=\upphi \left({\uppi}_{\mathrm{t}}^{\mathrm{e}}+{\mathrm{v}}_{\mathrm{t}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}}\right) $$

(7)

This relationship (7) gives rise to defining the Net Inflation Effect on Output, NIEO, as:

$$ {\mathrm{NIEO}}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{e}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}} $$

(8)

Hence, a positive difference between the expected and output-neutral inflation indicates that a positive effect on output of inflation will occur in time t, if there are no additional shocks to the system. A negative NIEO can be interpreted conversely. This observation leads to using this difference as a simple indicator of possible real effects of anti-inflationary policy. If, in time t-1, this difference is positive and of small magnitude and the monetary authorities are able, through their policy, to generate a reduction in inflation in time t, loss in output would be relatively small, ceteris paribus. In other words, the implication of Eq. (8) for the conduct of monetary policy is that if the central bank wishes to undertake an anti-inflation measure, it would be better to do so when the NIEO is relatively low, since in this case the expected output cost will be relatively smaller, i.e. a contractionary action will only generate a small output loss if the measure is undertaken when NIEO is close to zero or, ideally, zero. In other words, it is expected that anti-inflationary policy will be relatively more effective with negative NIEO than positive NIEO. Similarly, the expected output gain generated by an expansionary policy will be greater, when NIEO is positive rather than when NIEO ≤ 0. The knowledge of NIEO regimes might therefore recommend the proper timing for undertaking contractionary monetary policy, with least damage to output.

3 Methodology and Evaluation of NIEO

This section explains the methodology underlying the estimation of the NIEO indicator. This requires the computation of the two inflation measures discussed above. Following several recent contributions (Shapiro and Watson 1988; Blanchard and Quah 1989; Quah and Vahey 1995; Hahn 2001; Charemza and Makarova 2006; Martel 2008 and Charemza et al. 2015), this study uses a two variable VAR for growth and inflation to estimate the two components of headline inflation, where expected and output-neutral inflation are computed by decomposition of the residuals. This decomposition was also applied by Quah and Vahey (1995), who considered two types of shocks in the VAR model and then two types of inflation shocks; 1) the shock that has long-run influence on output; 2) the shock which does not have a long-run impact on output. The identification of the disturbances is based on a Cholesky decomposition of the long-run parameters matrix. Output-neutral inflation ${\uppi}_{\mathrm{t}}^{\mathrm{n}}$ is based on the long-run economic hypothesis proposed by Quah and Vahey.

Suppose that the VAR model can be written as⁷:

$$ \mathrm{A}\left(\mathrm{L}\right){\mathrm{Z}}_{\mathrm{t}}=\mathrm{K}+{\mathrm{U}}_{\mathrm{t}} $$

(9)

where ${\mathrm{Z}}_{\mathrm{t}}=\left[\begin{array}{l}{\mathrm{x}}_{\mathrm{t}}\\ {}{\uppi}_{\mathrm{t}}\end{array}\right]$, x_t is the fourth differences of the log of output, π_t is the fourth differences of the log of consumer prices, A(L) is the lag polynomial operator, $\mathrm{K}=\left[\begin{array}{l}{\mathrm{k}}_1\\ {}{\mathrm{k}}_2\end{array}\right]$ the vector of constants, ${\mathrm{U}}_{\mathrm{t}}=\left[\begin{array}{l}{\mathrm{u}}_{\mathrm{t}}^{\mathrm{y}}\\ {}{\mathrm{u}}_{\mathrm{t}}^{\uppi}\end{array}\right]$ shocks with zero expectations and variance-covariance matrix $\sum =\left[\begin{array}{l}{\upsigma}_{11}\kern1em {\upsigma}_{12}\\ {}{\upsigma}_{21}\kern1em {\upsigma}_{22}\end{array}\right]$. While output disturbance ${\mathrm{u}}_{\mathrm{t}}^{\mathrm{y}}$ might have long-lasting effects on both prices and output, inflationary shocks ${\mathrm{u}}_{\mathrm{t}}^{\uppi}$ are defined to have no long-run impact on output. Suppose further that the output shock ${\mathrm{u}}_{\mathrm{t}}^{\mathrm{y}}$ can be decomposed into the technological shock, w_t, and the real effect of the inflationary shock ${\mathrm{u}}_{\mathrm{t}}^{\uppi}$, i.e.:

$$ {\mathrm{u}}_{\mathrm{t}}^{\mathrm{y}}={\mathrm{w}}_{\mathrm{t}}+\updelta {\mathrm{u}}_{\mathrm{t}}^{\uppi} $$

(10)

where the inflationary shock and technology shock w_t are independent and $\updelta =\frac{\upsigma_{12}}{\upsigma_{22}}$, which implies that the variance-covariance matrix of ${\mathrm{W}}_{\mathrm{t}}=\left[\begin{array}{l}{\mathrm{w}}_{\mathrm{t}}\\ {}{\mathrm{u}}_{\mathrm{t}}^{\uppi}\end{array}\right]$ is diagonal. The vector moving average representation of (5) is

$$ {\mathrm{Z}}_{\mathrm{t}}=\mathrm{M}+\mathrm{C}\left(\mathrm{L}\right)\left[\begin{array}{l}1\kern1em \updelta \\ {}0\kern1em 1\end{array}\right]{\mathrm{W}}_{\mathrm{t}} $$

(11)

$$ {\mathrm{Z}}_{\mathrm{t}}=\mathrm{M}+\mathrm{S}\left(\mathrm{L}\right){\mathrm{W}}_{\mathrm{t}} $$

(12)

where M = [m₁,  m₁]^′ = EZ_t = C(1)K, C(L) = A^‐1(L) = I + C⁽¹⁾L + C⁽²⁾L⁽²⁾ + …, and ${\mathrm{S}}^{\left(\mathrm{i}\right)}={\mathrm{C}}^{\left(\mathrm{i}\right)}\left[\begin{array}{l}1\kern1em \updelta \\ {}0\kern1em 1\end{array}\right]$.

The expected inflation ${\uppi}_{\mathrm{t}}^{\mathrm{e}}$, being the rate which would occur along the economy’s long-run growth path⁸, can be estimated from Eq. (11) on the basis of inflation available at time t − 1 for time t.

$$ {\uppi}_{\mathrm{t}}^{\mathrm{e}}=\left[0,\kern0.5em 1\right].\left(\mathrm{M}+\sum \limits_{\mathrm{i}=1}^{\mathrm{t}-1}{\mathrm{S}}^{\left(\mathrm{i}\right)}{\mathrm{L}}^{\left(\mathrm{i}\right)}{\mathrm{W}}_{\mathrm{i}}\right) $$

(13)

The output-neutral inflation defined by Eq. (2) can be recovered by applying the Quah and Vahey (1995) long-run output-neutrality restriction. Decomposition into the unitary shocks is given by

$$ {\mathrm{Z}}_{\mathrm{t}}=\mathrm{M}+\Gamma \left(\mathrm{L}\right){\Phi}_{\mathrm{t}}, $$

(14)

where Γ(L) = Γ⁽⁰⁾ + Γ⁽¹⁾L + Γ⁽²⁾L⁽²⁾ + …,, Φ_t = [φ_1t, φ_2t]^′, the φ_2t is defined as the output-neutral component of disturbances and $\mathrm{E}{\Phi}_{\mathrm{t}}{\Phi}_{\mathrm{t}}^{\prime }=\mathrm{I}$ (identity matrix). The desired long-run output-neutral decomposition is defined as:

$$ \Gamma (1)={\Gamma}^{(0)}+{\Gamma}^{(1)}\mathrm{L}+{\Gamma}^{(2)}{\mathrm{L}}^{(2)}+\dots, =\left[\begin{array}{l}{\upgamma}_{11}\kern1em 0\\ {}{\upgamma}_{21}\kern1em {\upgamma}_{22}\end{array}\right], $$

where γ_kj (k, j = 1, 2) are elements of the long-run matrix Γ(1). After some manipulation, it gives:

$$ \Gamma (1)\times {\Phi}_{\mathrm{t}}=\mathrm{C}(1)\times {\mathrm{U}}_{\mathrm{t}}=\mathrm{S}(1){\mathrm{W}}_{\mathrm{t}}, $$

(15)

Where Γ(1) can be computed as the lower-triangular Cholesky factor of C(1) ∑ C(1)^′. The corresponding output-neutral component ${W}_t^n$ of moving average disturbances W_t given by Eq. (12). Further denote:

$$ {\mathrm{W}}_{\mathrm{t}}^{\mathrm{n}}=\mathrm{C}{(1)}^{-1}\Gamma (1){\Phi}_{\mathrm{t}}^{\mathrm{n}} $$

(16)

where ${\Phi}_{\mathrm{t}}^{\mathrm{n}}={\left[0\kern1em {\upvarphi}_{2\mathrm{t}}\right]}^{\prime }$ can be defined as the output-neutral measure of unitary disturbances Φ_t. The output-neutral inflation is given by

$$ {\uppi}_{\mathrm{t}}^{\mathrm{n}}=\left[0\kern1em 1\right].\left(\mathrm{M}+\sum \limits_{\mathrm{i}=1}^{\mathrm{t}-1}{\mathrm{S}}^{\left(\mathrm{i}\right)}{\mathrm{L}}^{\left(\mathrm{i}\right)}{\mathrm{W}}_{\mathrm{i}}^{\mathrm{n}}\mathrm{W}\right) $$

(17)

So that NIEO_t is given by:

$$ {\mathrm{NIEO}}_{\mathrm{t}}={\uppi}_{\mathrm{t}}^{\mathrm{e}}-{\uppi}_{\mathrm{t}}^{\mathrm{n}}=\left[0\kern1em 1\right].\left(\sum \limits_{\mathrm{i}=1}^{\mathrm{t}-1}{\mathrm{S}}^{\left(\mathrm{i}\right)}{\mathrm{L}}^{\left(\mathrm{i}\right)}\left({\mathrm{W}}_{\mathrm{i}}-{\mathrm{W}}_{\mathrm{i}}^{\mathrm{n}}\right)\right). $$

(18)

As NIEO_t is based entirely on information from the past, it can be used for economic policy analysis and various types of forecasting.

4 Empirical Results

The estimation uses quarterly time series data of growth and inflation rates⁹ of ten countries, including both developed and developing countries. These are the two variables corresponding to the theoretical model in Section 3 above. This paper analyses the real effect of inflation on the three highest (peak) inflation countries in the last three decades, namely Argentina, Iran and Venezuela, while for comparison we included seven more countries, with varied inflation histories. By the high inflation countries (Argentina, Brazil, India, Indonesia, Iran, Russia and Venezuela) we mean those cases where average annual inflation is more than 7% and there are frequent double digit inflation episodes (see Charemza et al. 2015). The three countries (Japan, UK and USA) where average annual inflation is less 3% in the period under consideration are deemed to be ‘low inflation’ countries. The reason to use quarterly data in our analysis is that the relatively short samples weaken the statistical importance of the results and degrees of freedom. There is also the trade-off between maximizing the sample size and minimizing the possibility of a large structural break. The data starts and ends with different dates because quarterly GDP data are not available for a longer period of time for some countries.¹⁰ The quarterly GDP for Argentina, Brazil, Iran, India, Indonesia and Russia is available from 1993Q1, 1995Q1, 1988Q1, 1996Q4, 1990Q1 and 1993Q1 respectively. Additionally, the official quarterly CPI data is missing between 1986Q2 to 1988Q2 and from 2014Q4 for Iran.¹¹ For Venezuela, the quarterly GDP data is taken from the Oxford Economics database, as it was not available from other sources such as the OECD or IFS. For Japan, UK and USA, data starts in 1988Q1; while earlier data is available, using this would make the panel less balanced (for example, the date for India starts in 1996Q1). This also excludes periods of volatility resulting from the oil shocks of the 1970s and early 1980s. We have considered those countries with the highest inflation and for which quarterly data was available for a long time span. We have not considered other high-inflation countries, such as Zimbabwe or some in south-east Europe, due to issues of data availability/reliability. All of the data have been converted to logarithms and seasonally adjusted. Given the problems related to the data availability and reliability, the different time-periods have been used: Argentina (1993Q1-2015Q4),¹² Brazil (1995Q1-2016Q2), India (1996Q4-2016Q2), Indonesia (1990Q1-2016Q2), Iran (1988Q3-2014Q4), Japan (1988Q1-2016Q2), Russia (1993Q3-2016Q2), UK (1988Q1-2016Q2), USA (1988Q1-2016Q2) and Venezuela (1988Q1-2015Q4).¹³

The application of the VAR model depends on the data properties, in particular that the data is stationary. However, the existing literature for or against stationarity of GDP growth and inflation is not conclusive (Charemza et al. 2005; Basher and Westerlund 2008; Cook 2009). The empirical evidence is vast and often contradictory, although the recent results (Perron 1989; Glynn et al. 2007; Caporale and Paston 2013) suggest stationarity even for the high inflation countries and under structural breaks. It is also desirable that the use of the VAR does not omit any long-run information contained within the data, specifically any cointegration relationships. Unit root and cointegration tests were conducted to investigate the stationarity properties of the series. We applied the standard Augmented Dickey-Fuller (ADF) and more powerful unit root tests, because the ADF unit test is known to experience, potentially, the problem of finite sample power, such as stationarity with a large AR root (DeJong et al. 1992). Kim and Perron (2009) introduced unit root tests that are valid when a break occurs at an unknown time under both the null and alternative hypotheses; it has been argued that tests which do not allow for multiple, unknown breaks have low power and may be likely to incorrectly fail to reject a unit root (Montañés and Reyes 2000). In this paper, we use the testing methodology proposed by Bai and Carrion-i-Silvestre (2009), Carrion-i-Silvestre et al. (2009), Elliott et al. (1996) and Ng and Perron (2001) to examine the data for non-stationarity against the possibility of structural breaks in essentially trend-stationary series. We test the inflation and growth data with several unit root tests, namely, ADF-GLS Elliott-Rothenberg-Stock(${MP}_T^{GLS}$), Ng-Perron (${MZ}_{\alpha}^{GLS}$), Silvestre-Kim-Perron (MSB^GLS) SKP-MZ_T Silvestre-Kim-Perron (${MP}_T^{GLS}$). The ADF and Ng and Perron tests indicate that both GDP growth and inflation are stationary for all countries, although in some there is a failure to reject the null of a unit root, as shown in Table 1. We find that GDP growth series for Argentina and Russia and inflation for Brazil and Russia are not stationary for all Ng and Perron tests but stationary by the ADF test. However, for both series we do find that almost all tests do reject the null of a unit root at 5% (see Table 1). This is consistent with the findings of Caporale and Paston (2013) that GDP growth and inflation are stationary even for countries with high inflation episodes and under structural breaks. Hence we conclude that it is reasonable to proceed treating the series as stationary (even though they are not necessarily close to ‘steady state’).

Table 1 Unit Root Test results for annual (quarterly data) GDP growth and inflation

From the results obtained with the Johansen cointegration test, shown in Appendix Table 4, there is no cointegration evidence among GDP and CPI at levels in most of the countries although we do find one cointegration relation for Russia at 5%. Since cointegration does not exist between GDP and consumer prices, we use the following formulation in order to test for Granger-causality¹⁴ from inflation to growth rates and vice versa, that is we specify a short-run relationship between the stationary variables. The results, reported in Appendix Table 5, of the Granger-causality/block (VAR based) exogeneity Wald tests, show that the null hypothesis that inflation does not Granger-causes growth is rejected at the 5% level for all countries, except Brazil and Japan. As Table 5 also indicates, the null hypothesis that growth does not Granger-cause inflation is rejected at the 5% level of significance for India and Russia, implying in this case that there is a one-way causality going from inflation to growth.

With the use of these inflation and growth series, the VAR model (11) has been estimated for each country by the multiple least squares method, where the number of lags has been set using the Akaike Information Criterion and Schwartz Bayesian criteria reported in Table 1.¹⁵ Using the Eqs. (13) and (17) the expected and output-neutral inflations are computed, respectively. Then, applying the estimated parameters, NIEO has been computed using Eq. (18). To check the VAR stability, Table 2 indicates that the absolute values of the roots of the polynomials of the parameter matrices is greater than one, which confirms stability of the VAR model¹⁶ for all countries (Lütkepohl 1991; Lütkepohl 2005). To check for autocorrelation of the residuals the Ljung-Box test is used and the Jarque-Bera test is used to test the normality of the residuals. The reported results support the null hypothesis of no autocorrelation in the residuals for all countries (with the exception of Indonesia). The p-values for the Jarque-Bera test shown in Table 2 indicate that the inflation residuals are non-Normal for all countries, while output residuals are Normal for some countries. Consequently, the estimation results are valid for the purpose of our application.

Table 2 Summary of the VAR estimations and diagnostic tests

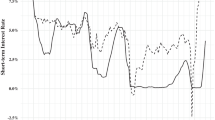
The NIEO is computed using Eq. (18) for the ten countries. In empirical applications, the expected (${\uppi}_{\mathrm{t}}^{\mathrm{e}}$) and output-neutral (${\uppi}_{\mathrm{t}}^{\mathrm{n}}$) inflation are not observable and are computed from the decomposition of the structural VAR residuals. We focus here on the results for Argentina, Iran and Venezuela (the three countries which exhibited very high inflation during the sample period).¹⁷ The results for the remaining countries are given in the appendix (Fig. 9), although we discuss the most relevant comparisons here also.¹⁸ The distributions of the indicator NIEO is unknown; therefore, the confidence intervals shown in the figures are derived by bootstrapping, following Efron (1979) and Davidson and MacKinnon (2007). Although there are some possible limitations to bootstrapped confidence intervals, bootstrapping has been found to perform well relative to other methods of confidence interval construction (e.g. Bollen and Stine 1990; Efron and Tibshirani 1993; Lockwood and MacKinnon 1998). In the empirical analysis the two-dimensional residuals are jointly resampled independently and with replacements in the VAR model. The idea of residual pairwise bootstraps proceeds as follows: first the VAR Model is estimated where the estimated residual pairs are obtained, and then bootstrap residual pairs are generated by randomly drawing with replacement from these estimated residuals. These bootstrap residual pairs are used to compute firstly bootstrap expected inflation, secondly output-neutral inflation and lastly NIEO estimates. The step is repeated 1500 times, and bootstrap distributions of the NIEO are obtained. Figures 1, 2, and 3 show confidence intervals (± two standard deviation around the computed value of NIEO) obtained by the residual pairwise bootstrap applied to the residuals of the VAR model, where the NIEO is represented by the middle line between confidence intervals (the dotted lines).

Fig. 1

NIEO and pairwise bootstrapping, Argentina

Fig. 2

NIEO and pairwise bootstrapping, Iran

Fig. 3

NIEO and pairwise bootstrapping, Venezuela

For all three countries, the significance of the NIEO indicator is mixed, however there are several periods of high and increasing inflation which follow positive and statistically significant NIEO. It can be seen from Fig. 4 that for Argentina there are several prolonged periods of positive and significant NIEO, from 2002 to 04, 2005–06 and 2010–11, coinciding with high inflation. Figure 5 shows that for Iran there was a high and increasing inflation rate throughout 1994–95, 2008–09 and 2012–14, which was associated with a positive and significant NIEO. Venezuela had an average annual inflation rate of 39% within the dataset. In 1996–98 the annual inflation rate was very high, exceeding 100% in some cases, however the NIEO at this time was not significant. From 1998 inflation declined steadily until 2002, at which point another high inflation episode began. As can be seen from Fig. 6, the NIEO became strongly positive and significant from 2002Q3-2003Q4 then became significantly negative once inflation started to fall in 2004.

Fig. 4

Effects of a monetary policy shock on GDP growth and inflation. GDP growth and impulse responses to an interest rate shock: left column for GDP and right column for inflation

Fig. 5

NIEO, GDP Growth and Inflation in %, Argentina

Fig. 6

NIEO, GDP Growth and Inflation in %, Iran

To investigate the validity and reliability of the NIEO, we further discuss the results of the seven other countries, as presented in Appendix Fig. 9. Japan, UK and USA had markedly lower average inflation than the three countries discussed above; it is noticeable that NIEO was statistically significant for several periods. For Japan, during the period 1990–92, inflation was between 2.2–3.5% and NIEO was significantly positive, whereas during 2009–10 there was a significant, negative NIEO (Fig. 9a4). During the period 1990–92, the UK experienced relatively high inflation (e.g. 8.4% in 1991Q2); there is a corresponding significant NIEO (Fig. 9a6). Similarly, for the USA, there are spells of significance of NIEO during 1998Q1 to 2001Q1, which was a period of gradually rising inflation. For Indonesia, NIEO is highly significant for the period 1998Q2 to 1999Q1 during the period of hyperinflation (inflation reached about 80%). Additionally, the findings are identical for Brazil, India and Russia, where NIEO is significantly positive during the episode of high inflation (Brazil: 2015Q2-2016Q2, India: 2010Q1-2013Q3, Russia: 1998Q4-1999Q2).

The findings, in general, suggest that (relative) high inflation episodes generate positive NIEO in all countries, during the periods of increasing inflation, including those countries which have low average inflation. It is generally the case that NIEO is positive while inflation is increasing and is negative (or at least decreasing) during periods of decreasing inflation. This might reflect the adjustment of inflation expectations in response to the observed outcomes, which in turn might lead to reinforcement of the current tendency, giving a partial causal role to the excess inflation expectations indicated by NIEO. This is consistent with the findings of Bruno and Easterly (1998), Charemza et al. (2015) and Charemza and Makarova (2006) that the high inflation periods correspond to a positive, relatively large, real effect.

5 Monetary Transmission Mechanism in the Selected Highest Inflation Countries

Currently, price stability is a key issue of monetary policy and is one of the main objectives of many central banks. For policy to be successfully conducted the policy-maker must have a correct assessment of the channels of the overall monetary transmission mechanism, as this will determine the impact of policy changes on the macro-economy.¹⁹ Lin and Ye (2009) find that both the level of inflation and its volatility are statistically significantly lower in those developing countries which have adopted inflation-targeting monetary policy, relative to those developing countries with alternative monetary policies. While they find a significant difference due to targeting, Lin and Ye (2009) also find that the size of the effect of targeting on inflation and inflation variability differs considerably across countries, due to idiosyncratic factors such as fiscal position, age of the targeting regime and the extent to which policy also aims to control the exchange rate.

An appropriate interpretation of the inflationary process is of key importance in those economies which have experienced the highest levels of inflation over the past few decades. Inflation is one of the main policy issues in Argentina, Iran and Venezuela. These economies have experienced repeated episodes of high inflation and recession. While inflation targeting is not the stated aim of monetary policy in any of these three countries, it is nonetheless apposite to consider the monetary transmission mechanism, i.e. the effect of interest rate changes on the levels of inflation and output growth. The starting conjecture is that an increase in the interest rate will bring about a fall in inflation and a reduction in growth.

The analysis uses a three-variable VAR model to investigate the response of growth and inflation to an interest rate shock. Examples of a similar approach include Sims and Zha (1998), Christiano et al. (1999), Kim and Roubini (2000), Stock and Watson (2001), Faust et al. (2004), and Bjørnland and Jacobsen (2013), all of whom have used VAR models to explore the monetary transmission mechanism. First, we define Z_t as the (3 × 1) vector of the variables discussed above, GDP growth x_t, inflation π_t and interest rate i_t, Z_t = [x_t, π_t, i_t]^′. The structural shocks of the model have been identified by using the Cholesky decomposition. We assume the n(n − 1)/2 economic restrictions, necessary to identify the structural model, are imposed as zero restrictions on the matrix S, that links the reduced form and the structural disturbances²⁰. That is, growth and inflation depends only on lagged values of the interest rate, whereas monetary policymakers might respond immediately to shocks to inflation and growth. Inflation depends on contemporaneous growth but not the interest rate. The economic interpretation and restrictions associated with this model depend on the ordering of the variables. The ordering of the variables specifies which shocks are not allowed to contemporaneously affect which variables, of the vector of endogenous variables Z_t = [x_t, π_t, i_t]^′. Equation (19) describes the relationship between the reduced form disturbances, $\left[{\upvarepsilon}_{\mathrm{t}}^{\mathrm{y}},\kern0.5em {\upvarepsilon}_{\mathrm{t}}^{\uppi},\kern0.5em {\upvarepsilon}_{\mathrm{t}}^{\mathrm{MP}}\right]$, and the structural shocks, $\left[{\mathrm{e}}_{\mathrm{t}}^{\mathrm{y}},\kern0.5em {\mathrm{e}}_{\mathrm{t}}^{\uppi},\kern0.5em {\mathrm{e}}_{\mathrm{t}}^{\mathrm{MP}}\right]$, by using the following ordering in the Cholesky decomposition

$$ \left[\begin{array}{l}{\upvarepsilon}_{\mathrm{t}}^{\mathrm{y}}\\ {}{\upvarepsilon}_{\mathrm{t}}^{\uppi}\\ {}{\upvarepsilon}_{\mathrm{t}}^{\mathrm{MP}}\end{array}\right]=\left[\begin{array}{l}{\mathrm{S}}_{11}\kern1em 0\kern2em 0\\ {}{\mathrm{S}}_{11}\kern1em {\mathrm{S}}_{11}\kern1.5em 0\\ {}{\mathrm{S}}_{11}\kern1em {\mathrm{S}}_{11}\kern1.5em {\mathrm{S}}_{11}\end{array}\right]\left[\begin{array}{l}{\mathrm{e}}_{\mathrm{t}}^{\mathrm{y}}\\ {}{\mathrm{e}}_{\mathrm{t}}^{\uppi}\\ {}{\mathrm{e}}_{\mathrm{t}}^{\mathrm{MP}}\end{array}\right] $$

(19)

Ordering growth first seemed most plausible as this implies that growth shocks, ${\mathrm{e}}_{\mathrm{t}}^{\mathrm{y}}$, may affect the reduced form disturbances of all variables and thus all variables in the system contemporaneously, while, in contrast, the reduced form disturbances of growth, ${\upvarepsilon}_{\mathrm{t}}^{\mathrm{y}}$, and thus the growth are not affected contemporaneously by any of the inflationary e^t_π and monetary policy shocks e^t_MP.

This analysis uses quarterly data on growth, inflation and interest rates from the periods described in Section 4. The interest rate data for Iran and Venezuela is not readily available, at a quarterly frequency, from reliable sources. Therefore, the deposit rate has been used as a proxy for the policy interest rate. For Iran, the quarterly deposit rate data is only available from the IFS database from 2003Q4 onwards; prior to this, the data series for 1988Q3 to 2003Q3 is interpolated from annual series, by using Simpson’s rule in numerical integration (see Al-Turki 1995). The annual series is downloaded from the Bank of Iran. The data are drawn from various sources including the database of Oxford Economics for the Argentina data and from the IFS database in the case of Venezuela.

We use a set of Ng and Perron²¹ unit root tests, along with ADF and PP tests, for the interest rate data and find that the interest rate is stationary for Argentina and Venezuela, while it is non-stationary for Iran.²² Given these results, for Argentina and Venezuela the VAR models of the three stationary variables are computed. For Iran, the interest rate is stationary at first difference. Given this, a Johansen cointegration test is applied (for Iran) to estimate the long-run relation among GDP, CPI and the interest rate, all of which are integrated I(1). According to the Trace and Maximum Eigenvalue tests given in Appendix Table 7, we cannot reject the null hypothesis that there is no cointegration vector. Consequently, the VAR approach is applied on two stationary variables (growth and inflation) and one non-stationary variable (interest rate) for Iran. This follows Stock and Watson (2001), Thoma (2008) and Bjørnland and Jacobsen (2013), who use the interest rate in levels because using differences would mean that information will be lost, since it is the level of the interest rate and not the change of it that matters when economic agents optimize.

Lag-length selection criteria suggest the use of six lags for Argentina, one lag for Iran and five lags for Venezuela. Furthermore, in order to take account of the effects of the Iraq-Kuwait war in 1990, the global financial crisis, an economic depression in 1998–2002 in Argentina, which began due to the Russian and Brazilian financial crises, the terrorist attacks in the USA in 2001 and the Iraq war in 2003, the computed VAR of the three endogenous variables includes dummies²³ as exogenous variables associated to capturing the above-mentioned structural break episodes (see Boivin and Giannoni 2006).

Table 8 (in the Appendix) summarizes the Granger causality results for the three variable VAR. We find that the interest rate causes inflation and output at the 1% significance level for Argentina and Venezuela, whereas for Iran the interest rate does predict growth at 5% but doesn’t cause inflation. Diagnostic tests show that the VAR is well-specified and stable.²⁴

Impulse response functions indicating the impact of variables on output and inflation are shown in Fig. 4, with the dotted lines representing ±2 standard error confidence intervals, with horizons of 20 quarters. A positive monetary policy shock affects output negatively for all three countries, although the effect is negligible for Iran. In the case of inflation, the positive monetary policy shock decreases inflation for Argentina and Venezuela, however, surprisingly for Iran the shock produces a negligibly positive (almost zero) response in inflation (although this increase is not significant).

The variance decomposition, reported in Table 3, demonstrates that interest rate shocks account for 17.4% of growth volatility, in the long-run, for Argentina. For Iran 2.6% of output variation is caused by interest rate shocks, while for Venezuela policy shocks cause 8.5% of output variability. The decompositions for inflation show that for Argentina, 43% of variation is due to policy shocks, in the long-run, while for Venezuela 21% of long-run variation is caused by policy shocks. This gives a clear indication that in these countries interest rate changes have a strong effect on macro-variables. This is consistent with the findings of Romer and Romer (2004) and Barakchian and Crowe (2013) that monetary policy has large and statistically significant effects on both growth and inflation. For Iran there is a very small effect on inflation, with only 0.08% of long-run inflation variability being caused by interest rate shocks. The findings for Iran are consistent with the previous results that interest rates do not Granger-cause inflation and that the response is statistically insignificant.

Table 3 Variance decomposition of GDP growth and Inflation in Argentina

6 NIEO and Monetary Policy

Having analysed the monetary transmission effects on output and inflation, we now consider the role of the NIEO indicator in suggesting the preferred timing of interest rate changes. One of the purposes of inflation targeting is to engender perceptions of central bank credibility and thereby influence inflation expectations towards the target inflation rate. The NIEO indicator can be utilised to determine the extent to which inflation expectations, relative to output-neutral inflation, impact upon growth. When attempting to ‘anchor’ expectations through anti-inflationary policy, the central bank could use NIEO to judge the possible resulting harmful effects on growth.

Figures 5, 6, and 7 show growth (columns, left-hand axis), inflation (solid line, right-hand axis) and NIEO (dashed line, left-hand axis) for each of the three countries studied. Figure 5 shows the results for Argentina. It can be seen that the NIEO is relatively small for the first few years of the sample, but as inflation increased during 2002 the NIEO increased considerably (Fig. 1 above shows that the NIEO was statistically significantly positive throughout this period). Argentina experienced negative annual growth from 1999 onwards, being −6% in 1999 and worsening to 17% in 2002. Over the same period, the monetary policy interest rate was increased from 8% (1999) to 39% (2002). However, inflation was not high; in fact, there was deflation of 1.8% in 1999, −0.64% in 2000 and 1.62 in 2001, before a spike in inflation in 2002. Throughout this period the NIEO was negative, suggesting that an expansionary monetary policy would have stimulated growth (and inflation). Since 2005 the NIEO has been low relative to headline inflation, with the difference between the two being roughly stable. This suggests that as actual inflation has been stable, inflation expectations have been similar to the output-neutral inflation rate.

Fig. 7

NIEO, GDP Growth and Inflation in %, Venezuela

Figure 6 shows the results for Iran. As previously discussed, Iran has had two episodes of high inflation within the sample period. The first, in the mid-1990s, can be seen to correspond to a 13% increase in the NIEO, as expectations adjusted to the short-term deviation of inflation from the long-run rate. At this time the growth rate was negative, with a minimum of −8%. The second period of high inflation occurred in 2011–13, with the NIEO becoming significantly positive during this period also (see the confidence intervals in Fig. 6 above). In response to rising inflation beginning in 2010 the interest rate was increased in 2012, from 11.16% to 14.81%; however, this did little to reduce inflation, with the annual inflation rate rising to almost 40% in 2013, while at the same time there was a recession (GDP growth of approx. -11%). The NIEO was positive during 2012, suggesting that anti-inflationary policy at this time would have reduced growth. The NIEO was negative in 2010 when inflation started increasing, so an anti-inflationary policy undertaken at this time might be expected to have had a less damaging effect on output.

Figure 7 provides the results for Venezuela. In this case, although there were episodes of high inflation in the mid-1990s and at the very end of the sample period, the NIEO does not generally seem to closely follow the inflation rate, suggesting that expected inflation remained close to output-neutral inflation (despite the large short-term deviations from it NIEO was significantly positive in 1999, as shown in Fig. 3 above, but not large in absolute terms). In 1998 the interest rate was increased to 35%, despite inflation following a downward trajectory after the peak in 1996. This led to a sharp recession in 1999 (annual growth of −9%). At the time of the interest rate increase the NIEO was positive, indicating that the increase was likely to damage output growth more. The NIEO was also positive in 1997, but of lower magnitude; hypothetically an increase in the interest rate in 1997 would have been less harmful to growth than that enacted in 1998. For Venezuela the largest values of NIEO occurred in relation to the severe recession in 2003 and subsequent positive growth in 2004. Had the policy rate been increased in 2001 rather than 2002, the NIEO suggests that the adverse effect on growth would have been smaller, as in 2001 NIEO was close to zero (and in some quarters negative), while in 2002 NIEO was positive (and increasing). In this case it seems that the NIEO indicator lagged actual inflation and the change in NIEO might reflect a large adjustment of expectations in response to the increase in inflation in 2002, which followed four years of relatively low and steadily-declining inflation. After this episode the NIEO was close to zero for the remainder of the sample period.

The overall experience of these three countries suggests that the undesirable effects of necessary monetary policy changes could potentially have been better-managed if the timing had been based on the NIEO. The same reductions in inflation could perhaps have been achieved with smaller harmful effects on growth, if policy had acted sooner while the NIEO was of lower magnitude, such that the changes in inflation would not have effected growth as strongly. A similar argument could be made for the other countries in our study, which were also shown to have significant, increasing NIEO during periods of increasing inflation.

To illustrate the evolution of the monetary policy implemented by the central banks under a counterfactual scenario reflecting the targeting of the NIEO, we compute a simple Taylor rule, originally proposed by Taylor (1993), as a description of interest rate policy in the countries under study. As in Castelnuovo (2007) and many other studies, we estimate the following Taylor rule:

$$ {\mathrm{r}}_{\mathrm{t}}={\upalpha}_0+{\upalpha}_1{\uppi}_{\mathrm{t}}+{\upalpha}_2{\mathrm{x}}_{\mathrm{t}}+{\mathrm{u}}_{\mathrm{t}} $$

(20)

where π_t is the inflation rate and x_t is the output growth. This equation may be considered as the baseline monetary policy reaction function of macroeconomic modelling for the evolution of the central bank’s key interest rate (r_t). Figure 8 shows the results where the black and orange lines (black and light grey when viewed in grey scale) correspond to the actual interest rate and the Taylor rule prescriptions obtained for NIEO indicator. As can be seen, the central bank would have had to respond with a much tighter monetary policy during the whole sample in the case of Argentina (Fig. 8a). It should be notice that, due to its forward-looking nature, the interest rate resulted from our counterfactual scenario reaches a peak in advance to the significant increase registered in 2002 following the abandonment of the peg with the USA dollar. As for the Iranian case (Fig. 8b), the monetary policy that the central bank would have followed if the NIEO had been targeted would had been much tighter at the beginning of the sample and around the Global Financial Crisis, indicating once again a much earlier response. Finally, in the case of Venezuela, the central bank would have reacted more actively since the 2002 recession.

Fig. 8

Interest rate and Taylor rule prescriptions

7 Conclusions

It has been found that for all ten countries, in periods of high inflation the NIEO is significantly positive and that when inflation is increasing the NIEO is also increasing. Consistent with this, those countries with low average inflation were also found to have increasing NIEO during periods of increasing inflation. This suggests that the NIEO could be a useful indicator of the likely effects of monetary policy, including in those countries which already have quite successful inflation-targeting policy. Regarding the analysis of the three high inflation countries (Argentina, Iran, Venezuela), which did not follow inflation-targeting policies, the interest rate policy changes still had a causal effect on growth and inflation (i.e. monetary policy is effective), which further implies that NIEO is relevant to the determination of growth and inflation in these countries. Moreover, our analysis found that output did respond negatively (as expected) to the interest rate, therefore policy makers ought to consider the effects of such changes, beyond the effect on inflation. This supports the argument of Barakchian and Crowe (2013) that active monetary policy could prevent high inflation and stabilizes growth.

Furthermore, comparison of the NIEO results with the monetary policy decisions which these countries have made provides some evidence to suggest that the policies might have been more effective and/or less harmful to output if their timing had accorded better with the NIEO. Typically, countries which undertook anti-inflationary actions while the NIEO was large suffered relatively more damaging effects on output, while if the same policies had been undertaken while the NIEO was small the likely outcome regarding output would have been less severe. In particular, our results suggest that anti-inflationary action is best taken at the beginning of rising inflation periods, before inflation expectations increase in excess of the output-neutral level. As discussed in Section 6 in relation to the high inflation countries, anticipatory policy responses of this type (ex-ante interest rate changes) would enable the central bank to achieve its goal of reducing inflation without suffering the loss of output which would occur if the policy was implemented at the ‘peak’ of the inflation (when NIEO is significantly positive for all countries). Similarly, for a country such as Indonesia during the period of the Asian crisis (1997–1998) inflation hit a peak of 75% and the policy response was to increase interest rates to a similar level (although of course there were other factors to this decision). Had some of this policy change taken place before NIEO had increased (Fig. 9a3) then the contractionary effect on output could have been much less. Our results therefore support the general movement towards anticipatory/forward-looking monetary policy and, especially, the results support the argument that NIEO can potentially be used as an advance indicator for the purpose of planning monetary policy actions, particularly the timing of interest rate changes, in order to control inflation without excessively destabilizing growth. This claim has been corroborated by the results from counterfactual scenarios suggesting that if the central banks would have targeted a NIEO indicator, they would have implemented a much tighter monetary policy in response to key episodes.

Appendix

1.1 Country Selection and Description

• (1) Argentina

At the start of the sample period Argentina had relatively low inflation, but inflation passed 500% in the mid-1980s and peaked at an annual rate in excess of 3000% in 1989. The policy interest rate was 62% and this had the effect of dramatically reducing inflation (down to 10.61% two years later) and growth (although growth was still positive, at 6%, two years later). Corresponding to these reductions, the interest rate was reduced to 11%. It can be seen from Fig. 1 that from 1994 to 1998 the economy was relatively stable, with single-digit growth and inflation. Over this period interest rates were in the range 7–12%. The principal feature of Argentine monetary policy during this period was the maintenance of a currency board, pegging the peso to the USA dollar. It was intended that this would allow Argentina to import credibility and stability, preventing high inflations such as those experienced at the beginning of the decade. From 1999 to 2002 Argentina experienced a recession of increasing severity, culminating in growth of −11% in 2002. In 2002 the peg to the USA dollar was abandoned and the subsequent depreciation of the peso resulted in a spike in inflation (to a rate of 26%). After this the economy recovered rather quickly, with the following decade characterized by real growth rates close to 10% and inflation below 10%. Figure 1 shows that towards the end of the sample period growth lessened and inflation began to increase, reaching 22% in 2014, with the interest rate being increased to 20% in response.

• (2) Iran

Iran is rich in natural resources and has a large public sector. Iran’s major exports are oil and gas, with the economy being heavily dependent on the revenues therefrom. Iran experienced increasing inflation between 1991 and 1995, from 17% to 50%, respectively. The interest rate was increased from 13% to 19% over the same period and, as shown by Fig. 2, this contributed to a reduction in inflation, which averaged roughly 16% for the following six years, during which time the interest rate was maintained at 19%. Within the same period growth was between 2% and 7%. The second major inflationary episode within the sample occurred in 2011–2014. Inflation peaked at 39% in 2013 and interest rates were increased to 17%, while at the same time growth fell from 4% to a low of −6.5% in 2012, gradually recovering to 1.5% in 2014.

Iranian monetary policy is not directly concerned with price stability, but rather is focused on the exchange rate and the balance of payments in order to maintain external stability (although these do of course have implications for the price level). Nonetheless, there is empirical evidence that the variations in interest rates have borne some similarity to the actions which an inflation targeting central bank would have taken (as partly described above).

• (3) Venezuela

Venezuela is also a major oil exporter, with this sector providing the majority of export earnings and state revenues. Similar to Iran, Venezuela has used monetary policy to manage the exchange rate and balance of payments, with exchange controls used to restrict the fluctuations of the currency, while also being concerned with the relatively frequent occurrences of high inflation. As Fig. 3 shows, Venezuela has had the highest average inflation of the three countries considered here, with two episodes of prolonged high inflation. Firstly, from 1991 to 1998 inflation was above 30%, with a peak of 100% in 1996. Growth was quite low in this period (although it did reach 6% in 1997) and interest rates were high (between 15% and 40%). Secondly, inflation increased from 21% in 2012 to 62% in 2014 (and inflation has increased further subsequently), while growth fell from 5.5% in 2012 to −4% in 2014.

Fig. 9

NIEO and pairwise bootstrapping, Brazil

Table 4 Cointegration test: Trace and Maximum Eigenvalues statistics

Table 5 Granger causality tests based on a linear VAR Model

Table 6 Unit Root tests for interest rate

Table 7 Cointegration test: Trace and Maximum Eigenvalues statistics (GDP growth, inflation and interest Rate)

Table 8 Granger causality tests based on a linear VAR Model

Table 9 Roots of Characteristic Polynomial test for VAR stability condition check