Abstract
In this paper, we derive a new method to compute the nodes and weights of simultaneous n-point Gaussian quadrature rules. The method is based on the eigendecomposition of the banded lower Hessenberg matrix that contains the coefficients of the recurrence relations for the corresponding multiple orthogonal polynomials. The novelty of the approach is that it uses the property of total nonnegativity of this matrix associated with the particular considered multiple orthogonal polynomials, in order to compute its eigenvalues and eigenvectors in a numerically stable manner. The overall complexity of the computation of all the nodes and weights is \(\mathcal {O}(n^2)\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider the computation of the nodes \(x_{j}\) and weights \(\omega _{j}^{(k)}\) of a simultaneous Gaussian quadrature rule
for r positive weight functions \( w^{(1)}(x), \ldots , w^{(r)}(x)\). It was shown in [3] that one gets an optimal set of Gaussian quadrature rules if the n quadrature nodes are the zeros of a polynomial \(p_{\overset{\rightarrow }{n}}(x)\) of degree \(n:=\mid \overset{\rightarrow }{n}\mid =n_1+\ldots +n_r\) (where \(\overset{\rightarrow }{n}=(n_1,\ldots ,n_r)\) is a multi–index), satisfying the orthogonality conditions
with respect to the weight functions \( w^{(1)}(x), \ldots , w^{(r)}(x)\).
Simultaneous Gaussian quadrature rules were introduced in [3], in order to evaluate computer graphics illumination models. In particular, the computation of a set of m definite integrals with respect to different weight functions and common integrand function was required. The aim was to minimize the evaluations of the integrand function and maximize the order of the considered quadrature rules. To this end, the author proposed a numerical scheme of m quadrature rules having the same set of nodes.
Furthermore, multiple orthogonal polynomials occur in the theory of simultaneous rational approximation, e.g., in the Hermite–Padé approximation of a system of functions [4,5,6, 18, 20].
The nodes and weights of such quadrature rules can be computed via the eigendecomposition of a banded lower Hessenberg matrix \(H_n\), built on the coefficients of recurrence relations leading to the multiple orthogonal polynomial \(p_{\overset{\rightarrow }{n}}(x)\) of type II [4], associated with the simultaneous Gaussian quadrature rule. The Golub–Welsch algorithm [13] is the customary way for constructing Gaussian quadrature rules related to classical orthogonal polynomials. It is based on the QR algorithm for computing the eigenvalue decomposition of a symmetric tridiagonal matrix and it is backward stable [9, 11]. The Golub–Welsh algorithm can be adapted to compute the eigendecomposition of \(H_n, \) but it suffers from tremendous instability due to the high non–normality [12] characterizing the latter matrix. In order to overcome the aforementioned instability, in [22] the eigenvalue decomposition is performed in variable precision arithmetic.
In this paper, we show that for the families of simultaneous Gaussian quadrature rules given in [22], the matrix \(H_n\) is totally nonnegative (TN, for short), i.e., the determinant of every square submatrix of \(H_n\) is a nonnegative number [8], and we discuss how this property can be verified efficiently. We then exploit the TN property of \(H_n\) to first scale it to a well–balanced matrix \(\hat{H}_n\), using a diagonal scaling \(\hat{H}_n:=S_n^{-1}H_nS_n\). This scaling is shown to improve the sensitivity of the eigenvalues tremendously when \(H_n\) is TN.
The straightforward test for a matrix \(H_n\) to be TN is to verify that all its minors are nonnegative, which can be quite cumbersome, even though there are results indicating that testing a small subset of minors is often sufficient (see [8]). For instance, a symmetric, invertible, and irreducible tridiagonal matrix \(T_n\) is TN if and only if it is nonnegative and positive definite. Therefore, one has only to test the positivity of its tridiagonal elements and of its leading principal minors. Moreover, there exists a bidiagonal Cholesky factorization with nonnegative elements, and this can be computed in \(\mathcal {O}(n)\) flops. We exploit this particular property since we show how to reduce our banded TN matrix \(H_n\) to a similar symmetric tridiagonal one \(\hat{T}_n\), with transformations preserving its TN property.
Using the results of Koev [15] for TN matrices, the eigenvalues of \(\hat{T}_n\) and, hence, also of \(\hat{H}_n\) and \(H_n\), can be computed to high relative accuracy if the factorization of \( H_n,\) as a product of nonnegative bidiagonal matrices, is known. Unfortunately, the latter factorization is not known a priori and, then, it must be computed involving subtractions, which do not preserve the high relative accuracy anymore. Therefore, the eigenvalues of the computed \(\hat{T}_n\) could be far from the exact eigenvalues of \(H_n, \) but they can be used as an initial guess of a variant of the Ehrlich–Aberth iteration [1, 2, 7] applied to \( \hat{H}_n. \) The considered implementation of the Ehrlich–Aberth iteration yields, for a computed eigenvalue of \( \hat{H}_n, \) also the corresponding left and right eigenvectors needed for the construction of the simultaneous Gaussian quadrature rule, with \( \mathcal{O}(n)\) computational complexity. Then, the overall computational complexity of the proposed algorithm is \( \mathcal{O}(n^2)\).
The left and right eigenvectors can be also computed by the QR method with \( \mathcal{O}(n^3)\) computational complexity [12]. We show, using a number of numerical experiments, that this approach works amazingly well and does not require the use of variable arithmetic anymore. We also provide an alternative method to compute the simultaneous Gaussian rule in case the matrix \( H_n\) is not TN.
Finally, the proposed algorithm can be adapted to compute simultaneous Gaussian quadrature rules for other classes of multiple orthogonal polynomials [24], whenever the recurrence relation coefficients are known. On the other hand, if such coefficients are unknown, they can be computed by the discretized Stieltjes–Gautschi procedure [19].
The paper is organized as follows. Notations used in the paper are listed in Section 2. In Section 3, we argue that the banded lower Hessenberg matrix \(H_n\) of the recurrence relations is TN, and we discuss how this can be verified. In Section 4, we give a scaling technique that significantly reduces the sensitivity of its eigenvalue decomposition. We then propose a similarity transformation that reduces the bandwidth of \(H_n\) to tridiagonal form in Section 5, exploiting the TN property of \(H_n. \) In Section 6, we show how to compute the eigenvalues and left and right eigenvectors of \(H_n\) in a fast and reliable manner. We provide the sketch of the proposed algorithm in Section 7. The stability of the new proposed method using some numerical examples is illustrated in Section 8, and Conclusions are reported in Section 9.
2 Notations
Matrices are denoted by upper–case letters \(A, B, \ldots ; \) vectors with bold lower–case letters \( {\varvec{x}}, {\varvec{y}}, \ldots , \varvec{\omega }, \ldots ;\) scalars with lower–case letters \( x, y, \ldots , \lambda ,\theta , \ldots \).
Matrices of size (m, n) are denoted by \( H_{m,n}\) or simply by \( H_{m}\) if \( m=n.\) The element i, j of a matrix A is generally denoted by \( a_{i,j}\) and the ith element of a vector \( {\varvec{x}}\) is denoted by \( x_i, \) if not explicitly defined.
Submatrices are denoted by the colon notation of Matlab: A(i : j, k : l) denotes the submatrix of A formed by the intersection of rows i to j and columns k to l, and A(i : j, : ) and A( : , k : l) denote the rows of A from i to j and the columns of A and from k to l, respectively.
The identity matrix of order n is denoted by \( I_n, \) and its ith column, \(i=1,\ldots ,n, \) i.e., the ith vector of the canonical basis of \( {\mathbb {R}}^{n}, \) is denoted by \( {\varvec{e}}_i\).
The notation \(\lfloor y \rfloor \) stands for the largest integer not exceeding \( y \in {\mathbb {R}}_{+}.\) The machine precision is denoted by \(\epsilon \).
3 Totally nonnegative band matrices
As explained in [22], the computation of the nodes and weights of the multiple orthogonal polynomials can be extremely sensitive, which is why the method proposed in [22] needs to be computed in variable precision arithmetic to get acceptable accuracy, even for matrices of order less than 20.
In this paper, we will restrict ourselves to the case of \(r=2\) simultaneous quadratures, since the instabilities already appear in this simple case. The simultaneous Gaussian quadrature problem derived in [3, 4, 22] then corresponds to a set of multiple orthogonal polynomials satisfying the 4–term recurrence relations :
and \(p_{-2}(x)=p_{-1}(x)=0.\)
Equation (2) can be written in matrix form,
i.e.,
where \(H_n \) and \(\varvec{p}_{i}(x), i=0,1,\ldots ,\) are, respectively, the \(n\times n\) banded lower Hessenberg matrix with 2 sub–diagonals and one upper-diagonal :
and
Hence, by (4), \({\bar{x}}\) is a zero of \( p_{n}(x)\) if and only if \({\bar{x}}\) is an eigenvalue of \(H_n\) with corresponding eigenvector \(\varvec{p}_{n-1}({\bar{x}})\), or equivalently, by (3), \(\varvec{p}_{n}({\bar{x}})\) is the vector spanning the null–space of \( \left[ \begin{array}{c|c}H_n- {\bar{x}}I_n&a_{n-1}\varvec{e}_n\end{array}\right] \).
Let us consider the following two examples, taken from [22], as a guide for our discussions in the rest of the paper.
Example 1
For the modified Bessel functions \(K_\nu (x)\) and \(K_{\nu +1}(x)\) of the second kind, given by
and for the weight functions
positive and integrable in the interval \([0, \infty ),\) it is shown in [22] that, for \(\alpha >-1\) and \(\nu \ge 0\), the recurrence relations for the corresponding monic multiple orthogonal polynomials are given by \(a_i=1\) for \(i\ge 0\), and
Example 2
For the modified Bessel functions \(I_\nu (x)\) and \(I_{\nu +1}(x)\) of the first kind and for the weight functions
positive and integrable in the interval \([0, \infty ),\) it is shown in [22] that, for \(c>0\) and \(\nu \ge -1\), the recurrence relations for the corresponding monic multiple orthogonal polynomials are given by \(a_i=1\) for \(i\ge 0\), and
The eigenvalues of \(H_n\) are the nodes \(x_{j}\) of the simultaneous quadrature rule (1), and the weights \({\omega }_{j}^{(k)}, j=1, \ldots ,n, \; k=1,2,\) can be obtained from their corresponding left and right eigenvectors [4, 22]. Moreover, the nodes are all nonnegative when the integration interval is nonnegative [16, Th. 23.1.4].
Remark 1
We point out that for both examples, the lower Hessenberg matrix \(H_n\) is irreducible and the sequences \(b_i\), \(c_i\), and \(d_i\) are positive and monotonically increasing with i, a property that will be used in Section 4. It also follows from the interlacing property of the eigenvalues of \(H_n\) and of \(H_{n+1}\) [12] that \(H_n\) must be invertible, since the spectrum of \(H_{n+1}\) is nonnegative.
It will be shown in Section 4 that the eigenvalue decomposition of the matrix \(H_n\) is very sensitive. In this paper, we argue that the matrix \(H_n\) corresponding to a positive integration interval is TN and, hence, this property should be exploited in order to improve the numerical sensitivity of the eigenvalue decomposition. It is indeed shown in [15] that the eigenvalues of a TN matrix can be computed reliably, even to full relative accuracy. We thus need to verify that the \(n\times n\) matrix \(H_n\), built on the 4–term recurrence relation (2), is indeed TN.
In order to make sure that \(H_n\) is a TN matrix, we first need to have all scalars nonnegative. For Example 1, all the scalars \(a_i, b_i, c_i,\) and \(d_i\) are positive for \(\alpha > -1\) and \(\nu \ge 0\) and in Example 2, they are positive for \(c> 0\) and \(\nu \ge -1\). For the \(2\times 2\) submatrices, we only have to verify the nonnegativity of the following “dense” matrices
because all other \(2\times 2\) submatrices are zero or are triangular and hence nonnegative because of the scalar conditions. If we want to verify the TN property of \(H_n\), one must also verify this for minors of dimensions 3, 4, and so on. This becomes rather tedious and can best be checked with computer algebraic software. We will develop an alternative test in Section 5, based on the existence of a Neville–type similarity transformation [8], and which requires only \(\mathcal {O}(n^2)\) floating point operations. This does not guarantee that \(H_n\) is TN for all possible values of \(\alpha \) and \(\nu \), but it is a cheap alternative for a given set of values.
4 Scaling
The matrix \(H_n\) in Example 1 has elements that grow quite quickly with n since \(b_n=\mathcal {O}(n^2)\), \(c_n=\mathcal {O}(n^4)\), and \(d_n=\mathcal {O}(n^6)\). We, therefore, recommend to first apply a diagonal scaling
to make sure the matrix is more “balanced” [21]. Then, since the sequences \(a_i\) and \(c_i\) and positive (see Remark 1), the following algorithm yields the scaled matrix \(\hat{H}_n\) whose tridiagonal submatrix is irreducible and symmetric (i.e., \(\hat{c}_i=\hat{a}_{i-1}>0\)) :
Algorithm Scale

Since all operations are multiplications, divisions, and square roots, they can be performed in a forward stable manner. The relative (forward) error on each element of \(\hat{H}_{i,j}\) is therefore bounded by \(\gamma _k \! \mid \! \hat{H}_{i,j}\!\mid \), where \(\gamma _k:=k\epsilon /(1-k\epsilon )\), k is the number of floating point operations involved in the computation of \(\hat{H}_{i,j}\), and \(\epsilon \) is the machine precision (see [14, Chaptar 3]). This leads to the following theorem, using the notation and results of [14, Chapter 3].
Theorem 1
Let \(\hat{H}_n:=S_n^{-1} H_n S_n\) be the matrix obtained by the Algorithm Scale, applied to the banded matrix \(H_n\), given in (5). Then, the forward error
satisfies the elementwise relative bound \(\mid \Delta _{\hat{H}_n}\mid \le \gamma _{3n}\mid \hat{H}_n \mid \).
Proof
The element that requires the largest number of floating point operations is \(\hat{d}_{n-1}\). It involves 3 flops in every update of the \(s_i\) elements and, hence, a total of \(3n + \mathcal {O}(1)\) flops. \(\square \)
Remark 2
A more detailed error analysis may be used to reduce the factor \(\gamma _{3n}\) by exploiting the relations between the consecutive values of the \(s_i\)’s. More importantly, the scaling factors \(s_i\) may be replaced by their rounded version to their nearest power of two, by, e.g., using the Matlab functions round and log2 :
The forward errors are then zero, since multiplication with, or division by a power of 2 can be executed without rounding error. The caveat is that the resulting matrix \(\hat{H}_n\) will not have an exact symmetric tridiagonal submatrix, but its off–diagonal elements will be within a factor \(\sqrt{2}\) of each other, i.e;
After the scaling procedure applied to Example 1, with \(\alpha =\nu =0.5\) and \(n=20\), the maximum element of \(\hat{H}_n\) is \(\hat{b}_{n-1}=1200\), while the maximum element of \(H_n\) is \(d_{n-1}=46883070\) (which is a factor of about 40,000). Moreover, the transformed matrix \(\hat{H}_n\) has a dominant diagonal. This is based on the following lemma, which will also be useful for the further treatment of the matrix \(\hat{H}_n\) in Section 5.
Lemma 1
Let the matrix \(\hat{H}_n=S_n^{-1}H_n S_n\) be the scaled version of \(H_n\), given in (5). If \(H_n\) is TN with monotonically increasing diagonal elements \(\hat{b}_i\), then the off–diagonal elements of the scaled matrix \(\hat{H}_n\) satisfy for \(i \ge 1\)
implying that \(\hat{d}_i< \hat{c}_i < \hat{b}_i\) for all \(i\ge 2\).
Proof
If the matrix \(H_n\) is TN, then so is the scaled matrix \(\hat{H}_n\). Then, the inequalities follow from the nonnegativity of the submatrices
and the monotonicity of the elements \(\hat{b}_i=b_i\). \(\square \)
The positive effect of this transformation is best visualized by the sensitivity of the eigenvalues of \(H_n\), which are measured by the angle between the left and right eigenvectors \({\varvec{u}}^{(j)}\) and \({\varvec{v}}^{(j)}, \)
and the corresponding sensitivities of the scaled matrix. After scaling, these sensitivities are reduced in Example 1, for \(\alpha =0.5\) and \(\nu =0.5, \) by a factor between \(10^{25}\) and \(10^{35}\) as it is shown in Fig. 1. It is interesting to point out here that the Matlab routine for balancing a standard eigenvalue problem, did not help here at all. The balanced matrix was only modified in the last few elements and still yielded very badly conditioned eigenvalues.
5 Reducing the bandwidth
In this section, we reduce a banded TN matrix \(H_n\) to a symmetric tridiagonal TN matrix, where we aim at guaranteeing the backward stability of the resulting similarity transformation. The matrix \(H_n\) has 2 diagonals below the main diagonal and one diagonal above the main diagonal. Moreover, it is assumed to be nonnegative and irreducible (i.e., all \(a_i\) are nonzero). Then, the total nonnegativity implies that \(b_i\) and \(c_i\) are also nonzero whenever \(d_i\) is nonzero. It follows from Theorem 2 (see below) that the TN property of a matrix is preserved when applying certain bidiagonal similarity transformations, and we will show that this applies to the matrix \(H_n\) and its reduction to tridiagonal form. We explain the reduction of the bandwidth of \(H_n\) by just showing the elimination procedure for the leftmost element in the bottom row of \(H_n\), using an \(8\times 8\) example. In the first three “snapshots” of the reduction process, we show the effect of a \(2\times 2\) elementary similarity transformation
where m is chosen to annihilate the element indicated by \({\varvec{0}}\) in the matrix, but it also creates a “bulge” indicated by \({\varvec{x}}\). The dashed lines indicate on what rows and columns this similarity transformation is operating. The “eliminator” m is positive and requires one division, while the transformations for that \(2\times 2\) similarity transformation require 14 flops, giving a total of 15 flops per elementary similarity transformation. Moreover, it is shown in the Appendix that all elements marked as \(\times \) remain positive if the matrix \(H_n\) is TN.


Since this requires \(\lfloor (n-1)/2\rfloor \) elementary similarity transformations, we need less than 15n/2 flops to eliminate the leftmost element in the bottom row of \(H_n\). The rest of the procedure just repeats the above scheme on the deflated \((n-1)\times (n-1)\) matrix shown in the last snapshot. The total complexity is therefore
In order to verify the TN property, we use a result due to Whitney [25].
Theorem 2
Suppose A is an \(n\times n\) matrix with \(a_{i,j}>0\), and \(a_{i,k} = 0\) for \(k < j-1\). Then, let B be the \(n\times n\) matrix obtained from A by using column j to eliminate \(a_{i,j-1}\) using \(E:= \left[ \begin{array} {cc}1 &{} 0 \\ -m &{} 1 \end{array} \right] \) with \(m=a_{i,j-1}/a_{i,j}\), operating on columns \(j-1\) and j. Then, A is TN if and only if B is TN.
Proof
The proof for the transposed matrix can be found in [8, Th. 2.2.1, pp. 48–49], but the statement also holds for the transposed matrices A and B. \(\square \)
It then follows that every right transformation E in the above reduction preserves the TN property because of Theorem 2. Moreover, every left transformation \(E^{-1}\) is a TN matrix and, hence, the TN property is preserved (see [8]).
If this reduction procedure is applied to \(\hat{H}_n\), rather than \(H_n\), one can hope to have eliminators \(m_i\) that are bounded by 1, because its largest elements seem to be on the main diagonal and are monotonically increasing. This is not guaranteed for the whole process of the reduction, but we show that it holds in the first “sweep” of \(\lfloor \frac{n-1}{2}\rfloor \) elementary transformations. Again, we use the \(8\times 8\) matrix to illustrate this.
The first one requires the eliminator \(m_1 =\hat{d}_7/\hat{c}_7\), which is bounded by 1, because of Lemma 1. The next two eliminators are respectively computed as
which are again smaller than 1 because of Lemma 1. After one such sweep, the assumptions \(\hat{b}_{i-1} \le \hat{b}_i\) and \(\hat{a}_{i-1} =\hat{c}_{i}\) of Lemma 1 are not guaranteed anymore, which means that the eliminators could grow. But in Example 1, all the eliminators were smaller than 0.57, and their average was 0.21, which implies that the condition number of the similarity transformation to triangular form has a very reasonable condition number.
Note that we have now obtained an irreducible nonnegative tridiagonal matrix \(T_n\). It is therefore easy to verify if it is TN. We can first perform a second scaling to make \(\hat{T}_n = \hat{S}_n^{-1} T_n \hat{S}_n\) symmetric. Finally, it is shown in [8] that an irreducible and invertible tridiagonal matrix \(\hat{T}_n\) is TN if and only if its Cholesky factorization \(LL^T\) has a bidiagonal factor L with positive elements. Since this is an \(\mathcal {O}(n)\) computational process, we can verify if \(H_n\) is TN by going through the transformation steps
in a total of \(\mathcal {O}(n^2)\) flops. In each of these transformations, the TN property is preserved, and hence \(H_n\) is TN if the different steps can be performed successfully. An unsuccessful reduction would therefore be detected by an eliminator m that is negative in the construction of \(T_n\), or a failure of the Cholesky decomposition yielding L.
6 Computing eigenvalues and eigenvectors
The nodes \( x_j, j=1,\ldots ,n, \) of a simultaneous Gaussian quadrature rule are the eigenvalues of the banded Hessenberg matrix \(H_n\). If we denote by \( {\varvec{u}}^{(j)}=[u_1^{(j)}, u_2^{(j)},\ldots , u_n^{(j)} ]^T, \) and \({\varvec{v}}^{(j)}=[v_1^{(j)}, v_2^{(j)},\ldots , v_n^{(j)} ]^T \) the left and right eigenvector of \( H_n\) associated with \( x_j, \) then the vectors of weights \(\varvec{\omega }^{(k)}=[\omega _1^{(k)},\omega _2^{(k)},\ldots , \omega _n^{(k)} ]^T, \;\) \( k=1,2,\) of the rules (1) are given by (see [22]) :
where the constants \(d_{i,k},\; i,k=1,2,\) are
Therefore, to compute the n–point simultaneous Gaussian rule for multiple orthogonal polynomials, all the eigenvalues of \(H_n\) and the corresponding left and right eigenvectors need to be computed.
Given an initial approximation \({\varvec{x}}^{(0)^T}=\left[ \begin{array}{cccc} x_1^{(0)},&x_2^{(0)},&\cdots x_{n-1}^{(0)},&x_n^{(0)} \end{array}\right] ^T\) for all the eigenvalues of \(H_n\), they can be simultaneously computed by the Ehrlich–Aberth iteration [1, 2, 7],
The generated sequence of approximations converges cubically, or even faster if the implementation is in the Gauss–Seidel style, to the eigenvalues of \(H_n\), because they are simple. In practice, as noticed in [2], the Ehrlich–Aberth iteration exhibits good global convergence properties, though no theoretical results seem to be known about global convergence.
The main requirements for the success of the Ehrlich–Aberth method are a fast, robust, and stable computation of the Newton correction \( p_n(x)/p'_n(x),\) and the availability of a good set of initial approximations for the zeros, \({\varvec{x}}^{(0)},\) so that the number of iterations needed for convergence is not too large. The initial approximation \({\varvec{x}}^{(0)}\) can be obtained by computing the eigenvalues of the symmetric tridiagonal matrix \(\hat{T}_n\). As an alternative, the initial approximation \({\varvec{x}}^{(0)}\) can be obtained by computing the eigenvalues of the symmetric tridiagonal submatrix \({\mathtt triu}(\hat{H}_n,-1), \) i.e., the matrix obtained from \(\hat{H}_n\) by setting \( \hat{d}_i=0,\; i=2, 3, \ldots , n-1. \)
We now show how to compute \( p_n({\bar{x}}) \) and \( p'_n({\bar{x}}),\) for a given point \( {\bar{x}}\). Let \( \hat{H}_{n+1}, S_{n+1} \in {\mathbb {R}}^{(n+1) \times (n+1)} \) be the matrices obtained by using Algorithm Scale of Section 4 for \( n+1. \) Let \(\hat{H}_{n,n+1} \) be the rectangular matrix obtained from \(\hat{H}_{n+1}\) by deleting its last row,
Let us consider the following subdivisions of \(\hat{H}_n,\)
and
Since \(\hat{H}_{n,n+1} = S_n^{-1} {H}_{n,n+1} {S}_{n+1} \), and, by (2) and (5), the vector
spans the null–space of \( {H}_{n,n+1} - {\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] , \) with \( I_n \) the identity matrix of order n and \( {\varvec{0}}_n \) the zero vector of length n. Then, the transformed vector
spans the null–space of \(\hat{H}_{n,n+1} -{\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] ,\) i.e., the polynomials \( {\hat{p}}_{j}({\bar{x}}),\; j =0,1, \ldots , n \) are the multiple orthogonal polynomials satisfying the recurrence relations generating the matrix \( \hat{H}_{n,n+1}, \)
If \(\hat{L}\hat{Q}=\hat{H}_{n,n+1} -{\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] \) is the LQ factorization of \( \hat{H}_{n,n+1} -{\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] ,\) with \( \hat{L}\in {\mathbb {R}}^{n\times (n+1)}\) lower triangular and \(\hat{Q}\in {\mathbb {R}}^{(n+1)\times (n+1)}\) orthogonal, then the last row of \(\hat{Q}\) spans the null–space of \( \hat{H}_{n,n+1} -{\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] \) [12, pp. 640–641].
Defining \( \hat{L}^{(0)}:=\hat{H}_{n,n+1} -{\bar{x}}\left[ \begin{array}{c|c} I_n&{\varvec{0}}_n \end{array} \right] , \) the matrix \(\hat{Q}\) can be computed as the product of n Givens rotations \(G_i \in {\mathbb {R}}^{(n+1)\times (n+1)}\),
such that for \( i=1,2,\ldots ,n,\) the updated matrix
has entry \((i,i+1) \) annihilated and \(\hat{\ell }^{(i)}_{i,i}=\sqrt{\hat{\ell }^{(i-1)^2}_{i,i}+\hat{\ell }^{(i-1)^2}_{i,i+1}}. \) It turns out that the vector spanning the null–space of \( \hat{H}_{n,n+1} \) is
Therefore, \(\hat{L}:=\hat{L}^{(n)} \) and \({\hat{p}}_n({\bar{x}}) = \gamma _n. \)
Let now
In order to compute \({\hat{p}}'_n({\bar{x}}), \) we differentiate (7) obtaining
Then, taking into account that \(\hat{p}'_0({\bar{x}})=0,\) it follows that the vector \({\hat{\varvec{p}}}'({\bar{x}})\) is the solution of the linear system
where
Therefore, the evaluation of \({\hat{p}}_n({\bar{x}}) \) and \( {\hat{p}}'_n({\bar{x}}) \) requires \(19 n +\mathcal {O}(1) \) and \(5n +\mathcal {O}(1) \) floating point operations.
If \(\hat{x} \) is a zero of \( {\hat{p}}_{n}(x)\), i.e., \( {\hat{p}}_{n}(\hat{x} )=0,\) then \({\hat{\varvec{p}}}_{n-1}(\hat{x}) \) is the right eigenvector of \( \hat{H}_n \) corresponding to the eigenvalue \( \hat{x}\). Moreover, let \( \tilde{L} \tilde{Q} = \hat{ H}_n - \hat{x}I_n, \) with \( \tilde{L} \) lower triangular and \(\tilde{Q}\) orthogonal. Then, \( \tilde{\ell }_{1,1} =0 \) and \( \tilde{Q}(:,1) \) is the left eigenvector of \( \hat{H}_n \) associated with \(\hat{x}\). The number of floating point operations needed to compute the left eigenvector, given the corresponding eigenvalue, is \(19 n +O(1) \) floating point operations. As shown in [23] the computation of the left and right eigenvectors is stable by using Givens rotations, since the eigenvalues of \(\hat{H}_n\) are well separated for the measures considered in Examples 1 and 2. Observe that, if \( \hat{\varvec{u}}^{(j)} \) and \( \hat{\varvec{v}}^{(j)} \) are respectively left and right eigenvectors of \(\hat{H}_n\) corresponding to the eigenvalue \( x_j, \) then \(\sigma _n \hat{\varvec{u}}^{(j)} \) and \( \sigma _n^{-1} \hat{\varvec{v}}^{(j)} \) are respectively left and right eigenvectors of \( H_n\) corresponding to the eigenvalue \( x_j. \)
Remark 3
Observe that also the condition number of the matrix \( \hat{C}_n,\) defined in (6) and involved in the linear system (8), significantly improves with respect to that of \( C_n:=H_{n+1}(1:n,2:n+1).\) For the sake of completeness, the condition numbers of \( C_n\) and \( \hat{C}_n,\) with \( n = 10, 20, \ldots , 90, 100, \) for Example 1, with parameters \( \alpha =1, \; \nu =0\) and Example 2, with parameters \( c=1, \; \nu =0\), are displayed in Table 1
A similar behavior is observed when choosing different parameter values for both Examples.
7 Outline of the algorithm
For the sake of clearness, here we shortly report the different steps of the proposed algorithm, along with the Sections where they are described.
- Step 1.:
-
Choice of the multiple orthogonal polynomials (Section 3);
- Step 2.:
-
Construction of the matrix \( H_n\) (Section 3);
- Step 3.:
-
Similarity transformation of \( H_n\) into \( \hat{H}_n, \) \( \hat{H}_n=S_n^{-1} H_n S_n, \) with \( S_n \) a diagonal matrix (Section 4);
- Step 4.:
-
Similarity transformation of \( \hat{H}_n \) into the unsymmetric tridiagonal matrix \(T_n: \) \(T_n= M_n \hat{H}_n M^{-1}_n\) (Section 5);
- Step 5.:
-
Transformation of \( T_n\) into the similar matrix \(\hat{T}_n = \hat{S}_n^{-1} T_n \hat{S}_n,\) with \(\hat{S}_n \) a diagonal matrix (Section 5);
- Step 6.:
-
Computation of the eigenvalues of \(\hat{T}_n: \) \( \varvec{x}_0 = \texttt {eig}(\hat{T}_n)\) (Section 6);
- Step 7.:
-
Refinement of the eigenvalues by the Ehrlich–Aberth method with initial guess \( \varvec{x}_0\) (Section 6);
- Step 8.:
-
Computation of the left and right eigenvectors of \( \hat{H}_n \) associated with the computed eigenvalues (Section 6);
- Step 9.:
-
Computation of the simultaneous Gaussian quadrature rule (Section 6).
8 Numerical results
In this section, the simultaneous Gaussian quadrature rules of the couple of weights \( w^{(1)}(x) \) and \( w^{(2)}(x)\) of Examples 1 and 2, are computed for different values of n. All the computations are performed with Matlab R2022a in floating point arithmetic with machine precision \( \epsilon \approx 2.2\times 10^{-16}. \) The computed nodes and weights, denoted respectively by \( x_j,\) \( {\omega }_j^{(1)} \) and \( {\omega }_j^{(2)} \) \( j=1, \ldots , n,\) are compared to those computed in extended precision (with 500 digits), denoted respectively by \( \hat{x}_j,\) \(\hat{\omega }_j^{(1)} \) and \(\hat{\omega }_j^{(2)} \) \( j=1, \ldots , n,\) which will therefore be considered as exact. In Fig. 2, the absolute errors \(\mid x_j -\hat{x}_j \mid \) and \( \epsilon \; x_j, \) for the weights \( w^{(1)}(x) \) and \( w^{(2)} (x)\) of Example 1, with \( \alpha =1, \) \( \nu =0,\) and \( n=40, \) are displayed on a logarithmic scale. The quantities \( \epsilon \; x_j \) were added to verify that \(\mid x_j-\hat{x}_j \mid \approx \epsilon \; x_j \) holds. Observe that if \(\mid x_j -\hat{x}_j \mid =0\) in floating point arithmetic, for some j, the corresponding symbol “ ” is not dispalyed in Fig. 2.
” is not dispalyed in Fig. 2.
Absolute errors \( \mid x_j - \hat{x}_j \mid \) (“ ”) and \( \epsilon x_j \) (“
”) and \( \epsilon x_j \) (“ ”) \( j=1,\ldots , n\) (Example 1, \(\alpha =1, \) \( \nu =0,\) and \( n=40 \))
”) \( j=1,\ldots , n\) (Example 1, \(\alpha =1, \) \( \nu =0,\) and \( n=40 \))
Absolute errors \( \mid \omega _j^{(1)} - \hat{\omega }_j^{(1)} \mid \) and \( \mid {\omega }_j^{(2)} - \hat{\omega }_j^{(2)} \mid \), \( j=1,\ldots , n\) (denoted by “ ” and “
” and “ ,” respectively), and lines representing \( \epsilon n \Vert \varvec{\omega }^{(1)}\Vert _2\) and \(\epsilon n \Vert \varvec{\omega }^{(2)}\Vert _2\) (denoted by “
,” respectively), and lines representing \( \epsilon n \Vert \varvec{\omega }^{(1)}\Vert _2\) and \(\epsilon n \Vert \varvec{\omega }^{(2)}\Vert _2\) (denoted by “ ” and “
” and “ ,” respectively), obtained for Example 1 (\(\alpha =1, \) \( \nu =0,\) and \( n=40 \) )
,” respectively), obtained for Example 1 (\(\alpha =1, \) \( \nu =0,\) and \( n=40 \) )
It can be noticed that each node is computed with high relative accuracy. In Fig. 3, the absolute errors \(\mid {\omega }_j^{(k)} -\hat{\omega }_j^{(k)} \mid \) and \( \epsilon n \Vert {\varvec{\omega }}^{(k)}\Vert _2\), for \( k=1,2, \) are shown on a logarithmic scale, for the weights \( w^{(1)}(x) \) and \( w^{(2)} (x)\) of Example 1, with \( \alpha =1, \) \( \nu =0 \) and \(n=40.\)
We can observe that the weights are computed with almost full absolute accuracy.
The proposed method is used to simultaneously compute the integrals [22]
where \(w^{(1)}(x) \) and \(w^{(2)}(x) \) are defined in Example 1, and \( \alpha = 1, \) \( \nu =0, \) for \(n= 10, 20,\ldots , 80, 90.\) The results are given in Table 2.
It can be noticed that the obtained approximations of the integrals are the same as those computed with Maple (with 100 digits precision) in [22].
In Fig. 4, the absolute errors \(\mid x_j -\hat{x}_j \mid \) for the weights \( w^{(1)}(x) \) and \( w^{(2)} (x)\) of Example 2, with \( c=1 \) \( \nu =0,\) and \( n=40, \) are shown on a logarithmic scale. The quantities \( \epsilon \; x_j \) were added to verify that \(\mid x_j-\hat{x}_j \mid \approx \epsilon \; x_j \) holds. Observe that if \(\mid x_j -\hat{x}_j \mid =0\) in floating point arithmetic, for some j, the corresponding symbol “ ” is not dispalyed in Fig. 4.
” is not dispalyed in Fig. 4.
Absolute errors \( \mid x_j - \hat{x}_j \mid \) (“ ”) and \(\epsilon x_j \) (“
”) and \(\epsilon x_j \) (“ ”), \(j=1,\ldots ,n \) (Example 2, \(c\!=\!1, \) \( \nu \!=\!0,\) and \( n\!=\!40 \) )
”), \(j=1,\ldots ,n \) (Example 2, \(c\!=\!1, \) \( \nu \!=\!0,\) and \( n\!=\!40 \) )
In Fig. 5, the absolute errors \(\mid {\omega }_j^{(k)} -\hat{\omega }_j^{(k)} \mid \) and \( \epsilon n \Vert {\varvec{\omega }}^{(k)}\Vert _2\), for \( k=1,2, \) are shown on a logarithmic scale, for the weights \( w^{(1)}(x) \) and \( w^{(2)} (x)\) of Example 2, with \( c=1, \) \( \nu =0,\) and \( n=40. \)
Absolute errors \( \mid \omega _j^{(1)} - \hat{\omega }_j^{(1)} \mid \) and \( \mid {\omega }_j^{(2)} - \hat{\omega }_j^{(2)} \mid \), \( j=1,\ldots , n\) (denoted by “ ” and “
” and “ ,” respectively), and lines representing \( \epsilon n \Vert \varvec{\omega }^{(1)}\Vert _2\) and \(\epsilon n \Vert \varvec{\omega }^{(2)}\Vert _2\) (denoted by “
,” respectively), and lines representing \( \epsilon n \Vert \varvec{\omega }^{(1)}\Vert _2\) and \(\epsilon n \Vert \varvec{\omega }^{(2)}\Vert _2\) (denoted by “ ” and “
” and “ ,” respectively), obtained for Example 2 (\(c=1, \) \( \nu =0,\) and \( n=40\))
,” respectively), obtained for Example 2 (\(c=1, \) \( \nu =0,\) and \( n=40\))
It can be observed that the eigenvalues are computed with high relative accuracy and the weights are computed with almost full absolute accuracy.
The proposed method is used to simultaneously compute the integrals [22]
where \(w^{(1)}(x) \) and \(w^{(2)}(x) \) are the weight functions defined in Example 2, with \( c= 1, \) and \( \nu =0, \) for \(n= 10, 20,\ldots , 50.\) The results are reported in Table 3.
It can be noticed that the obtained approximations of the integrals are the same of those computed with Maple (precision: 100 digits) in [22].
9 Concluding remarks
In this paper, we propose a new method to compute the nodes and weights of a simultaneous Gaussian quadrature rule with \(r=2\) integration rules. It uses a banded lower Hessenberg matrix with \(r=2\) subdiagonals derived from the multiple orthogonal polynomial linked to the simultaneous quadrature rule. An important contribution of this paper is a special balancing technique that significantly improves the sensitivity of the calculation of nodes and quadrature weights. We then use the Aberth–Ehrlich method for computing the nodes and an efficient null–space calculation to compute all left and right eigenvectors. The new method was shown to compute nodes to almost full relative accuracy and the vector of weights to almost full absolute accuracy. The method heavily relies on the property that the banded Hessenberg matrix is TN. The complexity of the method is \(\mathcal {O}(n^2)\) for all calculations, which compares very favorably with earlier methods that have a cubic complexity. We conjecture that this technique can be applied to all such quadrature rules with a nonnegative integration interval and that it also holds for r larger than 2, although we only coded and tested the method for \(r=2\) in this paper.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Code availability
The codes described in the manuscript are available from the authors, upon request.
References
Aberth, O.: Iteration methods for finding all zeros of a polynomial simultaneously. Math. Comp. 27, 339–344 (1973)
Bini, D.A., Gemignani, L., Tisseur, F.: The Ehrlich-Aberth method for the nonsymmetric tridiagonal eigenvalue problem. SIAM J. Matrix Anal. Appl. 27, 153–175 (2005)
Borges, C.F.: On a class of gauss-like quadrature rules. Numer. Math. 67, 271–288 (1994)
Coussement, J., Van Assche, W.: Gaussian quadrature for multiple orthogonal polynomials. J. Comput. Appl. Math 178, 131–145 (2005)
de Bruin, M.G.: Simultaneous Padé approximation and orthogonality, In: Brezinski, C. et al. (Eds.) Polynomes Orthogonaux et Applications, Lecture Notes in Mathematics, vol. 1171:74–83. Springer, Berlin(1985)
de Bruin, M.G.: Some aspects of simultaneous rational approximation. In: Numer Anal Math Model, Banach Cent Publ, PWN-Pol Sci Publishers, Wars 24, 51–84 (1990)
Ehrlich, L.W.: A modified Newton method for polynomials. Comm. ACM 10, 107–108 (1967)
Fallat, S.M., Johnson, C.R.: Totally nonnegative matrices, Princeton University Press (2011)
Francis, J.G.F.: The QR transformation a unitary analogue to the LR transformation-part 1. Comput. J. 4(3), 265–271 (1961)
Gantmacher, F., Krein, M.: Oscillation matrices and kernels and small vibrations of mechanical systems. AMS Chelsea, Providence, RI (2002)
Gautschi, W.: Construction of Gauss-Christoffel quadrature formulas. Math. Comput. 22(102), 251–270 (1968)
Golub, G.H., Van Loan, C.F.: Matrix computations, 4th edn. Johns Hopkins University Press, Baltimore (2013)
Golub, G.H., Welsch, J.H.: Calculation of gauss quadrature rules. Math. Comput. 23(106), 221–230+s1–s10 (1969)
Higham, N.: Accuracy and stability of numerical algorithms. SIAM Publ, Philadelphia (1996)
Koev, P.: Accurate eigenvalues and SVDs of totally nonnegative matrices. SIAM J. Mat. Anal. Appl. 27(1), 1–23 (2005)
Ismail, M.E.H., Van Assche, W.: Classical and quantum orthogonal polynomials in one variable, Encyclopedia of Mathematics and its Applications, vol. 98, Cambridge University Press (2005)
Laudadio, T., Mastronardi, N., Van Dooren, P.: On computing modified moments for half-range Hermite weights. Numer. Algoritm. 92, 767–793 (2022)
Mahler, K.: Perfect systems. Compos. Math. 19, 95–166 (1968)
Milovanovíc, G.V., Stanć, M.: Construction of multiple orthogonal polynomials by discretized Stieltjes-Gautschi procedure and corresponding Gaussian quadratures. Facta Univ. Ser. Math. Inform. 18, 9–29 (2003)
Nikishin, E.M., Sorokin, V.N.: Rational approximations and orthogonality, Translations of Mathematical Monographs, American Mathematical Society, vol. 92, Providence, RI (1991)
Parlett, B.N., Reinsch, C.: Balancing a matrix for calculation of eigenvalues and eigenvectors. Numer. Math. 13(4), 293–304 (1969)
Van Assche, W.: A Golub-Welsch version for simultaneous gaussian quadrature. Internal Report Dept. Mathematics, KULeuven (2023)
Van Dooren, P., Laudadio, T., Mastronardi, N.: Computing the eigenvectors of nonsymmetric tridiagonal matrices. Comput. Math. Math. Phys. 61, 733–749 (2001)
Van Assche, W., Coussement, E.: Some classical multiple orthogonal polynomials. J. Comput. Appl. Math. 127, 317–347 (2001)
Whitney, A.: A reduction theorem for totally positive matrices. J. Analyse Math. 2, 88–92 (1952)
Acknowledgements
This paper is dedicated to Marc Van Barel on the occasion of his retirement. The authors would like to thank the anonymous reviewers, whose valuable comments helped to improve the manuscript.
Funding
Open access funding provided by Consiglio Nazionale Delle Ricerche (CNR) within the CRUI-CARE Agreement. Teresa Laudadio and Nicola Mastronardi are members of the Gruppo Nazionale Calcolo Scientifico – Istituto Nazionale di Alta Matematica (GNCS–INdAM).
The work of Nicola Mastronardi was partly supported by MIUR, PROGETTO DI RICERCA DI RILEVANTE INTERESSE NAZIONALE (PRIN) 20227PCCKZ “Low–rank Structures and Numerical Methods in Matrix and Tensor Computations and their Application”, Università degli Studi di BOLOGNA CUP J53D23003620006.
Paul Van Dooren is partly Suported by Short Term Mobility of Consiglio Nazionale delle Ricerche.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work.
Corresponding author
Ethics declarations
Ethics approval
Not applicable
Conflict of interest
The authors declare no competing interests.
Additional information
Dedicated to Marc Van Barel on the occasion of his retirement.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Let us start with a matrix \(H_8\) that is TN and let all its elements marked as \(\times \) be positive. Then, the first right transformation with \(E:= \left[ \begin{array} {cc}1 &{} 0 \\ -m &{} 1 \end{array} \right] \) in columns 6 and 7, only modifies the boldface elements in column 6 :

Clearly, the boldface \(\textbf{x}'s \) can not be zero since it would violate the TN property in the minors of columns 5 and 6. The next step is then a left transformation with \(E:= \left[ \begin{array} {cc}1 &{} 0 \\ m &{} 1 \end{array} \right] \) in rows 6 and 7, only modifying the boldface elements in row 6 :

Clearly, the boldface \(\textbf{x}'s\) are again nonzero because a positive quantity was added to them.
The same reasoning can be applied to the later steps to show that only the elements that are meant to be eliminated, indeed become zero, while all other elements remain positive during the process.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Laudadio, T., Mastronardi, N. & Van Dooren, P. Computational aspects of simultaneous Gaussian quadrature. Numer Algor (2024). https://doi.org/10.1007/s11075-024-01785-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11075-024-01785-0



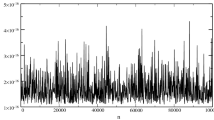


 ”) and unscaled matrix
”) and unscaled matrix  ”) of Example 1, with
”) of Example 1, with 


