Second-order Rosenbrock-exponential (ROSEXP) methods for partitioned differential equations

Abstract

In this paper, we introduce a new framework for deriving partitioned implicit-exponential integrators for stiff systems of ordinary differential equations and construct several time integrators of this type. The new approach is suited for solving systems of equations where the forcing term is comprised of several additive nonlinear terms. We analyze the stability, convergence, and efficiency of the new integrators and compare their performance with existing schemes for such systems using several numerical examples. We also propose a novel approach to visualizing the linear stability of the partitioned schemes, which provides a more intuitive way to understand and compare the stability properties of various schemes. Our new integrators are A-stable, second-order methods that require only one call to the linear system solver and one exponential-like matrix function evaluation per time step.

1 Introduction

Many scientific and engineering problems involve dynamics driven by several processes of different natures. Often such systems are modeled by differential evolution equations with a forcing term that is comprised of several additive components. These additive terms can represent the influence of each of the driving mechanisms. A well-known example of such a system is an advection–diffusion equation where the evolution is governed by the advective and diffusive forces modeled by two additive terms with first-order and second-order derivatives, respectively. In general, a two-term forcing model can be written as an initial-value problem of the form

$$\begin{aligned} y'&= f_1(y) + f_2(y) \end{aligned}$$

(1a)

$$\begin{aligned} y(t_0)&=y_0. \end{aligned}$$

(1b)

We only consider systems in the autonomous form as the non-autonomous case can be reduced to the autonomous one by introducing the time variable as an additional state variable. Frequently, the forcing terms $f_i(y)$ represent processes occurring over a wide range of temporal scales. As a result, the differential equations modeling such a system are stiff, with stiffness arising from either or both of the additive forcing terms. Such additive forcing structure can be exploited in constructing an efficient temporal numerical integrator to solve the model equations. This is often accomplished through the use of a splitting [1, 2] or a partitioned approach [3, 4]. Both of these approaches have advantages and disadvantages, and the construction of methods of either type, particularly of higher order, is still an active area of research. In this paper, we focus on the partitioning approach to develop new methods.

Some of the best-known partitioned integrators are implicit-explicit (IMEX) methods [5] which have been used for a wide range of applications [6,7,8,9]. IMEX techniques treat one component of the forcing term implicitly and the other explicitly; thus, these methods are appropriate for problems where one of the forcing terms is responsible for stiffness in the system. For problems with stiffness present in both forcing terms, partitioning approach has been extended to implicit-implicit methods [10] and implicit–exponential (IMEXP) integrators [11,12,13]. For IMEXP integrators, however, more attention has been dedicated to systems where one of the forcing terms is linear. Fewer options have been introduced for problems with nonlinear-nonlinear additive stiff forcing structure [12, 13].

In this work, we present a novel way to construct implicit-exponential-type methods for precisely such systems. In other words, we develop a new way to construct partitioned time integration schemes that treat $f_1$ implicitly and $f_2$ exponentially for problems where both of these functions are nonlinear and their Jacobians around $y_n$, $J_{1,n} = \frac{\partial f_1}{\partial y}(y_n)$ and $J_{2,n} =\frac{\partial f_2}{\partial y}(y_n)$ are stiff.

This approach is particularly advantageous when one of the forcing terms can be treated implicitly in a very efficient way, e.g., when a fast preconditioner exists for this portion of the Jacobian. We extend the work in [14] to problems where both $f_1$ and $f_2$ are nonlinear and introduce a new ansatz for constructing such partitioned implicit-exponential integrators which can potentially be extended to higher-order methods. We also describe a convenient way to visualize and assess the stability of the methods and choose schemes with favorable stability properties. The efficiency and accuracy of the new techniques are demonstrated on a set of test problems in a numerical study which also includes a thorough comparison of the performance of the new methods with previously introduced partitioned schemes for such problems. In the following, it is assumed that the partition into $f_1$ and $f_2$ is consistent with the problem to be solved and the Jacobians corresponding to each of the forcing terms are well-defined matrices such that their matrix exponentials or their inverses can be approximated in a stable manner.

The article is organized as follows. The first section briefly reviews the exponential and Rosenbrock methods, which serve as a building block of our new techniques. Section 3 introduces the novel ansatz for the partitioned implicit-exponential methods and presents the construction of the new second-order schemes of this type. Linear stability analysis of the new methods is included in Sect. 4 where we also show that some of our schemes are A-stable. Finally, in Sect. 5, we validate and compare the performance of our methods to other techniques using several numerical test problems.

2 Review of basic exponential and Rosenbrock methods

The new partitioned methods which will be introduced in Sect. 3 use both exponential and Rosenbrock-type integration to advance (1a) in time. Here, we present a brief overview of these two approaches as the building blocks of our new schemes.

Consider the following (unpartitioned) system of ordinary differential equations (ODEs)

$$\begin{aligned} \dfrac{d y}{d t} = f(y), \qquad y(t_0)=y_0, \qquad y \in \mathbb {R}^N, \ f: \mathbb {R}^N \rightarrow \mathbb {R}^N \end{aligned}$$

(2)

where y represents some unknown dynamically changing properties of the system, and f describes all forces driving the system. Suppose we are interested in computing the solution to this system over an interval $t \in [t_0, T]$. Letting h be the discretization step size and $y_n=y(t_n)$ denote the approximate solution at $t_n = t_0+h n$, one can expand (2) in a Taylor series to obtain

$$\begin{aligned} \dfrac{d y}{d t} (t)=f(y_n)+ J_n \cdot (y(t)-y_n)+r(y(t)), \end{aligned}$$

(3)

where $J_n=\dfrac{d f}{d y} (y_n)$ and

$$\begin{aligned} r(z)=f(z)-f(y_n) - J_n \cdot (z-y_n). \end{aligned}$$

(4)

Using the integrating factor $e^{- J_n \,t}$ on (3), we can write it in the form

$$\begin{aligned} \dfrac{d}{dt} \left( e^{-J_n\,t} y(t)\right) = e^{-J_n\,t}(f(y_n) - J_n y_n)+ e^{-J_n\,t} r(y(t)). \end{aligned}$$

(5)

Integrating over the time interval $[t_n,t_n+h]$ and multiplying by $e^{J_n(t_n+h)}$ leads to the integral form

$$\begin{aligned} y(t_n+h)=y_n+ \varphi _1(hJ_n) h f(y_n)+\int _{t_n}^{t_n+h} e^{J_n (t_n + h -t)} r(y(t)) dt, \end{aligned}$$

(6)

where the matrix function $\varphi _1$ is defined as $\varphi _1(A) = (e^{A} - I)A^{-1}$ and I is the identity matrix. This equation, called the Volterra equation among its other names, is the starting point for the construction of different exponential integrators by introducing approximations to the terms of the right-hand side to estimate $y_{n+1} \approx y(t_n + h)$.

For instance, a second-order exponential Euler method (EPI2) [15] can be constructed by neglecting the nonlinear integral in (6), e.g.,

$$\begin{aligned} y_{n+1} = y_n + \varphi _1(hJ_n) h f(y_n). \end{aligned}$$

(7)

The action of the matrix function $\varphi _1$ on a vector can be either evaluated exactly or approximated depending on the properties of the matrix $J_n$. For example, $\varphi _1(hJ_n)$ can be calculated exactly if $J_n$ is small or diagonal. When the Jacobian is large and sparse, a variety of approximation techniques such as Taylor expansions [16], Krylov-based algorithms [17], or Leja methods [18] can be used.

A one-stage second-order Rosenbrock scheme [19], denoted here ROS2, could be derived by analogously neglecting the integral in (6) but also replacing the $\varphi _1$ function by its Padé approximant of order (0/1):

$$\begin{aligned} y_{n+1} = y_n + h \left( I - \frac{h}{2}J_n\right) ^{-1}f(y_n) \end{aligned}$$

(8)

It is worth mentioning that the ROS2 scheme is very close in its formulation (differing only by a factor $\frac{1}{2}$ in front of the Jacobian) to the linearized Euler method

$$\begin{aligned} y_{n+1} = y_n + h \left( I - h J_n\right) ^{-1}f(y_n) \end{aligned}$$

(9)

However, the linearized Euler method is only first order.

Both EPI2 and ROS2 require evaluation of matrix functions of the full (unpartitioned) Jacobian $J_n$ and share similar properties in terms of linear stability. The choice between the two, therefore, depends on the nature of the problem to be solved. For example, when an efficient solver for a linear system of equations is available (e.g., a direct solver or a preconditioned iterative method), the ROS2 scheme may be a judicious choice. Otherwise, exponential approximation of $\varphi _1(hJ_n)f_n$ might be more efficient when used with a fast algorithm such as the KIOPS method [17]. The case where an efficient linear solver is only available for a portion of the Jacobian will be discussed in the next section.

3 New nonlinear-nonlinear partitioned Rosenbrock-exponential (ROSEXP) methods

3.1 General framework

Below, we introduce a framework for developing efficient numerical schemes for solving nonlinear-nonlinear partitioned problems of the form:

$$\begin{aligned} y' = f(y) = f_1(y) + f_2(y), \qquad y(t_0) = y_0, \end{aligned}$$

(10)

where $f_1$ and $f_2$ are both stiff. To develop such schemes, we use the idea of generalized EPI methods introduced in [20]. Specifically, in [20], it was proposed to construct approximation to the solution of (10) in the form

$$\begin{aligned} y_{n+1} = y_n + \sum _i \psi _i(hJ_n) f(z_i) \end{aligned}$$

(11)

where $\psi _i(hJ_n)$ are functions of a matrix $J_n$ which in some way approximates the Jacobian or a portion of the Jacobian, and $z_i$ are vectors approximating the solution on some nodes. The functions $\psi _i$ are chosen to construct integrators of a particular type. For example, these functions can be exponential or rational depending on whether an exponential, an implicit, or a hybrid method is being built.

We extend this idea to the case of a partitioned right-hand side and allow these functions to be a product of exponential or rational functions, each applied to either the Jacobian of $f_1$ or $f_2$. For low-order methods, this idea can be expressed using the following ansatz:

$$\begin{aligned} y_{n+1} = y_n + Q_{1,1}(hJ_{1,n}) Q_{2,1}(hJ_{2,n}) h f_1(y_n) + Q_{1,2}(h J_{1,n})Q_{2,2}(h J_{2,n}) h f_2(y_n) \end{aligned}$$

(12)

where $Q_{i,j}$ are analytic functions (rational or exponential-like functions), and $J_{1,n}$ and $J_{2,n}$ are respectively the Jacobians of $f_1$ and $f_2$ evaluated at $y_n$. Note that the multiplication order of the functions $Q_{1,i}$ and $Q_{2,i}$ in the above ansatz can be changed to derive different schemes. Since matrices $J_{1,n}$ and $J_{2,n}$ do not necessarily commute, we can also consider the following flipped ansatz that reverses the order of application of the functions:

$$\begin{aligned} y_{n+1} = y_n + Q_{2,1}(hJ_{2,n}) Q_{1,1}(hJ_{1,n}) h f_1(y_n) +Q_{2,2}(h J_{2,n}) Q_{1,2}(h J_{1,n}) h f_2(y_n) \end{aligned}$$

(13)

Because the functions $Q_{i,j}$ are only applied to either $J_{1,n}$ or $J_{2,n}$, availability of efficient solvers that estimate $Q_{i,j}$ applied to each of these matrices separately for some problems can result in significant computational savings compared to a method which involves only the full Jacobian $J_n = J_{1,n} + J_{2,n}$. This ansatz is very general and allows the construction of many methods. By analogy with splitting methods, it can be expected that to construct methods of order greater than two, the ansatz above has to be extended to include additional terms that will include more numerous products of $Q_{i,j}$ functions. The number of options to extend the ansatz in such a way is quite extensive and requires a separate systematic study. Additionally, the derivation presented above uses classical order conditions. General stiff order theories were previously proposed for nonpartitioned problems and partitioned systems with a linear term that was being exponentiated (e.g., [21]). To our knowledge, however, due to the complexity of such problems and their analysis, there are currently no general stiff arbitrary order theories for partitioned problems with general nonlinear-nonlinear partitioning. Only linear-nonlinear partitioned problems with methods of second order have been analyzed from the stiff order perspective in [14]. In addition, it is not clear if the full stiff order conditions are necessary to avoid order reduction for many problems [22]. Thus, both the construction of higher-order methods and exploration of analogues of stiff order conditions for generally partitioned problems are relegated to our future work. In this paper, we focus on the proof-of-concept derivation and testing of several efficient second-order schemes and will continue our work on extending these ideas to more generally applicable methods to future publications.

3.2 Construction of second-order schemes

In this section, we derive the classical order conditions necessary for a scheme based on the ansatz (12) to have second order of convergence. To do so, we assume that the numerical solution at time $t_n$ is exact ($y(t_n) = y_n$) and match the numerical solution at the next time step $y_{n+1}$ to $y(t_{n+1})$, the exact solution at time $t_{n+1}$ up to and including second-order terms. This will add some restrictions on the functions $Q_{i,j}$ that will be used to derive second-order schemes.

First, we assume that the functions $Q_{i,j}$ are analytic, so that we have the following Taylor series representation:

$$ Q_{i,j}(hA) = \alpha _{i,j} I + \beta _{i,j} h A + O(h^2) $$

Table 1 Second-order Rosenbrock-exponential schemes

Without loss of generality, we can assume that $\alpha _{i,j} =1$. If it is not the case, the function can be rescaled. Moreover, the product of the scaling coefficients must be equal to 1 for consistency. We use these expansions of $Q_{i,j}$ to obtain the following form of the numerical solution:

$$\begin{aligned} y_{n+1}= & {} y_{n}+Q_{1,1}\left( h J_{1,n}\right) Q_{2,1}\left( h J_{2,n}\right) h f_{1}\left( y_{n}\right) +Q_{2,1}\left( h J_{1,n}\right) Q_{2,2}\left( h J_{2,n}\right) h f_{2}\left( y_{n}\right) \\= & {} y_{n}+\left( I+\beta _{1,1} h J_{1,n}\right) \left( I+\beta _{2,1} h J_{2,n}\right) h f_{1}(y_{n}) \\{} & {} +\left( I+\beta _{1,2} h J_{1,n}\right) \left( I+\beta _{2,2} h J_{2,n}\right) h f_{2}(y_{n})+O\left( h^{3}\right) \\= & {} y_{n} + h\left( f_{1}\left( y_{n}\right) +f_{2}(y_{n})\right) \\{} & {} + h^{2} \left[ \left( \beta _{1,1} J_{1,n}+\beta _{2,1} J_{2,n}\right) f_{1}(y_{n}) + \left( \beta _{1,2} J_{1,n}+\beta _{2,2} J_{2,n}\right) f_{2}(y_{n})\right] +O\left( h^{3}\right) \end{aligned}$$

On the other side, the exact solution at time $t_{n+1}$ can be expanded as follows:

$$\begin{aligned} y(t_{n+1}) = y(t_n) + h (f_1(y_n) + f_2(y_n)) + \frac{h^2}{2} (J_{1,n}+J_{2,n}) (f_1(y_n) + f_2(y_n)) + O\left( h^3\right) \end{aligned}$$

After matching the terms up to thsecond order, we have the following conditions on the functions $Q_{i,j}$:

$$\begin{aligned} \beta _{1,1} = \beta _{2,1} = \beta _{1,2} = \beta _{2,2} = 1/2 \end{aligned}$$

Table 1 presents several schemes that satisfy these conditions. These methods were obtained by choosing the functions $Q_{i,j}$ to be exponential or rational functions similar to those found in formulas for the EPI2 and ROS2 schemes. For this reason, if we consider the extreme case partitioning $f_1 = 0, f_2 = f$, then all the schemes from Table 1 reduce to the EPI2 method. Likewise, if $f_1 = f, f_2 = 0$, then all the schemes simplify to the ROS2 scheme. It should be noted that we derived these methods using classical order conditions theory. In our future research, we plan to investigate whether stiffly accurate methods approach of [14] can be used to build similar partitioned methods.

As mentioned previously, implicit-exponential (IMEXP) schemes for linear-nonlinear partitioned problems were introduced in [14]. In particular, the scheme HImExp2N (Eq. (4.2) in [14]) is derived for problems of the type $y' = L y + N(y)$ where L is a linear operator and N is a nonlinear operator. Interpreting this scheme in the context of our ansatz and the derived order conditions, we can easily see that the method HImExp2N also satisfies the order conditions (14a). Thus, HImExp2N can also be used for the nonlinear-nonlinear partitioned problems and is, in fact, a second-order scheme for problems of the form (1a). Using the notation from this article, HImExp2N can be written as follows:

$$\begin{aligned} Y_1&= y_n + \frac{h}{2} \left( I - \frac{h }{2} J_{1,n}\right) ^{-1} f(y_n) \end{aligned}$$

(14a)

$$\begin{aligned} y_{n+1}&= y_n + h \left( I - \frac{h }{2}J_{1,n} \right) ^{-1} f(y_n) + 2h \varphi _2(h J_{2,n}) (f_2(Y_1) - f_2(y_n)) \end{aligned}$$

(14b)

where $\varphi _2(A) = (e^A - I - A/2) A^{-2}$.

Additional partitioned nonlinear-nonlinear schemes were also explored in [12, 13], but both of the methods derived in these publications are limited to first-order accuracy. We will include the SIERE and SBDF2ERE schemes derived in these papers in our comparisons:

• SIERE [13]:

  $$\begin{aligned} y_{n+1} = y_n + h \left( I - h J_{1,n}\right) ^{-1} \left( f_1(y_n) + \varphi _1(hJ_{2,n}) f_2(y_n) \right) \end{aligned}$$

• SBDF2ERE [12]:

  $$\begin{aligned} y_{n+1} = y_n + \frac{1}{3} \left( I - \frac{2\,h}{3} J_{1,n}\right) ^{-1} \left( y_n - y_{n-1} + 2\,h f_1(y_n) + 2\,h \varphi _1(hJ_{2,n}) f_2(y_n) \right) \end{aligned}$$

  Note that all the schemes are written so that the $f_1$ partition is treated using the rational function, while the $f_2$ partition is treated exponentially.

4 Linear stability

As mentioned in the previous section, our work focuses on nonlinear-nonlinear partitioning where both $f_1$ and $f_2$ are stiff. In this context, it is important to have good stability properties. In order to study the linear stability of partitioned integrators, we assume that the partitioned Jacobian terms $J_{1,n}$ and $J_{2,n}$ are simultaneously diagonalizable and consider the following problem:

$$\begin{aligned} y' = \lambda _1 y + \lambda _2 y \quad \text {where} \quad \lambda _1, \lambda _2 \in \mathbb C. \end{aligned}$$

(15)

Note that this problem is not able to give a full picture of the linear stability of additively partitioned problems. For example, it does not take into account the potential coupling between the two partitions. However, based on our experiments, this problem allows us to give a good description of the stability of the different methods.

Any one-step method applied to (15) reduces to the recurrence ${y_{n+1} = R(z_1, z_2) y_n}$ where $z_1 = h\lambda _1$, $z_2 = h\lambda _2$ and $R(z_1,z_2)$ is the stability function of the scheme. The scheme is then stable if $|R(z_1,z_2)| \le 1$. The stability functions for all one-step methods considered in this work are listed in Table 2.

Table 2 Stability functions for one-step methods

Because the SBDF2ERE scheme is a multi-step method, we determine stability differently. After applying the method to the linear problem (15), we obtain the recurrence

$$\begin{aligned} y_{n+1} + R_1(z_1,z_2) y_n + R_0(z_1,z_2) y_{n-1}= 0 \end{aligned}$$

where $R_1(z_1,z_2) = - \frac{2}{3-2z_1} (1+e^{z_2})$ and $R_0(z_1,z_2) = \frac{1}{3-2z_2}$. The method will be stable when $w_1$ and $w_2$, the roots of the polynomial $w^2 + R_1(z_1,z_2) w + R_0(z_1,z_2)$, satisfy the root condition.

Because both $z_1$ and $z_2$ are complex-valued, the stability regions for both one-step and multi-step methods are challenging to visualize. To simplify our presentation of stability, we will use $A(\varvec{\alpha })$-stability. For a stability function R(z) of a single complex variable, a method is said to be $A(\varvec{\alpha })$-stable if it includes a sector of an angle $\varvec{\alpha }$ in its stability region with $\varvec{\alpha }$ defined as follows:

$$\begin{aligned} \varvec{\alpha } = \max \{\alpha : \forall z \quad (z \in \mathbb {C}^- \wedge |\arg (z)-\pi | \le \alpha ) \Rightarrow |R(z)| \le 1 \}. \end{aligned}$$

(16)

For non-partitioned schemes, $\varvec{\alpha }$ is the maximum value of the angle such that the method is stable for all complex z values in the sector delimited by the lines with an angle $-\varvec{\alpha }$ and $+\varvec{\alpha }$ with respect to the negative real axis. This value ranges from $0^\circ$ if the method is only stable on the negative real axis to $90^\circ$ for a method that is stable in the entire left half-plane. When the angle of the $\varvec{\alpha }$-stability of a scheme is equal to $90^\circ$, we say that the method is A-stable.

By fixing either $z_1$ or $z_2$, we can reduce the stability function of a partitioned scheme to a function of a single complex variable. We can then compute the stability angle $\varvec{\alpha }$ in the remaining free variable. This can be expressed mathematically as

$$\begin{aligned} \text { fixing} z_1:{} & {} \varvec{\alpha }(z_1) = \max \{\alpha : \forall z_2 \quad (z_2 \in \mathbb {C}^- \wedge |\arg (z_2)-\pi | \le \alpha ) \Rightarrow |R(z_1,z_2)| \le 1 \}, \end{aligned}$$

(17a)

$$\begin{aligned} \text { fixing} z_2:{} & {} \varvec{\alpha }(z_2) = \max \{\alpha : \forall z_1 \quad (z_1 \in \mathbb {C}^- \wedge |\arg (z_1)-\pi | \le \alpha ) \Rightarrow |R(z_1,z_2)| \le 1 \}, \end{aligned}$$

(17b)

Fixing $z_1$ or $z_2$ over a grid of values and using color to represent the stability angle makes it possible to easily visualize the stability of each method. Figure 1 shows the $\varvec{\alpha }$-stability for the schemes presented in the previous section. Note that ordinarily, due to the high dimensionality of the stability function $R(z_1, z_2)$, it is difficult to assess the properties of the stability regions. Using the approach described above, it is easier to visualize the stability regions. To our knowledge, this approach to visualizing the linear stability of a method has not been used before. Plots like Fig. 1 provide a visual guide to the overall shape of the stability regions. Additional visualization can be done if one is interested in the geometric details of a subregion. For example, different types of plots, such as graph of the angle value along the real axes, can be created to better assess stability for eigenvalues on the real axes.

Fig. 1

$\varvec{\alpha }$-stability angles for the partitioned schemes when $z_1$ is fixed (left column) or $z_2$ is fixed (right column). The x and y axis of the plots in the left and right columns, respectively, correspond to the real and imaginary parts of $z_1$ and $z_2$. The color represents the stability angle $\varvec{\alpha }$ defined in (17a) and (17b). The white regions correspond to parameter values where the stability region is bounded and therefore not $\varvec{\alpha }$-stable even for $\varvec{\alpha } = 0$

In Fig. 1a, we see that $\varvec{\alpha } = 90^\circ$ for all values of $z_1$ and $z_2$. This implies that the schemes PartRosExp2, PartExpRos2, and SIERE are all A-stable. This can be formally proven by observing that the stability function for each of these methods is a product of two A-stable functions in $z_1$ and $z_2$, respectively (e.g., the stability functions of PartRosExp2 and PartExpRos2 are the products of the functions $R_1(z) = e^{z}$ and $R_2(z) = \frac{2 + z}{2-z}$). Since both of these functions are A-stable, the product must also be A-stable.

Figure 1b shows that the stability of the schemes RosExp2, ExpRos2 and HImExp2N is more restricted. Specifically, there are restrictions on stability in $z_1$ if values of $z_2$ are close to the imaginary axes. However, for problems with spectrum lying sufficiently away from the imaginary axes, stability is retained. Finally, the stability of the scheme SBDF2ERE, presented in Fig. 1c, is good overall, with some limitations close to the origin.

5 Numerical experiments

The stability properties of the new schemes for linear equations with constant coefficients provide necessary but not sufficient conditions for the stability of variable coefficients and nonlinear problems. In this section, we summarize numerical experiments that confirm that the conclusions of our analysis also apply to more complicated problems. Since we are interested in problems where it is known a priory that partitioning will be beneficial, we compare the new schemes with other methods that can take advantage of partitioning rather than general time integration schemes.

5.1 Advection–diffusion PDE (AdvDiff)

We consider the following 1D advection–diffusion PDE:

$$\begin{aligned} \frac{\partial u}{\partial t} + \frac{\partial }{\partial x} \left( \alpha _0 u + \alpha _1 u^2 \right) = \frac{\partial }{\partial x} \left[ (\beta _0 + \beta _1 u) \frac{\partial u }{\partial x} \right] , \quad x \in [0,1], \quad t \in [0, 0.1], \end{aligned}$$

(18)

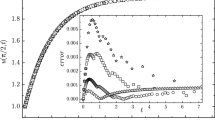
We use a Gaussian function as the initial condition $u(x, 0) = e^{-5000 (x - 0.2)^2}$ and homogeneous Dirichlet boundary conditions $u(0,t) = u(1,t) = 0$. We also consider two sets of parameters: the first corresponds to a linear problem with $\alpha _0 = 5$, $\alpha _1 = 0$, $\beta _0 = 10^{-2}$, and $\beta _1 = 0$, and the second represents a nonlinear problem with $\alpha _0 = 5$, $\alpha _1 = 5$, $\beta _0 = 5 \times 10^{-4}$, and $\beta _1 = 10^{-1}$. Figure 2 shows the solution u of this PDE at the initial and final time. Equation (18) is discretized in space using standard second-order centered finite differences with 1000 grid points. This discretization leads to a system of N ordinary differential equations that can be written as follows:

$$ u' = f_{\text {adv}}(u) + f_{\text {diff}}(u)$$

where $f_{\text {adv}}(u)$ correspond to the discretized advection term $\frac{\partial }{\partial x} \left( \alpha _0 u + \alpha _1 u^2 \right)$ and $f_{\text {diff}}(u)$ correspond to the discretized diffusion term $\frac{\partial }{\partial x} \left[ (\beta _0 + \beta _1 u) \frac{\partial u }{\partial x} \right]$. In the next section, we will explore the cases where $f_1 = f_{\text {adv}}, f_2 = f_{\text {diff}}$ (rational advection/exponential diffusion) as well as $f_1 = f_{\text {diff}}, f_2 = f_{\text {adv}}$ (rational diffusion/exponential advection).

Fig. 2

Solution at initial and final time for the PDE (18) with both sets of parameters

5.2 Schnakenberg with non-linear diffusion (Schnakenberg_NL)

The following equations describe two reacting and diffusing chemical species (u and v) evolving in two-dimensional space:

$$\begin{aligned} \frac{\partial u}{\partial t}&= \gamma (a - u + u^2 v) + \nabla . (u^{\beta _1} \nabla u ), \end{aligned}$$

(19a)

$$\begin{aligned} \frac{\partial v}{\partial t}&= \gamma (b - u^2 v) + d \ \nabla . (v^{\beta _2} \nabla v), \quad \quad (x,y) \in [0,1]^2 \end{aligned}$$

(19b)

where $a = 0.1, b = 0.9, d = 10, \beta _1 = \beta _2 = 10, t_{end} = 10^{-2}$, and $\gamma = 1000$. As in [23, Section 4.2], the initial condition is a perturbation of the stable equilibrium, and the boundary conditions are periodic in both directions. The diffusion terms are discretized using the standard second-order finite differences on a uniform grid with $N_x = N_y = 128$. The reaction terms are treated exponentially, while the diffusion terms are treated using the rational function.

Fig. 3

Convergence plots (error vs. time step) for the linear and nonlinear AdvDiff, Schnakenberg_NL, and Semilinear_para problems

5.3 1D semilinear parabolic problem (Semilinear_para)

Finally, we use the following one-dimensional semilinear parabolic problem described in [24] (note that we use the term “semilinear parabolic problem” as it was named in [24]):

$$\begin{aligned} \frac{\partial u}{\partial t}(x, t) - \frac{\partial ^2 u}{\partial x^2}(x,t) = \int _0^1 u(x,t)dx + \phi (x,t) \quad \quad x \in [0,1], t \in [0,1], \end{aligned}$$

(20)

with the homogeneous Dirichlet boundary conditions. The source function $\phi$ is chosen so that $u(x, t) = x (1-x)e^t$ is the exact solution. This problem was originally designed to demonstrate the order reduction that some exponential integrators can suffer when applied to stiff problems. It is therefore used here to validate that no such order reduction is exhibited by our schemes. The diffusion term is discretized using the standard second-order finite differences on a uniform grid with $N_x = 400$. The nonlinear terms on the right-hand side are treated exponentially, while the diffusion term is treated using the rational function.

Fig. 4

Stability comparison for the AdvDiff problem with different partitioning

5.4 Numerical results

Numerical examples presented below verify the order of convergence of the newly derived methods and compare their performance with the existing methods described above. The implementation of the integrators was done in MATLAB 2020b. For all the schemes, we use the KIOPS method introduced in [17] to approximate the products of exponential and $\varphi -$functions with vectors. This method allows us to approximate both exponential functions in the schemes PartExpRos2 and PartRosExp2 at once as a single computation. The rational functions are approximated using the GMRES method [25] with an incomplete LU factorization with no fill preconditioner (ILU(0)). Because the scheme BDF2ERE is a multi-step integrator where the solution at the current and previous time step must be known, the initial step must be treated differently. In this work, the initial time step is computed using the $2^{nd}$ order EPI2 method. The error is computed at the final time as the discrete $2-$norm between the approximate solution and a reference solution computed using MATLAB’s ode15s integrator with absolute and relative tolerances set to $10^{-14}$.

In the first set of tests, we verify the order of convergence of all the methods on the problems presented above. Figure 3 shows the convergence plot (error vs. time step in log-log scale) on the linear and nonlinear advection–diffusion PDE, Schnakenberg PDE, and the semilinear parabolic problems. Note that for the advection–diffusion PDE, we used $f_1=f_{\text {adv}}$ and $f_2 = f_{\text {diff}}$. We can see that, as expected, the methods SBDF2ERE and SIERE both converge at first order, while the methods introduced in Table 1 and the HImExp2N scheme converge at second order. We can also see that for the advection–diffusion and the Schnakenberg PDE, the order of multiplication of the functions $Q_{i,j}$ does not influence the accuracy of the solution (ansatz (12) vs. (13)). However, for the semilinear parabolic problem, the order does affect the accuracy. For this problem and this partitioning, applying the function of $J_{2,n}$ first leads to better accuracy. This case illustrates that the accuracy of the method does depend on the problem and the chosen partitioning.

Next, we want to validate the stability advantages of the new schemes that our analysis of Sect. 4 predicted. We showed that for the schemes ExpRos2, RosExp2, and HImExp2N, if $z_2$ is close to the imaginary axis, then stability for $z_1$ is either bounded or restricted. Figure 4 shows the convergence diagram for the advection–diffusion PDE problem. Figure 4a and b correspond to the problem with linear parameters while Fig. 4c and d correspond to the nonlinear parameters. The plots on the left (Fig. 4a and c) are obtained using the partitioning $f_1=f_{\text {adv}}, f_2 = f_{\text {diff}}$, and the plots on the right (Fig. 4b and d) are obtained using the partitioning $f_1=f_{\text {diff}}, f_2 = f_{\text {adv}}$. The eigenvalues corresponding to the advection term $f_{\text {adv}}$ are expected to be close to the imaginary axis, while the eigenvalues of the diffusion term are expected to be along the negative real axis. Therefore, based on the stability analysis, we are expecting the schemes ExpRos2, RosExp2, and HImExp2N to have worse stability for $f_2= f_{\text {adv}}$ (right plots). For both the linear and nonlinear parameters, we see that this is indeed the case, and these methods are stable only for a more restrictive range of time step sizes.

Fig. 5

Precision diagram (error vs. CPU time) for the linear and nonlinear AdvDiff, Schnakenberg_NL, and Semilinear_parabolic problems

We now compare the performance of the methods on the different test problems. Figure 5 shows the precision diagrams (error vs. CPU time) for the linear and nonlinear advection–diffusion PDE, Schnakenberg PDE, and the semilinear parabolic problems. As expected, the precision diagrams clearly demonstrate that the first-order methods SBDF2ERE and SIERE are less efficient than all of the second-order schemes. Also, for cases where the linear solve is sufficiently more costly than the exponential functions estimation, such as systems solved in Fig. 5a and c, method PartExpRos2 is less efficient since unlike all other second-order schemes, it requires two linear systems to be solved per iteration. Among the second-order methods, there is no clear winner in terms of efficiency, and the choice of the best methods should depend on the particulars of the operators $f_1$ and $f_2$ and the costs of evaluating these functions, their respective Jacobian contributions, and the corresponding costs of linear solves and exponential function evaluations.

6 Conclusion

In this paper, we presented a new framework for deriving partitioned integrators for stiff systems of ODEs with nonlinear-nonlinear additive forcing terms. The new time integrators constructed using this framework are particularly efficient for problems where both nonlinear forcing terms are stiff, but one of them can be solved efficiently using an implicit approach, and another can be integrated exponentially. The new ansatz that allowed us to derive specific second-order schemes can potentially be extended to construct higher-order methods, where the choice of the sequential order for the operators is also very important. We intend to pursue this line of research in our future work. We have used linear stability analysis and a novel way to visualize the properties of a stability function to demonstrate that several of the new methods are A-stable and thus offer superior stability compared to existing schemes for similar problems. Convergence and efficient performance of the new methods have been demonstrated using several numerical examples. A thorough comparison of these schemes with integrators proposed for such problems in previous publications has been performed. We showed that the novel exponential-Rosenbrock-type methods are both more accurate and more stable than previously published methods and can be effectively used for a variety of applications.