Rates of robust superlinear convergence of preconditioned Krylov methods for elliptic FEM problems

Abstract

This paper considers the iterative solution of finite element discretizations of second-order elliptic boundary value problems. Mesh independent estimations are given for the rate of superlinear convergence of preconditioned Krylov methods, involving the connection between the convergence rate and the Lebesgue exponent of the data. Numerical examples demonstrate the theoretical results.

1 Introduction

The preconditioned conjugate gradient (PCG) method is a widespread way for the iterative solution of discretized elliptic partial differential equations. It can be efficiently coupled with multigrid methods and, under certain conditions, operator preconditioning can provide mesh-independent convergence. Hence, its convergence has been widely analyzed, see, e.g., [1, 3] and references therein.

In particular, superlinear convergence is often a characteristic second stage in the convergence history: this notion expresses, roughly speaking, that the number of iterations required to achieve a new correct digit will be decreasing in course of the iteration. This phenomenon is also favorable when the PCG method is used as an inner iteration for an outer process. Such results were already obtained in [11, 15] on operator level.

This paper considers some types of second-order elliptic boundary value problems with variable zeroth order coefficients and their finite element discretizations. Our goal is to find relevant estimations for the rate of superlinear convergence of the PCG method for this type of problem; furthermore, we are interested in robust, that is, mesh independent rates, which can be given independently of the finite element mesh size. This means that the favorable behavior does not deteriorate as the mesh is refined.

This mesh-independence property of superlinear convergence was studied in various joint papers of the second author, see, e.g., [2] for a general result, [3] for a survey in this journal, and [5] for some recent applications. The starting point of the present paper is [10], where a superlinear rate was found in a particular situation with continuous zeroth order coefficient. Our goal is to extend this result to a family of estimations for general zeroth order (“linearized reaction”) coefficients, that is, which are unbounded, and belong to some Lebesgue space. Furthermore, we would like to explore the connection between the convergence rate and the Lebesgue exponent. A practical motivation for such situations is, among other things, the Newton linearization arising in reaction-diffusion models where the nonlinear rate of reaction is typically of polynomial order, thus leading to linearized coefficients with given Lebesgue exponent.

We present eigenvalue-based estimations of the rate of superlinear convergence for such problems, first for single equations, then we show that similar estimations can be obtained in the case of proper systems of PDEs, involving GMRES in the nonsymmetric case. Finally, some numerical examples are shown, which properly demonstrate our theoretical results.

2 Theoretical background

2.1 The abstract problem and its discretization

Let H be a real Hilbert space and let us consider a linear operator equation

$$\begin{aligned} Au=g \end{aligned}$$

(1)

with some $g \in H$, under the following

Assumption 2.1

• (i) The operator A is decomposed as

  $$\begin{aligned} A=S+Q \end{aligned}$$

  (2)

  where S is a symmetric operator in H with dense domain D and Q is a compact self-adjoint operator defined on the domain H.

• (ii) There exists $k>0$ such that $\langle Su,u \rangle \ge k \Vert u\Vert ^2$ ($\forall u \in D$).

• (iii) $\langle Qu,u \rangle \ge 0$ ($\forall u \in H$).

We recall that the energy space $H_S$ is the completion of D under the energy inner product

$$\begin{aligned} \langle u,v \rangle _S=\langle Su,v\rangle , \end{aligned}$$

(3)

and the corresponding norm is denoted by $\Vert \cdot \Vert _S$. Assumption (ii) implies $H_S \subset H$. Then, there exists a unique bounded linear operator, denoted by $Q_S: H_S \mapsto H_S$, such that

$$ \langle Q_Su,v\rangle _S=\langle Qu,v \rangle \qquad (\forall u,v \in H_S). $$

We replace (1) by its formally preconditioned form

$$ Bu\equiv S^{-1}Au=S^{-1}g, $$

that is, $(I+S^{-1}Q)u=S^{-1}g$ in $H_S$. This gives the weak formulation

$$\begin{aligned} \langle (I+Q_S)u,v \rangle _S= \langle g,v \rangle \qquad (\forall v \in H_S). \end{aligned}$$

(4)

Since by assumption (iii) the bilinear form on the left is coercive on $H_S$, by the Lax-Milgram theorem, there exists a unique solution $u \in H_S$ of (4).

Now (4) is solved numerically using a Galerkin discretization. Consider a given finite-dimensional subspace $V=\text {span}\{\varphi _1,\dots ,\varphi _n\}\subset H_S$, and let

$$\begin{aligned} \varvec{\textrm{S}}_h=\{\langle \varphi _i,\varphi _j\rangle _S\}^n_{i,j=1} \quad \text { and } \varvec{\textrm{Q}}_h=\{\langle Q\varphi _i,\varphi _j\rangle \}^n_{i,j=1} \end{aligned}$$

the Gram matrices corresponding to S and Q. We look for the numerical solution $u_V \in V$ of (4) in V, i.e., for which

$$\begin{aligned} \langle (I+Q_S) u_V,v \rangle _S= \langle g,v \rangle \qquad (\forall v \in V). \end{aligned}$$

(5)

Then, $u_V=\sum ^n_{j=1} c_j\varphi _j$, where $\varvec{\textrm{c}}=(c_1,\dots ,c_n) \in \mathbb {R}^n$ is the solution of the system

$$\begin{aligned} (\varvec{\textrm{S}}_h+\varvec{\textrm{Q}}_h)\varvec{\textrm{c}}=\varvec{\textrm{b}} \end{aligned}$$

(6)

with $\varvec{\textrm{b}}=\{\langle g,\varphi _j \rangle \}^n_{j=1}$. The matrix $\varvec{\textrm{A}}_h:=\varvec{\textrm{S}}_h+\varvec{\textrm{Q}}_h$ is SPD.

By using matrix $\varvec{\textrm{S}}_h$ as the preconditioner for the system (6), we shall work with the preconditioned system

$$\begin{aligned} (\varvec{\textrm{I}}+\varvec{\textrm{S}}_h^{-1}\varvec{\textrm{Q}}_h)\varvec{\textrm{c}}=\tilde{\varvec{\textrm{b}}}, \end{aligned}$$

(7)

where $\varvec{\textrm{I}}$ is the identity matrix in $\mathbb {R}^n$ and $\tilde{\varvec{\textrm{b}}}=\varvec{\textrm{S}}_h^{-1}\varvec{\textrm{b}}$. We apply the CGM for the solution of this system.

2.2 The preconditioned conjugate gradient method and superlinear convergence

Let us consider a general linear system $\varvec{\textrm{A}}_h \varvec{\textrm{u}}= \varvec{\textrm{g}}$ and its preconditioned form

$$\begin{aligned} \varvec{\textrm{B}}_h \varvec{\textrm{u}}= \tilde{\varvec{ \textrm{g}}}, \end{aligned}$$

(8)

where $\varvec{\textrm{B}}_h= \varvec{\textrm{S}}_h^{-1}\varvec{\textrm{A}}$ and $\tilde{\varvec{ \textrm{g}}}= \varvec{\textrm{S}}^{-1}_h \varvec{ \textrm{g}}$. The preconditioner $\textbf{S}_h$ induces the energy inner product $\langle \textbf{c}, \textbf{d}\rangle _{\textbf{S}_h}:= \textbf{S}_h\, \textbf{c}\cdot \textbf{d}$, where $\cdot$ denotes the standard Euclidean inner product.

Then, the PCG method is given by the following algorithm. Let $\varvec{\textrm{u}}_0$ be arbitrary, $\varvec{\mathrm {\rho }}_0= \varvec{\textrm{A}_h}\varvec{\textrm{u}}_0-\varvec{\textrm{g}}$, $\varvec{\textrm{S}}_h \varvec{\textrm{p}}_0=\varvec{\mathrm {\rho }}_0$, $\varvec{\textrm{r}}_0=\varvec{\mathrm {\rho }}_0$ and for $k \in \mathbb {N}$

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \varvec{\textrm{u}}_{k+1}=\varvec{\textrm{u}}_k+\alpha _k \varvec{\textrm{p}}_k, \\ &{} \varvec{\textrm{r}}_{k+1}=\varvec{\textrm{r}}_k+\alpha _k \varvec{\textrm{S}}^{-1}_h\varvec{\textrm{A}}_h \varvec{\textrm{p}}_k, \\ &{} \varvec{\textrm{p}}_{k+1}=\varvec{\textrm{r}}_{k+1}+\beta _k \varvec{\textrm{p}}_k \\ \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} \alpha _k=\frac{-\Vert \varvec{\textrm{r}}_k\Vert ^2_{\varvec{\textrm{S}}_h}}{\langle \varvec{\textrm{A}}_h \varvec{\textrm{p}}_k, \varvec{\textrm{p}}_k \rangle }, \quad \beta _k=\frac{\Vert \varvec{\textrm{r}}_{k+1}\Vert ^2_{\varvec{\textrm{S}}_h}}{\Vert \varvec{\textrm{r}}_k\Vert ^2_{\varvec{\textrm{S}}_h}}. \end{aligned}$$

In fact, the vector $\varvec{\textrm{z}}_k:=\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{A}}_h \varvec{\textrm{p}}_k$ is computed by solving the auxiliary problem

$$\begin{aligned} \varvec{\textrm{S}}_h \varvec{\textrm{z}}_k=\varvec{\textrm{A}}_h \varvec{\textrm{p}}_k \, . \end{aligned}$$

Moreover, setting $\varvec{\textrm{w}}_k=\varvec{\textrm{z}}_k-\varvec{\textrm{p}}_k$, this problem is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\varvec{\textrm{S}}_h \varvec{\textrm{w}}_k=\varvec{\textrm{Q}}_h\varvec{\textrm{p}}_k, \\ &{} \varvec{\textrm{z}}_k=\varvec{\textrm{w}}_k+\varvec{\textrm{p}}_k \, . \end{array}\right. } \end{aligned}$$

(9)

We are interested in the superlinear convergence rates for the CGM, and now recall the corresponding well-known estimation. Let $\varvec{\textrm{A}}_h=\varvec{\textrm{S}}_h+ \varvec{\textrm{Q}}_h$. Then, $\varvec{\textrm{B}}_h$ in (8) has the compact perturbation form $\varvec{\textrm{B}}_h=\varvec{\textrm{I}}_h+ \varvec{\textrm{E}}_h$ with $\varvec{\textrm{E}}_h:=\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{Q}}_h.$ Let us order the eigenvalues of the latter according to $|\lambda _1(\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{Q}}_h)|\ge |\lambda _2(\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{Q}}_h)| \ge \dots \ge |\lambda _n(\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{Q}}_h)|$. Then, the error vectors $\varvec{\textrm{e}}_k:=\varvec{\textrm{c}}_k-\varvec{\textrm{c}}$ are measured by $\left< \varvec{\textrm{B}}_h \varvec{\textrm{e}}_k, \varvec{\textrm{e}}_k\right>_{\varvec{\textrm{S}}_h}^{1/2}= \left<\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{A}}_h \varvec{\textrm{e}}_k, \varvec{\textrm{e}}_k\right>_{\varvec{\textrm{S}}_h}^{1/2}= \left<\varvec{\textrm{A}}_h \varvec{\textrm{e}}_k, \varvec{\textrm{e}}_k\right>^{1/2} =\left\| \varvec{\textrm{e}}_k\right\| _{\varvec{\textrm{A}}_h}$, and they are known to satisfy

$$\begin{aligned} \left( \frac{\Vert \varvec{\textrm{e}}_k\Vert _{\varvec{\textrm{A}}_h}}{\Vert \varvec{\textrm{e}}_0\Vert _{\varvec{\textrm{A}}_h}} \right) ^{1/k} \le \frac{2 \Vert \varvec{\textrm{B}}^{-1}_h\Vert _{\varvec{\textrm{S}}_h}}{k} \sum ^{k}_{j=1} |\lambda _j(\varvec{\textrm{S}}^{-1}_h\varvec{\textrm{Q}}_h)| \qquad (k=1,2,\dots ,n). \end{aligned}$$

(10)

This follows, e.g., from formula (13.13) in [1], see also (2.16) in [3].

For the discretized problem described in subsection 2.1, the following result allows us to give a convergence rate for the upper bound of (10) through the eigenvalues of the operator $Q_S$. This is a modification of Theorem 1 in [10] where the square of eigenvalues was considered.

Lemma 1

Let assumptions 2.1 hold. Then, for any $k=1,2,\dots ,n$

$$\begin{aligned} \sum ^{k}_{j=1}|\lambda _j(\varvec{\textrm{S}}_h^{-1}\varvec{\textrm{Q}}_h)|\le \sum ^{k}_{j=1}\lambda _j(Q_S). \end{aligned}$$

(11)

Proof

We have in fact

$$\begin{aligned} \sum ^{k}_{j=1}\sigma _j(\varvec{\textrm{S}}_h^{-1}\varvec{\textrm{Q}}_h)\le \sum ^{k}_{j=1}\sigma _j(Q_S), \end{aligned}$$

(12)

where the $\sigma _j$ denote the singular values of the given matrix or operator, see [4]. Now both the matrix $\varvec{\textrm{S}}_h^{-1}\varvec{\textrm{Q}}_h$ (with respect to the $\varvec{\textrm{S}}_h$-inner product) and the operator $Q_S$ (in $H_S$) are self-adjoint, hence their singular values coincide with the modulus of the eigenvalues. Since $Q_S$ is a positive operator from assumption (iii), the modulus can be omitted.$\square$

An immediate consequence of this lemma is the following mesh-independent bound.

Corollary 1

For any $k=1,2,\dots ,n$

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _{\varvec{\textrm{A}}_h}}{\Vert e_0\Vert _{\varvec{\textrm{A}}_h}} \right) ^{1/k} \le \frac{2 \Vert B^{-1}\Vert _S}{k} \sum ^{k}_{j=1} \lambda _j(Q_S)\qquad (k=1,2,\dots ,n). \end{aligned}$$

(13)

Proof

By [2, Prop. 4.1], we are able to estimate $\Vert \varvec{\textrm{B}}^{-1}_h\Vert _{\varvec{\textrm{S}}_h} \le \Vert B^{-1}\Vert _S$. This, together with (10) and (11), completes the proof. $\square$

Since $|\lambda _1(Q_S)|\ge |\lambda _2(Q_S)| \ge \dots \ge 0$ and the eigenvalues tend to 0, the convergence factor is less than 1 for k sufficiently large. Hence, the upper bound decreases as $k \rightarrow \infty$ and we obtain superlinear convergence rate.

3 Estimation of the rates of superlinear convergence

We present the rate estimates in the following stages. First, we develop the results in detail for single equations. The studied preconditioners have the advantage that the original PDE is reduced to simpler PDEs whose discretizations can be solved by proper optimal fast solvers. Then, we extend the estimates for systems of PDEs, first for the symmetric and then for the nonsymmetric case. This situation shows the real strength of the idea of preconditioning operators, since one can reduce large coupled systems of PDEs to independent single PDEs, hence the numerical solution of the latter can be parallelized. In each case, we provide an estimation of the rate of mesh-independent superlinear convergence such that the dependence of the rate on the integrability exponent of the reaction coefficient is determined.

3.1 Elliptic equations

Let $d\ge 2$ and $\Omega \subset \mathbb {R}^{d}$ be a bounded domain. We consider the elliptic problem

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}- \textrm{div} (G \nabla u) + \eta u=g, \\ &{} u|_{\partial \Omega }=0 \end{array}\right. } \end{aligned}$$

(14)

in the following situation.

Assumption 3.1

• (i) The symmetric matrix-valued function $G \in {L}^{\infty } (\overline{\Omega },\mathbb {R}^{d} \times \mathbb {R}^{d})$ satisfies

  $$ G(x) \xi \cdot \xi \ge m |\xi |^2 \qquad (\forall \xi \in \mathbb {R}^{d}) $$

  for some $m>0$ independent of $\xi$.

• (ii) We have $\eta \ge 0$; furthermore, there exists $2< p < \frac{2d}{d-2}$ such that

  $$\begin{aligned} \eta \in {L}^{p/(p-2)}(\Omega ) . \end{aligned}$$

  (15)

• (iii) $\partial \Omega$ is a Lipschitz boundary.

• (iv) $g \in {L}^{2}(\Omega )$.

Then, problem (14) has a unique weak solution in ${H}^1_{0}(\Omega )$. The relevance of the condition on p in (ii) is that the continuous embedding ${H}^1_{0}(\Omega )\subset L^p(\Omega )$ holds, which ensures the boundedness of the corresponding bilinear form.

In practice, we are mostly interested in the case when the principal part has constant or separable coefficients, whereas $\eta =\eta (x)$ is a general variable (i.e., nonconstant) coefficient. In this case, the principal part will be an efficient preconditioning operator, see Remark 1 for background and extensions.

Let $V_h \subset {H}^1_{0}(\Omega )$ be a given FEM subspace. We look for the numerical solution $u_h$ of (14) in $V_h$:

$$\begin{aligned} \int _{\Omega } (G {\nabla } u_h \cdot \nabla v+\eta u_hv)=\int _{\Omega } gv \qquad (\forall v \in V_h). \end{aligned}$$

(16)

The corresponding linear algebraic system has the form

$$(\varvec{\textrm{G}}_h+\varvec{\textrm{D}}_h)\varvec{\textrm{c}}=\varvec{\textrm{g}}_h,$$

where $\varvec{\textrm{G}}_h$ and $\varvec{\textrm{D}}_h$ are the corresponding weighted stiffness and mass matrices, respectively. We apply the matrix $\varvec{\textrm{G}}_h$ as preconditioner, thus the preconditioned form of (16) is given by

$$\begin{aligned} (\varvec{\textrm{I}}_h+\varvec{\textrm{G}}^{-1}_h\varvec{\textrm{D}}_h)\varvec{\textrm{c}}=\tilde{\varvec{\textrm{g}}}_h \end{aligned}$$

(17)

with $\tilde{\varvec{\textrm{g}}}_h=\varvec{\textrm{G}}^{-1}_h\varvec{\textrm{g}}_h$. Then, we apply the CGM to (17). The auxiliary systems with $\varvec{\textrm{G}}_h$ can be solved efficiently with fast solvers, see Remark 1.

Such equations for $\eta \in C(\overline{\Omega })$ were considered in [10]. That was a rather restrictive assumption, see also Remark 2 for the motivations of the more general case (15).

Theorem 1

Let Assumptions 3.1 hold. Then, there exists $C>0$ such that for all $k \in \mathbb {N}$

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _{\varvec{\textrm{A}}_h}}{\Vert e_0\Vert _{\varvec{\textrm{A}}_h}}\right) ^{\frac{1}{k}} \le Ck^{-\alpha }, \end{aligned}$$

(18)

where $\alpha =\frac{1}{d}-\frac{1}{2}+\frac{1}{p}$.

Proof

Let us consider the real Hilbert space ${L}^{2}(\Omega )$ endowed with the usual inner product. Let $D=H^1_{0,G}:=\{u \in {H}_{0}^{1}(\Omega ) \cap {H}^{2}(\Omega ):\ \ G \nabla u \in H(\mathrm {div, \Omega }) \}$. We define the operators

$$\begin{aligned} Su \equiv -\textrm{div}(G\nabla u) \quad (u \in D) \quad \text { and } \quad Qu\equiv \eta u \quad (u \in {H}_{0}^{1}(\Omega ))\, . \end{aligned}$$

(19)

Then,

$$\begin{aligned} \langle Su,u \rangle _{L^2} \ge m \int _{\Omega } |\nabla u|^2 \ge m C_\Omega \int _{\Omega } u^2 \qquad (\forall u \in D), \end{aligned}$$

(20)

where $C_\Omega$ is the Poincaré–Friedrichs constant and m is the lower spectral bound of G given by assumption (i). Hence the energy space $H_S$ is a well-defined Hilbert space with $\langle u,v \rangle _S=\int _{\Omega }G \nabla u \cdot \nabla v$. It is easy to see that $H_S={H}_{0}^{1}(\Omega )$ and that the following inequality holds:

$$\begin{aligned} \sqrt{m}\Vert u\Vert _{{H}_{0}^{1}(\Omega )}\le \Vert u\Vert _{H_S} \qquad (\forall u \in H_S). \end{aligned}$$

(21)

Since $p<\frac{2d}{d-2}$, the embedding $\mathcal {I}:{H}_{0}^{1}(\Omega ) \rightarrow {L}^{p}(\Omega )$ is compact, in particular, there exists $\hat{c}>0$ such that for all $u \in {H}_{0}^{1}(\Omega )$

$$\begin{aligned} \Vert u\Vert _{{L}^{p}(\Omega )} \le \hat{c}\Vert u\Vert _{{H}_{0}^{1}(\Omega )}. \end{aligned}$$

(22)

Then,

$$\begin{aligned} \Vert Q_S v\Vert _{H_S}=\underset{{\Vert u\Vert _{H_S}=1}}{\sup } |\langle Q_Sv,u\rangle _S|&=\underset{{\Vert u\Vert _{H_S}=1}}{\sup } \langle Qv,u \rangle \\ \nonumber&=\underset{{\Vert u\Vert _{H_S}=1}}{\sup }\int _{\Omega } \eta v u \\ \nonumber&\le \underset{{\Vert u\Vert _{H_S}=1}}{\sup } \left( \int _{\Omega }|\eta |^{\frac{p}{p-2}}\right) ^{\frac{p-2}{p}} \left( \int _{\Omega }|v|^p \right) ^{\frac{1}{p}} \left( \int _{\Omega }|u|^p \right) ^{\frac{1}{p}} \\ \nonumber&\le \hat{c} \underset{{\Vert u\Vert _{H_S}=1}}{\sup } \Vert \eta \Vert _{{L}^{p/(p-2)}(\Omega )} \Vert v\Vert _{{L}^{p}(\Omega )} \Vert u\Vert _{{H}_{0}^{1}(\Omega )} \\ \nonumber&\le \frac{\hat{c}}{\sqrt{m}}\underset{{\Vert u\Vert _{H_S}=1}}{\sup } \Vert \eta \Vert _{{L}^{p/(p-2)}(\Omega )} \Vert v\Vert _{{L}^{p}(\Omega )} \Vert u\Vert _{H_S} \\ \nonumber&= \frac{\hat{c}M}{\sqrt{m}} \Vert v\Vert _{{L}^{p}(\Omega )}, \\ \nonumber \end{aligned}$$

(23)

where $M=\Vert \eta \Vert _{{L}^{p/(p-2)}(\Omega )}$. Here, we applied the extension of Hölder’s inequality ([6, Th. 4.6]) with

$$1=\frac{1}{p}+\frac{1}{p}+ \frac{p-2}{p}.$$

Hence, $Q_{S}$ is compact in $H_{S}$. Altogether, $Q_{S}$ is a compact self-adjoint operator in $H_{S}$, hence, by [9, Ch.6, Th.1.5], we have the following characterization of the eigenvalues of $Q_{S}$:

$$\begin{aligned} \forall n \in \mathbb {N} :\quad \lambda _{n}(Q_{S})=\min \{\Vert Q_{S}-L_{n-1}\Vert : \ \ L_{n-1} \in \mathcal {L}(H_{S}),\ \textrm{rank}(L_{n-1}) \le n-1 \}. \end{aligned}$$

(24)

By taking the minimum over a smaller subset of finite rank operators, we obtain

$$\begin{aligned} \lambda _n(Q_{S}) \le \min \{\Vert Q_{S}-Q_{S}L_{n-1}\Vert : \ \ L_{n-1} \in \mathcal {L}(H_{S}), \ \textrm{rank}(L_{n-1}) \le n-1 \}. \end{aligned}$$

(25)

Now, by (23) and (21) we get

$$\begin{aligned} \Vert Q_S-Q_SL_{n-1}\Vert&=\sup _{u \in H_S} \frac{\Vert (Q_S-Q_SL_{n-1})u\Vert _{H_S}}{\Vert u\Vert _{H_S}} \\&=\sup _{u \in H_S} \frac{\Vert Q_S(u-L_{n-1}u)\Vert _{H_S}}{\Vert u\Vert _{H_S}} \\&\le \frac{\hat{c}M}{\sqrt{m}} \sup _{u \in H_S} \frac{\Vert u-L_{n-1}u\Vert _{{L}^{p}(\Omega )}}{\Vert u\Vert _{H_S}} \\&\le \frac{\hat{c}M}{\sqrt{m}\sqrt{m}} \sup _{u \in {H}_{0}^{1}(\Omega )} \frac{\Vert u-L_{n-1}u\Vert _{{L}^{p}(\Omega )}}{\Vert u\Vert _{{H}_{0}^{1}(\Omega )}}. \end{aligned}$$

This, together with (25) yields

$$\begin{aligned} {\begin{matrix} \lambda _n(Q_S) &{}\le \! \frac{\hat{c}M}{m} \min \{\Vert \mathcal {I}\!-\!L_{n-1}\Vert : \ \ L_{n-1} \!\in \! \mathcal {L}({H}_{0}^{1}(\Omega ),{L}^{p}(\Omega )),\ \textrm{rank}(L_{n-1}) \!\le \! n\!-\!1 \} \\ &{}:=\frac{\hat{c}M}{m}a_n(\mathcal {I}), \end{matrix}} \end{aligned}$$

(26)

where $a_n(\mathcal {I})$ denotes the approximation numbers of the compact embedding $\mathcal {I} :{H}_{0}^{1}(\Omega ) \mapsto {L}^{p}(\Omega )$, see [14]. Furthermore, we have the estimation from [8]:

$$\begin{aligned} a_n(\mathcal {I}) \le \hat{C} n^{-\alpha }, \qquad \text{ where } \quad \alpha =\frac{1}{d}-\frac{1}{2}+\frac{1}{p} \end{aligned}$$

(27)

for some constant $\hat{C}>0$. Therefore, we arrive at the inequality

$$\begin{aligned} \lambda _n(Q_S) \le \frac{\hat{C}\hat{c}M}{m} n^{-\alpha }. \end{aligned}$$

Now, taking the arithmetic mean on both sides and estimating the sum from above by an integral, we obtain

$$\begin{aligned} \frac{1}{k}\sum ^{k}_{n=1}\lambda _n(Q_S) \le \frac{\hat{C}\hat{c}M}{m} \frac{1}{k} \left( 1+\int ^k_{1}\frac{1}{x^{\alpha }}\, dx \right) \le \frac{\hat{C}\hat{c}M}{m(1-\alpha )} \frac{1}{k^{\alpha }}. \end{aligned}$$

(28)

Then, by (13), we conclude. $\square$

Remark 1

The PCG method requires the solution of auxiliary problems $\varvec{\textrm{S}}w_k=\varvec{\textrm{Q}}p_k$, see (9). In the main case, when the principal part has constant or separable coefficients, these problems can be solved easily with fast solvers due to the special structure of the operator $Su \equiv -\textrm{div}(G\nabla u)$ (in particular, when $Su=-\Delta u$), see, e.g., [7, 12].

Moreover, to generalize the above, one may also incorporate a constant lower order term in S, i.e., (in the case of Laplacian principal part) define $Su=-\Delta u + cu$ for some constant $c>0$. This gives a better approximation of $Lu=-\Delta u + \eta u$ and, since S has constant coefficients, the auxiliary problems can be still be solved by the mentioned fast solvers. Theorem 1 remains true, since $Qu=(\eta -c)u$ is still compact; it may be no more a positive operator, but the only arising difference is that in Corollary 1 we replace $\lambda _j(Q_S)$ by $|\lambda _j(Q_S)|$.

Remark 2

The relevance of the extension of the results of [10] on $\eta \in C(\overline{\Omega })$ to our more general case (15) is motivated, e.g., by the following model. Consider a reaction-diffusion equation

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}- \Delta z + q(z)= f, \\ &{} z|_{\partial \Omega }=0, \end{array}\right. } \end{aligned}$$

(29)

where $q\in C^1(\mathbb {R})$ and there exists $2< p < \frac{2d}{d-2}$ such that

$$\begin{aligned} 0\le q'(\xi ) \le \alpha + \beta |\xi |^{p-2} \qquad (\forall \xi \in \mathbb {R}^{d}). \end{aligned}$$

(30)

Here, q describes the rate of reaction, which is typically of polynomial order as required in (30). The restriction on p means that the continuous embedding ${H}^1_{0}(\Omega )\subset L^p(\Omega )$ holds, hence the above problem is well-posed in ${H}_{0}^{1}(\Omega )$. Then, the Newton linearization around some $z_n$ leads to the linear problem of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}- \Delta u + \eta u= g \\ &{} u|_{\partial \Omega }=0 \end{array}\right. } \end{aligned}$$

(31)

where

$$\begin{aligned} \eta =q'(z_n) \, \in {L}^{p/(p-2)}(\Omega ) \end{aligned}$$

(32)

due to the above assumptions. That is, we obtain a problem of the type (14).

Remark 3

Owing to the equality $\Vert e_k\Vert _{\varvec{\textrm{A}}_h} = \Vert A^{-1/2} r_k\Vert$, the estimate (18) implies a similar one for the residuals:

$$ \left( \frac{\Vert r_k\Vert }{\Vert r_0\Vert }\right) ^{\frac{1}{k}} \le \, \frac{C_1}{k^{\alpha }} $$

where $C_1=C\, cond(A)$.

3.2 Elliptic systems

In this section, we prove that the previous results can be extended to certain systems of elliptic PDEs. For simplicity and also due to practical occurrence, we only include Laplacian principal parts; however, the results remain similar when the principal parts have the form (19).

3.2.1 Symmetric systems

First let us consider systems of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}-\Delta u_i + \eta _{i1}u_1+ \dots \eta _{is}u_s= g_i, \\ &{} u_i|_{\partial \Omega }=0, \quad (i=1,\dots ,s), \end{array}\right. } \end{aligned}$$

(33)

where $\varvec{H}=\{\eta _{ij}\}^{s}_{i,j=1}$ is a symmetric positive semidefinite variable coefficient matrix such that

$$\begin{aligned} \eta _{ij} \in {L}^{p/(p-2)}(\Omega ) \qquad (\forall i,j \in \{1, \dots , s\}). \end{aligned}$$

Such systems arise, e.g., in the Newton linearization of gradient systems: if a nonlinear reaction-diffusion system corresponds to a potential  

$$ \phi (u_1,...,u_s) = {\int _\Omega } \Bigl ( {1\over 2} \sum \limits _{i=1}^s |\nabla u_i|^2 + F(u_1,...,u_s)\Bigr ), $$

then the linearized problems have the form (33), which extend (31)–(32) to systems and the gradient structure implies the symmetry of the Jacobians $\varvec{H}=F'(u_1,...,u_s)$.

We work with the space ${L}^{p}(\Omega )^s$ with the norm

$$ \Vert u\Vert _{{L}^{p}(\Omega )^s}=\left( \sum ^{s}_{j=1} \Vert u_j\Vert ^2_{{L}^{p}(\Omega )} \right) ^{1/2} \qquad (u=(u_1,\dots , u_s) \in {L}^{p}(\Omega )^s). $$

Let $H={L}^{2}(\Omega )^{s}$; furthermore, $D:= (H^1_{0,G})^s$, where $H^1_{0,G}$ was defined in subsection 3.1 before (19). Using notation $u=(u_1 \dots u_s)$, we define the operators

$$\begin{aligned} Su:= \begin{pmatrix} -\Delta u_1 \\ . \\ . \\ . \\ -\Delta u_s \end{pmatrix} \quad (u\in D), \qquad Qu:= \varvec{H}u \quad (u \in {H}_{0}^{1}(\Omega )^s). \end{aligned}$$

(34)

Clearly, S is a uniformly positive symmetric operator in H. In fact, from (20),

$$\begin{aligned} \langle Su,u \rangle \ge C_\Omega \sum ^{s}_{i=1}\Vert u_i\Vert ^2_{{L}^{2}(\Omega )}=C_\Omega \Vert u\Vert ^2_{H}\, . \end{aligned}$$

(35)

Then, the energy space $H_S$ is well defined with

$$\begin{aligned} \langle u,v \rangle _S= \sum ^{s}_{i=1}\int _{\Omega }\nabla u_i\cdot \nabla v_i, \qquad \Vert u\Vert ^2_{H_S}= \sum ^{s}_{i=1} \int _{\Omega }|\nabla u_i|^2 \end{aligned}$$

and so $H_S={H}_{0}^{1}(\Omega )^s$. Furthermore, by (22), we have that

$$\begin{aligned} \Vert u\Vert ^2_{H_S} \ge \frac{1}{\hat{c}^2}\sum ^{s}_{i=1} \Vert u_i\Vert ^2_{{L}^{p}(\Omega )}=\frac{1}{\hat{c}^2}\Vert u\Vert ^2_{{L}^{p}(\Omega )^s}. \end{aligned}$$

(36)

Then, there exists a unique bounded linear operator $Q_S :{H}_{0}^{1}(\Omega )^s \rightarrow {H}_{0}^{1}(\Omega )^s$ such that

$$\begin{aligned} \langle Q_S u,v \rangle _S= \int _{\Omega } \sum ^{s}_{i,j=1} \eta _{ij} u_jv_i. \end{aligned}$$

(37)

It is easy to see that $Q_S$ is self-adjoint in $H_S$. Analogously to (23), by (36), (35) and Hölder’s inequality, we get

$$\begin{aligned} \nonumber \Vert Q_Sv\Vert _{H_S}&= \sup _{\Vert u\Vert _S=1} | \langle Q_S v,u \rangle _S| \\ \nonumber&\le \sup _{\Vert u\Vert _{H_S}=1} \sum ^{s}_{i,j=1}\int _{\Omega }|\eta _{ij}||v_j||u_i| \\ \nonumber&\le \sup _{\Vert u\Vert _{H_S}=1} \sum ^{s}_{i,j=1} \Vert \eta _{ij}\Vert _{{L}^{p/(p-2)}(\Omega )}\Vert v_j\Vert _{{L}^{p}(\Omega )} \Vert u_i\Vert _{{L}^{p}(\Omega )} \\&\le M\sup _{\Vert u\Vert _{H_S}=1} \sum ^{s}_{j=1} \Vert v_j\Vert _{{L}^{p}(\Omega )} \sum ^{s}_{i=1} \Vert u_i\Vert _{{L}^{p}(\Omega )} \\ \nonumber&\le M \sup _{\Vert u\Vert _{H_S}=1} \sqrt{s}\left( \sum ^{s}_{j=1} \Vert v_j\Vert ^2_{{L}^{p}(\Omega )} \right) ^{1/2} \sqrt{s}\left( \sum ^{s}_{i=1} \Vert u_i\Vert ^2_{{L}^{p}(\Omega )}\right) ^{1/2} \\ \nonumber&= Ms \sup _{\Vert u\Vert _{H_S}=1} \Vert v\Vert _{{L}^{p}(\Omega )^s} \Vert u\Vert _{{L}^{p}(\Omega )^s}\\ \nonumber&\le M s \hat{c} \Vert v\Vert _{{L}^{p}(\Omega )^s}, \end{aligned}$$

(38)

where $M=\max _{i,j}\Vert \eta _{ij}\Vert _{{L}^{p/(p-2)}(\Omega )}$. Hence, we have proved that $Q_S$ is a compact self-adjoint operator in $H_S$. Then, the characterization (24) of the eigenvalues of $Q_S$ holds. The rest of the proof follows by modifying the scalar case. Now, instead of (25), we take the minimum in the following way over a smaller subset of finite rank operators:

$$\begin{aligned} \lambda _n(Q_S) \le \min \{\Vert Q_S-Q_SL_{n-1}\Vert : \ \ L_{n-1} \in \mathcal {L}_{\textrm{diag}}(H_S), \ \textrm{rank}(L_{n-1}) \le n-1 \}, \end{aligned}$$

where we define $L_{n-1} \in \mathcal {L}_{\textrm{diag}}(H_S)$ by requiring

$$ L_{n-1}u= \begin{pmatrix} L^s_{n-1}u_1 \\ . \\ . \\ . \\ L^s_{n-1}u_s \\ \end{pmatrix},\text { such that } L^s_{n-1} \in \mathcal {L}({H}_{0}^{1}(\Omega )) \text { and } \textrm{rank}(L^s_{n-1}) \le \left[ \frac{n-1}{s}\right] , $$

where [.] denotes the lower integer part. Furthermore, we shall use the approximation numbers

$$ a_{\left[ \frac{n-1}{s}\right] }=\min \left\{ \Vert I-T_{n-1}\Vert : \ \ T_{n-1} \in \mathcal {L}({H}_{0}^{1}(\Omega ),{L}^{p}(\Omega )), \ \, \textrm{rank}(T_{n-1})\le \left[ \frac{n-1}{s}\right] \right\} . $$

Note that if $n\le s$ then we can use the bound $\lambda _n(Q_S)\le \Vert Q_S\Vert$. For $n\ge s+1$, from (27), the above numbers are estimated by

$$\begin{aligned} a_{\left[ \frac{n-1}{s}\right] } \le \hat{C} \left[ \frac{n-1}{s}\right] ^{-\alpha }, \end{aligned}$$

(39)

with $\alpha =\frac{1}{d}-\frac{1}{2}+\frac{1}{p}.$ Then,

$$\begin{aligned} \Vert Q_S-Q_SL_{n-1}\Vert&=\sup _{u \in H_S} \frac{\Vert (Q_S-Q_SL_{n-1})u\Vert _{H_S}}{\Vert u\Vert _{H_S}} \\&=\sup _{u \in H_S} \frac{\Vert Q_S(u-L_{n-1}u)\Vert _{H_S}}{\Vert u\Vert _{H_S}} \\&\le Ms \hat{c} \sup _{u \in H_S} \frac{\Vert u-L_{n-1}u\Vert _{{L}^{p}(\Omega )^s}}{\Vert u\Vert _{H_S}} \\&= Ms \hat{c} \sup _{u \in H_S} \frac{\left( \sum ^s_{j=1}\Vert u_i-L^s_{n-1}u_i\Vert ^2_{{L}^{p}(\Omega )}\right) ^{1/2}}{\left( \sum ^{s}_{j=1}\Vert u_i\Vert ^2_{{H}_{0}^{1}(\Omega )}\right) ^{1/2}} \\&\le Ms \hat{c} \sup _{u \in H_S} \frac{\left( \Vert I-L^s_{n-1}\Vert ^2_{\mathcal {L}({H}_{0}^{1}(\Omega ),{L}^{p}(\Omega ))}\sum ^s_{j=1}\Vert u_i\Vert ^2_{{H}_{0}^{1}(\Omega )}\right) ^{1/2}}{\left( \sum ^{s}_{j=1}\Vert u_i\Vert ^2_{{H}_{0}^{1}(\Omega )}\right) ^{1/2}} \\&= Ms \hat{c} \Vert I-L^s_{n-1}\Vert _{\mathcal {L}\left( {H}_{0}^{1}(\Omega ),{L}^{p}(\Omega )\right) }.\\ \end{aligned}$$

Therefore,

$$\begin{aligned} \lambda _n(Q_S)&\le Ms\hat{c}\min \left\{ \Vert I-L^s_{n-1}\Vert _{\mathcal {L}\left( {H}_{0}^{1}(\Omega ),{L}^{p}(\Omega )\right) } : \ \ L^s_{n-1} \in \mathcal {L}({H}_{0}^{1}(\Omega ),{L}^{p}(\Omega )), \ \textrm{rank}(L^s_{n-1}) \le \left[ \frac{n-1}{s}\right] \right\} \\&=Ms\hat{c}a_{\left[ \frac{n-1}{s}\right] }. \end{aligned}$$

Hence, by (39), we obtain the estimations

$$\begin{aligned} \lambda _n(Q_S) \le Ms\hat{c} \hat{C} \left[ \frac{n-1}{s}\right] ^{-\alpha } \qquad (\forall n\ge s+1), \end{aligned}$$

(40)

$$\begin{aligned} \lambda _n(Q_S) \le \Vert Q_S\Vert \qquad (\forall n\le s). \end{aligned}$$

(41)

Note that there exists $k_0,k_1 >0$ such that

$$k_0\le \frac{\left[ x\right] }{x} \le k_1 \qquad (\forall x>1) $$

(in fact, $k_0=1/2$ and $k_1=1$). Thus, for $n\ge s+1$,

$$\begin{aligned} \left[ \frac{n-1}{s}\right] ^{-\alpha }&\le \frac{1}{k^{\alpha }_0}\frac{s^{\alpha }}{(n-1)^{\alpha }} \\&=\left( \frac{s}{k_0}\right) ^{\alpha }\left( \frac{n^{\alpha }}{(n-1)^{\alpha }} \right) \frac{1}{n^{\alpha }} \\&\le \left( \frac{(s+1)}{k_0}\right) ^{\alpha }\frac{1}{n^{\alpha }}. \end{aligned}$$

Hence, (40) becomes

$$\begin{aligned} \lambda _{n}(Q_S) \le Ms\hat{c}\hat{C}\left( \frac{(s+1)}{k_0}\right) ^{\alpha }\frac{1}{n^{\alpha }}:=C_1 \frac{1}{n^{\alpha }} \end{aligned}$$

and by taking arithmetic means on both sides and splitting the sum, we get

$$\begin{aligned} \frac{1}{k} \sum ^{k}_{n=1} \lambda _n(Q_S)&\le \frac{1}{k}\left( s\Vert Q_S\Vert +\sum ^{k}_{n=s+1}\lambda _n(Q_S)\right) \\&\le \frac{1}{k}\left( s\Vert Q_S\Vert +C_1\sum ^{k}_{n=s+1}\frac{1}{n^{\alpha }}\right) \\&\le \frac{1}{k}\left( s\Vert Q_S\Vert +C_1\int ^{k}_{s}\frac{1}{x^{\alpha }}\, dx\right) \\&\le \frac{s}{k}\Vert Q_S\Vert +\frac{C_1}{1-\alpha }\frac{1}{k^{\alpha }} \\&\le C_2 \frac{1}{k^{\alpha }}, \end{aligned}$$

where $C_2=\max \{s\Vert Q_S\Vert ,C_1(1-\alpha )^{-1}\}$. Finally, by Corollary 1, we obtain that there exists $C>0$ such that for all $k \in \mathbb {N}$

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _{\varvec{\textrm{A}}_h}}{\Vert e_0\Vert _{\varvec{\textrm{A}}_h}}\right) ^{\frac{1}{k}} \le \frac{C}{k^{\alpha }} \end{aligned}$$

(42)

with $\alpha =\frac{1}{d}-\frac{1}{2}+\frac{1}{p}$, that is, Theorem 1 holds in exactly the same from for the above systems of PDEs as well.

3.2.2 Extension to non-symmetric systems

Let us now study (33) for $\varvec{H}=\{\eta _{i,j}\}^{s}_{i,j=1}$ non-symmetric. We apply the generalized minimal residual (GMRES) method to the corresponding discretized system. This method is the most widespread Krylov type iteration for non-symmetric systems, see, e.g., [13].

By [5], we have an analog of Corollary 1 when A is non-Hermitian. In this case the GMRES method provides superlinear convergence estimates for the residuals $r_k$, and (11) is replaced by the more general case (12). Altogether, we have

$$\begin{aligned} \left( \frac{\Vert r_k\Vert }{\Vert r_0\Vert } \right) ^{1/k} \le \frac{\Vert B^{-1}\Vert _S}{k} \sum ^{k}_{j=1} s_j(Q_S) \qquad (\forall k=1,2,\dots ,n). \end{aligned}$$

(43)

To show that Theorem 1 still holds in this case, we follow the same steps as we did previously. We define the operators $S,Q,Q_S$ as before in (34), (37). Here $Q_S$ is no longer self-adjoint and its eigenvalues do not coincide with its singular values. Nonetheless, by [9, Ch.6, Th.1.5], we have the following characterization of the singular values of $Q_S$:

$$\begin{aligned} \forall n \in \mathbb {N} :\quad s_{n}(Q_S)=\min \{\Vert Q_S-L_{n-1}\Vert : \ \ L_{n-1} \in \mathcal {L}(H_S), \ \textrm{rank}(L_{n-1}) \le n-1 \}. \end{aligned}$$

(44)

Then, similarly to the proof for symmetric systems, we can see that there exists $C_1>0$ such that

$$\begin{aligned} \frac{1}{k} \sum ^{k}_{n=1} s_n(Q_S) \le \frac{C_1}{k^{\alpha }}, \qquad \text{ where } \ \alpha =\frac{1}{d}-\frac{1}{2}+\frac{1}{p}. \end{aligned}$$

(45)

Therefore, by (43), we obtain that there exists $C_2>0$ such that

$$\begin{aligned} \left( \frac{\Vert r_k\Vert }{\Vert r_0\Vert } \right) ^{1/k} \le \frac{C_2 }{k^{\alpha }}. \end{aligned}$$

(46)

3.2.3 The efficiency of the preconditioners

For elliptic systems, the auxiliary problem $\varvec{\textrm{S}}w_k=\varvec{\textrm{Q}}p_k$ is the FEM discretization of the elliptic system

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta (w_k)_1 &{}= \sum ^{s}_{j=1} \eta _{1j} (p_k)_j, \\ -\Delta (w_k)_2 &{}= \sum ^{s}_{j=1} \eta _{2j} (p_k)_j, \\ &{}. \\ &{}. \\ &{}. \\ -\Delta (w_k)_s&{}= \sum ^{s}_{j=1} \eta _{sj} (p_k)_j, \\ (w_i)|_{\partial \Omega }&{}=0 \qquad (i=1,\dots , s) \end{array}\right. } \end{aligned}$$

where $w_k = ( (w_k)_1, \dots , (w_k)_s )$ is the unknown function and the right-hand side arises from the known functions $(p_k)_1, \dots , (p_k)_s$. The main point is that (in contrast to the original one) this system is uncoupled, i.e., the above equations are independent of one another. Hence, they can be solved in parallel.

We note that the idea of Remark 1 can also be used here: one may include constant lower order terms in S, which is especially useful if $\varvec{H}$ has large entries. Then, $-\Delta (w_k)_i$ above is replaced by $-\Delta (w_k)_i + c_i (w_k)_i$. For instance, we may set $c_i= 1/2 \Vert \varvec{H}\Vert$ or $c_i= 1/2 \sum ^{s}_{j=1} \eta _{ij}$.

In practice, these types of systems can be very large, e.g., in [16], long-range transport of air pollution models are described by a system of PDEs with $s=30$. That is, whereas the original problem is a coupled PDE system of several components, the preconditioner leads to uncoupled problems corresponding to the FEM discretization of single PDEs, which is considerably cheaper. This shows the efficiency of the proposed preconditioners.

4 Numerical tests

Let us solve the following PDEs numerically:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}-\Delta u +\eta _1 u = f_i \quad \text { in } \Omega =[0,1]^2, \\ &{}u|_{\partial \Omega }=0, \end{array}\right. } \end{aligned}$$

(47)

with $i=1,2$, and

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}-\Delta u +\eta _2 u = f_1 \quad \text { in } \Omega =[0,1]^2, \\ &{}u|_{\partial \Omega }=0, \end{array}\right. } \end{aligned}$$

(48)

where $p>2$, and $\eta _1,\eta _2 \in {L}^{\frac{p}{p-2}}(\Omega )$ are defined as

$$\begin{aligned} \eta _1(x,y)=(x^2+y^2)^{-\beta } \end{aligned}$$

and

$$\begin{aligned} \eta _2(x,y)=((x-0.5)^2+(y-0.5)^2)^{-\beta } \end{aligned}$$

for some $0<\beta < \frac{p-2}{p}$. Furthermore,

$$\begin{aligned} f_1(x,y)=1, \end{aligned}$$

$$\begin{aligned} f_2(x,y)=1-x-y. \end{aligned}$$

Applying the finite element method to (47) and (48) with stepsize $h=1/(N+1)$, we obtain the algebraic system

$$\begin{aligned} (\varvec{\textrm{G}}_h+\varvec{\textrm{D}}_h)\varvec{\textrm{c}}_i=\varvec{\textrm{g}}^i_h, \quad i=1,2,3. \end{aligned}$$

(49)

The cases $i=1,2$ and $i=3$ refer to the FEM discretization of (47) and (48), respectively. Then, we apply $\varvec{\textrm{G}}_h$ as a preconditioner and we solve the preconditioned system using the CGM. We used Courant elements and the computations were executed in Matlab (Fig. 1).

Fig. 1

Graphs of the numerical solutions with $N=40$ for (47) with right-hand side $f_i$ ($i=1,2$) and $\beta =1/4$, and for (48) with right-hand side $f_1$ and $\beta =3/4$, respectively

Table 1 Norm of residual error $r^i_k$ at each iteration of PCGM applied to system (49). Here $N=40$ and $\beta =1/4$

Table 2 Values of $\hat{\delta }_k$ for different $\alpha$’s and $\beta$’s, with a fixed mesh size. Here $N=40$

Table 3 Values of $\hat{\delta }_k$ for different mesh sizes with $\beta =3/4, \alpha =0.12$

To measure the error of the PCGM, we use the energy norm

$$ \Vert e\Vert _{\varvec{\textrm{A}}_h}=\langle \varvec{\textrm{A}}_h e,e\rangle ^{\frac{1}{2}} \qquad (e \in \mathbb {R}^{N^2}), $$

where $\varvec{\textrm{A}}_h=\varvec{\textrm{G}}_h+\varvec{\textrm{D}}_h$. Table 1 shows the residual error obtained at each iteration $k\le 10$ of the method applied to (49) for $i=1,2,3$, respectively.

To test Theorem 1, note that $d=2$ and so $\alpha =\frac{1}{p}$. Furthermore, recall that

$$\eta _1, \eta _2 \in {L}^{\frac{p}{p-2}}(\Omega ) \quad \text { if } \beta <\frac{p-2}{p}=1-2\alpha .$$

That is, if $p > \frac{2}{1-\beta }$, we get that the theorem holds when $\alpha <\frac{1-\beta }{2}.$ Table 2 shows the values of

$$ \hat{\delta }_k=\left( \frac{\Vert r_k\Vert _{G_h}}{\Vert r_0\Vert _{G_h}}\right) ^{\frac{1}{k}}k^{\alpha } $$

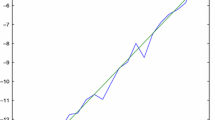
for $i=1,2,3$, respectively, with different choices of $\beta$ and $\alpha$ while fixing a mesh size. The value of $\hat{\delta }^i_k$ ($i=1,2$) corresponds to the system (47) with right-hand side $f_i$ and the case $i=3$ corresponds to the system (48). Note that residuals can be used when the exact solution is not known. In the symmetric case the bound (46) follows from the bound (18) owing to the equivalence of $\Vert e_k\Vert _{\varvec{\textrm{A}}_h}$ and $\Vert r_k\Vert$, see Remark 3. Altogether, the estimate (46) is equivalent to requiring that $\hat{\delta }_k$ is bounded by some constant as k increases, and this is indeed demonstrated by Table 2 and Fig. 2.

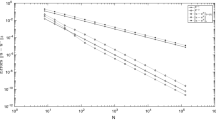
Finally, Table 3 and Fig. 3 show the values of $\hat{\delta }_k$ for different mesh sizes while fixing the values of $\beta$. The numbers demonstrate that the results of Theorem 1 are not sensitive to the size of the mesh.

Fig. 2

Graphical representation of Table 2

Fig. 3

Graphical representation of Table 3

5 Summary and conclusions

We have studied the mesh independent superlinear convergence of preconditioned Krylov methods for the iterative solution of finite element discretizations of second-order elliptic boundary value problems. We have proved mesh independent estimations for proper operator preconditioners for single equations and for systems, setting up a connection between the convergence rate and the Lebesgue exponent of the data. We have run numerical tests for equations with singular coefficients using different parameters. The tests have demonstrated the theoretical results.