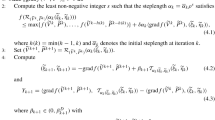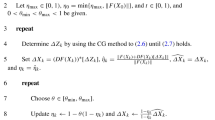Skip to main content
SpringerLink
Log in

Riemannian linearized proximal algorithms for nonnegative inverse eigenvalue problem

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

We study the issue of numerically solving the nonnegative inverse eigenvalue problem (NIEP). At first, we reformulate the NIEP as a convex composite optimization problem on Riemannian manifolds. Then we develop a scheme of the Riemannian linearized proximal algorithm (R-LPA) to solve the NIEP. Under some mild conditions, the local and global convergence results of the R-LPA for the NIEP are established, respectively. Moreover, numerical experiments are presented. Compared with the Riemannian Newton-CG method in Z. Zhao et al. (Numer. Math. 140:827–855, 2018), this R-LPA owns better numerical performances for large scale problems and sparse matrix cases, which is due to the smaller dimension of the Riemannian manifold derived from the problem formulation of the NIEP as a convex composite optimization problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Absil, P.A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press, Princeton (2008)

    Book  MATH  Google Scholar 

  2. Bapat, R.B., Raghavan, T.E.S.: Nonnegative Matrices and Applications, in Encyclopedia of Mathematics and its Applications, vol. 15. Cambridge University Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  3. Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences, in Classics in Applied Mathe-matics, vol. 9. SIAM, Philadelphia (1994)

    Google Scholar 

  4. Bonnans, J.F., Ioffe, A.: Second-order sufficiency and quadratic growth for nonisolated minima. Math. Oper. Res. 20, 801–817 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  5. Burke, J.V.: Descent methods for composite nondifferentiable optimization problems. Math. Program. 33, 260–279 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  6. Burke, J.V., Ferris, M.C.: A Gauss-Newton method for convex composite optimization. Math. Program. 71, 179–194 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  7. Burke, J.V., Ferris, M.C.: Weak sharp minima in mathematical programming. SIAM J. Control Optim. 31, 1340–1359 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  8. Do Carmo, M.P.: Riemannian Geometry. Birkhauser, Boston (1992)

    Book  MATH  Google Scholar 

  9. Chu, M.T.: Inverse eigenvalue problems. SIAM Rev. 40, 1–39 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chu, M.T., Golub, G.H.: Structured inverse eigenvalue problems. Acta Numer. 11, 1–71 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  11. Lewis, A.S., Wright, S.J.: A proximal method for composite minimization. Math. Program. 158, 501–546 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Helgason, S.: Differential Geometry, Lie Groups, and Symmetric Spaces. Academic Press Inc, New York (1978)

    MATH  Google Scholar 

  13. Hu, Y.H., Yang, X.Q., Sim, C.-K.: Inexact subgradient methods for quasi-convex optimization problems. Eur. J. Oper. Res. 240, 315–327 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hu, Y.H., Li, C., Yang, X.Q.: On convergence rates of linearized proximal algorithms for convex composite optimization with applications. SIAM J. Optim. 26, 1207–1235 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  15. Li, C., Ng, K.F.: Majorizing functions and convergence of the Gauss-Newton method for convex composite optimization. SIAM J. Optim. 18, 613–642 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, C., Ng, K.F.: The dual normal CHIP and linear regularity for infinite systems of convex sets in Banach spaces. SIAM J. Optim. 24, 1075–1101 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, C., Wang, X.: On convergence of the Gauss-Newton method for convex composite optimization. Math. Program. 91, 349–356 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  18. Pang, J.-S.: Error bounds in mathematical programming. Math. Program. 79, 299–332 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  19. Perfect, H.: Methods of constructing certain stochastic matrices. Duke Math. J. 20, 395–404 (1953)

    Article  MathSciNet  MATH  Google Scholar 

  20. Qi, L., Sun, J.: A nonsmooth version of Newton’s method. Math. Program. 58, 353–367 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  21. Robinson, S.M.: Stability theory for systems of inequalities, part II. Differentiable nonlinear systems. SIAM J. Numer. Anal. 13(4), 497–513 (1976)

  22. Rockafellar, R.T.: First- and second-order epi-differentiability in nonlinear programming. Trans. Amer. Math. Soc. 307, 75–108 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  23. Studniarski, M., Ward, D.E.: Weak sharp minima: Characterizations and sufficient conditions. SIAM J. Control Optim. 38, 219–236 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wang, J.H., Yao, J.C., Li, C.: Gauss-Newton methods for convex composite optimization on Riemannian manifolds. J. Global Optim. 53, 5–28 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. Womersley, R.S.: Local properties of algorithms for minimizing nonsmooth composite functions. Math. Program. 32, 69–89 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  26. Zheng, X.Y., Ng, K.F.: Strong KKT conditions and weak sharp solutions in convex-composite optimization. Math. Program. 126, 259–279 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Zheng, X.Y., Yang, X.Q.: Weak sharp minima for semi-infinite optimization problems with applications. SIAM J. Optim. 18, 573–588 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  28. Zhao, Z., Bai, Z.J., Jin, X.Q.: A Riemannian inexact Newton-CG method for constructing a nonnegative matrix with prescribed realizable spectrum. Numer. Math. 140, 827–855 (2018)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the editor and the anonymous referees for their helpful and valuable comments and suggestions.

Funding

Sangho Kum is supported by the National Research Foundation of Korea (grant NRF-2020R1A2C1A01010957). Chong Li is supported in part by the National Natural Science Foundation of China (grant 11971429). Jinhua Wang is supported in part by the National Natural Science Foundation of China (grant 12171131). Jen-Chih Yao is supported in part by the Grant MOST 111-2115-M-039-001-MY2.

Author information

Authors and Affiliations

  1. Department of Mathematics Education, Chungbuk National University, Cheongju, 28644, Korea

    Sangho Kum

  2. School of Mathematical Sciences, Zhejiang University, Hangzhou, 310027, People’s Republic of China

    Chong Li

  3. Department of Mathematics, Hangzhou Normal University, Hangzhou, 311121, People’s Republic of China

    Jinhua Wang

  4. China Medical University, Taichung, Taiwan, 40402, Republic of China

    Jen-Chih Yao

  5. Department of Systems Engineering and Engineering Management, The Chinese University of Hong Kong, Shatin, New Territories, Hong Kong

    Linglingzhi Zhu

Authors
  1. Sangho Kum
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinhua Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jen-Chih Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Linglingzhi Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jinhua Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kum, S., Li, C., Wang, J. et al. Riemannian linearized proximal algorithms for nonnegative inverse eigenvalue problem. Numer Algor 94, 1819–1848 (2023). https://doi.org/10.1007/s11075-023-01556-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-023-01556-3

Keywords

Mathematics Subject Classification (2010)

Search

Navigation